У.Клоксин, К.Меллиш
ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ПРОЛОГ
Для программистов и пользователей ЭВМ.
ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
Язык программирования Пролог появился в 1970 г. одновременно с такими сейчас широко распространенными языками, как Паскаль и Си. Его ориентация – «нетрадиционные» применения вычислительной техники: понимание естественного языка, базы знаний, экспертные системы и другие задачи, которые принято относить к проблематике искусственного интеллекта. Сила этого языка – в принципиально отличном от традиционных языков программирования подходе к описанию способа решения задачи: программа на Прологе описывает не процедуру решения задачи, а логическую модель предметной области – некоторые факты относительно свойств предметной области и отношений между этими свойствами, а также правила вывода новых свойств и отношений из уже заданных. Таким образом, Пролог – описательный язык. Как отмечено в авторском предисловии, такой логический подход к программированию создает и некоторые проблемы в распространении языка: основные понятия языка опытными программистами понимаются без труда, однако практическое претворение этого понимания в полезные программы вызывает затруднения.
Несмотря на очевидные и яркие достоинства, Пролог, в отличие от своих «сверстников» (Паскаля и Си), продолжительное время развивался, применялся и обсуждался в сравнительно узком кругу исследователей, работающих в области искусственного интеллекта. И лишь в последние годы Пролог попал в поле зрения широких кругов специалистов по информатике. Резкий рост его популярности объясняется, по-видимому, выходом теории искусственного интеллекта в область практического, «коммерческого» программирования.
В настоящее время растет круг практических систем, использующих достижения искусственного интеллекта на современных ЭВМ, появились престижные национальные проекты создания ЭВМ новых поколений, в которых интеллектуальный интерфейс с конечным пользователем (непрофессионалом в информатике) является центральным элементом. В японском проекте создания ЭВМ пятого поколения Пролог прямо называется базовым языком программирования. По-видимому, Пролог реально претендует на роль одного из основных инструментальных языков для «нетрадиционных» применений вычислительной техники, поэтому своевременное знакомство с ним отечественных специалистов, работающих в данной области, будет несомненно полезным.
В социалистических странах активное участие в разработках, связанных с Прологом, принимают ученые ВНР. В Институте по координации вычислительной техники (г. Будапешт) создана версия Пролога – МПролог, получившая международное признание. Не исключено, что МПролог будет широко доступен и пользователям нашей страны. Этим объясняется включение в русское издание специального приложения (F) посвященного МПрологу.
При переводе книги встретились значительные терминологические проблемы, поскольку установившаяся русская терминология в данной области практически отсутствует, а станет ли таковой англоязычный жаргон специалистов – покажет время. Для удобства читателей в предметном указателе приведены английские эквиваленты терминов, употребляемых в переводе.
Предисловие, главы 1,3-6, 9, 10 и Приложение В перевел М. М. Комаров, главы 7, 8, 11, Приложения А,С, D, E, F- А. В. Горбунов, главу 2 – Ю. М. Лазутин.
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
После выхода в 1981 г. первого издания книги «Программирование на языке Пролог» этот язык вызвал неожиданно большой интерес у специалистов по информатике, и в настоящее время он рассматривается как возможная основа для принципиально нового поколения языков и систем программирования.
Мы надеемся, что данная книга частично удовлетворила возрастающую потребность в простом и в то же время исчерпывающем введении в язык практического программирования, каким является Пролог. При подготовке второго издания книги мы воспользовались случаем, чтобы улучшить изложение материала и исправить различные незначительные ошибки. Мы благодарны многим читателям, высказавшим предложения по исправлению и улучшению книги.
У.
Клоксин К.
Меллиш
Кембридж, Англия, август 1984
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Язык программирования Пролог быстро завоевывает популярность во всем мире. С момента его создания, приблизительно в 1970 г., большое число программистов выбрали Пролог
для использования при решении задач в различных областях символьных вычислений, включающих:
• реляционные базы данных,
• математическую логику,
• решение абстрактных задач,
• понимание естественного языка,
• автоматизацию проектирования,
• символьное решение уравнений,
• анализ биохимических структур,
• различные области искусственного интеллекта.
До настоящего времени не было книг, ставивших своей целью обучить Прологу как языку практического программирования. Видимо, Пролог оказался настолько привлекательным для многих людей, что они стали его изучать, используя неизбежно краткие справочные руководства, небольшое число опубликованных статей и передаваемый устно среди пользователей языка «фольклор». Однако с внедрением Пролога в учебные программы для студентов и аспирантов многим из наших коллег понадобилось учебное руководство по Прологу. Мы надеемся, что наша небольшая книга до некоторой степени удовлетворит эту потребность.
Многие новички обнаруживали, что задача написания программы на Прологе не похожа на спецификацию алгоритма при программировании на традиционном языке программирования. Программист, использующий Пролог, больше интересуется тем, какие формальные отношения и объекты имеют место в решаемой задаче и какие отношения справедливы для разыскиваемого решения. Таким образом, Пролог можно рассматривать как язык
описаний, а не как язык
предписаний. Используемый в Прологе подход состоит главным образом в описании известных фактов и отношений, касающихся решаемой задачи, а не в предписании последовательности шагов, выполняя которые ЭВМ решит задачу. При реализации программы на Прологе фактическая последовательность вычислений, выполняемая ЭВМ, определяется частично логической декларативной семантикой Пролога, частично новыми фактами, которые Пролог может «вывести» из заданных ему фактов, и лишь отчасти управляющей информацией, явно заданной программистом.
Пролог является
практической и
эффективной реализацией многих принципов, относящихся к «интеллектуальному» выполнению программы, таких, как недетерминизм, параллельность, вызов процедур по образцу. Пролог имеет единообразную структуру данных, называемую
термом, на основе которой конструируются все данные и в том числе программы на Прологе. Программа на Прологе состоит из множества утверждений, каждое из которых является либо фактом о заданной информации, либо правилом, указывающим, как решение связано с заданными фактами или каким образом его можно из них вывести. Таким образом, Пролог можно считать первым шагом на пути к конечной цели –
программированию на языке логики. В этой книге мы не будем подробно рассматривать ни более широкие следствия, вытекающие из идеи логического программирования, ни вопрос о том, почему Пролог нельзя рассматривать как окончательный язык логического программирования. Вместо этого мы покажем, как, используя существующие сегодня системы программирования на Прологе, можно создавать
полезные программы.
Эта книга может служить нескольким целям. Мы не собираемся учить искусству программирования как таковому. Нам кажется, что нельзя научиться программированию, просто читая книги или слушая лекции. Вы должны
программировать, чтобы научиться делать это. Мы надеемся, что начинающие программисты, не имеющие математической подготовки, смогут освоить Пролог по этой книге, хотя в этом случае мы советовали бы, чтобы начинающий программист осваивал язык под руководством программиста, знающего Пролог, в рамках вводного курса по программированию как таковому. Предполагается, что начинающий программист может получить доступ к ЭВМ, на которой имеется Пролог-система, и что он прошел необходимый инструктаж по работе с терминалом. Опытному программисту не потребуется дополнительная помощь, но он также не должен впадать в уныние от наших усилий ограничить математические излишества. Мы использовали предварительный вариант этой книги при обучении выпускников университета, имевших математическую подготовку на уровне школьной программы и специализировавшихся в университете по философии и психологии.
Наш опыт показывает, что начинающим программы на Прологе представляются более понятными, чем соответствующие программы на традиционных языках программирования. Однако те же самые люди не склонны ценить те ограничения, которые накладывают традиционные языки на использование вычислительных ресурсов. С другой стороны, программист, имеющий опыт работы на традиционных языках программирования, лучше подготовлен к восприятию таких абстрактных понятий, как переменные и управление последовательностью действий. Но, несмотря на прежний опыт, приспособление к стилю программирования на Прологе может вызвать у него затруднения, и может потребоваться много убедительных примеров, прежде чем он начнет относиться к Прологу как к полезному средству программирования. Конечно, мы знаем много высококвалифицированных программистов, воспринявших Пролог с большим энтузиазмом. Тем не менее, цель этой книги не в том, чтобы «обратить в иную веру», а в том, чтобы научить программировать на Прологе.
Как и большинство других языков программирования, Пролог существует в множестве различных реализаций, каждая со своими семантическими и синтаксическими особенностями. Для описания в этой книге выбран «базовый» Пролог и все приводимые примеры написаны для стандартной версии, которая соответствует реализациям, разработанным главным образом в Эдинбурге для нескольких различных вычислительных систем: DEC-10 с операционной системой TOPS-10, DEC VAX и PDP-11 с операционной системой Unix, DEC LSI-11 с операционной системой RT-11 и ICL2980 с операционной системой ЕМА. Реализации для ЭВМ фирмы DEC являются, вероятно, наиболее распространенными. Все примеры, приведенные в этой книге, подходят для всех указанных реализаций. В приложениях приведены описания некоторых из существующих реализаций Пролога с указанием их отличий от стандарта. Читатель сможет убедиться, что большинство отличий имеет чисто «косметическую» природу.
Книга построена таким образом, что читать ее надо последовательно. Тем не менее, будет полезно прочитать гл. 8 в тот момент, когда читатель начнет писать программы на Прологе, состоящие более чем из десяти утверждений. Кроме того, разумно прочитать соответствующее приложение, содержащее описание используемой реализации Пролога. В приложениях говорится, как вводить утверждения, какие средства отладки имеются в системе, и рассматриваются другие практические вопросы. Не будет особого вреда, если вы лишь просмотрите книгу, но старайтесь при этом не пропускать главы.
Каждая глава книги делится на несколько разделов, и мы советуем читателю выполнять упражнения, приводимые в конце многих разделов. Решения к некоторым из этих упражнений даны в конце книги. Глава 1 представляет собой введение, цель которого – дать читателю почувствовать характер программирования на Прологе. Здесь вводятся основные идеи языка Пролог и читателю рекомендуется тщательно изучить их. В гл. 2 содержится более полное обсуждение идей и понятий, введенных в гл. 1. В гл. 3 рассматриваются структуры данных и приводятся в качестве примеров несколько небольших программ. В гл. 4 более подробно обсуждается механизм возврата, вводится символ «отсечения», используемый для управления механизмом возврата. В
гл. 5 вводятся имеющиеся в языке средства ввода-вывода. В гл. 6 описывается каждый встроенный предикат базовой версии языка Пролог. Глава 7 представляет собой «попурри» из примеров программ, взятых из многих источников и снабженных комментариями, поясняющими их работу. В гл. 8 даются некоторые советы по отладке программ на Прологе. В гл. 9 вводится синтаксис грамматических правил и изучаются предположения, лежащие в основе программ для анализа естественного языка с использованием грамматических правил. В гл. 10 описывается связь Пролога с идеями математического доказательства теорем и логического программирования, лежащими в основе языка. В гл. 11 представлен ряд проектов, на которых заинтересованные читатели могут поупражняться в развитии навыков программирования на Прологе.
Мы выражаем благодарность нашим учителям, сформировавшим наши взгляды на программирование: Роду Борстоллу, Питеру Скотту Лэнгстону и Робину Попплстоуну. Мы благодарны друзьям, участвовавшим вместе с нами в совершенствовании Пролога как практического и полезного средства программирования и поддерживавших нас в процессе подготовки этой книги: Алану Банди, Лоренсу Байрду, Роберту Ковальски, Фернандо Перейра и Дейвиду Уоррену. В частности, Лоуренс Байрд поддерживал работу по созданию книги с самого ее начала, предлагая программы, упражнения, некоторые проекты, приведенные в гл. 11, и много идей по организации книги. Мы также благодарны нашим друзьям, внесшим свой вклад в создание книги полезными замечаниями и советами по улучшению предварительного ее варианта: Джону Каннингаму, Ричарду О'Кифу, Элен Пейн, Фернандо Перейра, Гордону Плоткину, Роберту Реи, Питеру Россу, Максвеллу Шортеру, Арону Сломену и Дейвиду Уоррену. В этом отношении У. Клоксин особенно благодарен своим аспирантам из School of Epistemics и Department of Artificial Intelligence, которые помимо их воли стали объектом многочисленных экспериментов в области обучения программированию. При выборе примеров мы свободно пользовались распространенным программистским фольклором и в связи с этим приносим наши извинения всем, кто чувствует себя обойденным вниманием.
Эта книга была подготовлена в период работы авторов на факультете искусственного интеллекта Эдинбургского университета. Мы благодарны Джиму Хоу, возглавлявшему факультет, за создание благоприятных условий при работе над книгой.
У.
Клоксин К. Меллиш
Эдинбург, Шотландия, июнь 1981
ГЛАВА 1 ВВЕДЕНИЕ
Пролог – язык программирования, используемый для решения задач, сводимых к объектам и отношениям между объектами. В этой главе мы продемонстрируем основные элементы языка на примерах реальных программ, не вдаваясь особенно в детали, формальные правила и исключения. Исходя из этого, мы не старались, чтобы изложение было полным или достаточно точным. Мы хотим как можно быстрее подвести вас к тому моменту, когда вы сможете самостоятельно писать полезные программы, и чтобы добиться этого, мы должны сконцентрировать внимание на основных понятиях: фактах, запросах, переменных, конъюнкциях и правилах. Другие особенности языка Пролог, такие как списки и рекурсия, будут рассмотрены в последующих главах.
Пролог применяется в тех случаях, когда необходимо использовать ЭВМ для решения задачи, которая может быть выражена в терминах объектов и отношений между ними. Например, когда мы говорим: «Джон имеет книгу», мы объявляем, что между одним объектом «Джон» и другим объектом «книга» имеет место отношение обладания. Более того, это отношение имеет определенный порядок: Джон имеет книгу, но книга не имеет Джона! Когда мы задаем вопрос: «Имеет ли Джон книгу?», то нас интересует правильность именно отношения.
При констатации некоторых отношений не всегда упоминаются все объекты, включаемые в них. Например, когда мы говорим: «Драгоценные камни являются ценными», мы имеем в виду, что существует отношение, называемое «являться ценным», которое включает драгоценные камни. Для нас не имеет значения, кто считает, что драгоценные камни являются ценными, и почему он так считает. Это все зависит от того, что вы хотите сказать. При использовании Пролога, когда программируются отношения, подобные приведенным, уровень требуемой детализации также зависит от того, что вы хотите заставить делать ЭВМ
.
Существует еще один вопрос идейного плана, который следует упомянуть
, прежде чем приступать к программированию. Мы все знакомы с использованием правил для описания отношений между объектами. Например, правило «Два человека являются сестрами, если они оба женского пола и имеют одних и тех же родителей» объясняет нам, что значит быть сестрами. Оно также указывает, как определить, являются ли два человека сестрами: необходимо просто проверить, относятся ли они оба к женскому полу и имеют ли одних и тех же родителей. Важно отметить, что хотя правила обычно бывают упрощенными, тем не менее они приемлемы в качестве определений. В конце концов, не следует ожидать, что определение говорит нам все об определяемом объекте. Например, большинство людей согласится с тем, что в реальной жизни «быть сестрами» значит больше, чем это следует из приведенного правила. Однако, решая конкретную задачу, необходимо сосредоточить внимание именно на таких правилах, которые помогут ее решить. Таким образом, следует обратиться к схематичному и упрощенному определению, если его достаточно для достижения поставленной цели.
Программирование на языке Пролог состоит из следующих этапов:
• объявления некоторых
фактов об объектах и отношениях между ними,
• определения некоторых
правил об объектах и отношениях между ними и
• формулировки
вопросов об объектах и отношениях между ними.
Например, предположим, что мы записали на Прологе наше правило о сестрах. Мы могли бы сделать запрос о том, являются ли Мэри и Джейн сестрами. Пролог просмотрел бы все, что ему известно о Мэри и Джейн, и выдал бы ответ да или нет в зависимости от того, что ему известно. Таким образом, можно рассматривать Пролог как некоторое хранилище фактов и правил, используемых для поиска ответов на вопросы. Программирование на Прологе заключается в том, чтобы описать все эти факты и правила. Пролог-система позволяет использовать ЭВМ как хранилище фактов и правил и предоставляет механизм, позволяющий делать выводы, переходя от одних фактов к другим.
Пролог является диалоговым языком. Это следует понимать так, что пользователь и ЭВМ осуществляют некоторое подобие диалога. Предположим, что вам предложили поработать за терминалом ЭВМ и воспользоваться Прологом. Ваш терминал состоит из
клавиатуры и
дисплея. Вы используете
клавиатуру для ввода информации в ЭВМ, а ЭВМ использует
дисплей (может быть, экран либо бумажную ленту) для вывода полученных результатов. Пролог будет ждать, пока вы введете факты и правила, относящиеся к задаче, которую вы хотите решить. Затем, если вы сможете задать вопросы и если вы делаете это правильно, Пролог будет искать соответствующие ответы и выводить их на дисплей.
Теперь мы последовательно введем каждое из основных понятий языка Пролог. Не беспокойтесь о том, что вы не получите сразу полного представления о всех особенностях языка Пролог. В последующих главах будет дано их исчерпывающее описание и будет приведено и разобрано много примеров решения задач на языке Пролог.
1.1. Факты
Начнем обсуждение с
фактов об объектах. Предположим, мы хотим сообщить Прологу
[1]факт: «Джону нравится Мэри». Этот факт включает в себя два объекта, обозначенных именами «Мэри» и «Джон», и отношение, обозначенное словом «нравится». В языке Пролог используется стандартная форма записи фактов:
нравится (джон, мэри).
Важно соблюдать следующие правила:
• Имена всех отношений и объектов должны начинаться со строчной буквы. Например,
нравится, джон, мэри.
• Сначала записывается имя отношения. Затем через запятую записываются имена объектов, а весь список имен объектов заключается в круглые скобки.
• Каждый факт должен заканчиваться точкой.
Определяя с помощью фактов отношения между объектами, необходимо учитывать, в каком порядке перечисляются имена объектов внутри круглых скобок. Этот порядок может быть произвольным, но, выбрав один раз какой-то определенный порядок, мы должны везде следовать ему и далее. Например, в приведенном выше факте мы поставили на первое место в списке объектов «того, кому нравится», а объект «который нравится» стоит во второй позиции. Таким образом, факт
нравится(джон,мэри) не одно и тоже, что
нравится(мэри,джон). В соответствии с принятой нами (хотя и произвольным образом) договоренностью первый факт говорит о том, что Джону нравится Мэри, в то время как второй факт говорит, что Мэри нравится Джон. Если мы хотим сказать, что Мэри нравится Джон, то мы должны сформулировать это утверждение явно, в виде факта
нравится(мэри,джон).
Взгляните на следующие примеры фактов, приведенные вместе с возможной их интерпретацией на естественном языке:
ценный(золото). Золото является ценным,
женщина(джейн). Джейн — женщина.
владеет(джон,золото). Джон владеет золотом.
отец(джон,мэри). Джон является отцом Мэри.
дает(джон,книга,мэри). Джон дает Мэри книгу.
Всякий раз когда используется некоторое имя, оно указывает на определенный индивидуальный объект. В силу жизненного опыта нам совершенно ясно, что имена
джон и
джейн относятся к индивидуальным объектам. Но в некоторых других фактах мы использовали имена
золото и
ценный, и совсем не очевидно, что они значат. Логики называют имена такого сорта «словами, не имеющими определенного значения вне контекста». Используя такие имена, мы должны решить, как
интерпретировать эти имена. Например, имя золото могло бы относиться к некоторому объекту. В этом случае мысленный образ объекта имеет вид конкретного куска золота, который мы обозначаем именем
золото. И когда мы записываем на Прологе
ценный(золото), мы должны понимать это в том смысле, что этот конкретный кусок золота, для обозначения которого мы использовали имя
золото, является ценным. С другой стороны, мы могли бы интерпретировать имя
золото как
слово, обозначающее химический элемент золото с атомным весом 79, и, когда мы записываем
ценный(золото), мы должны понимать это так, что химический элемент золото является ценным. Таким образом, имеется несколько способов интерпретировать имя и именно автор программы определяет конкретную интерпретацию. До тех пор пока последовательно используется одна и та же интерпретация имен, никаких проблем не возникает. Выявлять отличия между различными интерпретациями необходимо с самого начала, с тем чтобы быть совершенно уверенным в том, что обозначают,имена.
Теперь пришла пора сказать несколько слов о терминологии. Имена объектов, список которых в каждом факте заключен в круглые скобки, называются аргументами. Заметим, что в программировании значение слова «аргумент» не имеет ничего общего с его общеупотребительным значением, используемым в контексте слов «диспут», «дебаты», «дискуссия», «спор» и т. п. Имя отношения, которое записывается непосредственно перед круглыми скобками, называется
предикат.[2] Таким образом,
ценный – это предикат, имеющий один аргумент, а
нравится – предикат с двумя аргументами.
Имена объектов и отношений являются полностью произвольными. Например, вместо терма
нравится(джон,мэри) мы могли бы с таким же успехом представить это как
a(b,c), помня при этом, что а значит
нравится, b означает
Джон, а
с –
Мэри. Однако обычно мы выбираем имена таким образом, чтобы они сами напоминали нам, что они значат. Следовательно, мы заранее должны решить, что значат наши имена и каким должен быть порядок аргументов. С этого момента необходимо последовательно придерживаться принятых соглашений.
Отношения могут иметь произвольное число аргументов. Если мы хотим определить предикат
играть, в котором упоминаются два игрока и игра, в которую они играют между собой, то необходимы три аргумента. Здесь приведены два примера, показывающие, как это можно сделать:
играть(джон,мэри,футбол).
играть(джейн, джим,бадминтон).
Как мы увидим далее, такой способ обеспечивает возможность представления сложных взаимодействий между отношениями.
В Прологе можно объявить факты, которые не являются истинными в реальном мире. Например, можно было бы написать
король(джон, франция), чтобы объявить, что
Джон является королем Франции. В реальном мире этот факт со всей очевидностью является ложным, в частности, потому, что монархия во Франции уничтожена приблизительно в 1792 г. Но Пролог не знает этого и не заботится об этом. Факты в Прологе просто позволяют выражать произвольные отношения между объектами.
Совокупность фактов в Прологе называется
базой данных. Мы будем пользоваться термином
база данных всякий раз при объединении вместе некоторых фактов (а в дальнейшем и правил) для совместного их использования при решении некоторой конкретной задачи.
1.2. Вопросы
Имея некоторую совокупность фактов, мы можем обращаться к Прологу с вопросами о них. В Прологе вопрос записывается почти так же, как и факт, за исключением того, что перед ним ставится специальный символ. Специальный символ состоит из вопросительного знака и следующего за ним тире. Рассмотрим вопрос:
?- имеет(мэри, книга).
Если мы интерпретируем
мэри как
человека по имени Мэри, а
книга - это какая-то конкретная книга, то смысл вопроса в следующем:
«Имеет ли Мэри (данную конкретную) книгу?» или
«Имеет ли место факт, что Мэри имеет данную книгу?». Мы не спрашиваем, имеет ли она все книги или книги вообще.
Обращение к Прологу с вопросом инициирует процедуру поиска в базе данных, ранее введенной в систему. Пролог ищет факты,
сопоставимые с фактом о вопросе. Два факта
сопоставимы (или соответствуют один другому), если их предикаты одинаковы (побуквенное совпадение) и их соответствующие аргументы попарно совпадают. Если Пролог находит факт, сопоставимый с вопросом, то он отвечает
да[3]. Если в базе данных такого факта не существует, то Пролог отвечает
нет. Ответ, выдаваемый Прологом, выводится на дисплей терминала непосредственно под запросом. Пусть имеется следующая база данных:
нравится(джо,рыба).
нравится(джо,мэри).
нравится(мэри,книга).
нравится(джо,книга).
Если все эти факты введены в Пролог-систему, то можно было бы делать следующие вопросы, ответы на которые Пролог написал бы непосредственно под текстом вопроса:
?- нравится(джо,деньги).
нет
?- нравится(мэри,джо).
нет
?- нравится(мэри,книга).
да
?- король(джон,франция).
нет
Ответы на три первых вопроса должны быть понятны. Кроме этого, Пролог отвечает
нет на вопрос о том, является ли Джон королем Франции. Система выдает такой ответ, так как среди фактов в базе данных, представленной приведенными выше четырьмя отношениями
нравится, нет отношений, указывающих на королевские звания. В Прологе ответ
нет используется в смысле
ничто в базе данных не согласуется с вопросом. Важно помнить, что ответ нет вовсе не эквивалентен ответу
является ложным. Предположим, например, что база данных содержит три факта об известных мыслителях Греции:
человек(сократ).
человек(аристотель).
афинянин(сократ).
Можно было бы сделать несколько вопросов:
?- афинянин(сократ).
да
?- афинянин(аристотель).
нет
?- грек(сократ).
нет
Хотя тот факт, что Аристотель жил когда-то в Афинах, может быть исторически верным, мы просто не можем
доказать его на основе фактов, представленных в базе данных. Более того, хотя в базе данных содержится факт о том, что Сократ жил в Афинах, это не
доказывает того, что он был греком, если только в базе данных нет дополнительной информации. Таким образом, когда Пролог на вопрос отвечает
нет, это значит
не доказуемо, не согласуется с базой данных.
В приведенном ранее примере Джону и Мэри нравится один и тот же объект. Мы знаем, что им нравится один и тот же объект, так как одно и то же имя
книга появляется в обоих фактах.
Обсуждавшиеся до сих пор факты и вопросы не представляют большого интереса. Все что мы можем сделать – это получить обратно ту же самую информацию, которую мы ввели в систему. Более полезны были бы вопросы вида:
«Какие объекты нравятся Мэри?». Именно для реализации такой возможности предназначены
переменные.
1.3. Переменные
Если вы хотите узнать, что нравится Джону, то было бы утомительно спрашивать
«Нравятся ли Джону книги?», «Нравится ли Джону Мэри?» и так далее, получая каждый раз ответ
да или
нет. Более разумно обратиться к Пролог-системе с просьбой назвать что-нибудь, что нравится Джону. Такой вопрос можно сформулировать следующим образом«
«Нравится ли Джону X?». Задавая вопрос, мы не знаем, для обозначения какого объекта использована литера
X. Нам хотелось бы, чтобы Пролог перечислил все имеющиеся возможности
для обозначения какого объекта использована литера X. В Прологе можно не только присваивать имена конкретным объектам, но и использовать имена, подобные
X, для обозначения объектов, которые должны быть определены Пролог-системой. Имена такого типа называются
переменными. Переменная в Прологе может иметь либо не иметь конкретное значение. Переменная конкретизирована, если имеется объект, который обозначает эта переменная. Переменная не конкретизирована, если еще не известно, что именно она обозначает. В Прологе используется соглашение, позволяющее отличать переменные от имен конкретных объектов –
каждое имя, начинающееся с прописной буквы, рассматривается как переменная.
При поиске ответа на вопрос Пролог организует просмотр всех фактов в базе данных, чтобы обнаружить объект, который эта переменная могла бы обозначать. Так, когда мы спрашиваем
«Нравится ли Джону X?», Пролог просматривает все известные ему факты для обнаружения тех вещей, которые нравятся Джону.
Такая переменная, как
X, сама по себе не является именем какого-то конкретного объекта, но она может быть использована для обозначения объектов, которым мы не можем дать имя. Например, мы не можем
чему-то, что нравится Джону, дать имя как объекту, поэтому для выражения подобных вопросов вместо вопросов вида
?- нравится(джон,
Что-то, что любит Джон).
Пролог позволяет использовать переменные и задавать вопросы в виде
?- нравится(джон,Х).
При желании можно давать переменным более длинные имена. Следующий вопрос вполне приемлем в Прологе:
?- нравится(джон, Что-точтонравитсяджону).
Почему? Потому что переменной может быть любое имя, начинающееся с прописной буквы. Рассмотрим следующую базу данных и запрос к Прологу:
нравится (джон,цветы).
нравится (джон,мэри).
нравится(поль,мэри).
?- нравится(джон,Х).
В вопросе спрашивается:
Существует ли что-нибудь, что нравится Джону? В ответ Пролог напечатает:
Х=цветы
а затем будет ждать дальнейших приказов; это мы вкратце обсудим далее. Как это произойдет? При поступлении такого вопроса в Пролог-систему переменная, входящая в вопрос, изначально является неконкретизированной. Пролог просматривает базу данных в поисках факта,
сопоставимого с вопросом. Если неконкретизированная переменная появляется в качестве аргумента, то Пролог считает, что такой аргумент сопоставим с
любым другим аргументом, находящимся в той же самой позиции факта. В нашем примере Пролог ищет любой факт с предикатом
нравится и первым аргументом
джон.
Второй аргумент в этом случае может быть каким угодно, так как в вопросе вторым аргументом является неконкретизированная переменная. При обнаружении такого факта переменная
X становится конкретизированной, обозначая объект, являющийся вторым аргументом найденного факта, каким бы этот аргумент ни был. Пролог просматривает факты базы данных в том порядке, в каком они вводились (на печатной странице это соответствует просмотру сверху вниз), поэтому факт
нравится(джон, цветы) найден первым. С этого момента переменная
X обозначает объект
цветы или, говоря другими словами, переменная
X конкретизируется значением
цветы. Пролог с помощью специального
маркера отмечает место в базе данных, в котором произошло сопоставление. Обсудим кратко причины, по которым оказалось необходимым использование такого маркера.
Обнаружив факт, соответствующий вопросу, Пролог печатает имена объектов, которые теперь обозначают переменные. В нашем примере есть только одна переменная
X, которой соответствует объект
цветы. Затем Пролог ждет дальнейших указаний, как об этом говорилось выше. Если в этой ситуации нажать на терминале клавишу
RETURN, указывая тем самым, что вы удовлетворены полученным ответом, то Пролог прекратит дальнейший поиск в базе данных. Если вместо этого нажать клавишу
; (и вслед за ней клавишу
RETURN), то Пролог продолжит поиск в базе данных,
начиная с места, отмеченного маркером. В такой ситуации, когда Пролог начинает поиск не с начала базы данных, а с места, отмеченного маркером, мы говорим, что Пролог пытается заново согласовать вопрос.
Предположим, что в ответ на первое найденное Прологом соответствие (
Х=цветы) мы предлагаем системе продолжить поиск (введя
;). Это значит, что мы хотим согласовать вопрос иначе; мы хотим найти другой объект, который могла бы обозначать переменная
X. Это также значит, что Пролог должен «забыть» о том, что переменная
X обозначает
цветы, и снова продолжить поиск с неконкретизированной переменной
X. Так как мы ищем альтернативное решение, то поиск продолжается с места, отмеченного маркером. Следующий найденный системой факт, соответствующий вопросу, есть
нравится(джон,мэри). Переменная
X вновь становится конкретизированной, обозначая
мэри, а Пролог отмечает маркером факт
нравится(джон,мэри). Пролог напечатает
Х=мэри и будет ожидать дальнейших команд. Если мы вновь введем точку с запятой, то Пролог продолжит поиск. В нашем примере нет больше ничего, что нравится Джону. Поэтому Пролог завершит поиск и предоставит нам возможность сделать новые запросы или ввести новые факты.
Что произойдет, если, имея те же факты, что и ранее, мы зададим вопрос:
?- нравится(Х,мэри).
В этом вопросе спрашивается:
«Существует ли объект, которому нравится Мэри?». Теперь вы сами можете понять, что в примере объектами, которые нравятся Мэри, являются
джон и
поль. Опять, если бы мы хотели увидеть все варианты, мы должны были бы вводить; после каждого ответа, выдаваемого Прологом:
?-
нравится(Х, мэри). наш вопрос
Х=джон; первый ответ. Мы вводим ;
Х=поль; второй ответ. Вновь вводим ;.
нет больше ответов нет.
1.4. Конъюнкции
Предположим, что мы хотим получать ответы на вопросы о более сложных отношениях, таких как:
«Нравятся ли Джон и Мэри друг другу?». Один из способов сделать это – узнать сначала, нравится ли Джону Мэри, и если Пролог ответит да, то спросить, нравится ли Мэри Джон. Таким образом, эта задача состоит из двух «целевых утверждений» (или целей), которые Пролог должен согласовать. Ввиду того что подобная комбинация часто используется при программировании на Прологе, для нее имеется специальное обозначение. Предположим, мы имеем следующую базу данных:
нравится(мэри,пища).
нравится(мэри,вино).
нравится(джон,вино).
нравится(джон,мэри).
Мы хотим узнать, нравятся ли Джон и Мэри друг другу. Для этого мы спрашиваем:
«Нравится ли Джон Мэри и
нравится ли Мэри Джон?». Связка
и выражает тот факт, что нас интересует конъюнкция двух указанных целей – мы хотим последовательно согласовать с базой данных обе цели. Мы выражаем это в вопросе, записывая обе цели через запятую:
?- нравится(джон,мэри),нравится(мэри,джон).
Запятая читается как «и» и используется для разделения произвольного числа различных целей, которые должны быть согласованы с базой данных для того, чтобы ответить положительно на вопрос. Если задана последовательность целей (разделенных запятыми), то Пролог пытается согласовать каждую цель по очереди, просматривая базу данных в поисках сопоставимых фактов. Чтобы согласовать с базой данных последовательность целей, необходимо согласовать все отдельные цели. Что должен напечатать Пролог в ответ на приведенный выше вопрос? Ответ будет
нет. Действительно, так как имеет место факт, что Джону нравится Мэри, то первая цель согласуется с базой данных. Однако вторая цель не согласуется с базой данных, так как в ней отсутствует факт
нравится(мэри,джон). Учитывая, что мы хотели знать, нравятся ли они
оба друг другу, окончательным ответом на вопрос является
нет.
Сочетая возможности конъюнкции и использования переменных, можно строить достаточно содержательные вопросы. Теперь, когда мы знаем, что нельзя выяснить, нравятся ли Джон и Мэри друг другу, мы спрашиваем:
«Существует ли что-нибудь такое, что нравится обоим -
Джону и Мэри?». Этот вопрос также содержит две цели:
• Существует ли такой объект
X, который нравится Мэри.
• Нравится ли Джону найденное значение
X.
В Прологе два указанных целевых утверждения следует объединить, используя конъюнкцию, как показано ниже:
?- нравится(мэри,Х), нравится(джон,X).
Пролог отвечает на вопрос, пытаясь подобрать соответствие для первой цели. Если в базе данных есть факт, соответствующий целевому высказыванию, то Пролог отметит найденное место и попытается согласовать вторую цель. Если и она достигнута, то Пролог также отмечает в базе данных соответствующее ей место, и таким образом находится решение, удовлетворяющее обеим целям.
Важно помнить, что каждая цель имеет свой собственный маркер для указания места в базе данных,
где найдены соответствующие им факты. Если, однако, вторая цель не согласуется с базой данных, то Пролог попытается найти новое соответствие для предыдущей цели (в данном случае для первой цели). Помните, что Пролог полностью просматривает базу данных для каждой из целей. Если случится так, что некоторый факт в базе данных можно сопоставить с заданной целью, то Пролог отметит это место в базе данных на случай, если впоследствии он будет вынужден снова искать для этой цели другое соответствие. И когда возникнет необходимость найти для цели другое соответствие, Пролог начнет поиск не с начала базы данных, а с места, отмеченного маркером, соответствующим этой цели. Наш предыдущий вопрос:
«Существует ли что-нибудь, что нравится и Мэри и Джону?» иллюстрирует пример такого поиска с возвратом («бектрекинга»). Пролог выполняет следующую последовательность действий:
1. База данных просматривается в попытке согласовать первую цель. Так как второй аргумент
(X) неконкретизирован, то ему может соответствовать все что угодно. Первый факт, сопоставимый с целью, в приведенной выше базе данных есть
нравится(мэри, пища). С этого момента
каждому появлению переменной
X в вопросе соответствует значение
пища. Пролог отмечает в базе данных то место, где был обнаружен соответствующий факт, так что при необходимости найти другой способ согласования цели с фактами он может вернуться в эту точку и продолжить поиск. Более того, следует помнить, что переменная
X была конкретизирована в этой точке и Пролог может «забыть» найденное для
X значение в случае необходимости найти новое соответствие в фактах для рассматриваемой цели.
2. Теперь в базе данных ищется факт
нравится(джон,пища), так как следующая цель – это
нравится (джон,X), а переменная
X теперь имеет значение
пища. Как можно видеть, база данных такого факта не содержит, так что эта цель с базой данных не согласуется. В этой ситуации мы должны попытаться найти новое соответствие в фактах для предыдущей цели. Поэтому Пролог предпринимает попытку найти новое соответствие для
нравится(мэри,X), при этом поиск в базе данных начинается с отмеченного маркером места. Но сначала необходимо «расконкретизировать» переменную
X так, чтобы
X опять могла быть сопоставлена с любым объектом.
3. Отмеченным маркером местом является факт
нравится(мэри, пища). Поэтому Пролог начинает поиск со следующего непосредственно за ним факта. Так как мы еще не достигли конца базы данных, то мы не исчерпали всех объектов, которые нравятся Мэри. Следующим сопоставимым фактом является
нравится(мэри, вино). Теперь переменная
X принимает значение
вино, и Пролог отмечает это место на случай, если потребуется найти новое соответствие для того, что нравится Мэри.
4. Как и ранее, Пролог пытается теперь согласовать с фактами вторую цель в вопросе, осуществляя поиск в базе данных факта
нравится(джон,вино). Пролог не пытается при этом использовать механизм поиска нового соответствия для этой цели. Это новая цель, которую он выбирает, продвигаясь, как и раньше, слева направо по списку целей в исходном вопросе, поэтому он должен начать поиск с начала базы данных. Когда после недолгого поиска будет найден сопоставимый факт, Пролог выдает надлежащее сообщение. Как только вторая цель согласована, Пролог отмечает соответствующий ей факт в базе данных на случай, если вдруг потребуется найти для нее новое соответствие. Для каждой цели, которую Пролог пытается согласовать, в базе данных имеется свой маркер, указывающий факт, поставленный в соответствие этой цели.
5. Теперь обе цели согласованы. Переменная
X обозначает имя
вино. Маркер первого целевого утверждения отмечает в базе данных факт
нравится(мэри,вино), а маркер второго целевого утверждения отмечает факт
нравится(джон,вино).
Как и в случае других запросов, как только Пролог находит ответ, он прекращает поиск и ожидает дальнейших указаний.
Если ввести
;, то Пролог продолжит поиск объектов, которые нравятся одновременно Джону и Мэри. Теперь мы знаем, что все
последующие попытки поиска новых ответов на вопрос с двумя целями начинаются с мест, отмеченных маркерами, которые оставили эти цели на предыдущем этапе.
Подводя итог, можно представить конъюнкцию целей в вопросе как список целей, упорядоченных слева направо и разделенных запятыми. Каждая цель может иметь соседа слева и соседа справа. Ясно, что цели, занимающие в списке крайнее левое и крайнее правое положения, не будут иметь соседей соответственно слева и справа. Обрабатывая конъюнкцию целей, Пролог пытается по очереди согласовать с базой данных каждую цель, просматривая вопрос слева направо. Если обнаруживается факт, сопоставимый с целью, то Пролог оставляет в этом месте базы данных маркер, связанный
с целью. Это можно наглядно представить с помощью стрелки, ведущей от цели к некоторому месту в базе данных, где находится соответствующий факт. Кроме того, некоторые ранее неконкретизированные переменные могут при этом быть конкретизированы, как это имело место выше на шаге 1. Если некоторая переменная конкретизируется, то конкретизируются и все вхождения этой переменной в вопрос. Далее Пролог пытается удовлетворить правого соседа этой цели, начиная поиск с вершины базы данных (наполнение базы данных в Прологе осуществляется сверху вниз, так что вершина – это факт, внесенный в базу данных первым). Как и любая другая цель, для которой найдено соответствие, она оставляет после себя в базе данных маркер (проводит еще одну стрелку от этой новой цели к соответствующему ей факту), на случай если впоследствии возникнет необходимость найти для цели другое соответствие. Каждый раз, когда целевое утверждение не выполняется (нельзя найти сопоставимого факта), Пролог возвращается и пытается найти новое соответствие для соседа
слева данной цели, начиная поиск с места, отмеченного соответствующим ему маркером. Кроме того, Пролог должен сначала расконкретизировать все переменные, которые были конкретизированы при достижении этой цели. Другими словами, когда Пролог ищет новое соответствие для цели, он должен «уничтожить» старое значение этих переменных. Если для цели, к рассмотрению которой был возврат справа, нельзя найти новое соответствие, то Пролог перейдет еще левее, постепенно приближаясь к левой границе конъюнкции. Если не удается найти новое соответствие для крайней слева цели, которая уже не имеет соседа слева, то в этом случае считается несогласуемой с базой данных вся конъюнкция целей в вопросе к Прологу. Такое поведение, когда Пролог неоднократно пытается согласовать (и вновь согласовать) цели, входящие в вопрос-конъюнкцию, называется поиском с возвратом (бектрекингом). В следующей главе дается краткое описание механизма возврата, а в гл. 4 проводится более полное и детальное рассмотрение этого процесса.
Разбирая примеры, полезно записывать под каждой переменной, входящей в целевое утверждение, значение (имя объекта), которое было присвоено этой переменной при установлении согласованности цели с базой данных. Следует также изображать стрелки, идущие от цели к соответствующему ей маркеру в базе данных. На рис. 1.1 приведен пример такой иллюстрации на бумаге работы Пролога, состоящий из четырех «мгновенных снимков» процесса поиска в приведенном выше примере. На каждом снимке показаны полная база данных и вопрос, а также пронумерованная последовательность комментариев. На рисунке цели, для которых найдены соответствия, заключены в прямоугольник.
На протяжении всей книги мы постараемся показать, где в рассматриваемых примерах имеет место возврат и какую роль он играет в решении задачи. Значение механизма возврата при поиске настолько велико, что ему полностью посвящена гл. 4.
Упражнение 1.1. Продолжить разбор рассмотренного выше примера с помощью карандаша и бумаги, предположив, что вы ввели точку с запятой;, инициируя возврат для того, чтобы определить, существует ли еще что-нибудь, что нравится одновременно Джону и Мэри.
 Рис. 1.1.
Рис. 1.1.
1.5. Правила
Предположим, мы хотим сформулировать утверждение, что Джону нравятся все люди. Один из способов сделать это заключается в записи для каждого человека, упоминаемого в базе данных, отдельного факта:
нравится(джон,альфред).
нравится(джон,бертран).
нравится(джон,чарлз).
нравится(джон,дейвид).
* * *
Это было бы очень утомительным, особенно если в нашей программе на Прологе упоминается несколько сот человек. Другой способ выразить факт, что Джону нравятся все люди, - это сказать
Джону нравится любой объект при условии, что этот объект является человеком. Здесь этот факт представлен в форме
правила для определения того, что нравится Джону, а не прямого перечисления всех людей, которые ему нравятся. В ситуации, когда Джону мог бы нравиться любой человек, представление утверждения в виде правила является значительно более компактным, чем список фактов.
В Прологе правила используются в том случае, когда необходимо сказать, что некоторый факт
зависит от группы других фактов. В естественном языке для выражения правила мы можем использовать слово
если. Например:
•
Я пользуюсь зонтом, если идет дождь.
•
Джон покупает вино, если оно дешевле, чем пиво.
Правила используются также для выражения определений, например:
X является птицей, если:
X является живым существом и X имеет перья.
или
X является сестрой Y, если:
X является женщино и X и Y имеют одних и тех же родителей.
В последних примерах мы использовали переменные
X и
Y. Важно помнить, что каждое вхождение переменной в правило обозначает один и тот же объект. Иначе мы разрушили бы саму суть определения. Например, используя приведенное выше определение птицы, мы не смогли бы показать, что Фред является птицей на основании того, что Фидо – это живое существо, а Мэри имеет перья. Этот принцип согласованной интерпретации переменных справедлив также и для правил в Прологе.
Правило – это некоторое
общее утверждение об объектах и об отношениях между ними. Например, мы можем сказать, что Фред является птицей, если Фред является живым существом и Фред имеет перья, мы можем также сказать, что Бертрам является птицей, если Бертрам является живым существом и Бертрам имеет перья. Таким образом, мы допускаем, что при каждом новом
использовании правила переменная обозначает новый, отличный от прежнего объект. Конечно, в рамках конкретного использования правила переменные интерпретируются согласованно, как на это указывалось выше.
Рассмотрим несколько примеров, начав с правила, содержащего одну переменную и конъюнкцию:
Джону нравится любой, кому нравится вино, или,
другими словами,
Джону нравится что-то, если чему-то нравится вино,
или, используя переменные,
Джону нравится X, если X нравится вино.
В Прологе правило состоит из
заголовка и
тела правила. Заголовок и тело соединяются с помощью символа :-, который состоит из двоеточия
: и тире
-. Символ ':-' читается
если.
Предыдущий пример записывается на Прологе следующим образом:
нравится(джон,X):- нравится(Х,вино).
Отметим, что правила также заканчиваются точкой. Заголовком этого правила является нравится(джон,Х). Заголовок правила описывает факт, для определения которого предназначено это правило. Тело правила, в данном случае нравится(Х,вино), описывает конъюнкцию целей, которые должны быть последовательно согласованы с базой данных, для того чтобы заголовок правила был истинным. Например, мы можем сделать Джона более разборчивым в выборе тех, кто ему нравится, просто добавив к телу правила еще несколько целевых утверждений, разделив их запятыми:
нравится(джон,X):- нравится(Х,вино), нравится(X,пища).
или, другими словами,
Джону нравится любой, кому нравятся вино и пища. Или, предположим, что Джону нравится любая женщина, которой нравится вино:
нравится(джон,Х):- женщина(Х), нравится(Х,вино).
Всякий раз, когда мы имеем дело с правилом в Прологе, необходимо отмечать все вхождения переменных. В последнем примере переменная
X использована три раза. Всякий раз, как переменная X конкретизируется некоторым объектом (ей присваивается значение), все вхождения
X в пределах
области действия этой переменной становятся конкретизированными. При каждом употреблении правила
область действия переменной
X – это все правило, начиная с заголовка и до точки '.' в конце этого правила. Так, если в приведенном выше правиле переменная X оказалась конкретизированной, принимая значение
мэри, то Пролог попытается согласовать с базой данных целевые утверждения
женщина(мэри) и
нравится(мэри,вино).
Теперь, чтобы продемонстрировать правило, использующее более одной переменной, рассмотрим базу данных, содержащую факты о семействе королевы Виктории. Мы будем использовать предикат
родители, имеющий три аргумента.
родители(Х, Y, Z) означает:
Родителями X являются Y и Z. Переменная
Y обозначает мать, а переменная
Z обозначает отца. Кроме того, мы будем использовать предикаты
женщина и
мужчина в их очевидном значении. Некоторая часть этой базы данных могла бы выглядеть следующим образом:
мужчина(альберт).
мужчина(эдуард).
женщина(алиса).
женщина(виктория).
родители(эдуард,виктория,альберт).
родители(алиса,виктория,альберт).
Здесь мы воспользуемся описанным ранее правилом
является_сестрой. Правило определяет предикат
является_сестрой, имеющий два аргумента, таким образом, что
является_сестрой(X, Y) истинно, если
X является сестрой
Y. Обратим внимание на использование в имени предиката символа подчеркивания '_'. Хотя до сих пор не было дано полных правил конструирования имен, отметим, что допускается использование подчеркивания в именах, а более подробно об этом будет сказано в следующей главе. Тогда
X является сестрой
Y, если:
•
X является женщиной,
•
X имеет мать
М и отца
F и
•
Y имеет тех же мать и отца, что и
X.
Это можно записать в виде следующего правила Пролога:
является_сестрой(X,Y):- женщина(X), родители(X,M,P), родители(Y,M,P).
Мы используем переменные
M и
F для обозначения
матери и
отца, хотя при желании мы могли бы использовать имена
Мать и
Отец. Отметим, что мы употребляем переменные, которые не появляются в заголовке правила. Эти переменные,
M и
F, обрабатываются таким же образом, как и любая другая переменная. Когда Пролог использует это правило, переменные
M и
F изначально будут неконкретизированными. Этим переменным будет присвоено некоторое значение в момент установления соответствия для предиката
родители(X,M,F). Однако, как только они конкретизируются, становятся конкретизированными и
все вхождения переменных
M и
F, соответствующие текущему использованию правила. Следующий пример должен помочь объяснить, как используются эти переменные. Давайте зададим вопрос:
?- является_сестрой(алиса,эдуард).
Имея описанные выше базу данных и правила
является_сестрой и получив такой вопрос, Пролог выполняет следующие действия:
1. Сначала вопрос сопоставляется с единственным правилом для предиката
является_сестрой, приведенным выше. При этом переменная
X конкретизируется, принимая значение
алиса, и переменная
Y конкретизируется значением
эдуард. Правило, с которым произошло сопоставление, отмечается маркером. Теперь Пролог пытается последовательно согласовать с базой данных три предиката, входящие в тело правила.
2. Так как на предыдущем шаге переменной
X присвоено значение
алиса, то первой целью является
женщина(алиса). Истинность этого предиката следует из списка фактов, так что цель достигнута. Поскольку данная цель согласована, то Пролог отмечает соответствующее ей место в базе данных (третье утверждение в
базе данных). При этом не
произошло никаких присвоений значений переменным. Далее Пролог пытается согласовать следующую цель.
3. Теперь Пролог ищет соответствие для предиката
родители(алиса,M,F), где переменные
M и
F сопоставимы с любыми аргументами, так как первоначально они неконкретизированы. Факт, с которым происходит сопоставление, есть
родители(алиса, виктория,альберт), и тем самым вторая цель достигнута. Пролог отмечает маркером соответствующее место в базе данных (шестое утверждение сверху) и записывает, что
M присвоено значение
виктория, a
F – значение
альберт. (Если хотите, вы можете делать соответствующую запись над целевым утверждением в правиле.) Затем Пролог пытается найти соответствие для следующего предиката в правиле.
4. Теперь Пролог ищет в базе данных факт
родители(эдуард,виктория,альберт), так как из запроса нам известно, что
Y – это
эдуард, а из предыдущего шага мы знаем, что
M и
F обозначают
виктория и
альберт. Эта цель достигается, поскольку найден подходящий факт (пятое утверждение сверху). Так как это последняя цель в конъюнкции, то и полное целевое утверждение является согласованным с базой данных, и тем самым доказано, что факт
является_сестрой(алиса, эдуард) является истинным, Пролог отвечает
да.
Предположим, мы хотим знать, является ли Алиса чьей-либо сестрой. Соответствующий вопрос на Прологе имеет вид
?- является_сестрой(алиса,X).
В ответ на вопрос Пролог выполняет следующие действия:
1. Вопрос сопоставляется с заголовком единственного правила для предиката
является_сестрой. Переменная
X, входящая в это правило, конкретизируется значением
алиса. Так как переменная
X в запросе неконкретизирована, то и переменная
Y в правиле также будет неконкретизированной. Однако эти две переменные теперь становятся
сцепленными. Как только одной из переменных присваивается некоторое значение, другая переменная становится конкретизированной тем же самым значением. Конечно, в данный момент они неконкретизированы.
2. Первая цель –
женщина(алиса), которая достигается так же, как и в предыдущем примере.
3. Вторая цель –
родители(алиса,М,F). Эта цель сопоставляется с
родители(алиса,виктория,альберт). Переменные
M и
F становятся конкретизированными.
4. Так как переменная
Y пока неизвестна, то третьей целью будет
родители(Y,виктория,альберт), и она сопоставляется с
родители(эдуард, виктория,альберт). Переменная
Y конкретизируется значением
эдуард.
5. Так как все целевые утверждения согласованы с базой данных, то тем самым согласовано и правило в целом, при этом переменная
X (как известно из вопроса) равна
алиса и
Y равна
эдуард. Учитывая, что
Y (в правиле) является
сцепленной с
X (в вопросе), то
X также конкретизирована значением
эдуард. Пролог печатает
Х=эдуард.
Как обычно, Пролог ожидает, пока вы сообщите ему, хотите ли вы найти все ответы на вопрос. Оказывается, что на данный вопрос имеется более одного ответа. Как Пролог находит оставшиеся ответы (ответ), является содержанием упражнения, приведенного в конце главы.
Как мы видели до сих пор, существуют два способа предоставить Прологу информацию относительно предиката, подобного предикату
нравится. Мы можем сделать это, используя как факты, так и правила. В общем случае предикат будет определен смесью фактов и правил. Эти факты и правила, определяющие предикат, называются
утверждениями[4]. Мы будем использовать слово
утверждение в случаях, когда мы ссылаемся либо на факт, либо на правило.
В качестве следующего примера, на этот раз не имеющего отношения к монархам, рассмотрим правило:
Человек может украсть что-либо, если этот человек вор и ему нравится вещь и эта вещь является ценной. На Прологе это записывается следующим образом:
может_украсть(P,T:- вор(P), нравится(P,T), ценный(T).
Предикат
может_украсть, который имеет две переменные
P и
T, представляет отношение:
некоторый человек P может украсть вещь T. Это правило зависит от утверждений, определяющих предикаты
вор, нравится и
ценный. Они могут быть представлены либо как факты, либо как правила в зависимости от того, что является более подходящим. Например, рассмотрим следующую базу данных, составленную в том числе из утверждений, обсуждавшихся ранее. Мы добавим к ним номера утверждений, заключенные между специальными скобками /*… */. Именно таким образом в Пролог-системе записывается
комментарий. Комментарии игнорируются Пролог-системой, но мы можем добавить их в программу для удобства. В последующем обсуждении мы будем ссылаться на номера предложений, представленные в виде комментариев.
/*1*/ вор(джон).
/*2*/ нравится(мэри, пища).
/*3*/ нравится(мэри,вино).
/*4*/ нравится(джон,X):- нравится(X,вино).
/*5*/ может_украсть(X,Y):- вор(X), нравится(X,Y).
Отметим, что определение предиката
нравится содержит три отдельных утверждения: два факта и правило. Для Пролога это не имеет значения. Единственное различие состоит в том, что когда осуществляется поиск в базе данных, чтобы согласовать с ней некоторую цель, то правило вызывает дальнейший поиск, чтобы согласовать его собственные предикаты-подцели. Факт не имеет подцелей, так что при сопоставлении
с фактом поиск либо сразу завершается, либо сразу происходит переход к следующему утверждению. Например, давайте проследим за тем, что получится, если обратиться к Прологу с вопросом:
Что Джон может украсть? Прежде всего этот вопрос транслируется на Прологе:
?- может_украсть(джон,Х).
Чтобы ответить на этот вопрос, Пролог осуществляет поиск следующим образом:
1. Прежде всего Пролог ищет в базе данных утверждение, описывающее предикат
может_украсть, и находит такое утверждение. Оно представлено в виде правила и имеет номер 5. Пролог отмечает это место в базе данных. Так как это утверждение является правилом, то, чтобы установить, согласуется ли заголовок правила с базой данных, необходимо попытаться согласовать с ней тело правила. Тогда переменной
X в правиле 5 присваивается значение
джон, которое берется из вопроса. Как и в предыдущих примерах, мы должны сопоставить неконкретизированные переменные (
X в вопросе и
Y в правиле), так что теперь они будут
сцеплены. Если вы не уверены, что до конца понимаете, что это значит, то необходимо вернуться назад к примерам с предикатом я
вляется_сестрой(X, Y). Для того чтобы правило выполнилось, необходимо согласовать цели с базой данных. Таким образом, теперь проверяется на согласованность с базой данных первое утверждение
вор(джон).
2. Эта цель достигается, так как факт
вор(джон) содержится в базе данных (утверждение 1). Пролог отмечает это место в базе данных, и при этом присвоения значений переменным не происходит. Далее Пролог пытается достигнуть вторую цель, применяя утверждение 5. Так как
X, как и ранее, обозначает
джон, то теперь Пролог ищет
нравится (джон, Y). Заметим, что к этому моменту
Y остается неконкретизированной.
3. Цель
нравится(джон, Y) сопоставляется с заголовком правила (утверждение 4). Переменная
Y, входящая в цель,
сцепляется с
X в заголовке правила, и обе эти переменные остаются неконкретизированными. Чтобы доказать это правило, теперь ищется
нравится(Х, вино).
4. Эта цель достигается, так как она сопоставляется с
нравится (мэри,вино) - фактом, являющимся утверждением с номером 3. Так что теперь
X становится
мэри.
5. Так как цель в утверждении 4 достигнута, то согласовано и правило в целом. Факт
нравится(джон, мэри) следует из утверждения 4, так как переменная
Y в утверждении 5 сцеплена с
X, и ей тоже присваивается значение
мэри.
6. Утверждение 5 теперь согласуется с базой данных при
Y, имеющем значение
мэри. Так как переменная
Y была сцеплена со вторым аргументом исходного вопроса, то переменная
X в вопросе конкретизируется, принимая значение
мэри. Приведем рассуждение, обосновывающее факт
Джон может украсть Мэри:
Для того чтобы украсть что-либо, прежде всего Джон должен быть вором. Из утверждения 1 следует, что это имеет место. Далее, Джону должен нравиться похищаемый предмет. Из утверждения 4 мы видим, что Джону нравится любой, кому нравится вино. Из утверждения 3 мы видим, что Мэри нравится вино. Следовательно, Джону нравится Мэри. Поэтому оба условия для похищения некоторого объекта имеют место, а значит, Джон может украсть Мэри.
Заметим, что факт (утверждение 2) о том, что Мэри нравится пища, не имеет никакого отношения к данному конкретному запросу, так как он нигде не понадобился.
В приведенном примере мы повторно использовали переменные
X и
Y в различных утверждениях. Например, в правиле
может_ украсть X обозначает объект, который может что-нибудь украсть. Но в правиле
нравится X обозначает объект, которому что-то нравится. Для того чтобы приведенная программа имела смысл, в Прологе должна иметься возможность указывать, что X может обозначать различные вещи в различных употреблениях утверждений. Помните, что знание
области действия переменной может разрешить любые неясности. Мы могли бы использовать более мнемоничные имена, чтобы попытаться предотвратить любые неясности, но мы используем простые имена, такие как X, чтобы продемонстрировать работу принципа области действия переменной.
1.6. Заключение и упражнения
К этому моменту мы уже обсудили большинство основных черт языка Пролог. В частности, мы рассмотрели:
• объявление фактов об объектах;
• задание вопросов относительно известных фактов;
• роль переменных и их области действия;
• конъюнкцию как способ описания
и-условий;
• представление отношений в виде правил;
• общую схему поиска с механизмом возврата.
С этим небольшим набором элементарных конструкций можно уже писать полезные программы для работы с простыми базами данных. Скорее всего, наиболее правильно так и поступить, работая над упражнениями, приведенными ниже.
Чтобы понять, как пользоваться этой книгой, вам следует прочитать предисловие, если вы не сделали это до сих пор. Кроме того, когда вы начнете писать программы для имеющейся в вашем распоряжении системы программирования на Прологе, вам следует обратиться к соответствующему приложению, чтобы узнать, как организуется взаимодействие с системой. Вы также найдете несколько практических советов в гл. 8.
Теперь, когда вы имеете в своем распоряжении достаточно большой арсенал средств Пролога, вам следует перейти к следующей главе, в которой обсуждаются некоторые вопросы, не рассматривавшиеся в этой главе. Кроме того, мы покажем, какие средства для работы с числами имеются в Прологе. Черты языка, рассматриваемые в нескольких последующих главах, делают очевидными выразительные возможности и удобство Пролога.
Упражнение 1.2. При применении правила
является_сестрой к обсуждавшейся ранее базе данных, содержащей информацию о семействе королевы Виктории, может быть получено несколько ответов. Объясните, как могут быть получены все ответы и каковы они.
Упражнение 1.3. В основу этого упражнения положено одно из упражнений из книги Kowalski R.
Logic for Problem Solving, North Holland, 1979. Предположим, что кем-то уже написаны на Прологе утверждения, определяющие следующие отношения:
отец(Х,Y) /* X является отцом Y */
мать(Х, Y) /* X является матерью Y */
мужчина(Х) /* X – мужчина */
женщина(Х) /* X - женщина */
родитель(Х,Y) /* X является родителем Y */
различны(Х,Y) /* X и Y различны */
Задача состоит в том, чтобы написать правила для следующих отношений:
является_матерью(Х) /* X является матерью */
является_отцом(Х) /* X является отцом */
является_сыном(Х) /* X является сыном */
является_сестрой(Х,Y) /* X является сестрой Y */
дедушка(Х, Y) /* X является дедушкой Y */
общие_родители(Х,Y) /* X и Y имеют общих родителей*/
Например, мы могли бы написать правило для предиката
тетя, при условии что у нас уже имеются правила для
женщина, общие_родители и
родитель.
тетя(Х,Y):- женщина(Х), общие_родители(X, Z), родитель(Z,Y).
Это можно также записать следующим образом:
тетя(Х,Y):- является_сестрой(Х,Z), родитель(Z, Y).
при условии что мы имеем правило для отношения
является_сестрой.
Упражнение 1.4. Используя правило для отношения
является_сестрой, определенное в тексте, объясните, каким образом становится возможным, что некто может быть своей собственной сестрой. Как можно было бы изменить это правило, если такое свойство нежелательно? Считайте, что предикат
различны из упр. 1.3 уже определен.
ГЛАВА 2 БОЛЕЕ ДЕТАЛЬНОЕ ОПИСАНИЕ
В данной главе приводится более полное описание тех элементов Пролога, которые были введены в предыдущей главе. Пролог предоставляет средства для структурирования данных, а также средства для структурирования той
последовательности, в которой совершаются попытки согласовать целевые утверждения с базой данных. Для структурирования данных необходимо знание синтаксических правил, используемых для обозначения данных. Структурирование последовательности, в которой будут совершаться попытки согласовать целевые утверждения с базой данных, предполагает знание принципов работы механизма возврата.
2.1. Синтаксические правила
Синтаксические правила языка описывают допустимые способы соединения слов. В соответствии с нормами английского языка предложение «I see a zebra» («я вижу зебру») является синтаксически правильным в отличие от предложения «zebra see I а» («зебра видит я»). В первой главе синтаксис Пролога явно не обсуждался, просто показывалось на примерах, как выглядят некоторые элементы Пролога. В данном разделе приводится краткое описание синтаксических правил для уже знакомых нам элементов Пролога.
Пролог-программы состоят из
термов. Терм – это либо
константа, либо
переменная, либо
структура. Каждый из этих термов фигурировал в предыдущей главе, но не назывался там таким именем. Терм записывается как последовательность
литер. Литеры делятся на четыре категории:
ABCDEFGHIJKLMNOPQRSTUVWXYZ
abсdefghijklmnopqrstuvwxyz
0123456789
+-*/\^<>~:.?@#$&
Первая строка состоит из
прописных букв. Вторая строка – из
строчных букв. В третьей строке –
цифры. В четвертой строке перечислены
специальные литеры (спецзнаки). В действительности спецзнаков больше, чем показано в четвертой строке, но остальные используются только в особых случаях, обсуждаемых ниже
[5]. Для термов каждого типа, таких как константа, переменная, структура, имеются свои правила образования имен термов из литер. Ниже вкратце обсуждаются каждый из типов термов.
2.1.1. Константы
Константами являются поименованные
конкретные объекты или
конкретные отношения. Существует два вида констант:
атомы и
целые числа. Примерами атомов являются имена, приводившиеся в предыдущей главе:
нравится мэри джон книга вино имеет драгоценности может_украсть
Специальные символы, используемые Прологом для обозначения вопросов '?-' и правил ':-', также являются атомами. Есть два вида атомов: составленные из букв и цифр и составленные из спецзнаков. Первые, как мы видели в предыдущей главе, должны обычно начинаться со строчной буквы. Атомы, составленные из спецзнаков, как правило, состоят
только из спецзнаков. Иногда возникает необходимость иметь атом, начинающийся с прописной буквы или цифры. Если атом заключается в одиночные кавычки, то его имя может содержать
любые литеры. И наконец, для простоты чтения внутрь атома можно включать специальную литеру – подчеркивание '_'. Ниже приведено несколько атомов:
а
свободный
=
'джордж-смит'
--›
джордж_смит
ieh2304
Следующие объекты не являются атомами:
2304ieh
джордж-смит
Пустой
_ альфа
Другой вид констант, целые числа, используется для представления числовых данных, что позволяет выполнять над ними арифметические операции. В предыдущей главе не обсуждались способы выполнения арифметических операций в Прологе, такие средства будут определены ниже. Целые числа состоят только из цифр и не могут содержать десятичной запятой. В этой книге будут использоваться сравнительно небольшие положительные числа, такие как
0 1 999 512 8192 14765 6224
Пролог реализован на различных ЭВМ и в зависимости от того, на какой именно ЭВМ работает программист, ему может быть разрешено или не разрешено использовать большие или отрицательные числа. Однако в данной книге приводятся только примеры, допустимые для любой из существующих версий Пролога. Можно утверждать, что всегда разрешается использовать числа из диапазона от 0 до 16 383. Возможно, что на доступной читателю ЭВМ допустимы и другие числа (превышающие 16 383 или отрицательные), однако дальнейшее изложение этого не учитывает. Может быть, это покажется удивительным, однако в задачах, в которых оказался полезным Пролог, как правило, не нужны средства для работы с очень большими, дробными или отрицательными числами. Тем не менее, поскольку Пролог является расширяемым языком, программист, обладающий соответствующими ресурсами, может без особого труда добавить к системе предикаты, определяющие такие возможности. Например, некоторые Пролог-системы предоставляют пользователям библиотечные программы, определяющие операции над рациональными числами и числами произвольной точности.
2.1.2. Переменные
Второй разновидностью термов в Прологе являются переменные. Переменные внешне похожи на атомы, за исключением того, что они начинаются с прописной буквы или знака подчеркивания '_'. Переменная служит для представления объекта, на который нельзя сослаться по имени. Здесь можно провести аналогию с использованием местоимений в естественном языке. В приведенных выше примерах фигурировали переменные с такими именами как
X,
Y и
Z. Однако имена могут быть сколь угодно длинными, например:
Ответ
Ввод
Большая_Выплата
_3_слепые_мыши
Иногда возникает необходимость в использовании переменной, имя которой не будет нигде употребляться. Например, если необходимо определить, нравится ли кому-нибудь Джон, и при этом не важно, кому именно он нравится, можно использовать
анонимную переменную.
Анонимная переменная – это одиночный знак подчеркивания '_'. Наш пример с Джоном записывается на Прологе следующим образом:
?- нравится(_,джон).
Если в одно утверждение входят несколько анонимных переменных, их можно интерпретировать неоднозначно. Это характерная особенность, присущая только анонимной переменной. Она позволяет избавить программиста от необходимости придумывать разные имена переменным в тех случаях, когда эти имена в утверждении нигде больше не употребляются.
2.1.3. Структуры
Третьим видом терма, присутствующим в Пролог-программах, является структура. Структура – это единый объект, состоящий из совокупности других объектов, называемых компонентами. Компоненты группируются в структуру для удобства их использования.
В реальной жизни одним из примеров структур является карточка-указатель для библиотечной книги. Карточка-указатель содержит несколько компонент: сведения об авторе, название книги, дату издания, место, где книга хранится в библиотеке, и т. д. Некоторые из компонент в свою очередь тоже можно разбить на компоненты. Например, сведения об авторе состоят из фамилии и инициалов.
Структуры служат средством организации данных в программе, поскольку они позволяют рассматривать как единый объект (карточку-указатель) группу отдельных элементов данных. Способ, которым осуществляется разложение данных на компоненты, зависит от решаемой задачи, В книге будут приведены некоторые рекомендации на этот счет.
Структуры полезны также в тех случаях, когда имеется общий тип и может существовать много конкретных экземпляров объектов этого типа. Например, книги. В главе 1 приводился факт
имеет(джон, книга).
обозначающий, что у Джона есть некоторая конкретная книга. Если затем будет сформулирован факт
имеет(мэри, книга).
то это означает, что у Мэри есть тот же самый объект, что и у Джона, поскольку в обоих фактах фигурирует одно и то же имя. Не существует другого способа указания факта, что объекты различны, кроме присвоения им различных имен. Можно было бы уточнить приведенные факты:
имеет(джон,грозовой_перевал).
имеет(мэри,моби_дик).
явно указав, какие именно книги есть у Джона и Мэри. Однако в больших программах обилие различных констант, смысл которых из контекста не очевиден, может вызвать затруднения. Человек, читающий данную Пролог-программу, может не знать, что константа
грозовой_перевал представляет собой название книги Эмили Бронте, жившей в Йоркшире (Англия) в 19-м веке. Можно было бы, скажем, предположить, что Джон назвал так своего любимого кролика. С помощью структур можно предоставить читателю необходимый контекст.
Структура записывается на Прологе с помощью указания ее
функтора и
компонент. Компоненты заключаются в круглые скобки и разделяются запятыми. Функтор записывается перед открывающей круглой скобкой. Рассмотрим факт, заключающийся в том, что у Джона есть книга с названием «Грозовой перевал», написанная Эмили Бронте:
имеет(джон,книга(грозовой_перевал, бронте)).
Внутри факта
имеет находится структура с именем
книга, имеющая две компоненты: название и автор. Поскольку структура
книга появляется внутри факта как один из его аргументов, она действует как объект, принимая участие в отношении. При желании можно было бы создать еще одну структуру – для идентификации автора, поскольку существовали три писательницы с фамилией Бронте:
имеет(джон,книга(грозовой_перевал, автор(эмили, бронте))).
Структуры с переменными в качестве компонент могут появляться в вопросах. Например, можно было бы спросить, есть ли у Джона какая-либо книга сестер Бронте:
?- имеет(джон,книга(Х,автор(Y, бронте))).
Если будет доказано, что это утверждение согласовано с базой данных, то значением
X будет название книги, а значением
Y – имя автора. В тех случаях, когда переменные в дальнейшем не используются, можно употребить анонимную переменную:
?- имеет(джон, книга(_, автор(_,бронте))).
Напомним, что анонимные переменные не «сцепляются» друг с другом.
Структуру
книга можно было бы еще улучшить, добавив аргумент, указывающий экземпляр книги. Например, третий аргумент, на место которого следует ставить целое число, дал бы нам возможность однозначно идентифицировать книгу:
имеет(джон, книга (улисc, автор(джеймс,джойс), 3129)).
что соответствует следующей фразе на естественном языке:
Джон имеет 3129-й экземпляр книги Джеймса Джойса «Улисс». Если у читателя сложилось впечатление, что синтаксис структур совпадает с синтаксисом фактов, то нам остается только подтвердить его правоту. Предикат (используемый в фактах и правилах) является на самом деле функтором некоторой структуры. Аргументы факта или правила – это компоненты структуры. Представление самих Пролог-программ в виде структур обладает многими достоинствами. Сейчас преждевременно обсуждать эти достоинства, однако читателю все же следует помнить, что все части Пролога, даже сами Пролог-программы, состоят из констант, переменных и структур.
2.2. Литеры
Имена констант и переменных образованы цепочками литер. Хотя для каждого вида имени (атом, целое число, переменная) имеются специальные правила, указывающие, из каких литер оно может составляться, полезно знать, что представляет собой весь набор литер, распознаваемых Прологом. Это связано с тем, что литера сама может рассматриваться как самостоятельный элемент данных. Поскольку мы уже знакомы с целыми числами, можно теперь описать, как литеры представляются небольшими целыми числами. Над литерами чаще всего выполняются операции «ввод» и «вывод». Эти операции будут обсуждаться в
гл. 5.
В Прологе имеются два типа литер:
печатаемые литеры и
непечатаемые литеры. Печатаемые литеры обладают визуальным образом, появляющимся на терминале при выводе. Непечатаемые литеры такого образа не имеют, но при выводе они вызывают выполнение некоторых действий. Этими действиями могут быть пропуск пустого места («печать» пробела), переход на новую строку, подача звукового сигнала. Ниже приведены все печатаемые литеры, которые можно использовать в Пролог-программах.
ABCDEFGHIJKLMNOPQRSTUVWXYZ
abedefghijklmnopqrstuvwxyz
0123456789
!"#$%&'()=–~^|\{}[] _`@ +;*:‹›,.?/
Читатель должен заметить, что данный набор более полон, чем приводившийся в начале главы. Некоторые из этих литер имеют специальное значение. Например, круглые скобки используются для выделения компонент структур. Однако, как мы увидим в последующих главах, любая литера может рассматриваться в Пролог-программе как и информационный элемент данных. Литеры могут печататься, вводиться с клавиатуры, сравниваться и принимать участие в арифметических операциях.
Литеры на самом деле интерпретируются как небольшие целые числа – из диапазона от 0 до 127. Каждой литере поставлено в соответствие некоторое целое число, называемое ее ASCII-кодом. Аббревиатура ASCII расшифровывается следующим образом: American Standard Code for Information Interchange (Американский стандартный код для обмена информацией)
[6]. Этот код широко используется на вычислительных машинах и в языках программирования во всем мире. Таблицу кодов ASCII можно найти почти в любом руководстве по работе на ЭВМ. Коды букв упорядочены в алфавитном порядке, так что выяснение порядка следования литер в алфавите сводится к сравнению их кодов с помощью операторов отношений, описываемых ниже в данной главе. Коды всех печатаемых литер больше 32.
Хотя польза кода ASCII в данный момент может быть для читателя и не очевидной, мы вновь вернемся к этому вопросу в разд. 3.2. и 3.5.
2.3. Операторы
Иногда удобно записывать некоторые функторы как
операторы. Это особая форма синтаксиса, облегчающая чтение соответствующих структур. Например, арифметические операции обычно записываются как операторы. В арифметическом выражении
x+y*z знаки сложения и умножения являются операторами. Если же данное арифметическое выражение записать в обычном для структур виде, то оно будет выглядеть следующим образом:
+(x,*(y,z)). Однако в некоторых случаях операторная форма записи удобнее потому, что мы со школьных лет привыкли использовать ее в арифметических выражениях. Кроме того, структурная форма требует заключения аргументов функтора в круглые скобки, что иногда обременительно.
Важно отметить, что операторы не вызывают выполнения каких-либо арифметических операций. Так, в Прологе
3+4 и
7 означают разные объекты. Терм
3+4 - другой способ записи терма
+(3,4), который является структурой. Позже будет описан способ интерпретации структур как арифметических выражений и вычисления их в соответствии с правилами арифметики.
Для начала необходимо знать, как читать арифметические выражения, содержащие операторы. Это требует знания трех свойств каждого оператора: его
позиции, его
приоритета и его
ассоциативности. В данном разделе будут описаны правила использования операторов Пролога с учетом этих свойств, но пока без излишних подробностей. В Пролог-программе можно определить много различных видов операторов, но мы будем иметь дело только с хорошо знакомыми атомами +, -, * и /.
Синтаксис терма, содержащего операторы, частично зависит от их
позиций. Операторы, подобные знакам сложения (+), вычитания (-), умножения (*) и деления (/), записываются между своими аргументами и называются поэтому
инфиксными операторами. Можно также помещать операторы перед их аргументами. Так, в выражении -
х+у минус перед
х обозначает арифметическую операцию изменения знака. Операторы, записываемые перед своими аргументами, называются
префиксными операторами. Наконец, некоторые операторы могут помещаться после своего аргумента. Например, оператор вычисления факториала, употребляемый математиками, помещается после числа, для которого необходимо вычислить факториал. В математических обозначениях факториал
х записывается как
x!
t где восклицательный знак обозначает операцию вычисления факториала. Операторы, записанные после своих аргументов, называются
постфиксными операторами. Таким образом, позиция оператора указывает его место по отношению к своим аргументам. Все операторы, рассматриваемые в следующем разделе, являются
инфиксными.
Теперь рассмотрим приоритет операторов. Когда нам необходимо проинтерпретировать терм
х+y*z как арифметическое выражение, мы знаем, что для того, чтобы получить правильное значение, нужно сначала перемножить
у и
z, а затем прибавить
х. Этими знаниями мы обязаны школе, где нас научили, что умножения и деления выполняются до сложений и вычитаний; исключениями являются случаи, когда порядок операций задается скобками. С другой стороны, структурная форма
+(x,*(y,z)) явно показывает порядок выполнения операций, поскольку структура с функтором * является аргументом структуры с функтором +. Для того чтобы ЭВМ правильно произвела соответствующие вычисления, необходимо сначала выполнить умножение – тогда в структуре с + будут известны значения аргументов. Таким образом, для использования операторов необходимы правила, указывающие порядок выполнения операций. Именно этой цели служит
приоритет.
Приоритет оператора определяет, какая операция выполняется первой. В Прологе каждый оператор связан со своим
классом приоритета. Класс приоритета представляет собой целое число, величина которого зависит от конкретной версии Пролога. Однако в любой версии оператор с большим приоритетом имеет класс
приоритета, более близкий к 1. Если классы приоритетов принимают значения из диапазона от 1 до 255, то оператор с первым классом приоритета выполняется первым, до выполнения операторов, принадлежащих (например) к классу 129. В Прологе операторы умножения и деления принадлежат к более высокому классу приоритетов, чем сложение и вычитание, поэтому терм
а-b/с эквивалентен терму
-(a,/(b,c)). Точное соответствие между операторами и классами приоритетов в данный момент не существенно, однако желательно запомнить относительный порядок выполнения операций.
Наконец, рассмотрим свойство
ассоциативности операторов. Необходимость знания этого свойства становится очевидной, когда нам требуется определить порядок выполнения операторов с одинаковым приоритетом. Например, какому выражению эквивалентно выражение «8/2/2» – «(8/2)/2» или «8/(2/2)»? В первом случае при интерпретации выражения было бы получено значение 2, во втором 8. Для того чтобы иметь возможность разделить эти два случая, необходимо знать, является ли данный оператор
левоассоциативным или
правоассоциативным. Левоассоциативный оператор должен иметь слева операции
одинакового или
низшего приоритета, а справа – операции
низшего приоритета. Например, все арифметические операции (сложить, вычесть, умножить и поделить) являются левоассоциативными. Это означает, что выражения, подобные «8/4/4», интерпретируются как «(8/4)/4», а выражение «5+8/2/2» эквивалентно «5+((8/2)/2)».
На практике в выражениях, понимание которых затрудняется правилами приоритета и ассоциативности, люди стремятся использовать круглые скобки. В нашей книге этот прием тоже будет использоваться, однако для полного понимания операторов надо знать синтаксические правила.
Напомним, что структура, образованная арифметическими операторами, подобна любой другой структуре. На самом деле никакие арифметические действия не выполняются до тех пор, пока не встретится предикат
'is' (есть), описанный в разд. 2.5.
2.4. Равенство и установление соответствия
В Прологе существует особый предикат
равенство, являющийся инфиксным оператором, обозначаемым литерой '='. Когда делается попытка доказать согласованность с базой данных целевого утверждения
?- X = Y.
(произносится
X равно Y), Пролог пытается
установить соответствие между
X и
Y; целевое утверждение «доказуемо», если такое соответствие имеется. Это действие можно представить себе как
попытку сделать X и Y равными. Предикат равенства является
встроенным, т. е. он уже определен в Пролог-системе. Предикат равенства работает так, словно определен следующий факт: X = X.
Внутри всякого утверждения
X всегда равно
X, и это свойство использовано нами при определении предиката равенства.
При согласовании с базой данных цели вида
X = Y, где
X и
Y – любые термы, в которых могут содержаться неконкретизированные переменные, действуют следующие правила:
• если
X представляет собой неконкретизированную переменную, а переменная
Y конкретизирована (какое именно значение ей дано, неважно), то
X и
Y равны. Кроме того,
X станет конкретизированной – ей будет дано то же значение, что и
Y. Например, следующий вопрос приведет к тому, что
X будет присвоено значение в виде структуры:
ехать(клерк, велосипед):
?- ехать(клерк, велосипед) = X.
• целые числа и атомы всегда равны самим себе. Например, попытки согласовать следующие целевые утверждения дадут результаты, показанные справа:
полицейский = полицейский /* верно */
бумага = карандаш /* ложно */
1066=1066 /* верно */
1206=1583 /* ложно */
• Две структуры равны, если они имеют один и тот же функтор и одинаковое число аргументов, причем все соответствующие аргументы равны. Например, при согласовании следующего целевого утверждения
X будет присвоено конкретное значение
велосипед:
ехать(клерк,велосипед) = ехать(клерк,Х).
Структуры могут быть вложены одна в другую на любую глубину. Если такие вложенные структуры проверяются на равенство, проверка займет больше времени, поскольку необходимо проверить все структуры. Попытка согласовать следующую цель:
a(b,C,d(e,F,g(h,i,J)))=a(B,c,d(E,f,g(H,i,j))).
будет успешной,
а переменные
В,
С,
F,
Е,
J будут конкретизированы, им будут присвоены соответственно значения
b,
с,
f,
e,
j. Что произойдет, если мы попытаемся приравнять две неконкретизированные переменные? Это специальный случай первого из вышеприведенных правил. Так, цель будет согласована и две переменные станут
сцепленными. Если две переменные сцеплены, то при конкретизации одной из них второй переменной будет автоматически присвоено то же самое конкретное значение, что и первой. Таким образом, в следующем правиле второй аргумент будет конкретизирован так же, как первый:
ничего_не_делать(Х,Y):- Х = Y.
Целевое утверждение X=Y всегда верно (т. е. согласуется с базой данных), если один из аргументов неконкретизирован. Более простой способ записи такого правила заключается в использовании того факта, что переменная равна самой себе:
ничего_не_делать(Х,Х).
Пролог предоставляет также предикат '\=' соответствующий
не равно. Целевое утверждение
Х\=Y верно в тех случаях, когда не доказуемо утверждение
X=Y, и наоборот. Таким образом,
Х\=Y означает, что
X не может быть сделано равным Y.
Упражнение 2.1. Скажите, верны ли следующие целевые утверждения, какие переменные будут конкретизированы и какие им будут даны значения:
пилоты(А, Лондон) = пилоты(лондон, париж)
точка(Х,Y,Z) = точка(Х1,Y1,Z1) = слово(буква)
существительное(альфа) = альфа
'викарий' = викарий
f(X,X) = f(a,b)
f(X,a(b,c)) = f(Z,a(Z,c)
2.5. Арифметика
ЭВМ часто используют для выполнения действий над числами. С помощью арифметических операций можно сравнивать числа и проводить вычисления. В данном разделе будут приведены примеры такого использования арифметических операций.
Рассмотрим сначала сравнение чисел. Для двух заданных чисел всегда можно сказать,
равно ли одно число другому,
меньше ли одно число другого,
больше ли одно число другого. Пролог предоставляет некоторые «встроенные» предикаты, позволяющие
сравнивать числа. Для этого могут использоваться обсуждавшиеся в разд. 2.4 предикаты '='и '\='. Их аргументами могут быть конкретизированные переменные, значениями которых являются целые числа, а также целые числа, записанные в виде констант. Существует еще несколько предикатов, позволяющих сравнивать числа. Перечислим здесь все эти предикаты, отметив предварительно, что каждый из них можно использовать в форме инфиксного оператора.
X = Y X и Y представляют одно и то же число
X \= Y X и Y представляют разные числа
X ‹ Y X меньше Y
X › Y X больше Y
X =‹ Y X меньше или равно Y
X ›= Y X больше или равно Y
Отметим, что символ «меньше или равно» записывается не так, как во многих других языках программирования (обычно ‹=). Это сделано в Прологе для того, чтобы программист мог использовать похожий на стрелку атом ‹= для своих собственных нужд.
Поскольку операторы сравнения являются предикатами, можно было бы предположить, что в Прологе допустим следующий факт:
2›3.
утверждающий, что 2 на самом деле больше 3. Факты, подобные этому, с формальной стороны полностью соответствует правилам Пролога. Однако Пролог не разрешает добавлять факты к «встроенным» предикатам. Такая особенность предотвращает непредсказуемые изменения смысла встроенных предикатов. В главе 6 будут описаны все встроенные предикаты, в том числе и те, с которыми мы уже познакомились.
В качестве первого примера использования чисел предположим, что у нас есть база данных, содержащая сведения о принцах, правивших Уэльсом в 9-м и 10-м веках. Предикат
правил(Х,Y,Z) истинен, если принц с именем
X находился у власти с года
Y по год
Z. Список фактов базы данных выглядит следующим образом:
правил(родри,844,878).
правил(анаравд,878,916).
правил(хивел_дда,916,950).
правил(лаго_ад_идвал,950,979).
правил(хивел_аб_иеуаф,979,985).
правил(кадваллон,985,986).
правил(маредудд, 986,999).
Теперь предположим, что мы хотим узнать, кто был на троне Уэльса в каком-то конкретном году. Можно было бы определить правило, аргументами которого являлись бы имя и дата и которое просматривало бы базу данных и сравнивало заданную дату с теми, что указаны в фактах. Давайте определим предикат
принц(X, Y), который истинен, если принц по имени
X был на троне в год
Y:
X был
принцем в год Y, если:
X правил с года А по год В и
Y находится между А и В или совпадает с А или В.
Первое целевое утверждение будет согласовываться с базой данных путем поиска подходящего факта. Второе целевое утверждение верно, если
Y равно
А, или
Y равно
В, или
Y лежит между
А и
В. Для проверки можно использовать утверждения
Y›=А и
Y=‹В. Переписав это на Прологе, получаем следующее правило:
принц (X,Y):-правил(Х,А,В),Y ›= А,Y =‹ В.
Ниже приведено несколько возможных запросов и ответов, даваемых Пролог-системой.
?- принц(кадваллон,986).
да
?- принц(родри,1979).
нет
?- принц(Х,900).
Х = анаравд
да
?- принц(X,979).
X = лаго_ад_идвал
;
X = хивел_аб_иеуаф да
Заметьте использование переменных в последних примерах. Убедитесь, что вы понимаете, как работает механизм поиска Пролога при ответе на подобные вопросы.
Арифметические операции могут также использоваться для вычислений. Например, если имеются сведения о населении и площади некоторой страны, то можно вычислить среднюю плотность населения для этой страны. Средняя плотность населения показывает, сколь тесно было бы в данной стране, если бы ее население было равномерно распределено по всей ее территории.
Рассмотрим следующую базу данных, содержащую сведения о населении и площади некоторых стран в 1976 г. Для представления связи между страной и ее населением будет использоваться предикат
нас. В наши дни население обычно характеризуется довольно большими числами. Не все версии Пролога позволяют работать с такими числами. Поэтому будем исчислять население в миллионах:
нас(Х, Y) означает, что население страны
X составляет примерно «
Y миллионов» людей. Предикат
площадь будет обозначать связь между страной и ее площадью (в миллионах квадратных километров):
нас(сша,203).
нас(индия, 548).
нас(китай,800).
нас(бразилия,108).
площадь(сша,8).
площадь(индия,3).
площадь(китай,9).
площадь(бразилия,8).
Теперь для того, чтобы найти среднюю плотность населения некоторой страны, мы должны использовать правило, гласящее, что значение плотности получается делением числа, представляющего население, на число, представляющее площадь.
Введем предикат
плотность(Х, Y), где X – это страна, a Y – плотность населения в данной стране, и запишем соответствующее правило на Прологе:
плотность(X,Y):-нас(Х,Р), площадь(Х,А), Y is Р/А.
Данное правило читается следующим образом:
Плотность населения страны X представляется числом Y, если:
Население X -
это Р, и Площадь X -
это A, и Y вычисляется делением Р на A.
В правиле используется оператор деления '/' введенный в предыдущем разделе. Операция деления выполняется на самом деле как целочисленное деление, сохраняющее только целую часть результата.
Новым здесь является инфиксный оператор
'is'. Его правый аргумент – терм, интерпретируемый как арифметическое выражение. Для того чтобы выполнить
'is', Пролог сначала вычисляет его правый аргумент в соответствии с правилами арифметики. Результат вычислений проверяется на соответствие с левыми аргументами, чтобы определить, доказуемо ли целевое утверждение. В вышеприведенном примере переменная
Y до исполнения
is не конкретизирована, и она остается в таком состоянии до вычисления выражения. Когда выражение вычислено,
Y принимает значение, равное полученной величине. Это означает, что должны быть известны значения всех переменных, находящихся справа от
is.
Предикат
is нужно использовать каждый раз, когда требуется вычислить арифметическое выражение. Напомним, что конструкции вида
Р/А являются такими же обычными структурами Пролога, как и
автор(эмили,бронте). Но если некоторая структура интерпретируется как арифметическое выражение, то к ней применяется специальная операция, заключающаяся в фактическом выполнении арифметических действий над двоичными представлениями элементов структуры и получении соответствующего результата. Эта операция называется
вычислением арифметического выражения. Не любую структуру можно вычислить как арифметическое выражение. Например, очевидно, что нельзя вычислить структуру
автор, поскольку функтор
автор не определен как арифметическая операция.
Вернемся к примеру со средней плотностью населения. Нетрудно видеть, что типичные вопросы и ответы на них выглядят следующим образом:
?- плотность(китай,X).
X=89
?= плотность(турция,X).
нет
Х=89 в первом вопросе представляет собой ответ Пролог-системы, означающий 89 человек на квадратный километр. Второй запрос не выполним, поскольку в базе данных нашего примера невозможно найти сведения о населении Турции.
Набор допустимых арифметических операций зависит от используемой ЭВМ. Однако все Пролог-системы обеспечивают выполнение следующих операций:
X+Y сумма X и Y
X–Y разность X и Y
X*Y произведение X и Y
X/Y частное от деления X на Y
X mod Y остаток от деления X на Y
Этот список вместе со списком операторов сравнения, приведенным выше, содержит все, что необходимо для решения простых арифметических задач. Поскольку Пролог в основном ориентирован на нечисловые задачи, арифметические возможности не так важны, как в других языках программирования.
2.6. Общая схема согласования целевых утверждений
Для ответа на вопрос, поступивший от программиста, Пролог выполняет решение некоторой задачи. Вопрос содержит
конъюнкцию целевых утверждений, которые необходимо попытаться доказать, т. е. проверить на согласованность с базой данных. Для доказательства целевых утверждений Пролог использует известные
утверждения. Факт может привести к немедленному доказательству (согласованию) целевого утверждения, в то время как правило может только свести данную задачу к конъюнкции предикатов-подцелей. Однако использование некоторого утверждения возможно только, когда оно «подходит» к рассматриваемому целевому утверждению, т. е. соответствует ему (сопоставимо с ним). Если целевое утверждение не доказано, возбуждается
процесс возврата. Процесс возврата заключается в пересмотре проделанной работы и попытках передоказать (вновь согласовать) целевые утверждения путем поиска альтернативных путей доказательства. Более того, если программист неудовлетворен ответом на свой вопрос, он может сам инициировать процесс возврата, нажав на клавиатуре клавишу ';', после того как Пролог информирует его о найденном решении. В данном разделе будут представлены диаграммы, показывающие, как Пролог пытается доказать и передоказать целевые утверждения.
2.6.1. Успешное доказательство конъюнкции целевых утверждений
Пролог пытается согласовать с базой данных входящие в конъюнкцию целевые утверждения в том порядке, в каком они написаны (слева направо), где бы они ни появились – в теле правила или в вопросе. Это означает, что Пролог не будет проверять некоторое утверждение, пока не будет доказан его сосед слева. А сосед справа будет рассматриваться только после доказательства данного целевого утверждения. Рассмотрим следующую простую программу о семейных связях:
родители (С,M,F):- мать(С,М), отец(C,F).
мать(джон,анна).
мать(мэри,анна).
отец(мэри,фред). отец(джон,фред).
Давайте рассмотрим последовательность событий, позволяющую дать ответ на вопрос:
?-женщина(мэри), родители(мэри,М,Р), родители(джон,М,Р).
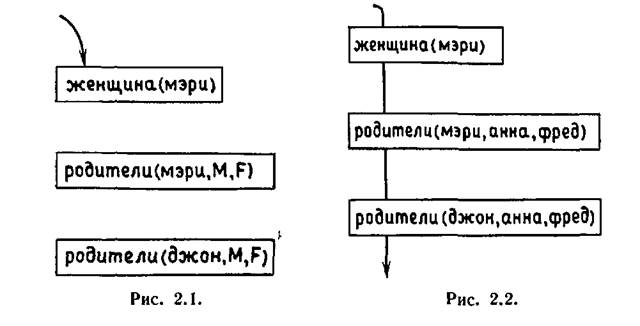
Данный вопрос позволяет определить, является ли
мэри сестрой
джона. Для того чтобы дать ответ Прологу, необходимо согласовать с базой данных последовательность подцелей, приведенных на рис. 2.1.
Представим целевые утверждения в виде прямоугольников, распределенных по странице. Стрелка, начинающаяся в верхней части страницы, указывает, какие целевые утверждения уже согласованы. Прямоугольники, через которые стрелка уже прошла, соответствуют согласованным целевым утверждениям. Прямоугольники, лежащие ниже острия стрелки, соответствуют целевым утверждениям, которые Пролог еще не рассматривал. При выполнении программы стрелка движется вверх и вниз по странице в соответствии с переходом Пролога от одного целевого утверждения к другому. Будем называть ее
цепочкой доказательств. В данном примере стрелка начинается в верхней части страницы, как показано выше. По мере согласования трех целевых утверждений она будет удлиняться вниз, проходя через соответствующие прямоугольники. Конечная ситуация представлена на рис. 2.2. Отметим, что в ходе доказательства согласованности целевых утверждений с базой данных были найдены значения для переменных
М и
F.
Такая диаграмма иллюстрирует общую структуру происходящего, но она не показывает,
как доказывались эти три целевых утверждения. Для того чтобы показать это, поместим внутрь прямоугольников больше информации. Давайте посмотрим, как доказывалось второе целевое утверждение. Доказательство согласованности целевого утверждения с базой данных включает в себя поиск в базе данных
соответствующих (сопоставимых) утверждений, пометку этого места базы данных и затем доказательств возникших подцелей. Этот процесс для второго целевого утверждения можно проиллюстрировать, включив в прямоугольник
родители индикацию выбранного утверждения и возникшие подцели. Выбранное утверждение обозначается числом в скобках, в данном случае
(1). Это число указывает
номер выбранного утверждения в наборе утверждений с соответствующим предикатом. Таким образом, число
1 означает, что было выбрано первое утверждение с данным предикатом. Эта информация достаточна для отметки места в базе данных. Подцели заключены в маленькие прямоугольники, помещенные в прямоугольник данного целевого утверждения. В момент, когда выбрано утверждение
родители, ситуация выглядит так, как показано на рис. 2.3.

Рис. 2.3.
Стрелка вошла в прямоугольник
родители и прошла через скобки, указывая, что выбрано некоторое утверждение. Данное утверждение создало две подцели –
мать и
отец. В данный момент для получения ответа на вопрос необходимо, чтобы стрелка прошла через два маленьких прямоугольника, вышла из прямоугольника
родители и затем прошла через второй прямоугольник
родители. Когда стрелка проходит через маленькие прямоугольники, необходимо выполнить те же самые шаги: выбор соответствующего утверждения и доказательство порождаемых им подцелей. В данном примере для каждого из этих двух целевых утверждений в базе данных находится соответствующий факт, и их согласованность с базой данных доказывается. На рис. 2.4 приведено более детальное изображение ситуации в момент получения ответа на вопрос.

Рис. 2.4.
Отметим, что для полноты картины нам необходимо было бы показать, как доказываются целевые утверждения
женщина(мэри) и
родители(джон,анна,фред). Однако столь подробная диаграмма не поместилась бы на одной странице.
Данный пример иллюстрирует общую схему рассмотрения целевых утверждений, объединенных в конъюнкцию, для случая, когда все цели согласуются с базой данных. Стрелка перемещается вниз по странице, по очереди проходя через прямоугольники. Когда стрелка входит в какой-либо прямоугольник, выбирается некоторое утверждение и отмечается его позиция. Если данное утверждение сопоставимо с целью и является фактом, стрелка может покинуть прямоугольник (такая ситуация имела место для целевых утверждений
мать и
отец). Если же утверждение сопоставимо с целью, но является правилом, создаются прямоугольники для подцелей, и стрелка должна пройти через них, прежде чем она сможет покинуть первоначальный прямоугольник.
2.6.2. Рассмотрение целевых утверждений при использовании механизма возврата
Когда целевое утверждение недоказуемо (проверены все возможные утверждения или пользователь нажал клавишу ';'), «цепочка доказательств» проходит назад тот путь, по которому она пришла в данную точку. Она возвращается в покинутые перед этим прямоугольники для того, чтобы попытаться
передоказать (вновь согласовать) соответствующие целевые утверждения. Когда стрелка возвращается в то место, где было выбрано какое-то утверждение (это событие изображается числом в скобках), Пролог пытается найти альтернативное утверждение, соответствующее данной цели. Сначала делаются неопределенными все переменные, которые были конкретизированы в ходе доказательства данного целевого утверждения. Затем возобновляется поиск в базе данных, начиная с того места, где был оставлен маркер. Если будет найдено другое утверждение, соответствующее целевому, Пролог помечает это место, и дальше события развиваются, как было описано выше в разд. 2.6.1. Отметим, что рассмотрение любых целевых утверждений, находящихся «ниже» данного (даже если они были пройдены в ходе рассмотрения предыдущей альтернативы), всегда начинается с самого начала. Пролог пытается доказать их без учета положения маркера (т. е. это не передоказательство). Если не удается найти другое подходящее утверждение, данное целевое утверждение считается недоказуемым и стрелка продолжает возвращаться назад до следующего маркера. В нашем примере, если целевое утверждение
родители(джон,анна,фред) недоказуемо, стрелка уйдет назад из прямоугольника
родители(джон,анна,фред) и войдет в прямоугольник
родители (мэри,анна,фред) снизу для того, чтобы попытаться передоказать данное целевое утверждение (см. рис. 2.5).

Рис. 2.5.
Отступая дальше, стрелка достигнет места, где было выбрано утверждение, соответствующее целевому утверждению отец. В первую очередь освобождаются все переменные, которые были конкретизированы в результате использования данного утверждения. Это означает, что переменная
F вновь становится неконкретизированной. Затем Пролог просматривает базу данных, начиная с утверждения, следующего за первым утверждением с предикатом
отец (здесь находится маркер), пытаясь найти альтернативное утверждение. Если предположить, что
мэри имеет только одного отца, то этот процесс успехом не завершится. Поэтому стрелка продолжит отступление. Она покинет прямоугольник
отец(мэри, F) (это целевое утверждение недоказуемо) и вернется в прямоугольник
мать(мэри,анна) (для того, чтобы попытаться передоказать данное целевое утверждение) (см. рис. 2.6).

Рис. 2.6.
Отступление стрелки будет продолжаться до успешного доказательства соответствующего целевого утверждения.
Эти примеры иллюстрируют общую схему повторного рассмотрения целевых утверждений в процессе возврата. Когда некоторое целевое утверждение недоказуемо, стрелка возвращается из соответствующего прямоугольника в прямоугольник с предшествующим целевым утверждением. Стрелка отступает до тех пор, пока не встретится маркер. Все переменные, которые были конкретизированы в результате предыдущего выбора сопоставимого утверждения, становятся неконкретизированными. Затем Пролог возобновляет поиск в базе данных сопоставимого утверждения, начиная с маркера. Если сопоставимое утверждение будет найдено, новое место помечается маркером, создаются прямоугольники для целевых подутверждений и стрелка опять начинает движение вниз. В противном случае стрелка продолжает отступать вверх в поисках другого маркера.
2.6.3. Установление соответствия
Правила, определяющие, подходит ли некоторое утверждение для согласования с целевым утверждением, выглядят следующим образом. Отметим, что при выборе утверждения все переменные сначала неконкретизированы.
• Неконкретизированная переменная соответствует любому объекту. Этот объект становится значением переменной.
• Целое число или атом соответствуют только самим себе.
• Между структурами можно установить соответствие, только если они имеют одинаковый функтор, одинаковое число параметров и соответствующие параметры соответствуют друг другу.
Особым случаем является установление соответствия между двумя неконкретизированными переменными. В этом случае мы говорим, что переменные
сцеплены. Две сцепленные переменные обладают следующим свойством: как только одна из них принимает конкретное значение, то же самое конкретное значение принимает и другая.
Если читатель заметил сходство между установлением соответствия и приравниванием аргументов (разд. 2.4), то он совершенно прав. Дело в том, что предикат '=' пытается сделать свои аргументы равными путем установления соответствия между ними.
Попытаемся применить на практике наши знания об операторах, арифметических действиях и установлении соответствия. Предположим, что в базе данных находятся следующие факты:
сумма(5).
сумма(З).
сумма(X+Y).
Рассмотрим вопрос:
?- сумма(2+3).
Какой из вышеприведенных фактов будет соответствовать данному запросу? Если вы думаете, что таковым будет первый факт, вам следует вернуться назад и еще раз прочесть разделы о структурах и операторах. В вопросе аргументом структуры
сумма является
структура с функтором + и компонентами 2 и 3. На самом деле указанной цели соответствует третий факт, при этом переменные
X и
Y принимают конкретные значения 2 и 3.
С другой стороны, если программист действительно хочет вычислить сумму, ему следовало бы воспользоваться предикатом is. Он должен был бы написать
?- X is 2+3.
или (в качестве развлечения) он мог бы определить предикат сложить, связывающий два целых числа и их сумму:
сложить (X, Y, Z):- Z is X+Y.
В этом определении
X и
Y должны быть конкретизированы, а
Z неконкретизирована.
ГЛАВА 3. ИСПОЛЬЗОВАНИЕ СТРУКТУР ДАННЫХ
Оксфордский толковый словарь английского языка определяет слово «рекурсия» следующим образом:
РЕКУРСИЯ. [Теперь употребляется редко, устаревшее.] Обратное движение, возвращение.
Это определение загадочно и, по-видимому, устаревшее. В настоящее время рекурсия является очень популярным и мощным средством в области нечислового программирования. Она используется в двух случаях: для описания структур, имеющих другие структуры в качестве компонент, и для описания программ, выполнению которых предшествует выполнение их собственной копии. Иногда начинающие программисты относятся к рекурсии с подозрением, не понимая, как это можно определить некоторое отношение через само себя? В Прологе рекурсия – это нормальный и естественный способ представления структур данных и программ. Мы надеемся, что тема этой главы – рекурсия – обретает ясность удобным и ненавязчивым образом.
3.1. Структуры и деревья
Чтобы легче было понять сложную структуру, ее обычно представляют в виде
дерева, в котором каждому функтору соответствует вершина, а компонентам соответствуют ветви дерева. Каждая ветвь может указывать на другую структуру, так что мы можем иметь структуры внутри структур. Обычно принято изображать дерево таким образом, чтобы корень дерева находился вверху, а ветви были направлены вниз, как это показано на рис. 3.1. Заметим, что два последних дерева имеют одинаковую форму, хотя корни и листья деревьев различны. Прежде чем читать дальше, вы должны быть уверены в том, что можете представить в виде дерева каждую из структур, с которыми вы уже сталкивались в предыдущих главах.
Предположим, у нас есть предложение «Джону нравится Мэри», и необходимо представить синтаксическую структуру этого предложения. В английском языке имеется очень простое синтаксическое правило построения предложений: предложение состоит из существительного, за которым следует глагольная группа. В свою очередь глагольная группа состоит из глагола и другого существительного. Это отношение между частями предложения может быть описано следующей структурой (которая представлена в виде дерева, приведенного на рис. 3.2):
предложение(существительное, глагольная_группа(глагол, существительное)).
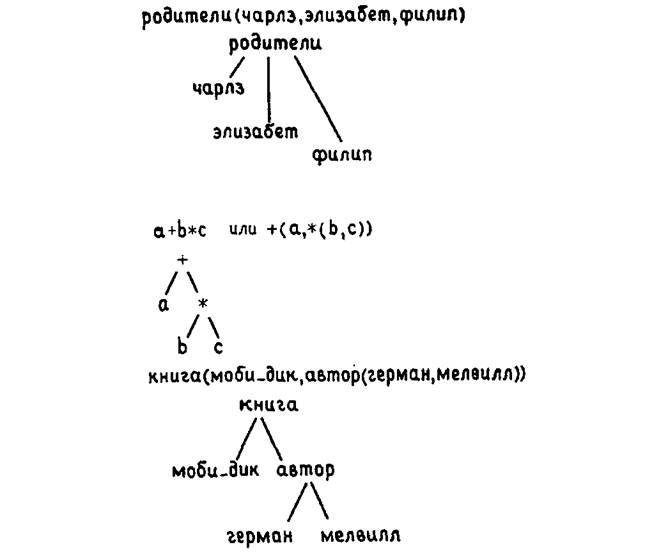
Рис. 3.1.
Если мы возьмем наше предложение («Джону нравится Мэри») и вставим слова из этого предложения в качестве аргументов функторов
существительное и
глагол в структуру предложения, то мы получим (см. рис. 3.3):
предложение(существительное(джон), глагольная_группа(глагол(нравится), существительное(мэри)))
Этот пример показывает, как можно использовать структуры в языке Пролог для представления синтаксиса очень простых предложений. В общем случае если мы знаем, какой частью речи является каждое слово в предложении, то можно записать структуру на Прологе, которая в явном виде описывает отношения между различными словами в предложении. Эта задача сама по себе представляет интересную тему исследования, и далее мы еще вернемся к вопросу о том, как, используя Пролог, заставить ЭВМ «понимать» некоторые простые предложения.
Деревья могут также применяться для графического описания переменных внутри структуры, в частности показывая, как сцеплены переменные, имеющие одинаковые имена (см. рис. 3.4).

Рис. 3.2.

Рис. 3.3.

Рис. 3.4.
3.2. Списки
Список - довольно широко используемая структура данных в области числового программирования. Список -это
упорядоченная последовательность элементов, которая может иметь произвольную длину. Признак
упорядоченный указывает на то, что порядок элементов в последовательности является существенным.
Элементами списка могут быть любые термы – константы, переменные, структуры, которые включают, конечно, и другие списки. Указанные свойства очень полезны в ситуации, когда мы не в состоянии заранее предсказать, насколько большим должен быть список и какую информацию он будет содержать. Более того, списки позволяют представить практически любой тип структуры, который может потребоваться при символьных вычислениях. Списки широко используются для представления деревьев синтаксического разбора, грамматик, карт городов, программ для ЭВМ и математических объектов, таких как графы, формулы и функции. Существует язык программирования – Лисп, в котором единственными доступными структурами данных являются константа и список. Однако в Прологе список – это просто один из частных видов структуры.
Списки могут быть представлены как специального вида дерево. Список – это любой
пустой список, не содержащий ни одного элемента, либо структура, имеющая две компоненты: голову и хвост списка. Конец списка обычно представляют как хвост, который является пустым списком. Пустой список записывают как [] – открывающая квадратная скобка, за которой следует закрывающая квадратная скобка. Голова и хвост списка являются компонентами функтора, обозначаемого точкой '.'. Так, список, состоящий из одного элемента '
а' есть
.(а, []), а его представление в виде дерева имеет вид

Аналогично список, состоящий из атомов
a,
b и
с, мог бы быть записан как
.(а,.(b,.(с,[]))), что изображается следующим образом:

Иногда функтор точка ('.') определяется как оператор, так что допустимо для Пролога два последних списка записать как
а.[] и
а.(b.(с.[]))). Второй список можно было бы записать просто как
а.b.с.[], так как функтор точка – правоассоциативный оператор. Списки являются упорядоченными последовательностями элементов, так что список
а.b отличается от списка
b.а.
Некоторые любят записывать древовидные диаграммы списков в виде дерева, «растущего» слева направо, ветви которого направлены вниз. Приведенный выше список, представленный диаграммой в виде такой «виноградной лозы» выглядит так:
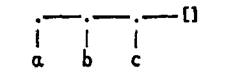
В этой диаграмме компонента функтора '.', соответствующая голове списка, «свисает» вниз, а компонента, соответствующая хвосту списка, «растет» вправо. Конец списка четко выделен тем, что последняя компонента – хвост списка – является пустым списком. Главное преимущество использования диаграммы для представления списка заключается в том, что она может быть записана справа налево на листе бумаги.
«Виноградная» диаграмма может оказаться удобной для записи списков на бумаге, когда нам необходимо видеть структуру списка, но в программах на Прологе для записи списков такие диаграммы не используются. Так как запись сложных списков с помощью функтора '.' часто оказывается неудобной, то в Прологе предусмотрена другая синтаксическая форма, которая может быть использована для записи списков в программе. Это так называемая
скобочная форма записи списка. Она представляет собой заключенную в квадратные скобки последовательность элементов списка, разделенных запятыми. Например, упоминавшиеся выше списки могут быть записаны в скобочной форме в виде
[а] и
[а, b, с]. Списки могут содержать другие списки или переменные. Например, в Прологе допустимы следующие списки:
[]
[конкретный, человек, [любит, ловить, рыбу]]
[а, V1, b, [X, Y]]
Переменные, входящие в списки, ничем не отличаются от переменных в любой другой структуре. Они в любой момент могут быть конкретизированы, так что умелое использование переменных может обеспечить образование «пустых мест» в списке, которые впоследствии могут быть заполнены данными.
Чтобы продемонстрировать структуру списков, содержащих в качестве элементов другие списки, приведем «виноградную» диаграмму для последнего из рассмотренных списков:

Из приведенной диаграммы ясно видно, что каждый ее горизонтальный уровень является списком, состоящим из некоторого числа элементов. Верхний уровень на приведенной диаграмме представляет список, содержащий четыре элемента, один из которых сам является списком. Второй уровень, содержащий два элемента, представляет четвертый элемент списка верхнего уровня. Работа со списками основана на расщеплении их
наголову и
хвост списка. Голова списка – это первый аргумент функтора '.', который используется для конструирования списка. Хвост списка – это второй аргумент функтора '.'. В случае когда для записи списка используется скобочная форма записи, головой списка является первый его элемент. Хвост списка представляет
список, состоящий из всех элементов исходного списка, за исключением первого его элемента. Следующие примеры демонстрируют расщепление списков на голову и хвост:
| Список |
Голова |
Хвост |
| [а, b, с] |
а |
[b, с] |
| [а,] |
а |
[] |
| [] |
|
|
| [[эта, кошка], сидела] |
[эта, кошка] |
[сидела] |
| [эта, [кошка, сидела]] |
эта |
[кошка, сидела]] |
| [эта, [кошка, села], на пол] |
эта |
[кошка, села], на пол] |
| [X+Y, х + y] |
X + Y |
[x + y] |
Заметим, что пустой список не имеет ни головы, ни хвоста. В последнем примере оператор ± используется как функтор для структур
+(Х, Y) и
+(х,у).
Так как операция расщепления списка на голову и хвост очень широко используется, то в Прологе введена специальная форма для представления списка с головой
X и хвостом
Y. Это записывается как
[X|Y], где для разделения
X и
Y используется вертикальная черта. При конкретизации структуры подобного вида
X сопоставляется с головой списка, a
Y – с хвостом списка, как это показано в следующем примере:
p([1, 2, 3]).
p([эта, кошка, сидела, [на, этой, подстилке]]).
?- p([X|Y]).
X = 1 Y=[2,3]
;
X=эта Y=[кошка, сидела, [на, этой, подстилке]]
?- p([_,_,_,[_|X]]).
X=[этой, подстилке]
Ниже приведено еще несколько примеров с использованием различных синтаксических возможностей записи списков, показывающих, каким образом производится сопоставление списков. В этих примерах делается попытка сопоставить два заданных списка, конкретизируя переменные, если это возможно.
| Список 1 |
Список 2 |
Конкретизация |
| [X, Y, Z] |
[джону,нравится,рыба] |
X=джону Y= нравится Z = рыба |
| [кошка] |
[X| Y] |
X= кошка |
| [X, Y | Z] |
[мэри,нравится,вино] |
X = мэри Y = нравится Z = [вино] |
| [[этот, Y]|Z] |
[[X, заяц], [находится, здесь]] |
X = этот Y = заяц Z = [[находится_ здесь]] |
| [X, Y|Z, W] |
(синтаксически некорректная конструкция списка) |
|
| [золотистый | T] |
[золотистый, норфолк] |
T= [норфолк] |
| [лошадь, X] |
[белая, лошадь] |
(сопоставление невозможно) |
| [белая | Q] |
[P | лошадь] |
P = белая Q = лошадь |
Как видно из последнего примера, используя скобочную форму записи списков, можно создавать структуры, похожие на списки, но не заканчивающиеся пустым списком. Одна из таких структур,
[белая|лошадь], обозначает структуру, головой которой является
белая, а хвостом –
лошадь. Константа
лошадь не является ни списком, ни пустым списком, и, как мы увидим далее, обработка таких структур требует большой осторожности, когда они используются в качестве хвоста списка.
Существует еще одна область применения списков – это представление строк литер. Иногда возникает необходимость в использовании строк литер для печати или ввода текста. Если строка литер заключена в двойные кавычки, то эта строка представляется как список кодов, соответствующих литерам строки. Для кодировки литер используется код ASCII, который обсуждался в разд. 2.2. Например, строка
"system" преобразуется в Прологе в следующий список:
[115, 121, 115,
116, 101, 109].
3.3. Принадлежность элементов списку
Предположим, что имеется некоторый список, в котором
X обозначает его голову, a
Y – хвост списка. Напомним, что такой список мы можем записать так:
[X|Y]. Этот список мог бы содержать, например, клички тех лошадей потомков жеребца
Coriander, которые все выиграли скачки в Великобритании в 1927 году:
[curragh_tip, music_star, park_mill, portland]
Теперь предположим, что мы хотим определить, содержится ли некоторая кличка в указанном списке. В Прологе это можно сделать, определив, совпадает ли данная кличка с головой списка.
Если совпадает, то наш список завершается успехом. Если нет, то мы проверяем, есть ли кличка в хвосте исходного списка. Это значит, что снова проверяется голова, но уже
хвоста списка. Затем проверяется голова
очередного хвоста списка. Если мы доходим до конца списка, который будет пустым списком, то наш поиск завершается неудачей: указанной клички в исходном списке нет.
Для того чтобы записать все это на Прологе, сначала надо установить, что между объектом и списком, в который этот объект может входить, существует отношение. Это отношение, называемое отношением принадлежности, представляет достаточно распространенное в повседневной жизни понятие. Так, мы говорим о людях, являющихся членами клубов, и о других тому подобных вещах. Для записи этого отношения мы будем использовать предикат
принадлежит: целевое утверждение
принадлежит(X, Y) является истинным («выполняется»), если терм, связанный с
X, является элементом списка, связанного с
Y. Имеются два условия, которые надо проверить для определения истинности предиката. Первое условие говорит, что
X будет элементом списка
Y, если X совпадает с головой списка
Y. На Прологе этот факт записывается следующим образом:
принадлежит(X,[X |_]).
Эта запись констатирует, что
X является элементом списка, который имеет X в качестве головы. Заметим, что мы использовали анонимную переменную '_' для обозначения хвоста списка. Это сделано потому, что мы никак не используем хвост списка в этом частном факте. Заметим,
что данное правило могло бы быть записано и по-другому:
принадлежит(X,[Y|_]:- X = Y.
К этому моменту вы должны уже понимать, почему можно использовать
X сразу в двух местах в первой, более короткой, версии этого правила.
Второе, и последнее, правило говорит о том, что
X принадлежит списку при условии, что он входит в хвост этого списка, обозначаемый через
Y. И нет лучшего пути, чем использовать тот же самый предикат
принадлежит для того, чтобы определить, принадлежит ли
X хвосту списка! В этом и состоит суть рекурсии. На Прологе это выглядит так:
принадлежит(X,[_ |Y]):- принадлежит(X,Y).
и констатирует, что X
является элементом списка, если X
является элементом хвоста этого списка. Заметим, что мы использовали анонимную переменную '_', так как нас не интересует имя переменной, обозначающей голову списка. Два этих правила в совокупности определяют предикат для отношения принадлежности и указывают Прологу, каким образом просматривать список от начала до конца при поиске некоторого элемента в списке. Наиболее важный момент, о котором следует помнить, встретившись с рекурсивно определенным предикатом, заключается в том, что прежде всего надо найти
граничные условия и способ
использования рекурсии.
Для предиката
принадлежит в действительности имеются два типа граничных условий. Либо объект, который мы ищем, содержится в списке, либо он не содержится в нем. Первое граничное условие для предиката
принадлежит распознается первым утверждением, которое приведет к прекращению поиска в списке, если первый аргумент предиката
принадлежит совпадает с головой списка, соответствующего второму аргументу. Второе граничное условие встречается, когда второй аргумент предиката
принадлежит является пустым списком.
Как мы можем убедиться в том, что граничные условия будут когда-либо удовлетворены? Для этого необходимо обратить внимание на то, как используется рекурсия во втором правиле для предиката
принадлежит. Заметим, что каждый раз, когда при поиске соответствия для целевого предиката
принадлежит происходит рекурсивное обращение к тому же предикату, новая цель формируется для
более короткого списка. Хвост списка всегда является более коротким списком, чем исходный список. Очевидно, что рано или поздно произойдет одно из двух событий: либо произойдет сопоставление с первым правилом для
принадлежит, либо в качестве второго аргумента
принадлежит будет задан список длины 0, т. е. пустой список. Как только возникнет одна из этих ситуаций, прекратится рекуррентное порождение целей для предиката
принадлежит. Первое граничное условие распознается фактом, который не вызывает порождения новых подцелей. Второе граничное условие не распознается ни одним из утверждений для
принадлежит, так что процесс поиска сопоставимого элемента списка для целевого утверждения принадлежит закончится неудачей. Это демонстрирует следующий пример на Прологе:
принадлежит(Х, [X | _]).
принадлежит(Х,[_|Y]):- принадлежит (X,Y).
?- принадлежит(d,[a,b,с,d,e,f,g]).
да
?- принадлежит(2,[3,a,4,f]).
нет
Предположим, мы введем вопрос
?- принадлежит(clugatе,[curraugh_tiр,music_star,раrk_mill, ortland]).
Так как
clygate не сопоставимо с
curragh_tip, то происходит сопоставление со вторым правилом для
принадлежит. Переменная Y получает значение
[music_star, park_mill, portland], и порождается следующая цель: определить, принадлежит ли
clygate этому списку. Опять происходит сопоставление со вторым правилом, и снова выделяется хвост списка. Текущей целью становится
принадлежит (clugate,[park_mill,portland]) Этот процесс рекурсивно повторяется до тех пор, пока мы не доберемся до цели, у которой
X есть
clygate, a
Y есть
[portland]. Происходит еще одно сопоставление со вторым правилом, и теперь
Y конкретизируется хвостом списка
[portland], который является пустым списком. Следующей целью становится
принадлежит(clygate,[]). Ни одно из правил в базе данных не сопоставимо с этой целью, так что цель оказывается ложной и ответ на вопрос будет отрицательным.
Важно помнить, что каждый раз, когда при согласовании
принадлежит с базой данных выбирается второе утверждение этого предиката, Пролог рассматривает рекурсивное обращение к предикату
принадлежит как попытку найти соответствие для некоторой новой его «копии». Это предотвращает путаницу переменных, соответствующих одному употреблению утверждения, с переменными, соответствующими другому употреблению этого же утверждения.
Предикат отношения принадлежности настолько полезен, что мы еще неоднократно будем использовать его в оставшейся части этой книги. Предикат
принадлежит важен еще и потому, что он представляет практически наименьший полезный пример рекурсивного предиката – определение предиката
принадлежит содержит утверждения, которые могут быть проверены с помощью только того же самого предиката
принадлежит. Рекурсивные определения часто встречаются в программах на Прологе, и они полностью равноправны с другими определениями. Однако надо быть осторожным, чтобы не допускать «закольцованные» определения, как, например, следующее:
родитель(X,Y):- ребенок(Y,X).
ребенок(A,B):- родитель(B,A).
В этом примере, чтобы согласовать с базой данных целевое утверждение
родитель, необходимо согласовать подцель
ребенок. Однако определение для ребенок приведет к появлению единственной подцели –
родитель. Вы должны понимать, почему вопрос, содержащий в качестве целей
родитель или
ребенок, приводит к циклу, находясь в котором Пролог не сможет найти какие-либо новые факты, и этот цикл никогда не завершится.
Одна важная проблема, на которую следует обращать внимание в рекурсивных определениях, - это
левосторонняя рекурсия. Она возникает в случае, когда правило порождает подцель, по существу эквивалентную исходной цели, которая явилась причиной использования этого правила. Так, если бы мы определили предикат
человек(X):- человек(Y), мать(Х,Y).
человек(адам).
и ввели вопрос
?- человек(X).
то Пролог сначала использовал бы правило и рекурсивно породил подцель
человек (Y). Попытка найти соответствие этой цели вновь привела бы к выбору первого правила и породила бы еще одну новую эквивалентную подцель. И так далее, до тех пор, пока не исчерпались бы вычислительные ресурсы. Конечно, если бы была возможность использовать механизм возврата, то был бы найден сообщенный в определении факт об Адаме и началось бы порождение решений
[7]. Ошибка заключается в том, что для того, чтобы начался возврат, Пролог должен потерпеть неудачу при проверке первого утверждения. В данном же случае поиск решения оказывается неопределенно длинным, и нет никакой возможности завершить этот поиск с успехом либо с неудачей. Из всего сказанного выше можно извлечь следующую мораль:
Не следует предполагать, что только потому, что вы предоставили все относящиеся к делу факты и правила, Пролог всегда найдет их. Создавая программу на Прологе, вы все время должны представлять, каким образом Пролог осуществляет поиск в базе данных и какие переменные будут конкретизированы, когда будет использовано одно из ваших правил.
Для приведенного примера имеется простой способ устранения ошибки – поместить факт перед правилом, а не после него. В действительности существует хороший эвристический принцип: помещать, где это возможно, факты перед правилами. Иногда при размещении правил в некотором конкретном порядке может возникнуть ситуация, когда они будут правильно работать для целей одного вида и не будут работать для целей другого вида. Рассмотрим следующее определение предиката
список (X), при котором предикат
список является истинным, если
X – список, последний элемент которого имеет в качестве хвоста пустой список:
список([A|B]):- список(B).
список([]).
Если мы используем эти правила для получения ответов на вопросы, подобные следующим:
?- список ([a,b,c,d]).
?- список([]).
?- список(f(1,2,3))
то данное определение будет работать хорошо. Но если мы сделаем запрос
?- список(X).
то программа зациклится. Предикат, аналогичный предикату
список, но неподверженный зацикливанию, задается следующими двумя фактами:
обобщенный_список([]).
обобщенный_список([_ |_]).
В этом варианте просто проверяется начало списка, а не тот факт, что последний хвост списка является пустым списком ([]). Последнее определение не является таким же строгим тестом правильности списка, как определение предиката
список, но оно не приведет к зацикливанию, если аргументом является переменная.
3.4. Пример: преобразование предложений
Рассмотрим программу на Прологе, которая в ответ на введенное с терминала предложение (на английском языке) печатает другое предложение, представляющее преобразованное исходное предложение. Эта программа для «ответов» программисту могла бы поддерживать следующий диалог:
Вы: you are a computer (Вы - ЭВМ)
Пролог: i am not a computer (Я – не ЭВМ)
Вы: do you speak french (Вы говорите по-французски?)
Пролог: no i speak german (Нет, я говорю по-немецки)
Хотя этот диалог может показаться натянутой, но все же осмысленной беседой, очень легко написать программу, выполняющую свою «часть» диалога. Для этого достаточно просто последовательно выполнять следующие действия:
1. Ввести предложение, набранное пользователем на терминале.
2. Заменить каждое вхождение слова
you на слово
i.
3. Аналогичным образом заменить
are на
am not.
4. Заменить
french на
german.
5. Заменить
do на
nо.
Если применить данную схему преобразования
к надлежащим образом подобранным предложениям, подобным использованным в приведенном выше диалоге, то получим осмысленные преобразованные предложения. Однако эта схема применима не ко всем предложениям. Например;
Вы: i do like you (я действительно люблю вас)
Пролог: i no like i (я не люблю себя)
Но если простая программа уже написана, то впоследствии ее можно модифицировать так, чтобы она справлялась и с предложениями, подобными приведенному.
Программа на Прологе, преобразующая одно предложение английского языка в другое, может быть реализована следующим образом. Прежде всего необходимо осознать, что имеется отношение между исходным предложением и преобразованным. В связи с этим нам следует определить предикат, называемый
преобразовать. Преобразовать(Х, Y) означает, что предложение
X может быть преобразовано в предложение
Y. Предложения
X и
Y удобно представлять в виде списков атомов, обозначающих слова, так что предложения могут быть записаны следующим образом:
[this,is,a,
sentence] (это некоторое предложение). Определив предикат
преобразовать, мы могли бы обращаться к Прологу с вопросами вида
?- преобразовать([dо,you,know,french],X). (Знаете ли вы французский)
на что Пролог отвечал бы
X=[no,i,know,german] (нет, я знаю немецкий).
Не следует обращать внимание на то, что вводимое и печатаемое в ответ предложения представлены в такой неестественной форме и не похожи на обычные предложения. В последующих главах мы обсудим способы ввода и вывода структур в виде, удобном для чтения. В данный момент нас интересуют лишь способы преобразования одного списка в другой.
Так как аргументами предиката
преобразовать являются списки, то прежде всего следует рассмотреть, что произойдет, если исходный список пустой. В этом случае мы скажем, что пустой список преобразуется в пустой список:
преобразовать([], [])
Или, иначе:
это факт, что преобразование пустого списка дает пустой список. Если причины для того, чтобы рассматривать пустой список, здесь не очевидны, то последующее изложение прояснит их. Далее нам следует разобраться в том, что основные действия предиката
преобразовать заключаются в следующем:
1. Заменить голову входного списка соответствующим словом и поместить это слово в выходной список в качестве головы.
2. Преобразовать хвост входного списка и сделать его хвостом выходного списка.
3. Если мы достигли конца входного списка, то к выходному списку больше ничего добавлять не надо, и мы можем завершить выходной список пустым списком [].
Переводя это на язык, более близкий к Прологу, можно сказать:
Преобразование списка с головой H и хвостом T дает список с головой X и хвостом Y,
если замена слова H дает слово X,
а преобразование списка T дает список Y.
Теперь следует сказать, что значит «заменить» одно слово на другое. Это может быть сделано при наличии в базе данных фактов вида
заменить(Х, Y), означающих, что слово
X может быть заменено словом
Y. В конце базы данных следует поместить факт-«ловушку», так как если слово не заменяется другим словом, то его следует заменить самим собой. Если сейчас не совсем понятно назначение «ловушки», то позднее, когда мы объясним, как работает программа, это должно стать ясным.
Роль такого факта-ловушки выполняет факт
заменить(Х,Х), который обозначает, что слово
X заменяется самим собой. Ниже приведена база данных, обеспечивающая указанные выше замены слов:
заменить(уоu,i).
заменить(аrе, [am,not]).
заменить(french,german).
заменить(dо,nо)
заменить(Х,Х). /* это факт-ловушка */
Заметим, что фраза
«am not» представлена как список, так что она входит в факт как один аргумент.
Теперь можно перевести приведенный выше текст на псевдо-Прологе в настоящую программу на Прологе, помня, что запись
[А|В] обозначает список, имеющий голову А и хвост В. Мы получаем нечто подобное следующему:
преобразовать([],[]).
преобразовать([Н|T],[X|Y]):-заменить(Н, X), преобразовать(Т,Y).
Первое утверждение в приведенной процедуре проверяет, является ли аргумент пустым списком. Оно же проверяет окончание списка. Как? Рассмотрим это на примере:
?- преобразовать([уоu,are,a,computer],Z).
Этот вопрос был бы сопоставлен с основным правилом для
преобразовать, при этом переменная
Н получила бы значение
you, а переменная
Т – значение
[are,a,computer]. Затем была бы рассмотрена подцель заменить
(you,Х), найден подходящий факт и переменная
X стала бы равной
i. Так как
X является головой выходного списка (в целевом утверждении преобразовать), то первое слово в выходном списке есть
i. Далее, поиск соответствия для подцели преобразовать
([are, a, computer], Y) привел бы к использованию того же правила. Слово are в соответствии с имеющейся базой данных заменяется на список
[am,not], и генерируется другая подцель с предикатом
преобразовать –
преобразовать([а,computer], Y). Ищется факт
заменить(а,X), но так как в базе данных нет факта заменить, первый аргумент которого равен а, то будет найден факт-ловушка, расположенный в конце базы данных, заменяющий '
а' на '
а'. Правило преобразовать вызывается еще раз с
computer в качестве головы входного списка и
пустым списком [] в качестве хвоста входного списка. Как и ранее,
заменить(computer, X) сопоставляется с фактом-ловушкой. Наконец, преобразовать вызывается с пустым списком на месте первого аргумента, и происходит сопоставление с первым утверждением предиката преобразовать. Результатом является пустой список, который заканчивает преобразованное предложение (напомним, что список заканчивается пустым хвостом). В заключение Пролог отвечает на вопрос, печатая
Z = [i,[am,not], a, computer]
Отметим, что фраза
[am,not] появляется в списке точно в таком же виде, как она была в него вставлена.
Теперь должны быть ясны причины появления в базе данных факта
преобразовать ([],[]) и факта-ловушки заменить
(Х,Х). Факты, подобные этим, часто включаются в программу, когда требуется проверить выполнение граничных условий. Из приведенного выше объяснения должно быть ясно, что выход на граничные условия происходит в случае, когда входной список становится пустым и когда оказываются просмотренными все факты для предиката
заменить. В обоих случаях выхода на граничные условия необходимо выполнить определенные действия. В случае когда входной список становится пустым, необходимо завершить выходной список (вставив пустой список в его конец). Если просмотрены все факты для предиката
заменить, но при этом не обнаружен факт, содержащий данное слово, то это слово должно остаться неизменным (путем замены его самим собой).
3.5. Пример: упорядочение по алфавиту
Как мы видели в гл. 2, в Прологе существуют предикаты для сравнения целых чисел. В приложениях, имеющих дело со словами, например работа со словарями, полезно иметь предикат для сравнения
слов в соответствии с алфавитным порядком.
Рассмотрим предикат, который мы назовем
меньше. Если предикат
меньше(Х, Y) используется в качестве целевого утверждения, то он истинен (т. е. согласуется с базой данных), если X и Y обозначают атомы и X по алфавиту предшествует Y. Так, предикат
меньше(арбуз, букварь) истинен, а
меньше(ветер,автомобиль) ложен. Точно так же должен быть ложен и предикат
меньше(картина,картина). Сравнивая два слова, мы сравниваем их последовательно, буква за буквой и при сравнении каждой буквы определяем, какое из следующих условий имеет место:
1. Достигнут конец первого слова, но не достигнут конец второго слова. Это имеет место, например, в случае
меньше(пар, паровоз). При возникновении такой ситуации предикат
меньше должен считаться истинным (т. е. согласованным с базой данных).
2. Очередная литера в первом слове предшествует в алфавите соответствующей литере во втором слове. Например,
меньше (слово,слон). Буква '
в' в слове
слово предшествует в алфавите букве '
н' в слове
слон. В этом случае предикат
меньше истинен.
3. Литера в первом слове совпадает с соответствующей литерой во втором слове. В этом случае следует использовать предикат
меньше для сравнения
оставшихся литер в обоих словах. Например, если дано
меньше(облако,одеяло), то, так как оба аргумента начинаются с буквы '
о', необходимо взять в качестве следующей цели
меньше(блако,деяло).
4. Одновременно достигнут конец первого и второго слов, как, например, в случае
меньше(яблоко,яблоко). При возникновении такого условия предикат
меньше должен быть ложным, так как оба слова являются одинаковыми.
5. Обработаны все литеры второго слова, но еще остались литеры в первом слове, как, например, в случае
меньше(алфавитный,алфавит). В такой ситуации предикат
меньше должен быть ложным.
После того как сформулированы перечисленные выше условия, задача перевода их на Пролог является довольно простой. Будем представлять слова в виде списков литер (целых чисел из некоторого диапазона). Для этого необходим способ преобразования атома в список литер. Эту функцию выполняет встроенный предикат Пролога
name(имя). Целевое утверждение
name(X, Y) согласуется с базой данных, когда атом, являющийся значением
X, состоит из литер, коды которых образуют список, являющийся значением
Y (используются коды ASCII). Отсылаем читателя к гл. 2, если он забыл, что такое коды ASCII. Если один из аргументов не определен, то Пролог предпримет попытку конкретизировать его, создавая соответствующую структуру. Поэтому можно использовать предикат
name для преобразования слова в список литер. Например, зная, что код ASCII для
'а' есть 97, код для
'l' – 108 и код для
'p' – 112, можно задавать следующие вопросы:
?- name (Х,[97,108,112])
Х=аlр
?- name (alp,X)
X=[97,108,112]
Первым утверждением в определении предиката
меньше является следующее правило:
меньше(Х, Y):- name(X,L),name(Y,M), меньше_l(L,M)
Это правило сначала преобразует слова в списки, используя предикат
name, и затем с помощью предиката
меньше_1 (будет определен ниже) сравнивает списки на соответствие алфавиту. Определение предиката
меньше_1 состоит из утверждений, реализующих приведенный выше набор условий. Первое условие является истинным, когда первый аргумент есть пустой список, а второй аргумент – это произвольный непустой список:
меньше_1([], [_|_]).
Второе условие записывается следующим образом:
меньше_1([X|_],[Y|_]):- X‹Y
Напомним, что аргументами предиката
меньше_1 являются списки чисел, так что разрешается сравнивать элементы этих списков, используя предикат '‹'. Третье условие записывается следующим образом:
меньше_1([А|Х],[В|Y]:- А=В, меньше_1(Х,Y).
Наконец, два последних условия описывают ситуации, когда предикат ложен, т. е. не согласуется с базой данных, так что если мы не предусмотрим никаких соответствующих им фактов или правил, то при используемом механизме поиска в базе данных доказательство согласованности любого целевого утверждения, для которого эти условия справедливы, закончится неудачей. Собирая все правила вместе, получим
меньше(Х,Y):- name(X,L), name(Y,M), меньше _1(L,M).
меньше_1([], [_|_]).
меньше_1([X|_],[Y|_]):- Х‹Y.
меньше_1([P|Q], [R|S]):- P = R, меньше_1(Q,S).
Заметим, что третье правило для
меньше_1 можно было бы записать более естественно так:
меньше_1([H|Q], [H|S]):- меньше_l(Q,S).
Упражнение 3.1. Подумайте, какое еще утверждение необходимо добавить к этому определению так, чтобы предикат был истинен и в том случае, когда два слова совпадают. В результате получится предикат, проверяющий, меньше или равен первый аргумент второму по алфавиту. Указание: обратите внимание на условие (4), приведенное выше, и вставьте утверждение, обрабатывающее это условие.
Упражнение 3.2. Почему в первом утверждении для предиката
меньше_1 в качестве второго аргумента использован список [_|_]? Почему недостаточно использовать список [.]?
3.6. Использование предиката присоединить и спецификация деталей
Предикат
присоединить, обрабатывающий списки, используется для создания нового списка, являющегося результатом соединения двух других списков. Например, верен следующей факт:
присоединить([а,b,с], [3,2,1], [а,b,с,3,2,1]).
Предикат
присоединить наиболее часто используется для создания нового списка в результате конкатенации двух других списков, как в следующем примере:
?- присоединить ([alpha,beta],[gamma,delta],X).
X=[alpha, beta, gamma, delta]
Но он может также использоваться и другим способом;
?- присоединить(Х,[b,c,d],[a,b,c,d]). Х=[а]
Предикат
присоединить имеет следующее определение;
присоединить([],L,L).
присоединить([Х|L1],L2,[Х|L3]):- присоединить (L1,L2,L3).
Выход на граничное условие происходит, когда первый аргумент является пустым списком. Любой список, присоединенный к пустому списку, дает тот же самый список. Во всех других случаях будет выполняться второе правило, смысл которого можно описать словами следующим образом:
1. Первый элемент первого списка
(X) всегда будет и первым элементом третьего списка.
2. Хвост третьего аргумента
(L3) всегда будет представлять результат присоединения второго аргумента
(L2) к хвосту первого списка
(L1).
3. Для присоединения одного списка к другому, о чем шла речь в пункте 2, необходимо использовать предикат
присоединить.
4. Так как при каждом обращении к правилу удаляется голова списка, являющегося первым аргументом, то постепенно этот список будет исчерпан и станет пустым, так что произойдет выход на граничное условие.
В дальнейших примерах будут встречаться ссылки на предикат
присоединить с необходимыми дополнительными пояснениями. В последующих главах мы обсудим различные свойства и применения этого предиката. Но сначала давайте применим его в другом простом примере рекурсии.
Предположим, что мы работаем на заводе, выпускающем велосипеды, и нам необходимо хранить спецификацию деталей велосипеда. Для того чтобы собрать велосипед, надо знать, какие детали заказать поставщикам. Каждая деталь велосипеда может состоять из более мелких элементов – поддеталей, например каждое колесо имеет спицы, обод и ступицу. Более того, ступица может состоять из оси и шестеренок. Давайте рассмотрим базу данных, организованную в виде дерева, которая позволит нам делать запросы о деталях, необходимых для изготовления некоторой части велосипеда. В одной из следующих глав предложенная здесь программа будет улучшена, с тем чтобы позволить вычислять, сколько экземпляров каждой детали нам потребуется.
Имеются два типа объектов, которые используются для изготовления велосипеда. Это
узлы и
детали. Каждый узел состоит из некоторого числа деталей, подобно тому как колесо состоит из спиц, обода и ступицы. Детали не имеют еще более мелких частей – они просто соединяются друг с другом, образуя узлы.
Можно представить детали как факты следующим образом:
деталь(обод). деталь(спица).
деталь(задняя_рама). деталь(руль).
деталь(шестерни). деталь(болт).
деталь(гайка). деталь(вилка).
Естественно, что это далеко не полный список деталей, необходимых для сборки велосипеда, но приведенные факты показывают основную идею. Узел может быть представлен именем узла, за которым следует список входящих в него деталей с указанием их количества. Например, следующий факт означает, что
велосипед - это узел, состоящий из двух колес и рамы:
узел(велосипед, [колесо, колесо, рама]).
Ниже представлена база данных узлов, необходимых для нашего упрощенного велосипеда:
узел(велосипед, [колесо,колесо,рама]).
узел(колесо, [спица,обод,ступица]).
узел(рама, [задняя_рама, передняя_рама]).
узел(передняя_рама, [вилка,руль]).
узел(ступица, [шестерни,ось]).
узел(ось, [болт,гайка]).
Заметим, что это частное множество утверждений неполностью описывает велосипед. Мы не делаем различия между передней и задней ступицами – обе имеют шестерни! Цепь и педали отсутствуют, и негде сидеть велосипедисту. Не указано также, как соединять детали друг с другом. Это просто перечисление некоторого числа требуемых деталей.
Теперь мы готовы написать программу, которая для заданной части перечислит все детали, необходимые для ее сборки. Если часть, которую мы хотим собрать, является деталью, то для нее ничего больше не требуется. Однако если мы хотим собрать некоторый узел, то необходимо применить этот процесс к каждой составной части узла. Определим предикат
часть (X, Y), где
X - имя части, a
Y – список деталей, необходимых для ее сборки. В первой версии программы мы не будем рассматривать вопрос о количестве деталей каждого типа, необходимых для сборки. Более полная программа будет представлена в гл. 7.
Выход на граничное условие происходит, когда
X является деталью. В этом случае
X просто возвращается в качестве элементарного списка:
часть(Х, [X]):- деталь(Х).
Следующее условие связано со случаем, когда
X является узлом. Здесь необходимо определить, имеется ли в базе данных соответствующий факт узел, и если такой имеется, то применить предикат
часть к каждому элементу списка подчастей. Для выполнения второй из указанных задач используется предикат, названный
список_частей.
часть(Х,Р):- узел(Х,Подчасти),
список_чаcтей(Подчасти, Р).
Предикат
список_частей берет список частей (из второго аргумента факта узел, представленного выше) и применяет предикат
часть к каждой части в списке. После вызова самого себя, необходимого для обработки хвоста списка, предикат
список_частей должен склеить полученные списки вместе, используя предикат
присоединить:
список_частей([Р|Хвост], Полный_список):- часть(Р,Части_головы)
список_частей(Хвост,Части_хвоста)
присоединить(Части_головы, Части_хвоста, Полный_список)
Список, созданный предикатом
часть, не будет содержать информации о требуемом количестве деталей, при этом элементы списка могут дублироваться. В гл. 7 будет представлена улучшенная версия программы, в которой эти недостатки отсутствуют.
Существуют две идеи, указывающие, как использовать предикат
часть для генерации предложений на английском языке. Во-первых, предложения могут быть представлены в виде иерархических структур: предложение имеет части
группа_существительного и
группа_глагола;
группа_существительного состоит из
определения и
существительного и т. д. Так что любая простая грамматика может быть выражена на языке «частей». Во-вторых, предикат
список_частей всегда обрабатывает элементы списка, представленного его первым аргументом, в порядке слева направо, и его результат (второй аргумент) накапливается в том же порядке. Два указанных свойства предиката
часть показывают, что можно использовать тот же метод для генерации предложений по некоторой грамматике. Типичный «узел» в этой грамматике мог бы выглядеть так:
узел(предложение,[группа_существительного,группа_глагола]).
узел(группа_существительного,[определение,существительное]).
узел(определение,[thе]).
узел(существительное, [clergyman]).
узел(существительное,[motorcar]).
А слова используемой лексики были бы определены как «детали»:
деталь(сlеrgуmаn).
деталь(motorcar)
Теперь у вас может возникнуть желание поэкспериментировать с таким подходом к генерации предложений. Для этого необходимо составить разумную грамматику и словарь. Убедитесь сами, что измененная таким образом программа будет выдавать все допускаемые грамматикой предложения, которые можно построить по заданным грамматике и словарю. Всякий раз, выдав очередное предложение, Пролог будет ожидать, когда вы введете точку с запятой, указывающую ему, что необходимо выполнить возврат для получения следующего предложения.
На приведенном здесь примере не заканчивается обсуждение проблемы обработки текстов на естественном языке в этой книге. Глава 9 полностью посвящена более детальному рассмотрению такого применения Пролога.
ГЛАВА 4. ВОЗВРАТ И ОТСЕЧЕНИЕ
Давайте подытожим всю информацию, которую мы почерпнули в гл. 1 и 2 о том, что может произойти с целевым утверждением (целью).
1. Может иметь место попытка
доказать согласованность целевого утверждения с базой данных. В процессе доказательства база данных просматривается, начиная с ее вершины. При этом возможны две ситуации:
(а) Может быть найден факт (или заголовок правила), сопоставимый с целевым утверждением. В этом случае мы говорим, что произошло
сопоставление цели с утверждением (фактом или правилом) в базе данных. Это место отличается в базе данных маркером и конкретизируются (присваиваются значения) соответствующие переменные, если они не были конкретизированы ранее. Если произошло сопоставление с правилом, то прежде всего необходимо попытаться доказать согласованность подцелей, вводимых этим правилом. Если цель согласуется с базой данных, то предпринимается попытка согласовать следующее целевое утверждение. В используемых нами диаграммах это будет цель, указанная в следующем, нижнем прямоугольнике, на который указывает стрелка. Если исходная цель входит в конъюнкцию, то это будет цель, расположенная в программе
непосредственно справа от исходной цели.
(б) В базе данных нет факта (или заголовка правила), сопоставимого с целевым утверждением. В этом случае мы говорим, что попытка доказать согласованность целевого утверждения потерпела
неудачу (цель не согласуется с базой данных). Тогда будет предпринята попытка (см. п.2)
вновь доказать согласованность целевого утверждения, указанного в прямоугольнике, расположенном выше стрелки. Если исходное целевое утверждение входит в конъюнкцию, то это будет целевое утверждение, расположенное в программе непосредственно слева от рассматривавшегося целевого утверждения.
2. Мы можем сделать попытку
вновь доказать согласованность целевого утверждения с базой данных. Для этого прежде всего необходимо попытаться вновь согласовать каждую из его подцелей, при этом стрелка возвращается в некоторую исходную позицию, поднимаясь вверх по странице. Если ни одна из подцелей вновь не может быть согласована каким-либо подходящим образом, делается попытка найти альтернативное утверждение для самой исходной цели. В этом случае необходимо вернуть в исходное (неопределенное) состояние каждую переменную, конкретизированную при выборе предыдущего утверждения. Эти действия мы называем «уничтожением» результатов, полученных ранее при доказательстве согласованности целевого утверждения. Затем возобновляется просмотр базы данных, но начинается этот просмотр с места, отмеченного маркером данной цели. Как и ранее, эта новая цель, выбранная при возврате, может оказаться либо согласованной, либо несогласованной с базой данных. При этом будет иметь место либо шаг (а), либо шаг (б).
В этой главе процесс возврата будет рассмотрен более подробно. Кроме того, будет рассмотрен специальный механизм – «отсечение», который может быть использован в программах на Прологе. Отсечение позволяет указывать, какие из ранее сделанных выборов альтернатив не следует более пересматривать.
4.1. Порождение множественных решений
Простейшая ситуация, в которой некоторое множество фактов допускает несколько ответов на вопрос, возникает, когда в этом множестве имеется несколько фактов, сопоставимых с вопросом. Например, имеются следующие факты:
отец(мэри, джордж).
отец(джон, джордж).
отец(сью,гарри).
отец(джордж,эдуард).
в которых
отец(X, Y) обозначает, что
Y является отцом
X. Вопрос
?- отец(X,Y).
имеет несколько возможных ответов. Если мы будем вводить после каждого ответа точку с запятой, то Пролог выдаст следующие ответы:
X = мэри, Y = джордж;
X = джон, Y = джордж;
X = сью, Y = гарри;
X = джордж, Y = эдуард.
Пролог найдет эти ответы, просматривая базу данных в поисках фактов и правил с предикатом
отец и печатая их в том порядке, в каком они представлены в базе данных. При этом Пролог не проявляет особого «интеллекта» – он ничего не помнит о предыдущих ответах. Так, если мы обратимся с вопросом
?- отец(_,X).
(для каких X верно то, что X является отцом), то мы получим
Х=джордж;
Х=джордж;
Х=гарри;
Х=эдуард.
при этом ответ
джордж повторен дважды, так как Джордж является отцом как Мэри, так и Джона. Если Пролог может сделать одно и то же двумя различными способами, то он рассматривает это как два различных решения.
Повторный просмотр выполняется точно таким же способом, если выбор среди альтернатив происходит на более глубоком уровне обработки. Например, для определения отношения «одним из детей
X является
Y» могло бы быть использовано правило
ребенок(Х,Y):- отец(Y,X).
Тогда вопрос
?- ребенок(Х,Y).
дал бы
X = джордж, Y = мэри;
X = джордж, Y=джон;
X = гарри, Y = сью;
X = эдуард, Y = джордж.
Так как
отец(Y, X) имеет четыре решения, то столько же решений имеет и
ребенок(Х, Y). Более того, решения порождаются в том же самом порядке. Единственное, что отличает эти решения, - это различный порядок аргументов в соответствии с определением для предиката
ребенок. Аналогично, если мы определили
отец(X):- отец(_,X).
(отец (X) обозначает, что X является чьим-либо отцом), то на вопрос
?- отец(X).
были бы получены ответы:
X = джордж;
X = джордж;
X
= гарри;
X = эдуард.
Если мы перемешаем факты и правила, то выбор альтернатив вновь будет производиться в соответствии с порядком, в котором представлены факты и правила. Так, мы могли бы определить:
человек(адам).
человек(X):- мать(X,Y).
человек(ева).
мать(каин,ева).
мать(авель,ева).
мать(иавал,ада).
мать(тувалкаин,цилла).
(
адам - человек; объект является человеком, если он имеет мать;
ева – человек. Перечисленные люди имеют указанных матерей). В этом случае если бы мы сделали запрос
?- человек (X).
то ответом было бы:
X = адам;
X = каин;
X = авель;
X = иавал;
X = тувалкаин;
X = ева.
Давайте рассмотрим более интересный случай, когда имеются два целевых утверждения, для каждого из которых есть несколько решений. Предположим, что мы планируем провести вечеринку и хотим порассуждать о том, кто с кем мог бы танцевать. Мы можем начать писать программу следующим образом:
возможная_пара(X, Y):- парень(Х), девушка(Y).
парень(джон).
парень(мармадук).
парень(бертрам).
парень(чарлз).
девушка(гризелда).
девушка(эрминтруда).
девушка(брунхильда).
В программе определено, что
X и
Y образуют возможную пару, если
X является парнем, a
Y — девушкой. Теперь давайте посмотрим, какие возможные пары имеются:
?- возможная_пара(X, Y).
X = джон, Y = гризелда;
X = джон, Y = эрминтруда;
X = джон, Y = брунхильда;
X = мармадук, Y = гризелда;
X = мармадук, Y = эрминтруда;
X = мармадук, Y = брунхильда;
X = бертрам, Y = гризелда;
X = бертрам, Y = эрминтруда;
X = бертрам, Y = брунхильда;
X = чарлз, Y = гризелда;
X = чарлз, Y = эрминтруда;
X = чарлз, Y = брунхильда.
Вы должны быть уверены, что понимаете, почему Пролог породил решения в таком порядке. Прежде всего он ищет сопоставление для цели
парень(X) и находит, что первым парнем является
джон. Затем он находит сопоставление для цели
девушка(Y), выбирая
гризелда в качестве первой девушки. В этом месте мы запрашиваем новое решение, вводя ';'. Пролог поэтому считает, что последнее доказательство согласованности цели потерпело неудачу, и делает попытку вновь доказать согласованность последней из рассматривавшихся целей. Этой целью является утверждение девушка, встретившееся при доказательстве согласованности целевого утверждения
возможная_пара. Обнаруживается альтернативный вариант
эрминтруда, и, следовательно, следующим решением является пара
джон и
эрминтруда. Аналогично порождается пара
джон и
брунхильда в качестве третьего решения. При следующей попытке доказать согласованность целевого утверждения
девушка(Y) Пролог обнаружит, что маркер, соответствующий этому целевому утверждению, находится в конце базы данных и, следовательно, попытка найти новое сопоставление для этого целевого утверждения терпит неудачу. Тогда делается попытка вновь доказать согласованность целевого утверждения
парень(Х), маркер которого был установлен на первый факт предиката
парень, и, следовательно, следующим найденным решением, соответствующим второму парню, является
мармадук. Теперь, когда для этого целевого утверждения найдено новое решение, Пролог определяет, что следует делать далее – он должен найти сопоставление для цели
девушка(Y), осуществляя поиск решения с самого начала базы данных. Так что он выбирает гризелда в качестве первой девушки. Следующие три решения содержат
мармадук и имена трех девушек. Очередная попытка найти альтернативное решение для цели
девушка заканчивается неудачей. Поэтому ищется другой парень, а поиск среди девушек производится с начала базы данных. Аналогичным образом происходит выполнение программы и далее.
В конце концов сложится ситуация, когда доказательство согласованности целевого утверждения
девушка закончится неудачей и при этом будут также исчерпаны все решения для целевого утверждения
парень. Программа не может более найти ни одной пары.
Все приведенные примеры являются очень простыми. Они содержат лишь определения большого числа фактов или используют правила для доступа к этим фактам. По этой причине они могут порождать только конечное число возможных решений. В некоторых случаях нам может потребоваться порождать бесконечное число возможных вариантов – не потому, что мы хотим рассмотреть их все, а потому, что мы не знаем заранее, сколько их понадобится. В этом случае необходимо рекурсивное определение (обсуждавшееся в предыдущей главе).
Рассмотрим следующее определение целого числа (здесь под «целым» числом понимается целое положительное число). Целевое утверждение
целое_
число(N) согласуется с базой данных, если переменная
N конкретизирована и ее значением является целое число. Если переменная
N неконкретизирована в момент рассмотрения целевого утверждения, то попытка найти соответствие для утверждения
целое_число (N) приведет к тому, что будет выбрано целое число, которое будет присвоено N в качестве значения.
/* 1 */ целое_число(0).
/* 2 */ целое_число (X):- целое_число (Y),X is Y+1)
Если мы зададим вопрос
?- целое_число (X).
то получим в качестве возможных ответов все целые числа в порядке возрастания (0, 1, 2, 3,…), по одному числу каждый раз. Всякий раз, когда инициируется возврат (возможно, в результате ввода точки с запятой ';'), для предиката
целое_число находится новое сопоставление, в результате чего его аргументу присваивается очередное целое число. Таким образом, это короткое определение порождает бесконечное число решений. Почему? На рис. 4.1, 4.2, 4.3 показана последовательность событий, приводящая к порождению трех первых решений. На каждом этапе самый нижний указатель (1) на рисунке указывает место, где впоследствии будет выбрано
иное решение. Первоначально для ответа на вопрос имеется выбор между фактом
1 и правилом
2. Если выбирается факт
1, то ничего более выбирать не придется, и мы получаем X = 0. В противном случае выбирается правило
2 и ищется соответствие для цели, порождаемой этим правилом. Если выбирается факт
1, то завершается доказательство целевого утверждения с ответом
X=1; в противном случае используется правило
2 и снова ищется соответствие для появившейся подцели. И так далее. На каждом этапе первое что делает Пролог – это выбирает факт
1. Только при выполнении возврата он изменяет последний сделанный им выбор. Каждый раз, когда он это делает, он возвращается к тому месту, где в последний раз выбирал факт
1, и выбирает вместо него правило
2. При этом выборе появляется новая подцель. Факт
1 представляет первую возможность для сопоставления с этой подцелью.

Рис. 4.1.
![]()
src="/i/5/81305/pic_16.jpg">
Рис. 4.2.

Рис. 4.3.
Большинство правил на Прологе будут порождать альтернативные решения, если они сопоставляются с целями, содержащими большое число неконкретизированных переменных. Например, отношение принадлежности элемента списку:
принадлежит(X,[X |_]
).
принадлежит(X,[_ |Y]):- принадлежит(X,Y).
порождает альтернативные решения. Если мы задаем вопрос
?- принадлежит(а,X).
(обратите внимание, что
X в вопросе является неконкретизированной переменной), то последовательные значения переменной
X будут представлять частично конкретизированные списки, в которых
а является первым, вторым, третьим и так далее элементом списка. Убедитесь, что вы понимаете, почему так получается. Другим следствием возврата, допускаемого при выполнении предиката принадлежит, является то, что вопрос
?- принадлежит(а,[а,b,r,а,с,а,d,а,b,r,а]).
фактически может быть согласован
пятью способами. Очевидно, что имеются приложения предиката
принадлежит, в которых требуется найти лишь одно решение, если оно вообще существует, и затем отбросить (обойти) остальные возможные решения. Такое отбрасывание оставшихся решений может быть реализовано с помощью «отсечения».
4.2. Отсечение
Этот раздел посвящен специальному механизму, используемому в программах на Прологе и называемому «отсечением»
[8]. Отсечение позволяет указать, какие из сделанных ранее выборов не следует пересматривать при возврате по цепочке согласованных целевых утверждений. Существуют две причины, побуждающие включать в программу такие указания:
• Программа будет выполняться быстрее, так как не будет тратиться время на попытки найти новые сопоставления для целей, о которых заранее известно, что они не внесут более ничего нового в решение.
• Программа может занимать меньше места в памяти ЭВМ, так как отсутствие необходимости запоминать точки возврата для последующего анализа позволяет более экономно использовать память.
В некоторых случаях включение отсечения в программу может означать переход от программы, которая не будет работать, к программе, которая будет работать.
Синтаксически использование в правиле отсечения выглядит как вхождение целевого утверждения с предикатом '!', не имеющим аргументов. Как целевое утверждение этот предикат всегда согласуется с базой данных и не может быть вновь согласован. Однако он имеет побочный эффект, который изменяет процесс последующего возврата. Эффект заключается в том, что маркеры некоторых целей становятся недоступными, так что для этих целей нельзя найти новые сопоставления. Рассмотрим, как это происходит на примере. Предположим, что вы заведуете библиотекой и имеете базу данных на Прологе, содержащую информацию о наличии книг, о том, кто и какие книги взял и когда книги должны быть возвращены. Один из вопросов, который мог бы вас интересовать,- это какие виды услуг, предоставляемых библиотекой, доступны каждому из читателей. Некоторые услуги, которые мы могли бы назвать основными, должны быть доступны любому читателю. Они включают пользование каталогом и справочным бюро. С другой стороны, дополнительные услуги, такие как пользование абонементом или получение книг из других библиотек, хотелось бы предоставлять читателю выборочно. Одно из правил могло бы состоять в том, что если читатель не возвратил в указанный срок книгу, то дополнительные виды услуг ему недоступны до тех пор, пока он не вернет книгу. Здесь приведена часть программы, которая использует это правило:
услуги(Читатель,Вид_услуг):-
книга_не_возвращена(Читатель,Книга),!,основные_услуги (Вид_услуг).
услуги(Читатель,Вид_услуг):-общие_услуги(Вид_услуг).
основные_услуги(пользование_каталогом).
основные_услуги(получение_справок).
дополнительные_услуги (абонемент).
дополнительные_услуги(межбиблиотечный_абонемент).
общие_услуги(X):-основные_услуги(X).
общие_услуги(X):-дополнительные_услуги(X).
книга_не_возвращена('С. Уотзер',книга10089),
книга_не_возвращена('А. Джонс', книга29907).
. . .
читатель('А.Джонс'). читатель('В.Метеск').
Зачем понадобилось использовать отсечение в этой программе и какой эффект оно оказывает? Предположим, что вы хотите просмотреть список всех читателей и определить, какие услуги им доступны. В этом случае вам надо обратиться к Прологу со следующим вопросом:
?- читатель(X), услуги(X,Y).
Начав поиск ответа, Пролог выберет первого читателя:
А.Джонс. Предположим, что этот читатель имеет на руках несколько не возвращенных в указанный срок книг. Для того чтобы определить, какие услуги доступны ему, Пролог воспользуется первым утверждением для предиката
услуги. Это приводит к появлению нового целевого утверждения –
книга_не_возвращена. После небольшого поиска среди фактов
книга_не_возвращена обнаружен факт о первой не возвращенной А. Джонсом в срок книги (второй факт для этого предиката). Следующее целевое утверждение – это отсечение. Эта цель автоматически согласуется с базой данных, и в результате этого в системе закрепляются все решения, принятые с момента выбора первого утверждения
услуги.
Мы можем представить ситуацию, возникшую непосредственно перед выполнением отсечения, в виде диаграммы, приведенной на рис. 4.4. Когда в программе встречается отсечение, то оно «отсекает» путь, представляющий цепочку выполненных доказательств таким образом, что следующая цель соединяется непосредственно с исходной (см. рис. 4.5). Результат действия отсечения в правиле для предиката
услуги (утверждение 1) заключается в том, что все цели, выбранные с момента, когда было выбрано это правило, запоминаются в системе как неизменяемые при обратном просмотре.
Путь, представляющий цепочку найденных доказательств, при этом изменяется так, что исключаются все маркеры, соответствующие целям, расположенным между
услуги и отсечением включительно. Таким образом, если впоследствии произойдет возврат на точку! (отсечение), то попытка согласовать цель
услуги немедленно потерпит неудачу. Система не будет рассматривать альтернативные решения для целевого утверждения
книга_не_возвращена ('А. Джонс', Книга), и это совершенно разумно, так как мы интересуемся лишь тем, числится ли за читателем
хотя бы одна не возвращенная в срок книга, а не тем, каковы
все книги, числящиеся за ним. Утверждение 2 в предикате
услуги тоже рассматриваться системой не будет, так как при возврате обходится и выбор правила, в котором встречается отсечение. Такое поведение системы в рассматриваемой ситуации тоже является разумным, так как мы не хотим порождать решения, указывающие на то, что
А. Джонсу доступны все услуги.

Рис. 4.4.

Рис. 4.5.
Действие отсечения в этом примере можно резюмировать следующим образом:
Если оказывается, что читатель имеет не возвращенную в срок книгу, то ему разрешается пользоваться лишь основными видами услуг, предоставляемыми библиотекой. Нет необходимости выявлять все книги, не возвращенные читателем в срок, равно как нет необходимости рассматривать какие-либо другие правила относительно услуг, предоставляемых читателю.
В этом примере использование отсечения привело к «сокращению» всех решений, принятых после выбора целевого утверждения
услуги. Оно называется
родительским целевым утверждением для отсечения, так как именно это целевое утверждение привело к использованию правила, содержащего отсечение. На наших диаграммах родительским целевым утверждением всегда является целевое утверждение, соответствующее наименьшему прямоугольнику, содержащему прямоугольник с '!'. Формальное определение эффекта, производимого отсечением, формулируется следующим образом:
Если отсечение встречается в качестве целевого утверждения, то после этого система лишается возможности изменять решения, принятые ею с момента вызова родительского целевого утверждения. Все альтернативы принятым решениям отбрасываются. Следовательно, попытка вновь доказать согласованность с базой данных любого целевого утверждения между родительским целевым утверждением и ! (отсечением) закончится неудачей.
Существуют различные способы описания того, что произошло с решениями, попавшими в область действия отсечения. Можно сказать, что эти решения отсекаются или замораживаются, что система лишается возможности изменять эти решения или что оставшиеся альтернативы отбрасываются. Можно также смотреть на символ отсечения как на некий разделитель (забор), отделяющий целевые утверждения. Так, при обработке конъюнкции целей
foo:- а, b, с,!, d, e, f
Пролог без каких-либо ограничений может выполнять возврат среди целей
a,
b и
с до тех пор, пока доказательство согласованности целевого утверждения
с с базой данных не приведет к тому, что Пролог «перешагнет» через «забор»! и приступит к доказательству согласованности целевого утверждения
d. Далее возврат может осуществляться между целевыми утверждениями
d,
e и
f, при этом, возможно, неоднократно будет достигаться согласованность всей конъюнкции целиком. Однако если произойдет неудача при доказательстве согласованности целевого утверждения
d, что вызовет «перешагивание через забор» справа налево, то никаких попыток вновь доказать согласованность целевого утверждения
с делаться не будет; доказательство согласованности конъюнкции целей в целом, а следовательно, и цели
foo потерпит неудачу.
Прежде чем перейти к рассмотрению других примеров с использованием отсечения, сделаем еще одно замечание. Мы сказали, что если отсечение появляется в некотором правиле и выбирается в качестве целевого утверждения, то Пролог-система лишается возможности
изменять все решения, принятые с момента вызова родительского целевого утверждения. Это значит, что выбор этого правила и всех решений, принятых после него, становится зафиксированным. Далее мы увидим, что есть возможность указывать альтернативы в
рамках одного правила, используя встроенный предикат ';' (обозначающий «
или»). На выбор альтернатив, сделанный с использованием этой возможности, эффект отсечения действует точно так же, т. е. при отсечении фиксируются все «
или»-выборы, сделанные с момента выбора правила, содержащего отсечение.
4.3. Общие случаи использования отсечения
Мы можем выделить три основных случая использования отсечения.
Первый связан с ситуациями, когда мы хотим указать Пролог-системе, что она нашла нужное правило для заданного целевого утверждения. В этом случае отсечение означает: «если вы дошли до этого места, то вы выбрали именно то правило, которое нужно для данного целевого утверждения».
Второй случай относится к ситуации, когда мы хотим указать Пролог-системе, что необходимо немедленно прекратить доказательство согласованности конкретного целевого утверждения, не пытаясь найти для него альтернативные решения. В этом случае используется конъюнкция отсечения с предикатом
fail, что означает; «если вы дошли до этого места, то вам следует прекратить попытки доказать согласованность данного целевого утверждения».
К третьему случаю относятся ситуации, когда мы хотим закончить порождение альтернативных решений механизмом возврата. В этом случае отсечение означает: «если вы дошли до этого места, то вы нашли единственное решение задачи и никакой возможности найти другие альтернативные решения нет».
Теперь мы рассмотрим несколько примеров использования отсечения в перечисленных выше ситуациях. Однако необходимо помнить, что во всех этих случаях отсечение имеет один и тот же смысл. Выделение трех случаев использования отсечения обусловлено чисто методическими соображениями, чтобы показать, по каким причинам в программах могут использоваться отсечения.
4.3.1. Подтверждение правильности выбора правила
При программировании на Прологе очень часто возникает желание использовать для описания одного предиката несколько утверждений. Одно утверждение будет использоваться, если аргументы имеют один вид, другое будет использоваться для аргументов иного вида и так далее. Часто мы можем указать, какое правило следует использовать для данного целевого утверждения, указав в качестве аргументов в заголовке правила необходимые образцы структур так, чтобы это правило могло быть сопоставлено лишь с соответствующими целевыми утверждениями. Однако это не всегда возможно. Если мы не можем сказать заранее, какого вида аргументы будут использоваться, или если мы не можем перечислить все множество возможных образцов аргументов, то мы можем принять компромиссное решение. Это значит, что задаются правила для аргументов определенных типов, а в конце задается правило-«ловушка» для всех остальных правил. В качестве примера такого способа рассмотрим следующую программу. Определим предикат сумма таким образом, что при выборе в качестве целевого утверждения
сумма(N, X), где
N – некоторое целое число, переменной
X присваивается значение, равное сумме всех целых чисел от
1 до
N. Так, например, возможен следующий диалог:
?- сумма(5,X).
X = 15;
нет
Полученный ответ объясняется тем, что 1+2+3+4+5 равно 15. Здесь приведена соответствующая программа.
сумма(1,1):-!.
сумма(N,Результат):- N1 is N-1, сумма(N1,Результат),Результат is Результат+N.
Приведенное определение является рекурсивным. Идея состоит в том, что выход на граничное условие происходит в случае, когда первый аргумент равен 1. В этом случае ответ тоже равен
1. Второе утверждение вводит рекурсивное целевое утверждение
сумма. Однако первый аргумент нового целевого утверждения на единицу меньше, чем первый аргумент в исходном целевом утверждении. Следующее целевое утверждение, которое будет порождено этим целевым утверждением, снова будет иметь первый аргумент на единицу меньше. И так далее до тех пор, пока не будет достигнуто граничное условие. Так как первый аргумент всегда на единицу меньше, то в конце концов произойдет выход на граничное условие (в предположении, что исходное целевое утверждение имеет первый аргумент не меньше 1) и выполнение программы закончится.
Представляет интерес то, как в этой программе организована обработка двух случаев: когда число, соответствующее первому аргументу, равно
1 и когда оно отлично от
1. Когда мы определяли предикаты для обработки списков, то было легко указать два типичных случая: когда список был пустым ([]) и когда он имел вид
[A|B]. Для чисел это не так просто сделать, потому что мы не можем задать такой аргумент, который был бы сопоставим только с целым числом, не равным 1. Приемлемое решение в данном примере состоит в том, чтобы выделить случай, когда первый аргумент равен 1, и обеспечить сопоставление для всех остальных случаев с помощью переменной. Мы знаем, что в соответствии со стратегией, используемой при поиске в базе данных, Пролог сначала будет пытаться произвести сопоставление с правилом для
1, и только в случае неудачи он попытается использовать второе правило. Таким образом, второе правило используется только для чисел, не равных
1. Но этим дело не кончается. Если когда-либо Пролог будет выполнять возврат и попытается пересмотреть выбор правила с первым аргументом, равным
1, то он обнаружит, что второе правило тоже применимо. Как можно видеть, оба правила являются альтернативными для целевого утверждения
сумма(1,X). Мы должны указать Прологу, что ни в коем случае не следует использовать второе правило, если число, соответствующее первому аргументу, равно 1. Один из способов сделать это – вставить отсечение в первое правило (как это и показано в записи этого правила). Это отсечение указывает Прологу, что если выбрано первое правило, то больше не следует принимать нового решения относительно того, какое правило использовать для целевого утверждения
сумма. В случае если число, соответствующее первому аргументу, действительно равно
1, может произойти только выбор первого правила.
Давайте посмотрим, как все это выглядит на языке диаграмм. Если мы обратимся к предикату
сумма(1,X) в следующем контексте:
выполнить:- сумма(1,X), foo(apples)
?-выполнить.
и для цели
foo(apples) нет сопоставления, то к моменту, когда обнаружится несогласованность
foo(apples) с базой данных, результат работы Пролога будет иметь вид, как показано на рис. 4.6. Если Пролог попытается найти новые сопоставления для целевых утверждений, просматривая их в обратном порядке, то обнаружится, что рассмотренные выше два альтернативных целевых утверждения не могут быть пересмотрены, так как они исключены из цепочки доказательства. Следовательно, наиболее верный путь – не пытаться найти другое сопоставление для предиката
сумма(1,X).

Рис. 4.6.
Упражнение 4.1. Что произойдет в процессе возврата при попытке найти новое сопоставление для целевогоутверждения
сумма, если из первого правила для предиката
сумма удалить отсечение? Какие альтернативные результаты будут получены (если вообще они будут возможны) и почему?
Последний пример показал, как можно использовать отсечение для того, чтобы сделать поведение Пролога чувствительным к случаю, когда мы не можем выделить все возможные случаи путем перечисления образцов в заголовках правил. Более типичная ситуация, в которой мы не можем указать структуру заголовков правил для выполнения сопоставления, возникает, если мы хотим ввести дополнительные условия в виде целевых утверждений Пролога, позволяющих в процессе согласования с базой данных выбрать соответствующие правила. Рассмотрим следующий альтернативный вариант решения последнего примера:
сумма(N,1):- N =‹ 1,!.
cyммa(N,R):- N1 is N-1, сумма(N1,R1), R is Rl+N
В этом случае указывается, что первое правило следует выбрать, когда заданное количество суммируемых чисел меньше или равно единице. Такое определение правила немного лучше, чем предыдущее, потому что соответствующая ему программа даст ответ (вместо того чтобы выполняться бесконечно), если в качестве первого аргумента будет задан
0 или отрицательное число. Если условие первого правила выполняется, то сразу же выдается результат
1 и не требуется прибегать к рекурсивному порождению целевых утверждений. Второе правило следует попытаться использовать лишь в случае, когда это условие не выполняется. Мы должны указать Прологу, что если уже обнаружено, что N
= ‹ 1, то не следует возвращаться к пересмотру выбора правила. Это как раз и достигается с помощью отсечения.
Общий принцип заключается в том, что использование механизма отсечения для указания Прологу на ситуации, когда он выбрал единственно правильное правило, может быть заменено использованием предиката
not. Это встроенный предикат Пролога, т. е. определение этого предиката заранее известно Пролог-системе. Поэтому его можно использовать, не выписывая каждый раз его определение (более полно встроенные предикаты описываются в гл. 6). Предикат
not определен таким образом, что целевое утверждение
not(X) истинно, только если X, рассматриваемое как целевое утверждение, не согласуется с базой данных. Таким образом,
not(X) означает, что
X недоказуемо как целевое утверждение Пролога, т. е. не согласовано с базой данных. В качестве примера использования
not вместо отсечения перепишем два варианта определения предиката
сумма следующим образом:
сумма(1,1).
cyммa(N,R):- not(N = 1), N1 is N-1, cyммa(N1,R1),R is N1 + R1.
или
сумма(N,1):- N =‹1.
сумма(N,R):- not(N=‹l), N1 is N-1, сумма(N1,R1
),R is N1 + R1.
В действительности в Прологе имеются другие удобные встроенные предикаты, которые могут заменить оба из приведенных вхождений предиката
not. Например, можно заменить
not(N=1) на
N\=1, a
not(N =‹
1) на
N›1. В общем случае это можно сделать не со всеми возможными условиями.
Использование предиката
not вместо отсечения свойственно для хорошего стиля программирования. Это связано с тем, что программы, содержащие отсечения, как правило, более трудны для чтения, чем программы, не содержащие их. Если удается локализовать все вхождения отсечения и заменить их с помощью предиката
not, то программа станет более понятной. Однако определение not предполагает попытку доказать, что заданное целевое утверждение согласуется с базой данных. Поэтому если мы имеем программу, в общем виде представимую как
A:-B, C
A:-not(B),D
то Прологу для успешного завершения программы может потребоваться две попытки согласовать
B. Он должен попытаться согласовать
B при просмотре первого правила. Но если затем будет выполнен возврат и рассмотрено второе правило, то он будет вынужден попытаться согласовать
B вновь, чтобы убедиться, может ли быть согласовано
not(B). Такое дублирование приводит к потере эффективности программы, когда условие
B достаточно сложно. Этого бы не произошло, если бы вместо приведенной программы мы имели:
A:-B,!,C
A:-D
Таким образом, иногда нужно взвесить преимущества ясной программы по сравнению с преимуществами ее быстрого выполнения. Обсуждение вопроса эффективности приводит нас к последнему примеру, в котором отсечение используется для фиксирования выбора правила. Рассмотрим определение предиката
присоединить:
присоединить([],X,X).
присоединить([А|В],С,[А|D]) – присоединить(В,С,D).
Если предикат
присоединить используется лишь в случаях, когда, имея два списка, мы хотим найти список, получающийся в результате добавления элементов второго списка в конец первого, то такая программа неэффективна, поскольку, если выполняется возврат при обработке целевого утверждения вида
присоединить([],[a,b,c,d],X), Пролог обязан сделать попытку использовать второе правило, несмотря на то что эта попытка заранее обречена на неудачу. В таком контексте пустота первого списка указывает на то, что первое правило является единственным возможным для использования и эта информация может быть сообщена Прологу с помощью отсечения. В общем случае при применениях Пролог-системы смогут лучше использовать имеющуюся память, если сообщать системе такие сведения, по сравнению с тем, когда она должна хранить информацию о выборе правил, которая в действительности использована не будет. Можно с этой целью переписать наше определение следующим образом:
присоединить([],X,X):-!.
присоединить([А|В],С,[А|D]:- присоединить(В,С,D).
При сделанных предположениях относительно применения предиката
присоединить это никак не повлияет на то, какие решения найдет программа, но несколько повысит ее эффективность по времени выполнения и объему занятой памяти. В качестве платы за это мы потеряли возможность использования предиката
присоединить в других ситуациях – он больше не будет работать ожидаемым образом, что будет показано в разд. 4.4.
4.3.2. Комбинация «отсечение-fail»
Во втором из перечисленных выше случаев применения отсечение используется в конъюнкции с встроенным предикатом
fail – еще одним встроенным предикатом, подобным
not. Предикат
fail не имеет аргументов, это означает, что выполнение целевого утверждения
fail не зависит от того, какие значения имеют переменные. Действительно, предикат
fail определен таким образом, что доказательство его согласованности как целевого утверждения всегда заканчивается неудачей и приводит к включению механизма возврата. Это в точности совпадает с тем, что происходит, когда мы пытаемся найти сопоставление для целевого утверждения, для которого в базе данных нет ни фактов, ни правил. Если
fail встречается после отсечения, то нормальное выполнение возврата изменится в результате действия механизма отсечения. Данная комбинация «отсечение-
fail» оказывается очень полезной на практике.
Давайте обсудим, как можно было бы использовать эту комбинацию в программе вычисления размера налога, который следует уплатить тому или иному человеку. Один из вопросов, на который мы хотели бы получить ответ – это является ли человек «средним налогоплательщиком». В этом случае вычисления были бы очень простыми и не требовали бы рассмотрения множества особых случаев. Давайте определим предикат
средний_налогоплательщик, где
средний_налогоплательщик(X) означает, что
X является средним налогоплательщиком. Например, Френд Влоггс, который женат, имеет двух детей и работает на велосипедном заводе, мог бы рассматриваться как действительно средний налогоплательщик. Однако директор-распорядитель нефтяной компании получает, по-видимому, достаточно много, а пенсионер – слишком мало, чтобы в обоих случаях был приемлем один и тот же способ вычисления налога. Нам следовало бы начать с особого случая. Возможно, что на иностранного гражданина распространяются особые налоговые законы, так как он может иметь налоговые обязательства также и в своей стране. Поэтому, каким бы средним он ни являлся в других отношениях, иностранец не будет классифицирован как средний налогоплательщик. Мы можем начать запись правил об этом следующим образом:
средний_ налогоплательщик(X):- иностранец(X), fail
.
средний_налогоплательщик(X):-…
В этой выдержке из программы
(которая является неверной) в первом правиле делается попытка сказать: «если X – иностранец, то доказательство согласованности целевого утверждения
средний_налогоплательщик(X) должно закончиться неудачей». Второе правило должно использовать общий критерий того, что значит быть средним налогоплательщиком в тех случаях, когда
X – не иностранец. Ошибка заключается в том, что если бы мы обратились с вопросом
?- средний_налогоплательщик(видслевип).
об иностранце по фамилии
видслевип, то произошло бы сопоставление с первым правилом и согласованность целевого утверждения
иностранец была бы доказана. Далее, целевое утверждение
fail инициировало бы возврат. При попытке найти новое сопоставление для цели
средний_налогоплательщик Пролог нашел бы второе правило, определяющее общие критерии вычисления налога, и начал бы применять это правило к
видслевип. Вполне вероятно, что этот иностранец удовлетворил бы общим критериям, что привело бы к неверному ответу «да».
Таким образом, первое правило оказалось абсолютно неэффективно при «отбраковке» нашего приятеля как среднего налогоплательщика. Почему так получается? Ответ кроется в том, что при возврате Пролог пытается найти новое сопоставление для
каждого целевого утверждения, рассматривавшегося ранее. Поэтому, в частности, будут исследованы альтернативные способы сопоставления для
средний_налогоплательщик(видслевип). Для того чтобы остановить поиск альтернатив в данном случае, необходимо отсечь сделанный выбор правила (заморозить решение), прежде чем будет выполнен предикат
fail. Мы можем сделать это, вставив отсечение перед
fail. Несколько более обстоятельное определение предиката
средний_налогоплательщик, включающее эти изменения, приведено ниже:
средний_налогоплателыцик(Х):- иностранец(Х),!,fail.
средний_налогоплательщика(X):-супруга(Х,Y), доход(Y,Доход), Доход › 3000,!, fail.
средний_налогоплателыцик(Х):- доход(X,Доход),2000 ‹ Доход, 20000 › Доход.
доход(Х,Y):- получаемое_пособие(Х,Р),Р‹5000,!, fail
.
доход(Х,Y):-жалованье(Х,Z),доход_от_капиталовложений(X,W),Y is Z + W.
доход_от_капиталовложений(Х,Y):-…
Обратите внимание на использование в этой программе других комбинаций «отсечение-
fail». Во втором правиле
средний_налогоплательщик говорится, что попытка показать, что некоторый человек является средним налогоплательщиком, может быть прервана, если можно показать, что заработок его супруги превышает некоторый порог. Точно так же в определении предиката
доход указано (в первом правиле), что если человек получает пособие, сумма которого меньше некоторого порога, то независимо от других обстоятельств мы будем рассматривать его как вовсе не имеющего дохода.
Интересный пример использования комбинации «отсечение-
fail» представляет предикат
not. Большинство реализаций имеют этот предикат как встроенный, но интересно рассмотреть, как можно описать его с помощью правил. Мы требуем, чтобы целевое утверждение
not(P), где
P обозначает некоторое другое целевое утверждение, было истинным тогда и только тогда, когда доказательство согласованности целевого утверждения
P терпит неудачу. Это не совсем точно соответствует нашему интуитивному пониманию «не является истинным» – далеко не всегда мы можем без опасения считать, что что-то не является истинным, если мы не в состоянии доказать это. Но как бы то ни было, здесь приводится соответствующее определение:
not(P):- call(P),!, fail.
not(P)
Определение предиката
not содержит обращение к аргументу
P как к целевому утверждению с использованием встроенного предиката
call. Предикат
call просто интерпретирует свой аргумент как целевое утверждение и пытается доказать его согласованность. Мы хотим, чтобы первое правило применялось в тех случаях, когда согласуется
P с базой данных, а в противном случае должно применяться второе правило. Таким образом, мы говорим, что если Пролог может согласовать
call(P), то он должен прекратить на этом правиле доказательство целевого утверждения
not. Другая возможность имеет место, если Пролог не может согласовать
call(P). В этом случае он никогда не дойдет до отсечения. Так как доказательство согласованности
call(P) потерпело неудачу, то происходит возврат, и Пролог обнаруживает второе правило. Следовательно, доказательство согласованности целевого утверждения
not(P) закончится успешно в случае, когда
P недоказуемо.
Как и в первом случае применения отсечения, мы можем заменить любое употребление комбинации «отсечение-
fail» использованием предиката
not. Такая замена требует несколько большей реорганизации программы, чем ранее, но при этом не приводит к потере эффективности. Если бы мы стали с этой целью переписывать нашу программу для предиката
средний_
налогоплательщик, то следовало бы начать ее примерно так:
средний_налогоплателыцик(X):-
nоt(иностранец(X)),not((супруга(X,Y),доход(Y,Доход), Доход›3000)), доход(Х, Доход1),…
Обратите внимание на то, что в этом примере конъюнкция целей, являющаяся аргументом
not, заключена в скобки. Для того чтобы однозначно показать, что запятые разделяют цели в конъюнкции (а не аргументы предиката
not), мы заключили аргумент предиката
not в дополнительные круглые скобки.
Теперь мы можем рассмотреть последнюю основную область применения отсечения в программах на Прологе – завершение последовательности порождения и проверки вариантов. Очень часто программа состоит из частей, соответствующих следующей общей модели. Имеется последовательность целей, которые могут быть согласованы множеством различных способов и которые порождают много возможных решений при возврате. Кроме того, имеются цели, проверяющие приемлемость порожденных решений для последующего использования. Если поиск сопоставлений для этих целевых утверждений закончится неудачей, то возврат приведет к тому, что будет предложено новое решение. Новое решение будет подвергнуто проверке на пригодность и так далее. Процесс завершится, либо когда будет порождено приемлемое решение (успех), либо когда нельзя больше найти решений (неудача). Мы можем назвать «генератором» целевые утверждения, которые порождают все возможные альтернативы, а целевые утверждения, которые проверяют пригодность решения, - «контролером». Давайте рассмотрим пример такой программы. Приводимый ниже фрагмент мог бы быть частью программы, играющей в крестики-нолики. Эта программа использует встроенные предикаты
var и
arg, которые подробно рассмотрены в гл. 6.
вынужденный ход(Доска,K):- линия(Клетки), угроза(Клетки,Доска,K),!.
линия([1,2,3]).
линия([4,5,6]).
линия([7,8,9]).
линия([1,4,7]).
линия([2,5,81).
линия([3,6,9]).
линия ([1,5,9]).
линия([3,5,7]).
угроза([X,Y,Z],B,X):- пусто(Х,В), крестик (Х,В), крестик(Z,B).
угроза([X,Y,Z],B,Y):- пусто(Y,B), крестик (Х,В), крестик(Z,B).
угроза([X,Y,Z],B,Z):- пусто(Z,B), крестик(Х,В), крестик(Y,B).
пусто(К,Доска):- arg(K,Дocкa,C), var(C).
крестик(К,Доска):- arg(K,Дocкa,C), nonvar(C), C=X.
нолик(К,Доска):- arg(К,Доска,С), nonvar(C), С=0.
Для тех, кто не знаком с этой игрой, вкратце объясним ее правила. Два игрока по очереди заполняют клетки на доске размером 3x3. Один игрок использует для этого символ 0, а другой игрок — символ X. Цель игры — расположить три своих символа подряд по одной линии (вертикальной, горизонтальной или диагональной). Мы можем перенумеровать девять клеток на доске следующим образом:

Предполагается, что программа действует за игрока, делающего свои ходы ноликами. Предикат
вынужденный_ход используется для ответа на вопрос: «Нужно ли делать вынужденный ход в конкретной позиции?» Такая ситуация имеет место, если игрок 0 (игрок, делающий ходы ноликами, т. е. программа) не может выиграть немедленно (мы не будем рассматривать этот слу- случай), но есть угроза того, что игрок
X может выиграть следую- следующим ходом. Например, в позиции

Игрок
0 вынужден поставить
0 в 4-й квадрат, так как если он не сделает этого, то его противник будет иметь возможность на следующем ходу заполнить линию 1-4-7. Программа работает, пытаясь найти линию, две клетки которой заполнены крестиками, а третья – пустая. Если такая линия имеется, то игрок 0 вынужден сделать ход, поставив нолик в пустую клетку. В утверждении для предиката
вынужденный_ход цель
линия(Клетки)
служит «генератором» возможных линий. Эта цель может быть согласована с базой данных несколькими способами, в частности, присваиванием в качестве значения переменной Клетки одного из возможных списков номеров клеток, находящихся на одной линии. Выбрав линию, необходимо проверить, существует ли угроза со стороны противника на этой линии. Это составляет задачу целевого утверждения, выполняющего функции «контролера»:
угроза(Клетки,Доска,К)
В этом целевом утверждении переменная
Доска используется для представления текущей позиции на доске (т. е. какие клетки заняты и какими символами), а переменная К получает в качестве значения номер клетки, в которой игрок 0 должен поставить нолик (при условии что доказательство этой цели завершается успешно).
Основная идея программы очень проста – предикат
линия выдает линию, а затем предикат
угроза проверяет, имеется ли на этой линии угроза. Если это так, то доказательство согласованности исходного целевого утверждения
вынужденный_ход заканчивается успешно. Иначе инициируется возврат, и предикат
линия предполагает другую возможную линию. Эта линия также подвергается проверке, и, возможно, снова произойдет возврат. Если мы окажемся в ситуации, когда предикат
линия не может более порождать линии, то доказательство согласованности целевого утверждения
вынужденный_ход закончится неудачей (вынужденных ходов нет).
Теперь рассмотрим, что происходит, если эта программа, являясь частью некоторой большей системы, успешно находит вынужденный ход. Переменная К получит в качестве значения номер клетки, в которой должен быть сделан ход, и эта информация будет использована где нибудь в другом месте в программе. Предположим, что в дальнейшем где-то в программе имеет место неудача при доказательстве согласованности некоторого утверждения и что Пролог в конце концов пытается вновь согласовать целевое утверждение
вынужденный_ход. Тогда предикат
линия начнет порождение новых возможных линий, которые должны быть проверены. Это бессмысленно, так как нет никакой пользы в том, чтобы искать альтернативный вынужденный ход. Если найден один из таких ходов, то мы не можем сделать ничего лучше, чем сделать этот ход – неудача при его осуществлении гарантировала бы проигрыш игры. В большинстве случаев, однако, альтернативных вынужденных ходов не будет, и при поиске сопоставления для цели
вынужденный_ход будут бесполезно просматриваться все неопробованные линии, прежде чем попытка доказать согласованность цели не закончится неудачей. Однако в случае альтернативных ходов известно, что даже если имеется другое решение, оно не может быть использовано без возникновения проблем с использованием первого решения Мы можем предотвратить потерю времени Прологом на поиск различных вынужденных ходов, поместив отсечение в конце соответствующего утверждения. Это приведет к замораживанию последнего успешного решения для предиката
линия. Введение отсечения равносильно следующему заявлению: «если ищутся вынужденные ходы, то важно найти только первое решение».
Чтобы понять такое использование отсечения, необходимо лишь рассмотреть общую структуру этой программы. Однако некоторые из деталей также представляют интерес. В программе предполагается, что игровую доску можно описать с помощью структуры, состоящей из девяти компонент. Каждая компонента представляет содержимое клетки с соответствующим номером. Таким образом, в любой момент времени содержимое четвертой клетки доски может быть получено путем выборки четвертого аргумента структуры, представляющей текущую позицию на доске (для этого мы используем встроенный предикат
arg). Если клетка ничем не заполнена, то переменная будет неконкретизи-рованной; иначе ее значение равно одному из атомов
О или
X. Мы используем предикаты
var и
nonvar для того, чтобы определить, занята клетка или нет.
Давайте рассмотрим другой пример программы, работающей по методу «порождения и проверки». Вернемся к вопросу о делении целых чисел, рассмотренному в разд. 2.5. Большинство Пролог-систем обеспечивают эту возможность автоматически, но здесь представлена программа для целочисленного деления, которая использует лишь операции сложения и умножения.
разделить(N1,N2,Результат):-
целое_число(Результат), Произведение_1 is Результат*N2, Произведение_2 is (Результат + 1)*N2, Произведение_1 =‹ N1, Произведение_2›N1,!.
Это правило использует предикат
целое_число (как он определен ранее) для порождения числа
Результат, которое является результатом «деления»
N1 на
N2. Так, например, результат деления
27 на
6 равен
4, так как
4×6 меньше или равно
27, а
5×6 больше чем
27.
Приведенное правило использует предикат
целое_число как «генератор», а остальные целевые утверждения выполняют функцию соответствующего «контролера». Мы заранее знаем, что если заданы конкретные значения
N1 и
N2, то предикат
разделить(N1, N2, Результат) может иметь значение «истина» лишь для одного возможного значения
Результат. Несмотря на то что
целое_число может породить бесконечное множество кандидатов, лишь для одного из них будут выполняться последние тесты. Мы можем явно выразить это наше знание, вставив отсечение в конце правила. Словами это можно сказать так: «если нам удалось породить число
Результат такое, что оно успешно проходит тесты для числа, являющегося результатом деления, то нет надобности пытаться получить другое решение». В частности, нет необходимости пересматривать какой-либо из выборов, которые были сделаны при поиске правил для
разделить, целое_число и так далее. Мы нашли единственное решение, и нет оснований искать другое. Если бы мы "не" добавили отсечение, то любой возврат в конце концов снова инициировал бы поиск альтернатив для
целое_число. Так что продолжилось бы порождение значений для переменной
Результат. Ни одно из новых значений не было бы правильным результатом деления, и, таким образом, генерация целых чисел продолжалась бы до бесконечности.
4.4. Проблемы, связанные с использованием отсечения
Мы уже убедились в том, что иногда необходимо учитывать стратегию, используемую в Прологе для поиска в базе данных, и что порядок записи утверждений в программе на Прологе влияет на результат доказательства согласованности целевых утверждений. Проблема, связанная с введением отсечений, заключается в том, что мы должны еще более детально знать, как именно будут использоваться правила программы. Ибо, когда правило используется одним способом, отсечение может быть безвредным или даже полезным, в то время как при другом способе употребления правила отсечение может привести к непредвиденному результату. Рассмотрим измененное определение предиката
присоединить, приведенное в предыдущем разделе:
присоединить([],Х,Х):-!.
присоединить[А|В],С,[А|D]:- присоединить(В,С,D).
Когда мы имеем дело с целевыми утверждениями, подобными
присоединить([а,b,с],[d,е],Х)
и
присоединить([а,b,с],Х,Y)
то использование отсечения вполне уместно. Если первый аргумент такого целевого утверждения уже имеет некоторое значение, то единственный смысл отсечения – это подтверждение того, что когда значение первого аргумента есть [], то только первое правило применимо. Однако рассмотрим, что произойдет, если мы имеем целевое утверждение
присоединить(Х,Y,[а,b,с]).
Это целевое утверждение будет сопоставлено с заголовком первого правила, что даст
X = [], Y = [a,b,c]
но затем встретится отсечение. Это приведет к тому, что будет заморожен сделанный нами выбор правила, и как следствие в случае если мы обратимся за новым решением, ответ будет «нет», даже если в действительности для данного запроса имеются другие решения.
Приведем другой интересный пример того, что может произойти, если правило, содержащее отсечение, используется незапланированным способом. Давайте определим предикат
число_родителей, который дает информацию о том, сколько родителей имеет человек. Мы можем определить его следующим образом:
число_родителей(адам,0):-!.
число_родителей(ева,0) :-!.
число_родителей(Х,2).
то есть число родителей для
адам и
ева равно 0, а для всех
остальных равно 2. Если мы всегда используем наше определение предиката
число_родителей для определения числа родителей некоторого данного человека, то все идет нормально. Мы получаем
?- число_родителей(ева,Х).
X = 0; нет
?- число_родителей(джон,Х).
X = 2;
нет
и так далее, как это и требуется. Отсечение необходимо, чтобы предотвратить процесс возврата, который мог бы привести к третьему правилу в случае, когда человек – это
адам или
ева. Однако рассмотрим, что произойдет, если мы используем те же самые правила, чтобы проверить, что данный человек имеет данное число родителей. Все хорошо, за исключением того, что мы получаем
?- число_родителей(ева,2).
да
Вам следует самостоятельно разобраться, почему так получается – это просто следствие стратегии, применяемой в Прологе для поиска в базе данных. Наша реализация обработки «остальных» случаев, основанная на использовании отсечения, просто больше не работает надлежащим образом. Существуют два способа изменить определение, которые позволили бы нам устранить указанный эффект:
число_родителей(адам,N):-!, N=0.
число_родителей(ева,N):-!, N=0.
число_родителей(Х,2).
или
число_родителей(адам,0).
число_родителей(ева,0).
число_родителей(Х,2):- X \= адам, X \= ева.
Конечно, эти определения по-прежнему не работают, если задать целевое утверждение вида
?- число_родителей(Х,Y).
ожидая, что возврат позволит перечислить все возможности. Таким образом, можно сделать следующий вывод:
Если вы вводите отсечения для того, чтобы обеспечить правильную работу программы для целевых утверждений определенной формы, то нет гарантии, что при появлении целевых утверждений иной формы будет происходить что-либо разумное. Отсюда следует, что надежное использование отсечения возможно лишь в том случае, когда вы имеете четкое представление о том, как ваши правила будут использоваться. Если характер использования правил меняется, то необходимо пересмотреть все случаи употребления отсечения.
ГЛАВА 5 ВВОД И ВЫВОД
В предыдущих главах фигурировал только один способ предоставления информации Пролог-программе – обращение к ней с вопросом. Точно так же единственный способ определить значение переменной на некотором этапе доказательства согласованности целевого утверждения с базой данных состоял в построении вопроса таким образом, чтобы Пролог-система напечатала ответ в виде «Х=ответ». В большинстве случаев такого непосредственного взаимодействия с программой посредством вопросов вполне достаточно, чтобы убедиться в том, что программа работает правильно. Однако во многих ситуациях удобно писать программу на Прологе так, чтобы она сама инициировала диалог с пользователем. Например, предположим, что имеется база данных, содержащая информацию о событиях, происходивших в мире в 16-м веке. Информация представлена в виде фактов, включающих дату события и его краткое содержание. Даты могут быть представлены как целые числа, а содержание – в виде списков атомов. Те атомы в списке, которые начинаются с прописной буквы, будут заключаться в одинарные кавычки, чтобы Пролог не принял их за переменные:
событие(1505, ['Начала','Евклида', переведены, на, латинский, язык]).
событие(1510, ['Начало', спора, между, 'Реучлином', и 'Пфефферкорном']).
событие(1523, [Кристиан, 'II', покинул, 'Данию']).
. . .
Теперь, для того чтобы узнать, что связано с конкретной датой, мы могли бы задать следующий вопрос:
?- событие(1505,Х).
на что Пролог напечатал бы ответ:
Х=['Начала', 'Евклида', переведены, на, латинский, язык]
Представление краткого содержания событий в виде списков атомов дает возможность определить дату событий по некоторым ключевым моментам, имевшим место. Например, рассмотрим предикат
когда, который мы определим ниже. Целевое утверждение
когда(Х, Y) доказуемо, если в заголовке события, имевшего место в году Y, упоминается X:
когда(Х,Y):- событие(Y,Z), принадлежит (X,Z).
?- когда(Кристиан,D).
D=1523
Один из недостатков использования списков атомов заключается в том, что их неудобно вводить в систему, особенно если атомы начинаются с прописной буквы. Другая возможность, которая имеет свои недостатки и преимущества,- это представлять названия событий в виде списков литер. Из предыдущих глав мы знаем, что списки литер представляются в виде строк литер, заключенных в двойные кавычки:
событие(1511, "Лютер посещает Рим").
событие(1521, "Генри III провозглашен защитником веры").
событие(1524, "Умер Васко да Гама").
событие(1529, "Берквин сожжен в Париже").
событие(1540, "Возобновление войны с Турцией").
. . .
Такая форма представления удобнее для ввода, но посмотрим, что произойдет, если задаться вопросом
?- событие(1524,X).
В ответ Пролог напечатает непонятный список кодов ASCII, соответствующих литерам строки, являющейся значением переменной
X! Хотя список литер легче ввести в систему, механизм 'вопрос – ответ' Пролога не позволяет получить ясный ответ. Было бы намного удобнее, если бы вместо того, чтобы обращаться к Прологу с подобными вопросами, можно было написать программу, которая вначале спрашивает, какая дата вас интересует, а затем выводит содержание соответствующего события на терминал. При этом названия событий можно было бы представлять в желаемом виде. Для выполнения задач подобного сорта в Прологе существует ряд встроенных предикатов, которые печатают свои аргументы на терминале. Имеются также предикаты, которые ожидают, пока пользователь введет текст с клавиатуры терминала, и присваивают переменной в качестве значения введенный текст. С помощью этих предикатов программа может взаимодействовать с вами, принимая от вас данные и печатая для вас результат. Когда программа ждет от вас данные, будем говорить, что она
читает или
вводит данные. Точно так же, когда программа печатает некоторый результат, будем говорить, что она
выводит результат. В этой главе мы описываем различные методы ввода и вывода данных. Один из рассматриваемых примеров связан с печатью кратких содержаний событий из базы данных исторических событий, а в заключение будет приведена программа, воспринимающая предложения на естественном языке и преобразующая их в список констант, который впоследствии может быть подвергнут обработке другими программами. Эта преобразующая программа, названная
ввести, может использоваться как некий «модуль», с помощью которого можно создавать программы для анализа предложений на естественном языке. Программы, выполняющие такой анализ, обсуждаются в последующих главах, особенно в гл. 9.
5.1. Ввод и вывод термов
5.1.1. Вывод термов
Наиболее удобный способ напечатать некоторый терм на дисплее терминала состоит, по-видимому, в использовании встроенного предиката
write. Если значением переменной
X является терм, то появление цели
write(X) вызовет печать этого терма на дисплее. В случае если переменная
X неконкретизирована, будет напечатано некоторое уникальное имя, которое состоит из одних цифр (например, '_253'). Однако если две переменные «сцеплены» в пределах одного и того же аргумента предиката
write, то им будет соответствовать одна и та же переменная. Предикат
write нельзя согласовать вновь. Этот предикат выполняется лишь один раз, и всякая попытка вновь согласовать его заканчивается неудачей. Нельзя ли использовать
write для вывода краткого содержания исторических событий в нашем примере? Вспомните, что строка литер в действительности представляется как список кодов литер. Если бы такой список был выведен с помощью предиката
write, то он был бы напечатан как заключенная в квадратные скобки последовательность целых чисел, разделенных запятыми!
Прежде чем мы познакомимся с первым примером использования предиката
write, нам нужно описать еще два предиката. Встроенный предикат
nl применяется для перехода на новую строку при печати данных на дисплее. Название «
nl» образовано от
«new line» (новая строка). Как и
write, предикат
nl выполняется только один раз. Следующий встроенный предикат
tab используется для печати пробелов на экране дисплея. Целевое утверждение
tab(X) выполняется только раз и вызывает перемещение курсора на
X позиций вправо. Предполагается, что значение переменной
X – целое число. Возможно, выбор имени
tab не очень удачен, так как в действительности этот предикат не имеет ничего общего с табуляцией на обычных пишущих машинках или на дисплеях терминалов.
При печати списков полезно печатать элементы списка таким образом, чтобы получаемый результат можно было легко понять. Списки, которые содержат другие «вложенные» списки, читать особенно трудно, тем более когда внутри них содержатся структуры. Определим предикат
рр (
pretty print – «хорошая печать») так, что целевое утверждение
рр(Х, Y) печатает в удобном виде список, присвоенный в качестве значения переменной
X. Смысл второго аргумента предиката рр будет объяснен позднее. Каждый автор программы, реализующей хорошую печать, имеет свой собственный стиль представления списков. Мы воспользуемся методом, при котором элементы списка печатаются в колонку. Если элемент сам является списком, то его элементы печатаются в колонке, которая смещена вправо по отношению к основной колонке. Такая форма представления по существу совпадает с рассмотренным в гл. 3 способом изображения списков. Например, список [1,2,3] «хорошо» печатается в следующем виде:
1
2
3
а список
[1,2,[3,4],5,6] печатается как
1
2
3
4
5
6
Заметим, что мы решили не печатать квадратные скобки и запятые, разделяющие элементы списка. Если элемент списка является структурой, то он будет обрабатываться точно таким же способом, что и атом. При таком подходе нам не нужно «раскрывать организацию» структур, чтобы «хорошо» напечатать их компоненты. Следующая программа реализует определенный нами способ хорошей печати:
pp([H|T],I):-!, F is I+3, pp(H,F), ppx(T,F),nl.
pp(X,I):- tab (I), write(X), nl.
ppx([],_).
ppx([H|T],I):- pp(H,I), ppx(T,I).
Теперь видно, что второй аргумент предиката
рр выполняет функции счетчика колонок. Целевое утверждение «верхнего уровня» для печати некоторого списка могло бы выглядеть как
… PP(L,0),…
при этом начальное значение счетчика колонок устанавливается равным 0. Первое утверждение предиката
рр обрабатывает специальный случай – когда первый аргумент является списком. Если это так, то необходимо установить новую колонку, увеличив счетчик на некоторое число (здесь 3). Затем мы должны отпечатать с помощью
рр голову списка, так как она сама может оказаться списком. Далее нужно напечатать все элементы хвоста списка, располагая каждый элемент в той же самой колонке. Это как раз и выполняет предикат
ррх. А предикат
ррх использует
рр, поскольку каждый элемент может быть списком. Второе утверждение предиката
рр соответствует случаю, когда нам необходимо напечатать что-либо, не являющееся списком. Мы просто делаем отступ на указанное число позиций, используем предикат
write для печати терма и
nl для перехода на новую строку. Первое утверждение для
рр также заканчивается
nl, поскольку печать каждого списка должна завершиться переходом на новую строку.
Отметим, что в предикате
рр мы поместили утверждение для обработки особого случая перед утверждением, обрабатывающим выход на граничное условие. Если бы мы поместили второе утверждение перед первым утверждением, то тогда список, являющийся первым аргументом предиката рр, был бы сопоставлен с переменной
X в заголовке второго правила. В результате получилось бы, что список был бы просто напечатан как единое целое без удобств и «хорошей» печати. Поэтому мы хотим, чтобы случай, когда аргумент является списком, проверялся первым. Именно поэтому мы выбрали такой порядок утверждений. Второе утверждение используется как правило-ловушка. Другой способ добиться такого же результата состоит в том, чтобы правило, осуществляющее проверку граничного условия, поставить первым и включить в его тело подцель, которая не выполняется, если первый аргумент является списком:
рр(Х,I):- not(список(Х)), tab(I), write(X), nl.
pp([H|T],I):- J is I+3, pp(H,J), ppx(T,J), nl.
/*ppx как и ранее */
список([]) список([_|_]).
Нам потребовалось определить соответствующий предикат
список таким образом, что целевое утверждение
список(Х) является согласованным, если
X – список. Первый факт определения этого предиката указывает, что пустой список является списком. Второй факт указывает, что структура, имеющая голову и хвост, является списком. Строго говоря, следовало бы проверить, что хвост структуры также является списком, но мы опустили здесь эту проверку.
Давайте вернемся к фактам, представляющим предикат событие, который мы обсуждали в начале этой главы. Если есть одно из кратких содержаний событий, представленное в виде списка атомов, то можно использовать предикат
write, чтобы напечатать каждый атом, вставляя пробел между атомами. Рассмотрим предикат
phh для печати краткого содержания событий:
phh([]):- nl.
phh([H|T]):- write(H), tab(l), phh(T).
Так, при следующем запросе было бы напечатано каждое событие, в содержании которого встречается «Англия»:
?- событие(_,L), принадлежит('Англия',L), phh(L).
Обратим внимание на использование механизма возврата для поиска в базе данных. Каждый раз, когда для целевого утверждения
принадлежит не находится сопоставление, делается попытка найти новое сопоставление для целевого утверждения
событие. В результате в поисках событий, в которых упоминается атом
«Англия», будет целиком просмотрена сверху вниз вся база данных.
Предикат
write печатает термы с некоторым «пониманием» того, что он делает, так как он учитывает, какие объявления операторов были сделаны. Например, если мы объявили некоторый атом как инфиксный оператор, то терм, имеющий этот атом в качестве функтора структуры с двумя аргументами, будет напечатан таким образом, что атом окажется между аргументами. Существует еще один предикат, который выполняет те же действия, что и
write, за тем исключением, что он игнорирует все сделанные объявления операторов. Этот предикат называется
display. Различие между
write и
display иллюстрирует следующий пример:
?- write(a+b*c*c),nl, display(a+b*c*c).
a+b*c*c
+(a,*(*(b,c),c))
да
Обратим внимание на то, что предикат
display обработал атомы + и * – точно так же, как и любые другие атомы, которые он печатает в этом терме. Как правило, нежелательно, чтобы печатаемые структуры выглядели подобным образом, так как наличие операторов обычно делает более понятными при чтении как вводимые, так и выводимые программой данные. Однако иногда, когда мы не совсем уверены в том, что знаем, каков приоритет операторов, использование предиката
display может оказаться очень полезным.
5.1.2. Ввод термов
Предикат
read читает следующий терм, набираемый пользователем на клавиатуре терминала. После вводимого терма должны следовать точка '.' и непечатаемая литера, такая как пробел или
RETURN. Если переменная
X не конкретизирована, то целевое утверждение
read(X) приведет к вводу следующего терма и этот терм будет присвоен в качестве значения переменной
X, Как и другие предикаты ввода-вывода, с которыми мы уже сталкивались, предикат
read выполняется лишь один раз. Если в момент рассмотрения целевого утверждения
read(X) его аргумент конкретизирован, то попытка доказать согласованность этого целевого утверждения с базой данных вызовет чтение следующего терма и попытку сопоставления его с аргументом, заданным в
read. Согласованность цели с базой данных зависит от результата этого сопоставления.
Используя предикаты
read и
phh, как они были определены выше, мы можем написать программу для печати краткого содержания исторических событий, хранящихся в базе данных, с помощью фактов с предикатом
событие. Эта программа имеет вид:
обращение:-
phh(['Какая',дата,вас,'интересует?'!),read(D),coбытиe(D,S),pph(S).
Мы определили предикат
обращение, не имеющий аргументов. Когда мы обращаемся к системе с вопросом
?- обращение.
Пролог напечатает
Какая дата вас интересует?
и будет ждать ответа. Предположим, что мы ввели с клавиатуры
1523.
Обратите внимание на то, что после 1523 необходимо ввести точку, так как этого требует предикат
read. И, как обычно, мы должны нажать клавишу
RETURN, чтобы сообщить ЭВМ, что мы закончили ввод строки текста. После этого Пролог ответит
Кристиан II покинул Данию
Обратите внимание, что в первой строке тела правила
обращение используется предикат
phh, хотя в этом случае печатается не краткое содержание исторического события. Это просто показывает, что
phh вполне подходит для печати
произвольного списка атомов независимо от того, откуда он взялся.
5.2. Ввод и вывод литер
Наименьшей единицей данных, которая может участвовать в операциях ввода-вывода, является литера. Мы уже знаем, что литеры интерпретируются как небольшие целые числа в соответствии с кодом ASCII. В Прологе имеется несколько встроенных предикатов для ввода и вывода литер.
5.2.1. Вывод литер
Если переменная
X имеет в качестве значения некоторую литеру (ее код ASCII), то эта литера будет напечатана при обработке целевого утверждения
put(X). Предикат
put всегда выполняется и не может быть пересогласован (это приводит к неудаче). В качестве «побочного эффекта»
put печатает литеру на дисплее терминала. Например, мы можем напечатать слово
hello довольно необычным способом:
?- put(104),put(101),put(108),put(108),put(111).
hello
Результатом такой конъюнкции целей является печать Прологом литер
h,
е,
l,
l,
о непосредственно под вопросом, как показано выше. Мы уже видели, что имеется возможность начать печать текста с начала следующей строки, использовав для этого предикат без аргументов nl. В действительности nl «печатает» некоторые управляющие литеры, что вызывает перевод курсора на дисплее терминала на начало следующей строки. Вопрос
?- put(104),put(105),nl,put(116),put(104),put(101),put(114), put(1O1).
вызвал бы следующую печать:
hi
there
Другой предикат, с которым мы уже познакомились, - это
tab(X), печатающий
X пробелов (ASCII код равен 32). Разумеется, переменной
X должно быть присвоено целое число. Отметим, что предикат
tab(X) мог бы быть определен так:
tab(0):- !.
tab(N):- put(32), M is N-1, tab(M).
Теперь мы можем определить предикат, который мы назовем
печать_строки. Если значением переменной
X является список кодов литер (строка), то целевое утверждение
печать_строки напечатает этот список (строку), используя
put для печати каждого элемента списка. Как и во всех подобных программах, граничным условием является появление пустого списка. Это условие мы и используем для завершения рекурсии. При непустом списке с помощью
put печатается голова списка, а затем используем
печать_строки – хвост списка:
печать_строки([]).
печать_строки([Н|Т]):- put(H), печать_строки(Т).
?- печать_строки(«Чарлз V отрекся от престола в Брюсселе»).
Чарлз V отрекся от престола в Брюсселе
Если мы решили представлять краткое содержание исторических событий как строки литер, а не как списки атомов, то такого определения вполне достаточно, чтобы печатать строки из базы данных для предиката событие.
5.2.2. Ввод литер
Для ввода литер, набираемых на клавиатуре терминала, могут быть использованы предикаты
get0(X) и
get(X). Эти предикаты всегда согласуются с базой данных, если их аргументы неконкре-тизированы, а попытка повторного согласования всегда неудачна. При обработке целей, включающих эти предикаты, ЭВМ ожидает до тех пор, пока пользователь не наберет на клавиатуре какую-либо литеру. Указанные предикаты немного различаются тем, что
get0(X) присвоит
X любую набранную на клавиатуре литеру независимо от ее вида. Напротив,
get(X) пропустит все
управляющие литеры и присвоит
X в качестве значения первую печатаемую литеру. Как отмечалось в гл. 2, печатаемая литера – это литера, которая визуализируется на дисплее терминала.
Если
X уже присвоено значение, то целевое утверждение
get(X) пропустит все управляющие литеры и сравнит следующую за ними печатаемую литеру со значением
X. Доказательство согласованности целевого утверждения зависит от результата этого сравнения. Целевое утверждение
get0(X) сравнивает
X со следующей литерой и в зависимости от совпадения считается согласованным с базой данных или нет.
В следующем разделе приводятся некоторые примеры с использованием предикатов для чтения литер. Заранее обращаем внимание читателя на те случаи, когда возникает необходимость в возврате за целевое утверждение
get.
5.3. Ввод предложений
В этом разделе мы представим программу, которая вводит предложение с терминала и преобразует его в список атомов языка Пролог. В программе определяется предикат
ввести, имеющий один аргумент. Программа должна уметь определять, где заканчивается одно вводимое слово и начинается следующее. Поэтому предположим, что слово состоит из нескольких букв, цифр или специальных литер. Буквы и цифры уже были представлены в разд. 2.1. Мы будем рассматривать одиночную кавычку ''' и дефис '-' как специальные литеры. Литеры
, ; : ? ! .
будут рассматриваться как отдельные слова. Все другие литеры являются разделителями между словами. Предложение считается законченным, когда встречается одно из слов '.', '!' или '?'. Прописные буквы автоматически преобразуются в строчные, так что одно и то же слово всегда превращается в один и тот же атом. В результате такого определения программа будет поддерживать диалог с пользователем, подобный следующему:
?- ввести(S).
The man, who is very rich, saw John's watch.
S = [the,man,',',who,is,very,rich,',',saw,'John's',watch,'.']
В действительности мы вставили в представление предложения дополнительные одинарные кавычки, чтобы выделить некоторые атомы.
Программа использует предикат
get0 для ввода литер с терминала. Затруднение, связанное с предикатом
get0, состоит в том, что если литера прочитана с терминала этим предикатом, то она «ушла навсегда» и никакое другое целевое утверждение
get0 или попытка вновь доказать целевое утверждение
get0 не позволит получить доступ к этой литере вновь. Поэтому следует избегать возврата за точку использования
get0, если мы хотим избежать «потери» литеры, которую он читает. Например, следующая программа, которая должна вводить литеры и печатать их снова, заменяя литеры
а на
b (код литеры
97 на код
98), не будет работать:
выполнить:- заменить_литеру, выполнить.
заменить_литеру:- get0(X) = 97,!, put(98).
заменить_литеру:- get0(X), put(X).
Приведенную программу в любом случае нельзя считать хорошей, потому что она будет работать вечно. Однако рассмотрим эффект попытки доказать согласованность целевого утверждения
заме-нить_литеру. Если первое правило определения предиката заме-нить_литеру используется для чтения литеры, код которой отличен от
97, то возврат приведет к тому, что будет сделана попытка воспользоваться вместо него вторым правилом. Однако согласование целевого утверждения
get0(X) во втором правиле приведет к тому, что X будет конкретизирована
следующей литерой. Это объясняется тем, что доказательство исходного целевого утверждения
get0 было
необратимым процессом. Таким образом, эта программа в действительности не печатала бы все литеры. Она даже иногда печатала бы литеры
а.
Как же программа
ввести преодолеет проблемы возврата при вводе? Ответ заключается в том, что программа конструируется таким образом, что она вводит литеры с опережением на одну литеру, а проверки литеры выполняются правилом, отличным от правила, в котором эта литера была прочитана. Если литера введена в каком-то месте программы и не может быть здесь же использована, то она возвращается обратно для возможного использования другими правилами. В соответствии со сказанным предикат для ввода одного слова читать_слово в действительности имеет три аргумента. Первый предназначен для литеры, которая была получена при последнем выполнении
get0 где-либо в программе, но которую оказалось невозможным использовать в месте ее получения. Второй предназначен для атома, который будет создан для прочитанного слова. Последний аргумент предназначен для литеры, следующей во вводимом предложении сразу за прочитанным словом. Для того чтобы определить, где кончается слово, необходимо ввести литеру, следующую непосредственно за словом. Эта литера должна быть сохранена, потому что она может оказаться первой литерой другого слова.
Здесь приведен текст программы:
/* Прочитать предложение */
ввести([Сл|Слс]):- get0(C), читать_слово(С,Сл,С1), остаток_предложения(Сл, С1, Слс).
/* Дано слово и литера после него, ввести остаток предложения */
остаток_предложения (Сл,_,П):- последнее_слово (Сл),!.
остаток_предложения(Сл,С,[Сл1|Слс]):- читать_слово(С, Сл, С1), остаток_предложения(Сл1,С1,Слс).
/* Ввести одно слово, имея начальную литеру и запомнив, какая литера идет после слова */
читать_слово(С,Сл,С1):- литера(С),!, name(Сл,С), get0(C1).
читать_слово(С,Сл,С2):- слово(С, Нс),!,get0(Cl),
остаток_слова(С1,Сс,С2),name(Сл,[Нс|Сс]).
читать_слово(С,Сл,С2):-get0(Cl), читать_слово (С1, Сл,С2).
остаток_слова(С,[Нс|Сс],С2):-слово(С,Нс),!,get0(Cl),остаток_слова (С1, Сс, С2
). остаток_слова(С, [],С).
/* Эти литеры образуют отдельные слова */
литера(44) /*, */
литера(59) /*; */
литера(58) /*: */
литера(63) /*? */
литера(ЗЗ) /*! */
литера(46) /*. */
/* Следующие литеры могут встретиться внутри слова */
/* Второй факт для предиката
слово преобразует прописные литеры в строчные
слово(С,С):- С › 96, С ‹ 123. /* a b… */
слово(С,М):- С › 64, С ‹ 91, M is С+ 32. /*А В… */
слово(С,С):- С › 47, С ‹ 58 /* 1 2… 9*/
слово(39,39). /* ' */
слово(45,45) /* – */
/* Следующие слова заканчивают предложение */
последнее_слово('.').
последнее_слово('!').
последнее_слово('?').
Упражнение 5.1. Объясните, для чего используется каждая переменная в приведенной программе.
Упражнение 5.2. Напишите программу, которая читает неограниченную последовательность литер и печатает ее, предварительно заменяя вхождения литеры
а литерой
b.
5.4. Чтение файлов и запись в файлы
Предикаты, обсуждавшиеся в этой главе ранее, использовались для ввода (чтения) и вывода (записи) данных при обмене лишь с терминалом, но они могут быть использованы и в более общих ситуациях. В Пролог-системе определяется
текущий входной поток данных, из которого производится чтение всех вводимых данных. Все выводимые данные записываются в
текущий выходной поток данных. В обычном состоянии текущий входной поток данных поступает с клавиатуры терминала, а текущий выходной поток данных направляется на дисплей терминала. Часто оказывается удобно выполнять операции чтения и записи данных над
файлами, которые представляют последовательность литер во вторичной внешней памяти. Конкретный вид этой памяти зависит от используемой ЭВМ, но сейчас файлы обычно хранятся на магнитных дисках. Предполагается, что каждый файл имеет собственное
имя(имя файла), используемое для идентификации файла. Для того чтобы содержание этой главы было понятно, читателю следует познакомиться с правилами организации и способом задания имен файлов в той операционной обстановке, в которой он работает. В Прологе имена файлов представляются атомами, но мы не можем исключить возможность каких-либо ограничений на синтаксис имен файлов, накладываемых конкретной обстановкой, в которой работает Пролог-система.
Файлы имеют определенную длину. Это означает, что они содержат определенное количество литер. В конце файла имеется специальный маркер, называемый
маркером конца файла. Мы не обсуждали маркер конца файла до сих пор, так как выход на конец файла является более обычным делом для файлов, расположенных во внешней памяти, чем при обмене с терминалом. Если программа производит чтение файла, то маркер конца файла может быть обнаружен и в случае, когда программа читает термы и когда читаются отдельные литеры. Если при выполнении
get0(X) встречается конец файла, то
X будет конкретизирована некоторой управляющей литерой, обычно имеющей код 26 в таблице кодов ASCII. Если конец файла встречается при выполнении
read(X), то
X будет конкретизирована некоторым специальным термом, значение которого зависит от конкретной Пролог-системы. При попытке прочитать файл далее маркера конца возникает ошибка.
Имеется встроенный (стандартный) файл, называемый
user. Чтение этого файла вызывает ввод данных с клавиатуры терминала, а запись в этот файл приводит к тому, что литеры печатаются на дисплее. Такой режим работы считается стандартным. При вводе с клавиатуры терминала признак конца файла генерируется при вводе управляющей литеры с кодом ASCII 26. Это окажет на выполнение
get0 и
read такое же воздействие, как если бы встретился конец файла.
5.4.1. Запись в файлы
Для записи в файлы термов и литер могут быть использованы в точности те же самые предикаты, что обсуждались ранее Единственное различие состоит в том, что когда мы хотим записать данные в файл, то нам надо сменить
текущий выходной поток данных так, чтобы им являлся файл, в который мы будем записывать данные, а не дисплей терминала. Текущий выходной поток данных изменяется с помощью предиката
tell. Если
X конкретизирована именем файла, которое должно быть атомом, то целевое утверждение
tell(X) переключает текущий выходной поток данных таким образом, что любая операция записи (выполняемая с помощью
write, put и других подобных предикатов) будет производиться в этот файл, а не на дисплей терминала. Целевое утверждение
tell(X) можно согласовать лишь один раз. Точно так же при выполнении Прологом возврата за целевое утверждение
tell не происходит восстановления прежнего текущего выходного потока данных. Наряду со сменой текущего выходного потока данных предикат
tell в зависимости от ситуации выполняет также другие операции. В первый раз, когда программа обращается к
tell с конкретным именем файла
X, Пролог считает, что необходимо завести новый файл с этим именем. Поэтому если
X конкретизирована некоторым именем файла и файл с таким именем уже существует, то все литеры, уже содержащиеся в этом файле, удаляются. Напротив, если файла с именем, являющимся значением
X, не существует, то файл с таким именем будет создан. В обоих случаях файл считается открытым (для записи в него). Это значит, что каждая последующая запись в этот файл будет добавлять литеры в конец файла до тех пор, пока не появится явное указание, что запись в файл полностью завершена (пока файл не будет закрыт). С данного момента если будет сделана новая попытка записи в этот файл, то Пролог, как и прежде, будет считать, что необходимо писать новую версию этого файла. При попытке выполнить
tell(X), когда переменная
X не имеет конкретного значения или ее значение не является именем файла, возникает ошибка. Реакция Пролог-системы на возникающие ошибки зависит от конкретной реализации.
Предикат
telling используется для определения имени файла, служащего текущим выходным потоком данных. Целевое утверждение
telling(X) считается согласованным, если
X имеет своим значением имя файла текущего выходного потока данных. Как вы, наверное, догадываетесь, если X неконкретизировано, то
telling конкретизирует
X атомом (именем файла), делающим это целевое утверждение верным.
Когда запись в файл полностью завершена, то выполнение предиката
told оформит конец файла и закроет его (для вывода). Кроме того, в результате его выполнения текущим выходным потоком данных снова станет дисплей терминала. Таким образом, типичная последовательность целевых утверждений для записи в файл некоторой совокупности литер имеет вид
… tеll(фред), write(X), told,…
Если текущий выходной поток данных переключается на другой файл без использования
told, то прежний файл не будет закрыт и останется доступным для записи в него. Это позволяет делать записи в файл с перерывами, как в следующем примере;
…tell (X), write(A), tell(user),write(B), tell(X), write(C), told.
5.4.2. Чтение файлов
Предикаты, которые предоставляет Пролог для переключения текущего входного потока данных, аналогичны предикатам, обсуждавшимся выше. Целевое утверждение
see(X) переключает текущий входной поток данных на файл с указанным именем. Так же как и
tell, это целевое утверждение не может быть доказано вновь, и выполненное предикатом изменение входного потока не переделывается при возврате. При первом выполнении
see(X) для некоторого файла
X этот файл становится открытым (для чтения), при этом чтение начинается с начала файла. Последующая операция чтения продолжает читать данные с того места, где закончила предыдущая операция. И так до тех пор, пока не будет сделано явного закрытия файла. С этого момента новая попытка читать из файла приведет к тому, что файл будет открыт и чтение начнется с начала файла, как и прежде. Текущий входной поток данных может быть определен в результате выполнения
seeing(X), и текущий входной поток данных может быть переключен обратно на ввод с терминала в результате выполнения целевого утверждения
seen, которое также закрывает файл.
5.4.3. Ввод программ
Чтение данных из файлов и запись данных в файлы наиболее полезны тогда, когда объем данных, с которыми работает наша программа и которые мы хотим поместить в базу данных, превосходит тот объем, который мы можем вводить вручную при каждом сеансе работы с ЭВМ. В Прологе файлы используются главным образом для хранения программ. Если текст Пролог-программы содержится в некотором файле, то мы можем прочитать все утверждения, содержащиеся в файле, и поместить их в базу данных, воспользовавшись для этого предикатом
consult. Если значением
X является имя файла, то цель
consult(X) прочитает утверждения (факты и правила) и целевые утверждения из этого файла. Большинство реализаций Пролога имеют специальную форму записи для предиката
consult, позволяющую прочитать последовательно один за другим список файлов. Если вопрос к Пролог-системе имеет вид списка атомов, то Пролог-система прочитает каждый файл из этого списка. В качестве примера использования такой формы записи приведем следующий вопрос:
?- файл1, отображение, эксперт.
Этот вопрос обрабатывается таким образом, как если бы Пролог выполнял целевое утверждение
consultall(X), где
X - это список, заданный в вопросе, а предикат
consultall определен следующим образом:
consultall([]).
consultall(H|T]):- consult(H), consultall(T).
Однако короткая списковая запись более экономична, а это особенно важно, если принять во внимание, что самое первое действие, которое выполняет работающий с Прологом программист,- это чтение из файлов своих предикатов. Предикат
consult автоматически прекращает чтение утверждений, когда встречается конец файла. В разд. 6.1 предикат
consult описывается более подробно.
5.5. Объявление операторов
Причина, по которой операторы рассматриваются в главе, посвященной вводу-выводу, состоит в том, что операторы предоставляют некоторые синтаксические удобства при чтении и записи термов. Никаких других причин для введения операторов нет. Для начала коротко напомним сказанное в разд. 2.3, а затем расскажем о том, как объявляются операторы.
Синтаксис языка разрешает использование операторов, обладающих следующими тремя свойствами: позицией, приоритетом и ассоциативностью. По занимаемой позиции операторы могут быть инфиксными, постфиксными или префиксными (оператор, имеющий два аргумента, может располагаться между аргументами; оператор с одним аргументом может находиться либо после аргумента, либо перед ним). Приоритет оператора – это некоторое целое число, диапазон изменения которого зависит от конкретной реализации Пролога. Предположим, что оно находится в диапазоне от
1 до
255. Приоритет используется для того, чтобы придать однозначную интерпретацию выражениям в тех случаях, когда синтаксис термов не задан явно с помощью скобок. Ассоциативность необходима для придания однозначной интерпретации выражениям, в которых имеются два оператора с одинаковыми приоритетами. Оператору в языке Пролог соответствует специальный атом, который специфицирует позицию и ассоциативность оператора. Для инфиксных операторов возможны следующие спецификации:
xfx xfy yfx yfy
Чтобы понять смысл этих спецификаций, их полезно рассматривать как «образцы» возможного использования операторов. В приведенных образцах буква
f представляет оператор, а
х и
у – аргументы. Таким образом, во всех приведенных выше образцах оператор должен находиться
между двумя аргументами, т. е. он является инфиксным оператором. В соответствии с этим соглашением
fx fy
есть две спецификации для префиксных операторов (оператор записывается перед его единственным аргументом). Точно так же
xf yf
представляют возможные спецификации для постфиксных операторов. Может вызвать недоумение использование двух букв для обозначения аргументов. Использование букв
х и
у в той или иной позиции позволяет выразить информацию об ассоциативности оператора. В предположении, что выражение не содержит скобок, буква у указывает, что соответствующий ей аргумент может содержать операторы с приоритетом, равным приоритету данного оператора или с более низким приоритетом. Напротив, буква
х указывает, что каждый оператор в соответствующем ей аргументе должен иметь строго более низкий приоритет по сравнению с приоритетом данного оператора. Рассмотрим, что это значит для оператора +, объявленного как
yfx. Если имеется выражение
а + b + с
то для него возможны две следующие интерпретации:
(а + b) + с а + (b + с)
Вторая интерпретация исключается, так как при этом аргумент, стоящий после первого вхождения +, содержит оператор с тем же самым приоритетом (второй оператор +). Это противоречит тому, что в спецификации оператора + после
f стоит
х.
Оператор, имеющий спецификацию
yfx, является левоассоциативным. Аналогично оператор со спецификацией
xfy является правоассоциативным. Если мы знаем необходимую ассоциативность объявляемого инфиксного оператора, то это значит, что однозначно определяется соответствующая оператору спецификация.
Заметим, что использование букв
х и
у в двух других случаях имеет тот же смысл относительно того, какие операторы могут появляться в соответствующей позиции при отсутствии скобок. Это значит, что, например, последовательность
not not a
допустима синтаксически, если оператор
not объявлен как
fy, и недопустима в случае, когда он объявлен как
fx.
Если мы хотим объявить на Прологе оператор с заданными позицией, приоритетом и ассоциативностью таким образом, чтобы Пролог распознавал его при вводе и выводе термов, то мы используем встроенный предикат
ор. Если
Имя - это оператор, который мы желаем иметь (атом, который мы хотим сделать оператором),
Приоритет - приоритет оператора (целое число в соответствующем диапазоне) и
Спецификация - спецификация, определяющая положение и ассоциативность оператора (один из приведенных выше атомов), то такой оператор может быть объявлен с помощью выполнения следующего целевого утверждения
?- ор (Приоритет,Спецификация,Имя).
Если объявление оператора является допустимым, то эта цель будет достигнута.
В качестве примера объявления операторов далее приводится полный список базовых операторов, обсуждаемых в данной книге. Конкретные реализации Пролога могут иметь несколько отличный набор «стандартных» операторов; может потребоваться масштабирование указанных приоритетов. Однако взаимный порядок операторов в иерархии приоритетов обычно остается неизменным.
?-op(255,xfx,':-').
?-op(255,fx,'?-').
?-op(254,xfy,';').
?-op(253,xfy,',').
?-op(250,fx,spy).
?-op(250,fx,nospy).
?-op(60,fx,not).
?-op(51,xfy,'.').
?-op(40,xfx,is).
?-op(40,xfx,' =..').
?-op(40,xfx,=).
?-op(40,xfx,\=).
?-op(40,xfx,‹).
?-op(40,xfx,=‹).
?-op(40,xfx,›=).
?-op(40,xfx,›).
?-op(40,xfx, ==).
?-op(40,xfx,\==).
?-op(31,yfx,-).
?-op(31,yfx,+).
?-op(21,yfx,/).
?-op(21,yfx,*).
?-op(ll,xfx, mod).
ГЛАВА 6. ВСТРОЕННЫЕ ПРЕДИКАТЫ
В этой главе будут описаны некоторые
встроенные предикаты, которые может обеспечивать Пролог-система. Что имеется в виду, когда мы говорим, что предикат является встроенным? Это значит, что определение этого предиката уже имеется в Пролог-системе и нет необходимости иметь собственное его описание. Встроенные предикаты предоставляют возможности, которые нельзя реализовать с помощью описаний на чистом Прологе. Они также могут предоставлять удобные средства, избавляя программиста от необходимости самому определять эти предикаты. В действительности мы уже встречались с некоторыми встроенными предикатами – это предикаты для ввода и вывода, обсуждавшиеся в гл. 5. Оператор «отсечения» тоже можно рассматривать как встроенный предикат.
Предикаты для ввода-вывода показывают, что встроенные предикаты могут иметь «побочные эффекты». Это значит, что при доказательстве согласованности целевого утверждения, содержащего такой предикат, помимо конкретизации аргументов предиката могут возникнуть дополнительные изменения. Это, естественно, не может случиться с предикатами, определенными на чистом Прологе. Другой важный факт, касающийся встроенных предикатов, состоит в том, что они могут быть определены только для аргументов конкретного вида. Например, рассмотрим предикат '‹' определенный таким образом, что
Х‹Y выполняется, если число
X меньше, чем число
Y. Подобное отношение не может быть определено в Прологе без помощи посторонних средств,
использующих некоторые знания о числах. Таким образом,
‹ – это встроенный предикат, а его определение использует некоторые операции вычислительной машины, на которой реализована Пролог-система, для определения относительной величины чисел (представленных в виде двоичного кода или каким-либо иным способом).
Что произойдет, если мы используем в качестве целевого утверждения предикат
X‹Y, где
X является атомом или даже более того, если как
X, так и
Y неконкретизированы? Определение предиката, данное на машинном языке, окажется просто неприменимым. Поэтому мы должны оговорить, что предикат
X‹Y может быть использован в качестве целевого утверждения, если на момент, когда делается попытка выполнить его, обе переменные
X и
Y имеют в качестве значений числа. Что произойдет в случае, когда это условие не выполняется, зависит от конкретной реализации Пролог-системы. Возможно, доказательство согласованности такого целевого утверждения просто закончится неудачей. А может быть, будет напечатано сообщение об ошибке и система выполнит ряд действий, соответствующих этой ситуации (подобных прекращению попыток ответить на текущий вопрос).
6.1. Ввод новых утверждений
Когда вы пишете программу на Прологе, вам следует сообщить системе, какие утверждения нужно использовать, и затем задавать относительно них вопросы. Возможно, вы захотите вводить утверждения с терминала или захотите указать Пролог-системе приготовленный вами заранее файл, откуда следует брать утверждения. В действительности обе эти операции с точки зрения Пролога одинаковы, так как терминал рассматривается как файл, имеющий имя
user. Имеются два основных встроенных предиката для ввода новых утверждений:
consult и
reconsult. Кроме того, в языке существует удобная форма записи на случай, когда вы захотите ввести утверждения сразу из нескольких файлов,- так называемая списковая форма записи. Для тех, кому это интересно, укажем, что в разд. 7.13 приведены простые определения на Прологе предикатов
consult и
reconsult.
consult(X)
Встроенный предикат
consult предназначен для использования в тех ситуациях, когда вы хотите добавить утверждения из некоторого файла /или вводимые с терминала) к утверждениям, уже имеющимся в базе данных. Аргумент предиката должен быть атомом, указывающим имя файла, из которого должны браться утверждения. Какие литеры составляют допустимое имя файла, естественно, зависит от конкретной, используемой вами ЭВМ. Ниже приведены примеры возможной записи целевого утверждения с предикатом
consult на различных ЭВМ:
?- consult(myfile).
?- consult('/us/gris/pl/chat').
?- consult('lib:iorout.pl'),
В случае когда Пролог должен доказать согласованность целевого утверждения consult, он просматривает файл, добавляя утверждения, которые он обнаруживает, в конец базы данных. В результате новые утверждения будут помещены после всех уже имевшихся утверждений для тех же предикатов. Если в файле будет обнаружен вопрос, то он будет рассматриваться точно так же, как обычный вопрос, за тем исключением, что ответ не будет напечатан. Обычно не имеет смысла вставлять вопросы в файл с новыми утверждениями, за исключением тех случаев, когда необходимо сделать операции, подобные объявлению новых операторов и печати полезных сообщений.
reconsult(X)
Предикат
reconsult аналогичен предикату
consult, за исключением того, что вводимые утверждения
заменяют все имеющиеся утверждения для того же самого предиката. Вследствие этого reconsult удобно использовать для исправления ошибок в программе. Если вы вводите некоторые файлы с утверждениями и затем обнаруживаете, что одно из утверждений содержит ошибку, то вы можете исправить ее, и для этого нет необходимости вводить заново все файлы. Чтобы сделать это, вам необходимо ввести с помощью
reconsult файл, содержащий совокупность правильных утверждений для предиката, содержащего ошибку. Вы можете ввести исправления либо непосредственно с терминала
(reconsult (user)), либо сначала отредактировать соответствующий файл, не выходя из Пролог-системы (такую возможность предоставляют не все реализации), и затем ввести этот файл с помощью
reconsult. Конечно, при вводе исправленных утверждений с терминала содержание
базы данных, с которой работает Пролог, изменится, но при этом исходный
файл, содержащий первоначальные утверждения с ошибками, останется неизменным! В разд. 8.5 показано использование предикатов
consult и
reconsult в процессе разработки программы.
Списковая форма записи
Пролог предоставляет специальную форму записи, позволяющую более удобно задавать предикаты
consult и
reconsult в качестве целевых утверждений, особенно в случае, когда вы хотите ввести более чем один файл. Для этого достаточно просто записать совокупность имен файлов (как атомов Пролога) в виде списка и задать этот список в качестве целевого утверждения. Если вы хотите, чтобы содержимое файла было просто добавлено к базе данных
(consult), то имя такого файла записывается в списке в том виде, как оно есть, если же вы хотите, чтобы при этом произошла замена уже имеющихся одинаковых предикатов
(reconsult), то перед именем файла ставится знак '-' (минус). Так, например, вопрос
?- [файл1,-файл2,'фред.1',-'билл.2'].
полностью эквивалентен следующему, но более длинному;
?- consult(файл1), reconsult(файл2), consult('фред:1'), reconsult('билл.2').
Списковая форма сводится к удобству записи, она не дает каких-либо дополнительных возможностей по сравнению с использованием предикатов
consult и
reconsult. Некоторые реализации Пролога могут использовать в списковой форме записи вместо знака '-' какой-нибудь иной знак, но эффект при этом останется прежним.
6.2. Выполнение и невыполнение целевого утверждения
При нормальном выполнении программы на Прологе целевое утверждение считается согласованным (с базой данных), когда это может быть доказано, и несогласованным в случае, когда доказательства найти не удается. В языке имеются два предиката, позволяющих удобно и явным образом определить случаи, когда целевое утверждение считается согласованным и когда несогласованным. Это предикаты
true и
fail.
true
Это целевое утверждение всегда согласуется с базой данных. В действительности этот предикат не является необходимым, так как утверждения в базе данных и цели могут быть переупорядочены или перегруппированы так, чтобы избежать использования предиката
true. Однако для удобства он входит в состав встроенных предикатов.
fail
Это целевое утверждение никогда не согласуется с базой данных. Имеются две ситуации, когда этот предикат оказывается полезным. Одна из них – это использование комбинации !-
fail, которая уже была описана в разд. 4.3. Конъюнкция целевых утверждений
…!, fail
применяется для того, чтобы указать, что
если процесс выполнения дошел до этого момента, то можно больше не пытаться доказать (согласовать) данное целевое утверждение. Конъюнкция считается несогласованной благодаря наличию предиката
fail, а родительское целевое утверждение не согласуется ввиду того, что использовано отсечение.
Другая ситуация, в которой используется предикат
fail, возникает, когда вы хотите явно указать, что для некоторого целевого утверждения нужно перебрать все решения. Возможно, вы захотите напечатать все возможные решения. Например, выполнение целевого утверждения
?- событие (X,Y), phh(Y), fail.
привело бы к печати всех событий, имеющихся в базе данных, рассмотренной в разд. 5.1, выбор событий и печать их краткого содержания выполняют предикаты событие и
phh, при этом цель окажется несогласованной с базой данных. Еще одно применение
fail рассмотрено в разд. 7.13 (в определении предиката
retrac-tall).
6.3. Классификация термов
Если вам надо определить предикаты, которые будут использоваться с аргументами различных типов, то полезно иметь возможность выделять в определении предиката ситуации, соответствующие каждому из возможных типов. В простейшем случае может понадобиться применять разные утверждения в зависимости от того, является ли аргумент целым числом или атомом. Разные утверждения могут потребоваться и для конкретизированных и неконкретизированных аргументов. Приводимые ниже предикаты позволяют программисту включить в утверждения эти дополнительные условия.
var(X)
Целевое утверждение
var(X) согласуется с базой данных, если на текущий момент
X является неконкретизированной переменной. Таким образом, возможен следующий диалог:
?- var(X).
да
?- var(23).
нет
?- X = Y, Y = 23, var(X).
нет
Неконкретизированная переменная может представлять часть некоторой структуры, которая еще не полностью заполнена. Примерами могут служить неотмеченные клетки на доске для игры в крестики-нолики, рассмотренной в разд. 4.3.3, и незаполненные части упорядоченного дерева, представляющего словарь в разд. 7.1. При работе с такими структурами предикат
var очень, полезен при определении, являются ли некоторые части структуры уже заполненными или нет. Это может предотвратить «случайную» конкретизацию переменной при попытке анализа ее значения. Например, при работе со словарем, представленным в виде упорядоченного дерева, может потребоваться узнать, имеется ли уже вход для некоторого ключа, не создавая такой вход в случае его отсутствия. При игре в крестики-нолики может возникнуть необходимость определить, занята или нет некоторая клетка. Попытка сопоставить неконкретизированную переменную с «
о» или «
х» привела бы просто к тому, что соответствующий символ был бы помещен в клетку, соответствующую переменной.
nonvar(X)
Целевое утверждение
nonvar(X) согласуется с базой данных, если
X на текущий момент не является неконкретизированной переменной. Предикат
nonvar является, таким образом, противоположным по отношению к предикату
var. Действительно, он может быть определен на Прологе следующим образом:
nonvar(X):- var(X),!, fail.
nonvar(_).
atom(X)
Целевое утверждение
atom(X) согласуется с базой данных, если текущее значение
X является атомом в смысле языка Пролог. Как следствие возможен следующий диалог:
?- atom(23).
нет
?- atom(apples).
да
?- atom('/us/qris/pl. 123').
да
?- atom("этo строка").
нет
?- atom(X).
нет
?- atom(book(bronte,w_h,X)).
нет
integer(X)
Целевое утверждение
integer(X) согласуется с базой данных, если на текущий момент
X обозначает целое число. Этот предикат можно использовать при определении простого предиката для упрощения арифметических выражений, где необходимо знать, является ли выражение целым числом (см., например, разд. 7.12).
atomic(X)
Целевое утверждение
atomic(X) согласуется с базой данных, если на текущий момент
X обозначает либо целое число, либо атом. Предикат
atomic может быть определен через предикаты
atom и
integer следующим образом:
atomic(X):- atom(X).
atomic(X):- integer(X)
6.4. Работа с утверждениями как с термами
Пролог позволяет программисту анализировать и изменять свою программу (т. е. утверждения, которые используются для доказательства согласованности его целевых утверждений). Это непосредственно следует из того, что утверждения можно рассматривать как обычные структуры языка Пролог. В связи с этим в Прологе есть встроенные предикаты, позволяющие программисту следующее:
• Создавать структуру, представляющую утверждения в базе данных.
• Добавлять к базе данных утверждение, представленное заданной структурой.
• Удалять из базы данных утверждение, представленное заданной структурой.
Большинство операций над базой данных могут быть выполнены с помощью этих предикатов и обычных операций языка Пролог для конструирования и декомпозиции структур. В дополнение к приведенным здесь примерам в разд. 7.8 представлены некоторые способы использования данных предикатов для добавления и удаления утверждений.
Прежде чем мы рассмотрим соответствующие предикаты, необходимо понять, как утверждения Пролога могут быть представлены в виде структур. Для простого факта такой структурой является соответствующий ему предикат с аргументами. То есть факт, подобный
нравится(джон,Х)
может рассматриваться как обычная структура с функтором
нравится (имеющим два аргумента) и аргументами
джон и
X. С другой стороны, правило можно рассматривать как структуру с главным функтором ':-'(с двумя аргументами). Этот функтор объявлен как инфиксный оператор. Первым аргументом является заголовок утверждения, а вторым – его тело. Так что
нравится(джон, X):- нравится(Х,вино)
есть не что иное, как
':-' (нравится(джон,Х), нравится(Х,вино))
– совершенно обычная структура. Далее, если правило содержит более одного целевого утверждения, то они считаются объединенными в структуры с функтором ',' (с двумя аргументами). Этот предикат также объявлен как инфиксный оператор. Так что
прародитель(Х, Z):- родитель(Х, Y), родитель(Y,Z)
есть в действительности просто
':-'(прародитель(Х,Z),Y(родитель(Х,Y),родитель(Y, Z))
Далее приведены предикаты, позволяющие программисту анализировать и изменять его утверждения.
listing (A)
Выполнение целевого утверждения
listing(A), когда значением
А является атом, приводит к тому, что все утверждения, предикат которых совпадает с этим атомом, будут записаны в виде термов Пролога в текущий файл вывода. Таким способом вы можете проверить, какие утверждения для некоторого предиката имеются в базе данных на текущий момент. Конкретный формат представления выводимых утверждений зависит от используемой вами реализации Пролог-системы. Заметим, что будут представлены все утверждения, предикат которых совпадает с атомом независимо от того, сколько аргументов они имеют. Использование предиката
listing может помочь вам обнаружить ошибки в программе. Так, в приведенном далее примере сеанса работы с системой программист обнаруживает, что он неправильно определил предикат
обр.
?- [test].
test consulted
да
?- обр([a,b,c,d],X).
нет
?- listing(обр).
обр([],[]).
обр ([_44|_45],_38):-обр(_45,_47),присоединить(_47,[_44],_38).
да
Печать утверждений предиката
обр показывает, что атом
присоединить написан в программе с ошибкой.
clause(X, Y)
Выполнение целевого утверждения вида
clause(X, Y) приводит к тому, что
X и
Y сопоставляются с заголовком и телом некоторого имеющегося в базе данных утверждения. При попытке выполнить указанное целевое утверждение переменная
X должна быть до такой степени конкретизирована, чтобы был известен главный предикат утверждения. Если для данного предиката нет утверждений, то доказательство согласованности целевого утверждения заканчивается неудачей. Если имеется несколько утверждений, соответствующих предикату, то Пролог выбирает первое из них. В этом случае если предпринимается попытка вновь согласовать целевое утверждение, то будет выбрано следующее утверждение и так далее.
Заметим, что в то время как предикат
clause всегда имеет аргумент, соответствующий телу утверждения, далеко не каждое утверждение действительно имеет тело. Если утверждение не имеет тела, то считается, что оно имеет фиктивное тело
true. Мы называли такие утверждения «фактами». В той или иной степени конкретизируя
X и
Y, можно искать либо все утверждения, соответствующие данному предикату с вполне определенным числом аргументов, либо все утверждения, соответствующие некоторому образцу. Так, например:
присоединить([], X, X).
присоединить([А|В]),С,[А|D]:- присоединить(В,С,D).
?- clause(присоединить(А,В,С),Y).
А=[], В =_23, С=_23, Y = true;
А = [_23|_24], В =_25, С = [_23|_26], Y = присоединить(_24,_25,_26);
нет
Предикат
clause очень полезен в том случае, если нам надо создать программы, анализирующие или исполняющие другие программы (см. разд. 7.13).
asserta(X), assertz(X)
Два встроенных предиката
asserta и
assertz позволяют добавлять новые утверждения в базу данных. Оба предиката действуют в точности одинаковым образом, за тем исключением, что
asserta добавляет утверждение в
начало базы данных, в то время как
assertz добавляет утверждение в ее
конец. Это отличие можно легко запомнить, учитывая, что «
а» является первой буквой английского алфавита, a «
z» его последняя буква. При выполнении целевого утверждения
asserta(X),
X должно иметь значением нечто, что можно представлять как утверждение; действительно, как и в случае
clause,
X должно быть достаточно конкретизировано, чтобы можно было установить главный предикат. Необходимо подчеркнуть, что результат добавления в базу данных утверждения не устраняется при выполнении возврата. Следовательно, если мы использовали предикат
asserta или
assertz для того, чтобы добавить новое утверждение, то это утверждение может быть удалено только в случае, если мы явно укажем это (используя предикат
retract).
retract(X)
Встроенный предикат
retract позволяет удалять утверждения из базы данных. Этот предикат имеет один аргумент, представляющий терм, с которым должно быть сопоставлено удаляемое утверждение. Указанный терм должен быть достаточно конкретизирован, чтобы можно было определить предикат утверждения (аналогично предикатам
asserta,
clause и т. д.). При попытке выполнить целевое утверждение
retract(X) находится первое утверждение в базе данных, с которым может быть сопоставлен
X, и это утверждение удаляется. При попытке вновь выполнить это целевое утверждение Пролог просматривает базу данных, начиная с места удаленного утверждения, в попытке найти другое сопоставимое утверждение. Если такое утверждение находится, то выполняются действия, рассмотренные выше. Если делается новая попытка согласовать целевое утверждение, то продолжается поиск следующего подходящего утверждения. И так далее. Заметим, что если утверждение было удалено, то оно ни при каких условиях не будет восстановлено вновь, даже при попытке вновь выполнить предикат
retract при возврате. Если в некоторый момент поиск не дает новых сопоставлений утверждений, то согласование целевого утверждения заканчивается неудачей.
Так как аргумент
X сопоставляется с удаляемым утверждением, то имеется возможность получить точное представление об удаляемом утверждении, даже если
X исходно означал некоторую структуру, содержащую множество неконкретизированных переменных. Это позволяет использовать предикат
retract вместо предиката
clause, в ситуации когда найденное утверждение сразу же удаляется. Такая ситуация как раз имеет место в определении предиката генатом (разд. 7.8).
6.5. Создание структур и работа с компонентами структур
Обычно когда мы хотим задать в программе на Прологе операции со структурой определенного вида, то мы делаем это, «упоминая» некоторым образом подобную структуру. Это значит, что если предикат используется для обработки множества структур различного вида, передаваемых ему в качестве аргумента, то обычно мы обеспечиваем отдельное утверждение для каждого класса структур. Хорошим примером такого подхода является программа для символьного дифференцирования, которая будет рассмотрена в разд. 7.1. В этой программе используются отдельные утверждения для функторов +, -, * и так далее. Мы знаем заранее, какие структуры могут появиться, и обеспечиваем утверждения для каждой из них.
В некоторых программах мы не можем предвидеть заранее все возможные структуры. Это имеет место, например, при написании программы «красивой печати», которая могла бы печатать произвольные структуры языка Пролог, размещая их в нескольких строках и используя отступы. (См. разд. 5.1, где представлена такая программа для печати списков.) Так, например, возможно, мы захотели бы напечатать терм
книга(629,автор(бронте, эмили),вх)
следующим образом:
книга
629
автор
бронте
эмили
вх
Важным моментом является то, что мы хотим, чтобы эта программа работала правильно, какую бы структуру мы ей ни задали. Понятно, что одна из возможностей сделать это – обеспечить отдельное утверждение для каждого функтора, какой только можно представить. Но это работа, которую мы никогда не завершим, потому что существует бесконечно много различных функторов! Написать подобную программу можно, используя встроенные предикаты для работы со структурами произвольного вида. Здесь мы опишем некоторые из них – это предикаты
functor,
arg и '
=..'. Мы опишем также предикат
name, выполняющий операции над атомами.
functor(T,F,N)
Предикат
functor определен таким образом, что
functor(T,F,N) означает, что
Т –
это структура с функтором F,
имеющим N аргументов. Этот предикат можно использовать двумя основными способами, В первом случае аргумент
Т уже имеет значение. Целевое утверждение считается несогласованным с базой данных, если
Т не является ни атомом, ни структурой. Если
Т – это атом или структура, то
F сопоставляется с функтором этой структуры, а
N присваивается значение, равное числу аргументов функтора. Заметим, что в данном контексте считается, что атом – это структура с числом аргументов 0. Ниже приведено несколько примеров целевых утверждений с предикатом
functor:
?- functor(f(a,b,g(Z)),F,N).
Z = _23, F = f
, N
= 3
?- functor(a+b,F,N).
F = +, N = 2
?- functor([a,b,c],F,N).
F =., N
= 2
?- functor(apple,F,N).
F = apple, N = 0
?- functor([a,b,c],'.',3).
нет
?- functor([a,b,c],a,Z).
нет
Прежде чем перейти к обсуждению предиката
arg, следует рассмотреть второй способ использования предиката
functor. В этом случае первый аргумент целевого утверждения
functor (Т, F, N) неконкретизирован. В этом случае два других аргумента должны быть конкретизированы, однозначно определяя функтор и число аргументов соответственно. Целевое утверждение такого вида всегда согласуется с базой данных, и в результате значением
Т становится структура с указанными функтором и числом аргументов. Таким образом, это некоторый способ
создания произвольных структур по заданным функтору структуры и числу ее аргументов. Аргументами такой структуры, созданной с помощью предиката
functor, являются неконкретизированные переменные. Следовательно, эта структура будет сопоставима с любой другой структурой, имеющей тот же функтор и одинаковое число аргументов.
Предикат
functor используется для создания структуры в основном тогда, когда нам надо получить «копию» некоторой уже существующей структуры с новыми переменными в качестве аргументов. Мы можем ввести для этого предикат
копирование, использующий
functor как целевое утверждение:
копирование(Старая, Новая):- functor(Cтapaя,F,N), functor(Hoвaя,F,N).
В этом определении подряд используются два целевых утверждения
functor. Если целевое утверждение
копирование имеет конкретизированный первый аргумент и неконкретизированный второй, то произойдет следующее. Первое целевое утверждение
functor будет соответствовать первому способу использования этого предиката (так как первый аргумент этого предиката конкретизирован). Следовательно,
F и
N конкретизируются, получив в качестве значений функтор и число аргументов этой существующей структуры. Второе целевое утверждение
functor соответствует второму способу использования этого предиката. На этот раз первый аргумент неконкретизирован, и информация, задаваемая
F и
N, используется для создания структуры
Новая. Эта структура имеет те же функтор и число аргументов, что и Старая, но ее компонентами являются переменные. Таким образом, возможен следующий диалог:
?- копирование(sentence(np(n(john)), v(eats)),X).
X = sentence(_23,_24)
Мы используем подобную комбинацию целевых утверждений
functor в определении предиката
reconsult в разд. 7.13.
arg(N,T,A)
Предикат
arg всегда должен использоваться с конкретизированными первым и вторым аргументами. Он применяется для доступа к конкретному аргументу структуры. Первый аргумент предиката
arg определяет, какой аргумент структуры необходим. Второй аргумент определяет структуру, к аргументу которой необходим доступ. Пролог находит соответствующий аргумент и затем пытается сопоставить его с третьим аргументом предиката
arg. Таким образом, цель
arg(N,T,A) согласуется с базой данных, если
N-й аргумент
Т есть
А. Давайте рассмотрим несколько целевых утверждений с
arg.
?- аrg(2,отношение(джон,мать(джейн)),Х).
X = мать(джейн)
?- arg(1,a+(b+c),X).
X =а
?- arg(2,[a,b,c],X).
X = [b,c]
?-arg(l,a+(b+c),b).
нет
Иногда мы захотим использовать предикаты
functor и
arg в ситуации, когда возможные структуры уже известны. Это связано с тем, что структура может иметь так много аргументов, что просто неудобно каждый раз перечислять их все. Рассмотрим пример, в котором структуры используются для описания книг. Мы могли бы иметь отдельную компоненту для названия книги, ее автора, издательства, года издания и так далее. Будем считать, что результирующая структура имеет четырнадцать компонент. Мы могли бы написать следующие полезные определения:
является _ книгой(книга(_,_,_,_,_,_,_,_,_,_,_,_,_,_)).
название(книга(Т,_,_,_,_,_,_,_,_,_,_,_,_,_),Т).
автор(книга(_,А,_,_,_,_,_,_,_,_,_,_,_,_),А).
. . .
В действительности мы можем записать это значительно более компактно следующим образом:
является_книгой(Х):- functor(X, книга, 14).
название(Х,Т):- является_книгой(Х), arg(1,X,T).
автор(Х,А):- является_книгой(Х), arg(2,X,T).
. . .
X=..L
Предикаты
functor и
arg дают один из способов создания произвольных структур и доступа к их аргументам. Предикат «=..» предоставляет альтернативный способ, полезный в том случае, когда необходимо одновременно получить все аргументы структуры или создать структуру по заданному списку ее аргументов. Целевое утверждение
X=..L означает, что
L есть список, состоящий из функтора структуры X,
за которым следуют аргументы X. Такое целевое утверждение может быть использовано двумя способами, так же как и целевое утверждение
functor. Если
X уже имеет значение, то Пролог создает соответствующий список и пытается сопоставить его с
L. Напротив, если
X неконкретизировано, то список будет использован для формирования соответствующей структуры, которая станет значением
X. В этом случае голова списка должна быть атомом (этот атом станет функтором X). Ниже приведено несколько примеров целевых утверждений, содержащих =..:
?- имя(а,b,с) =.. X.
X = [имя,а,b,с]
?- присоединить([А|В],С, [A|D]) =..L.
A = _2, В = _3, С = _4, D = _5, L = [присоединить,[_2|_3],_4,[_2|_5]]
?- [a,b,c,d] =..L.
L = ['.',a,[b,c,d]].
?- (a+b) =.. L.
L = [+,a,b].
?- (a+b) =..
[+,A,B] A = а, В = b
?- [a,b,c,d] =..
[A|B] A = '.', В = [a,[b,c,d]]
?- X =.. [a,b,c,d]
X = a(b,c,d).
?- X =.. [присоединить,[a,b,],[c],[a,b,c]].
X = присоединить([а,b],[с],[а,b,с])
Примеры использования предиката =.. приведены в разд. 7.12.
name(А,L)
В то время как предикаты
functor,
arg и
=.. используются для формирования произвольных структур и доступа к их аргументам, предикат
name используется для работы с произвольными атомами. Предикат
name сопоставляет атому список литер (их ASCII кодов), из которых состоит этот атом. Данный предикат можно использовать как для определения литер, составляющих указанный атом, так и для определения атома, содержащего заданные литеры. Целевое утверждение
name(A, L) означает, что
литеры, образующие атом А,
являются элементами списка L. Если аргументу А уже присвоено значение, то Пролог создает список литер и пытается сопоставить его с
L. В противном случае Пролог использует список
L для создания атома, который станет значением
А. Приведем примеры использования предиката
name:
?- name(apple,X).
X = [97,112,112,108,100]
?- name(X,[97,l12,112,108,100]).
X = apple
?- name(apple,"apple").
да
?- name(apple,"pear").
нет
В разд. 9.5 предикат
name используется для доступа к внутренней структуре слов английского языка, представляемых атомами Пролога.
6.6. Воздействие на процесс возврата
В Прологе есть два встроенных предиката, изменяющих нормальную последовательность событий, происходящих в процессе возврата. Предикат «
!» устраняет возможности для повторного согласования целевых утверждений, а предикат
repeat создает новые альтернативы там, где их не было ранее.
Отсечение
Символ отсечения ('!') можно рассматривать как встроенный предикат, который лишает Пролог-систему возможности изменить некоторые из решений, принятых ею ранее. Более подробное описание отсечения смотрите в гл. 4.
repeat
Встроенный предикат
repeat обеспечивает дополнительную возможность для порождения множественных решений в процессе возврата. Хотя он и является встроенным, его поведение полностью соответствует следующему определению:
repeat.
repeat:- repeat.
Что произойдет, если мы поместим предикат
repeat как целевое утверждение в одно из наших правил?
Во-первых, это целевое утверждение согласуется с базой данных, так как имеется соответствующий факт – первое утверждение определения предиката
repeat. Во-вторых, если в процессе возврата вновь будет достигнуто это место, то Пролог будет иметь возможность испробовать альтернативу – правило (второе утверждение). При использовании правила порождается другое целевое утверждение
repeat. Так как оно сопоставляется с фактом для предиката
repeat, то это целевое утверждение вновь согласуется с базой данных. Если процесс возврата снова дойдет до этого места, то Пролог вновь использует правило там, где он ранее использовал факт. Чтобы доказать согласованность вновь порожденного целевого утверждения, он снова выберет факт. И так далее. В действительности в процессе возврата целевое утверждение
repeat может быть согласовано бесконечное число раз. Обратим внимание на существенность порядка, в котором записаны утверждения для предиката
repeat. (Что произойдет, если факт будет записан после правила?)
Для чего нужно порождать целевые утверждения, которые всегда будут согласовываться в процессе возврата? Они нужны для того, чтобы создавать правила, в которых имеется возможность выбора вариантов, из правил, которые такой возможности не содержат. И тем самым мы можем заставить их порождать каждый раз различные значения.
Рассмотрим встроенный предикат
get0, который описан в гл. 5. Если Пролог пытается доказать согласованность целевого утверждения
get0(X), то он понимает это как указание взять очередную литеру (букву, цифру, пробел или что-либо еще), которая была введена в систему, и попытаться сопоставить целочисленный код этой литеры со значением
X. Если они будут сопоставимы, то целевое утверждение считается согласованным, в противном случае оно несогласовано. При этом нет никакого выбора – предикат
get0 всегда обрабатывает только текущую литеру, введенную в систему в момент обращения к предикату. При следующем обращении к целевому утверждению, включающему
get0, он возьмет следующую литеру, но при этом опять не будет никакого выбора. Мы можем определить новый предикат
new_get следующим образом:
new_get(X):- repeat, get0(X).
Предикат
new_get обладает следующим свойством: он порождает одно за одним значения всех последующих литер (в порядке их поступления) как альтернативные решения. Почему так получается? Когда мы первый раз вызываем
new_get(X), то подцель
repeat согласуется и подцель
getO(X) тоже, при этом переменная
X конкретизируется очередной литерой. Когда мы инициируем возврат, то выясняется, что последним местом, где имелся выбор, является
repeat. Пролог забывает все, что было сделано с того момента, а повторное согласование целевого утверждения
repeat успешно завершается. Теперь он вновь должен обратить свое внимание на
getO(X). К этому моменту текущей литерой является следующая литера, и в результате
X получает в качестве значения вторую литеру.
Мы можем использовать наше определение
new_get, чтобы определить другой полезный предикат. Предикат
get обычно является встроенным. Когда Пролог обрабатывает целевое утверждение
get(X), он рассматривает его как указание читать литеры до тех пор, пока он не найдет очередную неуправляющую литеру, имеющую изображение при печати (пробел, признак конца строки и т. д.). Затем он пытается сопоставить целочисленный код этой литеры со значением X. Мы можем написать приблизительное определение предиката
get следующим образом:
get(X):- new_get(X), X › 32.
Чтобы понять это определение, нужно вспомнить, что в кодировке ASCII все неуправляющие (печатаемые) литеры имеют код, превышающий 32, все остальные литеры имеют код, меньший или равный 32. Что происходит при попытке согласовать
get(X)? Прежде всего
new_get(X) сопоставляет X с текущей литерой, введенной в систему. Если ее код меньше или равен 32, то следующее целевое утверждение неверно и
new_get будет вынужден породить следующую литеру как следующее возможное решение. Эта литера будет затем сравнена с 32 и так далее. В конце концов
new_get найдет неуправляющую литеру, сравнение закончится успешно и код этой литеры будет возвращен в качестве результата
get.
Упражнение 6.1. Приведенное определение предиката
get не будет работать надлежащим образом, если мы обратимся к целевому утверждению
get(X) с уже определенным значением
X. Почему это происходит?
Неприятность, связанная с предикатом
repeat, состоит в том, что он всегда имеет альтернативное решение. Следовательно, в процессе возврата
repeat никогда не будут пересмотрены решения, принятые раньше, чем произошел последний вызов
repeat, если только мы не отсечем каким-либо образом эту постоянную возможность выбора. В силу сказанного предыдущие определения должны быть переписаны следующим образом:
new_get(X):- repeat, get0(X).
get(X):- new_get(X), X › 32,!.
Заметим, что это определение по-прежнему работает, лишь если мы пытаемся согласовать
get(X) с неконкретизированной значением переменной
X. Из-за проблемы, связанной с механизмом возврата за
repeat, в каждом применении
new_get необходимо предусматривать отсечение дальнейших вариантов, как только порождается литера, удовлетворяющая заданным условиям.
6.7. Формирование составных целевых утверждений
В правилах и вопросах вида
X:-Y или
?-Y терм, появляющийся на месте
Y, может состоять из единственного целевого утверждения либо представлять конъюнкцию целевых утверждений или их дизъюнкцию. Более того, можно употреблять в качестве целевых утверждений
переменные и успешно доказывать согласованность целевого утверждения, когда целевое утверждение в действительности не согласуется, используя для этого предикат
not. Предикаты, представленные в этом разделе, позволяют реализовать эти сложные способы выражения целевых утверждений.
Конъюнкция целей
Функтор ',' (запятая) определяет конъюнкцию целевых утверждений. Этот функтор был введен в гл. 1. Если
X и
Y – целевые утверждения, то целевое утверждение
X,
Y согласуется с базой данных, если согласуется
X и
Y. Если
X согласуется и затем
Y не согласуется, то делается попытка найти новое доказательство согласованности для
X. Если
X не согласуется, то не согласуется и конъюнкция в целом. Это и составляет суть механизма возврата. Функтор
Y является встроенным и определен как левоассоциативный инфиксный оператор, так что
X,
Y,
Z эквивалентно
(X,Y),Z.
Дизъюнкция целей
Функтор ';' определяет дизъюнкцию (означающую
или) целевых утверждений. Если
X и
Y – целевые утверждения, то целевое утверждение
X;
Y согласуется с базой данных, если согласуется
X или
Y. Если
X не согласуется, то делается попытка доказать согласованность
Y. Если и
Y не согласуется, то не согласуется и дизъюнкция в целом. Мы можем использовать функтор ';' для того, чтобы выразить альтернативы в
пределах одного утверждения. Например, будем считать, что некоторый объект является человеком, если этот объект – либо Адам либо Ева или если у объекта есть мать. Мы можем выразить это в одном правиле следующим образом:
человек(Х):- (Х=адам; Х = ева; мать(Х,Y)).
В этом правиле мы в действительности определили три альтернативы. Однако для Пролога это правило содержит две альтернативы, одна из которых сама содержит две альтернативы. Так как функтор ';' является встроенным и определен как правоассоциативный инфиксный оператор, то целевое утверждение в приведенном правиле в действительности можно переписать следующим образом:
';' (Х = адам, ';'(Х=ева,мать(Х, Y)))
Таким образом, первая возможность соответствует тому, что
X – это адам. Вторая возможность включает две альтернативы:
X это ева или у
X есть мать
Мы можем использовать дизъюнкцию в любом месте, где может быть использовано любое другое целевое утверждение на Прологе. Однако целесообразно использовать дополнительные скобки, чтобы избежать недоразумений, касающихся взаимодействия операторов ';' и ','. Обычно мы можем избежать применения дизъюнкции путем использования нескольких фактов и правил, содержащих, возможно, определения некоторых дополнительных предикатов. Например, приведенный выше пример в точности эквивалентен следующему:
человек(адам).
человек(ева).
человек(Х):- мать(Х,Y).
Этот вариант более традиционен и, возможно, проще для чтения. Для многих Пролог-систем он может быть более эффективным по сравнению с использованием ';'.
Результатом отсечения является невозможность изменить выбор альтернатив, обусловленных наличием дизъюнкций, сделанный с момента сопоставления с правилом, содержащим отсечение (см. гл. 4). Вследствие этого имеется ряд случаев, когда программа, содержащая отсечения, не может быть преобразована в обычную программу без использования дизъюнкций. Однако в общем случае не рекомендуется чрезмерно часто использовать ';'. В качестве предостережения отсылаем вас к гл. 8, где показано, как необдуманное использование ';' затрудняет понимание программ.
call(X)
Предполагается, что
X конкретизирован термом, который может быть интерпретирован как целевое утверждение. Целевое утверждение
саll(X) считается согласованным, если попытка доказать согласованность
X завершается успехом. Целевое утверждение
call(X) не согласуется с базой данных, если попытка доказать согласованность
X заканчивается неудачей. На первый взгляд этот предикат может показаться излишним, поскольку, естественно, возникает вопрос: почему аргумент
call не может быть записан непосредственно как целевое утверждение? Например, целевое утверждение
…, саll(принадлежит(а,Х)),…
всегда может быть заменено следующим:
…, принадлежит(a,X),…
Однако если мы создаем целевые утверждения, используя предикат '=..' или ему подобные, то возможны обращения к целевым утверждениям, функторы которых неизвестны на момент ввода программы в Пролог-систему. Так, например, в определении предиката
consult в разд. 7.13 нам надо иметь возможность рассматривать любой терм, прочитанный после
?-, как целевое утверждение. Предполагая, что
Р,
Х и
Y конкретизированы функтором и аргументами соответственно, можно использовать
call следующим образом:
…, Z =… [P,X,Y], call(Z),…
Последний фрагмент программы можно рассматривать как способ выражения обращения к целевому утверждению следующего вида:
…, P(X,Y),…
которое в рамках стандартной версии Пролога, рассматриваемой в этой книге, синтаксически некорректно. Однако некоторые версии языка Пролог допускают использование переменной в качестве функтора целевого утверждения.
not(X)
Предполагается, что
X конкретизирован термом, который может быть интерпретирован как целевое утверждение. Целевое утверждение
not(X) считается согласованным с базой данных, если попытка доказать согласованность
X заканчивается неудачей. Целевое утверждение
not(X) считается несогласованным, если попытка доказать согласованность X успешно завершается. В этом плане предикат
not очень похож на
call, за тем исключением, что согласованность или несогласованность аргумента, рассматриваемого как целевое утверждение, приводит к противоположному результату.
Чем отличаются следующие два вопроса?
/* 1 */?- принадлежит(Х,[а,b,с]), write(X).
/* 2 */?- not(not(принадлежит(Х,[а,b,с]))), write(X).
Может показаться, что между ними нет никакой разницы, так как в запросе 2
принадлежит(Х,[а,b,с,]) согласуется, поэтому
not(принадлежит(Х,[а,b,с,])) не согласуется и
not(not(принадлежит(Х,[а,b,с]))) согласуется. Это правильно лишь отчасти. В результате первого вопроса будет напечатан атом '
а', а в результате второго –
неконкретизированная переменная. Рассмотрим, что происходит при попытке доказать согласованность первого целевого утверждения из второго вопроса:
1. Целевое утверждение
принадлежит согласуется, и
X конкретизируется значением
а.
2 Предпринимается попытка доказать согласованность первого целевого утверждения
not, которая заканчивается неудачей, так как целевое утверждение
принадлежит, являющееся его аргументом, согласуется с базой данных. Теперь вспомним, что, когда целевое утверждение не согласуется, все конкретизированные переменные, такие как
X в нашем примере, должны теперь «забыть», что они обозначали до сих пор. Следовательно,
X становится неконкретизированной.
3. Предпринимается попытка доказать второе целевое утверждение
not, и эта попытка заканчивается успехом, так как его аргумент
(not(принадлежит(…))) не согласован. Переменная
X остается неконкретизированной.
4. Предпринимается попытка выполнить целевое утверждение
write с неконкретизированным значением
X. И, как описано в разд. 6.9, неконкретизированные переменные печатаются специальным образом.
6.8. Равенство
В этом разделе коротко рассматриваются различные встроенные предикаты, используемые для проверки равенства элементов и позволяющие делать их равными.
X=Y
Когда Пролог встречает целевое утверждение
X=Y, то он пытается сделать
X и
Y равными,
сопоставляя их друг с другом. Если сопоставление возможно, то целевое утверждение считается согласованным (а
X и
Y, возможно, становятся более конкретизированными). В противном случае целевое утверждение считается несогласованным. Более полное обсуждение этого предиката приведено в разд. 2.4. Предикат
равно определен таким образом, как если бы имел место факт
X = X.
Убедитесь, что вы понимаете, как это определение работает.
X\=Y
Предикат '
\=' является противоположным по отношению к предикату '
=' с точки зрения согласованности с базой данных. Это значит, что
X\=Y согласовано, если
X=Y не согласовано, и наоборот. Если целевое утверждение
X\ = Y согласовано (
X и
Y не могут быть сопоставлены друг с другом), то не произойдет никаких изменений в конкретизации
X и
Y. Если бы '
\=' не был встроенным предикатом, то мы могли бы определить его на Прологе следующим образом:
X \= Y:- X = Y,!, fail
. X \= Y.
X==Y
Предикат '==' выполняет значительно более строгую проверку на равенство, чем предикат '='. Это значит, что если
X==Y выполняется, то и тем более выполняется
X=Y. А обратное заключение не всегда имеет место. Отличие '==' состоит в том, что он более строг к переменным. Предикат '=' предполагает, что не-конкретизированная переменная может быть равна чему угодно, так как она сопоставима с чем угодно. С другой стороны, предикат '==' предполагает, что неконкретизированная переменная может быть равна другой неконкретизированной переменной, лишь когда они уже сцеплены друг с другом. Иначе проверка на равенство заканчивается неудачей. Таким образом, возможен следующий диалог:
?- X==Y.
нет
?- X==X.
X=_23
?- X = Y, X == Y. X = _23, Y = _23
?- присоединить([А|В],С) == присоединить(Х,Y).
нет
?- присоединить ([А|В],С) == присоединить([А|В],С).
А = _23, В = _24, С = _25
Х \== Y
Этот предикат находится в таком же отношении с '==' как '\=' с '='. Это значит, что целевое утверждение, содержащее этот предикат, согласуемо в точности тогда, когда целевое утверждение с '==' не согласуемо, и наоборот. И вновь мы могли бы считать, что этот предикат определен на Прологе следующим образом:
Х\== Y:- X == Y,!, fail.
Х\== Y.
6.9. Ввод и вывод данных
Предикаты для ввода и вывода литер и термов обсуждались в гл. 5. Здесь мы резюмируем наши знания о каждом из этих предикатов.
get0(X)
Это целевое утверждение согласуется с базой данных, если
X может быть сопоставлена с очередной литерой в текущем входном потоке данных. Цель
get0 выполняется лишь один раз (его нельзя согласовать повторно). Операция перехода к очередной литере не переделывается при возврате, так как не существует способа поместить литеру обратно в текущий входной поток данных.
get(X)
Это целевое утверждение согласуется с базой данных, если переменная
X может быть сопоставлена с очередной печатаемой (неуправляющей) литерой в текущем входном потоке данных. Печатаемые литеры имеют код ASCII, превышающий 32. Все управляющие литеры пропускаются. Предикат
get выполняется только один раз (он не может быть согласован вновь). Результат
get не устраняется при возврате, так как нет способа поместить литеру обратно в текущий входной поток данных.
skip(X)
Этот предикат читает и пропускает литеры в текущем входном потоке данных до тех пор, пока не встретится литера, сопоставимая с
X. Предикат
skip выполняется только один раз.
read(X)
Этот предикат читает очередной терм из текущего входного потока данных и сопоставляет его с
X. Предикат
read выполняется только один раз. Вводимый терм должен заканчиваться точкой '.' которая не становится частью этого терма. После точки должна следовать по крайней мере одна управляющая литера. Точка удаляется из текущего входного потока данных.
put(X)
Этот предикат записывает целое число
X в виде литеры (кодом которой и является
X) в текущий выходной поток данных. Предикат
put выполняется только один раз. Если
X неконкретизирован, то фиксируется ошибка.
nl
Записывает в текущий выходной поток данных последовательность управляющих литер, вызывающую переход на «новую строку». В случае вывода на дисплей все литеры, выводимые после
nl, будут размещены на следующей строке страницы;
nl выполняется только один раз.
tab(X)
Записывает
X «пробелов» в текущий выходной поток данных. Если
X неконкретизирован, то фиксируется ошибка,
tab выполняется только один раз.
write(X)
Этот предикат записывает терм
X в текущий выходной поток данных,
write выполняется только один раз. Каждая неконкретизированная переменная, входящая в
X, записывается как уникальное имя, начинающееся с подчеркивания ('_'), за которым следует уникальное число, как, например, '_239'. Переменные, сцепленные в пределах одного аргумента предиката
write, при печати будут иметь одинаковые имена. Предикат
write учитывает при печати термов имеющиеся объявления операторов. Так, например, инфиксный оператор будет напечатан между своими аргументами.
display(X)
Предикат
display работает в точности таким же способом, что и
write, за тем исключением, что он игнорирует все объявления операторов. Предикат
display печатает любую структуру, начиная с ее функтора, за которым в круглых скобках печатается список аргументов.
op(X,Y,Z)
Этот предикат объявляет оператор, имеющий приоритет X, позицию и ассоциативность
Y и имя
Z. Спецификация позиции и ассоциативности выбирается из числа следующих атомов:
fx fy xf yf xfx xfy yfx yfy
Если объявление оператора корректно, то
op считается согласованным. Более подробно этот предикат описан в разд. 5.5.
6.10. Обработка файлов
Предикаты для изменения текущего входного и текущего выходного потоков данных были введены в гл. 5. Здесь мы резюмируем наши знания о каждом из этих предикатов.
see(X)
Этот предикат открывает файл
X, если он еще не открыт, и определяет, что текущим входным потоком данных становится файл
X. Если
X неконкретизирована или
X конкретизирована именем несуществующего файла, то фиксируется ошибка.
seeing(X)
Это целевое утверждение согласуется с базой данных, если имя текущего входного потока данных (файла) сопоставимо с
X, и не согласуется в противном случае.
seen
Этот предикат закрывает текущий входной поток данных (файл) и определяет, что текущим входным потоком данных становится клавиатура терминала
(user).
tell(X)
Этот предикат открывает файл
X, если он еще не открыт, и определяет, что текущим выходным потоком данных, в который производится запись, является указанный файл. Если
X неконкретизирована, то возникает ошибка. Если
tell используется для. переключения выходного потока на еще неоткрытый файл и файл с именем, определяемым
X не существует, то файл с таким именем создается. Иначе, если файл, определяемый
X, уже существует, то предшествующее содержимое файла уничтожается.
telling(X)
Это целевое утверждение согласуется с базой данных, если X сопоставимо с именем текущего выходного потока данных, иначе оно не согласуется.
told
Этот предикат закрывает текущий выходной поток данных (файл) и записывает маркер конца файла в соответствующий файл. Текущим выходным потоком данных становится дисплей терминала (
user).
6.11. Вычисление арифметических выражений
Арифметические возможности языка Пролог первоначально обсуждались в разд. 2.5. Здесь мы подытожим наши знания об использовании предиката
'is' и о том, какие имеются функторы для формирований арифметических выражений.
X is Y
Y должен быть конкретизирован структурой, которую можно интерпретировать как арифметическое выражение (см. разд. 2.4). Сначала вычисляется выражение, которым конкретизирован
Y, и получается целое число, называемое
результатом. Результат сопоставляется с
X, и
is считается согласованным или несогласованным в зависимости от исхода сопоставления. Ниже описываются функторы, которые могут быть использованы для построения структуры, расположенной справа от предиката
is.
X + Y
Оператор сложения. При вычислении, инициированном предикатом
is, результатом является арифметическая сумма его аргументов. Аргументы должны быть конкретизированы структурами, которые можно вычислить и получить в качестве результатов целые числа.
X – Y
Оператор вычитания. При вычислении, инициированном предикатом
is, результатом является арифметическая разность его аргументов. Аргументы должны быть конкретизированы структурами, которые можно вычислить и получить в качестве результатов целые числа.
X * Y
Оператор умножения. При вычислении, инициированном предикатом
is, его результатом является арифметическое произведение его аргументов. Аргументы должны быть конкретизированы структурами, которые можно вычислить и получить в качестве результатов целые числа.
X / Y
Оператор целочисленного деления. При вычислении, инициированном предикатом
is, его результатом является целая часть частного от деления его аргументов. Аргументы должны быть конкретизированы структурами, которые можно вычислить и получить в качестве результатов целые числа.
X mod Y
Остаток от деления целых чисел (сравнение по модулю). При вычислении, инициированном предикатом
is, его результатом является целочисленный остаток, получаемый при делении
X на
Y. Аргументы должны быть конкретизированы структурами, которые можно вычислить и получить в качестве результатов целые числа.
Конкретные реализации Пролога могут включать и некоторые другие арифметические операции, такие, как возведение в степень. Примеры, приведенные в этой книге, используют лишь операции, перечисленные здесь.
6.12. Сравнение чисел
В Прологе имеются шесть предикатов для сравнения целых чисел. Эти предикаты первоначально были представлены в разд. 2.5, когда мы обсуждали арифметические возможности языка. Каждый такой предикат записывается как инфиксный оператор, имеющий два аргумента.
X = Y
Предикат проверки на
равенство, описанный в разд. 6.8, считается согласованным и в случае, когда его аргументами являются равные целые числа.
X \= Y
Предикат проверки на
несовпадение из разд. 6.8 также применим для целых чисел. Он выполняется, когда его аргументами являются различные числа.
X ‹ Y
Предикат
меньше выполняется, если целое число, соответствующее левому аргументу, меньше, чем число, соответствующее правому аргументу. Оба аргумента должны быть конкретизированы.
X › Y
Предикат
больше выполняется, когда целое число, соответствующее левому аргументу, больше, чем целое число, соответствующее правому аргументу. Оба аргумента должны быть конкретизированы, иначе возникает ошибка.
X ›= Y
Предикат
больше или равно выполняется, когда целое число, соответствующее левому аргументу, больше или равно целому числу, соответствующему правому аргументу. Оба аргумента должны быть конкретизированы.
X =‹ Y
Предикат
меньше или равно выполняется, когда левый аргумент меньше или равен правому аргументу. Оба аргумента должны быть конкретизированы. Заметим, что этот предикат записан как '=‹' а не '‹=' так что символ '‹=' является свободным и может быть использован в качестве оператора, который выглядит как стрелка.
6.13. Наблюдение за выполнением программы на Прологе
В этом разделе описаны встроенные предикаты, которые позволяют наблюдать за выполнением вашей программы. Здесь мы лишь опишем эти встроенные предикаты, а более подробное обсуждение отладки и трассировки программ содержится в гл. 8.
trace
Эффект выполнения предиката
trace заключается в установлении режима полной трассировки. Это значит, что после выполнения
trace вы получите возможность наблюдать за каждым из четырех основных типов событий
[9], которые происходят с каждым порождаемым вашей программой целевым утверждением.
notrace
Эффект выполнения предиката
notrace заключается в отмене режима полной трассировки. Однако сохраняется трассировка, вызываемая наличием контрольных точек (предикат
spy).
spy Р
Предикат
spy используется, когда необходимо обратить особое внимание на выполнение целевых утверждений, содержащих конкретные предикаты. Это можно сделать, установив на них
контрольные точки. Предикат
spy определен как префиксный оператор, и поэтому нет необходимости заключать в скобки его аргумент. Аргументом предиката может быть:
• Атом. В этом случае контрольная точка устанавливается на все предикаты с именем, соответствующим атому, независимо от того, сколько аргументов они имеют. Так, если бы мы имели утверждения для
сорт, имеющие как два, так и три аргумента, то целевое утверждение
spy сорт вызвало бы установку контрольных точек на оба множества утверждений.
• Структура вида
Имя/Размерность, где
Имя - это атом, а
Размерность - целое число. Эта запись определяет предикат с функтором
Имя, число аргументов которого равно
Размерность. Так
spy сорт/2 вызвало бы установку контрольных точек на целевые утверждения предиката
сорт с двумя аргументами.
• Список. В этом случае список должен заканчиваться пустым списком '[]', а каждый элемент списка сам должен быть допустимым аргументом для предиката
spy. Пролог установит контрольные точки во всех местах, указанных в списке. Так
spy[copт/2, присоединить/3] вызвал бы установку контрольных точек на предикат
сорт с двумя аргументами и на предикат
присоединить с тремя аргументами.
debugging
Встроенный предикат
debugging позволяет увидеть, какие контрольные точки установлены на текущий момент. В качестве подобного эффекта выполнения целевого утверждения
debugging печатается список всех контрольных точек.
nodebug
Целевое утверждение
nodebug вызывает устранение всех контрольных точек, установленных на текущий момент.
nospy
Подобно
spy,
nospy является префиксным оператором. Предикат
nospy является более селективным, чем
nodebug, так как вы можете точно указать, какие контрольные точки должны быть удалены. Это достигается путем указания аргумента, задаваемого в точности в такой же форме, как и для предиката
spy. Так, целевое утверждение
nospy[обр/2, присоединить/3] приведет к тому, что будут удалены все контрольные точки с предиката
обр с двумя аргументами и с
присоединить с тремя аргументами.
ГЛАВА 7. ЕЩЕ НЕСКОЛЬКО ПРИМЕРОВ ПРОГРАММ
В каждом разделе этой главы рассматривается некоторое конкретное применение Пролога. Мы советуем вам прочитать все разделы. Не огорчайтесь, если вы не поймете назначение какой-либо программы потому, что незнакомы с данной конкретной областью применения. Например, оценить значение символьного дифференцирования смогут лишь читатели, уже знакомые с дифференциальным исчислением. Тем не менее прочтите этот раздел, потому что программа нахождения символьных производных показывает, как установление соответствия между образцами используется при преобразовании структур одного вида (арифметическое выражение) в структуры другого вида. Самое главное – добиться понимания техники программирования на Прологе, находящейся в распоряжении программиста, независимо от конкретной прикладной задачи.
Мы надеемся, что набор задач достаточен, чтобы удовлетворить вкусам большинства читателей. Естественно, что все выбранные задачи относятся к таким областям, которые хорошо укладываются в те способы представления явлений реального мира, которые предлагает Пролог. Например, здесь отсутствует задача расчета потока тепла через трубу прямоугольного сечения. Правда, такие задачи тоже можно решать с помощью Пролога, однако выразительность и силу Пролога невыгодно демонстрировать на задачах, которые сводятся лишь к многократным повторениям вычислений над массивом чисел. Хотелось бы также рассмотреть и большие Пролог-программы, вроде тех, что используются в исследованиях по искусственному интеллекту для распознавания фраз естественного языка. К сожалению, цель такой книги как эта, не позволяет рассматривать программы, размеры которых превышают страницу текста и которые могут быть предложены лишь специально подготовленному читателю.
7.1. Словарь в виде упорядоченного дерева
Предположим, что мы хотим установить отношения между элементами информации с тем, чтобы использовать их, когда потребуется. Например, толковый словарь ставит в соответствие слову его определение, а словарь иностранного языка ставит в соответствие слову на одном языке слово на другом языке. Мы уже познакомились с одним способом составления словаря: с помощью задания фактов. Если нам нужно составить таблицу выигрышей на скачках, проводившихся на Британских островах в течение 1938 г., то мы можем просто определить факты вида
выигрыши(Х, Y), где
X - кличка лошади, a
Y – количество гиней (денежных единиц), выигранных этой лошадью. Следующая база данных может рассматриваться как часть этой таблицы:
Выигрыши(abaris,582).
Выигрыши(careful,17).
Выигрыши(jingling_silvee,300).
Bыигрыши(majola,356).
Если мы хотим узнать, какую сумму выиграла лошадь по кличке
maloja, нам нужно просто правильно построить вопрос и Пролог даст нам ответ:
?- Bыигрыши(maloja, X).
X=356
Напомним, что Пролог просматривает базу данных сверху вниз. Это значит, что если база данных нашего словаря упорядочена в алфавитном порядке, как в приведенном выше примере, то на поиск суммы выигрыша для
ablaze Пролог затратит меньше времени, чем на поиск суммы выигрыша для
zoltan. Однако хотя Пролог способен просмотреть свою базу данных гораздо быстрее, чем вы сможете просмотреть напечатанную таблицу, неразумно просматривать таблицу с начала до конца, если известно, что данные искомой лошади расположены в самом конце. Точно так же, хотя в Прологе имеются специальные средства быстрого просмотра базы данных, он не всегда проходит так быстро, как хотелось бы. В зависимости от размеров таблицы и от того, сколько информации хранится о каждой лошади, Прологу может потребоваться на просмотр таблицы неприемлемо большое время.
По этим и другим причинам специалисты по информатике потратили немало сил на поиски хороших способов организации хранения таких данных, как таблицы и словари. Сам Пролог использует некоторые из этих методов внутри себя при организации хранения своих собственных фактов и правил, но иногда их полезно использовать и в наших программах. Мы рассмотрим один такой метод организации словаря, который называется методом
упорядоченного дерева. Метод упорядоченного дерева является одновременно и эффективным способом использования словаря и средством демонстрации того, насколько полезны списки структур.

Рис. 7.1.
Упорядоченное дерево состоит из некоторого числа структур, называемых
узлами, причем каждому входу словаря соответствует один узел. Каждый узел содержит четыре компоненты. Сюда входят два связанных с узлом элемента данных, как в предикате
выигрыши в вышеприведенном примере. Один из этих элементов называется
ключом, его имя определяет место в словаре (кличка лошади в нашем примере). Другой элемент используется для хранения какой-либо другой информации о данном объекте (сумма выигрыша в нашем примере). Кроме того, каждый узел содержит ссылку (наподобие ссылки на хвост списка) на узел со значением ключа, которое лексикографически (по алфавиту)
меньше, чем имя, являющееся ключом данного узла, а также еще одну ссылку на узел со значением ключа лексикографически
большим, чем имя, являющееся ключом данного узла. Будем использовать структуру, которую обозначим как
в(Л,В,М, Б) (в - сокращение от «выигрыши»), где
Л – кличка лошади (атом), используемая в качестве ключа,
В – сумма выигрыша в гинеях (целое),
М – структура, соответствующая лошади, кличка которой меньше, чем та, что хранится в
Л, а
Б – структура, соответствующая лошади, кличка которой больше, чем значение в
Л. Когда для
М и
Б нет соответствующих структур, мы не будем их конкретизировать. Для небольшого множества лошадей указанная структура, будучи записанной в виде дерева, могла бы иметь вид, как представлено на рис. 7.1.
Если записать ее на Прологе в ступенчатом виде, учитывая ширину страницы, то она могла бы выглядеть так:
в(massinga,858,
в(braermar,385,
в(adela,588,_,_),
_),
в(panorama,158,
в(nettleweed,579,_,_),
_).
).
Теперь, располагая такой структурой, мы хотим «просмотреть» ее по кличкам лошадей, чтобы узнать их выигрыши в течение 1938 г. Как и раньше, структура должна иметь формат
в(Л,В,М, Б). Условие окончания поиска состоит в том, что кличка искомой лошади должна совпасть с
Л. В этом случае поиск удачен и не требуется пробовать другие варианты. В противном случае мы должны использовать предикат
меньше, определенный в гл. 3, чтобы определить, какую из «ветвей» дерева,
М или
Б, нужно рекурсивно просмотреть. Мы используем эти принципы при определении предиката
искать, причем
искать(Л,Т, Г) означает, что лошадь Л, если она найдена в таблице Т (которая организована в виде структуры формата в), выиграла
Г гиней:
искать (Л, в(Л,Г,_,),Г):- !.
искать Л, в(Л1,_,До,_),Г):-меньше(Л,Л1),искать(Л,До,Г).
искать(Л, в(Л1,_,_,После),Г):- not (меньше(Л,Л1)), искать(Л,После,Г).
Если при поиске по упорядоченному дереву использовать этот предикат, то в общем случае проверок будет меньше, чем если бы их данные были организованы в виде простого списка и просматривались бы с начала до конца.
Предикат
искать обладает одним интересным и удивительным свойством: когда вводим вопрос о лошади, клички которой нет в структуре, то любая информация, содержащаяся в вопросе, остается зафиксированной в этой структуре после окончания поиска. Иными словами, вопрос
?- искать(ruby_vintage,S,X).
имеет следующую интерпретацию:
построить структуру в, в которой кличке ruby_vintage поставлен в соответствие выигрыш X,
и присвоить ее в качестве значения переменной S. Таким образом,
искать осуществляет вставку новых компонент в частично заданную структуру. Поэтому многократно обратившись к
искать, можно построить словарь. Например, вопрос
?- искать(abaris,X,582), искать(maloja,X,356).
привел бы к тому, что значение переменной
X стало упорядоченным деревом из двух вхождений.
Понять то, каким образом
искать одновременно выполняет и создание и выборку компонент, можно на основе тех знаний о Прологе, которыми вы уже располагаете; мы настоятельно рекомендуем разобраться в этом самостоятельно. Подсказка: если
искать(Л,Т, Г) используется в конъюнкции целей, то «изменения» в структуре
Т сохраняются только в
области определения Т.
Упражнение 7.1. Поэкспериментируйте с предикатом
искать, чтобы установить, какие различия будут в словаре, если элементы в него вставлять каждый раз в разном порядке. Например, как будет выглядеть дерево словаря, если вставлять его элементы в таком порядке:
massinga, braemar nettleweed, panorama? А если в таком порядке:
adela, braemar, nettleweed, massinga?
7.2. Поиск в лабиринте
Стоит темная грозовая ночь. Когда вы ехали по пустынной сельской дороге, ваша машина сломалась и вы оказались перед входом сказочного дворца. Вы подошли к двери, обнаружили, что она открыта, и стали искать телефон. Как нужно осматривать дворец, чтобы не заблудиться и быть уверенным, что вы осмотрели каждую комнату? И каков кратчайший путь к телефону? Именно для таких крайних обстоятельств и разработаны методы поиска в лабиринте.
Во многих программах для ЭВМ, подобных программам поиска в лабиринте, полезно вести информационные списки и просматривать нужный список, когда впоследствии понадобится некоторая информация. Например, если мы решили найти во дворце телефон, нам может понадобиться список уже осмотренных комнат. Чтобы не плутать, снова и снова заходя в те же самые комнаты, нам нужно просто записывать на листке бумаги номера комнат, где мы уже побывали. Перед тем, как войти в комнату, мы проверяем, нет ли ее номера на нашем листке. Если он есть, мы пропускаем эту комнату, потому что уже должны были побывать там раньше. Если номера этой комнаты нет на листке, то мы записываем ее номер и входим в комнату, и так до тех пор, пока не найдем телефон.
Этот метод нуждается в некоторых уточнениях, но мы сделаем их позднее, при обсуждении проблем поиска на графе. А сначала давайте запишем по порядку наши шаги, чтобы знать, какие задачи предстоит решать:
1. Подойти к двери какой-либо комнаты. Если номер комнаты есть в нашем списке, то перейти к шагу 1.
2. Если в поле зрения нет ни одной комнаты, то «вернуться назад» через ту комнату, через которую мы прошли сюда, и посмотреть, нет ли возле нее каких-либо других комнат.
3. Иначе дописать номер комнаты к нашему списку.
4. Поискать телефон в этой комнате.
5. Если телефона нет, то перейти к шагу 1. Иначе мы останавливаемся, и наш список содержит путь, который мы прошли, чтобы попасть в нужную комнату.
Будем считать, что номера комнат являются константами (безразлично целыми числами или атомами). Сначала мы можем решить, как просматривать номера комнат, записанные на листке бумаги. Для этого можно использовать предикат
принадлежит, определенный в разд. 3.3, полагая, что содержимое листка бумаги представлено в виде списка. Теперь мы можем продвинуться в решении задачи поиска в лабиринте. Рассмотрим небольшой пример, где задан план дома, комнаты которого помечены буквами (см. рис. 7.2). Заметим, что просветы в стенах обозначают двери и что комната
а – это просто представление пространства вне дома. Имеются двери, ведущие из
а в
b, из
с в
d, из
f в
е, и так далее. Сведения о том, где имеются двери, могут быть представлены в виде фактов Пролога:
д(а,b).
д(b,е).
д(b,с).
д(d,c).
д(c,d).
д(e,f).
д(g,e).
Рис. 7.2.
Заметим, что информация о наличии дверей не избыточна. Например, мы сказали, что имеется дверь, ведущая из комнаты
g в комнату
е, но не сказали, что имеется дверь, ведущая из комнаты
е в комнату
g, т. е. мы не зафиксировали утверждение
д(e,g). Чтобы обойти эту проблему представления двухсторонних дверей, мы могли бы повторно записать д-факт для каждой двери с перестановкой аргументов. Или мы могли бы устроить программу таким образом, чтобы она понимала, что каждая дверь фактически может рассматриваться как двухсторонняя. Этот вариант мы и выбрали в нижеследующей программе.
Чтобы перейти из одной комнаты в другую, мы должны распознать один из следующих случаев:
• мы находимся в той комнате, которая нам нужна, или
• мы должны войти в дверь и распознать эти случаи снова (рекурсивно).
Рассмотрим целевое утверждение
переход(X,Y,T), которое доказуемо (согласуется с базой данных), если можно перейти из комнаты
X в комнату
Y. Третий аргумент
Т – это наш листок бумаги, который мы носим с собой и на котором записан перечень номеров комнат, в которых мы побывали до сего момента.
Граничное условие перехода из комнаты
X в комнату
Y состоит в том, что, возможно, мы уже находимся в комнате
Y (т. е., возможно,
X есть
Y). Это условие представлено в виде утверждения:
переход(Х,Х,Т).
В противном случае мы выбираем некоторую смежную комнату, назовем ее
Z, и смотрим, были ли мы в ней раньше. Если нет, то «переходим» из
Z в
Y, дописывая
Z в наш список. Все это выражается в виде следующего утверждения:
переход(Х, Y,T,):- Д(Х,Z),not(принадлежит(Z,Т)), переход(Z,Y,[Z|T]).
Словами это может быть выражено так: для того чтобы «перейти» из
X в
Y, не проходя через комнаты из списка
Т, надо найти дверь из
X куда-либо (т. е. в
Z), убедиться, что
Z еще не занесена в список
Т, и «перейти» из
Z в
Y, используя список
Т с дописанной в него
Z.
При использовании этого правила существуют три возможности возникновения ошибки: во-первых, если в
X вообще нет двери. Во-вторых, если дверь, которую мы выбрали, уже есть в списке. В-третьих, если «переход» в комнату
Z приведет в тупик на следующих уровнях. Если первое целевое утверждение
д(X, Z) не согласуется с базой данных, то и данное целевое утверждение
переход также недоказуемо. На «самом верхнем» уровне (не рекурсивный вызов) это означает, что из
X в
Y нет пути; на более глубоких уровнях это означает, что мы должны сделать «шаг назад» и поискать другую дверь.
Наша программа рассматривает каждую дверь как одностороннюю. Если мы считаем, что наличие двери из комнаты а в комнату
b – это то же самое, что наличие двери из комнаты
b в комнату а, то, как отмечалось выше, мы должны указать это явно. Кроме повторного задания
д-фактов с перестановкой аргументов, имеются два способа задать эту информацию в самой программе. Самый очевидный способ – это добавить еще одно правило, получая в итоге:
переход(Х,X,T).
переход(X,Y,T):- д(X,Z), not(принадлежит(Z,Т)),переход(Z,Y[Z|T]). переход(Х,Y,T):- д(Z,Х), not(принадлежит(Z,Т)),пeреход(Z,Y,[Z|T]).
Или, используя предикат ';' (обозначающий дизъюнкцию), можно записать:
переход(Х,Х,Т).
переход(Х,Y,T):- (д(Х,Z); д(Z,Х)), not(принадлежит (Z,T)),пepexод(Z,Y,[Z|T]).
Теперь о том, как найти телефон. Рассмотрим целевое утверждение
есть_телефон(X), которое согласуется с базой данных, если в комнате
X есть телефон. Если мы хотим сказать, что в комнате
g есть телефон, то мы просто записываем в нашу базу данных факт
есть_телефон(g). Предположим, мы начали поиск с комнаты
а. Один из способов узнать дорогу к телефону – это задать вопрос:
?- переход(а,Х,[]), есть_телефон(X).
Это – вопрос типа «создать и проверить», который находит достижимые комнаты и затем проверяет наличие в них телефона. Другой способ – это найти сопоставление сначала для предиката
есть_телефон(Х), а затем попробовать перейти из комнаты
а в
X:
?- есть_телефон(Х), переход(а,Х,[]).
Последний метод более эффективен, однако он подразумевает что мы «знаем», где телефон, еще до того, как начали поиск.
Начальная установка третьего аргумента пустым списком означает, что мы начинаем поиск, имея чистый лист бумаги. Изменяя эту начальную установку, можно получить разные варианты поиска. Вопрос
«найти телефону не заходя в комнаты d и f» можно выразить на Прологе так:
?- есть_телефон(X), переход (a,X,[d,f]).
В разд. 7.9 мы рассмотрим некоторые общие процедуры поиска по графу, в том числе программу, находящую кратчайший путь.
Упражнение 7.2. Допишите вышеприведенную программу так, чтобы она печатала такие сообщения, как «входим в комнату
X» и «телефон найден в комнате
Y», подставляя в них соответствующие номера комнат.
Упражнение 7.3. Может ли эта программа находить альтернативные пути? Если да, то где нужно
«отсечь», чтобы избежать нахождения более чем одного пути?
Упражнение 7.4. Чем определяется порядок, в котором просматриваются комнаты?
7.3. Ханойские башни
Ханойские башни - это игра, в которой используются три штыря и набор дисков. Все диски различаются диаметром и нанизываются на штыри через отверстие в центре каждого диска. Первоначально все диски находятся на левом штыре. Цель игры состоит в том, чтобы переместить все диски на центральный штырь. Правый штырь можно использовать как «запасной» для временного размещения дисков. При каждом перемещении диска с одного штыря на другой должны соблюдаться два ограничения: перемещать можно только самый верхний диск на штыре, и, кроме того, нельзя ставить диск на другой диск меньшего размера.
Многим из тех людей, которые играют в эту игру, практически никогда не удается обнаружить весьма простую стратегию, позволяющую успешно играть в Ханойские башни с тремя штырями и
N дисками. Чтобы не утомлять вас поисками решения этой задачи, мы откроем его:
• Граничное условие выполняется в случае, когда на исходном (левом) штыре нет дисков.
• Переместить N-1 дисков с исходного штыря на запасной (правый) штырь, используя итоговый штырь как запасной; отметим, что это перемещение осуществляется рекурсивно.
• Переместить один диск с исходного штыря на итоговый штырь. В этом месте наша программа будет выдавать сообщение об этом перемещении.
• Наконец, переместить N-1 дисков с запасного на итоговый, используя исходный штырь в качестве запасного.
Пролог-программа, реализующая данную стратегию, определяется следующим образом. Определяется предикат
ханой с одним аргументом, такой, что
xaной(N) означает выдачу сообщений о последовательности перемещений, когда на исходном штыре находится
N дисков. Из двух утверждений предиката
переместить один задает граничное условие, которое сформулировано выше, а второй – реализует рекурсивные случаи. Предикат
переместить имеет четыре аргумента. Первый аргумент – это число дисков, которые нужно переместить. Три другие представляют исходный, итоговый и запасной штыри для перемещения дисков. Предикат
сообщить использует предикат
write для печати названий штырей, участвующих в перемещении диска.
xaной(N):- переместить(N, левый,средний,правый).
переместить(О,_,_,_):-!.
переместить(N, А,В,С):-М is N-1,переместить(М,А,С,В),сообщить(А,В), переместить(М,С,В,А).
сообщить(Х,Y):-write([переместили,диск,со,штыря,Х,на, штырь,Y]),nl.
7.4. Справочник комплектующих деталей
В главе 3 мы рассматривали программу, выдающую на печать список деталей, необходимых при сборке некоторого узла на основе справочника комплектующих деталей. В данном разделе мы усовершенствуем эту программу, будем учитывать количество деталей путем суммирования числа требуемых деталей по мере перехода от узлов к их составляющим. Кроме того, усовершенствованная программа правильно обрабатывает повторения; процедура
собрать устраняет повторения при суммировании для каждой из требуемых деталей перед тем, как ответ выдается на печать.
Организация базы данных справочника сходна с тем, что описано в гл. 3. Сборочный узел представлен в виде списка структур вида
чис(X, Y), где
X – это имя некоторой детали (простой детали или узла), a
Y – необходимое количество таких деталей. Ниже перечислены все предикаты измененной программы с указанием их назначения:
Деталиузла(А): выдает на печать список всех простых деталей, требующихся для сборки узла
А, и количество каждой детали.
Деталиузлов(N,X,P): P - это список структур
чис(Дет, Кол), где
Дет - это название детали, а
Кол - это количество таких деталей, требующихся для сборки каждого из экземпляров узлов
X.
N - целое, а
X – атом, представляющий название некоторой детали.
Деталировка(N,S,Р): Р - это, как и выше, список структур
чис, требующихся для сборки всех узлов, представленных элементами списка
S;
N задает число экземпляров списка
S,
N – целое;
S – список структур
чис.
Собрать(Р, А):
Р и
А – списки структур
чис. А – это список, составленный из тех же элементов, что и
Р, но без повторений одной и той же детали. Причем количество каждой детали, указанное в списке
А, совпадает с суммой всех повторений этой детали в списке
Р. Предикат
собрать мы используем для того, чтобы собрать несколько описей наборов одинаковых деталей в одну опись. Например,
3 винта, 4 шайбы и 4 винта собираются вместе, давая 7
винтов и 4 шайбы.
Дособрать(Х,М, L,O,N) :
L и
О - это списки структур,
чис, О – это список всех элементов списка L, в состав которых не входит деталь X; X – это атом, задающий название некоторой детали;
N – это общее количество
X в списке
L, сложенное с
М;
М – это целое число, которое используется для суммирования количеств
X в
L и передается как аргумент в каждом вызове
дособрать. При выходе из рекурсии, который обеспечивается выполнением граничного условия,
М возвращается как
N.
Вывдеталейузла(Р):
Р – это список структур
чис, который выдается на печать по одной структуре на строке вывода. Цель
put(9) выводит литеру с кодом ASCII=9, что соответствует горизонтальной табуляции. С предикатом
присоединить мы уже неоднократно встречались ранее.
Полностью Пролог-программа выглядит так:
деталиузла(Т):-деталиузлов(1,Т,Р), co6paть(P,Q), вывдеталейузла(Q).
деталиузлов(N,Х,Р):-узел(Х,S), деталировка(N,S,Р).
деталиузлов(N,Х, [чис(Х,N)]):- деталь(Х).
деталировка(_, [], []).
деталировка(N, [чис(Х, Число) |L],T):-М is N * Число, деталиузлов(М,Х,Хдетали),деталировка (N, L,Остдетали,Т),присоединить(Хдетали,Остдетали,Т).
собрать([],[]).
coбpaть([чис(X,N)|R],[чис(X,Nитог)|R2]):-дособрать(Х,N,R,O,Nитог),собрать(О,R2).
досo6paть(_,N,[],[],N).
дособрать(Х,N,[чис(Х,Число)|Oст],Прочие,Nитог):-!,М is N+Число, дособрать(Х,М,Ост,Прочие,Nитог).
дособрать(Х,N,[Друг|Ост],[Друг|Прочие],Nитог):-дособрать(Х, N, Ост, Прочие, Nитог).
вывдеталейузла([]).
вывдеталейузла([чис(Х,N)|R):-tab(4),write(N),put(9),write(X),nl, вывдеталейузла(R).
7.5. Обработка списков
В этом разделе мы рассмотрим некоторые основные предикаты, полезные при работе со списками. Поскольку Пролог позволяет работать с произвольными структурами данных, списки не могут играть в нем той незаменимой роли, какая им отводится в других языках программирования, таких, как Лисп и Поп-2. Однако независимо от того, будут или не будут использоваться списки в ваших программах, всегда важно представлять себе, как работают предикаты, определения которых рассматриваются в данном разделе, поскольку они основаны на принципах, которые применимы при работе с любыми структурами данных.
Нахождение последнего элемента списка: Цель
последний(X, L) согласуется с базой данных, если элемент
X является последним элементом списка
L. Граничное условие выполняется, когда список
L содержит только один элемент. Это условие проверяется первым правилом. Второе правило задает общий рекурсивный случай:
последний(Х,[Х]).
последний(Х,[_,|Y]):- последний(Х,Y).
?- последний(Х,[talk,of,the,town]).
X = town
Проверка порядка следования элементов: Цель
следомза(Х, Y, L) согласуется с базой данных, если элементы
X и
Y являются последовательными элементами списка
L. Особенности работы переменных допускают, чтобы или
X, или
Y, или обе переменные были неконкретизированы перед попыткой согласовать цель. В первом утверждении, которое проверяет граничное условие, должно быть также предусмотрено, что после
X и
Y в списке могут быть другие элементы. Этим объясняется появление анонимной переменной, в которой сохраняется хвост списка:
следомза(Х,Y,[Х,Y|_]).
следомза(Х,Y,[_|Z]):- следомза(Х,Y,Z).
Объединение списков: С приводимым примером мы уже встречались ранее в разд. 3.6. Цель
присоединить(X, Y, Z) согласуется с базой данных в том случае, если
Z – это список, построенный путем добавления
Y в конец
X. Например,
?- присоединить([a,b,с],[d,e,f],Q).
Q=[a,b,c,d,e,f]
Определение предиката
присоединить выглядит следующим образом:
присоединить([],L,L).
присоединить([Х|L1],L2,[Х|LЗ]):- присоединить(L1,L2,LЗ).
Граничное условие выполняется тогда, когда первый аргумент является пустым списком. Действительно, пополнение какого-либо списка пустым списком не изменяет его. В дальнейшем мы постепенно приближаемся к граничному условию, поскольку каждое рекурсивное обращение к
присоединить удаляет один элемент из головы первого аргумента.
Заметим, что любые два аргумента
присоединить могут быть конкретизированы, и в этом случае
присоединить конкретизирует третий аргумент соответствующим результатом. Этим свойством, которое можно было бы назвать «недетерминированным программированием», обладают многие из определяемых в данной главе предикатов. Указанная гибкость
присоединить позволяет определить с его помощью ряд других предикатов, что мы и сделаем:
последний(Е1,Список):- присоединить(_,[Е1],Список).
следомза(Е11,Е12,Список):-
присоединить(_,[Е11,Е12|_], Список).
принадлежит(Е1,Список):- присоединить(_,[Е1|_],Список).
Обращение списка: Цель
обр(L,M) согласуется с базой данных, если результат перестановки в обратном порядке элементов списка
L есть список
М. В программе используется стандартный прием, когда обращенный список получается присоединением его головы к обращенному хвосту. Лучший способ обратить хвост – это использовать сам
обр. Граничное условие выполняется тогда, когда первый аргумент сократился до пустого списка, в этом случае результатом также является пустой список:
обр([],[]).
обр([Н|Т],L):- обр(T,Z), присоединить(Z,[Н],L).
Заметим, что на месте второго аргумента
присоединить стоит
Н в квадратных скобках. Причина в том, что
Н – это голова первого аргумента, а голова списка сама не обязана быть списком. Хвост же списка по определению всегда является списком. Для более эффективной реализации
обр мы можем встроить действия по объединению списков непосредственно в утверждения для
обр:
o6p2(L1,L2):- обрдоп(L1,[],L2).
обрдоп([X|L],L2
fL3):- обрдоп(L,[Х|L2],LЗ).
обрдоп([],L,L).
Второй аргумент
обрдоп используется для хранения «текущего результата». Каждый раз, когда выявляется новый фрагмент результата
(X), передаваемый в остальную часть программы, «текущий результат» представляет из себя старый «текущий результат», дополненный новым фрагментом
X. В самом конце последний «текущий результат» возвращается в качестве результата исходного целевого утверждения. Аналогичный прием используется в разд. 7.8 при определении предиката
имя_целого.
Исключение одного элемента: Цель
исключ1(Х, Y,Z)исключает первое вхождение элемента
X из списка
Y, формируя новый сокращенный список
Z. Если в списке
Y нет элемента
X, то целевое утверждение недоказуемо. Граничное условие выполняется тогда, когда мы находим искомый элемент
X, иначе осуществляется рекурсивная обработка хвоста списка
Y:
исключ1(А,[А|L],L):-!.
исключ1(А,[В|L],[В|М]):- исключ1(А,L,М).
Легко добавить утверждение, которое обеспечит доказательство предиката, когда второй аргумент сократится до пустого списка. Это утверждение, реализующее новое граничное условие, есть
исключ1(_,[],[])-
Исключение всех вхождений некоторого элемента; Цель
исключить(Х, L1, L2) создает список
L2 путем удаления всех элементов
X из списка
L1. Граничное условие выполняется тогда, когда
L1 является пустым списком. Это означает, что мы рекурсивно исчерпали весь список. Если
X находится в голове списка, то результатом является хвост этого списка, из которого
X тоже удаляется. Последний случай возникает, если во втором аргументе обнаружено, что-то отличное от X. Тогда мы просто входим в новую рекурсию.
исключить(_, [],[]).
исключить(Х,[Х|L],М):-!, исключить(Х,L,М).
исключить(Х,[Y|L1],[Y|L2]):- исключить(Х,L1,L2).
Замещение: Этот предикат очень напоминает
исключить, с той лишь разницей, что вместо удаления искомого элемента мы заменяем его некоторым другим элементом. Цель
заменить(Х, L,A,M) строит новый список
М из элементов списка
L, при этом все элементы
X заменяются на элементы
А. Здесь возможны 3 случая. Первый, связанный с граничным условием, в точности совпадает с тем, что было в
исключить. Второй случай – когда в голове второго аргумента содержится элемент
X, а третий – когда там содержится нечто отличное от
X:
заменить(_,[],_,[]).
заменить(Х,[Х|L],А,[А|М]):-!, заменить(Х,L,А,М).
заменить(Х,[Y|L],А,[Y|М]):- заменить(Х,L,А,М).
Подсписки: Список
X является подсписком списка
Y, если каждый элемент
X содержится и в
Y с сохранением порядка следования и без разрывов. Например, доказуемо следующее:
подсписок[[собрание, членов, клуба],[общее, собрание, членов, клуба, будет, созвано, позже]).
Программа
подсписок требует двух предикатов: один для нахождения совпадения с первым элементом, и второй, чтобы убедиться, что остальная часть первого аргумента поэлементно совпадает с соответствующей частью второго аргумента.
подсписок([Х|L],[Х|М]):- совпало(L,M),!.
подсписок(L,[_|М]):- подсписок(L,M).
совпало([],_).
совпало([Х|L],[Х|М]):- совпало(L,М).
Отображение: Это мощный метод, заключающийся в преобразовании одного списка в другой с применением к каждому элементу первого списка некоторой функции и использованием ее результата в качестве очередного элемента второго списка. Программа преобразования одного предложения в другое, которая рассматривалась в гл. 3, является одним из примеров отображения. Мы говорим, что «отображаем одно предложение в другое».
Отображение настолько полезно, что заслуживает отдельного раздела. Кроме того, поскольку списки в Прологе – это просто частные случаи структур, мы отложим обсуждение отображения списков до разд. 7.12. Отображение многолико. В разд. 7.11, посвященном символическому дифференцированию, описывается способ отображения одного арифметического выражения в другие.
7.6. Представление и обработка множеств
Множество - одна из наиболее важных структур данных, используемых как в математике, так и в программировании. Множество – это набор элементов, напоминающий список, но отличающийся тем, что вопрос о том, сколько раз и в каком месте что-либо входит в множество в качестве его элемента, не имеет смысла. Так, множество (1, 2, 3) – это то же самое множество, что и (1, 2, 3, 1), поскольку значение имеет только сам факт, принадлежит данный элемент множеству или нет. Элементами множеств могут также быть другие множества. Самой фундаментальной операцией над множествами является определение того,
принадлежит некоторый элемент данному множеству или нет.
Не должно вызывать удивления, что множества удобно представлять в виде списков. Список может содержать произвольные элементы, включая другие списки, и над списками можно определить предикат принадлежности. Однако условимся, что когда мы представляем множество в виде списка, такой список содержит только по одному элементу на каждый объект, принадлежащий множеству. При работе со списками без повторяющихся элементов упрощаются некоторые операции, такие, как удаление элементов. Итак, нам предстоит иметь дело только со списками без повторяющихся элементов. Предикаты, рассматриваемые ниже, соблюдают это свойство и опираются на него.
Над множествами обычно определяется следующий набор операций (мы будем применять и общепринятые математические обозначения для тех читателей, кто к ним привык):
Принадлежность множеству: X∈Y
X принадлежит некоторому множеству
Y, если
X является одним из элементов
Y.
Пример:
а∈{с,а,t}.
Включение: X⊂
Y
Множество
Y включает в себя множество
X, если каждый элемент множества
X является также элементом
Y. Множество
Y может содержать некоторые элементы, которых нет в
X.
Пример:
{x,r,u}⊂
{p,q,r,f,t,u,v,w,x,y,z}.
Пересечение: X∩Y
Пересечением множеств
X и
Y является множество, содержащее те элементы, которые одновременно принадлежат
X и
Y.
Пример:
{r,a,p,i,d} ∩
{p,i,c,t,u,r,e} =
{r,i,p}.
Объединение: X ∪
Y
Объединением множеств
X и
Y является множество, содержащее все элементы, принадлежащие
X или
Y или одновременно им обоим.
Пример:
{a,b,c} ∪
{с,d,е} = {a,b,c,d,e}.
Это – основные операции, которые обычно используются при работе с множествами. Теперь мы можем приступить к написанию Пролог-программ, реализующих каждую из них. Первая основная операция 'принадлежность' реализуется тем же самым предикатом
принадлежит, с которым мы уже встречались несколько раз. Однако в нашем определении
принадлежит в граничном случае нет символа «отсечения», поэтому мы можем создавать последовательные элементы списка, используя возвратный ход:
принадлежит(Х,[Х|_]).
принадлежит(Х,[_|Y]):- принадлежит(Х,Y).
Следующая операция 'включение' реализуется предикатом
включает, причем
включает(Х, Y) завершается успешно, если
X является подмножеством
Y, т. е.
Y включает
X. Второе утверждение в его определении опирается на математическое соглашение о том, что пустое множество является подмножеством любого множества. В Прологе это соглашение дает способ проверки граничного условия для первого аргумента, поскольку запрограммирована рекурсивная обработка его хвоста:
включает([А|Х],Y):- принадлежит(А,Y), включает(Х,Y).
включает([],Y).
Следом идет самый сложный случай, реализация пересечения. Целевое утверждение пересечение(Х, Y,Z) доказуемо, если пересечением
X и
Y является
Z. Это как раз тот случай, когда используется предположение, что данные списки не содержат повторяющихся элементов:
пересечение([], X, []).
пересечение([X|R],Y,[X|Z]):-принадлежит(Х, Y),!,пересечение(R, Y,Z).
пересечение([Х|R],Y,Z):- пересечение(R, Y,Z).
Наконец,
объединение. Целевое утверждение
объединение (X,Y,Z) доказуемо, если объединением
X и
Y является
Z. Заметим, что реализация предиката
объединение сконструирована на основе определений предикатов
пересечение и
присоединить:
объединение([],Х,Х).
объединение([Х|R],Y,Z):- принадлежит(Х,Y),!,
объединение(R,Y,Z). объединение([X |R],Y,[X|Z]):- объединение(R,Y,Z).
Этим исчерпывается наш перечень предикатов работы с множествами. И хотя использование множеств может оказаться не характерным для ваших программ, тем не менее полезно изучить эти примеры. Они позволяют вам получить ясное представление о том, как можно использовать рекурсию и возвратный ход.
7.7. Сортировка
Иногда полезно упорядочить список элементов в соответствии с заданным порядком их следования. Если элементами списка являются целые числа, то для того чтобы определить соблюден ли порядок следования, можно использовать предикат '‹'. Список (1, 2, 3) упорядочен, поскольку любая пара соседних целых чисел этого списка удовлетворяет предикату '‹'. Если элементами списка являются атомы, то мы можем воспользоваться предикатом
меньше, о чем уже говорилось в гл. 3. Список
[alpha,beta,gamma] упорядочен в алфавитном порядке, поскольку каждая пара соседних атомов этого списка удовлетворяет предикату
меньше.
Специалисты по информатике разработали много методов сортировки списков, когда задан некоторый предикат, который говорит нам о том, находятся ли соседние элементы списка в требуемом порядке следования. Мы рассмотрим Пролог-программы для четырех таких методов: наивная сортировка, сортировка включением (вставками), сортировка методом пузырька и быстрая сортировка. В каждой программе используется предикат упорядочено, который может быть определен через '‹'
меньше или любой другой предикат по вашему усмотрению, в зависимости от того, какого рода структуры вы сортируете. При этом предполагается, что целевое утверждение
упорядочено(Х, Y) доказуемо, если объекты
X и
Y удовлетворяют требуемому порядку следования, т. е. если
X в некотором смысле меньше чем
Y.
Один из способов сортировки чисел в порядке возрастания состоит в следующем: вначале создается некоторая перестановка чисел, затем проверяется расположен ли полученный список в порядке возрастания. Если это не так, то создается новая перестановка чисел. Этот метод известен под названием
наивная сортировка:
наивсорт(L1,L2):- перестановка(L1,L2),отсортировано(L2),!.
перестановка(L,[H|T]):-присоединить(V,[Н|U],L), присоединить(V,U,W), перестановка(W,Т).
перестановка([],[]).
отсортировано(L):- отсортировано(0,L).
отсортировано(_,[]).
отсортировано(N,[H|T]):- упорядочено(N,Н),отсортировано(Н,T).
Используемый здесь предикат
присоединить многократна определялся ранее. В этой программе предикаты имеют следующий смысл:
Наивсорт(L1, L2) означает, что
L2 – это список, являющийся упорядоченной версией списка
L1;
Перестановка(L1, L2) означает, что
L2- это список, содержащий все элементы списка
L1 в одном из многих возможных порядков их следования; в терминологии разд. 4.3 – это
генератор.
Предикат
отсортировано(L) означает, что числа в списке
L упорядочены в порядке возрастания; это –
'контролер'.
Процесс поиска упорядоченной версии списка заключается в создании некоторой перестановки элементов и проверки ее упорядоченности. Если это так, то единственный ответ найден. Иначе мы вынуждены продолжать создание перестановок. Это не очень эффективный метод сортировки списка.
При
сортировке включением каждый элемент списка рассматривается отдельно и включается в новый список на соответствующее место. Этот метод используется, например, при игре в карты, когда игрок сортирует имеющиеся на руках карты, вынимая и переставляя по одной карте за раз. Целевое утверждение
вклюсорт(X, Y) доказуемо тогда, когда список
Y является упорядоченной версией списка
X. Каждый элемент удаляется из головы списка и передается предикату
вклюсорт2, который включает этот элемент в список и возвращает измененный список.
вклюсорт([],[]).
вклюсорт([Х|L],М):- вклюсорт(L,N), вклюсорт2(Х,N,М).
вклюсорт2(Х,[А|L],[А|М]):- упорядочено(А,Х),!,вклюсорт2(Х,L,М).
вклюсорт2(Х,L,[Х |L]).
Чтобы сделать предикат сортировки включением более универсальным, удобно задавать предикат проверки порядка следования в качестве аргумента предиката
вклюсорт. Используем для этого предикат ' =..', который рассматривался в гл. 6:
вклюсорт([],[],_).
вклюсорт([Х|L],М,О):- вклюсорт(L,N,О),вклюсорт2(Х,N,М,О).
вклюсорт2(Х,[А|L],[А|М],0):-Р=..[O,А,Х], call(P),!
, вклюсорт2(Х,L,М,O).
вклюсорт2(Х,L,[Х|L],О).
Теперь мы можем использовать такие цели как
вклюсорт(А,В,'‹') и вклюсорт(А,В,меньше), т. е. отпадает необходимость в предикате
упорядочено. Этот метод может быть распространен.и на другие алгоритмы сортировки данного раздела.
При
сортировке методом пузырька в списке ищется пара соседних элементов, расположенных не по порядку следования. Если такие элементы находятся, то они меняются местами. Этот процесс продолжается до тех пор, пока перестановки станут ненужными. Если при сортировке включением выбранный элемент как бы «тонет», попадая на нужное место, то сортировка методом пузырька названа так потому, что здесь элементы, подобно пузырькам воздуха, постепенно «всплывают», занимая соответствующее место.
пусорт(L,S):-присоединить(Х,[А,В|Y],L),упорядочено(В,А),присоединить(Х, [В, А|Y],M),пусорт(M,S).
пусорт(L,L).
присоединить([],L,L).
присоединить([Н|Т],L[Н|V]):- присоединить(Т,L,V).
Заметим, что здесь применяется тот же самый предикат
присоединить, с которым мы встречались ранее. Этот пример отличается от предыдущих необходимостью возвратного хода после каждого найденного решения. Поэтому в первом правиле в определении
пусорт «отсечение» не используется. Эта программа еще один пример «недетерминированного» программирования,- для выбора элементов списка L здесь используется предикат
присоединить. При этом контроль полноты выполненных перестановок целиком возложен на
присоединить.
Быстрая сортировка - это более сложный метод сортировки, предложенный Хоором и применимый для сортировки больших списков. Для реализации быстрой сортировки на Прологе мы должны сначала разделить список, состоящий из головы
Н и хвоста
Т, на два списка
L и
М такие, что:
• все элементы
L меньше или равны
Н;
• все элементы
М больше чем
Н;
• порядок следования элементов в
L и
М такой же как в
[Н |Т].
После того, как мы разделили список, применяем быструю сортировку к каждому из полученных списков (это рекурсивная часть), и присоединяем
М к
L Цель
разбить(H,T,L,M) разделяет список
[Н |Т] на списки
L и
М, как сказано выше:
paзбить(H,[A|X],[A|Y],Z):- А=‹ Н, разбить(Н,Х,Y,Z).
разбить(Н,[А|Х],Y,[А|Z]):- А › Н, разбить(Н,Х,Y,Z).
разбить(_,[], [],[]).
Тогда программа быстрой сортировки примет вид:
бысорт([],[]).
бысорт([H|T],S):-разбить(Н,Т,А,В),бысорт(А,А1),бысорт(В,В1), присоединить(А1, [H|B1],S).
Предикат
присоединить можно встроить внутрь программы сортировки. Тогда получается другой предикат
бысорт2 ([H|T], S,X):-разбить(Н,T,А,В), бысорт2(А,S,[Н|Y]), бысорт2(B,Y,X).
бысорт2([],Х,Х).
В этом случае третий аргумент используется как временная рабочая область, и при обращениях к
бысорт2 этот аргумент должен заполняться пустым списком.
Более подробные сведения о методах сортировки можно найти в книге D. Knuth,
The Art of Computer Programming, v. 3 (Sort and Searching), Addison-Wesley, 1973 (Имеется перевод: Кнут Д. Искусство программирования для ЭВМ, т. 3 (Сортировка и поиск). М.: Мир, 1978.-
Перев.) Метод быстрой сортировки Хоора описан в его статье в Computer Journal n. 5 (1962), стр. 10-15.
Упражнение 7.5. Проверьте, что предикат
перестановка (L1, L2) строит все перестановки заданного списка
L1 (причем каждую по одному разу) и выдает их как альтернативные значения списка
L2. В каком порядке строятся эти решения?
Упражнение 7.6. Быстрая сортировка лучше всего работает ка больших списках, поскольку там она обеспечивает более быструю сходимость к решению. В то же время объем работы, выполняемой на каждом уровне рекурсии быстрой сортировки, превышает то, что делается в других методах, из-за использования разбить. Поэтому, при сортировке небольших списков рекурсивные вызовы
бысорт, видимо, можно заменить обращениями к другим методам сортировки, например, к сортировке включением. Разработайте «гибридную» программу, которая использует быструю сортировку для обработки больших подсписков (списков, полученных с помощью предиката
разбить), но переключается на другой метод (сортировка включением) при значительном уменьшении длины подсписка. Подсказка: поскольку
разбить должен просмотреть все элементы списка, то он может заодно подсчитать и длину списка.
7.8. Использование базы данных: random, генатом, найтивсе
Во всех программах, которые рассматривались до сих пор, база данных использовалась лишь для хранения фактов и правил, с помощью которых определяются предикаты. Можно использовать базу данных и для хранения обычных структур, т. е. таких, которые порождаются при выполнении программы. До сих пор для передачи таких структур от одного предиката к другому мы применяли механизм аргументов. Однако существуют доводы в пользу хранения этой информации в базе данных. Иногда некоторый элемент информации может потребоваться во многих частях программы. Передача его через механизм аргументов может привести к появлению одного – двух дополнительных аргументов у большинства предикатов. Другим доводом является возможность сохранения информации при возвратном ходе. В этом разделе мы рассмотрим три предиката, которые позволяют хранить в базе данных структуры, время жизни которых превышает то, что может быть обеспечено с помощью переменных. Вот эти три предиката:
random, вырабатывающий при каждом вызове псевдослучайное целое,
найтивсе, порождающий список всех структур, обеспечивающих истинность данного предиката, и
генатом, порождающий атомы с различающимися именами.
Генератор случайных чисел (random)
Цель
random(R, N) конкретизирует
N целым числом, случайно выбранным в диапазоне от
1 до
R. Метод выбора случайного числа основан на конгруэнтном методе с использованием начального числа («затравки») инициализируемого произвольным целым числом. Каждый раз, когда требуется случайное число, ответ вычисляется на основе существующего начального значения, и при этом порождается новое начальное число, которое сохраняется до тех пор, пока вновь не потребуется вычислить случайное число. Для хранения начального числа между вызовами
random мы используем базу данных. После того как начальное число использовано, мы убираем (с помощью
retract) из базы данных старую информацию о начальном числе, вычисляем его новое значение, и засылаем в базу данных новую информацию (с помощью
asserta). Исходное начальное значение – это просто факт в базе данных, с функтором
seed имеющим одну компоненту – целое значение начального числа.
seed(13).
random (R,N):-seed(S),N is (S mod R) + 1,retract(seed(S)),NewSeed is (125 * S + 1) mod 4096,asserta(seed(NewSeed)),!.
Используя семантику
retract можно упростить определение
random следующим образом:
random(R,N):-retract(seed(S)),N is (S mod R)+1,NewSeed is (125 * S +1) mod 4096,asserta(seed(NewSeed)),!.
Для того, чтобы напечатать последовательность случайных чисел, расположенных в диапазоне между 1 и 10, которая обры-вается после того, как будет порождено значение 5, нужно задать следующий вопрос:
?- repeat, random(10,X), write(X), nl, X=5.
Генератор имен (генатом)
Предикат
генатом позволяет порождать новые атомы Пролога. Если у нас есть программа, которая воспринимает информацию об окружающем мире (например, путем анализа описывающих его предложений на английском языке), то в случае появления в этом мире нового объекта возникают трудности с его обозначением. Естественно представлять объект атомом Пролога. Если объект ранее не встречался, мы должны убедиться в том, что тот атом, который мы ему сопоставляем, случайно не совпал с другим атомом, уже представляющим какой-то другой объект. Иными словами, нам необходимо иметь возможность формировать новые атомы. Мы можем также потребовать, чтобы созданный атом имел также некоторое мнемоническое значение: это облегчит понимание информации выводимой нашей программой. Если бы атомы представляли, скажем, студентов, то целесообразно было
бы назвать первого студента –
студент1, второго –
студент2, третьего –
студентЗ и т. д. Если к тому же нам нужно было бы работать с объектами представляющими еще и преподавателей, то можно было бы выбрать для их представления атомы
преподаватель1,
преподаватель2, преподавательЗ и т. д.
Функция программы
генатом состоит в том, чтобы порождать новые атомы от заданных корней (таких как
студент и
преподаватель). Для каждого корня программа запоминает, какой номер был использован в последний раз. Поэтому, когда в следующий раз от нее требуется породить атом с данным корнем можно гарантировать, что он будет отличаться от тех, что были порождены ранее. Так, когда вопрос
?- генатом(студент,X).
задан впервые, ответом будет
X = студент1
В следующий же раз ответом будет
X = студент2
и т. д.
Заметим, что эти различающиеся решения при возвратном ходе не порождаются (
генатом(Х, Y) нельзя согласовать вновь), они порождаются последующими целями, включающими этот предикат.
В определении
генатом используется вспомогательный предикат
тек_номер. Контроль за тем, какой номер использовать следующим для данного корня, осуществляется программой
генатом путем записи в базу данных фактов вида
тек_номер и удаления фактов, которые стали ненужными. Факт
тек_номер (Корень, Номер) означает, что последний номер, использованный с корнем
Корень, был
Номер. Иными словами, последний атом, порожденный для этого корня, состоял из литер, взятых из
Корень, за которыми был приформирован номер, взятый из
Номер. Когда Пролог пытается доказать согласованность цели
генатом, обычно делается следующее: последний факт
тек_номер для заданного корня удаляется из базы данных, к его номеру прибавляется 1, и новый факт
тек_номер запоминается в базе данных, заменяя исключенный факт. С этого момента новый номер может быть использован как основа для порождения нового атома. Хранить информацию о текущем номере в базе данных очень удобно. В противном случае каждый предикат, прямо или косвенно участвующий в выполнении
генатом, должен был бы пересылать информацию о текущих номерах через дополнительные аргументы.
Последние несколько утверждений этой программы определяют предикат
целое_имя, который используется для преобразования целого числа в последовательность литер-цифр. Атомы, порождаемые
генатом, формируются с помощью встроенного предиката
name, который формирует атом из литер корня, за которыми следуют цифры номера. В некоторых реализациях Пролога используется версия предиката
name, которая выполняет также функции предиката
целое_имя, однако весьма поучительно посмотреть, как его можно определить на Прологе. В этом определении неявно используется тот факт, что коды ASCII для цифр 0, 1, 2 и т. д. равны соответственно 48, 49, 50 и т. д. Поэтому, чтобы преобразовать число меньшее 10 в код ASCII соответствующей цифры, достаточно прибавить к этому числу 48. Перевести в последовательность литер число, большее 9, сложнее. Последнюю цифру такого числа получить легко, поскольку это просто остаток от деления на
10 (число mod 10). Таким образом, цифры числа легче формировать в обратном порядке. Мы просто циклически повторяем следующие операции: получение последней цифры, вычисление остальной части числа (результат его целого деления на 10). Определение этого на Прологе выглядит следующим образом:
цифры_наоборот(N,[С]):- N‹10,!, С is N+48.
цифры_наоборот(М,[С|Сs]):-С is (N mod 10) + 48,N1 is N/10,цифры_нaoбopот(N1,Cs).
Чтобы получить цифры в правильном порядке, применим трюк: в этот предикат добавим дополнительный аргумент – список «уже сформированных» цифр, С помощью этого аргумента мы можем получать цифры по одной в обратном порядке, но в итоговый список вставлять их в прямом порядке. Это делается следующим образом. Пусть у нас есть число 123. В начале список «уже сформированных» цифр есть []. Первым получаем число 3, которое преобразуется в литеру с кодом 51. Затем мы рекурсивно вызываем
целое_имя, чтобы найти цифры числа 12. Список «уже сформированных» цифр, который передается в это целевое утверждение, содержит литеру, вставленную в исходный список «уже сформированных» цифр – это список [51]. Вторая цель
целое_имя выдает код 50 (для цифры 2) и снова вызывает
целое_имя, на этот раз с числом 1 и со списком «уже сформированных» цифр [50, 51]. Эта последняя цель успешно выполняется и, поскольку число было меньше 10, дает ответ [49,50,51]. Этот ответ передается через аргументы разных целей
целое_имя и дает ответ на исходный вопрос – какие цифры соответствуют числу 123?
Приведем теперь всю программу полностью.
/* Породить новый атом, начинающийся с заданного корня, и оканчивающийся уникальным числом. */
генатом (Корень,Атом),выдать_номер(Корень,Номер), name(Корень,Имя1), целое_имя(Номер,Имя2), присоединить(Имя1,Имя2,Имя), name(Атом,Имя).
выдать_номер(Корень, Номер):-retract(тeк_номер(Корень, Номер1)),!,Номер is Номер 1 + 1, asserta(тек_номер(Корень, Номер)).
выдать_номер(Корень,1):- asserta(тек_номep(Kopeнь,l)).
/* Преобразовать целое в список цифр */
целое_имя(Цел,Итогспи):- целое_имя (Цел, [], Итогспи).
целое_имя(I,Текспи,[С|Текспи]:- I ‹10,!, С is I+48.
целое_имя(I,Текспи,Итогспи):-Частное is I/10, Остаток is I mod 10,С is Остаток+48.
целое_имя(Частное,[С|Текспи],Итогспи).
Генератор списков структур (найтивсе)
В некоторых прикладных задачах полезно уметь определять все термы, которые делают истинным заданный предикат. Например, мы могли бы захотеть построить список всех детей Адама и Евы с помощью предиката
родители из гл.
1 (и располагая базой данных с фактами
родители о родительских отношениях). Для этого мы могли бы использовать предикат по имени
найтивсе, который мы определим ниже. Цель
найтивсе(Х,G, L) строит список
L, состоящий из всех объектов
X таких, что они позволяют доказать согласованность цели
G. При этом предполагается, что переменная
G конкретизирована произвольным термом, однако таким, что
найтивсе рассматривает его как целевое утверждение Пролога. Кроме того переменная
X должна появиться где-то внутри
G. Таким образом
G может быть конкретизирована целевым утверждением Пролога произвольной сложности. Для того, чтобы найти всех детей Адама и Евы, необходимо было бы задать следующий вопрос:
?- найтивсе(Х, родители(Х,ева,адам), L).
Переменная
L была бы конкретизирована списком всех
X, для которых предикату
родители(Х,ева,адам) можно найти сопоставление в базе данных. Задача
найтивсе заключается в том, чтобы повторять попытки согласовать его второй аргумент, и каждый раз, когда это удается, программа должна брать значение X и помещать его в базу данных. Когда попытка согласовать второй аргумент завершится неудачно, собираются все значения
X, занесенные в базу данных. Получившийся при этом список возвращается как третий аргумент. Если попытка доказать согласованность второго аргумента
ни разу не удастся, то третий аргумент будет конкретизирован пустым списком. При помещении элементов данных в базу данных используется встроенный предикат
asserta, который вставляет термы перед теми, которые имеют тот же самый функтор. Чтобы поместить элемент
X в базу данных, мы задаем его в качестве компоненты структуры по имени
найдено. Программа для
найтивсе выглядит следующим образом:
найтивce(X,G,_):-asserta(найденo(мapкep)), call(G), asserta(найденo(X)),fail.
найтивсе(_,_,L):- собрать_найденное([],М),!, L=M.
собрать_найденное(S,L):- взятьеще(Х),!,собрать_найденное([Х |S],L).
собрать_найденное(L,L).
взятьеще(Х):- retract(найдено(Х)),!, Х\==маркер.
Предикат
найтивсе, начинает свою работу с занесения специального маркера, который представляет из себя структуру с функтором
найдено и с компонентой
маркер. Этот специальный маркер отмечает место в базе данных, перед которым будут занесены (с помощью
asserta) все
X, согласующие
G с базой данных при данном запуске
найтивсе. Затем делается попытка согласовать
G и каждый раз, когда это удается,
X заносится в базу данных в качестве компоненты функтора
найдено. Предикат
fail инициирует процесс возврата и попытку повторно согласовать
G (asserta согласуется не более одного раза). Когда попытка согласовать
G завершается неудачей, процесс возврата приводит к неудаче первого утверждения из определения
найтивсе, и делается попытка согласовать в качестве цели второе утверждение. Второе утверждение вызывает
собрать_найденное для выборки из базы данных всех структур найдено и включения их компонент в список. Предикат
собрать_найденное вставляет каждый элемент в переменную, где хранится список «уже собранных» элементов. Этот прием мы рассматривали выше при разборе программы ге-натом. Как только встречается компонента
маркер, взятьеще завершается неудачей, после чего выбирается второе утверждение для
собрать_найденное. При сопоставлении
его с текущей целью второй аргумент (результат) сцепляется с первым аргументом (с набранным списком)
Заметим, что присутствие в базе данных структуры
найдено (маркер) указывает на некоторое конкретное употребление
найтивсе. Это означает, что
найтивсе может вызываться рекурсивно – любое использование
найтивсе во втором аргументе другого
найтивсе будет обработано правильно.
В разд. 7.9 мы разработаем программу, которая использует предикат
найтивсе для построения списка всех потомков узла в графе. Этот список необходим для реализации программы поиска по графу вширь.
Упражнение 7.7. Напишите Пролог-программу
случайный_выбор такую, что цель
случайный_выбор(L, Е) конкретизирует Е случайно выбранным элементом списка
L. Подсказка: используйте генератор случайных чисел и определите предикат, который возвращает N-й элемент списка.
Упражнение 7.8. Задана цель
найтивсе(Х,G, L). Что произойдет, если в
G имеются неконкретизированные переменные не сцепленные с
X?
7.9. Поиск по графу
Граф – это сеть, состоящая из узлов, соединенных дугами. Например, географическую карту можно рассматривать как граф, где узлами являются населенные пункты, а дугами, соединяющие их дороги. Если вы хотите найти кратчайший маршрут между двумя населенными пунктами, вам предстоит решить задачу нахождения кратчайшего пути между двумя узлами графа.
Проще всего описать граф в базе данных с помощью фактов, представляющих дуги между узлами графа. На рис, 7.3 приведен пример графа и его представления с помощью фактов. Чтобы пройти от узла
g к узлу
а, мы можем пойти по пути
g,
d,
e,
а или по одному из многих других возможных путей. Если мы представляем ориентированный граф, то предикат а следует понимать так, что
а(Х, Y) означает, что существует дуга из
X в
Y, но из этого не следует существование дуги из
Y в
X. В данном разделе мы будем иметь дело только с неориентированными графами, у которых все дуги двунаправленные. Это допущение совпадает с тем, которое мы делаем в разд. 7.2 при поиске в лабиринте.

Простейшая программа поиска по графу, представленному так, как указано выше, выглядит следующим образом:
переход(Х,X).
переход(Х,Y):- (a(X,Z);a(Z,X)), переход(Z,Y).
К сожалению, эта программа может зацикливаться. Поэтому, как и раньше, мы используем список Т для хранения перечня тех узлов, в которых мы уже побывали в какой-либо рекурсии предиката.
переход(Х,Х,Т).
переход(Х,Y,T):- (a(X,Z);a(Z,X)), not (принадлежит(Z, Т)),переход(Z, Y,[Z|T]).
Эта программа, разработанная в разд. 7.2, осуществляет так называемый поиск «вглубь», поскольку вначале рассматривается только один из соседей узла по графу, Другие же соседи игнорируются до тех пор, пока неудачные попытки согласовать цели в рекурсивных вызовах не возвратят Пролог к рассмотрению данного узла.
Теперь давайте рассмотрим такой поиск по графу, который мог бы быть полезен на практике. Как быть, если мы должны спланировать маршрут поездки из одного города Северной Англии в другой? Для этого потребуется база данных с информацией о дорогах между городами в Северной Англии и их протяженности:
а(ньюкасл,карлайл,58).
а(карлайл,пенрит,23).
а(дарлингтон,ньюкасл,40).
а(пенрит, дарлингтон,52).
а(уэркингтон,карлайл,33).
а(уэркингтон,пенрит,39).
На некоторое время мы можем забыть о расстояниях и определить новый предикат:
a(X,Y):- a(X,Y,Z).
С помощью этого определения предиката а уже имеющаяся программа поиска по графу (
переход) будет находить пути, по которым можно переезжать из одного места на графе в любое другое. Однако программа
переход имеет недостаток: когда она успешно завершается, мы не знаем, какой путь она нашла. По меньшей мере мы вправе ожидать от программы переход
выдачи нам в нужном порядке списка мест, которые придется посетить. Тем более, что в программе имеется перечень этих мест, правда, в порядке, обратном тому, какой нам нужен. Чтобы получить правильный список, мы можем воспользоваться программой
обр, определенной в разд. 7.5. Тогда мы получим новое определение программы
переход, которая возвращает найденный маршрут через свой третий аргумент:
переход(Старт,Цель,Путь):- переход0(Старт,Цель,[],R),обр(R, Путь).
переход0(Х,Х,Т,[Х|Т]).
переход0(Место,Y,Т,R):-следузел(Место,Т,Сосед),переход0(Сосед,Y,[Место|T],R).
следузел(Х,Бывали,Y):- (a(X,Y); a(Y,X)),not (принадлежит(Y,Бывали)).
Заметим, что предикат
следузел позволяет получать для узла
X «правильный» узел
Y, т. е. такой, к которому можно непосредственно перейти от узла
X. Ниже приводится пример работы этой программы при поиске маршрута из Дарлингтона в Уэркингтон:
?- переход(дарлингтон,уэркингтон,Х)
Х=[дарлингтон,ньюкасл,карлайл,пенрит,уэркингтон]
Это не самый лучший маршрут, однако, программа найдет другие маршруты если мы инициируем процесс возврата.
У этой программы много недостатков. Она совершенно не управляет выбором следующего участка пути, поскольку у нее нет доступа к полному набору возможных вариантов, а те выборы, которые у программы имеются, не представлены явно в виде структуры, которая может анализироваться программой, а неявно предопределены схемой работы механизма возврата.
Ниже приведен переработанный вариант программы, который отличается большей универсальностью. В дальнейшем мы увидим, как с помощью простых изменений в этой программе можно получить разнообразные методы поиска.
переход(Старт,Цель,Путь):- переход1([[Старт]],Цель,R),обр(R, Путь).
переход1([Первый|Ост],Цель,Первый):- Первый =[Цель|_].
переход1([[Послед|Бывали]|Прочие],Цель,Путь):-найтивсе([Z, Послед|Бывали], следузел(Послед, Бывали,Z), Список), присоединить(Список, Прочие, НовПути), переход1(НовПути,Цель,Путь).
Предикат
следузел остается прежним. Предикату
переход1 передается список рассматриваемых путей вместе с конечным пунктом, и в последнем аргументе он возвращает удачный путь. Список рассматриваемых путей – это просто все дороги, начинающиеся в начальной точке, которые мы уже рассмотрели. Мы надеемся, что одна из них при продлении даст путь, который приведет нас в конечный пункт. Все пути представлены в виде обратных списков населенных пунктов, так что они могут также выполнять функции перечня мест, где мы уже бывали.
В самом начале имеется только один возможный путь, который можно пытаться продлить. Это просто путь, который начинается в исходном пункте и никуда не ведет. Если мы стартуем из Дарлингтона, то это будет
[дарлингтон]. Если теперь исследовать пути ведущие из Дарлингтона в соседние города, то можно обнаружить, что имеются два возможных пути
[ньюкасл, дарлингтон] и
[пенрит, дарлингтон]. Поскольку Уэркингтон не встречается ни на одном из этих путей, необходимо решить, какой из этих путей следует продолжить. Если принято решение продлить первый путь, то мы обнаружим, что существует всего один доступный узел – последний город на этом пути. Итак, кроме пути Дарлингтон – Пенрит у нас есть новый путь:
[карлайл, ньюкасл, дарлингтон].
Наш «изыскатель»,
переход1 ведет полный список путей, по которым, может быть, стоит двигаться. Как же он решает какой из путей следует рассмотреть первым? Он просто выбирает
первый попавшийся. Затем он ищет все возможные способы продления этого пути до следующего населенного пункта (используя
найтивсе для построения списка всех таких продленных путей) и помещает получившиеся пути в
начало списка для рассмотрения их на следующем уровне рекурсии.
В результате,
переход1 ведет себя таким образом, что он попробует все возможные способы продления первого пути прежде чем будет рассматривать альтернативные пути. Такая стратегия поиска является одним из вариантов
поиска вглубь. Между прочим,
переход1 рассматривает пути совершенно в том же порядке, что и
переход0. Быть может вам будет интересно выяснить, почему это так.
Если нас интересует кратчайший путь от Дарлингтона до Уэркингтона, то имеющаяся программа для этого не подходит. Первое найденное ею решение – это не кратчайший путь, а наоборот, самый длинный (в данном случае). Нам нужно изменить программу таким образом, чтобы она строила пути в порядке возрастания их длины. Если мы изменим ее так, чтобы она всегда продлевала более короткие пути, прежде чем рассматривать более длинные, то она будет вынуждена находить вначале кратчайшие пути (если измерять длину пути числом городов на нем). Полученная программа будет осуществлять
поиск вширь. Единственное, что нужно сделать для этого – это вставлять новые альтернативы в конец всего списка возможностей, а не в начало, как в последнем примере. Мы просто исправим второе утверждение в определении
переход1, чтобы он выглядел следующим образом:
переход1([[Послед|Бывали]|Прочие],Цель,Путь):-найтивсе([Z,Послед|Бывали], следузел(Послед, Бывали,Z),Список), присоединить(Прочие,Список,НовПути), переход1(НовПути,Цель, Путь).
Теперь исправленная программа находит возможные пути из Дарлингтона в Уэркингтон в следующем порядке:
[дарлингтон,пенрит,уэркингтон]
[дарлингтон,ньюкасл, карлайл,уэркингтон]
[дарлингтон,пенрит,карлайл,уэркингтон]
[дарлингтон,ньюкасл,карлайл,пенрит,уэркингтон]
Мы можем значительно упростить эту программу, если уверены, что ответ на вопрос всегда существует и если нам нужно только первое решение. В этом случае отпадает необходимость в проверке на зацикливание. Попробуйте самостоятельно выяснить, почему это так.
К сожалению, путь через наименьшее число городов не обязательно будет самым кратчайшим по километражу. До сих пор мы не принимали во внимание информацию о расстояниях, имеющуюся в нашем графе. Если же мы добавим к нашему графу несколько фиктивных городов, чтобы получить:
а(ньюкасл,карлайл,58).
а(карлайл,пенрит,23).
а(городБ,городаА,15).
а(пенрит, дарлингтон,52).
а(городБ,городВ,10).
а(уэркингтон, карлайл, 33).
а(уэркингтон,городВ,5).
а(уэркингтон,пенрит,39).
а(дарлингтон,городА,25).
то путь, кратчайший по километражу, фактически будет построен последним, поскольку он проходит через большое число городов. С каждым путем, который может быть продолжен, нам нужно связать и поддерживать в процессе работы программы указатель текущей длины этого пути. Тогда программа будет всегда продлевать путь с наименьшим километражем. Такая стратегия называется поиском по критерию
первый-лучший. Будем теперь представлять путь в списке альтернативных путей в виде структуры
г(М, П), где
М – общая длина пути в километрах, а
П – список мест, где мы уже побывали. Модифицированный предикат
переходЗ находит кратчайший путь в списке альтернатив. Предикат кратчайший выделяет кратчайший путь в отдельный список, а остальные пути – в другой список. Предикат
продлить находит все допустимые продолжения текущего кратчайшего пути и добавляет их к списку. Это в свою очередь требует новой версии предиката
следузел, которая прибавляет расстояние до следующего города к уже вычисленному расстоянию. В целом программа выглядит так:
переходЗ (Пути,Цель,Путь):-кратчайший (Пути,Кратчайший,ОстПути), продлить(Кратчайший,Цель,ОстПути,Путь).
продлить(г(Расст,Путь),Цель,_,Путь):- Путь = [Цель|_].
продлить(г(Расст,[Послед| Бывали]),Цель,Пути,Путь):-найтивсе(г(D1,[Z,Послед|Бывали]),следузел(Послед,Бывали,Z,Расст,D1),Список), присоединить(Список,Пути,НовПути), переходЗ(НовПути,Цель,Пути).
кратчайший([Путь[Пути],Кратчайший,[ПутьЮст]):-кратчайший(Пути,Кратчайший,Ост), короче(Кратчайший,Путь),!.
кратчайший(Путь|Ост],Путь,Ост). короче(г(М1,_),г(М2, _):- M1 ‹ М2.
следузел(Х,Бывали,Y,Расст,НовРасст):-(a(X,Y,Z); a(Y,X,Z)),not(принадлежит(Y,Бывали)),НовРасст is Расст+Z.
Чтобы использовать эту программу, необходимо задать вопрос, содержащий предикат переход, определенный следующим образом:
переход (Старт,Цель,Путь):-переход3([г(0,[Старт])],Цель,R), обр(R,Путь).
Эта новая программа успешно строит возможные пути в по-рядке возрастания их фактической протяженности. Может быть, вам захочется изменить ее так, чтобы вместе с ответами она печатала длины различных путей.
Мы лишь затронули вопрос о возможных способах организации поиска по графу. Сведения о том, как осуществлять поиск по графу с использованием более эффективных критериев, чем «первый лучший», можно найти в литературе по искусственному интеллекту. Например: Nilsson N.
Principles of Artificial Intelligence, Springer-Verlag,
1982[10] и Winstone
P. Artificial Intelligence, (second edition), Addison-Wesley, 1984.
[11]
7.10. Просеивай Двойки, Просеивай Тройки
Просеивай Двойки,
Просеивай Тройки,
Эратосфена Решето,
Пусть все кратные им отсеем,
Простые числа получим зато.
Аноним
Простое число – это целое положительное число, которое делится нацело только на 1 и на само себя. Например, число 5 – простое, а число 15 – нет, поскольку оно делится на 3. Один из методов построения простых чисел называется «решетом Эратосфена». Этот метод, «отсеивающий» простые числа, не превышающие N, работает следующим образом:
1. Поместить все числа от 2 до N в решето.
2. Выбрать и удалить
из решета наименьшее число.
3. Включить это число в список простых.
4. Просеять через решето (удалить) все числа, кратные этому числу.
5. Если решето не пусто, то повторить шаги 2-5.
Чтобы перевести эти правила на Пролог, мы определим предикат
целые для получения списка целых чисел, предикат
отсеять для проверки каждого элемента решета и предикат
удалить для создания нового содержимого решета путем удаления из старого всех чисел, кратных выбранному числу. Это новое содержимое опять передается предикату
отсеять. Предикат
простые - это предикат самого верхнего уровня, такой что
простые(N, L) конкретизирует
L списком простых чисел, заключенных в диапазоне от
1 до
N включительно.
простые(Предел,Рs):- целые(2,Предел,Is),отсеять(Is,Рs).
целые (Min,Max,[Min|Oct]):-Min=‹Max,!, М is Min+1,целые(М,Мах,Ост).
целые(_,_,[]).
отсеять([],[]).
отсеять([I|Is],[I|Ps]):-удалить(I,Is,Нов),отсеять(Нов,Рs).
удалить(Р,[],[]).
удалить (P,[I|Is],[I|Nis]):-not(0 is I mod Р),!,удалить(Р,Is,Nis).
удалить (P,[I|Is],Nis):-0 is I mod Р,!,удалить(Р,Is,Nis).
Продолжая эту арифметическую тему, рассмотрим Пролог-программу, реализующую рекурсивную формулировку алгоритма Евклида для нахождения наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) двух чисел. Целевое утверждение
нод(I,J,K) доказуемо, если
K является наибольшим общим делителем чисел
I и
J. Целевое утверждение
нок(I,J,K) доказуемо, если
K является наименьшим общим кратным чисел
I и
J:
нод(I,0,I).
нод(I,J,K):- R is I mod J, нод(J,R,K).
нок(I,J,K):- нод(I,J,R), K is (I*J)/R.
Заметим, что из-за особенностей способа вычисления остатка эти предикаты не являются «обратимыми». Это означает, что для того чтобы они работали, необходимо заблаговременно конкретизировать переменные
I и
J.
Упражнение 7.10. Если числа
X,
Y и Z таковы, что квадрат Z равен сумме квадратов
X и
Y (т. е. если
Z²=
X²+
Y²), то про такие числа говорят, что они образуют
Пифагорову тройку. Напишите программу, порождающую Пифагоровы тройки. Определите предикат
pythag такой что, задав вопрос
?- pythag(X,Y,Z).
и запрашивая альтернативные решения, мы получим столько разных Пифагоровых троек, сколько пожелаем. Подсказка: используйте предикаты, подобные
целое_число из гл.
4.
7.11. Символьное дифференцирование
Символьным дифференцированием в математике называется операция преобразования одного арифметического выражения в другое арифметическое выражение, которое называется
производной. Пусть
U обозначает арифметическое выражение, которое может содержать переменную
х. Производная от
U по
х записывается в виде
dU/dx и определяется рекурсивно с помощью некоторых правил преобразования, применяемых к
U. Вначале следуют два граничных условия. Стрелка означает «преобразуется в»;
U и
V обозначают выражения, а
с – константу:
dc/dx →
0
dx/dx →
1
d(-U)/dx →
-(dU/dx)
d(U+V)/dx → dU/dx+dV/dx
d(U-V)/dx →
dU/dx-dV/dx
d(cU)/dx →
c(dU/dx)
d(UV)/dx →
U(dV/dx) + V(dU/dx)
d(U/V)dx →
d(UV-1)/dx
d(Uc)/dx →
cUc-l(dU/dx)
d(lnU)/dx →
U-1(dU/dx)
Этот набор правил легко написать на Прологе, поскольку мы можем представить арифметические выражения как структуры и использовать знаки операций как функторы этих структур. Кроме того, сопоставление целевого утверждения с заголовком правила мы можем использовать как сопоставление образцов. Рассмотрим цель
d(E,X, F), которая считается согласованной, когда производная выражения
E по константе
[12] X есть выражение
F. Помимо знаков операций +, -, *, /, которые имеют встроенные определения, нам нужно определить операцию ^, такую, что
X^Y означаете
xy, а также одноместную операцию ~, такую что
~Х означает «минус
X». Эти определения операций введены исключительно для того, чтобы облегчить распознавание синтаксиса выражений. Например, после того как
d определен, можно было бы задать следующие вопросы:
?- d(x+1,x,X).
X = 1+0
?- d(x*x-2,x,X).
X = х*1+1*х-0
Заметим, что само по себе простое преобразование одного выражения в другое (на основе правил) не всегда дает результат в приведенной (упрощенной) форме. Приведение результата должно быть записано в виде отдельной процедуры (см. разд. 7.12). Программа дифференцирования состоит из определений дополнительных операций и построчной трансляции приведенных выше правил преобразования в утверждения Пролога:
?- op(10,yfx,^).
?- op(9,fx,~).
d(X,X,1):-!.
d(C,X,0):- atomic(C).
d(~U,X,~A):- d(U,X,A).
d(U+V,X,A+B):- d(U,X,A), d(V,X,B).
d(U-V,X,A-В):- d(U,X,A), d(V,X,B).
d(C*U,X,C*A):- atomic(C), C\=X, d(U,X,A),!.
d(U*V,X,B*U+A*V):- d(U,X,A), d(V,X,B).
d(U/V,X,A):- d(U*V^~1),X,A).
d(U^C,X,C*U^(C-1)*W):- atomic(C),C\=X,d(U,X,W).
d(log(U),X,A*U^(~1)):- d(U,X,A).
Обратите внимание на два места, в которых задан предикат
отсечения. В первом случае отсечение обеспечивает тот факт, что производная от переменной по ней самой распознается только первым утверждением, исключая возможность применения второго утверждения. Во втором случае предусмотрено два утверждения для умножения. Первое – для специального случая. Если имеет место специальный случай, то утверждение для общего случая должно быть устранено из рассмотрения.
Как уже говорилось, данная программа выдает решения в неприведенной форме (т. е. без упрощений). Например, всякое вхождение
х*1 может быть приведено к х, а всякое вхождение вида
х*1+1*х-0 может быть приведено к
2*х. В следующем разделе рассматривается программа алгебраических преобразований, которую можно использовать для упрощения арифметических выражений. Примененный способ очень похож на тот, каким выше выводились производные.
7.12. Отображение структур и преобразование деревьев
Если некоторая структура покомпонентно копируется с целью образования новой структуры, то мы говорим, что одна структура
отображается в другую. Обычно при копировании каждая компонента слегка изменяется подобно тому, как в гл. 3 мы изменяли одно предложение, превращая его в другое. В том примере нам иногда нужно было скопировать какое-то слово в точности в том виде, в каком оно встретилось в исходном предложении, а иногда при копировании нам нужно было изменить слово. Для этого мы использовали следующую программу, которая
отображает первый аргумент предиката
преобразовать во второй его аргумент:
преобразовать([],[]).
преобразовать([А|В],[С|D]):- заменить(А,С),преобразовать(В,D).
Поскольку отображение имеет довольно широкое применение, мы можем определить предикат
отобспис такой, что целевое утверждение
отобспис(Р, L, M) согласуется с базой данных, применяя предикат
Р к каждому элементу списка
L и образуя в результате новый список
М. При этом предполагается, что предикат
Р имеет два аргумента: первый аргумент для передачи «входного» элемента, а второй аргумент – для измененного элемента, подлежащего включению в список
М.
отобспис((_,[],[]).
отобспис((P,[X|L],[Y|M]):- Q =..[P,X,Y],call(Q),отобспис(Р,L,М).
Об этом определении следует сказать несколько слов. Во-первых, определение содержит граничное условие (первое утверждение) и общий рекурсивный случай (второе утверждение). Во втором утверждении используется оператор '=..', формирующий целевое утверждение на основе предиката
(Р), входного элемента
(X) и переменной
(Y), которую предикат
Р должен конкретизировать, чтобы образовать измененный элемент. Затем делается попытка согласовать цель
Q, в результате чего
Y конкретизируется, образуя голову третьего аргумента данного вызова предиката
отобспис. Наконец, рекурсивный вызов отображает хвост первого аргумента в хвост второго.
Функции предиката
преобразовать может выполнять предикат
отобспис. Полагая, что предикат
заменить определен как в гл. 3, такое использование
отобспис могло бы выглядеть следующим образом:
?- отобспис(заменить,[уоu,аrе,а,computer],Z).
Z = [i, [am, not], a, computer]
Путем упрощения предиката
отобспис получается предикат
обрабспис, который просто обрабатывает список, применяя некоторый предикат от одного аргумента к каждому элементу списка. При этом новый список не порождается.
обрабспис(_,[]).
обрабспис(Р,[Х|L]):-Q =…[Р,Х],call(Q),обрабспис(Р,L).
Заметим, что предикат
печать_строки из гл. 5 можно было бы заменить запросом вида
обрабспис(put, L), где
L – это строка, которую нужно напечатать.
Отображение применимо не только к спискам; оно может быть определено для структуры любого вида. Например, рассмотрим арифметическое выражение, составленное из функторов * и +, имеющих по два аргумента. Пусть мы хотим отобразить одно выражение в другое, устраняя при этом все умножения на 1. Это алгебраическое приведение могло быть определено с помощью предиката
s такого, что
s(Op, L, R,Ans) означает, что выражение, состоящее из операции
Ор с левым аргументом
L и правым аргументом
R приводится к упрощенному выражению
Ans. Факты, необходимые для устранения умножений на 1, могли бы выглядеть так (из-за коммутативности умножения нужны два факта):
s(*,X,1,X).
s(*,1,X,X).
Эта таблицы упрощений позволяет нам любое выражение вида 1*Х отобразить в X. Посмотрим, как можно воспользоваться этим в программе.
При приведении выражения
Е с помощью такой таблицы упрощений, мы вначале должны привести левый аргумент
Е, затем привести правый аргумент
Е и, наконец, посмотреть, подходит ли этот приведенный результат под случаи, предусмотренные в нашей таблице. Если это так, то мы порождаем новое выражение в соответствии с указаниями таблицы. В качестве «листьев» дерева, представляющего выражение, фигурируют целые числа или атомы, поэтому для приведения листьев к ним самим в граничном условии мы должны использовать встроенный предикат
atomic. Как и выше, мы можем использовать ' =..', чтобы разложить выражение
Е на функтор и компоненты;
привести(Е,Е):- atomic(E), 1.
привести(Е,F):-Е =.. [Op,L,R],привести(L,Х),привести(R, Y),s(Op,X,Y,F).
Итак, предикат
привести отображает выражение
Е в выражение
F, используя для этого факты, имеющиеся в таблице упрощений
s. А что делать, если невозможны никакие упрощения? Чтобы избежать в этом случае неудачного завершения
s(Op,X, Y, F), мы должны поместить в конец каждого раздела таблицы упрощений, относящегося к определенному оператору, правило-ловушку. Приведенная ниже таблица упрощений содержит правила для сложения и умножения. Кроме того, в ней выделены правила-ловушки для каждого вида операций.
s(+,X,0,X).
s(+,0,X,X).
s(+,X,Y,X + Y) /* ловушка для + */
s(*,_,0,0).
s(*,0,_,0).
s(*,1,X,X).
s(*,X,1,X).
s(*,X,Y,X*Y). /* ловушка для * */
При наличии правил-ловушек возникает вопрос о выборе способа упрощения некоторых выражений. Например, если нам дано выражение 3+0, мы можем либо использовать первый факт, либо применить правило-ловушку для +. Благодаря способу упорядочения фактов, прежде чем применить правило-ловушку Пролог всегда будет пытаться применить правила для специальных случаев. Поэтому первое решение, полученное предикатом
привести, всегда будет являться действительно упрощенным выражением (если оно возможно). Однако альтернативные решения будут иметь не самый простой вид из всех возможных.
Другое упрощение, используемое при выполнении алгебраических преобразований с помощью ЭВМ, известно как свертка констант. В выражении
3*4+a константы 3 и 4 могут быть «свернуты», что дает в результате выражение
12+а. Правила свертки констант могут быть добавлены
в соответствующие места приведенной выше таблицы упрощений. Правило для сложения констант выглядит следующим образом:
s(+,X,Y,Z):- integer(X), integer(Y), Z is X+Y.
Соответствующие правила для других арифметических операций имеют аналогичный вид.
В коммутативных операциях, таких как умножение и деление, указанные выше упрощения могут давать различный эффект на выражениях, которые записаны по-разному, но алгебраически эквивалентны. Например, если правило свертки констант задано для умножения, то предикат
привести совершенно правильно преобразует
2*3*а в
6*а, но
а*2*3 или
2*а*3 будут преобразовываться в самих себя. Чтобы понять, почему это так, подумайте над тем, как выглядят деревья, представляющие эти выражения (см. рис. 7.4).
В первом дереве самое нижнее умножение
2*3 можно свернуть, получив
6, но во втором дереве нет поддеревьев, которые было бы можно свернуть. Однако, используя коммутативность умножения, можно добавить к таблице следующее правило, которое позволит справиться с данным конкретным случаем:
s(*,X*Y,W,X*Z):- integer(Y), integer(W), Z is Y*W.
Более общая алгебраическая система может быть построена путем простого добавления дополнительных s-утверждений вместо увеличения объема программы для
привести.

Рис. 7.4
7.13. Применение предикатов clause и retract
В этой книге мы неоднократно сталкивались с применением встроенных предикатов. На самом деле многие из них можно определить на Прологе, используя более простые встроенные предикаты. В этом разделе мы рассмотрим несколько таких определений. Они могут найти практическое применение у тех программистов, которые используют неполную в каких-либо отношениях Пролог-систему, однако в любом случае они интересны, как примеры программирования на Прологе. Может быть, они наведут вас на мысль о разработке несколько отличающихся версий этих предикатов для своего собственного применения.
Мы можем определить с помощью предиката
clause некоторую версию процедуры
listing. Определим предикат
распеч1 такой, что при согласовании цели
распеч1(Х) с базой данных из последней будут выводиться на печать утверждения, заголовки которых совпадают с
X. Поскольку определение
распеч1 включает использование предиката
clause, у которого
X задан как первый аргумент, то мы вынуждены поставить условие, что переменная
X конкретизирована таким образом, что главный функтор утверждения известен. Рассмотрим определение
распеч1:
распеч1(Х):-clause(Х,Y),выв_утвержд(Х,Y),write('.'),nl,fail.
распеч1(Х).
выв_утвержд(Х,true):-!, write(X).
выв_утвержд(Х,Y):- write((X:- Y)).
При попытке согласовать с базой данных цель
распеч1(Х) первое утверждение осуществляет поиск в базе данных такого утверждения, у которого заголовок совпадает с
X. Если такое утверждение найдено, то оно выводится на печать и затем с помощью предиката
fail инициируется механизм возврата. Возвратный ход опять приводит нас к предикату
clause, который находит другое такое же утверждение, если оно имеется, и т. д. Когда таких утверждений больше нет, цель
clause больше не удается согласовать с базой данных. В этом случае будет выбрано второе утверждение определения предиката
распеч1, и потому цель будет согласована с базой данных. «Побочным эффектом» этих действий является печать соответствующих утверждений. Определение предиката
выв_утвержд задает способ печати найденных утверждений. Выделяется специальный случай, когда тело утверждения есть
true. В этом случае на печать выводится только заголовок утверждения. Иначе на печать выводится заголовок и тело утверждения, соединенные функтором ':-'. Отметим, что использование «отсечения» здесь имеет целью указать, что в случае, когда тело есть
true, можно применять только первое правило. Поскольку данный пример построен на использовании механизма возврата, то задание отсечения здесь существенно.
Встроенный предикат
clause можно также применить при написании Пролог-интерпретатора на самом Прологе. Это означает, что мы можем определить действия, которые представляют собой выполнение Пролог-программы, причем исполнителем этих действий также является Пролог-программа. Ниже приводится определение предиката
интерпрет такого, что цель
интерпрет(Х) согласуется в том и только в том случае, когда
X, рассматриваемая как цель, согласуется с базой данных.
Предикат
интерпрет напоминает встроенный предикат
call, но является более ограниченным.
интерпрет(true):-!.
интерпрет((Gl,G2)):-!, интерпрет(G1), интерпрет(G2).
интерпрет(Цель):-clause(Цель,ЕщеЦели), интерпрет(ЕщеЦели).
Первые два утверждения рассчитаны на специальные случаи, когда цель есть
true и когда цель представляет собой конъюнкцию целей. Последнее утверждение рассчитано на случай простой цели. Данная процедура находит утверждение, заголовок которого совпадает с заданной целью, и затем интерпретирует цели, входящие в тело этого утверждения. Заметим, что приведенное определение не рассчитано на программы, где используются встроенные предикаты, поскольку у таких предикатов нет определяющих их в обычном смысле утверждений.
Рассмотрим определение предиката
consult. Разумеется, предикат
consult предусмотрен среди встроенных предикатов большинства Пролог-систем, однако интересно посмотреть, как он может быть определен на Прологе.
consult(Файл):-seeing(Input),sее(Файл),repeat,read(Tepм),обработать(Терм),seen,see(Input),!.
обработать(Терм):- маркер_конца_файла(Терм),!.
обработать((?- Q)):-!, call(Q),!, fail.
обработать(Утвержд):- assertz(Утвержд), fail.
Это определение отличается рядом интересных особенностей. Во-первых, цель
seeing(Input) и ее партнер
see(Input) призваны гарантировать, что текущий файл ввода не будет «забыт» после применения предикат
consult. Во-вторых, предикат
маркер_конца_файла здесь использован без определения. По замыслу он должен быть истинным только в том случае, когда его аргумент конкретизирован термом, используемым для представления конца файла (который мог бы встретиться при выполнении
read). В разных реализациях Пролога для представления «конца файла» используются разные термы, поэтому
маркер_конца_файла в разных реализациях может быть определен по-разному. Одно из возможных определений выглядит так:
маркер_конца_файла(конец_файла).
В определении предиката
обработать интересна организация выполнения соответствующих действий для каждого терма, считанного из входного файла. Целевое утверждение
обработать доказуемо только, когда его аргументом является маркер конца файла. Иначе после соответствующего действия имитируется неудача доказательства и инициируется механизм возврата, который возвращает программу к предикату
repeat. Отметим важность «отсечения» в конце определения предиката
consult. Оно фиксирует выбор, сделанный предикатом
repeat[13]. И последнее замечание. Если терм, считанный из файла, представляет собой вопрос (см. второе утверждение определения предиката
обработать), то делается попытка немедленно согласовать соответствующую цель с помощью предиката
call (см. разд. 6.7).
В качестве примера использования предиката
retract здесь приведено определение полезного предиката
уберивсе. При согласовании с базой данных целевого утверждения
уберивсе(Х) все утверждения, заголовки которых совпадают с
X, удаляются из базы данных. Поскольку в данном определении используется предикат
retract, то переменная
X не может быть неконкретизированной, так как в противном случае не с чем будет сопоставлять утверждения из базы данных. Данное определение должно распознавать два вида утверждений с заголовками, совпадающими с
X, - факты и правила. При обработке этих двух видов утверждений в вызове
retract задаются разные аргументы. В определении используется то свойство, что
retract будет срабатывать при возврате до тех пор, пока все утверждения, сопоставимые с его аргументами, не будут удалены из базы данных.
уберивсе(Х):- retract(X), fail.
уберивсе(Х):- retract((X:- Y)), fail. уберивсе(_).
В качестве примера использования предиката
убери все здесь приведено определение предиката
reconsult на Прологе. Назначение предиката
reconsult сходно с назначением предиката
consult, с той лишь разницей, что при
reconsult каждое считанное утверждение замещает существующее утверждение того же предиката, а не добавляется к нему (см. разд. 6.1).
reconsult(Файл):-уберивсе(сделано(_)),seeing(Старый),sее(Файл),repeat,read(Терм),проверить(Терм),seen,see(Старый),!.
проверить(Х):- маркер_конца_файла(Х),!.
проверить((?- Цели)):-!, call (Цели),!, fail.
проверить(Утверждение):-заголовок(Утверждение, Заголовок), запись_сделана(3аголовок), assertz(Утверждение), fail.
запись_сделана(3аголовок):- сделано(Заголовок),!.
запись_сделана(3аголовок):- functor(Заголовок,Func,Arity), functor(Proc,Func,Arity), asserta(cдeлaнo(Proc)), уберивсе(Ргос),!.
заголовок((А:- В), А):-!.
заголовок (А, А).
Это определение похоже на определение
consult, в котором вместо предиката
обработать используется предикат
проверить. Основное различие заключено в предикате
запись_сделана. Когда в файле появляется первое утверждение для данного предиката, то, прежде чем к базе данных будет добавлено хотя бы одно новое утверждение, из нее должны быть удалены все старые утверждения для данного предиката. Удаление этих утверждений нельзя откладывать до момента, когда в базе данных появятся их новые версии, поскольку в этом случае мы удалили бы из базы данных те утверждения, которые только что были введены. Как же определить, что некоторое утверждение в файле является первым для соответствующего предиката? Ответ заключается в том, что мы регистрируем в базе данных предикаты, для которых уже нашлись утверждения в файле. Это делается с помощью предиката
сделано. Когда из файла считывается первое утверждение например, для предиката
foo с двумя переменными, то имеющиеся утверждения удаляются и новое утверждение добавляется к базе данных. Кроме того, к базе данных добавляется факт:
сделано(foo(_,_)).
В дальнейшем, при чтении остальных утверждений для предиката
too, мы сможем проверить, что старые утверждения уже удалены из базы данных. Тем самым удается избежать ошибочного удаления новых утверждений. Для данного определения важно, что мы не добавляем в базу данных что-нибудь вроде:
сделано(foо(а,Х)).
поскольку в этом случае аргумент предиката
сделано не обязательно совпадает с заголовком утверждения для
foo. Пара запросов
…,functor(Заголовок,Func,Arity),functor(Proc,Func,Arity),…
конкретизирует
Ргос структурой, имеющей тот же функтор, что и заголовок
Заголовок, но с переменными в качестве аргументов (см. разд. 6.5).
ГЛАВА 8. ОТЛАДКА ПРОЛОГ-ПРОГРАММ
На приведенных выше примерах вы уже приобрели опыт применения программ и научились их изменять, а также успели написать и свои собственные программы. Теперь самое время заняться вопросом: что делать, когда программа ведет себя не так, как ожидалось. Подобные неожиданности связаны с наличием ошибок в программе, а процесс устранения этих ошибок называется отладкой. По нашему убеждению самым разумным подходом к программированию является тот, который может быть охарактеризован как «программирование с предупреждением ошибок». Перефразируя старую поговорку, можно сказать, что
грамм тщательного программирования стоит килограмма отладки. В этой главе мы расскажем о некоторых методах отладки, но начнем с того, как избежать проникновения ошибок в программы. Сознавая, что в общем виде эта проблема неразрешима, мы хотим просто поделиться некоторыми неформальными приемами, которые уже приносили пользу другим программистам, работающим на Прологе.
Как и всякое творчество, будь то сочинение музыки, литература или архитектура, программирование располагает множеством способов
представления объектов и
обработки этих объектов и отношений между ними в конкретной программе. В общем случае для некоторого элемента данных в программе существует несколько возможных способов его представления или обработки. Всякий раз, когда программист решает использовать в данной программе один из них, мы говорим, что программист принял
проектное решение.
Новички, впервые столкнувшиеся с задачей выбора проектных решений, часто испытывают трудности. Помочь им может знание возможных вариантов решений, и, кроме того, важно, чтобы руководитель разъяснил им методику программирования в целом, поскольку искусство принятия проектных решений в программировании – это самостоятельная дисциплина. Мы уже пытались затронуть эту проблему в разд. 1.1, где обсуждались различные способы интерпретации утверждений. Эти вопросы связаны с
представлением объектов и отношений. В разд. 7.7 мы снова столкнулись с этой проблемой при описании трех различных способов упорядочения списка объектов. Эти вопросы связаны с разными способами
обработки объектов и отношений.
В данной книге мы старались оказать помощь в выборе проектных решений двумя путями. Во-первых, наличие в книге большого числа примеров программ должно способствовать усвоению идей некоторых решений, выработанных опытными программистами. Во-вторых, в данной главе можно найти некоторые советы и рекомендации, специфические для Пролога.
8.1. Расположение текстов программ
После того как программист принял решение о том, как представлять и обрабатывать объекты и отношения в программе, ему следует убедиться в том, что текст программы расположен удобно для чтения и ее синтаксические конструкции ясны. Набор утверждений для данного предиката называется
процедурой. Возможно, вы уже обратили внимание на то, что в примерах данной книги каждое утверждение в процедуре начинается с новой строки, а между собой процедуры разделяются одной пустой строкой. Например, один из способов определения предиката эквивалентности для множеств (при представлении множеств в виде списков) состоит в использовании трех предикатов, каждый из которых определяется с помощью процедуры из двух строк:
равмнож(Х,Х):-!.
равмнож(Х,Y):- равспис(Х,Y).
равспис([],[]).
равспис([Х|L1],L2):- удалить(Х,L2,LЗ), равспис(L1,LЗ).
удалить(Х,[Х|Y],Y).
удалить(Х,[Y|L1],[Y|L2]):- удалить(Х,L1,L2).
Данный пример, возможно, не является наилучшим определением эквивалентности множеств, однако он показывает, как нужно размещать тексты процедур. Заметим, что утверждения каждой процедуры сгруппированы вместе, а процедуры разделяются пустой строкой. Другое соглашение, которого придерживаются многие программисты на Прологе, - это писать каждое утверждение на отдельной строке, если оно на ней умещается. Если нет, то писать заголовок утверждения и знак ':-' на первой строке, а каждую цель в конъюнкции целей писать с новой строки со сдвигом. Для примера рассмотрим запись программы порождения всех перестановок списка:
перест([],[]).
перест(L,[Н|Т]):-
присоединить(Y,[Н|U],L),
присоединить(V,U,W),
перест(W,T).
В этом определении перестановки элементов списка выполняет предикат
присоединить, а механизм возврата при каждой попытке вновь согласовать целевое утверждение
перест(Х, Y) обеспечивает порождение из
X новой перестановки
Y. Следует обратить внимание на способ размещения на странице конъюнктов второго утверждения.
Главное – остановить свой выбор на каком-либо согласованном наборе правил оформления текста программы, а на каком – не так уж важно. Как правило, полезно добавлять комментарии, надлежащим образом группировать термы, в случае сомнений относительно приоритета выполнения операций – использовать круглые скобки, а также разумно распоряжаться пустым пространством (пробелами и пустыми строками). Комментарии должны подсказывать, как следует интерпретировать аргументы структур или утверждений: в каком порядке они поступают и каким структурам данных (константам или структурам) они должны соответствовать. Полезно также указывать в комментариях, как должны конкретизироваться переменные в результате согласования данного утверждения с базой данных.
В плане общей организации программы полезно разделять текст программы на более или менее замкнутые части, например, желательно, чтобы все процедуры обработки списков оказались в одном и том же файле. Процедура Пролога, содержащая более пяти – десяти правил, может оказаться трудной для понимания, поэтому путем определения более мелких предикатов попытайтесь как можно более естественным образом разбить ее на части. Если в программе используется много фактов, таких как правила упрощения из разд. 7.12, то все эти факты должны содержаться в одном файле. Большое количество фактов легче читается, чем большое количество правил, и хотя даже несколько правил могут быть трудны для понимания, многие страницы описания конкретного факта могут не вызвать затруднений, поскольку сама семантика фактов более проста.
Еще один момент, который влияет на легкость чтения Пролог-программ, - это использование точки с запятой («или») и восклицательного знака («отсечение»). С проблемами, связанными с чрезмерно широким использованием «отсечения», мы познакомились в гл. 4. Всегда следует пытаться обойтись без ';', возможно за счет дополнительных утверждений. Например, следующая программа:
nospy(X):-
проверить(Х,Функтор,ЧисАрг,А), !,
(контрточка(_,Функтор,А), !,
(отказ(контрточка(Заголовок, Функтор, ЧисАрг),_),
устконтрточку(Заголовок, Тело),
отказ(3аголовок, Тело),
write('контр.точка с терма'), печтерм(Функтор, ЧисАрг),
write(' удалена.'),nl,
fail
; true
)
; write('Heт контр.точек на терме'),
write(X), put(46), nl
),
!.
гораздо труднее для понимания, нежели:
nospy(X):-проверить(Х,Функтор,ЧисАрг,А),!,
попыт_убр(Х,Функтор,ЧисАрг,А).
попыт_убр(_,Функтор, ЧисАрг,А):- контрточка(_,Функтор,А),!,убрконтрточку(Функтор, ЧисАрг, А).
попыт_убр(Х,_,_,_):- write('Heт контр.точек на терме '), write(X), put(46), nl,!.
убрконтрточку(Функтор, ЧисАрг, А):-
отказ(контрточка(Заголовок,Функтор, ЧисАрг), _), устконтрточку(Заголовок,Тело), отказ(3аголовок, Тело),
write('Koнтp.точка с терма'), печтерм(Функтор, ЧисАрг), write(' удалена.'), nl, fail.
убрконтрточку (_,_,_).
которая делает в точности то же самое. Если же вам действительно необходимо использовать «или», то полезно так организовать текст конъюнкции целей, чтобы «или» не терялось среди целей. Полезно также заключить соответствующие цели в скобки, чтобы явно выделить область действия этого «или».
На протяжении всей книги подчеркивалась важность умения учитывать при решении многих задач наряду с общим правилом и граничные условия. Всюду, где это возможно, мы старались разместить граничные условия перед всеми другими утверждениями процедуры. Это выделяет граничные условия и, кроме того, служит в какой-то мере защитой от циклических определений. Однако бывают случаи, когда желательно размещать граничные условия после всех утверждений процедуры. Очевидно, что правила-«ловушки», с которыми мы уже сталкивались несколько раз, нужно размещать в конце процедуры.
Разбирая Пролог-процедуру
всегда полезно обращать внимание на следующие важнейшие моменты ее записи:
• Проверьте
посимвольно, как записано имя каждого предиката и каждой переменной в процедуре. Ошибки в написании имен довольно распространены.
• Проверьте
число аргументов каждого функтора, используемого в процедуре. Убедитесь в том, что число аргументов (и порядок их следования) соответствуют вашим проектным решениям.
• Выделите из утверждений все
операторы и определите их приоритет, ассоциативность, а также то, где находятся их аргументы. Это можно сделать на основании определений операторов, и исходя из наличия скобок. Если есть сомнения, добавьте дополнительные скобки. Для проверки соответствия действия оператора вашим представлениям попробуйте распечатать некоторые простые термы, используя display.
• Обратите внимание на
область определения каждой переменной и выделите в этой области переменные, сходные с ней по имени. Проследите, какие переменные «сцепляются», когда одной из них будет присвоено значение. Проверьте, встречаются ли в теле утверждения переменные из его заголовка.
• Постарайтесь определить, какие переменные конкретизированы, а какие нет в момент перед применением утверждения.
• Выделите утверждения, составляющие граничные условия. Проверьте, учтены ли все возможные граничные условия.
После того как подобным образом процедура будет разобрана «по косточкам», вы поймете ее гораздо лучше.
8.2. Типичные ошибки
В этом разделе мы рассмотрим те ошибки, которые допускают как начинающие, так и опытные программисты, использующие Пролог. Эти ошибки делятся на две группы:
синтаксические ошибки и ошибки
управления последовательностью обработки.
После того, как программист решил, какую программу он будет писать и как разместит ее текст на странице печатающего устройства (или на экране видеотерминала), ему остается ввести текст программы, записав его в файл или непосредственно в базу данных Пролог-системы. Основная задача данного этапа – это обеспечить
синтаксическую правильность программы. Ниже приводится список типичных синтаксических ошибок. Если программист сам не выявит эти ошибки, то при попытке выполнить предикат
consult Пролог может выдать соответствующее сообщение.
• Одной из типичных синтаксических ошибок является отсутствие точки '.' в конце утверждения. Точкой должен заканчиваться и любой терм, считываемый с помощью предиката
read. После точки нужно оставлять хотя бы один пробел. Поэтому избегайте заканчивать файл вместе с вводом точки последнего утверждения – убедитесь в том, что в самом конце вы не забыли нажать клавишу
RETURN.
• Некоторые специальные литеры используются парами. К ним относятся круглые скобки '(' и ')', используемые для группирования термов, квадратные скобки '[' и ']', используемые для задания списков, и фигурные скобки '{' и '}', используемые для записи правил грамматики (см. гл. 9). Сюда же относятся двойные кавычки '"' используемые для ограничения строк и одиночная кавычка '", используемая для задания атомов. Составные скобки '/*' и '*/' используются для ограничения комментариев. Убедитесь, что скобок каждого вида задано не больше и не меньше чем необходимо.
• Остерегайтесь неправильного написания слов, особенно имен встроенных предикатов. Это может привести к самым неожиданным ошибкам, поскольку неверно записанные имена предикатов вряд ли сопоставятся с каким-либо утверждением в базе данных. Или наоборот, они могут неожиданно сопоставиться с утверждениями, заголовок которых случайно совпадает с получившимся именем.
• Еще одним источником возможных ошибок являются операторы. Когда вы не уверены в ассоциативных свойствах оператора, то используйте круглые скобки, чтобы задать нужные свойства явно. Проверяйте экспериментально действие введенных вами операторов с помощью предиката
display.
• Когда имеете дело с операциями над списками, проверяйте себя с помощью следующих вопросов и ответов:
• Как сопоставляются
[а,b,с] и
[X|Y]? (
X конкретизируется значением a, a
Y -
значением [b,с]).
• Сопоставимы ли
[а] и
[X|Y]?
(Да, причем X конкретизируется значением a,
a Y –
значением []).
• Сопоставимы ли
[] и
[X|Y]?
(Нет).
• Имеет ли смысл запись
[X, Y|Z]?
(Да).
• Имеет ли смысл запись
[X|Y,Z]?
(Нет).
• Имеет ли смысл запись
[Х|[Y|Z]?
(Да, это то же самое, что [X,Y|Z])
• Как сопоставляются
[a, b] и
[А |В]? (
А конкретизируется значением а, а
В -
значением [b]).
• Существует ли более одного способа сопоставления приведенных выражений?
(Нет, никогда).
Необходимо подчеркнуть, что когда приходится иметь дело со списками или другими структурами подобного рода, полезно прибегать к помощи «древовидных диаграмм», о которых говорилось в гл. 2.
Даже в тех случаях, когда вы уверены, что в программе нет синтаксических ошибок, она все-таки при попытке согласования целевых утверждений может вести себя непредсказуемо; характерными признаками этого являются: впечатление, что программа никогда не остановится («бесконечный цикл»), неожиданные появления отрицательных ответов
(нет), или конкретизация переменных не теми значениями, какие ожидались. Приведем обычные причины подобных ошибок:
• Циклические определения, о которых упоминалось в гл. 3.
• Недостаточность граничных условий или какая-либо другая недоопределенность задачи.
• Бесполезные процедуры, которые переопределяют встроенные предикаты.
• Задание неверного количества аргументов для функтора. Это не рассматривается как синтаксическая ошибка, поскольку количество аргументов функтора может быть разным.
• Неожиданный выход на конец файла при выполнении предиката чтения
read.
Остерегайтесь следующих заблуждений относительно принципов работы механизма возврата:
•
Заблуждение: Одна из причин использования возвратного хода состоит в том, что Пролог может вернуться к предыдущему сопоставлению и выполнить его снова некоторым другим способом.
На самом деле: Когда Пролог просматривает базу данных, пытаясь сопоставить цели что-либо из базы данных (какой-нибудь факт или заголовок правила), то сопоставление бывает либо успешным, либо неудачным. Пролог никогда не делает возвратный ход ни к какому сопоставлению, в попытке осуществить его по-другому, поскольку сопоставить конкретную цель с конкретным утверждением в базе данных можно только одним-единственным способом.
•
Заблуждение: Запись списка
[X|Y] может быть сопоставлена с любым отрезком списка, и при этом разбиение списков на части может быть осуществлено несколькими разными способами. Именно этим объясняется действие предиката
присоединить (X, Y, [a,b,c,d]).
На самом деле: В записи списка
[X|Y] X сопоставляется только с головой списка, a
Y сопоставляется только с его хвостом. Цели с предикатом
присоединить способны находить разные разбиения списков благодаря возможностям возвратного хода, а не возможностям сопоставления.
8.3. Модель трассировки
Метод, используемый Прологом при попытках согласовать цели с базой данных, можно рассматривать с разных точек зрения. Мы уже познакомились с одной моделью описания этого метода, которую можно представить в виде «цепочки доказательств», проходящей через прямоугольники, изображающие цели. Теперь мы познакомимся с другой моделью описания работы Пролога, которая применяется во многих средствах отладки программ, таких как
трассировка. Существованием этой модели мы обязаны главным образом нашему коллеге Лоренсу Бэрду. Вам следует изучить эту модель, прежде чем вы приступите к использованию средств отладки Пролога.
При использовании трассировки Пролог-система выводит на печать информацию о последовательности отработки целей, чтобы показать, какой стадии выполнения достигла программа. При этом, для того чтобы разобраться в том, что происходит, важно понять, когда и почему определенные цели выводятся на печать. В обычных языках программирования особый интерес представляют моменты входа в подпрограммы и выхода из них. Однако Пролог допускает написание недетерминированных программ, а это вносит сложности, связанные с механизмом возврата. Дело не ограничивается последовательностью входов в утверждения и выходов из них. Механизм возврата может неожиданно вновь запустить выполнение каких-либо утверждений, чтобы построить альтернативное решение. Кроме того предикат отсечения 'Г указывает для каких целей нельзя искать другие решения. Наибольшие трудности, с которыми приходится сталкиваться начинающим программистам, связаны именно с пониманием принципов работы механизма возврата: что на самом деле происходит, когда попытка согласования цели завершается неудачей и система неожиданно начинает возвратный ход. Мы надеемся, что этот процесс достаточно подробно описан в предыдущих главах. Впрочем, в предыдущих главах рассматривалась не только последовательность обработки целей, но также и то, как происходит конкретизация переменных, как цели сопоставляются с заголовками утверждений из базы данных, и, наконец, как согласуются с базой данных подцели. В модели трассировки выполнение Пролог-программ описывается в терминах четырех видов происходящих событий: CALL(ВЫЗОВ), ЕХIT(ВЫХОД), REDО(ПЕРЕДЕЛКА), FAIL(HEУДАЧА).
CALL
Событие CALL фиксирует начало попытки Пролога согласовать цель с базой данных. На наших диаграммах это обозначено стрелкой, входящей в прямоугольник сверху.
EXIT
Событие EXIT фиксирует момент, когда некоторая цель только что согласована с базой данных. На наших диаграммах это обозначается стрелкой, выходящей снизу из прямоугольника.
REDO
Событие REDO фиксирует момент, когда система возвращается к цели, пытаясь повторно согласовать ее с базой данных. На наших диаграммах это обозначается стрелкой, которая возвращается в прямоугольник снизу.
FAIL
Событие FAIL фиксирует момент, когда попытка согласовать цель с базой данных заканчивается неудачно. На наших диаграммах это соответствует выходу стрелки вверх из прямоугольника.
Средства отладки сообщают нам о моментах возникновения событий этих четырех видов в ходе выполнения наших программ. Эти события будут происходить со всеми целями, которые Пролог рассматривает во время выполнения программы. Чтобы можно было различать, к каким целям относятся происходящие события, каждой цели присваивается уникальный целочисленный идентификатор, который называется его
номером обращения.
Обратимся к примеру. Рассмотрим следующее определение предиката
потомок:
потомок(Х,Y):- отпрыск(Х,Y).
потомок(X,Z):- отпрыск(Х,Y), потомок(Y,Z).
Этот фрагмент программы находит прямых потомков некоторого лица по заданным в базе данных фактам
отпрыск, например:
отпрыск(авраам,измаил).
отпрыск(авраам,исаак).
отпрыск(исаак,исав).
. . .
Первое утверждение программы указывает, что
Y является потомком
X если
Y есть отпрыск
X, а второе утверждение указывает, что
Z является потомком
X если
Y есть отпрыск
X и если
Z является потомком
Y. Рассмотрим вопрос:
?- потомок(авраам,Ответ), fail.
и проследим за ходом выполнения программы чтобы увидеть, когда возникают разные события указанных видов. Важно, чтобы вы
попытались проследить за процессом трассировки, мысленно воссоздавая поведение цепочки доказательств, которая входит в прямоугольники, обозначающие цели и выходит из них. Время от времени мы будем представлять текущее состояние в виде диаграмм.
В заданном вопросе после первой цели следует
fail. Это сделано для того, чтобы инициировать механизм возврата и тем самым, получить все возможные решения для цели потомок. Таким образом, в целом вопрос никак не может иметь положительного ответа. Однако цель нашей трассировки состоит в том, чтобы наглядно представить себе ход выполнения программы, вызванный несогласуемостью второй цели
(fail).
В начале мы имеем прямоугольники, обозначающие две цели, в которые пока не входила стрелка, представляющая цепочку доказательств (см. рис. 8.1). Первое событие состоит в ВЫЗОВе (CALL) цели
потомок. Это - обращение номер 1.

Риc. 8.1
(1) CALL: потомок(авраам,Ответ)
(2) CALL: отпрыск(авраам,Ответ)
Мы сопоставили с целью первое утверждение процедуры потомок и это привело к ВЫЗОВ цели
отпрыск. В результате возникла ситуация, где стрелка движется вниз (см. рис. 8.2). Мы продолжаем:

Рис. 8.2.
(2) EXIT: отпрыск (авраам,измаил)
Сразу успешно согласуется первое утверждение и следует ВЫХОД
(EXIT) из цели.
(1) EXIT
: потомок(авраам,измаил)
Таким образом, мы согласовали первое утверждение процедуры
потомок.
(3) CALL: fail
(3) FAIL: fail
(1) REDO: потомок(авраам,измаил)
Затем мы пытаемся согласовать
fail, и, как и следовало ожидать, эта попытка завершается НЕУДАЧЕЙ (FAIL). Стрелка возвращается из прямоугольника
fail назад выше в прямоугольник
потомок. Изображение этой ситуации приведено на рис. 8.3. Стрелка движется вверх. Продолжаем:

Рис. 8.3.
(2) REDO: отпрыск(авраам,измаил)
(2) EXIT: отпрыск(авраам,исаак)
Для цели
отпрыск выбрано альтернативное утверждение. Поэтому стрелка может снова выйти вниз из этого прямоугольника.
(1) EXIT: потомок(авраам,исаак)
(4) CALL: fail
(4) FAIL: fail
(1) REDO: потомок(авраам,исаак)
И снова
fail заставляет нас отвергнуть это решение и начать возвратный ход. Заметим, что это было совершенно новое обращение к
fail (мы вошли в него заново «сверху»).
(2) REDO: отпрыск(авраам,исаак)
(2) FAIL: отпрыск(авраам,Ответ)
На этот раз мы не можем предложить другое сопоставление для цели
отпрыск, и потому продолжаем возвратный ход, стрелка отступает вверх, покидая прямоугольник
отпрыск.
(5) CALL: отпрыск(авраам,Y)
Здесь произошло следующее: мы выбрали второе утверждение процедуры
потомок и выполнили совершенно новое обращение
к отпрыск, соответствующее первой подцели (рис. 8.4). Стрелка теперь снова движется вниз. Продолжаем:

Рис. 8.4.
(5) EXIT: отпрыск(авраам,измаил)
(6) CALL: потомок(измаил,Ответ)
Это дает решение, с которым мы теперь уже рекурсивно вызываем
потомок. Следует новое обращение к
потомок.
(7) CALL: отпрыск(измаил,Ответ)
(7) FAIL
: отпрыск(измаил,Ответ)
(8) CALL
: отпрыск(измаил, Y2)
(8) FAIL
: отпрыск(измаил,Y2)
(6) FAIL
: потомок(измаил,Ответ)
У Измаила нет детей (в данном примере) поэтому в обоих утверждениях процедуры
потомок подцель
отпрыск завершается неудачей, что приводит к неудаче всей цели потомок.
(5) REDO: отпрыск(авраам,измаил)
Мы возвращаемся назад для выбора новой альтернативы.
(5) EXIT: отпрыск(авраам.исаак)
(9) CALL: потомок(исаак,Ответ)
(10) CALL: отпрыск(исаак,Ответ)
(10) EXIT: отпрыск(исаак,исав)
Запускаем новое обращение
к потомок и попытка согласовать подцель
отпрыск завершается удачно (рис. 8.5). Продолжаем:

(9) EXIT: потомок(исаак,исав)
(1) EXIT: потомок(авраам,исав)
(11) CALL: fail
(11) FAIL: fail
(1) REDO: потомок(исаак,исав)
(9) REDO: потомок(исаак,исав)
Это дает окончательное решение исходного вопроса, однако fail вновь вынуждает включиться механизм возврата, поэтому мы возвращаемся назад по событиям REDO:
(10) REDO: отпрыск(исаак,исав)
(10) EXIT: отпрыск(исаак,иаков)
(9) EXIT: потомок(исаак,иаков)
(1) EXIT: потомок(авраам,иаков)
Для подцели
отпрыск найдено другое сопоставление, которое порождает другой результат для исходной цели
потомок. Уже сейчас можно заметить, что это последний потомок Авраама, однако еще остается выполнить определенный объем работы. Проследим далее за последовательностью событий по мере того, как механизм возврата заставляет нас отступать к началу.
(12) CALL: fail
(12) FAIL: fail
(1) REDO: потомок(авраам,иаков)
(9) REDO: потомок(исаак,иаков)
(10) REDO: отпрыск(исаак,иаков)
(10) FAIL: отпрыск(исаак,Ответ)
(13) CALL: отпрыск(исаак,YЗ)
Теперь мы пытаемся применить второе утверждение процедуры
потомок.
(13) EXIT: отпрыск(исаак,исав)
(14) CALL; потомок(исав, Ответ)
Еще одна рекурсия
(15) CALL: отпрыск(исав,Ответ)
(15) FAIL: отпрыск(исав,Ответ)
(16) CALL: отпрыск(исав,Y4)
(16) FAIL: отпрыск(исав,Y4)
(14) FAIL: потомок(исав,Ответ)
(13) REDO: отпрыск(исаак,исав)
(13) EXIT: отпрыск(исаак,иаков)
(17) CALL: потомок(иаков,Ответ)
Пытаемся использовать Иакова.
(18) CALL: отпрыск (иаков,Ответ)
(18) FAIL: отпрыск (иаков, Ответ)
(19) CALL: отпрыск(иаков,Y5)
(19) FAIL: отпрыск (иаков, Y5)
(17) FAIL: потомок(иаков,Ответ)
(13) REDO: отпрыск(исаак,иаков)
(13) FAIL: отпрыск(исаак,YЗ)
(9) FAIL: потомок(исаак,Ответ)
(1) FAIL: потомок(авраам,Ответ) нет
Наконец мы закончили. Надеемся, что этот утомительный пример дал вам возможность понять последовательность событий, происходящих при выполнении Пролог-программы. Вы, вероятно, уже заметили, что для любой цели всегда бывает только один ВЫЗОВ (событие CALL) и одна НЕУДАЧА (событие FAIL), хотя может быть сколько угодно ПЕРЕДЕЛОК (событие REDO) и соответствующих ВЫХОДов (событие EXIT). В следующем разделе мы рассмотрим процесс трассировки для более сложного примера – предиката
присоединить.
Упражнение 8.1. В приведенной выше модели ничего не говорится о том, как обрабатывается цель – отсечение '!'. Расширьте эту модель, включив туда учет действия отсечения.
8.4. Трассировка и контрольные точки
Обнаружив, что программа не работает (порождает сообщения об ошибках, просто отвечает
'нет' или выдает неверный ответ) вы, наверное, захотите побыстрее найти ошибки с тем, чтобы исправить их. В этом разделе описывается набор встроенных предикатов, позволяющих «проследить» за выполнением программы. С их помощью вы можете вновь запустить программу на той же задаче и проследить за ее выполнением, чтобы найти место, с которого она начинает работать неверно. При этом вы увидите, когда происходят разные события трассировочной модели, подобно тому, как это было в предыдущем разделе, где мы наблюдали за процедурой
потомок. Точный набор возможностей, предоставляемых предикатами отладки, зависит от конкретной реализации Пролога, однако то, что мы собираемся сообщить вам, даст представление об имеющихся средствах, так что вы сможете разобраться в том, что предлагает вам ваша система. В любом случае мы настоятельно советуем ознакомиться с документацией по вашей Пролог-системе, прежде чем начать использование средств отладки.
Основное назначение трассировки и контрольных точек состоит в том, чтобы программист получил информацию о попытках согласования определенных целей, возникающих в ходе выполнения его программы. Программист может принять решения относительно интересующих его целей и относительно уровня своего вмешательства в процесс их согласования. Первое решение сводится к выбору определенной комбинации
полной трассировки и трассировки по
контрольным точкам. Вообще говоря, полная трассировка означает выдачу информации обо
всех целях, а контрольные точки позволяют программисту получить информацию лишь о тех предикатах, которые он задал. Однако эти возможности могут различными способами комбинироваться. Используемые при этом встроенные предикаты рассмотрены в разд. 6.13. Контрольная точка для какого-либо предиката устанавливается с помощью предиката
spy (отмена контрольной точки выполняется предикатом
nospy). Установка режима полной трассировки осуществляется предикатом
trace (а ее отмена – предикатом
notrace).
Второе решение заключается в выборе уровня управления процессом трассировки. При неуправляемой трассировке информация о целях выдается на терминал и программа продолжает выполнение. При управляемой трассировке, выдав информацию о цели, система каждый раз спрашивает у программиста, что бы он хотел сделать. Он может изменить уровень трассировки, изменить нормальный ход выполнения программы и дать ряд других указаний. Ваша Пролог-система может обеспечивать раздельный выбор уровня управления трассировкой для каждого из четырех видов событий:
• Когда впервые делается попытка согласовать некоторую цель с базой данных, когда данная цель встречается впервые (событие CALL);
• Когда цель успешно согласована (событие EXIT);
• Когда готовится попытка повторного согласования цели (событие REDO), и
• Когда устанавливается несогласуемость цели с базой данных, поскольку все попытки вновь согласовать ее оказались безуспешными (событие FAIL).
Например, разумным представляется такой выбор: задать трассировку событий CALL и REDO как управляемую, а трассировку событий EXIT и FAIL – как неуправляемую. Более подробное описание этих четырех событий, происходящих при согласовании целей с базой данных, приведено в разд. 8.3,
Рассмотрим теперь, что за информация выдается пользователю, когда происходит некоторое событие с интересующей его целью. Прежде всего выдается название цели с указанием вида произошедшего события и, возможно, номера обращения. Если для данного события задана неуправляемая трассировка, то это все. Если же задана управляемая трассировка, то Пролог потребует указаний относительно того, что ему делать дальше. Протокол полной неуправляемой трассировки мог бы выглядеть следующим образом:
?- [user].
присоединить([],Y,Y).
присоединить([А|В],С,[А|D]):- присоединить(В,С,D).
/* введите здесь литеру – признак конца файла */
да
?- присоединить ([а][b],Х).
CALL присоединить([a],[b],_43)
CALL присоединить([],[b],_103)
EXIT присоединить([],[b],[b])
EXIT присоединить([a],[b],[a,b])
X = [a,b];
REDO присоединить([a],[b],[a,b])
REDO присоединить([],[b],[b])
FAIL присоединить([],[b],_103)
FAIL присоединить ([a], [b],_43)
нет
?- присоединить(Х,Y,[а])
CALL присоединить(_37,_38,[а])
EXIT присоединить([],[а],[а])
X = [], Y = [a];
REDO присоединить([],[a],[a])
CALL присоединить(_93,_38,[])
EXIT присоединить([],[],[])
EXIT присоединить([а],[],[a])
X = [a], Y = [];
REDO присоединить([a],[],[a])
REDO присоединить([],[],[])
FAIL присоединить (_93,_38,[])
FAIL присоединить(_37,_38,[])
нет
Здесь на терминал выведены сведения обо всех четырех событиях для всех целей. Однако программист не может приостановить выполнение программы в какой-либо точке, изменить по ходу выполнения объем трассировочной информации, или как-либо еще повлиять на ход выполнения трассировки. Эти возможности предоставляются при управляемой трассировке.
Прежде чем перейти к рассмотрению управляемой трассировки, следует сделать несколько замечаний о том, как Пролог выдает сведения о целях во время трассировки. На самом деле, способ выдачи сведений о целях средствами трассировки не обязательно совпадает с тем, который используется предикатом
write. Это происходит потому, что для выдачи сведений о целях пользователю разрешается задавать свои собственные определения. Вы можете воспользоваться этой возможностью для того, чтобы вывести какие-либо общие структуры, используемые в вашей программе, особым способом, который обеспечивает большую наглядность и выразительность, чем обычный вывод с помощью предиката
write. Эта возможность осуществляется следующим образом. Стандартный способ выдачи сведений о целях опирается на использование встроенного предиката
print с единственным аргументом. Предикат
print действует, как если бы он был определён следующим образом:
print(X):- portray(X),!.
print(X):- write(X).
Предикат
portray уже не является встроенным, поэтому вы можете сами задать утверждения для его определения. Если эти утверждения таковы, что они позволяют согласовать с базой данных цель
portray(X) для одной из ваших целей Х,то считается, что выдачу всех необходимых сведений сделают эти утверждения. В противном же случае данные об этой цели X будут выданы с помощью предиката
write. Например, если по каким-то причинам вы не хотите выдавать значение третьего аргумента цели
присоединить, то это может быть обеспечено с помощью следующего утверждения:
portray(присоединить(А,В,С)):- writе('присоединить('), write(A), write(','), write(B), write(','), write('‹foo›)').
Каждый раз когда встретится цель X, содержащая предикат
присоединить, приведенное утверждение будет обеспечивать успешное согласование цели
portray(X), и вывод трассировочной информации будет полностью возложен на данное утверждение. В случае цели, содержащей любой другой предикат, цель
port-гау(Х) не согласуется с базой данных и потому сведения об X будут выданы с помощью предиката
write(X). Если бы приведенное выше утверждение присутствовало в базе данных, то соответствующая часть приведенного выше протокола трассировки выглядела бы следующим образом:
?- присоединить ([a],[b],X).
CALL присоединить([а],[b],‹fоо›)
CALL присоединить ([],[b],‹foo›)
EXIT присоединить([],[b],‹fоо›)
EXIT присоединить([a],[b],‹foo›)
X = [a,b];
REDO присоединить([a],[b],‹foo›)
REDO присоединить([],[b],‹foо›)
FAIL присоединить([],[b],‹foo›)
FAIL присоединить ([a],[b],‹foo›) нет
Т
еперь рассмотрим управляемую трассировку. Если вы задали управляемую трассировку для событий некоторого типа, то Пролог спросит у вас, что нужно сделать после того, как наступит событие заданного типа. На терминале это может выглядеть примерно так:
?- присоединить ([а],[b],Х).
CALL присоединить([а],[b],_43)?
После вывода литеры '?' программа останавливается. Теперь от вас требуется ответ – команда, которой вы зададите одно из возможных действий. Если затребованное вами действие означает продолжение обычного выполнения программы, то она продолжит выполнение до тех пор, пока трассировка не дойдет до следующего управляемого события для прослеживаемого предиката. И опять вам будет задан вопрос вида:
CALL присоединить([],[b],_103)?
Одной из команд может быть выдача списка допустимых команд на терминал. Рассмотрим некоторые из них.
Выдача информации о цели
Первая группа команд предназначена для выдачи информации о цели в различных форматах. Как мы уже знаем, стандартным средством выдачи сведений о цели является предикат
print, в рамках которого с помощью определяемого пользователем предиката
portray можно выводить нужные сведения в нужном формате. Однако у пользователя могут возникнуть сомнения в правильности утверждений, определяющих
portray, или он может пожелать увидеть цель в обычной форме. Поэтому Пролог предоставляет команду, дающую вам возможность вывести сведения о текущей цело с помощью предиката
write или
display. В этом случае программа не продолжает выполняться, а пользователя просят задать еще одну команду, которая укажет как следует продолжать выполнение программы. Как правило, этот диалог имеет следующий вид:
?- присоединить([a],[b],X).
CALL присоединить([а],[b],‹fоо›)? write
CALL присоединить([а],[b],_103)?
Обычно в качестве альтернативного способа вывода сведений о цели используют
write. Предикат
display может понадобиться в том случае, когда цель содержит много операторов, и вы забыли приоритеты их выполнения. В этом случае
display поможет вам однозначно определить вложенность функторов.
Выдача информации о предшественниках
Предшественниками данной цели называются те цели, согласованность которых зависит от согласованности данной цели. На наших диаграммах с прямоугольниками это те цели, прямоугольники которых включают данную цель. Так, каждая цель имеет предшественника, который в свою очередь является одной из целей исходного вопроса – той целью, согласованию которой помогает текущая цель. Аналогично, когда речь идет о правиле, каждая цель, порожденная телом правила, имеет в качестве предшественника ту цель, которая сопоставлена с заголовком правила. Рассмотрим некоторые примеры предшественников. Обратимся к следующей простой программе обращения списка (которая рассматривалась в разд. 7.5):
обр([],[]).
oбp([H|T],L):- oбp(T,Z), присоединить(Z,[H],L).
присоединить([],X,Х).
присоединить([А|В],С,[А|D]):- присоединить(В,С,D).
Пусть мы задали исходный вопрос:
?- oбp([a,b,c,d],X).
(A)
Тогда, вследствие второго утверждения, возникают две подцели, каждая из которых в качестве своего непосредственного предшественника имеет цель, составляющую содержание исходного вопроса. Вот эти подцели:
oбp([b,c,d],Z)
(B)
присоединить(Z,[a],X)
(C)
Поскольку второе утверждение будет снова использовано при согласовании
(B), снова возникают две подцели:
oбp([c,d],Z1)
(D)
присоединить(Z1,[a],Z)
(E)
Их предшественниками являются цели
(A) и
(B). Заметим, что цель
(C) не является их предшественником, поскольку от них непосредственно зависит только согласованность
(B), от которой, в свою очередь, зависит согласованность
(А). Цели
(D) и
(E) никак не влияют на согласованность
(C). Когда процесс согласования исходного вопроса заходит уже достаточно далеко, возникает цель вида:
присоединить([с],[b],Y)
На этом этапе текущая цель и ее предшественники могут быть представлены в следующем виде:
oбp([a,b,c,d],_46) (цель
A)
oбp([b,c,d],[d|_50]) (цель
B)
присоединить([d,с],[b],[d|_51])
присоединить([с],[b],_52)
Прежде чем читать дальше, вам следует убедиться в том, что вы понимаете, почему это предшественники данной цели, а также почему у нее нет никаких других предшественников. С приведенным здесь изображением предшественников связана одна особенность, которая может проявиться и в вашей Пролог-системе. Существуют два способа выдачи информации о предшественнике на печать – при первом способе информация соответствует состоянию предшественника при первой попытке согласовать его, при втором – текущему состоянию, с теми значениями переменных, которые они получили в результате конкретизации. Здесь у нас принят второй способ. Когда выполнение впервые дошло до цели
(B), второй аргумент предиката
обр не был конкретизирован. Тем не менее, в списке предшественников этот аргумент показан как имеющий значение. Это объясняется тем, что теперь переменная, которая задана в этой позиции, оказалась конкретизированной, а именно, теперь мы выяснили, что для
[b, с, d] первым элементом обращенного списка является
d.
Глядя на предшественников текущей цели можно получить ясное представление о том, что происходит с программой и почему она делает то, что наблюдается. Одной из команд, которые пользователю разрешается вводить при наступлении управляемого события для некоторой цели может быть выдача сведений о каких-либо из ее предшественников. Таким образом, если вы чувствуете, что ваша программа тратит где-то много времени и подозреваете, что это может быть результатом зацикливания, то верная стратегия состоит в том, чтобы прервать выполнение, включить полную трассировку, а затем посмотреть на предшественников, чтобы понять, где вы находитесь.
Изменение уровня трассировки
Другой набор команд, которыми можно воспользоваться при наступлении управляемого события, связан с изменением желаемого объема трассировки. Некоторые из более грубых управляющих воздействий состоят в следующем.
• Удаление всех контрольных точек. Это имеет тот же эффект, что и вызов цели
nodebug (см. разд. 6.13).
• Отключение полной трассировки. Это имеет тот же эффект, что и вызов цели
notrace (см. разд. 6.13).
• Включение полной трассировки. Это имеет тот же эффект, что и вызов цели
trace (см. разд. 6.13).
При задании любой из этих команд ваша программа продолжит затем выполнение в указанном режиме до тех пор, пока не дойдет до цели, которую вы намеревались прослеживать. В некоторых версиях Пролога могут быть предусмотрены более тонкие средства управления трассировкой. Эти средства помогут вам быстро пройти через те участки выполнения программы, которые не представляют интереса с тем, чтобы сосредоточиться на участках, где, вероятно, имеются ошибки. Здесь возможны следующие команды:
• «creep» (ползти): Продолжить выполнение программы с полной трассировкой до тех пор, пока не поступит новое указание (при наступлении следующего управляемого события).
• «skip» (пропустить): Продолжить выполнение программы без выдачи какой-бы то ни было трассировочной информации до тех пор, пока не наступит какое-либо событие, относящееся к текущей цели.
• «leap» (перескочить); Продолжить выполнение программы без выдачи трассировочной информации до тех пор, пока либо не будет достигнута контрольная точка, либо не наступит событие, относящееся к текущей цели.
Первая из этих команд соответствует случаю, когда вы хотите, начиная с данного момента, тщательно проследить за ходом выполнения программы. Вторая команда соответствует случаю, когда вас не интересует ход согласования какой-либо цели, а нужно побыстрее перейти к тому, что происходит дальше. Третья команда относится к случаю, когда в ходе согласования некоторой цели выполняется большой объем не интересующей вас деятельности, но где-то в середине возникает интересующая вас цель (имеющая контрольную точку). Поэтому вам желательно пропускать все до тех пор, пока не будет достигнута нужная контрольная точка или (если программа ошибочна) пока текущая цель не окажется согласованной или несогласованной не достигнув контрольной точки. Ниже приводится пример использования команд «creep» и «skip». Предположим, что в простой программе сортировки, приведенной в разд. 7.7, есть ошибка, но при этом мы уверены, что наша программа порождения перестановок работает правильно. Если вы помните, определение программы
наивсорт начинается так:
наивсорт(Х,Y):- перестановка(Х,Y), отсортировано(Y),!.
Чтобы избежать необходимости просматривать массу детальных сведений о том, как работает программа перестановка, можно воспользоваться командой «skip» и получить трассировку, которая начинается так:
CALL наивсорт([3,6,2,9,20],_45)? creep
CALL перестановка([3,6,2,9,20],_45)? skip
EXIT перестановка([3,6,2,9,20],[3,6,2,9,20])? creep
CALL упорядочено(ЕЗ,6,2,9,20])? creep
CALL упорядочено(0,[3,6,2,9,20])? creep
CALL 0‹3?
. . .
Вмешательство в процесс согласования цели
Здесь рассматриваются команды, которые позволяют изменять порядок работы программы. С их помощью можно повторить некоторые фрагменты, которые желательно изучить более подробно, обойти случаи про которые известно, что они не относятся к делу и наоборот, заставить программу рассмотреть случаи, которые иначе она могла бы и не обнаружить. Все это способно значительно ускорить отладку, поскольку позволяет подвергнуть многократной проверке особо сложные части программы не повторяя заново весь ее запуск с самого начала.
• «retry» (повторить): Если вы задали команду «retry» после какого-либо события для некоторой цели, то Пролог вернется к тому месту, где он первоначально осуществил ВЫЗОВ (событие CALL) этой цели. Все будет в точности так же, как и в момент первоначального появления этой цели (кроме каких-либо добавлений к базе данных, которые могли быть сделаны). Это означает, что вы можете еще раз проследить за тем, что происходит при согласовании данной цели. На практике обычно сочетают использование команд «retry» и «skip». Если вы сомневаетесь в том, что ошибка возникает при согласовании некоторой цели, вы можете сперва пропустить (с помощью команды «skip») трассировку процесса ее согласования. Это означает, что вы не намерены пробираться через массу трассировочных данных, относящихся к цели, процесс согласования которой выполняется совершенно правильно. Если же возникла ошибка, и цель либо не согласуется с базой данных, либо дает неверный результат, то у вас сохраняется возможность после всего этого (с помощью команды «retry») вернуться назад и проследить за всем более внимательно.
• «or» (или): Эта команда, в точности как ';', означает просьбу о выборе альтернативного решения некоторого вопроса. Если вы находитесь в точке ВЫХОДа из цели (событие EXIT), вы также можете попросить о выборе альтернативы. Таким образом, если известно, что первый найденный ответ не позволяет успешно завершить остальную часть программы, можно тут же попросить о поиске другого решения. Это означает, что вы сможете быстрее добраться до той части программы, где содержится ошибка. Без такого режима вам пришлось бы «караулить» возможную неудачу процесса согласования после того, как была найдена первая альтернатива.
• «fail» (неудача): Эта команда в основном используется при наступлении события CALL. Если вы знаете, что данная цель в конце концов окажется несогласованной с базой данных, и что эта цель для вас не представляет интереса, то вы можете тут же принудительно завершить процесс согласования неудачно, задав эту команду.
Ниже приводится пример использования различных рассмотренных команд при изменении порядка согласования одного вопроса:
?- принадлежит(Х,[а,b,с]), принадлежит(Х,[b,d,е]).
CALL принадлежит(_ 44,[a, b,с])? creep
EXIT принадлежит(a, [а,b,с])? or
REDO принадлежит(a, [а,b,с])? creep
CALL принадлежит(_44,[b,с])? fail
FAIL принадлежит(_44,[b,с])? creep
FAIL принадлежит(_44,[a,b,с])? retry
CALL принадлежит(_44,[а,b,с])? creep
EXIT принадлежит(а,[а,b,с])? creep
CALL принадлежит(а,[d,с,е])? fail
FAIL принадлежит(a,[d,c,e])? creep
REDO принадлежит(а,[а,b,с])? creep
CALL принадлежит(_44,[b,с])? creep
EXIT принадлежит(b,[b,с])? or
REDO принадлежит(b,[b,с])? creep
CALL принадлежит(_ 44,[с])? fail
FAIL принадлежит(_44,[с])? retry
CALL принадлежит(_44,[с])? creep E
XIT принадлежит(с,[с])? creep
EXIT принадлежит(с,[b,c])? creep
EXIT принадлежит(c,[a,b,с])? creep
CALL принадлежит(c,[d,c,e])? creep
CALL принадлежит(c,[c,e])? creep
EXIT принадлежит(c,[c,e])? creep
EXIT принадлежит(c,[d,c,e])? or
REDO принадлежит(c,[d,c,e])? creep
REDO принадлежит(c,[c,e])? creep
CALL принадлежит(c,[e])? creep
CALL принадлежит(c,[])? creep
FAIL принадлежит(c,[])? creep
FAIL принадлежит(c,[е])? creep
FAIL принадлежит(c,[с,е])? retry
CALL принадлежит(c,[с,e])? creep
EXIT принадлежит(c,[c,e])? creep
EXIT принадлежит(с,[d,с,е])? creep
Другие команды
Рассмотрим другие возможные команды, которые могут быть доступны вам при наступлении управляемого события;
• «break» (пауза): Эта команда вызывает приостановку выполнения текущей программы, причем вам предоставляется новая копия Пролог-интерпретатора, Вы можете воспользоваться этим для задания вопросов относящихся к утверждениям, которыми вы располагаете, для расстановки контрольных точек или для чего-нибудь еще. Когда вы выйдете из этой копии интерпретатора (путем ввода литеры, являющейся признаком конца файла), то выполнение вашей прежней программы будет продолжено.
• «abort» (аварийное завершение): Эта команда вызывает прекращение выполнения всех ваших текущих программ, и вы «проваливаетесь» в Пролог-интерпретатор, который готов к вашему новому вопросу.
• «halt» (стоп): Эта команда вызывает полный выход из Пролога. Она может потребоваться вам, когда вы обнаружите ошибку и захотите для ее исправления отредактировать файл с той программой, где находится ошибка.
Заключение
В заключение хочется обратить внимание на три вопроса, ответы на которые следует продумать, прежде чем приступать к трассировке выполнения программы:
1. За какими целями вы собираетесь следить? Если вы хотите следить за всем (задав полную трассировку с помощью предиката
trace), то вы можете захлебнуться тем потоком информации, который будет поступать на ваш терминал. С другой стороны, если прослеживать только то, что происходит с небольшим числом предикатов (расставляя контрольные точки с помощью предиката
spy), то можно пропустить момент, когда программа начинает работать неверно. Вероятно, лучшим решением является компромисс между аккуратным использованием контрольных точек, позволяющих сузить район поиска, и полной трассировкой на заключительном этапе, что позволяет точно обнаружить место ошибки.
2. Какой уровень управления выполнением программы вы намерены осуществить через терминал? Если задать все типы событий как неуправляемые, то вы не сможете оказать никакого влияния на ход выполнения программы, которая быстро проскочит через место ошибки прежде чем вы сможете это заметить, а тем более – внимательно рассмотреть. С другой стороны, если вы зададите все события как управляемые, то вам придется постоянно подталкивать программу, сообщая ей, что нужно продолжить выполнение при каждом новом событии.
3. Намерены ли вы задать специальные средства вывода информации о прослеживаемых целях? Это может оказаться полезным в тех случаях, когда некоторые из целей содержат в качестве аргументов чрезмерно большие структуры, которые не представляют особого, интереса, и только отвлекают внимание от действительно интересных аргументов. В этом случае для подавления выдачи ненужной информации можно воспользоваться возможностями предиката
portray.
8.5. Фиксация ошибок
Если вы проследили за ходом выполнения программы и обнаружили, что она работает неверно, то вам захочется зафиксировать ошибку и запустить программу снова. Предположим, что ваша программа имеет разумные размеры, тогда она скорее всего уже хранится в файле на диске. Чтобы изменить эти файлы, вам придется использовать программу редактирования файлов. Здесь имеются две возможности:
• Ваша Пролог-система позволяет использовать редактор, а затем вернуться в Пролог с той же базой данных, что и прежде. Может быть, существует возможность сделать это прямо, с помощью соответствующего встроенного предиката. Возможен и другой вариант, когда Пролог позволяет вам сохранить текущее состояние базы данных в специальном файле, а позднее снова восстановить его. Тогда вы сохраняете ваше текущее состояние, выходите из Пролога, изменяете программу, запускаете Пролог снова и восстанавливаете предыдущее состояние базы данных. Вернувшись туда же, где вы были раньше, но с изменениями в одном или нескольких программных файлах, вам необходимо лишь выполнить предикат
reconsult для этих файлов, чтобы заменить старые определения измененных программ новыми.
• Если ваша Пролог-система не позволяет вернуться к прежнему состоянию после использования редактора и изменения ваших программных файлов, то вам придется запустить Пролог и применить предикат
consult ко всем вашим программным файлам, находящимся на внешней памяти.
Этот процесс можно упростить, если завести отдельный файл, состоящий из команд для Пролога, предписывающих применить предикат
consult ко всем файлам вашей программы. Тогда для того, чтобы считать в память всю программу, достаточно предложить Прологу применить
consult к этому отдельному файлу. Например, если вы предложите Прологу применить
consult к файлу, содержащему:
?- [filel,file2,file3].
?- [file4,file5,fileб].
то в результате будут считаны в память все файлы
file1,
file2,
file3,
file4,
file5, file6.
Иногда изменения в программе кажутся столь незначительными, что их можно ввести с терминала с помощью предикатов
consult(user) или
reconsult(user). Однако не следует пользоваться этим способом слишком часто. По невнимательности можно легко забыть какие-либо мелкие изменения, которые вносились таким способом, и при выполнении программы вновь столкнуться с теми же ошибками, которые встречались при прошлом запуске программы. Кроме того, поскольку в конечном итоге вы намерены внести исправления в ваши программные файлы, то нерационально повторять их прямой ввод с терминала. Итак, не поддавайтесь искушению вводить утверждения прямо с терминала в надежде поскорее заставить программу работать.
Ниже приводится небольшой пример того, как можно использовать предикаты
consult и
reconsult, чтобы внести изменения в программу с терминала. Этот сеанс работы начинается, когда в базе данных программиста нет ни одного утверждения.
?- присоединить([а,b,с,d],[е],Х).
нет
?- consult (user).
присоединить([А|В],С,[А|D]):- присоединить(А,С,D).
присоединить([],Х,Х).
обр([],[]).
обр([А|В],С):- o6p(B,D), присоединить(D,[А],С).
/* ввод литеры – признак конца файла */
да
?- обр([a,b,c,d,e],X).
нет
?- присоединить([а,b,с,d,е], [f],Х).
нет
?- присоединить([],[а,b,-],Х).
X = [а,b,с]
да
?- reconsult(user)
присоединить([А|В],С,[А|D]):- присоединить(В,С,D).
/* ввод литеры – признак конца файла */
да
?- oбp([a,b,c,d],X).
нет
?- consult (user).
присоединить([],Х,Х).
/* ввод литеры – признак конца файла */
да
?- oбp([a,b,c,d,e],X). X = [e,d,c,b,a].
да
В приведенном сеансе работы наш беспечный программист начинает с ввода через терминал утверждений для предикатов
присоединить и
обр. Конечно, он мог бы сначала ввести их в файл, а затем предложить Прологу применить к этому файлу предикат
consult. Впрочем, для такого маленького примера этого, может быть, и не стоило делать. К несчастью, в первом утверждении для
присоединить допущена ошибка – в цели задано
А, хотя на этом месте должно быть
В. Эта ошибка обнаруживается, когда система не может ответить на вопросы, содержащие
присоединить и
обр. Каким-то образом программист догадывается, что
его определение
присоединить неверно (в реальном сеансе для этого, вероятно, потребовалось бы использовать средства отладки). Так или иначе, он решает заменить имеющееся определение новым, используя для этого предикат
reconsult. К сожалению, в своем новом определении он забывает задать граничное условие (случай []). Поэтому программа по-прежнему не работает. К этому моменту исходное определение для
присоединить, состоящее из двух утверждений, заменено новым определением из одного утверждения, которое оказалось неполным. Наш программист замечает, что он допустил ошибку и что ситуацию можно исправить, просто добавив к уже имеющемуся определению одно утверждение. Это делается также с помощью предиката
consult. На этот раз программа заработала.
В заключение дадим еще один совет: при внесении изменений в программу ответьте на те же контрольные вопросы, на которые вы отвечали при написании первоначальной версии программы. Убедитесь, что ваши добавления согласуются с вашим прежним замыслом о том, какие переменные должны быть конкретизированы, когда и какие аргументы используются и для каких целей. Наконец, попытайтесь взглянуть еще раз на программу в целом – в ней могут быть и какие-либо другие ошибки.
ГЛАВА 9. ИСПОЛЬЗОВАНИЕ ГРАММАТИЧЕСКИХ ПРАВИЛ В ПРОЛОГЕ
9.1. Проблема синтаксического анализа
Предложения на естественном языке, таком как английский представляют собой нечто большее, чем просто произвольные последовательности слов. Мы не можем соединить вместе произвольное множество слов и получить при этом предложение, имеющее смысл. По крайней мере результат должен соответствовать тому, что мы называем грамматически правильным предложением.
Грамматика языка – это множество правил, позволяющих определить, какие последовательности слов приемлемы в качестве предложений этого языка. Она определяет, как из слов образуются словосочетания и какие последовательности этих словосочетаний допустимы. Если задана грамматика некоторого языка, то для любой последовательности слов мы можем сказать, является ли она допустимым предложением. И в случае, когда это предложение действительно является допустимым, в результате проверки мы определим, какие естественные группы слов имеются и как они связаны друг с другом. То есть будет определена внутренняя структура предложения.
Очень простой класс грамматик составляют так называемые контекстно-свободные грамматики. Вместо того, чтобы давать формальное определение понятия контекстно-свободной грамматики, мы проиллюстрируем его на одном простом примере. Приведенные ниже правила можно рассматривать как начальную часть грамматики предложений английского языка:
предложение--› группа_существительного, группа_глагола.
группа_существительного--› определитель, существительное.
группа_глагола--› глагол, группа_существительного.
группа_глагола--› глагол.
определитель--› [the].
существительное--› [apple].
существительное--› [man].
глагол--
› [eats].
глагол--› [sings].

Рис. 9.1.
Эта грамматика состоит из множества правил, каждое из которых записано в отдельной строке. Каждое правило определяет форму словосочетания определенного вида. Первое правило показывает, что предложение состоит из словосочетания, называемого
группа_существительного, за которым следует словосочетание, называемое
группа_глагола. Эти два словосочетания есть не что иное, как
подлежащее и
сказуемое предложения (см. рис. 9.1).
Чтобы представлять, что значит правило в контекстно-свободной грамматике, их следует читать следующим образом:
X--›Y как «
X может иметь вид Y», а '
X,
Y' как «
X,
за которым следует Y». Так первое правило может быть прочитано:
предложение может иметь вид: группа_существительного, за
которой следует группа_ глагола.
Все это очень хорошо, но что представляют собой
группа_существительного и
группа_глагола? Как мы должны распознавать подобные объекты и как узнать их грамматическую структуру? Ответы на эти вопросы следуют из второго, третьего и четвертого правил грамматики. Например,
группа_существительного
может иметь вид: определитель,
за которым следует существительное.
Неформально, группа существительного – это группа слов, служащая для обозначения некоторого объекта (или объектов). Такая группа содержит слово – существительное, которое определяет главный класс, которому принадлежит этот объект. Так «
the man» (человек) обозначает человека, «
the program» (программа) обозначает программу и так далее. Кроме того, в соответствии с приведенной грамматикой, существительному должна предшествовать группа слов, названная «определитель» (см. рис. 9.2). Аналогично, внутренняя структура словосочетания
группа_глагола описывается соответствующими правилами. Заметим, что для этого словосочетания существуют два правила. Это вызвано тем, что оно может принимать два вида. Словосочетание
группа_глагола может содержать словосочетание
группа_существительного, как в предложении
«the man eats the apple» (человек ест яблоко), или
группа_существительного может отсутствовать, как в предложении
«the man sings» (человек поет).
Для чего нужны остальные правила грамматики? Эти правила показывают, как некоторые словосочетания могут быть построены из настоящих слов, а не сводят их к совокупности более мелких словосочетаний. Слова английского языка записываются в квадратных скобках, так что правило:
определитель--› [the].
можно читать так:
определитель
может иметь вид: слово the.
Теперь, когда мы получили достаточно полное представление о грамматике, мы можем поговорить о том, какие последовательности слов являются грамматически правильными предложениями в соответствии с приведенной грамматикой. Наша грамматика очень проста и нуждается в целом ряде расширений. Основной недостаток заключается в том, что она допускает предложения, составленные лишь из пяти различных слов. Если мы хотим определить, является ли заданная последовательность слов предложением, в соответствии с тем, как оно определяется грамматикой, то необходимо применить первое правило, чтобы получить ответ на следующий вопрос:
можно ли разбить заданную последовательность на два словосочетания таким образом, чтобы первое из них было группа_существительного, а второе группа_глагола?
Затем, чтобы проверить, является ли первое словосочетание группой существительного, необходимо применить второе правило, которое можно интерпретировать как вопрос:
можно ли разбить словосочетание на определитель и существительное, следующее за определителем?

Рис. 9.2.
И так далее. В результате этой процедуры, если она завершится успешно, мы выделим все словосочетания и их части, входящие в заданное предложение, в соответствии с тем, как они определены грамматикой, и получим структуру, подобную приведенной на рис. 9.3. Эта диаграмма, показывающая структуру разбиения предложения на словосочетания, называется
деревом (синтаксического) разбора предложения.
Мы увидели, как, имея грамматику языка, можно построить деревья разбора для предложений этого языка, чтобы показать их структуру. Задача построения дерева разбора предложения по заданной грамматике называется
задачей синтаксического разбора (анализа). Программа для ЭВМ, которая строит деревья разбора для предложений языка, называется
синтаксическим анализатором.
В этой главе будет показано, как задача синтаксического анализа может быть сформулирована в рамках языка Пролог. Будет введен используемый в Прологе формализм грамматических правил, значительно облегчающий создание синтаксических анализаторов на Прологе. Область применения вводимых далее идей не ограничивается синтаксисом естественных языков. Действительно, те же самые методы применимы к любой задаче, объектом рассмотрения которой является упорядоченная последовательность элементов, которая некоторым естественным образом может быть разбита на группы, а порядок этих групп может быть определен множеством правил. Однако, ради простоты, в оставшейся части этой главы будет рассматриваться задача синтаксического анализа предложений на английском языке, а обобщение изложенных далее идей и методов на другие области предоставляется читателю.
предложение

Рис. 9.3.
9.2. Описание синтаксического анализа на языке Пролог
Основная структура данных, о которой идет речь при обсуждении задачи
синтаксического анализа, представляет последовательность слов. Предполагается, что можно выделить подпоследовательности этой структуры, представляющие различные словосочетания, допустимые грамматикой, и, основываясь на этом, показать, что последовательность в целом допустима в качестве словосочетания типа
предложение. Так как стандартным способом представления последовательности является список, то входные данные для синтаксического анализатора будут представлены как список языка Пролог. А какое же представление имеют сами слова? Для решаемой здесь задачи знание внутренней структуры слов представляется несущественным, так как все, что необходимо делать,- это сравнивать слова друг с другом. Поэтому естественно представлять слова как атомы языка Пролог,
Давайте разработаем программу, позволяющую определять, является ли заданная последовательность слов предложением в соответствии с приведенной выше грамматикой. Для того чтобы сделать это, программа будет должна выявить внутреннюю структуру заданных ей предложений. Далее будет показано, как разрабатывать программу, которая запоминает эту структуру и делает ее доступной для обозрения, но здесь этот вопрос не будет рассматриваться, чтобы не усложнять программу. Так как программа проверяет, является ли некоторая последовательность слов предложением, то давайте определим предикат предложение. Этот предикат использует лишь один аргумент и соответствует следующему утверждению:
предложение(Х) означает, что X является последовательностью слов, образующей грамматически правильное предложение.
Таким образом, предполагается, что можно задавать вопросы, подобные следующему:
?- предложение ([the, man, eats, the apple]).
Ответом на этот вопрос будет «да», если «the man eats the apple» является предложением, и «нет» в противном случае.
Представляется довольно неудачным, что мы должны задавать предложения искусственным способом, используя для этого списки атомов языка Пролог. Для более серьезных применений было бы желательно иметь возможность печатать английские предложения на терминале в их естественном виде. В главе 5 было показано, как может быть определен предикат
ввести для того, чтобы преобразовывать напечатанное предложение в список атомов языка Пролог. Очевидно, что мы могли бы использовать этот предикат в нашем синтаксическом анализаторе, чтобы обеспечить естественный способ общения с пользователем программы. Однако здесь мы не будем прибегать к таким «косметическим» средствам, а сконцентрируем внимание на реальных проблемах собственно синтаксического анализа.
В чем состоит проверка последовательности слов на принадлежность множеству правильных предложений? В соответствии с первым правилом грамматики, исходная задача сводится к нахождению словосочетания
группа_существительного в начале заданной последовательности слов, а затем словосочетания
груп-
па_глагола в оставшейся части последовательности. К концу этого процесса мы должны использовать в точности все слова последовательности, ни одним словом больше и ни одним словом меньше. Введем предикаты
группа_существительного и
группа_глагола, чтобы выразить свойства принадлежности группе существительного и группе глагола:
группа_существительного(Х) означает, что последовательность X является группой существительного. Аналогично, группа_глагола(Х) значит, что последовательность X является группой глагола.
Используя эти предикаты, мы можем дать определение предиката предложение. Последовательность X является предложением, если ее можно разбить на две подпоследовательности
Y и
Z, где
Y – это
группа_существительного,
Z –
группа_глагола. Так как мы представляем последовательности как списки, то у нас уже есть предикат
присоединить, выполняющий разбиение списка на два других. Таким образом, можно записать:
предложение(Х):-присоединить(Y,Z,Х), группа_существительного(Y), группа_глагола(Z).
Аналогично
группа_существительного(Х):- присоединить(Y,Z,Х), определитель(Y), существительное(Z).
группа_глагола(Х):- присоединить(Y,Z,Х), глагол(Y), группа_существительного(Z).
группа_глагола(Х):- глагол(Х).
Отметим, что два правила для предиката
группа_ глагола превращаются в два утверждения для нашего предиката, что соответствует двум возможным способам проверки последовательности на принадлежность классу
группа_глагола. И наконец, не составляет труда написать утверждения, соответствующие правилам, вводящим слова:
определитель([the]).
существительное([аррlе]).
существительное([man]).
глагол([eats]).
глагол([sings]).
Теперь наша программа завершена. Действительно, эта программа успешно идентифицирует последовательности слов, являющиеся предложениями для приведенной грамматики. Однако, прежде чем считать задачу решенной, следует посмотреть, что в действительности произойдет, когда мы зададим вопрос о некоторой последовательности слов. Рассмотрим утверждение для предиката
предложение:
предложение(Х):- присоединить(Y,Z,Х), группа_существительного(Y), группа_глагола(Z).
и следующий вопрос:
?- предложение([the, man, eats, the, apple]).
Переменная
X в правиле конкретизируется значением
[the, man, eats, the, apple], а переменные
Yи
Z не будут конкретизированы, так что данная цель будет порождать возможные пары значений для
Y и
Z такие, что результат присоединения списка
Z к списку
Y равен
X. С помощью механизма возврата будут порождены все возможные пары, по одной при каждом возврате. Цель
группа_ существительного будет выполняться лишь при условии, что
Y действительно приемлем как
группа_существительного. Иначе она не выполняется и присоединить будет вынужден найти другое значение для
Y. Так что последовательность выполнения первой части предиката
предложение будет следующей:
1. Целью является
предложение(thе, man, eats, the, apple]).
2. Разбиение исходного списка на два списка
Y и
Z. Возможны следующие варианты разбиения;
Y = [], Z = [the,man,eats,the,apple] Y = [the], Z = [man,eats,the,apple]
Y= [the,man], Z = [eats,the,apple]
Y= [the,man,eats], Z = [the,apple]
Y= [the,man,eats,the], Z = [apple]
Y= [the, man, eats, the, apple], Z = []
3. Выбор варианта значений для
Y и
Z из приведенного выше списка вариантов и проверка принадлежности
Y классу
группа_существительного. То есть, попытка согласования подцели
группа_существительного(Y).
4. Если
группа_существительного выполняется для
Y, то перейти к
группа_глагола. Иначе возвратиться к шагу 3 и попробовать другой вариант.
Очевидно, что при таком подходе выполняется совершенно ненужный поиск. Цель
присоединить(Y,Z,X) порождает множество решений, большая часть которых бесполезна и не может быть идентифицирована как группа существительного. Должен существовать более прямой путь получения решения. Как следует из нашей грамматики,
группа_существительного должна содержать в точности два слова. Этим можно было бы воспользоваться, чтобы не прибегать к поиску среди возможных вариантов разбиения исходной последовательности слов. Опасность заключается в том, что это не всегда так, если мы изменяем грамматику. Даже небольшое изменение в правиле для определитель могло бы повлиять на возможную длину группы существительного, а значит и на способ идентификации группы существительного. При разработке программы было бы хорошо сохранять некоторую модульность. Если мы хотим изменить одно утверждение, то это не должно вызывать изменение программы в целом.
Таким образом, эвристика относительно длины группы существительного имеет слишком частный характер, чтобы ее использовать в программе. Тем не менее, ее можно рассматривать как частный случай некоторого общего принципа. Если мы хотим выделить подпоследовательность, которая является группой существительного, то мы можем использовать свойства этой группы, чтобы ограничить набор подходящих для этого последовательностей. Если определение группы существительного подвержено изменениям, то это можно сделать, только передав всю ответственность по проверке соответствующих свойств утверждению
группа_существительного. Так как именно утверждение
группа_
существительного выражает свойства, которыми обладает группа существительного, то почему не предположить, что этот предикат сам может решить, на что должна быть похожа соответствующая последовательность? Давайте потребуем, чтобы предикат
группа_существительного сам решил, какая часть последовательности ему необходима и что необходимо оставить для последующей обработки предикатом
группа_глагола.
Это обсуждение приводит нас к новому определению предиката
группа_существительного, который теперь имеет уже два аргумента:
группа_существительного(Х, Y) истинно, если начальная часть последовательности X является группой существительного, а остальная часть последовательности есть Y.
Таким образом, можно было бы ожидать, что следующие вопросы:
?- группа_существительного([the,man,eats,the,apple], [eats, the,apple]).
?- группа_существительного([thе,аррlе,sings], [sings]).
должны иметь ответ «да». Теперь, чтобы отразить это изменение, мы должны пересмотреть определение предиката
группа_существительного. Для этого надо решить, как последовательность, выбранная в качестве группы существительного, разбивается на последовательность, представляющую определитель, за которой следует последовательность, являющаяся существительным. Мы можем вновь предоставить решение задачи о том, какую часть последовательности следует выбрать, непосредственно тем утверждениям, которые обрабатывают соответствующие группы слов, положив:
группа_существительного(Х,Y):- определитель(Х,Z), существительное(Z, Y).
Таким образом, в начале последовательности
X имеется
группа, существительного, если мы можем выделить определитель в начале
X, обозначив оставшуюся часть
Z, а затем можем выделить существительное в начале
Z. Часть последовательности, остающаяся после выделения группы существительного, совпадает с последовательностью, следующей за существительным. На диаграмме это выглядит так:
[the, man, eats, the, apple]
|--------------X--------------|
|-----------Z-----------|
|-------Y-------|
Для того чтобы все происходило так, как здесь описано, мы должны будем принять относительно предикатов
определитель и
существительное соглашение, подобное тому, какое мы приняли для предиката
группа_существительного.
Приведенное утверждение для предиката
группа_существи-тельного говорит о том, как задачу выделения группы существительного свести к задаче выделения определителя и следующего за ним существительного. Это аналогично сведению задачи разбора предложения к выделению группы существительного, за которой следует группа глагола. Все это очень абстрактно. Ничто из сказанного не говорит нам о том, как много слов входят в состав определителя, группы существительного или предложения. Эта информация должна извлекаться, исходя из нашей версии правил, которые фактически вводят английские слова. Мы вновь можем представить их в виде утверждений языка Пролог, но на этот раз мы должны добавить дополнительный аргумент, как например:
определитель([the|Х],Х).
Это правило (грамматики) выражает тот факт, что определитель стоит в начале последовательности, начинающейся со слова
the. Более того, определитель занимает лишь первое слово этой последовательности и оставляет все следующие за ним.
В действительности, для того чтобы показать, как в этой группе слов «используются» слова из последовательности и какая часть последовательности остается необработанной, к каждому предикату, распознающему группу слов некоторого вида, можно добавить дополнительный аргумент. В частности, для единообразия было бы разумно сделать то же самое и с предикатом
предложение. Как теперь выглядит исходная цель, с которой мы обращаемся к программе? Необходимо решить, какие два аргумента задавать в вопросе для предиката
предложение. Эти аргументы обозначают последовательность, с которой начинается обработка, и последовательность, оставшуюся после ее завершения. Очевидно, что первый из аргументов – тот же самый, что мы задавали ранее в предикате
предложение. Кроме того, так как мы хотим выделить предложение, которое включает в себя всю последовательность целиком, то нам надо, чтобы после того, как предложение выделено, ничего не осталось, т. е. чтобы осталась лишь пустая последовательность. Поэтому мы должны обратиться к программе следующим образом:
?- предложение(the,man,eats,the,аррlе],[]).
Посмотрим теперь, как выглядит грамматика в целом после того, как мы переписали ее с учетом обсуждавшихся выше изменений:
предложение(S0,S):- группа_существительного(S0,S1), группа_глагола(S1,S).
группа_существительного(S0,S):- определитель(S0,S1), существительное(S1,S).
группа_глагола(S0,S):- глагол(S0,S).
группа_глагола(S0,S):- глагол(S0,S1), группа_существительного(S1,S).
определитель([the|S],S).
существительное([man|S],S).
существительное([аррle|S],S).
глагол([eats|S],S).
глагол([sings|S],S).
Таким образом, теперь мы получили эффективную версию программы для распознавания предложений, допустимых грамматикой. Однако, к сожалению, последняя запись программы выглядит несколько беспорядочной по сравнению с предыдущей версией. Все дополнительные аргументы засоряют ее и их необходимость не очевидна. Теперь мы рассмотрим, как преодолеть эту проблему.
9.3. Запись грамматических правил в Прологе
Специальная форма записи грамматических правил в языке Пролог была разработана, чтобы помочь программисту в написании синтаксических анализаторов, использующих описанные только что методы. Такая форма записи облегчает чтение программы, так как скрывается вся информация, не представляющая интереса. В силу того, что эта форма записи является более краткой, чем обычная для Пролога, вероятность сделать глупую опечатку также меньше, если для написания синтаксических анализаторов используются грамматические правила.
Хотя форма записи грамматических правил, о которой здесь идет речь, вводится сама по себе, важно помнить, что это лишь сокращенная запись обычных Пролог-программ. Вы можете воспользоваться грамматическими правилами либо потому, что ваша Пролог-система уже знает, как их обрабатывать, либо потому, что имеется библиотечный пакет программ, позволяющий использовать специальную форму предиката
consult. В любом случае, способ обработки грамматических правил системой заключается в распознавании их при вводе и трансляции на обычный Пролог. Таким образом, грамматические правила превращаются в обычные утверждения Пролога, хотя, естественно, выглядят несколько по-иному по сравнению с тем, что программист обычно вводит в систему.
Рассматриваемая форма записи основывается на форме записи, использованной в начале этой главы для контекстно-свободных грамматик. Действительно, если бы грамматика, представленная в разд. 9.1 (она воспроизведена ниже), была введена в Пролог-систему, то она (грамматика) была бы оттранслирована в точности в те же самые утверждения, которые составляют последнюю версию программы синтаксического анализатора, приведенной в конце предыдущего раздела.
предложение--› группа_существительного, группа_глагола.
группа_существительного--› определитель, существительное.
группа_глагола--› глагол.
группа_глагола -› глагол, группа_существительного, определитель--› [the].
существительное--› [man].
существительное--› [apple].
глагол--› [eats].
глагол--› [sings].
На самом деле грамматические правила представляют структуры языка Пролог с главным функтором '--›' который объявлен как инфиксный оператор. Все, что должна сделать Пролог-система,- это проверить, имеет ли вводимый терм (при использовании предиката
consult и ему подобных) указанный функтор и, если это так, оттранслировать его в соответствующее утверждение.
Как происходит эта трансляция? Прежде всего, каждый атом, обозначающий класс словосочетания, должен быть оттранслирован в предикат с двумя аргументами – для входной последовательности и последовательности, остающейся после обработки, как в нашей программе. Затем, всякий раз, когда в правиле встречаются идущие одно за другим имена словосочетаний, соответствующие предикаты должны быть расположены так, чтобы аргументы показывали, что последовательность, которая остается после обработки одного словосочетания, образует входную последовательность для следующего словосочетания. И наконец, всякий раз, когда в правиле указывается, что словосочетание может быть реализовано как последовательность более мелких словосочетаний, аргументы должны говорить о том, что число слов, входящих в словосочетание, равно суммарному числу слов, входящих в более мелкие словосочетания, упоминаемые в правой части правила. Эти критерии гарантируют, например, что правило:
предложение-› группа_существительного, группа_глагола.
транслируется в утверждение:
предложение (S0, S):- группа_существительного(S0,S1), группа_глагола(S1,S).
или
Между началом S0 и S имеется предложение, если между началом S0 и S1 имеется группа существительного, и если между началом S1 и S имеется группа глагола.
Наконец, система должна знать, как транслировать правила, вводящие реальные слова. Трансляция таких правил производится путем включения слов в списки, образующие аргументы соответствующих предикатов, так что, например, правило
определитель--› [the].
транслируется в утверждение:
определитель(the|S],S).
Если программа синтаксического анализатора представлена в виде совокупности грамматических правил, то каким образом надо задать целевые утверждения, чтобы можно было обработать их программой? Так как известно, как грамматические правила транслируются в утверждения обычного Пролога, то можно выразить целевые утверждения обычным образом, добавив при этом дополнительные аргументы. Первый добавляемый аргумент представляет обрабатываемый список слов, а второй аргумент соответствует списку слов, оставшемуся после обработки, который как правило является пустым списком []. Таким образом, целевое утверждение можно задать так:
?- предложение([thе, man, eats,the,apple],[]).
?- группа_существительного([the,man,sings],X).
В некоторых реализациях Пролога в качестве альтернативы имеется встроенный предикат
phrase, который просто добавляет дополнительные аргументы. Предикат определен следующим образом:
phrase (P,L) истинно, если список L является допустимым словосочетанием типа Р.
Таким образом, можно было бы заменить первое из приведенных выше целевых утверждений следующим:
?- phrase(прeдложeниe, [the,man,eats,the,apple]).
Заметим, что определение предиката
phrase предполагает, что обрабатывается весь список целиком, а список, оставшийся после обработки должен быть пустым. Поэтому второе целевое утверждение нельзя изменить, используя предикат
phrase. Если в реализации Пролога нет встроенного предиката
phrase, то его можно легко определить следующим образом:
phrase(P,L):- Goal =.. [P,L,[]], call(Goal).
Отметим однако, что данное определение будет не приемлемо, если используются более общие грамматические правила, о которых мы скажем в следующем разделе.
Упражнение 9.1. Может быть вы захотите определить на
Прологе процедуру
translate таким образом, что
translate(X,Y) истинно, если
X – грамматическое правило (подобное тем, с какими мы сталкивались в этом разделе), a
Y – терм, представляющий соответствующее утверждение Пролога. Это упражнение довольно трудное. Процедуры подобные
translate имеются в Пролог-системе либо как встроенные, либо в виде библиотечных программ. Но если вы действительно напишите процедуру
translate, то это поможет вам понять, что представляет собой процесс трансляции.
9.4. Присоединение дополнительных аргументов
До сих пор рассматривался лишь довольно ограниченный класс грамматических правил. В этом разделе мы введем одно полезное расширение, позволяющее использовать в грамматических правилах дополнительные аргументы. Это «расширение» не выходит за рамки стандартных средств, предоставляемых в Прологе для записи грамматических правил.
Уже было показано, как имя некоторого класса словосочетаний, встретившееся в грамматическом правиле, транслируется в предикат, имеющий два дополнительных аргумента. Таким образом, грамматические правила приводят к множеству предикатов с двумя аргументами. Иногда при написании синтаксических анализаторов, помимо аргументов, служащих для представления обрабатываемой последовательности, могут потребоваться дополнительные аргументы, тем более, что предикаты в Прологе могут иметь произвольное число аргументов. Предлагаемая здесь форма представления грамматических правил обеспечивает такую возможность.
Давайте рассмотрим пример, показывающий, когда такие дополнительные аргументы полезны. Разберем задачу «согласования числа» между подлежащим и сказуемым предложения. Последовательности слов подобные
*The boys eats the apple.
*The boy eat the apple.
не являются грамматически правильными предложениями, даже если бы они и допускались грамматикой после незначительного ее расширения ('*' используется для обозначения грамматически неправильных предложений). Причина, по которой они не могут считаться грамматически правильными, состоит в том, что, если подлежащее в предложении употребляется в единственном числе, то и сказуемое в этом предложении должно быть глаголом в единственном числе. Аналогично, если подлежащее употребляется во множественном числе, то и сказуемое должно быть в форме множественного числа. Это можно было бы выразить в грамматических правилах, указав, что существуют два типа предложений: предложения с подлежащим в единственном числе и предложения с подлежащим во множественном числе. Предложение первого типа должно начинаться с группы существительного в единственном числе, в которую должно входить существительное, стоящее в форме единственного числа, и так далее. Это привело бы к следующему множеству правил:
предложение--› предложение_едч.
предложение--› предложение_мнч.
группа_существительного--
› группа_существительного_едч.
группа_существительного--› группа_существительного_мнч.
предложение_едч--› группа_существительного_едч, группа_глагола_едч.
группа_существительного_едч--› определитель_едч, существительное_едч.
группа_глагола_едч--› глагол_едч, группа_существительного.
группа_глагола_едч--› глагол_едч.
определитель_едч--› [the].
существительное_едч--› [boy].
глагол_едч--› [eats].
Аналогичное множество правил можно написать и на случай множественного числа. Такой способ согласования числа не очень изящен и скрывает тот факт, что структура предложений для единственного и множественного числа во многом совпадает. Более удачный способ состоит в том, чтобы связать с классами словосочетаний дополнительный аргумент, указывающий на использование единственного или множественного числа. Так
предложение(едч) обозначает словосочетание
предложение, употребленное в форме единственного числа. В общем случае,
предложение (X) обозначает предложение, форма числа которого равна
X. При этом правила согласования числа сводятся к условиям согласованности значений этих аргументов. Форма числа подлежащего в группе существительного должна совпадать с формой числа группы глагола и так далее. Переписав соответствующим образом грамматические правила, получаем:
предложение--› предложение(Х).
предложение(Х)--
› группа_существительного(Х), группа _глагола(Х).
группа_существительного(Х)--› определитель(Х), существительное(Х).
группа_глагола(Х)--› глагол(Х).
группа_глагола(X)--› глагол(Х), группа_существительного(Y).
существительное(едч)--› [boy].
существительное(мнч) -› [boys].
определитель(_)--› [the].
глагол(едч)--› [eats].
глагол(мнч)--›[eat].
Обратим внимание на способ, каким можно определить форму числа для
the. С этого слова могло бы начинаться словосочетание, употребленное в форме как единственного, так и множественного числа, и поэтому форма числа этого слова может быть сопоставлена с чем угодно. Отметим также, что во втором правиле для предиката
группа_глагола имена переменных выражают факт, что форма числа группы глагола (которая должна быть согласована с формой числа подлежащего) определяется по форме числа глагола, а не по форме числа объекта, если таковой имеется.
Можно ввести аргументы, выражающие другую важную информацию помимо согласования числа подлежащего и сказуемого. Например, их можно использовать для хранения перечня элементов, составляющих предложения, встретившихся не на своем обычном месте, и тем самым обрабатывать ситуации, называемые лингвистами «смещением». Или же они могут быть использованы для отражения
семантических характеристик, указывающих, каким образом значение
(смысл) словосочетания составляется из значений более мелких словосочетаний, входящих в исходное. Эти вопросы далее не будут обсуждаться, хотя в разд. 9.6 приведен простой пример использования семантической информации в синтаксическом анализаторе. Однако существует один момент, который здесь необходимо отметить. Лингвистам, возможно, интересно знать, что если в грамматические правила введены дополнительные аргументы, то нельзя гарантировать, что язык, определяемый этой грамматикой, по-прежнему остается контекстно-свободным языком, хотя довольно часто он будет таковым.
Представляется важной возможность использования дополнительных аргументов для возврата дерева разбора, являющегося результатом синтаксического анализа. В главе 3 было показано, как можно представить деревья в виде структур Пролога. Здесь это будет использовано при расширении синтаксического анализатора с целью включить в него построение дерева разбора. Польза деревьев синтаксического разбора в том, что они дают структурное представление предложения. Удобно писать программы, которые обрабатывают эти структурные представления подобно тому, как обрабатывались арифметические формулы и списки в гл. 7. Новая программа для грамматически правильного предложения, такого например, как
The man eats the apple.
строит в качестве результата структуру вида:
предложение(
группа_существительного(
определитель(thе), существительное(man)),
группа_глагола(
глагол(eats), группа_существительного(определитель(the),существительное(аррlе))
)
)
Чтобы добиться этого, необходимо лишь добавить дополнительные аргументы к каждому предикату, указывая, каким образом дерево, соответствующее всему словосочетанию в целом, конструируется из деревьев для частей этого словосочетания. Так первое правило можно изменить следующим образом:
предложение(Х,предложение(NP,VP))--› группа_существительного(X,NP), группа_глагола(X,VP).
Это правило указывает, что, если можно найти последовательность, составляющую группу существительного с деревом разбора
NP, за которой следует последовательность, составляющая группу глагола, с деревом разбора
VP то можно найти последовательность, составляющую полное предложение, и деревом разбора для этого предложения является
предложениe(NP,VP). Или, в более процедурной формулировке: для того, чтобы выполнить разбор предложения необходимо найти группу существительного, за которой следует группа глагола, и затем объединить деревья разбора этих двух составляющих, используя функтор
предложение для построения дерева разбора предложения. Отметим, что аргументы
X – это аргументы, использовавшиеся ранее для согласования формы числа, и решение поставить аргументы для построения дерева разбора после, а не перед ними является совершенно произвольным. Если вам трудно понять это расширение возможностей грамматических правил, то полезно напомнить, что последнее правило представляет собою всего лишь краткую запись следующего утверждения на языке Пролог:
предложение(Х,предложение(NР,VP),S0,S):-группа_существительного(Х,NР,S0,S1),
группа_глагола(Х,VР,S1,S).
где
S0,
S1 и
S – части входной последовательности слов. Аргументы, предназначенные для построения дерева разбора, можно ввести в правила грамматики обычным образом. Здесь приведен получившийся после этого фрагмент грамматики (аргумент, используемый для согласования формы числа, для ясности опущен):
предложение(предложение(NР,VP))--›группа _существительного (NP), группа _ глагола (VP).
группа_глагола(группа_глагола(V))--› глагол(V).
существительное(существительное(man)) – › [man].
глагол(глагол(eats))--› [eats].
Механизм трансляции, необходимый для перевода грамматических правил с дополнительными аргументами в утверждения Пролога, представляет простое расширение описанного ранее механизма. Ранее, для каждого класса словосочетаний создавался новый предикат с двумя аргументами, представляющими входную последовательность и последовательность, оставшуюся после обработки. Теперь надо создать предикат, имеющий на два аргумента больше, чем имеет соответствующее ему грамматическое правило. По соглашению, эти два дополнительных аргумента записываются в конце списка аргументов предиката (хотя в других Пролог-системах может использоваться иное соглашение). Таким образом, грамматическое правило
предложение(Х)--› группа_существительного(Х),группа_глагола(Х).
транслируется в утверждение
предложение(Х,S0,S):- группа_существительного(Х,S0,S1),группа_глагола(Х,S1,S).
При вызове целевых утверждений, содержащих грамматические правила, с самого верхнего уровня интерпретатора (т. е. из вопросов, задаваемых программистом.-
Ред.) или из обычных правил Пролога, необходимо явным образом указать дополнительные аргументы, добавив их в конец списка аргументов. Таким образом, правильное целевое утверждение, содержащее обращение к функтору
предложение, должно быть таким:
?- предложение(Х,[a,clergyman,eats,a, cake],[]).
?- предложение(Х, [every, bird, sings,and,pigs,can,fly],L).
Упражнение 9.2. Напишите новый вариант предиката
phrase, допускающий использование грамматических правил с дополнительными аргументами. Этот предикат должен допускать целевые утверждения вида:
?- phrase(предложение(Х),[the, man,sings]).
9.5. Введение дополнительных условий
Рассматривавшиеся до сих пор грамматические правила, входящие в программу синтаксического анализатора, содержали информацию лишь о том, какая часть входной последовательности обрабатывается каждым из правил. Каждый элемент описания правил должен содержать указание о том, как обрабатывать два дополнительных аргумента, добавленных транслятором грамматических правил. Так что каждое целевое утверждение в результирующем утверждении Пролога обрабатывало определенную часть входной последовательности. Иногда может возникнуть желание определить целевые утверждения иного типа, не связанные непосредственно с обработкой входной последовательности, и рассматриваемый формализм грамматических правил позволяет сделать это. В языке принято следующее соглашение: каждое целевое утверждение, заключенное в фигурные скобки {}, при трансляции не меняется.
Рассмотрим несколько примеров ситуаций, в которых было бы полезно использовать эту возможность. Мы покажем, как можно улучшить «словарь» синтаксического анализатора, т. е. его «знания» о словах обрабатываемого языка.
Прежде всего рассмотрим накладные расходы, связанные с введением нового слова в программу, в которой используются оба множества дополнительных аргументов (для согласования формы числа и для построения дерева разбора). Если нужно добавить новое слово, например
banana, то для этого необходимо добавить хотя бы правило
существительное(едч, существительное(banana))--› [banana].
которое сводится к следующему факту на Прологе:
существительное(едч, существительное(banana),[banana|S],S).
Это слишком большой объем информации для определения каждого существительного, особенно когда мы знаем, что каждое существительное представляется лишь одним элементом входного списка и порождает небольшое дерево с функтором
существительное. Значительно более экономичный способ представления основывается на разделении информации. Информация, общая для всех существительных, помещается в одном месте, а информация о конкретных словах в другом месте. Это можно сделать, если одновременно использовать возможности грамматических правил и обычного Пролога. Общая информация о том, каким образом существительные входят в другие словосочетания, представляется с помощью грамматического правила, а информация о том, какие слова являются существительными, представляется с помощью обычных утверждений Пролога. Этот подход можно применить к последнему примеру следующим образом:
существительное(S,существительное(N)) --› [N], {является_существительным(N,S)}.
где обычный предикат
является_существительным указывает, какие слова являются существительными и в какой форме - единственного или множественного числа – они употребляются.
является_существительным(banana,едч).
является_существительным(bananas,мнч).
является_существительным(man,едч).
. . .
Давайте подробно разберем, что означает это грамматическое правило. Оно указывает, что словосочетание класса
существительное может состоять из единственного слова
N (переменная, определенная в списке), удовлетворяющего некоторому ограничению. Это ограничение заключается в том, что
N должно входить в число слов, представленных предикатом
является_существительным, с указанием конкретной формы числа
S. В этом случае, форма числа словосочетания также
S, а порождаемое дерево разбора состоит из двух вершин: вершины
существительное и расположенной под ней вершины
N. Почему целевое утверждение
является_существительным (N,S) должно быть заключено в фигурные скобки? Потому, что оно выражает отношение, не имеющее ничего общего с обработкой входной последовательности. Если убрать фигурные скобки, то результат трансляции будет выглядеть примерно так:
является_существительным(N,S,S1,S2)
и это целевое утверждение никогда не было бы сопоставлено с утверждениями для
является_существительным. Заключив целевое утверждение в фигурные скобки, мы тем самым предотвращаем какие-либо его изменения при трансляции. Так что правило будет правильно оттранслировано в следующее утверждение
существительное(S,существительное(N),[N|Посл],Посл):- является_существительным(N,S).
Несмотря на внесенное изменение, используемый способ обработки отдельных слов по-прежнему остается недостаточно изящным. Неудобство этого способа состоит в том, что для каждого вновь вводимого слова надо записывать два утверждения
является_существительным – одно для формы единственного числа, а другое для формы множественного числа. Но в этом нет необходимости, поскольку для большинства существительных формы единственного и множественного числа связаны простым правилом:
Если X –
существительное в форме единственного числа, то слово, получаемое в результате прибавления 's' к концу слова X,
является формой множественного числа этого существительного.
Это правило можно использовать для пересмотра определения для
существительное. В результате будет получено новое множество условий, которым должно удовлетворять слово
N, для того, чтобы быть существительным. Так как эти условия связаны с внутренней структурой слова и не имеют никакого отношения к обработке входной последовательности, то они будут записаны с использованием фигурных скобок. Слова английского языка представляются как атомы Пролога и поэтому обсуждение вопроса разбиения слов на буквы сводится к рассмотрению литер, составляющих соответствующие атомы. Следовательно, в новом определении необходимо будет использовать предикат
name. Улучшенный вариант правила выглядит следующим образом:
существительное(мнч,существительное(КореньN))--›
[N], {(name(М,Мнимя), присоединить(Едимя,"s",Мнимя), name(КореньN,Едимя), является_существительным(КореньN,едч))}.
Конечно, представленное здесь общее правило о форме множественного числа существительных справедливо не во всех случаях (например, множественное число для «fly» не совпадает с «flys»), И по-прежнему необходимо исчерпывающим образом описывать все исключения. Обратите внимание на использование двойных кавычек для представления списка, содержащего литеру
's'. Теперь необходимо определять утверждения для предиката
является_существительным лишь для существительных в единственном числе, если форма множественного числа для них образуется по указанному выше правилу. Заметьте, что в соответствии с приведенным определением в дерево разбора вставляется существительное в форме единственного, а не множественного числа. Это может оказаться полезным при последующей обработке дерева разбора. Обратите также внимание на то, как использованы фигурные скобки. В различных реализациях Пролога некоторые детали синтаксиса могут немного отличаться, но наиболее безопасно заключать содержимое фигурных скобок в дополнительные круглые скобки, если оно состоит более чем из одного целевого утверждения, и оставлять пропуск между фигурной скобкой и точкой, завершающей правило.
Большинство трансляторов синтаксических правил, помимо целевых утверждений, заключенных в фигурные скобки, оставляют неизменными и некоторые другие целевые утверждения. Так, обычно нет необходимости заключать в фигурные скобки '!' или дизъюнкции (;) целевых утверждений.
9.6. Заключение
В этом разделе мы подведем итог тем сведениям, которые мы получили о синтаксисе грамматических правил. Затем будут указаны некоторые из возможных расширений и показаны некоторые интересные способы использования грамматических правил. Лучший способ описать синтаксис грамматических правил – сделать это с помощью самих же грамматических правил. Таким образом, здесь приводится некоторое неформальное описание синтаксиса. Отметим, что оно не является абсолютно строгим, так как в нем не учитывается влияние приоритета операторов на синтаксис.
грамматическое правило--› заголовок, ['--›'], тело.
заголовок--› нетерминальный_символ.
заголовок--› нетерминальный_символ, [','], терминальный_символ
тело--› тело, [','], тело.
тело--› тело, [';'], тело.
тело--› элемент_тела.
элемент_тела--› ['!'].
элемент_тела--› ['{'], целевые_утверждения_пролога, ['}'].
элемент_тела--› нетерминальный_символ.
элемент_тела--› терминальный_символ.
Ряд элементов описания неопределен. Здесь приведены их определения на естественном языке.
нетерминальный_символ обозначает класс словосочетаний, которые могут входить во входную последовательность. Он имеет вид структуры языка Пролог, функтор которой обозначает категорию словосочетаний, а аргументы дают дополнительную информацию (форму числа, значение и так далее).
терминальный_символ указывает ряд слов, которые могут быть частью входной последовательности. Он имеет вид списка языка Пролог и может быть либо пустым списком [], либо списком некоторой фиксированной длины. Элементы этого списка должны быть сопоставимы со словами последовательности в соответствии с заданным порядком.
целевые_утверждения_пролога -
это любые целевые утверждения языка Пролог. Они могут быть использованы для записи дополнительных условий и действий, ограничивая возможные пути анализа и указывая, как сложные результаты строятся из простых.
При трансляции на Пролог,
целевые_утверждения_пролога остаются неизменными, а
нетерминальный_символ получает два дополнительных аргумента, которые вставляются после явно указанных аргументов. Дополнительные аргументы соответствуют последовательности, в которой выделяется словосочетание, и последовательности, которая остается после выделения словосочетания. Терминальные символы появляются среди дополнительных аргументов нетерминальных символов. При вызове предиката, определенного грамматическими правилами, с верхнего уровня интерпретатора или из обычного правила Пролога необходимо явно указать два дополнительных аргумента.
Во втором правиле для предиката
заголовок описывается класс грамматических правил, с которыми нам еще не приходилось сталкиваться. До сих пор определения терминальных и нетерминальных символов содержали информацию лишь о том, как они обрабатывают входную последовательность. Иногда может возникнуть желание определить правила таким образом, чтобы они вставляли элементы во входную последовательность (для обработки другими правилами). Например, предложение в повелительном наклонении можно было бы анализировать следующим образом. В исходное предложение
Eat your supper.
вставляется дополнительное слово:
You eat your supper.
Получившееся предложение имеет правильную структуру, согласующуюся с нашими представлениями о структуре предложений. Это можно сделать, используя грамматическое правило вида:
предложение--› императив, группа_существительного, группа_глагола.
императив,[you]--› [].
императив--› [].
Из приведенных здесь правил лишь одно заслуживает внимания. Это первое правило для
императив, которое транслируется в утверждение
императив(L,[уоu|L]).
То есть, последовательность, возвращаемая после обработки, длиннее исходной последовательности. В общем случае, левая часть грамматического правила может включать нетерминальный символ, за которым, через запятую, следует список слов. Смысл такого правила состоит в том, что в процессе разбора предложения слова, указанные в списке, вставляются во входную последовательность после того, как завершится обработка целевыми утверждениями в правой части правила.
Упражнение 9.3. Приведенное определение для
грамматических правил, даже если бы оно было полным, не сможет выполнить функции синтаксического анализатора, если на вход ему подавать последовательность знаков. Почему?
В заключение рассмотрим пример грамматических правил, используемых для непосредственного извлечения «смысла» предложений, минуя этап построения дерева разбора. Этот пример взят из статьи Pereira, Warren, Artificial Intelligence, v. 13. Представленные далее правила транслируют предложения из ограниченного подмножества предложений английского языка в некоторое представление на языке исчисления предикатов, отражающее смысл этих предложений. Описание исчисления предикатов и используемой формы записи даны в гл. 10. В качестве примера работы программы мы приведем предложение «every man loves a woman» и соответствующую структуру, отражающую его смысл:
[14]
all(X,(man(X)→exists(Y,(woman(Y)& loves(X,Y)))))
Здесь представлены грамматические правила программы:
?- op(100,xfy,&)
?- op(150,xfy,→)
предложение(Р)--› группа_существительного(Х,Р1,Р),группа_глагола(Х,Р1).
группа_существительного(Х,Р1,Р)--›определитель(Х,Р2,Р1,Р),существительное(Х,Р3), отн_утверждение(Х,Р3,Р2).
группа_существительного(Х,Р,Р)--› наст_существительное(Х).
группа_глагола(Х,Р)--› перех_глагол(Х,Y,Р1),группа_существительного(Y,Р1,Р).
группа_глагола(Х,Р)--› неперех_глагол(Х,Р).
отн_утверждение(Х,Р1,(Р1&Р2))--› [that], группа_глагола(Х,Р2).
отн_утверждение(_,Р,Р)--› [].
определитель(Х,Р1,Р2,аll(Х,(Р1>Р2)))--› [every].
определитель(Х,Р1,Р2,ехists(Х,(Р1&Р2)))--› [а].
существительное(Х,man(Х))--› [man].
существительное(Х, woman (X))--› [woman].
наст_существительное(john)--› [john].
пepex_глагол(X,Y,loves(X,Y))--› [loves].
неперех_глагол(Х,lives(Х)))--› [lives].
В этой программе аргументы используются для построения структур, представляющих смысл словосочетаний. Смысл каждого словосочетания определяет последний аргумент соответствующего правила. Однако смысл словосочетания может зависеть от некоторых других факторов, представленных другими аргументами. Например, глагол
lives (живет) порождает высказывание вида
lives(X), где
X – это объект, обозначающий человека, который живет. Смысл слова
lives не позволяет заранее определить, чем будет являться
X. Чтобы быть полезным, понятие подобное
lives должно быть применимо к некоторому конкретному классу объектов. Что представляет этот объект, будет определено из контекста, в котором используется глагол
lives. Таким образом, имеем следующее определение: для любого
X, применение глагола
lives к
X имеет смысл
lives(X). Слово, подобное
every (каждый), является значительно более сложным. В этом случае понятие, соответствующее слову, должно применяться к некоторой переменной и к двум высказываниям, содержащим эту переменную. Результат можно сформулировать так: если подстановка некоторого объекта вместо переменной в первом утверждении делает что-то истинным, то подстановка того же объекта вместо переменной во втором утверждении также сделает что-то истинным.
Упражнение 9.4. Разберитесь в приведенной программе. Попробуйте проследить выполнение программы при обращении к ней с вопросами типа
?- предложение(Х, [every, man, loves, a, woman],[]).
Во что транслируются программой предложения «Every man that lives loves a woman» и «Every man that loves a woman lives». Предложение «Every man loves a woman» является в действительности двусмысленным - может существовать либо единственная женщина, которая нравится каждому мужчине, либо несколько женщин, каждая из которых нравится мужчине. Может ли программа породить альтернативные решения, описывающие смысл каждой из двух указанных интерпретаций предложения? Если нет, то почему? Какое простое предположение о построении структуры, отражающей смысл предложения, было сделано при написании программы?
ГЛАВА 10. ПРОЛОГ И МАТЕМАТИЧЕСКАЯ ЛОГИКА
Язык программирования Пролог был разработан коллективом во главе с Колмерауэром приблизительно в 1970 году. Это была первая попытка в разработке языка, который позволял бы программисту описывать свои задачи средствами математической логики, а не с помощью традиционных для программирования конструкций, указывающих
что и
когда должна делать вычислительная машина. Эта идея нашла отражение в названии языка программирования «Пролог» (английское название «Prolog» является сокращением для Programming in
Logic.-
Перев.).
В этой книге основное внимание было уделено вопросам, связанным с использованием Пролога в качестве инструментального средства для решения практических задач. При этом ничего не говорилось о путях достижения конечной цели – создании системы логического программирования, шагом к которой является Пролог. В этой главе мы намереваемся отчасти исправить это несоответствие, рассмотрев вкратце связь Пролога с математической логикой и вопрос о том, в какой степени программирование на Прологе соответствует идее логического программирования.
10.1. Краткое введение в исчисление предикатов
Если мы намерены обсуждать связь Пролога с математической логикой, то прежде всего необходимо установить, что мы понимаем под логикой. Первоначально логика развивалась как некоторый способ представления определенного класса высказываний, так чтобы можно было, используя формальную процедуру, проверить, справедливы они или нет. Таким образом, логика может быть использована для выражения высказываний, отношений между высказываниями и
правил вывода одних высказываний из других. Логическое исчисление специального вида, о котором будет идти речь в этой главе, называется
исчисление предикатов. Здесь мы лишь затронем некоторые вопросы исчисления предикатов. Хорошим введением в математическую логику является книга Hodges W.
Logic, Penguin Books, 1977. Более подробное обсуждение предмета дано в книге Mendelson E.
Intro ductiontoMathematicalLogic, VanNostrandReinhold.
[15] Вы так же можете обратиться к любой книге по математической логике. Другая книга, представляющая интерес, написана Chin L. С, Lee R. С.-Т.
Symbolic Logic and Mechanical Theorem Proving, Academic Press, 1973.
[16]
Для того чтобы делать высказывания о мире, необходимо уметь описывать объекты этого мира. В исчислении предикатов объекты представляются с помощью
термов. Существуют термы трех типов:
•
Константа. Это символ, обозначающий индивидуальный объект или понятие. Константы можно рассматривать как атомы языка Пролог и далее будет использоваться соответствующая форма записи. Так,
грек,
агата и
мир являются константами.
•
Переменная. Это символ, используемый в разное время для обозначения разных индивидуальных объектов. Переменные вводятся лишь одновременно с кванторами, о которых будет сказано далее. Термы, являющиеся переменными, можно рассматривать как переменные языка Пролог и далее для их обозначения будет использоваться синтаксис, принятый в Прологе. Таким образом,
X,
Человек и
Грек являются переменными.
•
Составной терм. Составной терм состоит из
функционального символа и упорядоченного множества термов, являющихся его
аргументами. Идея состоит в том, что составной терм обозначает тот или иной индивидуальный объект, зависящий от других индивидуальных объектов, представленных его аргументами. Функциональный символ описывает характер зависимости. Например, можно было бы иметь функциональный символ, обозначающий «расстояние» и имеющий два аргумента. В этом случае составной терм обозначает расстояние между объектами, представленными его аргументами. Составной терм можно рассматривать как структуру языка Пролог, имеющую в качестве функтора функциональный символ. Составные термы будут записываться по правилам синтаксиса Пролога так, что, например,
жена(генри) может обозначать жену Генри,
расстояние(точка1, X) может обозначать расстояние между некоторой заданной точкой и каким-то другим объектом, который будет указан, а
классы(мэри, на_следующий_ день_после(Х)) может обозначать классы, в которых преподавала Мэри на следующий после
X (необходимо указать день).
Таким образом, способы, используемые для представления объектов в исчислении предикатов, в точности соответствуют способам, имеющимся для этого в Прологе.
Для того чтобы делать высказывания об объектах, необходимо иметь возможность описывать отношения между объектами. Это делается с помощью
предикатов. Атомарное высказывание (атомарная формула) состоит из предикатного символа и соответствующего ему упорядоченного множества термов, являющихся его аргументами. Это полностью аналогично целевому утверждению Пролога. Так, например,
человек(мэри), владеет(Х,осел(Х)) и
нравится (Мужчина, вино) являются атомарными высказываниями (атомарными формулами). В языке Пролог структура может быть использована как в качестве целевого утверждения, так и в качестве аргумента для другой структуры. В исчислении предикатов дело обстоит иначе. Там имеется строгое разделение между функциональными символами, используемыми в качестве функторов для построения аргументов, и предикатными символами, используемыми в качестве функторов для построения высказываний (формул).
Используя атомарные высказывания, можно различными способами создавать составные высказывания. Именно здесь начинают появляться понятия не имеющие непосредственных аналогов в языке Пролог. Существует несколько способов построения более сложных высказываний из более простых. Прежде всего, можно использовать
логические связки. Таким способом можно выразить понятия 'не', 'и', 'или', 'влечет' и 'является эквивалентным'. Далее приведено краткое описание этих связок и вкладываемых в них значений. Здесь ? и ? используются для обозначения произвольных высказываний (формул). В следующей таблице приводятся традиционная форма записи высказываний, используемая в исчислении предикатов, и форма записи, используемая в этой главе.
| Логическая связка |
Исчисление предикатов |
Обозначение в книге |
Значение |
| Отрицание |
⌉α |
~α |
«не α» |
| Конъюнкция |
α∧β |
α&β |
«α и β» |
| Дизъюнкция |
α∨β |
α#β |
«α или β» |
| Импликация |
α⊃β |
α-›β |
«α влечет β» |
| Эквивалентность |
α≡β |
α‹-›β |
«α эквивалентна β» |
Так, например, конструкция
мужчина(фред) # женщина (фред)
могла бы быть использована для представления высказывания о том, что Фред является мужчиной
или Фред является женщиной. Конструкция
мужчина(джон) -› человек (джон)
могла бы представлять высказывание: то, что Джон является мужчиной,
влечет то, что он является человеком
(если Джон мужчина, то он – человек). Понятия импликации и эквивалентности иногда при первом знакомстве с ними представляются несколько сложными. Мы говорим, что α влечет β, если всякий раз, когда α истинно, то β также истинно. Мы говорим, что α эквивалентно β, если α истинно в точности в тех же случаях, что и β. В действительности, эти понятия могут быть определены через понятия 'и', 'или', 'не'. А именно:
α-›β значит то же самое, что (~α)#β
α‹-›β значит то же самое, что и (α&β)#(~α&~β)
α‹-›β также значит то же самое, что и (α-›β)&(α-›β)
До сих пор ничего не было сказано о том, что значат переменные, входящие в состав высказывания. В действительности, использование переменных имеет смысл лишь в случае, когда они вводятся с помощью
кванторов. Кванторы позволяют делать высказывания о множествах объектов и формулировать утверждения, истинные для этих множеств. В исчислении предикатов имеются два квантора. Если ν обозначает переменную, а ρ – это произвольное высказывание, то коротко значение кванторов можно выразить так:
| Исчисление предикатов |
Обозначение в книге |
Значение |
| ∀ν. ρ |
all(ν, ρ) |
«ρ истинно для всех значений переменной ν» |
| ∃ν.ρ |
exists(ν, ρ) |
«существует такое значение переменной ρ, для которого ν истинно» |
Первый из кванторов называется
квантором общности, так как он указывает на все объекты, существующие во вселенной («для всех ν,…»). Второй квантор называется
квантором существования, так как он указывает на существование некоторого объекта (или объектов) («существует ν такой что…»). В качестве примера приведем формулу
all(X, мужчина(Х) -› человек(Х))
которая значит, что какое бы значение
X мы не выбрали, если
X является мужчиной, то тогда
X – человек. Эту формулу можно прочитать так:
для любого X,
если X является мужчиной, то X является человеком. Или в более простой формулировке:
каждый мужчина является человеком. Аналогично
exists(Z, отец(джон,2)& женщина(Z)))
значит, что существует объект, обозначаемый
Z такой, что Джон является отцом
Z и
Z – женщина. Эту формулу можно прочитать так:
существует Z такой, что Джон является отцом Z и
Z –
женщина. Или в более естественной формулировке:
Джон имеет дочь. Ниже приведены две более сложные формулы исчисления предикатов:
all(X, животное(Х) -› exists(Y,мать(X,Y)))
all(X, формула_исчисления_предикатов(Х) ‹-› атомарная_формула(Х) # составная_формула(Х))
10.2. Приведение формул к стандартной форме
Как было показано в предыдущем разделе, формулы исчисления предикатов, записанные с использованием связок -› (импликация) и ‹-› (эквивалентность), могут быть переписаны лишь с использованием связок& (конъюнкция), # (дизъюнкция) и ~ (отрицание). В действительности, существует множество разных форм записи формул, и мы ни в коей мере не принесли бы в жертву выразительность формул, если бы должны были полностью отказаться от использования, например,
#,
-›,
‹-› и
exists(X, P). Как следствие этой избыточности, существуют много различных способов записи одного и того же высказывания. При необходимости выполнять формальные преобразования формул исчисления предикатов это оказывается очень неудобным. Было бы значительно лучше, если бы все, что мы хотим сказать, можно было выразить единственным способом. Поэтому здесь будет рассмотрен способ преобразования формул исчисления предикатов к специальному виду –
стандартной форме, - обладающему тем свойством, что число различных способов записи одного и того же утверждения меньше по сравнению с использованием других форм. В действительности будет показано, что высказывание исчисления предикатов, представленное в стандартной форме, очень похоже на некоторое множество утверждений языка Пролог. Так что исследование стандартной формы имеет существенное значение для понимания связи между Прологом и математической логикой. В приложении В будет коротко описана программа на Прологе, автоматически транслирующая формулы исчисления предикатов в стандартную форму.
Процесс приведения формулы исчисления предикатов к стандартной форме состоит из шести основных этапов.
Этап 1 - исключение импликаций и зквивалентностей
Процедура начинается с замены всех вхождений -› и ‹-
› в соответствии с их определениями, данными в разд. 10.1. Так, например, формула
аll(Х,мужчина(Х) -› человек(Х))
будет преобразована в формулу
аll(Х,~мужчина(Х) # человек(Х))
Этап 2 - перенос отрицания внутрь формулы
На этом этапе обрабатываются случаи применения отрицания к формулам, не являющимся атомарными. Если такой случай имеет место, то формула переписывается по соответствующим правилам. Так, например, формула
~(человек (цезарь)& существующий (цезарь))
преобразуется в
~человек(цезарь) # существующий (цезарь)
а
~аll(Х, человек (X))
преобразуется в
exists(Х,~человек(Х))
Преобразования, выполняемые на втором этапе, основаны на следующих фактах:
~(α&β) значит то же самое, что и
(~α) # (~β)
~exists(ν,ρ) значит то же самое, что и
all(ν,~ρ)
~all(ν,ρ) значит то же самое, что и
exists(ν,~ρ)
После завершения второго этапа каждое вхождение отрицания в формулу будет относиться лишь к атомарным подформулам. Атомарная формула или ее отрицание называется
литералом. На всех последующих этапах литералы обрабатываются как единый элемент, а то, какие литералы представлены отрицанием, будет существенным лишь в самом конце.
Этап 3 - сколемизация
На следующем этапе удаляются кванторы существования. Это делается путем введения новых констант –
сколемовских констант - вместо переменных связанных (введенных) квантором существования. Вместо того чтобы говорить, что существует объект, обладающий некоторым множеством свойств, можно ввести имя для такого объекта и просто сказать, что он обладает данными свойствами. Это соображение лежит в основе введения сколемовских констант. Сколемизация более существенно изменяет логические свойства формулы, чем все обсуждавшиеся ранее преобразования. Тем не менее, она обладает следующим важным свойством. Если имеется формула, то интерпретация, в которой эта формула истинна, существует тогда и только тогда, когда существует интерпретация, в которой истинна формула, полученная из первой в результате сколемизации. Такая форма эквивалентности формул вполне достаточна для наших целей. Так, например, формула
exists(X,женщина(X)& мать(Х,ева))
в результате сколемизации преобразуется в формулу
женщина(g1)& мать(g1, ева)
где
g1 – некоторая новая константа, не использовавшаяся ранее. Константа
g1 представляет некоторую женщину, мать которой есть Ева. То, что для обозначения константы использован символ» отличный от использовавшихся ранее, существенно, так как в высказывании ничего не говорится о том, что какой-то конкретный человек является дочерью Евы. В утверждении говорится лишь о том, что такой человек существует. Может оказаться, что
g1 будет соответствовать тот же самый человек, который соответствует другой константе, но это уже дополнительная информация, никак не выраженная в высказывании.
Если формула содержит кванторы общности, то процедура сколемизации уже не столь проста. Например, если в формуле
[17]
аll(Х, человек(Х) -› exists(Y,мать(X,Y)))
(«каждый человек имеет мать») заменить каждое вхождение переменной V, связанной квантором существования, на константу
g2 и удалить квантор существования, то получится:
all(X, человек(Х) -› мать(X,g2))
Последнее высказывание говорит о том, что все люди имеют
одну и ту же мать, обозначенную в формуле константой
g2. Если в формуле есть переменные, введенные посредством кванторов общности, то при сколемизации необходимо вводить не константы, а
составные термы (функциональные символы с множеством переменных аргументов) для того, чтобы отразить, как объект, о существовании которого идет речь,
зависит от того, что обозначают переменные. Таким образом, при сколемизации предыдущего примера должно получиться
all(X, человек(Х) -› мать(Х, g2(Х)))
В этом случае функциональный символ
g2 соответствует функции, которая каждому конкретному человеку ставит в соответствие его мать.
Этап 4 - вынесение кванторов общности в начало формулы
Этот этап очень прост. Каждый квантор общности просто выносится в начало формулы. Это не влияет на значение формулы. Так, например, формула
all(X, мужчина(Х) -› аll(Y,женщина(Y) -› нравится (X,Y)))
преобразуется в
аll(Х, аll(Y,мужчина(Х) -› (женщина(Y) -› нравится (X,Y))))
Так как теперь каждая переменная в этой формуле вводится посредством квантора общности, находящегося в начале формулы, то кванторы сами по себе не несут больше какой-либо дополнительной информации. Поэтому можно сократить формулу, опустив кванторы. Необходимо лишь помнить, что каждая переменная вводится посредством не указанного явно квантора, который опущен при записи формулы. Таким образом, формулу
аll(Х,живой(Х) # мертвый(Х)& аll(Y,нравится(мэри,Y) #грязный(Y))
теперь можно представить так:
(живой(Х) # мертвый(Х))& (нравится(мэри,Y) # грязный (Y))
Эта формула значит, что, какие бы
X и
Y ни были выбраны, либо
X живой, либо
X мертвый, и либо Мэри нравится
Y, либо
Y – грязный.
Этап 5 - использование дистрибутивных законов для & и #
На этом этапе исходная формула исчисления предикатов претерпела довольно много изменений. Формула больше не содержит в явном виде кванторов, а из логических связок в ней остались лишь & и # (помимо отрицания, входящего в состав литералов). Теперь формула преобразуется к специальному виду
- конъюнктивной нормальной форме, характерной тем, что дизъюнктивные члены формулы не содержат внутри себя конъюнкцию. Таким образом, формулу можно преобразовать к такому виду, когда она будет представлять последовательность элементов, соединенных друг с другом конъюнкциями, а каждый элемент является либо литералом, либо состоит из нескольких литералов, соединенных дизъюнкцией. Чтобы привести формулу к такому виду, необходимо использовать следующие два тождества:
(А&В) # С эквивалентно
(А # С)&(В # С)
А # (В&С) эквивалентно (
А # В)&(А # С)
Так, например, формула:
выходной(Х) # (работает(крис, X) & (сердитый (крис) # унылый(крис)))
(Для каждого
X либо
X – выходной день, либо Крис работает в день
X и при этом он либо сердитый, либо унылый) эквивалентна следующей:
выходной(Х) # (работает(крис,Х)) & (выходной(Х) # (сердитый(крис) # унылый(крис)))
(Для каждого
X, во-первых,
X является выходным днем или Крис работает в день
X; во-вторых, либо
X – выходной день, либо Крис сердитый или унылый).
Этап 6 - выделение множества дизъюнктов
Формула, имеющаяся к началу этого этапа, в общем случае представляет совокупность конъюнктивных членов, являющихся литералами или состоящих из литералов, соединенных дизъюнкцией. Давайте сначала рассмотрим структуру формулы на верхнем уровне, не вникая в детали организации конъюнктивных членов. Формула могла бы иметь, например, следующий вид:
(А & В) & (С & (D & Е))
где переменные обозначают, возможно, сложные высказывания (формулы), но при этом они не содержат внутри конъюнкций. На данном этапе нет никакой необходимости знать структуру вложенности, представляемую использованием скобок, так как все высказывания
(А & В) & (С & (D
& Е)) А
& (( В& С) & (D
& Е)) (А & В) & ((С
& D)
& Е
)
обозначают одно и то же. И хотя
структурно эти формулы различны, они имеют один и тот же смысл. Это объясняется тем, что если установлена истинность
всех высказываний из некоторого множества, то не имеет значения каким образом они группируются в сложное конъюнктивное высказывание. Не имеет значения, например, как сказать «
А истинно и
В и
С также истинны» или «
А и
В истинны и
С тоже истинно». Следовательно, скобки никак не влияют на смысл формулы. Можно просто написать (неформально):
A & B & C & D & E
Далее, порядок записи этих формул также не имеет значения. Безразлично, как сказать: «
А и
В истинны» или «
В и
А истинны», так как оба эти высказывания имеют одно и то же значение. И наконец, нет необходимости указывать знак конъюнкции (&) между формулами, так как заранее известно, что на верхнем уровне формула является конъюнкцией составляющих ее частей. Поэтому, в действительности, значение представленной формулы можно выразить значительно короче, представив ее в виде
совокупности {А, В, С, D, Е}. Название «совокупность» подчеркивает, что порядок элементов не имеет значения. Совокупность
{А, В, С, D, Е} в точности то же самое, что и
{В, А, С, Е, D},
{Е, D, В, С, А} и так далее. Формулы, являющиеся элементами совокупности, полученной в результате преобразования некоторой формулы исчисления предикатов, называются дизъюнктами. Таким образом, каждая формула исчисления предикатов эквивалентна (в некотором смысле) совокупности дизъюнктов.
Давайте рассмотрим несколько подробнее, что представляют собой эти дизъюнкты. Как уже было сказано, они состоят из литералов, соединенных друг с другом с помощью дизъюнкции. В общем случае, дизъюнкт выглядит примерно так:
((V # W) # X) # (Y # Z)
где переменные являются литералами. Теперь те же самые рассуждения, которые были сделаны о структуре формулы на верхнем уровне, можно применить к дизъюнктам. Как и выше, скобки не влияют на значение дизъюнкта. Точно так же несуществен и порядок литералов. Таким образом, можно просто сказать, что дизъюнкт – это
совокупность литералов (неявно соединенных дизъюнкцией). В последнем примере это будет
{V, W, X, Y, Z}
Теперь исходная формула представлена в стандартной форме. Более того, использовавшиеся для преобразования правила не зависят от того, существует или нет интерпретация, при которой формула истинна. Стандартная форма состоит из совокупности дизъюнктов, каждый из которых представляет совокупность литералов. Литерал – это либо атомарная формула, либо отрицание атомарной формулы. Эта форма является достаточно лаконичной, так как в ней опущены логические связки конъюнкций, дизъюнкций и кванторы всеобщности. Но при этом, очевидно, следует помнить о принятых соглашениях. И каждый раз, имея дело со стандартной формой, понимать, где и что в ней опущено. Рассмотрим, что представляет собой стандартная форма некоторых формул (предполагается, что уже выполнены первые пять этапов преобразования). Прежде всего вернемся к уже рассматривавшемуся примеру:
(выходной(Х) # работает(крис,Х)) & (выходной(Х) # (сердитый(крис) # унылый(крис)))
Эта формула порождает два дизъюнкта. Первый дизъюнкт содержит литералы:
выходной(Х), работает(крис,Х)
а второй литералы:
выходной(Х), сердитый(крис), унылый(крис)
Другой пример. Формула
(человек(адам)& человек(ева))&
((человек(Х) # ~мать(Х,Y)) # ~человек(#))
дает три дизъюнкта. Два из них содержат по одному литералу каждый
человек (адам)
и
человек (ева)
Другой содержит три литерала:
человек(Х), ~мать(Х,Y), ~человек(Y)
В заключении этого раздела рассмотрим еще один пример, демонстрирующий все этапы приведения формулы к стандартному виду. Начнем с формулы
all(X, аll(Y,человек(Y) -› почитает(Y,Х) -› король(Х))
утверждающей, что, если все люди относятся с почтением к некоторому человеку, то этот человек является королем. (Для каждого
X, если каждый
Y является человеком, почитающим
X, то
X – это король). После устранения импликации (этап 1) получаем:
аll(Х,~(аll(Y,~человек(Y) # почитает(Y,Х))) # король(Х))
Перенос отрицания внутрь формулы (этап 2) приводит к следующему:
аll(Х,ехists(Y,человек(Y) & ~почитает(Y,Х)) # король(Х))
Затем, в результате сколемизации (этап 3) формула преобразуется к виду:
аll(Х,(человек(f1(Х)) & ~почитает(f1Х),Х)) # король(Х))
где f1 -сколемовская функция. Теперь производится удаление кванторов всеобщности (этап 4), что приводит к формуле;
(человек(f1(X)) & ~почитает(f1(Х),X)) # король(Х)
Затем формула преобразуется к конъюнктивной нормальной форме (этап 5), в которой конъюнкция не появляется внутри дизъюнктов:
(человек(f1(Х) # король(Х)) & (~почитает(f1(Х), X) # король(Х))
Эта формула содержит два дизъюнкта (этап 6). Первый дизъюнкт имеет два литерала:
человек(f1(Х)), король(Х)
а второй дизъюнкт имеет литералы:
почитает(f1(Х),Х), король(Х)
10.3. Форма записи дизъюнктов
Очевидно, что для записи формул, представленных в стандартной форме, необходим соответствующий способ. Рассмотрим его. Прежде всего, стандартная форма представляет совокупность дизъюнктов. Договоримся записывать дизъюнкты последовательно один за другим, помня при этом, что порядок записи не имеет значения. В свою очередь, дизъюнкт является совокупностью литералов, часть из которых содержит отрицание, а часть не содержат его. Примем соглашение записывать сначала литералы без отрицания, а затем литералы с отрицанием. Эти две группы литералов будем разделять знаком ':-'. Литералы без отрицания при записи будем отделять друг от друга точкой с запятой (;) (помня, конечно, при этом, что порядок записи литералов в каждой группе неважен), а литералы с отрицанием будем записывать без знака отрицания (~), разделяя литералы запятыми. Запись каждого дизъюнкта будет заканчиваться точкой. При такой форме записи дизъюнкт, содержащий отрицания литералов
K,
L,… и литералы
А,
В,… мог бы быть представлен так:
A; B;…:- K, L,…
Хотя принятые предположения о форме записи дизъюнктов представляются произвольными, в них заложен некоторый мнемонический смысл. Если записать дизъюнкт, явно указав все знаки дизъюнкций и отрицаний и отделив литералы с отрицаниями от литералов без отрицаний, то получится примерно следующее;
(А # В #…) # (~К # -L #…)
что эквивалентно
(A # B # …) # ~(K & L & …)
Это в свою очередь эквивалентно (К & L &…) -› (А # В #…)
Если записать ',' вместо 'и', ';' вместо 'или' и ':-' вместо 'является следствием', то дизъюнкт естественным образом примет следующий вид:
A; B;…:- K, L,…
С учетом этих соглашений формула
(человек(адам) & человек(ева)) &((человек(Х) # ~мать(Х,Y)) # ~человек(Y))
записывается так:
человек(адам):-.
человек(ева):-.
человек(Х):- мать(Х,Y), человек(Y).
Это выглядит уже довольно знакомо. В действительности, это выглядит в точности как определение на Прологе того, что значит быть человеком. Однако другие формулы дают более загадочный результат. Так, для примера о выходном дне имеем:
выходной(Х); работает(крис,X):-.
выходной(Х); сердитый(крис); унылый(крис):-.
Сразу не так очевидно, чему это может соответствовать в Прологе. Этот вопрос будет подробнее рассмотрен в следующем разделе.
В приложении В представлена программа на Прологе, печатающая дизъюнкты в рассмотренном здесь виде. Так, дизъюнкты, приведенные в конце предыдущего раздела, в соответствии с принятыми соглашениями печатаются программой в следующем виде:
человек(f1(X)); король(Х):-.
король(Х):- почитает(f1(Х),Х).
10.4. Принцип резолюций и доказательство теорем
Теперь, когда мы имеем способ, позволяющий представлять формулы исчисления предикатов в такой аккуратной и привлекательной форме, рассмотрим, что можно делать с ними далее. Очевидно, можно исследовать вопрос о том,
следует ли что-либо интересное из некоторой заданной совокупности высказываний. То есть интересно исследовать, к каким
следствиям они приводят. Высказывания, которые исходно считаются истинными, называются
аксиомами или
гипотезами, а высказывания, которые следуют из них, называются
теоремами. Введенные понятия согласуются с терминологией, используемой при описании такого подхода к математике, когда работа математика представляется как процесс получения все новых и новых интересных теорем из таких хорошо аксиоматизированных областей, какими являются теория множеств и теория чисел. В этом разделе будут кратко рассмотрены вопросы получения интересных следствий для заданного множества высказываний, то есть вопросы доказательства теорем.
В 60-х годах в этой области наблюдалась большая активность, связанная с возможностью использования вычислительных машин для автоматического доказательства теорем. Именно эта область научной деятельности, по-прежнему остающаяся источником новых идей и методов, дала жизнь идеям, легшим в основу Пролога. Одним из фундаментальных достижений того времени явилось открытие Дж. А. Робинсоном
принципа резолюций и его применение к автоматическому доказательству теорем. Резолюция – это
правило вывода, говорящее о том, как одно высказывание может быть получено из других. Используя принцип резолюций, можно полностью автоматически доказывать теоремы, выводя их из аксиом. Необходимо лишь решать, к каким из высказываний следует применять правило вывода, а правильные следствия из них будут строиться автоматически.
Правило резолюций разрабатывалось применительно к формулам, представленным в стандартной форме. Если заданы два дизъюнкта, связанных между собой определенным образом, то это правило породит новый дизъюнкт, являющийся следствием двух первых. Главная идея состоит в том, что, если одна и та же атомарная формула появляется как в левой части одного дизъюнкта, так и в правой части другого дизъюнкта, то дизъюнкт, получаемый в результате соединения этих двух дизъюнктов, из которых вычеркнута упоминавшаяся повторяющаяся формула, является следствием указанных дизъюнктов. Например,
Из
унылый(крист); сердитый(крис):- рабочий_день(сегодня), идет_дождь(сегодня).
и
неприятный(крис):- сердитый(крис), усталый(крис).
следует
унылый(крис); неприятный(крис):- рабочий_день(сегодня), идет_дождь(сегодня), усталый(крис).
На естественном языке это звучит так. Если сегодня рабочий день и идет дождь, то Крис – унылый или сердитый. Кроме того, если Крис сердитый и усталый, то он неприятен. Поэтому, если сегодня рабочий день, идет дождь и Крис усталый, то Крис является унылым или неприятным.
В действительности, мы сильно упростили ситуацию, опустив два момента. Прежде всего, ситуация усложняется, когда дизъюнкты содержат переменные. В такой ситуации две атомарные формулы не обязательно должны быть идентичными – они должны быть лишь «сопоставимы». Кроме того, дизъюнкт, являющийся следствием двух других дизъюнктов, получается в результате их соединения (с удалением повторяющейся формулы) с помощью некоторой дополнительной операции. Эта операция включает в
себя «конкретизацию» переменных до такой степени, чтобы две сопоставляемые формулы стали идентичными. Используя терминологию Пролога, можно сказать, что, если имелось два дизъюнкта, представленных в виде структур, и было выполнено сопоставление соответствующих подструктур, то результат соединения этих структур и был бы представлением нового дизъюнкта. Второе упрощение состоит в том, что в общем случае, правило резолюций допускает сопоставление нескольких литералов в правой части одного дизъюнкта с
несколькими литералами в левой части другого дизъюнкта. Здесь будут рассматриваться лишь примеры, когда из каждого дизъюнкта выбирается один литерал.
Рассмотрим один пример применения правила резолюций при наличии переменных:
человек(f1(Х)); король(Х):-. (1)
король(Y):- почитает(f1(Y),Y). (2)
почитает(Z,артур):- человек(Y). (3)
Два первых дизъюнкта представляют стандартную форму формулы, которую можно выразить так: «если каждый человек почитает кого-то, то этот кто-то – король». Переменные переименованы для удобства объяснения. Третий дизъюнкт выражает высказывание о том, что каждый человек почитает Артура. Применяя правило резолюций к (2) и (3) (сопоставляя два соответствующих литерала), получаем:
король(артур):- человек(f1(артур)). (4)
(
Y в (2) сопоставлен с
артур в (3), a
Z в (3) сопоставлен с
fl(Y) в (2)). Теперь можно применить правило резолюций к (1) и (4), что дает:
король(артур); король(артур):-.
Это эквивалентно факту, гласящему, что Артур является королем.
В формальном определении метода резолюций процедура «сопоставления», на которую мы неформально ссылались, называется
унификацией. Интуитивно, множество атомарных формул
унифицируемо, если эти формулы могут быть сопоставлены друг с другом как структуры языка Пролог. В действительности, как это будет показано в одном из следующих разделов, процедура сопоставления, используемая в большинстве реализаций языка Пролог, не совпадает в точности с унификацией.
Как можно использовать метод резолюций для доказательства конкретных утверждений? Один из возможных способов состоит в том, чтобы последовательно, шаг за шагом, применять правило резолюций к имеющимся гипотезам и посмотреть, не появилось ли при этом то, что мы хотим доказать. К сожалению, нельзя гарантировать, что это в конце концов произойдет, даже если интересующее нас высказывание действительно следует из имеющихся гипотез. Так, например, в последнем примере нельзя вывести простой дизъюнкт
король(артур), исходя из данного множества дизъюнктов и используя лишь указанный метод, несмотря даже на то, что это очевидное следствие. Следует ли отсюда, что метод резолюций не является достаточно мощным средством для наших целей? К счастью, ответом на этот вопрос является «нет», так как можно переформулировать постановку задачи таким образом, что метод резолюций гарантированно сможет решить ее, если это в принципе возможно.
Метод резолюций имеет одно важное формальное свойство – он является
полным для доказательства несовместности множества дизъюнктов. Это значит, что если множество дизъюнктов
несовместно, то используя метод резолюций всегда можно вывести из данного множества дизъюнктов пустой дизъюнкт:
:-.
Кроме того, так как метод резолюций является
корректным, то единственное, что он может вывести в такой ситуации – это пустой дизъюнкт. Множество формул несовместно, если не существует интерпретации предикатов, констант и функциональных символов, делающей истинными одновременно все эти формулы. Пустой дизъюнкт является логическим выражением
ложности - он представляет высказывание, которое ни при каких условиях не может быть истинным. Таким образом, метод резолюций наверняка определит, когда заданное множество формул является несовместным, выведя пустой дизъюнкт, являющийся выражением противоречия.
Каким образом это свойство метода резолюций может помочь нам? Имеет место следующий факт:
Если множество формул {
А1, A2,…, Аn} совместно, то формула
В является следствием формул {
Al, A2,…, An} тогда и только тогда, когда множество формул {
А1, A2,…, Аn ⌉
В} - несовместно.
Таким образом, если множество гипотез совместно, то необходимо лишь добавить к нему дизъюнкты, соответствующие отрицанию высказывания, которое следует доказать. Резолюция даст пустой дизъюнкт в точности тогда, когда доказываемое высказывание следует из данных гипотез. Дизъюнкты, добавляемые к множеству гипотез, называются
целевыми дизъюнктами. Отметим, что целевые дизъюнкты ничем не отличаются от гипотез – и те и другие являются дизъюнктами. Так что, если задано множество дизъюнктов {
А1, А2, …,
Ап} и требуется проверить несовместность этого множества дизъюнктов, то в действительности невозможно определить, идет ли речь о доказательстве того, что ⌉
А1 следует из
A2,
А3, …,
Ап или что ⌉
А2 следует из
A1, A3, …,
Аn, или что ⌉
А3 следует из
А1, А2, A4,…,
Аn и так далее. Именно это является причиной того, что необходимо указывать какие дизъюнкты в действительности являются целевыми дизъюнктами. Для системы, использующей метод резолюций, все перечисленные задачи эквивалентны.
Легко увидеть, как можно получить пустой дизъюнкт в примере с королем Артуром, если добавить целевой дизъюнкт:
:- король(артур). (5)
(это дизъюнкт для
~король(артур)). Ранее уже было показано, как дизъюнкт
король(артур); король(артур):-. (6)
может быть выведен из гипотез. Применяя правило резолюций к (5) и (6) (сопоставляя любую из атомарных формул в (5)), получаем:
король(артур):-. (7)
И наконец, резолюция дизъюнктов (6) и (7) дает
:-.
Таким образом, использование метода резолюций позволило доказать следствие, что Артур является королем.
Полнота метода резолюций является полезным математическим свойством. Это свойство означает, что, если некоторый факт следует из гипотез, то имеется возможность доказать его истинность (показав несовместность множества дизъюнктов, содержащего гипотезы и отрицание доказываемого факта)» используя для этого метод резолюций. Однако, когда мы говорим, что методом резолюций можно вывести пустой дизъюнкт, это значит, что существует последовательность шагов, на каждом из которых правило резолюций применяется к аксиомам или к дизъюнктам выведенным на предыдущих шагах, и эта последовательность заканчивается выводом дизъюнкта, не содержащего литералов. Единственная проблема – найти соответствующую последовательность шагов. Так как, хотя метод резолюций и говорит о том, как получить следствие двух дизъюнктов, он не сообщает, какие дизъюнкты выбрать для очередного шага и какие литералы в этих дизъюнкциях необходимо «сопоставить». Обычно, если имеется большое количество гипотез, то существует и много вариантов выбора среди них. Более того, на каждом шаге выводится новый дизъюнкт и он тоже становится кандидатом на участие в последующей обработке. Большинство из имеющихся возможностей выбора дизъюнктов и литералов в них не имеют отношения к решаемой задаче и, если не производить тщательного отбора среди кандидатов, то можно потратить слишком много времени на бесплодные поиски, а путь, ведущий к решению, так и не найти.
На решение этих вопросов направлено много различных улучшений исходного принципа резолюций. В следующем разделе рассматриваются некоторые из них.
10.5. Хорновские дизъюнкты
Рассмотрим теперь модификацию метода резолюций, разработанную для случая, когда все дизъюнкты имеют некоторый определенный вид – когда они являются
хорновскими дизъюнктами, Хорновский дизъюнкт – это дизъюнкт, содержащий не более одного литерала без отрицания. Оказывается, что если процедура доказательства теорем используется для определения значений вычислимых функций, то вполне достаточно использовать для этого лишь хорновские дизъюнкты. Так как метод резолюций в случае хорновских дизъюнктов также является относительно простым, то естественно выбрать хорновские дизъюнкты в качестве основы для процедуры доказательства теорем, применяемой в
практической системе программирования, Рассмотрим коротко, что представляет метод резолюций, если ограничиться хорновскими дизъюнктами.
Прежде всего, очевидно, что существуют два вида хорнов-ских дизъюнктов – дизъюнкты, содержащие один литерал без отрицания и дизъюнкты, не содержащие таких литералов. Будем называть эти два типа хорновских дизъюнктов соответственно дизъюнктами с
заголовком и дизъюнктами
без заголовка. Следующие примеры иллюстрируют указанные типы дизъюнктов (необходимо помнить, что литералы без отрицания записываются слева от знака ':-'):
холостяк(Х):- мужчина(Х), неженат(Х).
:- холостяк(Х).
В действительности, рассматривая множества хорновских дизъюнктов (включая целевые утверждения), необходимо выделять лишь такие множества, в которых все дизъюнкты за исключением одного имеют заголовки. Это значит, что каждая разрешимая задача (задача доказательства теоремы), которая может быть выражена с помощью хорновских дизъюнктов, может быть представлена в таком виде, что:
• Имеется только один дизъюнкт без заголовка. Все остальные дизъюнкты имеют заголовки.
Так как совершенно не имеет значения, какие дизъюнкты считать целевыми, то можно принять решение рассматривать дизъюнкт без заголовка как целевой, а все остальные дизъюнкты – как гипотезы. Такое решение выглядит довольно естественно.
Почему мы должны рассматривать лишь такие совокупности хорновских дизъюнктов, которые вписываются в эту схему? Во-первых, легко видеть, что для того, чтобы задача была разрешима, необходимо наличие по крайней мере одного дизъюнкта без заголовка. Это объясняется тем, что в результате применения правила резолюций к двум хорновским дизъюнктам с заголовками вновь получается хорновский дизъюнкт с заголовком. Поэтому, если все дизъюнкты имеют заголовки, то единственное что можно делать – это выводить другие дизъюнкты с заголовками. Так как пустой дизъюнкт не имеет заголовка, то он никогда не будет выведен. Второе требование – это необходим лишь один дизъюнкт без заголовка – обосновать несколько труднее. Од-нако оказывается, что, если среди аксиом имеют несколько дизъюнктов без заголовка, то каждое доказательство нового дизъюнкта методом резолюций может быть преобразовано в доказательство, в котором используется не более чем один из них. Поэтому, если пустой дизъюнкт следует из данного множества аксиом, то он следует и из его подмножества, содержащего все дизъюнкты с заголовками и не более одного дизъюнкта без заголовка.
10.6. Пролог
Давайте подведем итог и посмотрим, как Пролог вписывается в рассмотренную выше схему. Как было показано, некоторые формулы, представленные в виде совокупности дизъюнктов, выглядят в точности так же, как и утверждения в Прологе, в то время как другие формулы имеют несколько отличный вид. Формулы, имевшие вид утверждений Пролога, есть в действительности не что иное, как формулы, представимые в виде хорновских дизъюнктов. При записи хорновского дизъюнкта в соответствии с принятыми соглашениями, количество атомарных формул слева от знака ';-' не может превышать одну. В общем случае, дизъюнкты могут иметь несколько таких формул (они соответствуют литералам, представляющим атомарные формулы без отрицания). В Прологе непосредственно можно представить только хорновские дизъюнкты. Утверждения программы на Прологе соответствуют хорновским дизъюнктам с заголовком (в рамках определенной процедуры доказательства теорем). А что в Прологе соответствует целевому дизъюнкту? Очень просто, вопрос в Прологе
?-
A1, A2,…, An
в точности соответствует хорновскому дизъюнкту без заголовка:-
A1, A2,…,
Ап
В предыдущем разделе уже говорилось о том, что для решения любой задачи, представленной с помощью хорновских дизъюнктов, достаточно иметь в точности один дизъюнкт без заголовка. В Прологе это соответствует ситуации, когда все утверждения «программы» имеют заголовки и в каждый момент времени рассматривается лишь одно целевое утверждение (не имеющее заголовка).
Пролог-система основывается на процедуре доказательства теорем методом резолюций для хорновских дизъюнктов. Конкретная стратегия, используемая при этом, является разновидностью
линейной входной резолюции. При использовании этой стратегии, выбор дизъюнктов для резолюции на каждом шаге ограничен следующими условиями. Процедура начинается с применения правила резолюций к целевому дизъюнкту и к одной из гипотез, что дает новый дизъюнкт. Затем производится резолюция этого дизъюнкта и одной из гипотез, что дает еще один новый дизъюнкт. Затем правило резолюций применяется к последнему полученному дизъюнкту и к одной из гипотез и так далее. На каждом этапе правило резолюций применяется к последнему из вновь полученных дизъюнктов и к одной из исходных гипотез. Правило резолюций никогда не применяется, если оба дизъюнкта были выведены на предыдущих этапах или являются исходными гипотезами. С точки зрения Пролога, последний выведенный дизъюнкт можно рассматривать как конъюнкцию целевых утверждений, которые еще надо доказать (согласовать с базой данных). В начальный момент это вопрос, а в конце процесса, при благоприятных условиях,- это пустое утверждение. На каждом этапе ищется утверждение, заголовок которого сопоставим с одним из целевых утверждений. Если необходимо, происходит конкретизация переменных. Удаляется целевое утверждение, с которым произошло сопоставление, а затем к целевым утверждениям, которые необходимо согласовать, добавляется тело найденного утверждения, в котором произведена конкретизация переменных. Так, например, начав с вопроса
:- мать(джон,Х), мать(Х,Y).
и утверждения
мать(U,V):- родитель(U,V), женщина(V).
получаем
:- родитель(джон,Х), женщина(Х), мать(Х,Y).
В действительности, используемая в Прологе стратегия является более ограниченной по сравнению с общей линейной входной резолюцией. В этом примере для сопоставления был выбран первый литерал целевого дизъюнкта, но с таким же успехом можно было бы сопоставить и второй литерал. В Прологе выбор литерала для сопоставления всегда происходит одним и тем же способом – всегда выбирается первый литерал в целевом дизъюнкте. Кроме того, новые целевые утверждения, полученные при использовании некоторого утверждения помещаются в начале целевого дизъюнкта. Это значит, что Пролог завершит доказательство согласованности всех подцелей прежде чем перейдет к обработке следующих целей.
Все сказанное относится к событиям, происходящим после того, как Пролог выбрал утверждение для сопоставления с первой целью. Но как организуется исследование альтернативных утверждений для удовлетворения той же самой цели? В Прологе используется стратегия
поиска вглубь, а
не поиска вширь. Это значит, что Пролог в каждый момент времени рассматривает лишь одну альтернативу, упорно следуя подразумеваемому предположению о правильности сделанного выбора. Выбор утверждений для каждой цели производится в строго фиксированном порядке, а пересмотр выбранных ранее утверждений происходит лишь в случае, когда все последующие попытки не привели к решению. В качестве альтернативы можно было бы предложить стратегию, при которой система запоминает одновременно все альтернативные пути решения. При этом система переходила бы по кругу от одной альтернативы к другой, прослеживая каждую альтернативу на небольшую глубину, а затем переходя к следующей. Такая стратегия поиска вширь имеет одно преимущество – если решение существует, то оно обязательно будет найдено. Используемая в Прологе стратегия поиска вглубь может привести к «зацикливанию» и, следовательно, никогда не будут исследованы некоторые альтернативы. С другой стороны такая стратегия намного проще и требует меньших затрат памяти при реализации на вычислительных машинах с традиционной архитектурой.
И наконец, небольшое замечание о возможных различиях между процедурой сопоставления, используемой в Прологе, и процедурой унификации, используемой в методе резолюций. Большинство Пролог-систем допускают обращение с вопросами, подобными следующему:
равны(X,X).
?- равны(foo(Y),Y).
Это возможно по той причине, что в Прологе разрешается сопоставлять некоторый терм с его собственным подтермом. В этом примере
foo(Y) сопоставляется с
Y, который сам является частью этого терма. В результате этого
Y становится равным
foo(Y) что в свою очередь равно
foo(foo(Y)) (учитывая значение
Y), что равно
foo(foo(foo(Y))) и так далее. Так что в результате
Y обозначает некоторую бесконечную структуру. Заметим, что хотя Пролог-системы могут допускать использование подобных конструкций, большинство из них будут не в состоянии напечатать окончательный результат сопоставления. В соответствии с формальным определением унификации, подобного вида «бесконечные термы» никогда не должны появляться. Так что, Пролог выполняет эту процедуру неправильно в сравнении с тем, как это делается при доказательстве теорем методом резолюций. Для того чтобы сделать процедуру корректной, необходимо добавить проверку условия, заключающегося в том, что переменная не может быть конкретизирована некоторым значением, содержащим эту переменную. Такая проверка,
проверка на вхождение, не представляла бы труда для ее реализации, но значительно замедляла бы выполнение программы на Прологе. Так как число программ, в которых может встретиться такая конструкция, невелико, то в большинстве реализаций такая проверка просто не делается.
10.7. Пролог и логическое программирование
В нескольких последних разделах было показано, как используются в Прологе идеи доказательства теорем. Можно видеть, что наши программы довольно похожи на гипотезы о проблемной области, а вопросы очень похожи на теоремы, которые нам хотелось бы доказать. Таким образом, программирование на Прологе имеет мало общего с процессом выдачи машине указаний о том, что и когда следует делать. Оно скорее состоит в передаче машине информации, которая предполагается истинной, и обращении к ней с вопросами о возможных следствиях из этой информации. Идея о том, что программирование должно выглядеть именно так, привлекательна и она привела многих специалистов к исследованию концепции
логического программирования, то есть
программирования на языке логики, как практической альтернативы обычному. Такой подход резко отличается от использования традиционных языков программирования подобных Фортрану или Лиспу, при программировании на которых необходимо как можно более подробно описать что и когда должна делать вычислительная машина. Преимущества логического программирования должны проявиться в том, что программы станут более понятными. Они не будут содержать затрудняющие понимание детали относительно того
как решать задачу, а скорее будут напоминать описание того,
что собой представляет результат решения. Кроме этого, если программа выглядит как описание (спецификация) того, что предполагается получить, то и относительно проще проверить (вручную или, возможно, используя какие-то автоматические средства), делает ли она в действительности то, что требуется. Подводя итог, можно сказать: преимущества языка логического программирования были бы следствием того, что программы обладают как
декларативной семантикой, так и
процедурной. Мы бы знали
что программа вычисляет, а не
как она это делает. Мы не будем здесь рассматривать логическое программирование вообще. Интересующемуся этим вопросом читателю рекомендуем обратиться к книге Ко-walski R.
Logic for Problem Solving, North Holland, 1979.
Давайте рассмотрим Пролог как кандидата на место языка логического программирования и посмотрим, насколько хорошо он для этого подходит. Прежде всего, ясно, что некоторые программы на Прологе действительно представляют описание проблемной области на языке логики. Запись:
мать(Х,Y):- родитель(Х,Y), женщина(Y).
можно рассматривать как описание того, что значит быть матерью (это значит быть женщиной и быть одним из родителей). Это утверждение выражает высказывание, которое, как мы предполагаем, должно быть истинным, и, кроме того, указывает, как показать, что кто-то является матерью. Аналогично, утверждения;
присоединить([], X, X).
присоединить([А|В],С[А|D]):- присоединить (B,C,D).
говорят о том, что собой представляет добавление одного списка в начало другого списка. Если пустой список помещается в начало некоторого списка
X, то результатом будет
X. С другой стороны, если непустой список присоединяется в начало некоторого списка,
то головой списка-результата будет голова присоединяемого списка. Кроме того, хвостом списка-результата будет список, получаемый в результате присоединения хвоста первого списка ко второму списку. Можно считать, что эти утверждения описывают отношение присоединить, так же как и (возможно) то, как в действительности присоединить один список к другому.
Это все верно лишь для некоторых программ на Прологе. А какое возможное логическое значение можно приписать утверждениям подобным следующим?
memberl(X, List):- var(List),!,fail.
memberl(X,[X|_]).
memberl(X,[_|List]):- memberl(X,List).
print(0):-!.
print(N):- write(N), N1 is N-1, print(N1).
noun(N):- name(N,Name1), append(Name2, [ll5],Namel), name(RootN,Name2), noun(RootN).
implies(Assum,Concl):-asserta(Assum), call(Concl), retract(Concl).
Эта проблема имеет место для всех «встроенных» предикатов, используемых в программах на Прологе. Предикат подобный
Var(List) ничего не говорит о принадлежности элемента списку, а проверяет состояние переменной (является ли указанная переменная неконкретизированной), возникающее в процессе доказательства. Аналогично, «отсечение» говорит кое-что о доказательстве высказывания (выбор каких альтернатив можно игнорировать), а не о самом этом высказывании. Два указанных «предиката» можно рассматривать как способ выражения
управляющей информации о том, как должно выполняться доказательство. Точно так же, предикаты подобные
write(N) не имеют каких-либо интересных логических свойств, но заранее предполагают, что в ходе доказательства будет достигнуто определенное состояние (
N конкретизируется) и начинают обмен информацией с программистом, сидящим за терминалом. Целевое утверждение
name(N, Name1) говорит кое-что о внутренней структуре объекта, который в исчислении предикатов был бы неделимым символом. В Прологе можно преобразовывать символы в строки литер, структуры в списки и в утверждения. Эти операции нарушают замкнутость высказываний исчисления предикатов. В последнем примере, использование предиката
asserta означает, что правило, о котором идет речь, добавляет что-то к множеству аксиом. В логике каждое правило или факт сохраняет истинность независимо от того, существуют ли какие либо другие факты или правила. В данном случае мы имеем дело с правилом, которое грубо нарушает этот принцип. Кроме того, если мы используем это правило, то окажемся в ситуации, когда на разных этапах доказательства имеется различное множество аксиом. Наконец, то что в одном из правил предполагается использовать терм
Concl в качестве целевого утверждения, означает, что допускается, чтобы переменная обозначала высказывание, встречающееся в некоторой аксиоме. Такая конструкция не относится к числу тех, которые могут быть выражены на языке исчисления предикатов, но напоминает возможности, которые могут быть представлены
логикой более высокого порядка.
На приведенном примере можно видеть, что некоторые программы на Прологе, можно понять
лишь в терминах, описывающих что и когда может произойти при выполнении программ и каким образом программы сообщают системе о том, что нужно делать. В качестве крайнего случая, можно привести программу для генатом представленную в
гл. 7. Вряд ли вообще может быть дана какая-либо декларативная интерпретация этой программы. Имеет ли тогда смысл рассматривать Пролог как язык логического программирования? Можем ли мы реально надеяться на какие-то преимущества логического программирования применительно к нашим программам на Прологе? На оба этих вопроса можно дать положительный ответ и основанием для этого служит то, что приняв соответствующий стиль программирования, мы все же можем получить некоторые преимущества благодаря связи Пролога с логикой. Ключевым моментом является использование разбиения программ на части, ограничивающие использование нелогических операций небольшим множеством утверждений. В качестве примера в гл. 4 было показано, как в некоторых случаях «отсечение» может быть заменено предикатом
not. В результате таких замен, программу, содержавшую целый ряд «отсечений» можно свести к программе, в которой «отсечение» используется лишь однажды (в определении
not). Использование предиката
not даже если он не совсем точно соответствует логическому '~' позволяет восстановить часть логической основы программы. Аналогично, ограничивая область применения предикатов
asserta и
retract определениями небольшого числа предикатов (таких как
генатом и
найтивсе), можно добиться того, что в целом программа становится более понятной по сравнению с программой, в которой эти предикаты свободно используются где угодно.
Таким образом, с появлением Пролога конечная цель, состоящая в создании языка логического программирования, не была достигнута. Тем не менее, Пролог дал практическую систему программирования, обладающую в некоторой степени свойствами, которыми должен обладать язык логического программирования – ясностью и декларативностью. Между тем ведутся работы по разработке улучшенных версий Пролога, которые более близки к логике чем имеющиеся в настоящее время. К числу наиболее важных работ в этой области относятся работы по созданию практической системы программирования, в которой нет необходимости использовать «отсечение» и которая имеет вариант предиката
not точно соответствующий логическому понятию отрицания.
ГЛАВА 11. ПРОГРАММНЫЕ ПРОЕКТЫ НА ПРОЛОГЕ
В этой главе рассматривается перечень программных проектов, которые вы могли бы попытаться осуществить для развития навыков программирования на Прологе. Некоторые из этих проектов довольно просты, зато другие вполне могут быть предложены в качестве «курсовой работы» в рамках учебного курса по Прологу. Более простые проекты следует использовать как дополнение к упражнениям, приведенным в предыдущих главах. В целом при перечислении проектов мы не придерживались какого-то определенного порядка, хотя те из них, что содержатся в разд. 11.2, в большей мере допускают расширения, содержат вызов честолюбию, но и требуют некоторой подготовки или знакомства с литературой по различным вопросам искусственного интеллекта и информатики. Небольшая часть проектов требует знаний из определенных разделов науки, поэтому если вы не специалист в области математической физики, то не отчаивайтесь, если не сможете написать программу дифференцирования трехмерных векторных полей.
Целая подборка Пролог-программ опубликована в отчете Coehlo H., Cotta J. С, Pereira L. M.
How to solve it with Prolog, Laboratorio Nacional de Engenharia Civil, Lisbon, Portugal. В нем содержится свыше ста небольших примеров, задач и упражнений из таких областей как вывод умозаключений на основе базы данных, естественный язык, символьное решение уравнений, и т. д. Этот отчет по своему характеру не рассчитан на использование для обучения, поэтому приведенные в нем Пролог-программы снабжены лишь краткими пояснениями.
11.1. Простые проекты
1.Определить предикат
лин для «линеаризации» списка путем построения нового списка, не содержащего списков в качестве элементов, но включающего все атомы исходного списка. Например, следующее целевое утверждение будет согласовано с базой данных:
?- лин([а,[b,с],[[d],[],е]], [a,b,c,d,e]).
Существует по меньшей мере шесть различных способов написания этой программы.
2. Составить программу для вычисления интервала (в днях) между двумя датами, заданными в формате День-Месяц, считая что обе они относятся к одному и тому же невисокосному году. Заметим, что '-' это просто инфиксная форма задания 2-х местного функтора. Например, следующее целевое утверждение будет
согласовано с базой данных:
интервал(3-март, 7-апрель, 35).
3. В главе 7 приведены сведения, достаточные для составления программ дифференцирования и упрощения арифметических выражений. Усовершенствуйте эти программы так, чтобы они могли обрабатывать выражения с тригонометрическими функциями и, если есть желание, с операциями дифференциальной геометрии, такими как div, grad и rot.
4. Написать программу, осуществляющую символическое отрицание выражения исчисления высказываний. Это выражение строится из атомов, одноместного функтора
not и двухместных функторов
and (и),
or (или) и
implies (импликация). Задать соответствующие описания операторов для этих функторов. Выражение, являющееся результатом отрицания, должно быть представлено в простейшей форме, когда
not применяется только к атомам. Например, отрицание выражения
р implies (q and not r)
должно выглядеть следующим образом: р and (not q or r)
5. Частотный словарь – это перечень слов, встречающихся в данном тексте, выписанный в алфавитном порядке с указанием числа вхождений каждого слова в тексте. Написать программу составления частотного словаря по списку слов, представленных в виде строк Пролога. Учтите, что строки – это списки кодов ASCII.
6. Написать программу, воспринимающую простые английские предложения, имеющие следующий формат

На основе ранее введенных предложений программа должна выдавать соответствующий ответ (yes (да), no (нет), ok (принято), unknown (неизвестно)). Например,
John is a man.
ok
A man is a person.
ok
Is John a person?
yes
Is Mary a person?
unknown
Каждое предложение должно транслироваться в утверждение Пролога, которое затем в зависимости от его характера, либо помещается в базу данных, либо выполняется как целевое. Так, результаты трансляции предложений приведенного выше примера выглядят следующим образом:
man(john).
person(X):- man(X).?- person (john).?- person(mary).
Если это окажется удобным, используйте правила грамматики. Головное утверждение
для управления диалогом может иметь вид:
беседа:- repeat, read (Предложение), анализ(Предложение, Утверждение), ответ(Утверждение), Утверждение = stop.
7. Альфа-бета (α-β) алгоритм – это один из методов обхода дерева игры, который упоминается во многих книгах по искусственному интеллекту. Реализуйте альфа-бета алгоритм на Прологе.
8. Задача об N-ферзях также широко распространена в литературе по программированию. Реализовать программу нахождения всех способов размещения 4 ферзей на шахматной доске размером 4?4, причем так, чтобы ни один ферзь не угрожал другому. Один из возможных подходов состоит в создании генератора перестановок, который затем проверяет каждую перестановку, чтобы убедиться, что все ферзи размещены правильно.
9. Написать программу, которая переписывает выражение исчисления высказываний (см. задачу 4), заменяя все вхождения
and,
or,
implies и
not единственной связкой
nand. Определение связки nand задается следующим тождеством
(α nand β)⌉≡(α∧β)
10. Один из способов представления целых положительных чисел состоит в том, чтобы представлять их в виде термов Пролога с использованием целого числа 0 и функтора
S с одним аргументом. Так, число 0 представляет само себя, 1 представляется как
S(0), 2 как
S(S(0)) и т. д. (каждое число представляется в виде функтора S примененного к представлению числа, на единицу меньшего, чем данное). Написать определение стандартных арифметических операций: сложение, умножение и вычитание, использующих указанное представление чисел. Например, нужно определить предикат
plus который действует следующим образом:
?- plus(s(s(0)),s(s(s(0))),X)
X=s(s(s(s(s(0)))))
(2+3=5). Для вычитания нужно ввести соглашение о том, что делать, когда результат операции не является положительным целым числом. Определите также предикат «меньше чем». Какие аргументы нужно конкретизировать, чтобы ваши определения работали правильно? Что произойдет, если этого не сделать? Как это соотносится со стандартными арифметическими операциями Пролога? Попытайтесь определить более сложные арифметические операции, такие как деление нацело и извлечение квадратного корня.
11.2. Более сложные проекты
Может показаться, что некоторые проекты данного раздела невозможно выполнить до конца, однако все они были реализованы на Прологе. Некоторые из них просто являются усложнениями программ, которые рассматривались ранее, а другие – совершенно новые и требуют знакомства с литературой по искусственному интеллекту или по информатике.
1. Дана карта, которая описывает дороги, соединяющие города. Написать программу планирования поездки между двумя городами, которая выдает расписание предполагаемой поездки. Данные, описывающие карту, могут включать расстояния, состояние дороги, уклон дороги, возможность заправки топливом вдоль разных дорог.
2. В существующих Пролог-системах встроенные арифметические операции предусмотрены только для целых чисел. Разработайте пакет программ, поддерживающий арифметические операции над рациональными числами, представленными в виде целой и дробной частей или в виде мантиссы и порядка.
3. Написать процедуры обращения и умножения матриц.
4. Компиляцию с языка высокого уровня на язык низкого уровня можно представить себе как последовательное преобразование синтаксических деревьев. Написать такой компилятор сначала для компиляции арифметических выражений. Затем добавить управляющие структуры (типа
if-
then-else). Точное соблюдение синтаксиса ассемблера в данном случае не столь существенно. Например, арифметическое выражение
х+1 может быть «упрощено» до ассемблерной операции
inc x, где
inc определена как одноместная операция. Проблема распределения регистров может быть отложена на потом за счет предположения, что объектный код предназначен для выполнения на машине с магазинной (стековой) памятью (безадресная машина),
5. Разработать представление для сложной настольной игры, такой как шахматы или го, и разобраться в том, как возможности Пролога в части сопоставления образцов могут быть использованы при реализации стратегий для этих игр.
6. Разработать формализм для описания набора аксиом, например, из теории групп, евклидовой геометрии, денотационной семантики, и исследовать проблему создания программы доказательства теорем для этих областей.
7. Интерпретатор утверждений Пролога может быть написан на самом Прологе. Напишите интерпретатор, реализующий иные семантики выполнения Пролога, такие как более гибкий порядок выполнения (вместо жесткого слева-направо), возможно, с использованием какого-нибудь «расписания» или планировщика.
8. Ознакомиться по литературе по искусственному интеллекту с вопросом построения планов решения задач, и реализовать генератор планов.
9. Решить с помощью средств Пролога задачу интерпретации контурного рисунка в терминах некоторой лежащей в его основе сцены. Характеристики рисунка могут быть помечены переменными, представляющими соответствующие характеристики сцены. Тогда рисунок соответствует набору ограничений, которым должны удовлетворять эти переменные.
10. Написать программу, которая, используя правила грамматики, осуществляет разбор предложений вида;
Fred saw John.
Магу was seen by John.
Fred told Mary to see John.
John was believed to have been seen by Fred.
Was John believed to have told Mary to see Fred?
11. В исследованиях по искусственному интеллекту используется система специальных правил (продукций), которая представляет собой последовательность правил вида «
Если ситуация,
то действие». Как оказалось, в задачах искусственного интеллекта с помощью таких правил удобно описывать «экспертные знания». Например, для реальных экспертных систем, использующих такие правила, типичны следующие предложения, содержащие «экспертные знания»:
Фармакология: Если агент X есть четырехвалентная соль аммония и противоаритмическое средство, а агент Y есть салицилат, то X и Y будут реагировать, порождая повышенную абсорбцию за счет образования ионной пары.
Игра в шахматы; Если белый король может быть придвинут к черному слону и при этом расстояние от белого короля до этого слона более одной клетки, то тогда этот слон в безопасности.
Медицина: Если культура высевается из крови и граммреакция организма отрицательна и морфологически организм есть палочка, и пациент является «хозяином» организма, то имеется 60% шансов на то, что этот организм есть
Pseudomonas aeruqinosa.
Напишите Пролог-программу интерпретации набора продукционных правил. Рассмотрите такие области как определение растений или животных по характерным признакам. Например, подобное правило из ботаники могло бы выглядеть так:
Если растение имеет стебель квадратного сечения, парные листья, двухгубчатые закрытые цветы, а его плод состоит из четырех маленьких орешков, заключенных в кожуру, то это растение принадлежит семейству
Labiatae.
Таким образом, если программа спросит нас: «у цветка квадратный стебель?», то ответив «нет» мы тем самым исключаем возможность того, что он принадлежит семейству
Labiatae.
12. Написать программу переводящую определенный класс предложений на английском языке на язык исчисления предикатов.
13. Написать программу доказательства теорем в исчислении предикатов.
14. Написать программу-«психиатр», которая выдает ответы, основанные на ключевых словах, имеющихся во вводимой информации. Эта программа напоминает ту, что рассматривалась в гл. 3, и которая заменяла ключевые слова в предложении на другие слова. Типичный диалог такой программы мог выглядеть следующим образом (ответы программы выделены курсивом):
What is your problem? На что жалуетесь?
This is too much work. Очень много работы.
What else do you regard as too much work? Что еще вы имеете в виду, говоря, что очень много работы?
Writing letters. Написание писем.
I see. Please continue.Понятно, продолжайте.
Also washing my mother's car. А также мытье машины моей матери.
Tell me more about your family. Расскажите подробнее о вашей семье.
Why should I? Зачем это?
Why should you what? Что зачем?
Здесь ключевыми словами были
this is, mother и
why. Недостаток подходящих ключевых слов вызывал ответ
I see. Please continue.
15. Написать программу, разбирающую предложения с сообщениями о событиях в некотором учреждении, такие как
«Smith will be in his office at 3 pm for a meeting.» (Смит будет в своем учреждении в 3 часа дня для участия в собрании). Программа должна выдавать на печать «суть» предложения, сообщая кто, где и когда, следующим образом:
who: smith Кто: Смит
where: office Где: контора
when: 3 pm Когда: 3 часа дня
what: meeting Что: собрание
Эта «суть» должна быть занесена в базу данных в виде утверждений, с тем чтобы можно было получить ответ на такие вопросы:
Where is Smith at 3 pm? Где Смит в 3 часа?
where: office Где: контора
what: meeting Что: собрание
16. Написать интерфейс для общения на естественном (английском) языке с файловой системой вашей ЭВМ, чтобы можно было получать ответы на такие вопросы:
How many files David own? Сколько файлов принадлежат Дейвиду?
Does Chris share PROG.MAC with David? Использует ли Крис файл PROG.MAC совместно с Дейвидом?
When did Bill change file Когда Билл изменил свой VIDEO.C? файл VIDEO.C?
Программа должна уметь опрашивать различные характеристики файловой системы, такие как принадлежность файлов и даты.
ПРИЛОЖЕНИЕ А. ОТВЕТЫ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
Сюда вошли предлагаемые авторами ответы на некоторые из упражнений, встречающихся в тексте. Для большинства упражнений по программированию редко существует единственный правильный ответ, и, вполне возможно, что у вас получится другой верный ответ, который несколько отличается от предложенного нами. В любом случае следует обязательно опробовать вашу программу на Пролог-системе, имеющейся в вашем распоряжении, чтобы практически проверить, работает она или нет. Но даже в том случае, если вы написали правильную, но отличающуюся от нашей программу, может оказаться поучительным потратить немного времени на изучение альтернативного подхода к решению той же самой задачи.
Упражнение 1.2. Здесь представлены возможные определения семейных отношений.
явл_матерью(М):- мать(М,Ребенок).
явл_отцом(О):- отец(О, Ребенок).
явл_сыном(Сын):- родитель(Род,Сын), Мужчина(Сын).
явл_сестрой(Сес,Ч):- родитель(Род,Сес), родитель(Род,Ч), женщина(Сес), различ(Сес,Ч).
дедушка, (Дед,X):- родитель(Род,Х), отец(Дед,Род).
брат_или_сестра (S1,S2):- родитель(Род,Б1), родитель(Род, S2), различ(S1,S2).
Заметим, что нам приходится использовать предикат
различ в определении предикатов
явл_сестрой и
брат_или_сестра. Это гарантирует нам, что система не будет считать, что кто-то может быть сестрой или братом самому себе. Дать определение предиката
различ на этом этапе вы не сможете.
Упражнение 5.2. Следующая программа циклически считывает символы (из текущего файла ввода) и печатает их, заменяя при этом все строчные буквы 'а' на 'b'.
go:- repeat, get0(C), deal_with(C), fail.
deal_with(97):-!, put(98).
deal_with(X):- put(X).
Наличие «отсечения» в первом правиле предиката
deal_with существенно (почему?). Числа 97 и 98 есть значения кодов ASCII для символов '
а' и '
b' соответственно.
Упражнение 6.2. Почему следующее определение предиката
get не работает, если целевое утверждение
get задано с конкретизированным аргументом?
get(X):- new_get(X), X›32.
new_get(X):- repeat, getO(X).
Предположим, мы задали Пролог-системе целевое утверждение get(97) (проверить, является ли следующий печатаемый символ строчной буквой 'а'?), тогда как на самом деле этот следующий символ есть '
b'. Чтобы согласовать
get(97), делается попытка согласовать
new_get(97). Цель
repeat успешно согласуется, но затем цель
get0(97) оказывается несогласуемой (так как следующий символ не 'а'). Тогда начинается возвратный ход. Цель
get0 не может быть повторно согласована, а цель
repeat - может. Итак, целевое утверждение
repeat снова согласуется с базой данных, и вновь делается попытка согласовать
get0(97). На этот раз, конечно, следующим символом будет тот, что следует за '
b'. Если это не '
а', то цель оказывается несогласуемой, a
repeat снова завершается успешно. Теперь будет проверяться следующий символ и так далее. Фактически происходит следующее: программа считывает новые и новые символы до тех пор пока она, наконец, не находит тот, что совпадает с аргументом. Но это не то, что должен делать предикат
get. Правильное определение предиката
get, которое обходит эту проблему, а также содержит «отсечение», устраняющее возможность повторного согласования
repeat выглядит следующим образом:
get(X):- repeat, get0(Y), 32‹Y,!, X-Y.
Упражнение 7.10. Вот программа, которая порождает пифагоровы тройки.
pythag(X,Y,Z):- intriple(X,Y,Z), Sumsq is Х*Х + Y*Y, Sumsq is Z*Z.
intriple(X,Y,Z):- is_integer(Sum), minus(Sum,X,Sum1), minus(Sum1,Y,Z).
minus(Sum,Sum,0).
minus(Sum,Dl,D2):- Sum›0, Suml is Sum-1, minus(Suml,Dl,D3), D2 is D3+1.
is_integer(0).
is_integer(N):- is_integer(N1), N is N1 + 1.
С помощью предиката
intriple программа порождает все возможные тройки чисел
X,
Y,
Z, а затем проверяет, является ли данная тройка чисел пифагоровой тройкой. Определение
intriple гарантирует, что рано или поздно все возможные тройки чисел будут порождены. Прежде всего порождается целое число, являющееся суммой
X,
Y и
Z. Затем с помощью недетерминированного предиката вычитания
minus из него порождаются значения
X,
Y и
Z.
Упражнение 9.1. Здесь приведена программа, транслирующая простое правило грамматики в процедуру на языке Пролог. При этом предполагается, что это правило не содержит; классов словосочетаний с дополнительными аргументами, целевых утверждений внутри фигурных скобок, а также дизъюнкций и отсечений.
?- op(255,xfx,--›).
трансляция ((P1--›P2), (Gl:-G2)):- левая_часть(Р1,S0,S,G1), правая_частъ(Р2,S0,S,G2).
левая_часть(Р0,S0,S,G):- nonvar(PO), tag(P0,S0,S,G).
правая_часть((Pl,P2),S0,S,G):-!, правая_часть(Р1,S0,S1,G1), правая_чacть(P2,S1,S,G2), и(G1, G2,G).
правая_часть(P,S0,S,true):- явл_списком(Р),!, присоединить(Р,S,S0).
правая_часть(P,S0,S,G):- tag(P,S0,S,G).
tag(P,S0,S,G):- atom(P), G =.. [P,S0,S].
и(true,G,G):-!.
и(G,true,G):-!.
и(G1,G2, (G1,G2)).
явл_списком([]):-!.
явл_списком([_ |_]).
присоединить([А|В],C,[A|D]):- присоединить(В,С,D).
присоединить([], Х,Х).
В этой программе переменные, начинающиеся с латинской буквы Р, используются для обозначения описаний словосочетаний (в виде атомов или списков слов) в правилах грамматики. Переменные, начинающиеся с G, обозначают целевые утверждения Пролога. Переменные, начинающиеся с S, обозначают аргументы целевых утверждений Пролога (которые представляют последовательности слов). Для тех, кто заинтересуется, ниже приведена программа, которая способна обрабатывать более общие случаи трансляции правил грамматики. Один из приемов приспособления Пролог-системы к обработке правил грамматики состоит в использовании измененной версии предиката
consult, где предложение вида
А--›B транслируется перед занесением его в базу данных.
?- op(251,fx,{).
?- op(250,fx,}).
?- op(255,XFX,>).
трансляция((Р0--›Q0), (P:- Q)):- левая_часть(P0,S0,S,P), правая_часть(Q0, S0,S,Q1), лин(Q1, Q).
левая_часть((NT,Ts),S0,S,P):- !, nonvar(NT), явл_списком(Тs), tag(NT,S0,Sl,P), присоединить(Ts, S0,S1).
левая_часть (NT,S0,S,P):- nonvar(NT), tag(NT,SO,S,P).
правая_часть((Х1,Х2),S0,S,Р):- правая_часть(Х1,S0,S1,Р1), правая_часть(X2,Sl,S,P2), и(Р1,Р2,Р).
правая_часть((Xl;X2),S0,S,(P1;P2)):-!, или(Xl,S0,S,P1), или(Х2,S0,S,Р2).
правая_часть(Р,S,S,Р):-!.
правая_часть(!,S,S,!):-!.
правая_часть(Ts,SO,S,true):- явл_списком(Тs),!, присоединить(Ts, S,S0).
правая_часть(Х,S0,S,P):- tag(X,S0,S,P).
или(Х,S0,S,Р):- правая_часть(X,S0a,S,Pa), (var(S0a), S0a=S,!, S0=S0a, P=Pa; P=(S0=S0a,Pa)).
tag(X,S0,S,P):- X =..[F|A], присоединить(А,[S0,S],АХ), P =.. [F|AX].
и(true,P,P):-!.
и(P,true,P):-!.
и(P,Q,(P,Q)).
лин(А,А):- var(A),!.
лин((А,В),С):-!, лин1(А,С,R), лин(В,R).
лин(А,А).
лин1(А,(А,R),R):- VAR(A),!.
лин1((А,В),С,R):-!, лин1(А,С,R1), лин1(В,R1,R).
лин1(A,(A,R),R)
.
явл_списком([]):-!.
явл_списком([_|_]).
присоединить([А|В],С,[А|D]):- присоединить(В,С,D).
присоединить([], X, X).
Упражнение 9.2. Определение универсальной версии предиката
phrase (словосочетание) выглядит следующим образом:
phrase(Cтип,Слова):- Стип =.. [Pred|Args], присоединить(Args,[Слова,[]],Newargs), Цель =.. [Pred|Newargs], call (Цель).
где
присоеднить определен так же как в разд. 3.6.
ПРИЛОЖЕНИЕ В. ПРОГРАММА ПРИВЕДЕНИЯ ФОРМУЛ ИСЧИСЛЕНИЯ ПРЕДИКАТОВ К СТАНДАРТНОЙ ФОРМЕ
Как было обещано в гл. 10, мы проиллюстрируем процесс преобразования формулы исчисления предикатов в стандартную форму, представив фрагменты программы на Прологе, выполняющей это преобразование. Верхний уровень программы выглядит следующим образом:
translate(X):-
implout(X,Xl), /* Этап 1 */
negin(Xl,X2), /* Этап 2 */
skolem(X2,X3,[]), /* Этап 3 */
univout(X3,X4), /* Этап 4 */
conjn(X4,X5), /* Этап 5 */
clausify(X5,Clauses, []), /* Этап 6 */
pclauses(Clauses). /* Печать дизъюнктов */
Здесь приведено определение предиката
translate, действующего таким образом, что, если выполнить целевое утверждение
translate(X), где
X – это формула исчисления предикатов, то программа напечатает эту формулу в стандартной форме в виде последовательности дизъюнктов. В этой программе формулы исчисления предикатов представляются в виде структур языка Пролог, как на это указывалось ранее (в гл. 10). Однако мы сделаем некоторое отступление от предыдущего описания и будем представлять переменные, входящие в формулы исчисления предикатов, атомами языка Пролог, с целью облегчить их обработку. Предполагается, что можно отличить переменные в формулах исчисления предикатов от констант, используя некоторое соглашение относительно формы записи имен. Например, можно считать, что имена переменных всегда начинаются с одной из букв х, у, z. В действительности, переменные всегда вводятся в формулу посредством кванторов и, следовательно, их легко можно опознать. Лишь при чтении результата, печатаемого программой, программисту необходимо помнить, какие имена соответствуют переменным формул исчисления предикатов, а какие константам.
Прежде всего, необходимо объявить операторы для логических связок, используемых в формулах:
?- op(30,fx,~).
?- op(100,xfy,#).
?- op(100,xfy,&).
?- op(150,xfy,-›).
?- op(150,xfy,‹-›).
Следует обратить внимание на то, как определены операторы. В частности ~ имеет более низкий приоритет чем # и &. Для начала, необходимо сделать одно важное предположение. Предполагается, что переменные переименованы таким образом, что в обрабатываемой формуле одна и та же переменная никогда не вводится более чем одним квантором. Это необходимо, чтобы предотвратить возможные конфликты в употреблении имен в дальнейшем.
Для преобразования формул к стандартной форме мы используем метод преобразования дерева, обсуждавшийся в разд. 7.11 и 7.12. При представлении логических связок как функторов, формулы исчисления предикатов превращаются в структуры, которые могут быть изображены в виде деревьев. Каждый из шести основных этапов перевода в стандартную форму представляет некоторое преобразование дерева, которое отображает входное дерево в выходное.
Этап 1 - исключение импликаций
Определим предикат
implout так, что
implout(X, Y) означает, что формула
Y получается из формулы
X путем исключения всех импликаций.
implout((P ‹-› Q), (P1 & Q1) # (~Р1 & ~Q1))):- !, implout(P,Pl), implout(Q,Ql).
implout((P -› Q),(~P1 # Q1)):-!, implout(P,P1), implout(Q,Q1).
implout(all(X,P),all(X,P1)):- !.
implout(exists(X,P),exists(X,P1)):-!, implout(P, P1).
implout((P & Q),(P1 & Q1)):- !, implout(P,P1), implout(Q,Q1).
implout((P # Q),(P1 # Q1)):-!, implout(P,P1), implout(Q,Q1).
implout((-P),(~Pl)):-!, implout(P,P1).
implout(P,P).
Этап 2 - перенос отрицания внутрь формулы
Здесь необходимо определить два предиката –
negin и
neg. Целевое утверждение
negin(X, Y) означает, что формула
Y получена из
X в результате применения к ней преобразования «перенос отрицания». Этот предикат является основным и именно к нему производится обращение из программы. Целевое утверждение
neg(X, Y) означает, что формула
Y получена из формулы
~X с помощью того же преобразования, что и в
negin. В обоих случаях предполагается, что формула прошла обработку на первом этапе и, следовательно, не содержит -› и ‹-›
negin((~P),P1):-!, neg(P,P1).
negin(all(X,P),all(X,P1)):-!, negin(P,P1).
negin(exists(X,P),exists(X,P1)):-!, negin(P,P1).
negin((P & Q),(P1 & Q1)):-!, negin(P,P1), negin(Q,Q1).
negin((P # Q),(P1 # Q1)):-!, negin(P,P1), negin(Q,Q1).
negin(P,P).
neg((~P),P1):-!, negin(P,P1).
neg(all(X,P), exists(X,P1)):-!, neg(P,P1).
neg(exists(X,P),all(X,P1)):-!, neg(P,P1).
neg((P
& Q),(P1 # Q1)):-!, neg(P,P1), neg(Q, Q1).
neg((P # Q),(P1 & Q1)):~!, neg(P,P1), neg(Q, Q1).
neg(P,(~P)).
Этап 3 - сколемизация
Предикат
skolem имеет три аргумента, соответствующих: исходной формуле, преобразованной формуле и списку переменных, которые на текущий момент были введены посредством кванторов общности.
skolem(all(X,P),all(X,P1),Vars):-!, scolem(P,Pl,[X|Vars]).
skolem(exists(X,P),P2,Vars):-!, gensym(f,F), Sk =..[F|Vars], subst(X,Sk,P,P1), skolem(P1,P2,Vars).
skolem((P # Q),(P1 # Q1),Vars):-!, skolem(P,P1,Vars), skolem(Q,Q1,Vars).
skolem((P & Q),(P1 & Q1), Vars):-!, skoIem(P,P1,Vars), skolem(Q,Q1,Vars).
skolem(P,P,_).
В этом определении используются два новых предиката. Предикат
gensym должен быть определен таким образом, что целевое утверждение
gensym(X, Y) вызывает конкретизацию переменной
Y значением, представляющим новый атом, построенный из атома
X и некоторого числа. Он используется для порождения сколемовских констант, не использовавшихся ранее. Предикат
gensym определен в разд. 7.8 как
генатом. Второй новый предикат, о котором уже упоминалось, это
subst. Мы требуем, чтобы
subst(Vl,V2,F1,F2) было истинно, если формула
F2 получается на
F1 в результате замены всех вхождений
V1 на
V2. Определение этого предиката оставлено в качестве упражнения для читателя. Оно аналогично определениям, приведенным в разд. 7.5 и 6.5.
Этап 4 - вынесение кванторов общности в начало формулы
После выполнения этого этапа, естественно, будет необходимо иметь возможность указывать, какие атомы Пролога представляют переменные формулы исчисления предикатов, а какие атомы представляют константы. Мы больше не сможем воспользоваться удобным правилом, согласно которому переменными являются в точности те символы, которые вводятся с помощью кванторов. Здесь представлена программа, выполняющая операции вынесения и удаления кванторов общности.
univout(all(X,P), P1):- !, univout(P,P1).
univout((P & Q),(P1 & Q1)):-!, univout(P,P1), univout(Q,Q1).
univout((P # Q),(P1 # Q1)):- !, univout(P,P1), univout(Q,Q1).
univout(P,P).
Эти правила определяют предикат
univout таким образом, что
univout(X, Y) означает, что
Y получается из
X в результате вынесения и удаления кванторов общности.
Необходимо отметить, что данное определение
univout предполагает, что указанные операции будут применяться лишь после того, как полностью будут завершены первые три этапа преобразования. Следовательно, формула не должна содержать импликаций и кванторов существования.
Этап 5 - использование дистрибутивных законов для. & и #
Реальная программа для преобразования формулы в конъюнктивную нормальную форму является значительно более сложной по сравнению с последней программой. При обработке формулы вида
(Р # Q), где
Р и
Q – произвольные формулы, прежде всего, необходимо преобразовать
Р и
Q в конъюнктивную нормальную
форму, скажем
P1 и
Q1. И только после этого можно применять одно из преобразований, дающих эквивалентную формулу. Процесс обработки должен происходить именно в таком порядке, так как может оказаться, что ни
Р ни
Q не содержат& на верхнем уровне, а
Р1 и
Q1 содержат. Программа имеет вид:
conjn((P # Q),R):-!, conjn(P,P1), conjn(Q,Q1), conjn1((P1 # Q1),R).
conjn((P& Q),(P1& Q1)):-!, conjn(P,P1), conjn(Q,Q1).
conjn(P,P).
conjn1(((P & Q) # R), (P1 & Q1)):- !, conjn((P # Q), P1), conjn((Q # R), Q1).
conjn1((P # (Q & R)),(P1 & Q1)):-!, conjn((P # Q), P1), conjn((P # R), Q1).
conjn1(P,P).
Этап 6 - выделение множества дизъюнктов
Здесь представлена последняя часть программы приведения формулы к стандартной форме. Прежде всего, определим предикат
clausify, который осуществляет построение внутреннего представления совокупности дизъюнктов. Эта совокупность представлена в виде списка, каждый элемент которого является структурой вида
cl(A, В). В этой структуре
А – это список литералов без отрицания, а
В – список литералов с отрицанием (знак отрицания ~ явно не содержится). Предикат
clausify имеет три аргумента. Первый аргумент для формулы, передаваемой с пятого этапа обработки, Второй и третий аргументы используются для представления списков дизъюнктов. Предикат
clausify создает список, заканчивающийся переменной, а не пустым списком (
[]) как обычно, и возвращает эту переменную посредством третьего аргумента. Это позволяет другим правилам добавлять элементы в конец этого списка, конкретизируя соответствующим образом указанную переменную. В программе выполняется проверка с целью выявления ситуаций, когда одна и та же атомарная формула входит в дизъюнкт как с отрицанием, так и без него. Если такая ситуация имеет место, то соответствующий дизъюнкт не добавляется к списку, так как подобные дизъюнкты являются тривиально истинными и не дают ничего нового. Выполняется также проверка неоднократного вхождения литерала в дизъюнкт.
clausify((P& Q),C1,C2):-!, clausify(P,C1,C3), clausify(Q,C3,C2).
clausify(P,[cl(A,B)|Cs],Cs):- inclause(P,A,[],B,[]),!.
clausify(_,C,C).
inclause((P # Q), A, A1, B, B1):-!, inclause(P,A2,A1,B2,B1),inclause(Q,A,A2,B,B2).
inclause((~P),A,A,B1,B):-!, notin(P,A), putin(P,B,B1).
inclause(P,A1,A,B,B):- notin(P,B), putin(P,A,A1).
notin(X,[X|_]):-!, fail.
notin(X,[_|L]):-!, notin(X,L).
notin(X,[]).
putin(X,[],[X]):-!.
putin(X,[X|L],L):-!.
putin(X,[Y|L], [Y|L1]):- putin(X,L,L1).
Печать утверждений
Теперь будет определен предикат
pclauses печатающий формулу, представленную указанным способом, в соответствии с принятой формой записи.
pclauses([]):-!, nl, nl.
pclauses([cl(A,B)|Cs]):- pclause(A,B), nl, pclauses(Cs).
pclause(L,[]):-!, pdisj(L), write('.').
pclause([],L):-!, write(':-'), pconj(L), write('.').
pclause(L1,L2):- pdisj(L1), write(':-'), pconj(L2), write('.').
pdisj([L]):-!, write(L).
pdisj([L|Ls]):- write(L), write(';'), pdisj(Ls).
pconj([Lj):-!, write(L).
pconj([L|Ls]):- write(L), write(','), pconj(Ls).
ПРИЛОЖЕНИЕ С. РАЗЛИЧНЫЕ ВЕРСИИ ЯЗЫКА ПРОЛОГ
В настоящее время существует много различных версий Пролога, которые можно встретить во многих организациях. Разнообразие версий отчасти объясняется разнообразием имеющихся ЭВМ. Нет двух ЭВМ, для которых с одинаковой легкостью писались бы все возможные программы. Это нашло отражение в том, что различные реализации Пролога отличаются друг от друга по своим возможностям. Но даже две ЭВМ одного и того же типа могут работать с разными операционными системами. Операционная система – это программа, осуществляющая общее управление работой ЭВМ, в том числе контроль за эффективным распределением ресурсов между пользователями ЭВМ. Одни операционные системы разрешают программисту использовать широкий набор возможностей, обеспечиваемых ЭВМ. Набор допустимых средств других более скромен. Отсюда и различия между Пролог-системами. Наконец, создатели Пролог-систем часто расходятся в представлениях о том, какие возможности являются лишь эстетически приятными, а какие действительно необходимы. В результате никакие две Пролог-системы не совпадают полностью по возможностям, и не похоже, что эта ситуация вскоре изменится, поскольку относительно реализаций Пролога постоянно возникают новые идеи и усовершенствования.
В этой книге описана версия Пролога, которая не соответствует в точности никакой существующей системе. Скорее наоборот, она была задумана как описание «базового» Пролога, который похож на все системы сразу. Если вы усвоили идеи, изложенные в этой книге, то вам не составит большого труда приспособиться к какой-либо конкретной Пролог-системе, с которой вам придется работать. Синтаксис языка и некоторые встроенные предикаты могут отличаться, но в остальном это будет все тот же базовый Пролог, который описан здесь.
Лучший способ изучения Пролог-системы, которой вы располагаете,- это чтение руководства пользователя, входящего в комплект ее документации. Правда, изложение там может быть сжатым, однако, имея общее представление о языке, вы без особого труда сможете разобраться, чем данная система отличается от того, с чем вы знакомы. В данном приложении отмечается несколько моментов, на которые стоит обратить внимание, а также сообщаются подробные сведения о двух конкретных Пролог-системах, которые довольно широко распространены. При этом мы хотели бы еще раз подчеркнуть, что многие существующие Пролог-системы постепенно меняются, и поэтому ничто не заменит вам изучения свежей версии руководства по Пролог-системе для вашей ЭВМ. Ниже рассматриваются характеристики Пролог-систем, различия в которых наиболее вероятны для разных реализаций Пролога.
Синтаксис
У каждого имеются свои представления о том, какая форма синтаксиса наиболее естественна и наглядна. К счастью, синтаксис Пролога довольно прост и не дает большого простора для вариаций. Один из спорных вопросов – как следует отличать переменные от атомов. Здесь для обозначения переменных используются имена, начинающиеся с прописной буквы, а для обозначения атомов – со строчной. Кроме того, мы допускаем атомы, составленные из последовательностей знаков, таких как '*', '.' и '='. Некоторые Пролог-системы придерживаются в отношении использования прописных и строчных букв обратного соглашения (когда имена переменных начинаются со строчной буквы). Другие различают имена переменных за счет того, что начинают их со специальной литеры, как, например,
'_PERSON' или
'*PERSON'. Это удобно для систем, где прописные и строчные буквы не различаются. Другим моментом, где возможны расхождения, является способ записи утверждений – как заголовок утверждения отделяется от тела, как разделяются отдельные цели в теле и как обозначаются вопросы к системе. Для этого вполне могут употребляться атомы, отличные от ':-', '.' и '?-', или использоваться более сложные методы. В одной из ранних систем заголовок и цели утверждения размещались одно за другим, причем перед заголовком утверждения ставили знак '+', а перед каждой из подцелей – знак '-'. Короче говоря, вам могут встретиться способы записи утверждений, приведенные ниже, а также и отличные от них.
uncle(X,Z):- parent(X,Y), brother(Y,Z).
Uncle(x,z) ‹- Parent(x,y) & Brother(y,z).
UNCLE(_X,_Z):- PARENT(_X,_Y), BROTHER(_Y,_Z).
+UNCLE(*X,*Z) -PARENT(*X,*Y) -BROTHER(*Y,*Z).
((UNCLE X1 ХЗ) (PARENT X1 Х2) (BROTHER X2 ХЗ))
uncle(X,Z): parent(X,Y); brother(Y,Z).
Различные ограничения
Поскольку на разных ЭВМ управление памятью организовано по-разному, то создатели Пролог-систем не всегда могут позволить неограниченный рост некоторых объектов. Среди характеристик, которые подвержены изменениям при переходе от одной ЭВМ к другой, можно указать максимальную величину целого числа в Прологе, возможность использования чисел с плавающей точкой, максимально допустимое число аргументов функтора, максимальное количество литер в атоме, максимальное число утверждений в определении предиката и т. д.
Возможности окружения
Из-за различий в возможностях отдельных операционных систем в некоторых Пролог-системах можно прервать программу в ходе ее выполнения, отредактировать файл на диске без потери текущего состояния сеанса работы с Пролог-системой, одновременно выполнять несколько Пролог-программ, получать входные и передавать выходные данные через специальные устройства, Однако нельзя ожидать, чтобы какая-то из этих возможностей обеспечивалась на всех системах, поэтому здесь также могут встретиться различия. Как и в вопросе допустимого набора указанных возможностей, конкретная операционная система на вашей ЭВМ может отличаться тем, что некоторым вводимым литерам она будет придавать специальное значение. Например, литера, которая вводится для обозначения «конец файла» в конце предиката
consult(user) в разных ЭВМ различна. Другие литеры могут рассматриваться как запросы на выдачу информации о состоянии ЭВМ или как запросы на изменение последней введенной литеры. Подобные возможности не являются частью Пролог-системы, но тем не менее, важны для того, кто решил практически использовать эту систему.
Компиляция
Большинство Пролог-систем работает с представлением утверждений, которое близко к их исходному тексту. Когда какое-либо утверждение в такой системе начинает выполняться система должна проанализировать утверждение и предпринять соответствующие действия. Такая система называется
интерпретатором. Другая возможность состоит в том, что система транслирует ваши предложения в последовательности инструкций, которые могут непосредственно исполняться ЭВМ. Такая система называется
компилятором. Использование компилятора дает то преимущество, что ваша программа выполняется непосредственно, а не проходит процесс интерпретации. Это означает, что вы вправе ожидать, что ваша программа будет выполняться быстрее. Но, с другой стороны, поскольку при использовании компилятора текст программы не сохраняется в исходном виде, не следует надеяться на получение той же информации при ее отладке (например, вам нельзя будет запросить выдачу текстов ваших предложений). В некоторых системах имеется возможность выбора между компиляцией и интерпретацией утверждений. В этом случае следует тщательно взвесить преимущества каждого подхода.
Специальные встроенные предикаты
Хотя основные средства механизма выполнения программ в большинстве Пролог-систем действуют одинаково, специальные встроенные предикаты могут все-таки различаться. Иногда это выражается в том, что для тех возможностей, которые легко обеспечить на данной ЭВМ, вводятся дополнительные предикаты. Иногда одни и те же основные возможности реализуются с помощью предикатов, которые дают несколько отличающиеся результаты. Например, для любой Пролог-системы было бы достаточно располагать предикатами
functor и
arg или предикатом '=..'. Действительно, первые два могут быть выражены через третий и обратно. Вам, возможно, придется приспособиться к использованию имеющихся средств с тем, чтобы имитировать действие тех средств, к которым вы привыкли. Некоторые Пролог-системы могут предоставлять библиотеки полезных программ, обеспечивающих дополнительные возможности сверх тех, что дают встроенные предикаты. Например, грамматические правила могут быть предоставлены как часть базовой системы или может иметься возможность загрузить из библиотеки Пролог-программу, обеспечивающую такие возможности.
Средства отладки
Вопрос о том, какие средства отладки лучше всего подходят для Пролога, окончательно еще не решен. Тем временем разные системы предлагают свои подходы к выбору необходимых средств отладки. Остается надеяться, что общее введение в этот вопрос, приведенное в гл. 8, вооружит читателя всем необходимым для работы с любыми подобными средствами.
ПРИЛОЖЕНИЕ D. ПРОЛОГ ДЛЯ ЭВМ DEC SYSTEM-10
В этом приложении кратко описывается Пролог-система для ЭВМ DECsystem-10
[18], которую реализовали Дейвид Уоррен, Фернандо Перейра и Льюис Перейра. Эта реализация стала фактическим стандартом, и реализации, сделанные по этому образцу, имеются теперь на многих других ЭВМ от микро-ЭВМ 2-80 до ЭВМ семейства VAX фирмы DEC. Описанный в этой книге «базовый» Пролог также в основном совпадает с Прологом-10. В данном приложении рассматриваются только те его особенности, которые существенно отличаются от базового Пролога. В начале мы покажем, как выглядит сеанс работы с Прологом-10, а затем перейдем к более подробному изучению отличий этой системы от нашего базового Пролога. В конце приводится список Пролог-систем, сделанных по образцу Пролога-10, которые можно использовать на других ЭВМ.
Пример сеанса работы
Здесь приводится пример сеанса работы с Прологом-10. В нем в точности воспроизводится все, что происходит на терминале во время такого сеанса. Кроме того, здесь даются пояснения к тому, что происходит.
Сначала мы находимся на уровне монитора операционной системы TOPS-10 и просим запустить Пролог.
.r prolog
Prolog-10 version 3.3
Copyright (С) 1981 by D. Warren, F. Pereira and L. Byrd
|?- likes(X,Y).
no
Содержимое заголовка, конечно, может несколько меняться от одной версии системы к другой. Литеры «|?-» выданы Прологом как «приглашение». Тем самым он сообщает нам, что ждет вопроса. Мы задали вопрос и получили ответ
no (нет). Это неудивительно, поскольку сейчас в базе данных еще нет никаких фактов. Теперь мы полагаем, что существует файл,
test.pl, и мы заполняем базу данных его содержимым.
|?- ['test.pl'].
test.pl consulted 58 words 0.01 sec.
yes
Чтобы заставить Пролог считывать утверждения из файла, мы задаем вопрос, состоящий из имени файла, заключенного (в виде атома Пролога) в квадратные скобки. В данном случае это файл, состоящий из утверждений об отношении «нравится» (likes) между людьми.
|?- likes(john,bertrand).
no
|?- likes(john,albert).
no
Это просто ряд вопросов о том, кто кому нравится. Пролог не может найти в базе данных сопоставимых фактов.
|?- listing(likes).
likes(john,alfred).
likes(alfred,john).
likes(bertrand,john).
likes(david,bertrand).
likes(john,_l):- likes(_l,bertrand).
yes
Чтобы узнать, какие утверждения с заданным предикатом имеются в базе данных, мы задаем вопрос с помощью специального встроенного предиката
listing. Этот специальный вопрос заставляет Пролог выдать все утверждения, содержащие предикат
likes. Заметим, что неконкретизированные переменные Пролог выводит в виде литеры подчеркивания, за которой следует число. Последнее утверждение в базе данных было записано в файле в виде:
likes(john,X):- likes(X,bertrand).
Продолжим наш пример:
|?- likes(john,X).
X = alfred;
X = david;
no
Здесь, с помощью нажатия клавиш «;» и «RETURN» мы запрашиваем альтернативные ответы на заданный вопрос. Было выдано два возможных ответа; больше Пролог ничего не смог найти.
|?- likes(X,Y).
X = john,
Y = alfred;
X = alfred,
Y = john;
X = bertrand,
Y = john;
X = david,
Y = bertrand;
X = john,
Y = david;
no
На этот раз ответ системы состоит из значений, которыми конкретизированы обе переменные. И опять для получения альтернативных ответов мы вводим «;» и «RETURN» до тех пор, пока новых ответов не окажется.
|?- [user].
Теперь мы просим Пролог читать утверждения из файла user. Это означает, что утверждения следует читать с терминала. Прочитанные утверждения будут дописаны в конец базы данных. Перед вводом утверждений (в отличие от ввода вопросов) в качестве приглашения Пролог выдает символ «|» вместо «|?-».
[likes(timothy,bertrand).
|
user consulted 10 words 0.03 sec.
yes
После ввода первого утверждения мы сообщаем Прологу, что хотим прекратить чтение утверждений. Это делается путем одновременного нажатия клавиш «CONTROL» и «Z». При этом перед вводом комбинации «CONTROL Z» мы могли бы ввести не один, а несколько фактов и правил. Теперь Пролог завершил обработку предыдущего вопроса и ждет ввода нового.
|?- likes(john,X).
X = alfred;
X = david;
X = timothy;
no
Здесь мы снова просим выдать альтернативные ответы. Заметим, что ввод нового утверждения привел к появлению нового ответа, который ранее при том же вопросе не выдавался.
|?- likes(bertrand,Y).
Y = john
yes
Здесь показан другой способ работы с альтернативами. После первого ответа мы ввели «RETURN». Это привело к тому, что весь вопрос завершился успешно, и Пролог перешел к ожиданию следующего вопроса.
|?- core 36864 (7680 lo-seg + 29184 hi-seg)
heap 2560 = 1573 in use + 987 free
global 1177 = 16 in use + 1161 free
local 1024 = 16 in use + 1008 free
trail 511 = 0 in use + 511 free
0.36 sec. runtime
В ответ на последнее приглашение «|?-» мы ввели комбинацию «CONTROL Z», чтобы показать, что мы закончили работу с системой. В ответ Пролог выдал нам некоторую статистическую информацию, и мы снова вернулись в монитор TOPS-10. Полный протокол этого сеанса работы был записан в файл
prolog.log.
Синтаксис
Синтаксис Пролога-10 в основном совпадает с нашим описанием, Правда, он несколько менее строг в отношении того, что считать правильными атомами и переменными, чем те правила, которые приведены в книге. Каждый пример из этой книги удовлетворяет требованиям синтаксиса Пролога-10. Приведем одно важное замечание относительно операторов с высоким приоритетом: поскольку ',' является оператором, то настоятельно рекомендуется во избежание двусмысленности заключать в скобки все термы, записанные с использованием операторов одинакового или более высокого приоритета. Это гарантирует, например, что конструкция
foo(a,b,c)
может быть истолкована только как структура с функтором too от трех аргументов, а не, например, что-нибудь типа
foo(a,','(b,c))
или
foo(','(a,','(b,c)))
Если бы мы хотели записать именно этот последний терм, то это следовало бы сделать так
foo((a,b,c))
Правило относительно операторов высокого приоритета касается только нескольких операторов, таких как ':-' и ';'. Оно означает, что запись вида:
?- retract(parent(A,B):- father(A,B)).
является синтаксически неправильной в смысле Пролога-10. Чтобы сделать ее правильной, нужно добавить пару скобок.
В том случае, если вы работаете с терминалом или с операционной системой, в которых не предусмотрено одновременного использования прописных и строчных букв, можно использовать имеющийся в Прологе-10 альтернативный вариант синтаксиса. В этом синтаксисе отличие переменных от атомов состоит в том, что имена переменных начинаются с литеры подчеркивания «_». Для перехода на этот вариант синтаксиса предусмотрен встроенный предикат
nolc (нет строчных букв). Другой встроенный предикат,
lс (строчные буквы), позволяет снова переключиться на нормальный синтаксис.
И еще одно маленькое замечание. Функтор '.' (с двумя аргументами) в Прологе-10 не является заранее определенным оператором. При желании вы можете определить его сами, хотя в этом нет необходимости, если при работе со списками вы всегда пользуетесь специальным способом задания списков.
Различные ограничения
В Прологе-10 предусмотрены ограничения, с которыми пользователь вряд ли столкнется на практике. Приоритеты операторов должны быть в диапазоне от 1 до 1200. Целые числа должны находиться в диапазоне от -131 072 до 131 071, однако в ходе вычислений целых выражений промежуточные результаты могут выходить за эти границы. Вещественные числа (с плавающей точкой) не предусмотрены.
Возможности окружения
В Прологе-10 предусмотрена очень полезная возможность протоколирования сеанса работы. При обычной работе с Прологом система фиксирует в файле
plolog.log на диске почти все, что появляется на терминале. После того как работа закончена, вы можете просмотреть этот файл и точно определить, что происходило во время сеанса работы. Файл
prolog.log содержит полезную информацию о том, что и когда делала ваша программа, и какие изменения вы в ней делали. На тот случай, если вы не хотите протоколировать все подряд, предусмотрены встроенные предикаты, обеспечивающие включение и выключение протоколирования.
В Прологе-10 можно прервать выполнение программы путем одновременного ввода комбинации символов «CONTROL С». Система отвечает приглашением и ждет от вас указаний о том, какое действие нужно выполнить далее. Набор допустимых команд включает
break,
continue (продолжить выполнение программы),
exit (выход из Пролога),
trace и
notrace. Последние две команды вызывают продолжение выполнения программы после изменения вида или объема трассировки. Команда
break позволяет приостановить выполнение текущей программы и предоставляет вам возможность работы с новой «копией» Пролог-системы. После выхода из команды
break приостановленная программа продолжит свое выполнение.
В Прологе-10 в качестве литеры, играющей роль признака конца файла используется комбинация «CONTROL Z» (клавиша CONTROL одновременно с Z). Ее ввод, в зависимости от ситуации, в которой вы находитесь, приводит к выходу из Пролога, к завершению режима
break или к завершению выполнения предиката
consult. Встроенный предикат
read в случае выхода на конец файла сравнивает свой аргумент с атомом
end of file.
В Прологе-10 предусмотрены разнообразные средства, помогающие экономить время при повторном считывании программы. Можно сохранить «состояние» Пролог-системы, включая текущее состояние ее базы данных, в файле на диске, причем таким образом, что восстановление этого состояния происходит значительно быстрее, нежели чтение программы и приведение ее в то же самое состояние. Кроме того, в начале каждого сеанса работы, прежде чем начать ввод с терминала, Пролог-10 автоматически читает любую информацию, которая записана в файле
plolog.ini.
Если во время выполнения Пролога-10 фиксируется ошибка, то система выводит сообщение, говорящее о том, что произошло. Большинство ошибок вызывают просто неудачу в согласовании тех целей, которые их породили, так что ваша программа может продолжать выполнение. Однако некоторые ошибки более серьезны. В этих случаях система прекращает выполнение всех имеющихся в данный момент программ и просит ввести очередной вопрос.
Компиляция
В Прологе-10 предусмотрена возможность выборочной компиляции некоторых из ваших утверждений, что позволяет значительно увеличить эффективность программ по времени выполнения и занимаемой памяти. Для этого имеется встроенный предикат, который действует подобно предикату
consult, с той лишь разницей, что утверждения из файла не интерпретируются, а компилируются. Эффективность выполнения откомпилированных утверждений может быть увеличена за счет использования так называемых описаний режима, которые позволяют указать, как будут использованы данные утверждения (какие аргументы будут конкретизированы в различных ситуациях). Существуют определенные ограничения на пригодность утверждений для компиляции. Кроме того, системе необходимо задать некоторые другие описания, чтобы она смогла должным образом выполнять смесь интерпретируемых и откомпилированных утверждений.
Различия во встроенных предикатах
В Прологе-10 предусмотрены все встроенные предикаты, о которых говорилось в этой книге. Кроме того, он нормально обрабатывает грамматические правила, когда они встречаются в обычном
consult. В данном разделе рассматриваются некоторые отличия от приведенных описаний.
Действие предиката
display всегда состоит в выдаче аргументов этого предиката на терминал, а не в текущий файл вывода, как было описано.
При рассмотрении арифметических выражений мы говорили, что арифметическое выражение вычисляется только тогда, когда оно задано в качестве второго аргумента предиката
is. Во всех других случаях структура вида '24-3' просто обозначает саму себя. В Прологе-10 это не так. Там вычисляются и арифметические выражения, заданные как аргументы других предикатов. Примером этого служат операторы отношения '‹', '=‹' и т. д., а также предикат
put. Это означает, что приводимый ниже пример в Прологе-10 будет работать, а в нашем базовом Прологе выдаст ошибку или приведет к неудаче в согласовании цели.
?- 2+4‹12*(2+8).
yes
Еще одна особенность. Структура, представляющая собой список, состоящий из одного числа, рассматривается как арифметическое выражение, значением которого является число. Иными словами в Прологе-10 имеем:
?- X is [25].
X = 25
yes
Благодаря такой комбинации возможностей, вывод одиночных литер может быть задан в мнемоническом виде, например:
?- put("a"), put("b").
ab
yes
(не забывайте, что "а" – это список, состоящий из одного числового кода, соответствующего первой строчной букве алфавита).
Синтаксис отрицания. Предикат с именем
not не предусмотрен, но вместо него используется инфиксный оператор '\+' Отсутствует оператор «не равно» ('\=').
Переменные как целевые утверждения. На самом деле это скорее вопрос синтаксиса, чем чего бы то ни было другого. Мы уже видели, как с помощью предиката
call можно вызвать целевое утверждение, соответствующее текущему значению переменной Пролога. В Прологе-10 предусмотрен другой способ осуществления этого. Вместо того чтобы вставлять утверждение-цель вида
…, call(X),…
достаточно поставить на место цели саму эту переменную:
…, X,…
При этом использование варианта с
call также возможно. Более того, при применении к такому утверждению
asserta или
assertz система преобразует цель X в цель
call(X).
Задание аргументов для
retract. Из-за трудностей, связанных с использованием переменных в качестве целей, в Прологе-10 существуют отличия в том, как должны задаваться тела утверждений в предикате
retract. Трудность заключается в том, что когда мы задаем вопрос
?- retract((mother(A,B):- С)).
это может быть истолковано или как просьба об удалении утверждения, имеющего конкретный вид:
mother(A,B):- С.
где в теле утверждения переменная обозначает цель или как просьба об удалении утверждения для предиката
mother с любым телом, как, например:
mother(X,Y):- parent(X,Y), female(Y).
Для устранения возможной двусмысленности, в подобных случаях Пролог-10 всегда начинает с замены неконкретизированных переменных, обозначающих одиночные или множественные целевые утверждения в аргументах для
retract соответствующими структурами с функтором
call. Таким образом, вопрос
?- retract((mother(A,B):-С)).
фактически рассматривается как
?- retract((mother(A,B):-call(C))).
Если мы хотим удалить первое утверждение для предиката
mother независимо от его тела, то для этого можно было бы задать:
?- clause(mother(A,B),C), retract((mother(A,B):-С)).
В этом случае первая цель с
clause делает С достаточно конкретизированной, чтобы избежать преобразования.
Дополнительные встроенные предикаты
Помимо встроенных предикатов, описанных нами, в Прологе-10 предусмотрено много других возможностей.
«Условная» форма задания целей, которая позволяет задавать цели в следующем виде:
…, (likes(john,X) --› wooden(X); plastic(X)),…
Идея такой составной цели состоит в следующем. Если цель - «условие», которая задается перед стрелкой --›, согласуется с базой данных, то осуществляется вызов второй цели, заданной непосредственно после --›, иначе осуществляется вызов третьей цели. Любая из этих целей может представлять собой последовательность целей Пролога. Указанные условные цели действуют точно так же, как если бы они были определены в Прологе-10 следующим образом:
?- op(1050,xfy,-›).
?- op(1100,xfy,';').
(X -› Y; Z):- call(X),!, call(Y).
(X -› Y; Z):- call(Z).
Индексированная база данных. Это средство позволяет сопоставлять элементы информации в базе данных с конкретными значениями и обходить стандартный механизм доступа к базе данных, имеющийся в Прологе. Например, если бы вы захотели хранить информацию о возрастах сотен людей, то стандартный подход потребовал бы завести сотни утверждений для некоторого предиката age (возраст). И когда затем вы бы пожелали выяснить возраст конкретного человека, Пролог должен был бы осуществить просмотр всех утверждений, пока не нашел бы нужный. Беда в том, что при обычном подходе информация сопоставляется с предикатом и, когда предикат содержит много утверждений, объем поиска может быть большим. Индексированная база данных позволяет сопоставлять информацию с конкретным именем более прямым способом.
Возможность доступа к предшественникам. В главе о средствах отладки мы рассматривали понятие целей-предшественников. В Прологе-10 предусмотрены встроенные предикаты, обеспечивающие доступ к предшественникам из Пролог-программы.
Статистическая информация. В Прологе-10 предусмотрены встроенные предикаты, позволяющие получить данные о скорости выполнения вашей программы и объеме памяти, необходимой для ее выполнения.
Средства отладки
В Прологе-10 предусмотрены средства отладки, соответствующие тому, что было нами рассмотрено. В дополнение к встроенным предикатам отладки, описанным в гл. 8, предусмотрен предикат, позволяющий указать, какие события являются управляемыми во время трассировки.
Литература
DECsystem-10 Prolog User's Manual, Department of Artificial Intelligence, University of Edinburg, Scotland.- Представляет собой руководство пользователя Пролога-10.
C-Prolog User's Manual, CAAD Studio, Department of Architecture, University of Edinburg, Scotland.- Описывается система, работающая под управлением операционной системы UNIX,
Prolog-1 User's Manual, Expert Systems Ltd, 9 West Way, Oxford, England.- Описывает систему, работающую на многих ЭВМ, от Z-80 под управлением операционной системы СР/М до VAX 11 под управлением операционной системы VMS.
ПРИЛОЖЕНИЕ Е. МИКРО-ПРОЛОГ
В этом приложении рассматриваются некоторые возможности системы микро-Пролог, разработанной для микро-ЭВМ на базе микропроцессора Z-80, работающих под управлением операционной системы СР/М.
Пример сеанса работы
Все приводимые примеры соответствуют «базовому» синтаксису. При желании можно воспользоваться другими формами синтаксиса, включая тот, что совместим с Прологом для ЭВМ DECsystem-10.
Ниже приводится последовательность сообщений, которая может появиться на вашем терминале в ходе обычного сеанса работы с микро-Прологом. Прежде всего мы задаем для СР/М команду запуска Пролога.
A›PROLOG
Micro-Prolog 3.00 S/N
(С) 1982 Logic Programming Associates Ltd.
9999 Bytes Free
&.?((likes x y))
Clause error at (likes x y)
В микро-Прологе литеры «&» выдаются в качестве приглашения. Их появление означает, что система ожидает от нас ввода команды. Ввод литеры «?» означает, что мы хотим задать вопрос. Вслед за ним должна следовать последовательность целей, заключенная в круглые скобки (которую следует понимать как конъюнкцию этих целей). Каждая цель внутри скобок представляет собой последовательность из имени предиката и следующих за ним аргументов. Переменные обозначаются именами, начинающимися с х, у, z, X, Y, Z, за которыми могут следовать числа. В вопросе, приведенном выше, спрашивается о том, нравится ли кто-либо кому-либо. Но поскольку в базе данных нет утверждений для предиката
likes (нравится), то микро-Пролог сообщает об ошибке.
&.LOAD TEST
Другая важная команда – это
LOAD. Далее следует имя файла. Ввод этой команды приводит к чтению содержимого файла
TEST.LOG и дополнению этим содержимым базы данных, подобно тому, как это делалось при
consult. Теперь можно задавать вопросы:
&.?((likes john bertrand))
?
&.?((likes john alfred))
&.
Заметим, что отрицательный ответ на вопрос обозначается в микро-Прологе литерой «?», а положительный ответ – повторной выдачей приглашения. Чтобы узнать, какие утверждения имеются для предиката
likes, мы задаем команду
LIST. Можно запросить выдачу текста всей программы или выдачу утверждений для некоторого набора предикатов. Посмотрим, какие утверждения существуют для предиката
likes:
&. LIST(likes)
((likes john alfred))
((likes alfred john))
((likes bertrand john))
((likes david bertrand))
((likes john x) (likes x bertrand))
В некоторых случаях для того, чтобы получить ответ на заданный вопрос, приходится прибегать к помощи встроенных предикатов. Предикат РР обеспечивает выдачу его аргументов на терминал, а предикат FAIL вызывает неудачное согласование целевого утверждения.
&.?((likes john х) (РР х) (FAIL))
alfred
david
?
Так мы получили два ответа на вопрос: «Кто нравится Джону?». Если мы хотим добавить к базе данных новые утверждения с терминала, нам не нужно прибегать к помощи специальных команд – мы можем просто ввести эти утверждения. Синтаксис утверждений микро-Пролога будет рассмотрен в следующем разделе.
&.((likes timothy bertrand))
&.?((likes john x) (PP x) (FAIL))
alfred
david
timothy
?
Чтобы выйти из микро-Пролога и вернуться в СР/М, достаточно задать команду QT, за которой следует поставить точку:
&. QT.
А›
Синтаксис
Синтаксис микро-Пролога существенно отличается от синтаксиса, рассматриваемого в данной книге, однако освоить его можно довольно быстро. Основная идея заключается в том, что существует всего один вид терма – список. Если мы хотим построить терм с функтором
f и четырьмя аргументами, то для этого используется список из пяти элементов, куда
f входит в качестве головы, а остальные элементы соответствуют четырем аргументам в порядке их следования. Таким образом то, что в базовом синтаксисе было бы записано в виде:
f(a,g(2,3),c)
на микро-Прологе должно быть записано как:
(f a (g 2 3) с)
Здесь мы сталкиваемся также и с иным синтаксисом задания списков, где списки заключены в круглые скобки, а элементы списков разделяются пробелами.
Утверждения представляются как списки термов, где первый терм – это заголовок утверждения, а остальные термы – цели, которые, будучи взятыми в конъюнкции, образуют тело утверждения. Рассмотрим более сложное утверждение:
((alter (zl|z2) (x|y)) (change zl x) (alter z2 у)
Это – второе утверждение для предиката
alter (преобразовать) из разд. 3.4. Заметим, что вертикальная черта имеет здесь то же значение, что и в базовом синтаксисе.
Различные ограничения
Микро-Пролог может обрабатывать числа с плавающей точкой с точностью до восьми значащих цифр и с порядком (по основанию 10) в диапазоне от -127 до 127. Имена атомов (называемые в микро-Прологе «константами») могут содержать до 60 литер, а терм не может содержать более 64 переменных. Эти ограничения на практике не вызывают трудностей.
Возможности окружения
Микро-Пролог предоставляет множество средств, помогающих при разработке программ за терминалом. Предикаты
LOAD и
SAVE позволяют, соответственно, читать и записывать программы в файлы на диске. Мощный строчный редактор и структурный редактор позволяют вносить изменения в тексты программ, не выходя из Пролог-системы. Выполнение микро-Пролог-программы может быть прервано путем ввода комбинации «CONTROL С».
Специальные встроенные предикаты
Имена и назначение встроенных предикатов сильно отличаются от рассмотренных в данной книге. Ниже приводится краткое описание некоторых из предусмотренных средств.
Тип терма можно проверить с помощью предикатов
NUM, CON, VAR, которые согласуются с базой данных, соответственно, в случае чисел, констант (атомов) и переменных. Кроме того, предикат
SYS проверяет, является ли константа именем встроенного предиката, предикат
1NT обеспечивает проверку на целое число.
Для работы с базой данных используются предикаты:
ADDCL (аналогичен
assert), CL (аналогичен
clause) и
DELCL (аналогичен
retract) В этих предикатах можно задавать дополнительный целочисленный аргумент
N с тем, чтобы можно было обрабатывать
N-e утверждение процедуры.
Поскольку единственным видом терма в микро-Прологе является список, то предикат вида ' =..' здесь не нужен. Предикат
STRING позволяет программисту создавать новые атомы и осуществлять доступ к внутренней структуре имени атома аналогично тому, как это делается с помощью предиката
name.
Составные цели в микро-Прологе можно конструировать с помощью встроенных предикатов
OR, NOT и
IF. Предикат
FAIL вызывает немедленную неудачу в согласовании цели. Предусмотрено также и «отсечение», которое обозначается с помощью литеры '/'.
Арифметические действия реализуются посредством нескольких предикатов, вместо одного is. Арифметические предикаты максимально «обратимы», поэтому, например, цель
(SUM х у
г)
вызывает сопоставление z с суммой х и у, если х и у конкретизированы. С другой стороны, если сначала конкретизированы у и r, а х – нет, то х будет конкретизирован разностью z-у.
Операции с файлами в микро-Прологе аналогичны тем, что имеются в базовом Прологе, с той лишь оговоркой, что здесь нет понятия текущего потока ввода или текущего потока вывода. Вместо этого вывод в файл и ввод из файла осуществляются, соответственно, через предикаты
WRITE и
READ с указанием каждый раз имени файла. Предусмотрены специальные предикаты, обеспечивающие удобства при вводе-выводе через терминал пользователя.
Микро-Пролог позволяет программисту разрабатывать программы по частям, которые называются модулями. Такая возможность сокращает вероятность случайных конфликтов имен в про-граммах и облегчает обмен программами между программистами.
Средства отладки
В микро-Прологе предусмотрена возможность трассировки программы, однако средства трассировки должны быть предварительно загружены с помощью предиката
LOAD. При трассировке выдается информация о процессе согласования всех целей, не содержащих встроенных предикатов. В моменты возникновения событий
CALL,
EXIT и
FAIL, которые именуются, соответственно, как
ENTER,
FINISH и
FAIL, выдаются соответствующие сообщения. Пользователю разрешается в момент события
CALL вмешиваться в ход трассировки и задавать команды
CONTINUE (продолжить выполнение с трассировкой),
SKIP (прервать трассировку до завершения текущей цели),
FINISH (немедленное согласование текущей цели) и
FAIL (немедленная неудача в согласовании текущей цели).
Литература
Clark K.L., Mc-Cabe F.G.
Micro-PROLOG: Programming in Logic, Prentice-Hall, 1984. [Русский перевод: Клар К., Маккейб Ф. Введение в логическое программирование на микро-Прологе.- М,; Радио и Связь, 1987.]
ПРИЛОЖЕНИЕ F. СИСТЕМА МПРОЛОГ[19]
В этом приложении описывается система МПролог, разработанная в Институте по координации вычислительной техники (SZKI), г. Будапешт. Название системы МПролог отражает тот факт, что в этой системе предусмотрены средства для модульной разработки программ. Кроме того, в ней поддерживается более 200 встроенных предикатов, рассчитанных на различные области применения.
Синтаксис МПролога совместим с синтаксисом Пролога-10 (см. приложение D), и почти все встроенные предикаты Пролога-10 предусмотрены также и в МПрологе.
Пролог доступен на следующих вычислительных комплексах:
| ЭВМ |
Операционные системы |
| VAX-11 |
VMS, UNIX |
| IBM |
VM/CMS, MVS |
| Siemens |
BS2000 |
| M68000 |
UNOS, UNIX-подобные системы |
Одна из версий МПролога (так называемый мини-МПролог) предназначена для микро- и мини-ЭВМ. Первая реализация этой системы применяется на ЭВМ IBM PC с ОС MSDOS.
Пример сеанса работы
Ниже приводится пример сеанса работы с подсистемой разработки программ (PDSS) системы МПролог,
В системе МПролог средства диалоговой разработки программ отделены от интерпретатора и реализованы в подсистеме PDSS, которая исполняет команды первичного ввода, редактирования, выполнения, трассировки и другой обработки модулей МПролога. Подсистема PDSS также позволяет задавать значительное число глобальных параметров, определяющих режимы работы команд. Например, параметр
line_length (длина_строки) задает длину выводимых строк при специально
форматированном выводе утверждений.
DO $S.MPRO.PDSS
MPROLOG (V1.4) Program Development Subsystem 1.4:4 (
c) 1982 Institute for Coordination of Computer Techniques (SZKI), Budapest.
По команде
help выводится общая вспомогательная информация о возможностях PDSS (# означает приглашение системы)
[20];
* help Команда; h[elp] [ТЕМА…]
Выводит вспомогательную информацию по заданной теме или о возможностях самой команды
help, если аргумент опущен.
Можно получить информацию по следующим темам:
all_global all_symbolic all_visible body bye coded consult declaration delete dynpart edit enter exception_handling execute export face focus global goal help hidden import insert interface list local match_order mode modify module move next nonprolog operator options previous query read rename replace reply reset rungoal savemod selectors set solutions status symbolic trace type untimed untrace visible =
Сведения по конкретной теме, например по теме
module, указанной в третьей колонке, можно получить следующим образом:
*help module
Команда: m[odule]
[ИМЯ]
Делает модуль
ИМЯ текущим модулем. Если
ИМЯ опущено, то текущим модулем становится `неименованный_модуль'. После этой команды никакое утверждение не помещается в поле зрения.
Возможности PDSS позволяют разрабатывать несколько модулей. Данный сеанс начинается с команды
module, создающей модуль, в который затем будут помещаться определения предикатов.
* module first
MODULE first
* enter hates(ann,john).
PREDICATE hates/2
*?- hates(kate,X).
NO
Команда
enter используется здесь для дополнения модуля
first новым утверждением. На основе одного этого утверждения ответ на вопрос
hates(kate, X) получается отрицательным.
В то же время, когда утверждений, относящихся к данному целевому утверждению, вообще нет, система ведет себя по-другому: такая ситуация рассматривается как особая, и она обрабатывается стандартным обработчиком особых ситуаций PDSS:
*?- likes(X,Y).
Exception -505: undefined predicate In call of likes(_425,_426) Function (h for help)?
* h
p – enter new PDSS level
b – backtrace
a – abandon execution
с – continue
f – fail
s – contents of the stack
r - redo the broken call
i – user handled interrupt
h – help Function (h for help)'
* f
NO
Здесь
enter new PDSS level означает выход на новый уровень команд PDSS (аналогично команде
break в Прологе-10),
backtrace означает вывод списка предшественников ошибочного вызова (аналогично команде
backtrace в Прологе для PDP-11 с ОС UNIX).
После завершения указанных выше действий пользователь может запросить другие действия. Предикаты
continue и
fail продолжают приостановленное выполнение программы так, как если бы вместо особой ситуации имела место согласованность или несогласованность цели с базой данных. В данном случае ввод
f приводит к ответу
NO.
Однако систему МПролог можно заставить вести себя так, как Пролог-система, описанная в книге. Для этого достаточно в качестве обработчика особой ситуации для
undefined predicate задать целевое утверждение
fail:
*?- newhandler("undefined predicate",fail).
Yes
*?- likes(X,Y).
No
Будем считать, что файл
test содержит ту же самую последовательность утверждений, что и в предыдущих приложениях. Тогда мы можем считать содержащиеся в нем утверждения в базу данных. При этом, если параметр
auotostate не в состоянии «off» (выключено), то будет выводиться функтор (т. е. имя/число аргументов) читаемых из файла предикатов.
*?- [test]. likes/2
Yes
*?- listing(likes/2).
likes(john,alfred).
likes(alfredjohn).
likes(bertrandjohn).
likes(david,bertrand).
likes(john,ANYBODY):
- likes(ANYBODY,bertrand).
Yes
Переменные (в данном случае
ANYBODY) записаны прописными буквами как в Прологе-10. Однако в МПрологе предусмотрена особая возможность сохранения символьных имен переменных в пользовательской программе.
Альтернативным способом вывода заданного предиката или некоторых из определяющих его утверждений является использование команды
type:
* type likes/2
likes(john,alfred).
likes(alfred,john).
likes(bertrand,john).
likes(david,bertrand).
likes(john,ANYBODY):- likes(ANYBODY,bertrand).
Второе и четвертое утверждения данного предиката можно просмотреть с помощью команды;
* type likes / 2 CL (2,4)
likes(alfred, john).
likes(david,bertrand).
А все утверждения, включающие
bertrand выбираются следующим образом:
* type likes / 2 CL (bertrand)
likes(bertrand, john).
likes(david,bertrand).
likes(john,ANYBODY):- likes(ANYBODY,bertrand).
Получение альтернативных решений для целевого утверждения осуществляется немного иначе, чем в Прологе-10:
*?- likes(john,Who).
WHO = alfred Continue (y/n)?
* y
WHO = david Continue (y/n)?
* у
NO
Новые утверждения можно добавлять как с помощью команды
enter, так и путем чтения псевдо-файла
user (как в Прологе-10):
*?- [user].
likes(timothy,bertrand).
likes/2+6
* bye
Yes
Команда ввода вопроса (?-) не выдает сведений о времени его выполнения. Эту информацию можно получить путем задания команды execute (в краткой форме ':'):
* :likes(john,X).
(*** CPU time: 0.27 sec, 1 calls, 0 backtracks ***)
Подсистема PDSS гибко реагирует на синтаксические ошибки. В стандартном режиме при возникновении такой ошибки пользователю предоставляется выбор: отредактировать ошибочное утверждение или выполнить целевое утверждение:
*?- likes(john,ann)). full stop expected at) Enter the editor (y/n)?
* y
10: likes(john,ann))
*** Enter editor commands
* 10: likes(john,ann)
*** Line 10 replaced ***
* end NO
Команда
end закрывает цикл редактирования. Затем делается попытка согласовать отредактированную цель, и в результате получается ответ
NO.
Тот же метод применим и в случае чтения файла в базу данных: ошибочные утверждения могут быть отредактированы, а затем процесс чтения файла продолжается.
Сеанс работы с PDSS завершается по команде bye. При этом система предупреждает пользователя о возможности утраты модулей, которые не были записаны в файлы.
* bye
*** The following module(s) have not been saved: ***
first Do you want to exit (y/n)?
* y
Normal exit from MPROLOG PDSS
Синтаксис
Синтаксис МПролога в основном совместим с синтаксисом Пролога-10. Правда, позиции операторов, их приоритеты и ассоциативность в МПрологе отличаются, однако, для обеспечения совместимости с тем, что описано в данной книге, предусмотрен встроенный предикат
ор. Списки можно задавать как с помощью точечной записи (используя для этого предварительно описанный оператор '.'), так и с помощью скобочной записи [].
Строки в МПрологе не эквивалентны списку кодов, составляющих их литер. Это означает, что пример из гл. 5 (база данных исторических событий) с вопросом
событие(1524,Х) будет работать и ответом будет 'Васко да Гама умер'.
Модульность
В самом языке и в системе разработки программ предусмотрены средства модульного построения программ. МПролог-программа может состоять из нескольких модулей, которые взаимодействуют между собой только через заданные интерфейсы модулей.
Например, предикат
найти для работы со словарем, имеющим вид упорядоченного дерева (см. разд. 7.1), может быть заключен в такой модуль:
module dictionary.
export (найти / 3, печ_дерево / 3).
import (меньше / 2).
visible (таблица, подряд), body.
найти(Н, b(H,G,_,_), G):-!.
найти(Н, в(Н1,_,BEFORE,_),G):- меньше(Н,Н1)?найти(Н,ВЕFОRЕ,G).
найти(Н,в(Н1,,_,AFTER),G):- not(меньше(Н,Н1)), найти (H,AFTER,G).
печ_дерево(T,FORM,KEYWORD):- var(T),!.
печ_дерево(в(H,W,L,G),F,K):- печ_дерево(L,F,K), печ_элемент(Н,W,F,K), печ_дерево(G,F,K).
печ_элемент(Н,W,таблица,K):- !, outterm(H), outtab(15), outterm(K),outspaces(l), outterm(W), newline.
печ_элемент(Н,W,подряд,K):- outterm(H), outspaces(l), outterm(K), outspaces(1), outterm(W), outterm(",").
end mod /* dictionary */.
Этот модуль «экспортирует» (т. е. делает доступным для других модулей) предикаты
найти/3 и
печ_дерево/3, и только эти предикаты данного модуля могут быть использованы вне его. Предикат
печ_дерево может выводить на печать заданное дерево в двух возможных форматах в соответствии с аргументом
FORM, который может иметь значения
таблица и
подряд. Эти два имени описаны как видимые, что указывает на то, что они используются не только внутри данного модуля например, как конструктор в-структур. Видимость имени не обязательно обозначает сохранение его символьного представления в другом модуле, однако, если оно используется в другом модуле как видимое имя, то эти два вхождения унифицируются.
Заметим, что конкретное представление дерева скрыто в данном модуле.
Рассмотрим еще один модуль, использующий определенные выше предикаты. Предположим, что у нас есть список лошадей, участвующих в бегах, в порядке их финиширования, а нам нужно получить алфавитный перечень их кличек с указанием занятого места. Для этого можно воспользоваться предикатом
печ_ индекс, который по списку кличек порождает дерево, а затем выводит его на печать.
module index.
export(печ_индекс/0).
import(найти/3, список_кличек/1, печ_дерево/3).
visible(таблица).
body.
печ_индекс:- список_кличек(L),созд_дерево(L, 1, Т, печ_дерево(Т,таблица,": ").
созд_дерево([],_,_):- !.
созд_дерево([NАМЕ|L,N,Т):- найти(NAME,T,N), M is N+1, созд_дерево(L,М,T).
endmod /* index */.
Здесь снова имя таблица задано как видимое, тогда как параметр
KEYWORD предиката
печ_дерево (здесь он имеет значение ".") заключен в двойные кавычки. Это означает, что символьное представление этого имени должно быть сохранено.
Компоненты системы МПролог
Ядром системы МПролог является интерпретатор. Другой основной компонентой системы является подсистема разработки программ
PDSS, которая сама написана на МПрологе и работает под управлением интерпретатора. Подсистема
PDSS обеспечивает возможности диалоговой разработки программ.
После того как фаза разработки программ закончена, можно воспользоваться тремя другими компонентами системы, обеспечивающими эффективность выполнения программы.
Претранслятор системы МПролог преобразует МПролог-модули во внутреннее представление, допускающее эффективное выполнение. Он обрабатывает элементы программы, осуществляя их оптимизацию, управляемую пользователем. Например, использование описаний вида
match_order и
mode позволяет значительно повысить эффективность поиска утверждений.
Второй компонентой системы является консолидатор, который объединяет двоичные модули в выполняемую программу. Объединение может осуществляться по шагам. Это означает, что несколько двоичных модулей можно объединить в один новый двоичный модуль с внешним интерфейсом, заданным пользователем.
Третьей из указанных выше компонент системы является компилятор, который преобразует двоичные модули (порождаемые претранслятором), заменяя представление программы, необходимое для интерпретатора, на непосредственно исполняемый машинный код. Система МПролог допускает объединение в готовую программу интерпретируемых и откомпилированных модулей.
Различные ограничения
Целые числа могут изменяться в диапазоне от -8 388 607 до 8 388 607. Действительные числа не предусмотрены. Приоритеты операторов могут изменяться от -3000 до 3000.
Дополнительные встроенные предикаты
В МПрологе предусмотрены некоторые дополнительные встроенные предикаты. Например, допускающие повторное согласование при возвратном ходе предикаты ввода, разнообразные предикаты вывода, работы со строками, с базой данных, а также предикаты обработки особых ситуаций.
Два основных предиката ввода
insymb(X) и
interm(X) допускают повторное согласование при возврате. Это означает, что при возвратном ходе выполненные ими действия «отменяются». Например, если первый вводимый символ не совпадает с
аааа, то вопрос
? insymb(aaaa).
не согласуется, причем в этом случае
аааа сохраняется во входном потоке и может быть считан последующими предикатами ввода
[21].
Эти предикаты обеспечивают дополнительные возможности для задания грамматических правил. Например, правила, приведенные в разд. 9.3, могут быть непосредственно преобразованы в следующие предикаты:
предложение:- группа_существительного, группа_глагола.
группа_существительного:- определитель, существительное.
группа_глагола:- глагол.
группа_глагола:- глагол, группа_существительного.
определитель:- insymb(the).
существительное:- insymb(man).
существительное:- insymb(apple).
глагол:- insymb(eats).
глагол:- insymb(sings).
Приведенный выше предикат
предложение завершается успешно, если из входного потока поступает предложение, удовлетворяющее заданной грамматике. Заметим, что обработка синтаксических ошибок и команда '=' реализуются на основе предикатов ввода, допускающих повторное согласование при возврате. Предикаты для работы с базой данных в МПрологе также имеют версии, допускающие повторное согласование. Например,
fdelclause(EXPR)
исключает первое утверждение, заголовок которого может быть сопоставлен с
EXPR, тогда как
fsupclause(EXPR)
только подавляет его. Это означает, что при возвратном ходе это утверждение возвращается на свое место. С помощью этого предиката можно, например, по-другому определить предикат
перейти из разд. 7.2:
перейти(X,X).
перейти(X,X):- в_след_комн(Х,Z), перейти(Z,Y).
в_след_комн(Х,Z):- fsupclause(d(X,Z)); fsupclause(d(Z,X)).
Здесь нам уже не нужен вспомогательный третий аргумент (содержащий список комнат, где мы уже бывали). Вместо этого, чтобы быть уверенным в том, что в каждую дверь мы входим только один раз, мы просто подавляем на период поиска факты, соответствующие дверям, через которые мы уже прошли.
Имеется большой набор предикатов вывода, позволяющий осуществлять разнообразные виды форматированного вывода. Например, можно задавать границы строк и предельную глубину вывода. Задание глубины вывода полезно при выводе очень сложных термов (или даже бесконечных термов поскольку в МПрологе соответствующих проверок не делается), когда нас интересует только их общая структура. Задание глубины вывода равной
N означает, что фактически выводиться будут только первые
N уровней терма, а подтермы уровня
N+1 будут представлены как
(…).
Предикаты обработки особых ситуаций МПролога позволяют программисту самому программировать действия по восстановлению при ошибках. Например, ниже представлен простой вариант средства 'спроси у пользователя', позволяющего запросить у пользователя указания, как продолжать выполнение, если встретился неопределенный предикат.
ask_the_user:- broken _call(С), outterm("How to continue from: "), outterm(C), outterm("?"), nl, interm(C), ineot.
где
broken_call(С) - это стандартный предикат, конкретизирующий переменную С ошибочным целевым утверждением. Выполнив целевое утверждение
newhandler("undefined predicate", ask_the_user)
система будет вызывать
ask_the_user (спроси_у_пользователя) всякий раз, когда что-либо окажется неопределенным. Например, определив предикаты
плотность и
нас как в разд. 2.5, но оставив неопределенным предикат
площадь:
плотность(X,Y):- нас(X,Р), площадь(X,A), Y is P/A.
нас(китай,800).
. . .
мы можем наблюдать следующий диалог:
*? плотность(китай,D).
How to continue from площадь(китай,_101)?
* площадь(китай,4).
D = 200
Continue (y/n)?
* y
NO
*? плотность(китай,D).
How to continue from площадь(китай,_101)?
* n.
NO
Другой важный встроенный предикат – это
error_protect (Call, Handler), который выполняет целевое утверждение
Call в защищенном окружении: когда внутри
Call возникает особая ситуация (не обрабатываемая текущим обработчиком особых ситуаций), выполняется
Handler.
Средства отладки
Средства трассировки МПролога аналогичны тем, что имеются в Прологе-10.
Литература
MPROLOG Language Reference Manual
MPROLOG User's Guide /VAX/11-VMS/ MPROLOG User's Guide /VAX/11 – UNIX/ MPROLOG User's Guide /IBM – VM/CMS/ MPROLOG User's Guide /Siemens BS2000/
Getting Started with MPROLOG
Указанная литература может быть получена через институт по координации вычислительной техники (SZKI), г. Будапешт, ВНР
.
Примечания
1
В книге термин «Пролог» употребляется в трех значениях: 1) Пролог – язык программирования с совокупностью синтаксических и семантических правил записи программ; 2) Пролог – программная система (интерпретатор), реализующая язык; эта система и осуществляет диалог с пользователем; 3) Пролог – машина, на которой Пролог-система выполняет (интерпретирует) программы, написанные на языке Пролог. Как правило, из контекста всегда ясно, какое значение используется в каждом конкретном случае. При необходимости явного указания при переводе использовались термины: «язык Пролог», «Пролог-система», «Пролог-машина». - Прим. пepeв.
(обратно)
2
Связь введенного понятия с математической логикой обсуждается в гл. 10. - Прим. ред.
(обратно)
3
В записи программ на Прологе и в ответах Пролог-системы используются слова двух типов: 1) имена, определяемые пользователем (например,
джон, книга, нравится)
; 2) имена и служебные слова, определенные в языке Пролог (например,
is,
get). Учитывая, что слова первого типа имеют некоторую смысловую нагрузку (для читателя, но не для Пролога), все они переведены на русский язык. Слова второго типа зарезервированы в языке Пролог. Поэтому в тексте они оставлены в исходном виде, за исключением переведенных на русский язык ответов Пролога на вопросы
yes - да,
no – нет.-
Прим. перев.
(обратно)
4
В оригинале – clause for a predicate – термин, определяющий конъюнкты предиката, переменные которых связаны квантором общности. Связь этого понятия с математической логикой обсуждается в гл. 10.- Прим. ред.
(обратно)
5
В книге ничего не говорится о буквах русского алфавита. Мы будем считать, что в набор допустимых литер Пролога входят русские буквы – строчные и прописные. - Прим. ред.
(обратно)
6
Код ASCII соответствует коду КОИ-7, широко распространенному на ЭВМ нашей страны. Различие имеет место лишь для кириллицы, отсутствующей в коде ASCII. - Прим. перев.
(обратно)
7
Это могло бы привести к успеху при соответствующем определении предиката
мать. - Прим. ред.
(обратно)
8
В оригинале использован термин Пролога «cut», и при переводе точнее было бы применить термин «сокращение». Однако, следуя терминологии более ранних публикаций о Прологе, мы сохраним термин «отсечение». - Прим. ред.
(обратно)
9
Модель, лежащая в основе трассировки, подробно описывается в гл. 8. - Прим. ред.
(обратно)
10
Имеется перевод: Нильсон Н. Принципы искусственного интеллекта. - М.: Радио и связь, 1985. - Прим. перев.
(обратно)
11
Имеется перевод 1-го издания: Уинстон П., Искусственный интеллект. - М.: Мир, 1980. - Прим. перев.
(обратно)
12
Имеется в виду константа в смысле Пролога. - Прим. ред.
(обратно)
13
Тем самым обеспечивает возможность вновь согласовать предикат consult. В противном случае механизм возврата никогда не смог бы миновать repeat, у которого всегда есть альтернативное решение. - Прим. ред.
(обратно)
14
На «ломаном» русском языке этот пример можно представить следующим образом: «Каждый мужчина нравится некоторая женщина».
все (X, мужчина (X)--› существует (Y, (женщина (Y) & нравится (X))))
. - Прим. ред.
(обратно)
15
Имеется перевод: Мендельсон Э. Введение в математическую логику.- М.: Наука, 1971.- Прим. перев.
(обратно)
16
Имеется перевод: Чень Ч., Ли Р. Математическая логика и автоматическое доказательство теорем.- М.: Наука, 1983.- Прим. перев.
(обратно)
17
В некоторых последующих примерах допущена неточность: в формулах используется импликация, хотя все импликации должны быть удалены на первом этапе.- Прим. перев.
(обратно)
18
В дальнейшем – Пролог-10.- Прим. перев.
(обратно)
19
The MPROLOG System, SZKI, Budapest, 1986.
© SZKI, Budapest, 1986
© перевод на русский язык, «Мир», 1987
(обратно)
20
Вспомогательная информация, выдаваемая по команде help, переведена на русский язык.- Прим. ред.
(обратно)
21
Здесь допущена неточность: во входном потоке при возвратном ходе сохраняется не
аааа, а то, что прочитано из него до возврата. - Прим. ред.
(обратно)
Оглавление
ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
ГЛАВА 1 ВВЕДЕНИЕ
1.1. Факты
1.2. Вопросы
1.3. Переменные
1.4. Конъюнкции
1.5. Правила
1.6. Заключение и упражнения
ГЛАВА 2 БОЛЕЕ ДЕТАЛЬНОЕ ОПИСАНИЕ
2.1. Синтаксические правила
2.1.1. Константы
2.1.2. Переменные
2.1.3. Структуры
2.2. Литеры
2.3. Операторы
2.4. Равенство и установление соответствия
2.5. Арифметика
2.6. Общая схема согласования целевых утверждений
2.6.1. Успешное доказательство конъюнкции целевых утверждений
2.6.2. Рассмотрение целевых утверждений при использовании механизма возврата
2.6.3. Установление соответствия
ГЛАВА 3. ИСПОЛЬЗОВАНИЕ СТРУКТУР ДАННЫХ
3.1. Структуры и деревья
3.2. Списки
3.3. Принадлежность элементов списку
3.4. Пример: преобразование предложений
3.5. Пример: упорядочение по алфавиту
3.6. Использование предиката присоединить и спецификация деталей
ГЛАВА 4. ВОЗВРАТ И ОТСЕЧЕНИЕ
4.1. Порождение множественных решений
4.2. Отсечение
4.3. Общие случаи использования отсечения
4.3.1. Подтверждение правильности выбора правила
4.3.2. Комбинация «отсечение-fail»
4.4. Проблемы, связанные с использованием отсечения
ГЛАВА 5 ВВОД И ВЫВОД
5.1. Ввод и вывод термов
5.1.1. Вывод термов
5.1.2. Ввод термов
5.2. Ввод и вывод литер
5.2.1. Вывод литер
5.2.2. Ввод литер
5.3. Ввод предложений
5.4. Чтение файлов и запись в файлы
5.4.1. Запись в файлы
5.4.2. Чтение файлов
5.4.3. Ввод программ
5.5. Объявление операторов
ГЛАВА 6. ВСТРОЕННЫЕ ПРЕДИКАТЫ
6.1. Ввод новых утверждений
6.2. Выполнение и невыполнение целевого утверждения
6.3. Классификация термов
6.4. Работа с утверждениями как с термами
6.5. Создание структур и работа с компонентами структур
6.6. Воздействие на процесс возврата
6.7. Формирование составных целевых утверждений
6.8. Равенство
6.9. Ввод и вывод данных
6.10. Обработка файлов
6.11. Вычисление арифметических выражений
6.12. Сравнение чисел
6.13. Наблюдение за выполнением программы на Прологе
ГЛАВА 7. ЕЩЕ НЕСКОЛЬКО ПРИМЕРОВ ПРОГРАММ
7.1. Словарь в виде упорядоченного дерева
7.2. Поиск в лабиринте
7.3. Ханойские башни
7.4. Справочник комплектующих деталей
7.5. Обработка списков
7.6. Представление и обработка множеств
7.7. Сортировка
7.8. Использование базы данных: random, генатом, найтивсе
7.9. Поиск по графу
7.10. Просеивай Двойки, Просеивай Тройки
7.11. Символьное дифференцирование
7.12. Отображение структур и преобразование деревьев
7.13. Применение предикатов clause и retract
ГЛАВА 8. ОТЛАДКА ПРОЛОГ-ПРОГРАММ
8.1. Расположение текстов программ
8.2. Типичные ошибки
8.3. Модель трассировки
8.4. Трассировка и контрольные точки
8.5. Фиксация ошибок
ГЛАВА 9. ИСПОЛЬЗОВАНИЕ ГРАММАТИЧЕСКИХ ПРАВИЛ В ПРОЛОГЕ
9.1. Проблема синтаксического анализа
9.2. Описание синтаксического анализа на языке Пролог
9.3. Запись грамматических правил в Прологе
9.4. Присоединение дополнительных аргументов
9.5. Введение дополнительных условий
9.6. Заключение
ГЛАВА 10. ПРОЛОГ И МАТЕМАТИЧЕСКАЯ ЛОГИКА
10.1. Краткое введение в исчисление предикатов
10.2. Приведение формул к стандартной форме
10.3. Форма записи дизъюнктов
10.4. Принцип резолюций и доказательство теорем
10.6. Пролог
10.7. Пролог и логическое программирование
ГЛАВА 11. ПРОГРАММНЫЕ ПРОЕКТЫ НА ПРОЛОГЕ
11.1. Простые проекты
11.2. Более сложные проекты
ПРИЛОЖЕНИЕ А. ОТВЕТЫ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
ПРИЛОЖЕНИЕ В. ПРОГРАММА ПРИВЕДЕНИЯ ФОРМУЛ ИСЧИСЛЕНИЯ ПРЕДИКАТОВ К СТАНДАРТНОЙ ФОРМЕ
ПРИЛОЖЕНИЕ С. РАЗЛИЧНЫЕ ВЕРСИИ ЯЗЫКА ПРОЛОГ
ПРИЛОЖЕНИЕ D. ПРОЛОГ ДЛЯ ЭВМ DEC SYSTEM-10
ПРИЛОЖЕНИЕ Е. МИКРО-ПРОЛОГ
ПРИЛОЖЕНИЕ F. СИСТЕМА МПРОЛОГ[19]
*** Примечания ***

 Рис. 1.1.
Рис. 1.1.


 Рис. 2.4.
Отметим, что для полноты картины нам необходимо было бы показать, как доказываются целевые утверждения женщина(мэри) и родители(джон,анна,фред). Однако столь подробная диаграмма не поместилась бы на одной странице.
Данный пример иллюстрирует общую схему рассмотрения целевых утверждений, объединенных в конъюнкцию, для случая, когда все цели согласуются с базой данных. Стрелка перемещается вниз по странице, по очереди проходя через прямоугольники. Когда стрелка входит в какой-либо прямоугольник, выбирается некоторое утверждение и отмечается его позиция. Если данное утверждение сопоставимо с целью и является фактом, стрелка может покинуть прямоугольник (такая ситуация имела место для целевых утверждений мать и отец). Если же утверждение сопоставимо с целью, но является правилом, создаются прямоугольники для подцелей, и стрелка должна пройти через них, прежде чем она сможет покинуть первоначальный прямоугольник.
Рис. 2.4.
Отметим, что для полноты картины нам необходимо было бы показать, как доказываются целевые утверждения женщина(мэри) и родители(джон,анна,фред). Однако столь подробная диаграмма не поместилась бы на одной странице.
Данный пример иллюстрирует общую схему рассмотрения целевых утверждений, объединенных в конъюнкцию, для случая, когда все цели согласуются с базой данных. Стрелка перемещается вниз по странице, по очереди проходя через прямоугольники. Когда стрелка входит в какой-либо прямоугольник, выбирается некоторое утверждение и отмечается его позиция. Если данное утверждение сопоставимо с целью и является фактом, стрелка может покинуть прямоугольник (такая ситуация имела место для целевых утверждений мать и отец). Если же утверждение сопоставимо с целью, но является правилом, создаются прямоугольники для подцелей, и стрелка должна пройти через них, прежде чем она сможет покинуть первоначальный прямоугольник.
 Рис. 2.5.
Отступая дальше, стрелка достигнет места, где было выбрано утверждение, соответствующее целевому утверждению отец. В первую очередь освобождаются все переменные, которые были конкретизированы в результате использования данного утверждения. Это означает, что переменная F вновь становится неконкретизированной. Затем Пролог просматривает базу данных, начиная с утверждения, следующего за первым утверждением с предикатом отец (здесь находится маркер), пытаясь найти альтернативное утверждение. Если предположить, что мэри имеет только одного отца, то этот процесс успехом не завершится. Поэтому стрелка продолжит отступление. Она покинет прямоугольник отец(мэри, F) (это целевое утверждение недоказуемо) и вернется в прямоугольник мать(мэри,анна) (для того, чтобы попытаться передоказать данное целевое утверждение) (см. рис. 2.6).
Рис. 2.5.
Отступая дальше, стрелка достигнет места, где было выбрано утверждение, соответствующее целевому утверждению отец. В первую очередь освобождаются все переменные, которые были конкретизированы в результате использования данного утверждения. Это означает, что переменная F вновь становится неконкретизированной. Затем Пролог просматривает базу данных, начиная с утверждения, следующего за первым утверждением с предикатом отец (здесь находится маркер), пытаясь найти альтернативное утверждение. Если предположить, что мэри имеет только одного отца, то этот процесс успехом не завершится. Поэтому стрелка продолжит отступление. Она покинет прямоугольник отец(мэри, F) (это целевое утверждение недоказуемо) и вернется в прямоугольник мать(мэри,анна) (для того, чтобы попытаться передоказать данное целевое утверждение) (см. рис. 2.6).


 Рис. 3.2.
Рис. 3.2.
 Рис. 3.3.
Рис. 3.3.
 Рис. 3.4.
Рис. 3.4.
 Аналогично список, состоящий из атомов a, b и с, мог бы быть записан как .(а,.(b,.(с,[]))), что изображается следующим образом:
Аналогично список, состоящий из атомов a, b и с, мог бы быть записан как .(а,.(b,.(с,[]))), что изображается следующим образом:
 Иногда функтор точка ('.') определяется как оператор, так что допустимо для Пролога два последних списка записать как а.[] и а.(b.(с.[]))). Второй список можно было бы записать просто как а.b.с.[], так как функтор точка – правоассоциативный оператор. Списки являются упорядоченными последовательностями элементов, так что список а.b отличается от списка b.а.
Некоторые любят записывать древовидные диаграммы списков в виде дерева, «растущего» слева направо, ветви которого направлены вниз. Приведенный выше список, представленный диаграммой в виде такой «виноградной лозы» выглядит так:
Иногда функтор точка ('.') определяется как оператор, так что допустимо для Пролога два последних списка записать как а.[] и а.(b.(с.[]))). Второй список можно было бы записать просто как а.b.с.[], так как функтор точка – правоассоциативный оператор. Списки являются упорядоченными последовательностями элементов, так что список а.b отличается от списка b.а.
Некоторые любят записывать древовидные диаграммы списков в виде дерева, «растущего» слева направо, ветви которого направлены вниз. Приведенный выше список, представленный диаграммой в виде такой «виноградной лозы» выглядит так:
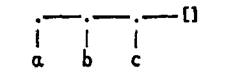 В этой диаграмме компонента функтора '.', соответствующая голове списка, «свисает» вниз, а компонента, соответствующая хвосту списка, «растет» вправо. Конец списка четко выделен тем, что последняя компонента – хвост списка – является пустым списком. Главное преимущество использования диаграммы для представления списка заключается в том, что она может быть записана справа налево на листе бумаги.
«Виноградная» диаграмма может оказаться удобной для записи списков на бумаге, когда нам необходимо видеть структуру списка, но в программах на Прологе для записи списков такие диаграммы не используются. Так как запись сложных списков с помощью функтора '.' часто оказывается неудобной, то в Прологе предусмотрена другая синтаксическая форма, которая может быть использована для записи списков в программе. Это так называемая скобочная форма записи списка. Она представляет собой заключенную в квадратные скобки последовательность элементов списка, разделенных запятыми. Например, упоминавшиеся выше списки могут быть записаны в скобочной форме в виде [а] и [а, b, с]. Списки могут содержать другие списки или переменные. Например, в Прологе допустимы следующие списки:
[]
[конкретный, человек, [любит, ловить, рыбу]]
[а, V1, b, [X, Y]]
Переменные, входящие в списки, ничем не отличаются от переменных в любой другой структуре. Они в любой момент могут быть конкретизированы, так что умелое использование переменных может обеспечить образование «пустых мест» в списке, которые впоследствии могут быть заполнены данными.
Чтобы продемонстрировать структуру списков, содержащих в качестве элементов другие списки, приведем «виноградную» диаграмму для последнего из рассмотренных списков:
В этой диаграмме компонента функтора '.', соответствующая голове списка, «свисает» вниз, а компонента, соответствующая хвосту списка, «растет» вправо. Конец списка четко выделен тем, что последняя компонента – хвост списка – является пустым списком. Главное преимущество использования диаграммы для представления списка заключается в том, что она может быть записана справа налево на листе бумаги.
«Виноградная» диаграмма может оказаться удобной для записи списков на бумаге, когда нам необходимо видеть структуру списка, но в программах на Прологе для записи списков такие диаграммы не используются. Так как запись сложных списков с помощью функтора '.' часто оказывается неудобной, то в Прологе предусмотрена другая синтаксическая форма, которая может быть использована для записи списков в программе. Это так называемая скобочная форма записи списка. Она представляет собой заключенную в квадратные скобки последовательность элементов списка, разделенных запятыми. Например, упоминавшиеся выше списки могут быть записаны в скобочной форме в виде [а] и [а, b, с]. Списки могут содержать другие списки или переменные. Например, в Прологе допустимы следующие списки:
[]
[конкретный, человек, [любит, ловить, рыбу]]
[а, V1, b, [X, Y]]
Переменные, входящие в списки, ничем не отличаются от переменных в любой другой структуре. Они в любой момент могут быть конкретизированы, так что умелое использование переменных может обеспечить образование «пустых мест» в списке, которые впоследствии могут быть заполнены данными.
Чтобы продемонстрировать структуру списков, содержащих в качестве элементов другие списки, приведем «виноградную» диаграмму для последнего из рассмотренных списков:
 Из приведенной диаграммы ясно видно, что каждый ее горизонтальный уровень является списком, состоящим из некоторого числа элементов. Верхний уровень на приведенной диаграмме представляет список, содержащий четыре элемента, один из которых сам является списком. Второй уровень, содержащий два элемента, представляет четвертый элемент списка верхнего уровня. Работа со списками основана на расщеплении их наголову и хвост списка. Голова списка – это первый аргумент функтора '.', который используется для конструирования списка. Хвост списка – это второй аргумент функтора '.'. В случае когда для записи списка используется скобочная форма записи, головой списка является первый его элемент. Хвост списка представляет список, состоящий из всех элементов исходного списка, за исключением первого его элемента. Следующие примеры демонстрируют расщепление списков на голову и хвост:
Из приведенной диаграммы ясно видно, что каждый ее горизонтальный уровень является списком, состоящим из некоторого числа элементов. Верхний уровень на приведенной диаграмме представляет список, содержащий четыре элемента, один из которых сам является списком. Второй уровень, содержащий два элемента, представляет четвертый элемент списка верхнего уровня. Работа со списками основана на расщеплении их наголову и хвост списка. Голова списка – это первый аргумент функтора '.', который используется для конструирования списка. Хвост списка – это второй аргумент функтора '.'. В случае когда для записи списка используется скобочная форма записи, головой списка является первый его элемент. Хвост списка представляет список, состоящий из всех элементов исходного списка, за исключением первого его элемента. Следующие примеры демонстрируют расщепление списков на голову и хвост:
 Рис. 4.1.
Рис. 4.1.

 Рис. 4.4.
Рис. 4.4.
 Рис. 4.5.
Действие отсечения в этом примере можно резюмировать следующим образом:
Если оказывается, что читатель имеет не возвращенную в срок книгу, то ему разрешается пользоваться лишь основными видами услуг, предоставляемыми библиотекой. Нет необходимости выявлять все книги, не возвращенные читателем в срок, равно как нет необходимости рассматривать какие-либо другие правила относительно услуг, предоставляемых читателю.
В этом примере использование отсечения привело к «сокращению» всех решений, принятых после выбора целевого утверждения услуги. Оно называется родительским целевым утверждением для отсечения, так как именно это целевое утверждение привело к использованию правила, содержащего отсечение. На наших диаграммах родительским целевым утверждением всегда является целевое утверждение, соответствующее наименьшему прямоугольнику, содержащему прямоугольник с '!'. Формальное определение эффекта, производимого отсечением, формулируется следующим образом:
Если отсечение встречается в качестве целевого утверждения, то после этого система лишается возможности изменять решения, принятые ею с момента вызова родительского целевого утверждения. Все альтернативы принятым решениям отбрасываются. Следовательно, попытка вновь доказать согласованность с базой данных любого целевого утверждения между родительским целевым утверждением и ! (отсечением) закончится неудачей.
Существуют различные способы описания того, что произошло с решениями, попавшими в область действия отсечения. Можно сказать, что эти решения отсекаются или замораживаются, что система лишается возможности изменять эти решения или что оставшиеся альтернативы отбрасываются. Можно также смотреть на символ отсечения как на некий разделитель (забор), отделяющий целевые утверждения. Так, при обработке конъюнкции целей
Рис. 4.5.
Действие отсечения в этом примере можно резюмировать следующим образом:
Если оказывается, что читатель имеет не возвращенную в срок книгу, то ему разрешается пользоваться лишь основными видами услуг, предоставляемыми библиотекой. Нет необходимости выявлять все книги, не возвращенные читателем в срок, равно как нет необходимости рассматривать какие-либо другие правила относительно услуг, предоставляемых читателю.
В этом примере использование отсечения привело к «сокращению» всех решений, принятых после выбора целевого утверждения услуги. Оно называется родительским целевым утверждением для отсечения, так как именно это целевое утверждение привело к использованию правила, содержащего отсечение. На наших диаграммах родительским целевым утверждением всегда является целевое утверждение, соответствующее наименьшему прямоугольнику, содержащему прямоугольник с '!'. Формальное определение эффекта, производимого отсечением, формулируется следующим образом:
Если отсечение встречается в качестве целевого утверждения, то после этого система лишается возможности изменять решения, принятые ею с момента вызова родительского целевого утверждения. Все альтернативы принятым решениям отбрасываются. Следовательно, попытка вновь доказать согласованность с базой данных любого целевого утверждения между родительским целевым утверждением и ! (отсечением) закончится неудачей.
Существуют различные способы описания того, что произошло с решениями, попавшими в область действия отсечения. Можно сказать, что эти решения отсекаются или замораживаются, что система лишается возможности изменять эти решения или что оставшиеся альтернативы отбрасываются. Можно также смотреть на символ отсечения как на некий разделитель (забор), отделяющий целевые утверждения. Так, при обработке конъюнкции целей
 Рис. 4.6.
Упражнение 4.1. Что произойдет в процессе возврата при попытке найти новое сопоставление для целевогоутверждения сумма, если из первого правила для предиката сумма удалить отсечение? Какие альтернативные результаты будут получены (если вообще они будут возможны) и почему?
Последний пример показал, как можно использовать отсечение для того, чтобы сделать поведение Пролога чувствительным к случаю, когда мы не можем выделить все возможные случаи путем перечисления образцов в заголовках правил. Более типичная ситуация, в которой мы не можем указать структуру заголовков правил для выполнения сопоставления, возникает, если мы хотим ввести дополнительные условия в виде целевых утверждений Пролога, позволяющих в процессе согласования с базой данных выбрать соответствующие правила. Рассмотрим следующий альтернативный вариант решения последнего примера:
Рис. 4.6.
Упражнение 4.1. Что произойдет в процессе возврата при попытке найти новое сопоставление для целевогоутверждения сумма, если из первого правила для предиката сумма удалить отсечение? Какие альтернативные результаты будут получены (если вообще они будут возможны) и почему?
Последний пример показал, как можно использовать отсечение для того, чтобы сделать поведение Пролога чувствительным к случаю, когда мы не можем выделить все возможные случаи путем перечисления образцов в заголовках правил. Более типичная ситуация, в которой мы не можем указать структуру заголовков правил для выполнения сопоставления, возникает, если мы хотим ввести дополнительные условия в виде целевых утверждений Пролога, позволяющих в процессе согласования с базой данных выбрать соответствующие правила. Рассмотрим следующий альтернативный вариант решения последнего примера:
 Предполагается, что программа действует за игрока, делающего свои ходы ноликами. Предикат вынужденный_ход используется для ответа на вопрос: «Нужно ли делать вынужденный ход в конкретной позиции?» Такая ситуация имеет место, если игрок 0 (игрок, делающий ходы ноликами, т. е. программа) не может выиграть немедленно (мы не будем рассматривать этот слу- случай), но есть угроза того, что игрок X может выиграть следую- следующим ходом. Например, в позиции
Предполагается, что программа действует за игрока, делающего свои ходы ноликами. Предикат вынужденный_ход используется для ответа на вопрос: «Нужно ли делать вынужденный ход в конкретной позиции?» Такая ситуация имеет место, если игрок 0 (игрок, делающий ходы ноликами, т. е. программа) не может выиграть немедленно (мы не будем рассматривать этот слу- случай), но есть угроза того, что игрок X может выиграть следую- следующим ходом. Например, в позиции
 Игрок 0 вынужден поставить 0 в 4-й квадрат, так как если он не сделает этого, то его противник будет иметь возможность на следующем ходу заполнить линию 1-4-7. Программа работает, пытаясь найти линию, две клетки которой заполнены крестиками, а третья – пустая. Если такая линия имеется, то игрок 0 вынужден сделать ход, поставив нолик в пустую клетку. В утверждении для предиката вынужденный_ход цель
Игрок 0 вынужден поставить 0 в 4-й квадрат, так как если он не сделает этого, то его противник будет иметь возможность на следующем ходу заполнить линию 1-4-7. Программа работает, пытаясь найти линию, две клетки которой заполнены крестиками, а третья – пустая. Если такая линия имеется, то игрок 0 вынужден сделать ход, поставив нолик в пустую клетку. В утверждении для предиката вынужденный_ход цель

 Рис. 7.2.
Заметим, что информация о наличии дверей не избыточна. Например, мы сказали, что имеется дверь, ведущая из комнаты g в комнату е, но не сказали, что имеется дверь, ведущая из комнаты е в комнату g, т. е. мы не зафиксировали утверждение д(e,g). Чтобы обойти эту проблему представления двухсторонних дверей, мы могли бы повторно записать д-факт для каждой двери с перестановкой аргументов. Или мы могли бы устроить программу таким образом, чтобы она понимала, что каждая дверь фактически может рассматриваться как двухсторонняя. Этот вариант мы и выбрали в нижеследующей программе.
Чтобы перейти из одной комнаты в другую, мы должны распознать один из следующих случаев:
• мы находимся в той комнате, которая нам нужна, или
• мы должны войти в дверь и распознать эти случаи снова (рекурсивно).
Рассмотрим целевое утверждение переход(X,Y,T), которое доказуемо (согласуется с базой данных), если можно перейти из комнаты X в комнату Y. Третий аргумент Т – это наш листок бумаги, который мы носим с собой и на котором записан перечень номеров комнат, в которых мы побывали до сего момента.
Граничное условие перехода из комнаты X в комнату Y состоит в том, что, возможно, мы уже находимся в комнате Y (т. е., возможно, X есть Y). Это условие представлено в виде утверждения:
Рис. 7.2.
Заметим, что информация о наличии дверей не избыточна. Например, мы сказали, что имеется дверь, ведущая из комнаты g в комнату е, но не сказали, что имеется дверь, ведущая из комнаты е в комнату g, т. е. мы не зафиксировали утверждение д(e,g). Чтобы обойти эту проблему представления двухсторонних дверей, мы могли бы повторно записать д-факт для каждой двери с перестановкой аргументов. Или мы могли бы устроить программу таким образом, чтобы она понимала, что каждая дверь фактически может рассматриваться как двухсторонняя. Этот вариант мы и выбрали в нижеследующей программе.
Чтобы перейти из одной комнаты в другую, мы должны распознать один из следующих случаев:
• мы находимся в той комнате, которая нам нужна, или
• мы должны войти в дверь и распознать эти случаи снова (рекурсивно).
Рассмотрим целевое утверждение переход(X,Y,T), которое доказуемо (согласуется с базой данных), если можно перейти из комнаты X в комнату Y. Третий аргумент Т – это наш листок бумаги, который мы носим с собой и на котором записан перечень номеров комнат, в которых мы побывали до сего момента.
Граничное условие перехода из комнаты X в комнату Y состоит в том, что, возможно, мы уже находимся в комнате Y (т. е., возможно, X есть Y). Это условие представлено в виде утверждения:
 Простейшая программа поиска по графу, представленному так, как указано выше, выглядит следующим образом:
Простейшая программа поиска по графу, представленному так, как указано выше, выглядит следующим образом:
 Рис. 7.4
Рис. 7.4
 Риc. 8.1
(1) CALL: потомок(авраам,Ответ)
(2) CALL: отпрыск(авраам,Ответ)
Мы сопоставили с целью первое утверждение процедуры потомок и это привело к ВЫЗОВ цели отпрыск. В результате возникла ситуация, где стрелка движется вниз (см. рис. 8.2). Мы продолжаем:
Риc. 8.1
(1) CALL: потомок(авраам,Ответ)
(2) CALL: отпрыск(авраам,Ответ)
Мы сопоставили с целью первое утверждение процедуры потомок и это привело к ВЫЗОВ цели отпрыск. В результате возникла ситуация, где стрелка движется вниз (см. рис. 8.2). Мы продолжаем:



 (9) EXIT: потомок(исаак,исав)
(1) EXIT: потомок(авраам,исав)
(11) CALL: fail
(11) FAIL: fail
(1) REDO: потомок(исаак,исав)
(9) REDO: потомок(исаак,исав)
Это дает окончательное решение исходного вопроса, однако fail вновь вынуждает включиться механизм возврата, поэтому мы возвращаемся назад по событиям REDO:
(10) REDO: отпрыск(исаак,исав)
(10) EXIT: отпрыск(исаак,иаков)
(9) EXIT: потомок(исаак,иаков)
(1) EXIT: потомок(авраам,иаков)
Для подцели отпрыск найдено другое сопоставление, которое порождает другой результат для исходной цели потомок. Уже сейчас можно заметить, что это последний потомок Авраама, однако еще остается выполнить определенный объем работы. Проследим далее за последовательностью событий по мере того, как механизм возврата заставляет нас отступать к началу.
(12) CALL: fail
(12) FAIL: fail
(1) REDO: потомок(авраам,иаков)
(9) REDO: потомок(исаак,иаков)
(10) REDO: отпрыск(исаак,иаков)
(10) FAIL: отпрыск(исаак,Ответ)
(13) CALL: отпрыск(исаак,YЗ)
Теперь мы пытаемся применить второе утверждение процедуры потомок.
(13) EXIT: отпрыск(исаак,исав)
(14) CALL; потомок(исав, Ответ)
Еще одна рекурсия
(15) CALL: отпрыск(исав,Ответ)
(15) FAIL: отпрыск(исав,Ответ)
(16) CALL: отпрыск(исав,Y4)
(16) FAIL: отпрыск(исав,Y4)
(14) FAIL: потомок(исав,Ответ)
(13) REDO: отпрыск(исаак,исав)
(13) EXIT: отпрыск(исаак,иаков)
(17) CALL: потомок(иаков,Ответ)
Пытаемся использовать Иакова.
(18) CALL: отпрыск (иаков,Ответ)
(18) FAIL: отпрыск (иаков, Ответ)
(19) CALL: отпрыск(иаков,Y5)
(19) FAIL: отпрыск (иаков, Y5)
(17) FAIL: потомок(иаков,Ответ)
(13) REDO: отпрыск(исаак,иаков)
(13) FAIL: отпрыск(исаак,YЗ)
(9) FAIL: потомок(исаак,Ответ)
(1) FAIL: потомок(авраам,Ответ) нет
Наконец мы закончили. Надеемся, что этот утомительный пример дал вам возможность понять последовательность событий, происходящих при выполнении Пролог-программы. Вы, вероятно, уже заметили, что для любой цели всегда бывает только один ВЫЗОВ (событие CALL) и одна НЕУДАЧА (событие FAIL), хотя может быть сколько угодно ПЕРЕДЕЛОК (событие REDO) и соответствующих ВЫХОДов (событие EXIT). В следующем разделе мы рассмотрим процесс трассировки для более сложного примера – предиката присоединить.
Упражнение 8.1. В приведенной выше модели ничего не говорится о том, как обрабатывается цель – отсечение '!'. Расширьте эту модель, включив туда учет действия отсечения.
(9) EXIT: потомок(исаак,исав)
(1) EXIT: потомок(авраам,исав)
(11) CALL: fail
(11) FAIL: fail
(1) REDO: потомок(исаак,исав)
(9) REDO: потомок(исаак,исав)
Это дает окончательное решение исходного вопроса, однако fail вновь вынуждает включиться механизм возврата, поэтому мы возвращаемся назад по событиям REDO:
(10) REDO: отпрыск(исаак,исав)
(10) EXIT: отпрыск(исаак,иаков)
(9) EXIT: потомок(исаак,иаков)
(1) EXIT: потомок(авраам,иаков)
Для подцели отпрыск найдено другое сопоставление, которое порождает другой результат для исходной цели потомок. Уже сейчас можно заметить, что это последний потомок Авраама, однако еще остается выполнить определенный объем работы. Проследим далее за последовательностью событий по мере того, как механизм возврата заставляет нас отступать к началу.
(12) CALL: fail
(12) FAIL: fail
(1) REDO: потомок(авраам,иаков)
(9) REDO: потомок(исаак,иаков)
(10) REDO: отпрыск(исаак,иаков)
(10) FAIL: отпрыск(исаак,Ответ)
(13) CALL: отпрыск(исаак,YЗ)
Теперь мы пытаемся применить второе утверждение процедуры потомок.
(13) EXIT: отпрыск(исаак,исав)
(14) CALL; потомок(исав, Ответ)
Еще одна рекурсия
(15) CALL: отпрыск(исав,Ответ)
(15) FAIL: отпрыск(исав,Ответ)
(16) CALL: отпрыск(исав,Y4)
(16) FAIL: отпрыск(исав,Y4)
(14) FAIL: потомок(исав,Ответ)
(13) REDO: отпрыск(исаак,исав)
(13) EXIT: отпрыск(исаак,иаков)
(17) CALL: потомок(иаков,Ответ)
Пытаемся использовать Иакова.
(18) CALL: отпрыск (иаков,Ответ)
(18) FAIL: отпрыск (иаков, Ответ)
(19) CALL: отпрыск(иаков,Y5)
(19) FAIL: отпрыск (иаков, Y5)
(17) FAIL: потомок(иаков,Ответ)
(13) REDO: отпрыск(исаак,иаков)
(13) FAIL: отпрыск(исаак,YЗ)
(9) FAIL: потомок(исаак,Ответ)
(1) FAIL: потомок(авраам,Ответ) нет
Наконец мы закончили. Надеемся, что этот утомительный пример дал вам возможность понять последовательность событий, происходящих при выполнении Пролог-программы. Вы, вероятно, уже заметили, что для любой цели всегда бывает только один ВЫЗОВ (событие CALL) и одна НЕУДАЧА (событие FAIL), хотя может быть сколько угодно ПЕРЕДЕЛОК (событие REDO) и соответствующих ВЫХОДов (событие EXIT). В следующем разделе мы рассмотрим процесс трассировки для более сложного примера – предиката присоединить.
Упражнение 8.1. В приведенной выше модели ничего не говорится о том, как обрабатывается цель – отсечение '!'. Расширьте эту модель, включив туда учет действия отсечения.

 Рис. 9.2.
И так далее. В результате этой процедуры, если она завершится успешно, мы выделим все словосочетания и их части, входящие в заданное предложение, в соответствии с тем, как они определены грамматикой, и получим структуру, подобную приведенной на рис. 9.3. Эта диаграмма, показывающая структуру разбиения предложения на словосочетания, называется деревом (синтаксического) разбора предложения.
Мы увидели, как, имея грамматику языка, можно построить деревья разбора для предложений этого языка, чтобы показать их структуру. Задача построения дерева разбора предложения по заданной грамматике называется задачей синтаксического разбора (анализа). Программа для ЭВМ, которая строит деревья разбора для предложений языка, называется синтаксическим анализатором.
В этой главе будет показано, как задача синтаксического анализа может быть сформулирована в рамках языка Пролог. Будет введен используемый в Прологе формализм грамматических правил, значительно облегчающий создание синтаксических анализаторов на Прологе. Область применения вводимых далее идей не ограничивается синтаксисом естественных языков. Действительно, те же самые методы применимы к любой задаче, объектом рассмотрения которой является упорядоченная последовательность элементов, которая некоторым естественным образом может быть разбита на группы, а порядок этих групп может быть определен множеством правил. Однако, ради простоты, в оставшейся части этой главы будет рассматриваться задача синтаксического анализа предложений на английском языке, а обобщение изложенных далее идей и методов на другие области предоставляется читателю.
предложение
Рис. 9.2.
И так далее. В результате этой процедуры, если она завершится успешно, мы выделим все словосочетания и их части, входящие в заданное предложение, в соответствии с тем, как они определены грамматикой, и получим структуру, подобную приведенной на рис. 9.3. Эта диаграмма, показывающая структуру разбиения предложения на словосочетания, называется деревом (синтаксического) разбора предложения.
Мы увидели, как, имея грамматику языка, можно построить деревья разбора для предложений этого языка, чтобы показать их структуру. Задача построения дерева разбора предложения по заданной грамматике называется задачей синтаксического разбора (анализа). Программа для ЭВМ, которая строит деревья разбора для предложений языка, называется синтаксическим анализатором.
В этой главе будет показано, как задача синтаксического анализа может быть сформулирована в рамках языка Пролог. Будет введен используемый в Прологе формализм грамматических правил, значительно облегчающий создание синтаксических анализаторов на Прологе. Область применения вводимых далее идей не ограничивается синтаксисом естественных языков. Действительно, те же самые методы применимы к любой задаче, объектом рассмотрения которой является упорядоченная последовательность элементов, которая некоторым естественным образом может быть разбита на группы, а порядок этих групп может быть определен множеством правил. Однако, ради простоты, в оставшейся части этой главы будет рассматриваться задача синтаксического анализа предложений на английском языке, а обобщение изложенных далее идей и методов на другие области предоставляется читателю.
предложение
 Рис. 9.3.
Рис. 9.3.
 На основе ранее введенных предложений программа должна выдавать соответствующий ответ (yes (да), no (нет), ok (принято), unknown (неизвестно)). Например,
John is a man.
ok
A man is a person.
ok
Is John a person?
yes
Is Mary a person?
unknown
Каждое предложение должно транслироваться в утверждение Пролога, которое затем в зависимости от его характера, либо помещается в базу данных, либо выполняется как целевое. Так, результаты трансляции предложений приведенного выше примера выглядят следующим образом:
На основе ранее введенных предложений программа должна выдавать соответствующий ответ (yes (да), no (нет), ok (принято), unknown (неизвестно)). Например,
John is a man.
ok
A man is a person.
ok
Is John a person?
yes
Is Mary a person?
unknown
Каждое предложение должно транслироваться в утверждение Пролога, которое затем в зависимости от его характера, либо помещается в базу данных, либо выполняется как целевое. Так, результаты трансляции предложений приведенного выше примера выглядят следующим образом: