

Предлагаемая вниманию читателей книга Э. Тейлора и Дж. Уилера — учебник по частной теории относительности для младших студентов -физиков и старших школьников, написанный в том новом стиле, который, получив заслуженное признание, успешно пробивает себе дорогу в современных вузах и, будем надеяться, в скором времени завоюет и среднюю школу. Это учебник для начинающих физиков, а так как идеи теории относительности стали в наши дни краеугольным камнем общечеловеческой культуры, это и учебник для всех людей, интересующихся естественными науками. Он написан просто, но скрупулёзно строго: его авторы — крупные физики и отличные педагоги.
Книги такого рода полезно читать в два-три, а то и более приёмов: сначала как увлекательный роман, а затем как запутанную детективную повесть, в которой нужно разобраться до конца, и знание дальнейшего развития «фабулы» здесь помогает лишь лучше понять суть дела и делает более острой «интригу» .
Успехи XIX столетия в развитии механики, электромагнетизма и изучении свойств материи были гармонично объединены в XX веке великими принципами относительности и квантов. Изучать даже начальный курс физики, не пользуясь всей мощью этих основополагающих принципов, — это то же самое, что заниматься мучительной процедурой деления, пользуясь римскими цифрами вместо куда более подходящих арабских.


EDWIN F. TAYLOR
Massachusetts Institute of Technology
JOHN ARCHIBALD WHEELER
Princeton University
SPACETIME PHYSICS
W. H. Freeman and Company
San Francisco and London 1966
Э.Ф. Тейлор, Дж. А. Уилер
ФИЗИКА
ПРОСТРАНСТВА-
ВРЕМЕНИ
Перевод с английского
Н. В. Мицкевича
ИЗДАНИЕ ВТОРОЕ, ДОПОЛНЕННОЕ
ИЗДАТЕЛЬСТВО • МИР •
МОСКВА 1971
УДК 530.12(07)
Редакция космических исследований, астрономии и геофизики
Инд. 2-6-2, 2-3-2
102-71
ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
Предлагаемая вниманию читателей книга — учебник по частной теории относительности 1) для студентов-физиков младших курсов и школьников старших классов, написанный в том новом стиле, который, получив заслуженное признание, успешно пробивает себе дорогу в современных вузах и, будем надеяться, в скором времени завоюет также среднюю школу. Эта книга — учебник для начинающих физиков, а так как идеи теории относительности стали в наши дни краеугольным камнем общечеловеческой культуры, это и учебник для всех молодых людей, интересующихся естественными науками. Он написан просто и скрупулёзно строго: его авторы — крупные физики и отличные педагоги. Особенно хорошо известно имя Джона Арчибалда Уилера, «старожила» Принстона, одного из патриархов ядерной физики. Того самого Уилера, который вместе с Нильсом Бором является автором знаменитой теории деления атомных ядер, открывшей эпоху технических приложений ядерной энергии; ядерщика, «на старости лет» (да простит мне эти слова Уилер, который всегда остаётся молодым) переключившегося на гравитацию. Именно участие Уилера в создании этой книги наложило на неё отпечаток специфической деловитости и вместе с тем непринуждённости, наглядного и творческого в своей основе подхода к самым сокровенным и глубоким «тайнам» теории относительности. Профессор Эдвин Ф. Тейлор известен больше как педагог. Следует сказать, однако, что и Уилер много внимания уделил преподаванию, и его ученики добились больших успехов: достаточно назвать Ричарда П. Фейнмана, лауреата Нобелевской премии по физике.
1) Часто говорят: «специальная теория относительности», отдавая тем самым дань буквенному (но не всегда буквальному) совпадению английского слова «special»— специальный, частный (например, «special case» — частный случай), и русского слова «специальный», имеющего чаще всего иной оттенок. Как известно, Эйнштейн творил на немецком языке (если не считать интернационального языка формул), где впервые и прозвучало в данном контексте слово «speziell». Заметим, что французы говорят «relativite restreinte»— именно частная теория относительности. Неискушённому читателю иногда даже кажется, что «общая» теория относительности предназначена «для всех», для широкого круга людей, а «специальная»— лишь для избранных специалистов, тогда как дело обстоит фактически наоборот! Читатель может убедиться, что специальную теорию относительности именует частной не один лишь переводчик этой книги,— для этого достаточно прочесть полезную во всех отношениях статью академика В. Л. Гинзбурга в журнале «Наука и жизнь» (№№ 1-3 за 1968 г.).
Безусловно, на характер изложения теории относительности в книге Тейлора и Уилера наложили отпечаток программы американских (и вообще западных) вузов. Программы английской и американской систем вузов построены более утилитарно, чем наши. Это естественно: многие студенты кончают университет, проучившись всего три года, т.е. пройдя курс усиленного техникума (степень бакалавра — bachelor); другие остаются ещё на два-три года и получают степень магистра (master). Чтобы примирить оба эти варианта, приходится разобщать концентры обучения (до некоторой степени аналогичные нашим) в большей степени, чем это имеет место в наших вузах. В этих условиях теоретическая подготовка оказывается менее существенным вопросом, и, например, принципы теоретической механики либо вовсе не читаются, либо читаются уже после курса квантовой механики. Однако в курсе общей физики больший удельный вес приобретают теоретические вопросы; в ряде западных учебников для первых курсов университетов петитом даются детали, подлежащие обычно освещению лишь в курсе теоретической физики. Поскольку в американских и английских вузах больший упор в преподавании делается на демонстрационный эксперимент и запоминание фактического материала, советским студентам оказывается легче усваивать абстрактную сторону теории в книгах типа той, что вы держите сейчас в руках: авторы предельно разжёвывают теоретические вопросы. Поэтому нашим студентам следует рекомендовать решать больше упражнений в этой книге, чем предлагают её авторы. Для них будут достаточно простыми и упражнения, помеченные одной звёздочкой.
Вообще при чтении этой книги необходимо выработать и соблюдать строгую систему (которую не мешает перенести и на работу с другими книгами!). Изложение сплошь и рядом может показаться слишком простым, если не примитивным, но в действительности авторы очень глубоко продумали все средства воздействия (в том числе эмоционального) на читателя, так что нельзя оставлять без внимательных размышлений ни одной притчи в этой книге. Таким образом, важно несколько раз возвращаться к одной и той же теме, и вы каждый раз будете находить в ней что-нибудь новое и содержательное, что прежде ускользало от вашего внимания, и вместе с тем такое, что должно играть принципиальную роль в понимании явлений. Книги такого рода полезно читать в два-три, а то и более приёмов: сначала как увлекательный роман, а затем как запутанную детективную повесть, в которой нужно разобраться до конца, и знание дальнейшего развития «фабулы» здесь может лишь помочь лучше понять суть дела. Решать же упражнения следует всегда в одной тетради или на собираемых в папке листах, уж во всяком случае не на каких-нибудь обрывках. Эти советы ясны для любого студента (хотя он и не всегда им, к сожалению, следует), но их полезно повторить специально для школьников, которые очень много выиграют, если возьмутся осилить эту книгу. Они получат большое удовольствие и ещё большую реальную пользу. Заметим, что многие упражнения без звёздочек составлены вполне на школьном уровне!
Теория относительности — довольно разнородная как по составу, так и по своему состоянию область науки. Частная теория уже практически устоялась, и в ней возможны главным образом чисто методические усовершенствования. Общая теория, напротив, если и достаточно полна по своей общей геометрической формулировке, но в физическом отношении пока ещё туманна и не завершена (на это жаловался уже сам Эйнштейн). Тейлор и Уилер лишь слегка касаются в своей книге общей теории относительности, стараясь сделать акцент на геометрической концепции Вселенной (позиции чисто уилеровские!), и здесь полезно сделать некоторые оговорки.
Уилер уже много лет (см. его книгу «Гравитация, нейтрино, Вселенная», ИЛ, 1962) провозглашает и проводит в жизнь программу построения «физики как геометрии», противопоставляя ей динамическую теорию полей и частиц. Этот подход логически вполне последователен, лишь его выражение страдает определёнными пороками. Уилер, провозглашая первенствующую роль геометрии, забывает, что геометрия (в его же концепции!) — опытная наука, а не априорная, т.е. это та же физика, но выраженная специфическим языком. Именно поэтому и все понятия физики сохраняют жизненность и ценность, подвергаясь диалектическому переосмыслению в общей теории относительности. Именно поэтому слова Уилера о «массе без массы» и о «материи без материи» остаются лишь словами, ибо в современной физике уже давно под массой понимают отнюдь не только массу механических образований, но и массу поля. Что же касается материи, то можно с уверенностью утверждать, что и электромагнитное, и гравитационное, и все другие физические поля — это разные конкретные виды материи. Заметим при этом, что сведение всего к полям — программа привлекательная, но, увы, по сей день она остаётся лишь программой.
Стремясь избавиться от динамической трактовки явлений, авторы призывают отказаться от термина «гравитационное поле», вводя вместо него «приливное поле», и тут же поясняют, что оба термина — синонимы. Трудно ожидать, что этот новый термин привьётся, так как его преимущества сомнительны даже в чисто методическом отношении. Главное в их аргументации — факт отсутствия «гравитационной силы» в локально инерциальной системе отсчёта. Если наш читатель в дальнейшем познакомится с общей теорией относительности детальнее (например, по отличной стандартной книге Л. Д. Ландау и Е. М. Лифшица «Теория поля», изд-во «Наука», 1967), то он заметит, что на пробную частицу, конечно, вообще не действует никакая ковариантная (т.е. в данном случае 4-векторная) гравитационная сила. Однако достаточно взять две пробные массы, столь малые, чтобы их взаимодействием можно было пренебречь, и тогда «разность» этих, «равных нулю», гравитационных векторных сил, действующих со стороны на наши частицы, окажется отличной от нуля, если в данной четырёхмерной области пространство-время искривлено, т.е. если здесь объективно присутствует гравитация. Читателю предлагается поразмыслить над тем, насколько эта ситуация (эффект девиации геодезических) напоминает приведённую в книге притчу о двух путешественниках.
Однако есть (очень немногие) пункты, касающиеся и частной теории относительности, когда авторы оказываются в плену традиционных не вполне точных представлений. Таков вопрос о соотношении между преобразованием Галилея и преобразованием Лоренца. Эти преобразования действительно отличаются друг от друга не только по форме записи; различие между ними сводится к тому, что второе из них относится к классу ортогональных преобразований, первое же — нет, если рассматривать его с 4-мерной точки зрения. Теория относительности доказывает не безусловную непригодность преобразования Галилея при больших скоростях, а несостоятельность подхода к нему как к 3-мерному преобразованию. Если же последовательно учитывать, что преобразование Галилея есть 4-мерное преобразование координат пространства-времени, то отсюда автоматически следует лишь недекартов характер системы координат, к которой оно приводит (вспомним, например, недекартовы координаты в случаях сферической или полярной систем, сравнительно простые ввиду своей ортогональности и 3-мерности).
Как показал Мёллер в своей книге (С. Мøller, The Theory of Relativity, Oxford, 1952), единственным отличием системы координат, к которой приводит преобразование Галилея, от декартовой (получаемой при преобразовании Лоренца) является неортогональность оси времени к пространственным осям, причём здесь применим стандартный метод ортогонализации, и тогда в совокупности преобразование Галилея и преобразование, ортогонализирующее все 4 координатные оси, автоматически даёт обычное преобразование Лоренца! Это преобразование ортогонализации уже не затрагивает системы отсчёта, так что преобразования Галилея и Лоренца физически эквивалентны. И можно без труда показать, что первое приводит в точности к тем же релятивистским эффектам, к каким приводит второе. Всё дело в том, что не всякое координатное время тождественно физическому (наблюдаемому) времени, и физическим является только то время, которое ортогонально пространственным измерениям. Итак, в ряде случаев переход к физическому времени в теории сводится к стандартным математическим вычислениям, и его можно совершить, используя так называемый формализм хронометрических инвариантов Зельманова [А. Л. Зельманов, Доклады АН СССР, 107, 815 (1956)].
Кстати сказать, этот формализм позволяет исследовать уже в рамках частной теории относительности физические эффекты в неинерциальных системах отсчёта, вопреки широко распространённому противоположному взгляду, разделяемому, очевидно, и авторами этой книги. Но в монографии В. А. Фока «Теория пространства, времени и тяготения» (Физматгиз, 1961) частная теория относительности уже была сформулирована в произвольных (в том числе ускоренно движущихся) системах координат и, следовательно, в неинерциальных системах отсчёта. Если теперь к подходу Фока добавить аппарат формализма Зельманова, то мы непосредственно придём к связи между математическим выражением теории в неинерциальных системах отсчёта и физическими наблюдаемыми величинами, так что синтез этих двух формулировок даёт все эффекты неинерциальных систем наряду с обычными «инерциальными» релятивистскими эффектами. Однако детальное изложение вопроса требует более мощного математического аппарата, чем используемый в книге Тейлора и Уилера, и мы не будем здесь касаться его подробнее, отсылая читателя к нашей книге «Физические поля в общей теории относительности» («Наука», 1969), где наряду с другими вопросами излагаются основы формализма Зельманова и некоторые его применения.
Тем не менее факт применимости частной теории относительности к описанию неинерциальных систем отсчёта не следует понимать как полное приравнивание неинерциальных систем к инерциальным. Следует помнить, что в неинерциальных системах отсчёта физические законы специфически видоизменяются. Этот факт играет определяющую роль при переходе к общей теории относительности, где инерциальную систему отсчёта можно вводить лишь локально (неголономность инерциальных систем в присутствии истинной гравитации, т.е. искривления пространства-времени).
Если это предисловие прочтёт начинающий физик, студент или школьник (правда, предисловиям редко выпадает такая честь), пусть он не думает, что переводчик решил подавить его своей учёностью. Мои цели совсем иные. Я не сомневаюсь, что яркая, оригинальная книга Тейлора и Уилера произведёт большое впечатление, вдохновляющее молодого читателя на изучение физики; надеюсь, что она и после прочтения много лет не будет сдана им в макулатуру. Иными словами, пусть читатель возвращается к этому учебнику вновь и вновь; может быть, прочтя тогда сделанные в предисловии замечания, он задумается над путями развития теории относительности и — кто знает? — возможно, из-под его пера выйдет ещё более совершенный учебник. А пока для него главное — читать эту книгу и систематически решать упражнения.
* * *
Второе издание книги дополнено ответами на упражнения, присланными авторами. Читателя, таким образом, ожидает искушение сразу заглянуть в эти ответы, не утруждая себя решением упражнений. Если он пойдёт на это — тем хуже для него. Напротив, уже решив упражнение, полезно посмотреть ответ и сравнить свой метод решения с предлагаемым авторами.
В этом издании мы добавили новую задачу, по духу близкую к составленным самими авторами и касающуюся одного визуально наблюдаемого эффекта, где наряду с обычной релятивистской кинематикой важную роль играют законы распространения света (задача № 54а).
Редакция и переводчик благодарят авторов книги за любезную присылку ответов на упражнения.
Н. Мицкевич
1. ГЕОМЕТРИЯ ПРОСТРАНСТВА-ВРЕМЕНИ
1. ПРИТЧА О ЗЕМЛЕМЕРАХ
Жили-были в тридевятом царстве два племени — дневное и ночное, и правил ими король. Королевские земли для нужд дневного племени мерил дневной землемер. Направления на север и на восток он определял по магнитной стрелке компаса. Работая, он откладывал к востоку от центра столичной площади расстояния в метрах (𝑥 в метрах), а расстояния в северном направлении, которые считались священными, он измерял в других единицах — милях (𝑦 в милях). Он делал своё дело аккуратно и добросовестно, так что люди его племени часто пользовались записями своего землемера.
Дневной землемер ориентировался на магнитный северный полюс
Люди ночного племени пользовались услугами другого землемера, который определял направления на север и на восток по Полярной звезде. И этот землемер отсчитывал расстояния к востоку от центра столичной площади в метрах (𝑥' в метрах), а священные расстояния к северу — в милях (𝑦' в милях). Он тоже делал своё дело аккуратно и добросовестно. Все углы земельных участков характеризовались в его реестре значениями двух координат: 𝑥' и 𝑦'.
Ночной землемер ориентировался на Полярную звезду
Однако настал день, когда в землемерном училище появился студент, лишённый предубеждений. Вопреки установившейся традиции он стал посещать занятия, которые вели и дневной, и ночной землемеры — главы обоих соперничающих направлений. Первый из них научил нашего студента на дневных занятиях, как определять положение городских ворот и углов земельных участков по своему методу. На ночных занятиях студент изучил метод другого землемера. Шли дни и ночи, и наш студент всё больше задумывался над тем, как привести в разумное соответствие оба эти метода определения местоположения объектов. Он произвёл сравнение данных о положении городских ворот относительно центра столичной площади, полученных обоими землемерами, и получил табл. 1.
Таблица 1.
Две разные системы данных, характеризующие одну и ту же точку
Точка (место)
Данные, взятые относительно координатных осей дневного землемера, ориентированных по магнитному компасу
(
𝑥
в метрах,
𝑦
в милях
)
Данные, взятые относительно координатных осей ночного землемера, ориентированных по Полярной звезде
(
𝑥'
в метрах,
𝑦'
в милях
)
Городская площадь
0
0
0
0
Ворота
𝐴
𝑥
𝐴
𝑦
𝐴
𝑥
𝐴
'
𝑦
𝐴
'
Ворота
𝐵
𝑥
𝐵
𝑦
𝐵
𝑥
𝐵
'
𝑦
𝐵
'
Прочие ворота
…
…
…
…
В нарушение всех традиций студент сделал смелый и еретический шаг и перевёл результаты измерений в северном направлении, прежде всегда выражавшиеся в милях, в метры с помощью постоянного множителя перевода 𝑘. Тогда он обнаружил, что величина √(𝑥𝐴)²+(𝑘𝑦𝐴)², вычисленная по данным дневного землемера о положении ворот 𝐴, численно в точности равна величине √(𝑥𝐴')²+(𝑘𝑦𝐴')², вычисленной по данным ночного землемера для тех же ворот 𝐴. Проделав эти операции с данными о положении ворот 𝐵, студент и для них нашёл полное согласие. Возбуждение студента достигло предела, когда он испробовал свой метод на данных о всех других городских воротах и во всех случаях получил подтверждение своей догадки. Он решил дать имя новооткрытой величине и назвал
√
(𝑥)²+(𝑘𝑦)²
(1)
расстоянием точки (𝑥,𝑦) от центра города. Он заявил, что им открыт принцип инвариантности расстояния, т.е. что расстояния, вычисленные с помощью координат дневного и ночного землемеров, в точности совпадают, хотя сами значения этих координат совершенно различны.
Открытие: расстояние инвариантно
Эта притча иллюстрирует то примитивное состояние, в котором находилась физика до того, как Эйнштейн в Берне, Лоренц в Лейдене и Пуанкаре в Париже открыли частную теорию относительности. Насколько примитивное?

Рис. 1. Схема города и городских ворот с нанесёнными на неё осями координат, используемыми двумя разными землемерами.
1. Землемеры мифического королевства измеряли расстояния в северном направлении в священных единицах — милях, иных, чем единицы, в которых они измеряли расстояния в восточном направлении. Аналогично люди, занимавшиеся физикой, измеряли время в священных единицах — секундах, иных, чем единицы, в которых они измеряли пространство. Никому не приходило в голову применить и здесь и там одни и те же единицы или попытаться комбинировать друг с другом возведённые в квадрат пространственную и временную координаты, выраженные в метрах. Множитель перехода между секундами и метрами, а именно скорость света 𝑐=2,997925⋅10⁸ метра в секунду, считался священным числом. Никто не считал его просто множителем перехода, подобным множителю перехода между милями и метрами, т.е. множителем, который возник лишь благодаря исторической случайности и лишён глубокого физического смысла.
2. В нашей притче северные координаты 𝑦 и 𝑦', определённые разными землемерами, не очень сильно отличались друг от друга, потому что соответствующие направления на север были разделены лишь малым углом 10°. Наш мифический студент сначала думал, что малое различие между 𝑦 и 𝑦' вызвано просто ошибками в геодезической съёмке. Аналогично этому люди думали, что время между взрывами двух хлопушек будет одним и тем же, кто бы его ни измерял. И лишь в 1905 г. мы узнали, что разница во времени между двумя событиями (первое из которых берётся в качестве начала отсчёта —«опорное событие») в действительности неодинакова (равна 𝑡 и 𝑡') для наблюдателей, находящихся в разных состояниях движения. Пусть первый наблюдатель неподвижен относительно лаборатории, а второй наблюдатель пролетает мимо в сверхскоростной ракете. Ракета влетает через парадный вход, проносится через длинный коридор и вылетает в дверь чёрного хода. В коридоре взрываются сначала первая хлопушка («опорное событие»), а затем вторая («событие 𝐴»). Оба наблюдателя уславливаются между собой, что опорное событие определяет начало отсчёта времени и начало отсчёта расстояния.
Пусть второй взрыв произошёл, например, через 5 сек после первого по данным лабораторных часов и на 12 м дальше по коридору. Тогда его временна́я координата равна 𝑡𝐴 = 5 сек, а пространственная 𝑥𝐴 = 12 м.
Дальнейшие взрывы и события также происходят по длине коридора. Данные обоих наблюдателей представлены в табл. 2.
Таблица 2.
Пространственные и временные координаты одних и тех же событий, получаемые двумя наблюдателями, движущимися относительно друг друга. Для простоты значения координат 𝑦 и 𝑧 приняты равными нулю, а ракета считается движущейся в направлении оси 𝑡
Событие
Значения координат, измеренные наблюдателем, находящимся
в покое в лаборатории
(
𝑥
в метрах
,
𝑡
в секундах
)
в ракете (движущийся с нею)
(
𝑥'
в метрах
,
𝑡'
в секундах
)
Опорное событие
0
0
0
0
Событие
𝐴
𝑥
𝐴
𝑡
𝐴
𝑥
𝐴
'
𝑡
𝐴
'
Событие
𝐵
𝑥
𝐵
𝑡
𝐵
𝑥
𝐵
'
𝑡
𝐵
'
Прочие события
…
…
…
…
Первый наблюдатель использует лабораторную систему отсчёта
Второй наблюдатель использует систему отсчёта ракеты
3. Открытие понятия расстояния мифическим студентом подобно открытию в 1905 г. Эйнштейном и Пуанкаре понятия интервала. Интервал, вычисленный по данным измерений одного наблюдателя,
Интервал =
√
(𝑐𝑡
𝐴
)²-(𝑥
𝐴
)²
(2)
в точности равен интервалу, вычисленному по данным измерений другого наблюдателя,
Интервал =
√
(𝑐𝑡
𝐴
')²-(𝑥
𝐴
')²
(3)
даже если фигурирующие в этих вычислениях координаты по отдельности не равны друг другу. Два наблюдателя припишут пространственным и временном координатам событий А, Б, В, … относительно одного и того же опорного события разные значения, но, вычислив эйнштейновские интервалы между этими событиями, они обнаружат, что соответствующие величины совпадают. Эта инвариантность интервала (его независимость от выбора системы отсчёта) вынуждает признать, что время невозможно отделить от пространства. Пространство и время — части единого целого, которое называется пространством-временем. Геометрия пространства-времени в действительности характеризуется четырьмя измерениями. Можно сказать, что «направление временной оси» зависит от состояния движения наблюдателя точно так же, как направление оси 𝑦 землемера зависело от его метода ориентации на «север».
Открытие: интервал инвариантен
В остальной части этой главы мы будем заниматься развитием аналогии между снятием планов в пространстве и взаимным сопоставлением событий в пространстве-времени. Обзор, предвосхищающий наши выводы, представлен в табл. 3. Для того чтобы почувствовать единство пространства и времени, мы обращаемся к способу, помогающему лучше разглядеть ландшафт; для этого нужно посмотреть на него под разными углами. Поэтому мы сравниваем пространственную и временную координаты одного и того же события в двух разных системах отсчёта, движущихся относительно друг друга.
Таблица 3.
Детализация притчи о землемерах, предвосхищающая дальнейший анализ
Притча о землемерах — геометрия
пространства
Физическая параллель—геометрия
пространства-времени
Задача землемера — определить положение точки (ворот А), пользуясь одной из двух систем координат, повёрнутых относительно друг друга
Задача физика — определить положение в пространстве и времени события (взрыв хлопушки А), пользуясь одной из двух движущихся относительно друг друга систем отсчёта
Две системы координат — ориентированная по магнитному компасу и ориентированная по Полярной звезде
Две системы отсчёта — лабораторная система отсчёта и система отсчёта ракеты
Для удобства все землемеры условились измерять положения относительно общего начала (центр городской площади)
Для удобства все физики условились измерять положения событий в пространстве и во времени относительно общего опорного события (взрыв опорной хлопушки)
Анализ результатов, полученных землемером, упрощается, если координаты точки 𝑥 и 𝑦 измерены в одинаковых единицах — метрах
Анализ результатов, полученных физиком, упрощается, если координаты события 𝑥 и 𝑡 измерены в одинаковых единицах — метрах
Взятые по отдельности, координаты 𝑥𝐴 и 𝑦𝐴 ворот А имеют разные значения в двух системах координат, повёрнутых относительно друг друга
Взятые по отдельности, координаты 𝑥𝐴 и 𝑡𝐴 события А имеют разные значения в двух системах отсчёта, равномерно движущихся относительно друг друга
Инвариантность длины. Расстояние (длина) √𝑥𝐴²+𝑦𝐴² от ворот А до городской площади получается одинаковым, если его вычислять по результатам измерений в любой из двух повёрнутых относительно друг друга систем (𝑥𝐴 и 𝑦𝐴 измерены в метрах)
Инвариантность интервала. Интервал √𝑡𝐴²-𝑥𝐴² между событием А и опорным событием получается одинаковым, если его вычислять по результатам измерений в любой из двух систем отсчёта, движущихся относительно друг друга 𝑥𝐴 и 𝑡𝐴 измерены в метрах)
Преобразование поворота. Пользуясь эвклидовой геометрией, землемер может решить следующую задачу: по данным значениям координат 𝑥𝐴' и 𝑦𝐴' ворот А в системе ночного землемера и относительному наклону соответствующих осей найти координаты 𝑥𝐴 и 𝑦𝐴 тех же самых ворот в системе дневного землемера
Преобразование Лоренца. Пользуясь лоренцевой геометрией, физик может решить следующую задачу: по данным значениям координат 𝑥𝐴' и 𝑡𝐴' события А в системе ракеты и скорости ракеты относительно лабораторной системы отсчёта найти координаты того же самого события 𝑥𝐴 и 𝑡𝐴 в лабораторной системе
Притча о землемерах подсказывает нам, что было бы полезно перейти к одинаковым единицам для измерения как пространства, так и времени. Поэтому возьмём в качестве такой единицы метр. В метрах можно измерять и время. Если установить на обоих концах полуметрового стержня по зеркалу, то между этими зеркалами может отражаться взад и вперёд луч световой вспышки. Такое устройство представляет собой часы. Можно сказать, что эти часы издают «тик-так» каждый раз, когда свет возвращается к первому зеркалу. Между всеми последовательными возвращениями свет вспышки проходит путь, в общей сложности равный 1 метру. Мы назовём поэтому промежуток времени между двумя последовательными «тик-так» таких часов 1 метром светового времени или, проще, 1 метром времени. (Проверьте, что 1 секунда приблизительно равна 3⋅10⁸ метрам светового времени).
Время измеряется в метрах
Одна из целей физики — отыскание простых взаимосвязей между событиями. В нашем случае для этого целесообразно выбрать специальную систему отсчёта, относительно которой законы физики имеют простую форму. Заметим, что вблизи Земли все предметы подвержены действию силы тяжести. Это действие усложняет известные нам по обыденному опыту законы движения. Чтобы исключить подобные усложняющие обстоятельства, мы сконцентрируем наше внимание в следующем параграфе на свободно падающей вблизи Земли системе отсчёта. В такой системе отсчёта сила тяжести не ощущается, и мы назовём эту лишённую тяготения систему отсчёта инерциальной. В частной теории относительности исследуются классические законы физики, взятые относительно инерциальной системы отсчёта.

Рис. 2. Рисунок из первых изданий «Из пушки на Луну» Ж. Верна. Кличка бедного пса была Спутник.
Упрощение: переход к свободно падающей лаборатории
Принципы частной теории относительности замечательно просты. Они много проще аксиом геометрии Эвклида или правил управления автомобилем. Однако и геометрия Эвклида, и автомобиль были созданы поколениями обыкновенных людей, даже не испытавшими в полной мере удивления, которого заслуживали плоды их творчества. Некоторые из лучших умов XX в. выступали против идей теории относительности, и не потому, что их природа темна, а по той простой причине, что человеку трудно преодолеть установившийся взгляд на вещи. Теперь относительность уже выиграла сражение. Мы уже можем выразить её понятия так просто, что правильный взгляд на вещи устанавливается сам собой,— это значит «делать плохое трудным, а хорошее —простым» 1). Понимание теории относительности отныне не есть проблема обучения, а просто дело интуиции — практикуемого подхода к вещам. При таком подходе громадное число прежде непостижимых опытных данных становятся совершенно естественными и понятными 2).
1) Высказывание Эйнштейна по аналогичному поводу в письме архитектору Корбюзье.
2) Исчерпывающий список литературы по частной теории относительности для начинающих, а также ряд оттисков работ см. в книге Special Relativity Theory, Selected Reprints, опубликованной Американским институтом физики для Американской ассоциации учителей физики в 1963 г. [В советском издании обширную библиографию по частной теории относительности см. в книге: У. И. Франкфурт, Очерки по истории специальной теории относительности, Изд-во АН СССР, М., 1961.— Прим. перев.]
2. ИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЁТА
Менее чем через месяц после того, как капитуляцией при Аппоматоксе закончилась гражданская война в Америке (1861—1865), французский писатель Жюль Верн начал писать свой роман «Из пушки на Луну». В этом романе рассказывалось о том, как выдающиеся американские артиллерийские инженеры отлили в специальной шахте во Флориде гигантскую пушку, направленную жерлом в небо. Из этой пушки был выпущен десятитонный снаряд, в котором находились трое людей и несколько животных. Когда снаряд устремился в свободный полёт к Луне, покинув канал ствола пушки, его пассажиры могли, как обычно, ходить внутри снаряда по дну, расположенному ближе к Земле (см. рис. 3а). При дальнейшем полёте пассажиры чувствовали, что их всё меньше и меньше прижимает к полу космического корабля, пока, наконец, в той точке, где Земля и Луна притягивают к себе тела с равной силой, но в противоположных направлениях, эти пассажиры стали свободно парить, оторвавшись от пола. Затем, приближаясь к Луне, они снова смогли ходить, но теперь уже по противоположной стороне своего корабля, обращённой к Луне. В начале полёта одна из находившихся в снаряде собак погибла от ран, полученных при запуске. Пассажиры выбросили её труп в люк на дне снаряда, но обнаружили, что он следует за снарядом в течение всего путешествия.

Рис. 3а. Неправильное предсказание. Жюль Верн полагал, что пассажир свободно летящего снаряда будет стоять на том дне снаряда, которое ближе к Земле или к Луне, в зависимости от того, притяжение которой из них сильнее, но что собака будет парить рядом со снарядом в течение всего путешествия.

Рис.3б. Правильным было бы предсказание, что и пассажир будет парить внутри снаряда в течение всего путешествия. Жюль Верн прав, описывая движение собаки.
Пассажиры жюльверновского космического корабля ощущали свой вес
Этот рассказ приводит к парадоксу, играющему решающую роль для теории относительности. Жюль Верн считал возможным, что гравитационное притяжение со стороны Земли способно прижимать пассажира к стороне снаряда, обращённой к Земле, на первоначальном этапе путешествия. Он считал также естественным, что труп собаки будет всё время оставаться вблизи снаряда, так как и снаряд, и собака независимо друг от друга движутся по одной и той же траектории в пространстве. Но если собака летит снаружи рядом с космическим кораблём в течение всего путешествия, то почему бы и пассажиру не парить свободно внутри космического корабля? Ведь если бы мы распилили снаряд на две части, не стал ли бы пассажир, оказавшийся теперь «снаружи», свободно парить над полом?
Парадокс пассажира и собаки
Наш опыт в области реальных космических полётов позволяет разрешить этот парадокс. Жюль Верн ошибался, описывая состояние пассажира внутри космического корабля. Подобно находящейся снаружи корабля собаке, пассажир внутри корабля совершает тот же путь в пространстве, что и космический корабль. Поэтому он должен свободно парить относительно корабля в течение всего путешествия (рис. 36). Конечно, гравитационное поле Земли действует на пассажира. Но оно действует и на космический корабль. В самом деле, относительно Земли ускорение космического корабля под действием её гравитационного поля в точности равно ускорению пассажира под действием этого поля. Ввиду равенства этих ускорений между пассажиром и космическим кораблём не будет существовать относительного ускорения. Итак, космический корабль служит системой отсчёта («инерциальной системой отсчёта»), по отношению к которой пассажир не испытывает ускорения.
Пассажир реального космического корабля испытывает состояние невесомости
Утверждение о том, что ускорение пассажира относительно космического корабля равно нулю, вовсе не равносильно утверждению, что их относительная скорость обязательно равна нулю. Пассажир может отталкиваться от пола или стен, в результате чего он пролетит внутри корабля и ударится о стену. Но если его начальная скорость относительно корабля была равна нулю, то этот случай будет самым интересным, так как равная нулю скорость будет постоянно сохраняться и в дальнейшем. И пассажир, и космический корабль будут следовать в пространстве одним и тем же путём. Как это замечательно, что пассажир, даже лишённый возможности взглянуть наружу, тем не менее следует строго предопределённой орбите! Лишённый возможности двигаться, он даже с закрытыми глазами не касается стен. Можно ли в большей степени исключить влияние тяготения?!

Рис.4. Космический корабль, свободно падающий вблизи Земли.
Пусть современный космический корабль с пассажиром на борту запускается вертикально вверх с Земли, поднимается и падает обратно (рис. 4). (Пассажир в лифте испытывает близкое подобие этого падения, когда обрывается трос лифта). Выберем такой свободно падающий космический корабль в качестве наилучшей возможной системы отсчёта для физических опытов. Эта система отсчёта является самой лучшей, потому что наряду со всем прочим законы движения частиц имеют наиболее простой вид в свободно падающем корабле. В таком корабле свободная частица, находившаяся первоначально в покое, сохранит состояние покоя. Если лёгким толчком придать этой частице скорость, она будет двигаться в корабле по прямой линии с постоянной скоростью. Другие опыты подтверждают, что все законы механики имеют простое выражение, если их выразить относительно свободно падающего корабля. Такой свободно поднимающийся или свободно падающий (а вообще говоря, свободно движущийся в пространстве) космический корабль мы называем инерциальной системой отсчёта.
Понятие инерциальной системы отсчёта
Взглянем на свободно падающий космический корабль с поверхности Земли. Мы увидим, как проста причина того, что первоначально покоившаяся свободная частица сохраняет своё состояние покоя относительно корабля. Причина эта в том, что по отношению к поверхности Земли как корабль, так и частица падают с одним и тем же ускорением (рис. 4). Именно благодаря такому равенству ускорений относительные положения частицы и космического корабля не меняются, если наша частица первоначально покоилась относительно корабля.

Рис. 5. Железнодорожный вагон, свободно падающий в горизонтальном положении вблизи Земли.
Вопределении инерциальной системы отсчёта содержится требование, чтобы в ней не ощущались гравитационные силы. Если в качестве такой системы взят космический корабль, находящийся вблизи Земли, то он не должен быть очень большим, так как помещённые в него на большом расстоянии друг от друга частицы будут испытывать разное воздействие со стороны неоднородного гравитационного поля Земли. Так, если двум частицам с разных концов корабля предоставить возможность свободно падать, каждая из них будет притягиваться к центру Земли, и они будут сближаться друг с другом в ходе падения (рис. 5). В качестве другого примера возьмём две частицы, раздвинутые в вертикальном направлении, строго одна над другой (рис. 6). Их ускорение под действием силы тяжести будет иметь одно и то же направление, но более близкая к Земле частица будет мало-помалу оставлять другую позади, и по мере падения космического корабля расстояние между частицами будет увеличиваться. В обоих случаях законы механики не будут простыми в очень большом космическом корабле — большой космический корабль не представляет собой инерциальной системы отсчёта.

Рис. 6. Железнодорожный вагон, свободно падающий в вертикальном положении вблизи Земли.
Земное притяжение неоднородно, и большой космический корабль не может служить инерциальной системой отсчёта
Однако нам нужно, чтобы законы механики имели в космическом корабле простой вид. Поэтому необходимо устранить все относительные ускорения, вызванные внешними факторами, «устранить» в том смысле, чтобы сделать величину этих ускорений ниже обнаружимого предела, когда они уже не будут искажать картины более важных ускорений, подлежащих изучению (например, возникающих при столкновении частиц). Это может быть достигнуто при выборе достаточно малого космического корабля. Чем меньше космический корабль, тем меньше и величина относительных ускорений объектов в разных точках этого корабля. Пусть мы располагаем приборами, измеряющими относительные ускорения с любой заданной степенью точности. Как бы высока ни была точность (чувствительность) этих приборов, мы можем всегда взять космический корабль настолько малых размеров, что эти паразитные относительные ускорения окажутся ниже предела чувствительности приборов. В рамках выбранной точности такой космический корабль можно считать инерциальной системой отсчёта.
Пример космического корабля, имеющего достаточно малые размеры, чтобы быть пригодным в качестве инерциальной системы, отсчета
Когда можно сказать, что космический корабль или другая лаборатория имеет размеры достаточно малые, чтобы его можно было назвать инерциальной системой отсчета? Иначе говоря, когда относительные ускорения свободных частиц, помещенных в разных концах лаборатории, слишком малы, чтобы быть наблюдаемыми? Разбор ситуации в какой-то одной лаборатории послужит иллюстрацией для наших рассуждений. Допустим, что железнодорожный вагон 25 м длины в горизонтальном положении сброшен с высоты 250 м на поверхность Земли (рис. 5). Время, прошедшее от начала до конца падения, будет равно приблизительно 7 сек, т.е. около 21⋅10⁸ м светового времени. Пусть в первый момент падения в воздухе в противоположных концах вагона будут предоставлены самим себе два маленьких шарика от подшипника. За время падения они приблизятся друг к другу на 10⁻³ м (толщина 10 страниц этой книги) под действием различия в направлениях действующей на них силы земного притяжения (см. упражнение 32). В другом случае предположим, что тот же вагон сбрасывается в вертикальном положении, причем нижний его конец вначале находится на высоте 250 м над поверхностью Земли (рис. 6). Вновь освободим при этом в противоположных концах вагона два шарика от подшипника. Теперь за время падения шарики удалятся друг от друга на 2⋅10⁻³ м, так как нижний из них испытывает большее гравитационное ускорение, чем верхний. В каждом из этих примеров будем считать, что используемые в вагоне измерительные приборы не обладают достаточной чувствительностью, чтобы зафиксировать относительное движение шариков. Тогда, пользуясь приборами указанной степени чувствительности и в указанные ограниченные сроки наблюдения, мы можем принять наш железнодорожный вагон (или рассмотренный прежде свободно падающий космический корабль) в качестве инерциальной системы отсчёта. Повысив чувствительность измерительного оборудования, мы уже не сможем использовать данный космический корабль в качестве инерциальной системы отсчёта, если не изменим постановку опыта. Для этого следует либо укоротить 25-метровый отрезок, на котором проводились наблюдения, либо сократить длительность последних во времени. Лучше всего, однако, сократить в некоторой согласованной комбинации как пространственные, так и временные размеры исследуемой области. Наконец, как последнюю альтернативу можно предложить отправить с помощью ракеты (часть «в» упражнения 32) всю систему в такую область пространства, где невозможно измерить «дифференциал гравитационного ускорения» между двумя противоположными концами вагона. Эту же мысль можно выразить иначе: ускорение частиц относительно вагона должно стать нечувствительно малым. Эти относительные ускорения могут быть измерены внутри вагона без привлечения каких-либо внешних наблюдений. И только если эти относительные ускорения слишком малы, чтобы быть замеченными, существует система отсчёта, относительно которой законы движения имеют простой вид,— инерциальная система отсчёта.
Определение инерциальной системы отсчёта
Система отсчёта называется инерциальной в некоторой области пространства и времени, если во всей этой области пространства-времени с некоторой данной степенью точности любая первоначально покоившаяся пробная частица сохраняет своё состояние покоя, а любая пробная частица, первоначально двигавшаяся, продолжает своё движение без изменения величины и направления своей скорости. Инерциальную систему отсчёта называют также лоренцевой системой отсчёта. При таком определении инерциальные системы всегда с необходимостью локальны, т.е. инерциальны лишь в ограниченной области пространства-времени.
Определение области пространства-времени
«Область пространства-времени»— каков точный смысл этого понятия? Длинный и узкий железнодорожный вагон, использованный в нашем примере, служил средством для исследования пространства-времени на ограниченном отрезке времени и в том или ином пространственном направлении. Его можно было направить с севера на юг, с востока на запад либо сверху вниз. При каждой ориентации могло быть измерено относительное ускорение двух маленьких шариков от подшипника, освобождённых в противоположных концах вагона. Как можно показать с помощью вычислений, во всех трёх направлениях (как и в промежуточных) относительный «дрейф» этих двух пробных частиц составлял половину (или менее) минимальной поддающейся обнаружению величины. Тогда во всём кубе с рёбрами 25 м пространства и на протяжении 7 сек времени всевозможными способами движущиеся пробные частицы отклоняются от прямолинейного движения на не поддающуюся обнаружению величину. Другими словами, данная система отсчёта является инерциальной в области пространства-времени с размерами
⎛
⎜
⎝
25 м × 25 м × 25 м
пространства
⎞
⎟
⎠
×
⎛
⎜
⎝
21⋅10⁸ м
времени
⎞
⎟
⎠
Обсуждение областей пространства-времени, размеры которых превышают размеры таких локальных инерциальных систем, см. в гл. 3.
Определение пробной частицы
«Пробная частица». Насколько мала должна быть частица для того, чтобы её можно было принять за пробную? Её масса должна быть настолько малой, чтобы присутствие этой частицы в пределах некоторой заданной степени точности не влияло на движение других близких к ней частиц. На языке ньютоновской механики это означает, что гравитационное притяжение между пробной частицей и другими частицами должно быть пренебрежимо малым (с заданной степенью точности). Рассмотрим, например, частицу с массой 10 кг. Если поместить другую частицу с меньшей массой в ¹/₁₀ м от неё, то первоначальное состояние покоя этой второй частицы нарушится настолько, что она сдвинется менее чем за 3 мин на 10⁻³ м. Итак, 10-килограммовый объект не есть пробная частица в этой смысле. Пробная частица подвергается действию гравитационных сил, но сама не вызывает появления сколько-нибудь заметной гравитационной силы.

Рис. 7. Новейшая инерциальная система отсчёта. Вырезка из журнала Engineering Opportunities за март 1964 г.
СТРОИТЕЛЬСТВО
В прошлом месяце был предложен подряд на строительство нулевого цикла 500-футовой башни свободного падения, обеспечивающей условия невесомости на период до 10 сек, в Льюисовском исследовательском центре НАСА в Кливленде. Пролёт свободного падения высотой около 400 фут обеспечит пятисекундный период невесомости. Пневматическое поршневое устройство на дне шахты позволит подбрасывать образцы в 6000 фунт весом и 4 фут в диаметре до вершины башни, продлевая тем самым период невесомости до 10 сек. Для торможения образцов будет использован пенопласт. Система вакуумных насосов позволит поддерживать в шахте давление, соответствующее высоте около 50 миль, так что отпадает необходимость окружать образец экранами, компенсирующими сопротивление воздуха. Сооружение будет использовано для исследований жидких и газообразных систем в условиях невесомости в рамках проблемы запуска жидкостных двигателей в условиях космоса в ходе орбитальных полётов. Функционирующая в настоящее время в Льюисе малая башня свободного падения обеспечивает невесомость лишь на период от 2 до 4 сек и допускает испытания образцов лишь 10 дюйм в диаметре.
Инерциальную систему удаётся ввести, потому что все тела падают с одним и тем же ускорением
Инерциальную систему отсчёта было бы невозможно определить, если бы не существовало замечательного природного феномена. Все частицы различных размеров, формы и состава падают в одном и том же месте с одним и тем же ускорением относительно Земли. Если бы это было не так, наблюдатель внутри падающего космического корабля заметил бы относительное ускорение у разных частиц, даже когда эти частицы находятся вблизи друг друга. По крайней мере некоторые из частиц, покоившихся первоначально, вышли бы из состояния покоя, что означало бы непригодность космического корабля как инерциальной системы отсчёта согласно определению последней. В какой мере мы уверены в том, что все частицы в одном и том же месте, но разные по своему составу падают на Землю с одним и тем же ускорением? Как говорит легенда, Галилей бросал для проверки этого предположения с «Падающей башни» в Пизе шары, сделанные из разных веществ 1). В 1922 г. барон Роланд фон Этвёш установил с точностью 5:10⁹, что дерево и платина испытывают одинаковое ускорение со стороны Земли. Недавно Роберт Дикке указал, что Солнце является более удобным источником гравитационного ускорения для измерений (см. упражнение 35). Изменение каждые 12 час направления солнечного притяжения на противоположное позволяет производить фантастически большое усиление путём резонанса. Цилиндры из алюминия и золота подвергались ускорению со стороны Солнца (0,59⋅10⁻² м/сек²), одинаковому с точностью 3:10¹¹, как показали Р. Дикке и Питер Ролл 2). Это была одна из наиболее чувствительных проверок фундаментальнейшего физического принципа: тождества ускорения, вызванного силой тяжести у пробной частицы любой природы.
1) О том, производил ли в действительности Галлией этот эксперимент, см. книгу Lloyd W. Taylor, Phisics the Pioneer Science, Vol. 1, Dover Publications, New York, 1959, p. 25.
2) См. главу по эксперименту в теории относительности, написанную Дикке в книге Relativity, Groups, and Topology, ed. by C. and B. DeWitt, Gordon and Breach, New York, 1964, p. 173—177, или в книге R.H. Diсke, The Theoretical Significance of Experimental Relativity, Gordon and Breach, New York, 1964.
Из этого принципа вытекает, что для выяснения, является ли данная система отсчёта инерциальной, в качестве пробной частицы может быть использована частица, состоящая из любого вещества. Система отсчёта, инерциальная для пробных частиц одного вида, будет также инерциальной для пробных частиц любых других видов.
3. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
Перекрывающиеся инерциальные системы отсчёта движутся относительно друг друга прямолинейно и равномерно
Мы описываем движение пробных частиц по отношению к некоторой системе отсчёта, с тем чтобы выяснить, является ли эта система инерциальной. Движения тех же пробных частиц, а также их столкновения (если таковые происходят) могут быть описаны и по отношению более чем к одной инерциальной системе. Носителем одной системы отсчёта может быть космический корабль, выполненный в форме полого цилиндра (рис. 8, а), тогда как носителем другой системы отсчёта может быть подобная же конструкция с несколько меньшим диаметром, таким, чтобы при встрече с первой она могла пролететь внутри неё (рис. 8, б). При этом существует область пространства-времени, общая для внутренней части обоих кораблей во время их взаимного совмещения. Множество пробных частиц могут пролетать в том или ином произвольно выбранном направлении через эту область. Путь каждой из них будет прямолинейным, если изобразить его в координатах одной из систем отсчёта, а также в координатах другой, так как они обе являются инерциальными системами отсчёта. Такая прямолинейность путей возможна лишь благодаря тому, что любые две перекрывающиеся друг с другом инерциальные системы отсчёта движутся друг относительно друга равномерно. Напротив, если второй космический корабль включает двигатели и ускоряется во время прохождения сквозь первый (рис. 8, в), то по наблюдениям с этого второго корабля траектории пробных частиц будут искривлены. Если имеющееся оборудование позволяет заметить кривизну таких траекторий, то эту ускоренную систему отсчёта нельзя считать инерциальной.

а) Движение типичной пробной частицы, наблюдаемое в первой инерциальной системе.
б) Движение той же частицы, наблюдаемое во второй инерциальной системе отсчёта, движущейся относительно первой.
в) Движение той же пробной частицы, наблюдаемое в ускоренной, а потому неинерциальной системе отсчёта.
Рис. 8. Сравнение инерциальных систем отсчёта с ускоренной системой.
Если даны две инерциальные системы отсчёта, равномерно движущиеся друг относительно друга, то любая находящаяся в движении пробная частица будет относительно них сохранять величину и направление скорости своего движения неизменными, хотя бы даже эти величина и направление её скорости были совершенно различными в каждой из двух систем. В самом деле, ведь мы определили понятие инерциальной системы отсчёта так, чтобы в любой инерциальной системе был справедлив следующий закон механики (первый закон Ньютона): «Всякое тело сохраняет состояние покоя или прямолинейного равномерного движения, пока и поскольку оно не понуждается внешними силами изменить это состояние». Кроме этого закона механики, существуют и другие. Каждый из них также будет справедлив в любой инерциальной системе отсчёта, о чём свидетельствует эксперимент.
Относительность: законы физики одинаковы во всех инерциальных системах отсчёта
Сохраняют ли справедливость во всех инерциальных системах отсчёта и другие законы физики? Должен ли инженер-электротехник, рассчитывая электрические цепи для реактивного самолёта, применять иные законы электротехники на том основании, что самолёту предстоит двигаться? Не придётся ли пользоваться иными законами электромагнитного излучения при расчёте радиопередатчика для космического корабля, потому что этот корабль будет двигаться? Не придётся ли применять новые законы для истолкования экспериментов по столкновениям протонов с атомами мишени, если и компактный протонный ускоритель, и мишень, и счётчики частиц установлены на равномерно движущейся железнодорожной платформе? Насколько нам известно, ответом на эти три вопроса, как и на другие, подобные им, является «нет». Несмотря на самые усердные поиски, никто никогда не обнаружил каких-либо нарушений следующего принципа:
Все законы физики одинаковы во всех инерциальных системах отсчёта.
Это утверждение мы будем называть принципом относительности. Принцип относительности утверждает, что, установив законы физики в одной инерциальной системе отсчёта, мы можем применять их без всякого изменения в любой другой инерциальной системе отсчёта. В любой инерциальной системе отсчёта одинаковы как форма законов физики, так и численные значения физических констант, фигурирующих в этих законах. Все инерциальные системы эквивалентны с точки зрения любого закона физики. Выражая это утверждение негативно, можно сказать, что принцип относительности утверждает полную невозможность отличить одну инерциальную систему отсчёта от другой с помощью законов физики, точно так же, как измерительная рулетка и уровень землемера не могут показать, используем ли мы направление на север по Полярной звезде или по магнитной стрелке компаса!
О чём нам НЕ говорит принцип относительности
Отметим, о чём нам не говорит принцип относительности. Он не говорит, что промежуток времени между событиями А и Б будет одним и тем же, если его измерять в разных инерциальных системах отсчёта. Не говорит он и о том, что расстояние в пространстве между этими двумя событиями будет одним и тем же в этих двух системах. Как правило, ни промежутки времени, ни расстояния не будут одинаковыми в двух разных инерциальных системах, точно так же как разности северных и восточных координат ворот А и Б не совпадают при их определении дневным и ночным землемерами. В результате импульс данной частицы в одной системе будет иметь другое значение, чем её же импульс во второй системе. Даже скорость изменения импульса во времени будет, как правило, различной в разных системах отсчёта, и то же относится к величине силы. Поэтому при изучении движения заряженной частицы два движущихся относительно друг друга наблюдателя не обязательно определят одни и те же величины напряжённостей электрического и магнитного полей, действующих на эту частицу. Полная сила, вызванная совместным действием электрического и магнитного полей, будет разной в каждой инерциальной системе отсчёта.
И тем не менее, несмотря на всю свою специфичность в разных системах отсчёта, физика в них будет одна и та же! Физические величины в разных системах отличаются по своим численным значениям, но удовлетворяют одним и тем же законам. Скорость изменения импульса во времени, взятая в одной системе, равна полной силе, измеренной в этой же системе (второй закон Ньютона). Скорость изменения импульса во времени, взятая во второй системе, равна полной силе, измеренной во второй же системе:
лабораторная система
⎧
⎪
⎪
⎪
⎩
Скорость
изменения
импульса
во времени
⎫
⎪
⎪
⎪
⎭
←
равна
→
(Силе)
↑
↑
как правило,
НЕ равны
как правило,
НЕ равны
↓
↓
⎧
⎪
⎪
⎪
⎩
Скорость
изменения
импульса
во времени
⎫
⎪
⎪
⎪
⎭
←
равна
→
(Силе)
система ракеты
И не только законы механики, но и законы электромагнетизма и все прочие законы физики, выполняющиеся в одной инерциальной системе отсчёта, точно так же строго выполняются и в любой другой инерциальной системе отсчёта. Именно этот факт мы имеем в виду, когда говорим, что «принцип относительности утверждает полную невозможность отличить одну инерциальную систему отсчёта от другой с помощью законов физики».
Законы электродинамики (электромагнетизма), выполняющиеся в одной инерциальной системе отсчёта, точно так же строго выполняются и в любой другой инерциальной системе отсчёта. Численное значение величины скорости света (𝑐=2,997925⋅10⁸ м/сек) является одной из постоянных, фигурирующих в законах электродинамики. Согласно принципу относительности, это экспериментальное значение должно быть одинаковым в любой из двух инерциальных систем отсчёта, равномерно движущихся друг относительно друга. Подтверждается ли это на опыте? Ответ на этот вопрос: ДА, хотя современные эксперименты страдают совершенно неудовлетворительной чувствительностью для того, чтобы решить столь важный вопрос. Давайте поэтому, подобно улитке, «втянем рога» и сосредоточимся на более простом вопросе, на который можно дать окончательный ответ. В законах электродинамики нет выражений, которые зависели бы от направления. Поэтому следует ожидать, что скорость распространения вспышки света по замкнутому пути будет одинакова, когда свет распространяется по линии север — юг или восток — запад, т.е. скорость света изотропна. Пусть, однако, те же самые вспышки света наблюдаются с равномерно движущейся ракеты. Не окажется ли, что скорость света на замкнутом пути по отношению к этой ракете будет различной в зависимости от направления прямой, вдоль которой распространяется свет? На это принцип относительности отвечает НЕТ: скорость света, будучи изотропной в одной инерциальной системе отсчёта, сохранит свою изотропность в любой другой инерциальной системе, охватывающей прежнюю пространственно-временную область.
Опыт Майкелъсона — Морли: скорость света изотропна во всех инерциальных системах отсчёта
Этот результат поистине удивителен. Мы знаем, что скорость звука в воздухе одинакова во всех направлениях, когда воздух неподвижен. Но достаточно подуть сильному ветру или, с тем же успехом, поехать при спокойном воздухе на автомобиле, чтобы «скорость звука по течению» оказалась больше, чем «скорость звука против течения» (в случае автомобиля берётся «течение» воздуха относительно него). Элементарный расчёт показывает, что обе эти скорости отличаются от скорости звука, измеренной поперёк течения. Скорость распространения звука по замкнутому пути, измеренная относительно автомобиля, будет различной в различных направлениях. Этот вывод верен и для любого другого вида волнового движения, но не для света! Почему же мы настолько уверены, что подобного результата не дадут опыты со светом? Наша уверенность основывается на ряде тончайших экспериментов, начиная с классического опыта А. Майкельсона и Е. Морли 1), проделанных с 1880 г. В них в качестве движущейся системы отсчёта была использована сама Земля. (Напомним, что Земля практически является инерциальной системой отсчёта при локальных опытах со светом; см. упражнение 31). Земля движется со скоростью около 30 км/сек по своей орбите вокруг Солнца. По существу Майкельсон и Морли сравнивали скорость распространения света по замкнутому пути вдоль направления движения Земли и поперёк этого направления. Этот опыт они повторяли в разное время года, когда Земля двигалась в различных направлениях относительно неподвижных звёзд. При этом не было обнаружено никакого воздействия движения Земли на относительную скорость света в двух взаимно перпендикулярных направлениях. Степень точности опыта позволила им определить, что измеряемая скорость света в двух взаимно перпендикулярных направлениях одинакова с точностью до ¹/₆ величины скорости движения Земли по орбите (см. упражнение 33). Более новые опыты снизили эту неопределённость до 3% величины скорости движения Земли по орбите 1). Из опыта Майкельсона — Морли и его последних улучшенных вариантов следует, что в любой инерциальной системе отсчёта скорость распространения света по замкнутому пути одинакова во всех направлениях, т.е. скорость света изотропна как в лабораторной системе отсчёта, так и в системе ракеты в согласии с утверждением принципа относительности. Однако утверждения принципа относительности этим не исчерпываются. Скорость света должна быть не только изотропна и в лабораторной системе отсчёта, и в системе ракеты, но также, если этот принцип верен, в этих обеих системах отсчёта должно быть одинаково и численное значение величины изотропной скорости света: 𝑐=2,997925⋅10⁸ м/сек. Поддаётся ли экспериментальной проверке и это утверждение? Да, такая проверка была произведена Кеннеди и Торндайком примерно через 50 лет после того, как Майкельсон и Морли поставили свой опыт 2).
1) A.A. Michelson, W. Morley, American Journal Of Science, 34, 333 (1887).
1) Т.S. Jasеja, A. Javan, J. Murray, С. Н. Townes, Physical Review, 133, А1221 (1964).
2) R. J. Kennedy, E. M. Thorndike, Physical Review, 42, 400 (1932).
Эксперимент Кеннеди и Торндайка: скорость света имеет одну и ту же численную величину во всех инерциальных системах отсчёта
Подобно Майкельсону и Морли, Кеннеди и Торндайк использовали в качестве движущейся системы отсчёта Землю. Они пытались обнаружить хоть какое-нибудь изменение величины скорости распространения света по замкнутому пути, когда Земля в разное время года двигалась в различных направлениях вокруг Солнца. Их результат был отрицательным, и из степени его точности можно заключить, что нет никакого изменения величины скорости света, по крайней мере большего 2 м/сек, когда свет распространяется по замкнутому пути в двух системах отсчёта, движущихся с относительной скоростью 60 км/сек (удвоенная скорость движения Земли по орбите; см. упражнение 34). В эксперименте Кеннеди — Торндайка эталоном длины было плечо самого интерферометра — цельный кусок плавленого кварца, находящегося в вакууме при температуре, постоянной с точностью около одной тысячной градуса. В качестве эталона времени был взят собственный период колебаний, связанный с зелёной линией в спектре атома ртути. Единственной и важнейшей трудностью в этом эксперименте, проводившемся в Пасадене (Калифорния), было поддержание постоянных условий в течение ряда месяцев, тогда как в опыте Майкельсона — Морли в Кливленде (Огайо) каждая серия сравнений (в разных направлениях) могла проводиться за один день. В этом же состояло и различие между обоими экспериментами. Их результаты сопоставлены в табл. 4 на следующей странице.
Таблица 4.
Современные критерии для решения вопроса: «Различна ли скорость света на замкнутом пути в разных системах отсчёта?»
ДВЕ СИСТЕМЫ ОТСЧЁТА
Первая система отсчёта
Земля при её движении в одном направлении относительно Солнца, например в январе
Вторая система отсчёта
Земля при её движении в противоположном направлении (по отношению к неподвижным звёздам) в июле
РЕЗУЛЬТАТЫ ОПЫТОВ
Результаты опыта Майкельсона — Морли
Первоначальный вариант
Ни в какой системе отсчёта наблюдатели (может быть
один и тот же
наблюдатель на Земле, повторяющий свой опыт спустя 6 месяцев) не могут заметить разницы в скорости света на замкнутом пути в любых двух взаимно перпендикулярных направлениях, большей чем
¹
/
₆
скорости движения Земли по орбите
Модернизированный вариант
Ни в какой системе отсчёта наблюдатели не могут заметить разницы в скорости света на замкнутом пути в любых двух взаимно перпендикулярных направлениях, большей чем 3% скорости движения Земли по орбите
Результаты эксперимента Кеннеди — Торндайка
Скорость света на замкнутом пути одинакова в любой из определённых выше «сезонных» систем отсчёта с точностью приблизительно до 2
м/сек
ИСТОЛКОВАНИЕ ОПЫТНЫХ ФАКТОВ
Модернизированный вариант опыта Майкельсона — Морли
Скорость Земли по ее орбите вокруг Солнца равна
30
км/сек
= 1/10 000 скорости света
Тогда
разница
в величине скорости света на замкнутом пути,
измеренной в двух взаимно перпендикулярных направлениях,
меньше 3/100 от 1/10 000 скорости света,
т.е. меньше 3/1 000 000 скорости света.
Итак,
принцип относительности
подтверждается этим модернизированным вариантом опыта с точностью
3 : 1 000 000
Эксперимент Кеннеди — Торндайка
Разница
в величине скорости света на замкнутом пути, измеренной в двух системах отсчета,
меньше приблизительно 2
м/сек
,
т.е. меньше 1/100 000 000 скорости света
Итак,
принцип относительности
подтверждается этим экспериментом с точностью
1 : 100 000 000
Хотя ни один из этих экспериментов не обладал чувствительностью экспериментов Этвёша и Дикке (3 : 1011), их результаты тем не менее изумительно точно подтвердили принцип относительности. К тому же планируется повысить чувствительность эксперимента Кеннеди—Торндайка1). Такое повышение чувствительности очень важно. Ведь принятие метра в качестве единицы времени имеет смысл, лишь если свет проходит один метр длины за одно и то же время во всех системах отсчёта. Равенство скорости света в системе отсчёта ракеты и в лабораторной системе допускает простой способ сравнения часов в этих системах (разд. 5). Возможность такого сравнения решающим образом зависит от отрицательного результата эксперимента Кеннеди — Торндайка.
1) Т.S. Jasеja, A. Javan, J. Murray, С. Н. Townes, Physical Review, 133, А1221 (1964). Подробный анализ экспериментальных оснований частной теории относительности см. в статье Робертсона «Сравнение постулатов и наблюдений в частной теории относительности», Н. P. Robertson, Reviews of Modern Physics, 21, 378 (1949).
Структура пространства-времени приводит к тому, что Станфордский ускоритель стоит 300 миллионов долларов
В 1905 г. принцип относительности был явной ересью, открытым вызовом интуиции и восприятию природы в рамках «здравого смысла», свойственных большинству тогдашних физиков. Потребовались долгие годы, чтобы привыкнуть к нелепой на первый взгляд мысли о том, что некоторая конкретная скорость обладает одной и той же величиной, в какой бы из двух перекрывающихся и движущихся относительно друг друга инерциальных систем отсчёта её ни измеряли. Теперь принцип относительности применяется ежедневно во множестве областей физики, и там он непрерывно и строго проверяется. Например, Станфордский линейный ускоритель электронов (приблизительная стоимость 300 миллионов долларов) должен иметь длину в 2 мили для того, чтобы разгонять электроны до скорости, почти равной скорости света (разница в скоростях всего лишь 8 : 10¹¹). Если бы были справедливы доэйнштейновские, ньютоновские законы механики, то для такого ускорения было бы достаточно» длины менее чем в один дюйм (см. упражнение 55)!
4. КООРДИНАТЫ СОБЫТИЯ
Почему мы используем координаты?
Для студента-физика инерциальная система отсчёта представляет собой то же, что сетка линий с севера на юг и с востока на запад на местности для землемера. Землемер изучает положение объектов в пространстве. Студент-физик изучает положение событий в пространстве и во времени. Дневной и ночной землемеры могли отказаться от использования координат в направлениях север — юг и восток — запад и попросту измерять расстояния между каждыми двумя городскими воротами, хотя сначала они даже не подозревали о существовании такой величины, как расстояние. Подобным же образом мы могли бы в этой главе ограничиться при определении положений событий в пространстве-времени измерением интервалов между любыми двумя событиями, не рассматривая по отдельности «пространственных» и «временной» координат 2). Однако следует начать с положения физики до 1905 г., совершенно не опираясь на понятие интервала. Это понятие само привлечёт наше внимание подобно тому, как понятие расстояния привлекла к себе внимание землемера. Так, два человека измеряли координаты в направлениях север — юг и восток — запад в двух разных системах координат, и лишь позднее они заметили взаимосвязь между совсем разными числами в своих записях («инвариантность расстояния»). Мы начнём подобным же образом с пространственных и временных координат событий в лабораторной системе отсчёта и с пространственных и временных координат тех же событий в системе отсчёта ракеты. И тогда у нас будут солидные основания для вывода о тождественном равенстве друг другу интервала между двумя событиями, вычисленного из лабораторных координат, и интервала между теми же двумя событиями, вычисленного из совсем других чисел — значений координат, полученных при измерениях в системе отсчёта ракеты («инвариантность интервала»).
2) Такой подход сформулирован Робертом Ф. Марцке и Джоном А. Уилером в сборнике Gravitation and Relativity, eds. H.-Y. Chiu and W. F. Hofmann, W. A. Benjamin, New York, 1964. (Имеется русский перевод: Гравитация и относительность, под ред. X. Цзю и В. Гофмана, изд-во «Мир», М., 1965, стр. 107.— Прим. перев.)
Определение понятия события
В геодезии основным понятием является место. В физике основное понятие — событие. Событие характеризуется не только местом, но и моментом времени, в который оно произошло. Вот примеры событий: испускание частицы или световой вспышки (взрывы); отражение или поглощение частиц или световых вспышек; столкновения и почти столкновения, именуемые совпадениями.
Как определить место и время, где и когда происходит событие в данной инерциальной системе отсчёта? Представим себе, что мы построили тело отсчёта, собрав из метровых стержней кубическую решётку, вроде того подобия «шведских стенок», которые стоят на детских площадках (рис. 9).

Рис. 9. Решётка из метровых стержней и часов. Опорные часы выделены.
Решётка из часов
Закрепим в каждом узле этой решётки часы. Часы могут быть любой конструкции, но они проградуированы в метрах времени. Возможность такой градуировки обсуждалась в разд. 1, когда мы заставляли световую вспышку бегать, отражаясь между двумя зеркалами, отстоящими друг от друга на полметра. Мы говорили, что такие часы издают «тик-так» каждый раз, когда свет возвращается к первому зеркалу. Между соседними «тик-так» свет проходит замкнутый путь 1 м, и мы условились называть полученную таким образом единицу времени 1 метром светового времени или, проще, 1 метром времени. В обычных единицах скорость света имеет измеренную величину 𝑐=2,997925⋅10⁸ м/сек. Путь 1 м свет проходит за время, равное 1 метр/с = 3,335640⋅10⁻⁹ сек. Значит, 1 метр светового времени равен 3,335640⋅10⁻⁹ секунд или около 3,3 наносекунд, если говорить на языке электроники сверхвысоких частот. Итак, мы полагаем, что все часы решётки, какова бы ни была их конструкция, проградуированы в метрах светового времени.
Синхронизация часов решётки
Каким образом синхронизировать друг с другом разные часы в решётке? Это можно сделать так: примем одни из этих часов за стандартные и перенесём в них начало системы координат 𝑥, 𝑦, 𝑧. Начнём на этих опорных часах отсчёт времени с 𝑡=0 и пошлём из них в этот момент световой сигнал во всех направлениях. Будем называть такой сигнал также опорным. Когда опорный сигнал достигает часов, находящихся на расстоянии 5 м, мы считаем, что эти часы должны показывать 5 метров светового времени. Пусть тогда находящийся при них ассистент ещё до начала эксперимента поставит стрелки этих часов на 5 метров времени, установит их в 5 м расстояния от опорных часов и запустит, лишь когда до него дойдёт опорный сигнал. Когда все приставленные к часам решётки ассистенты проделают аналогичную процедуру, т.е. каждый поставит стрелки своих часов на время в метрах, равное своему расстоянию от опорных часов, и запустит их, когда до него дойдёт опорный сигнал, то часы решётки будут синхронизированы между собой.
Возможны и другие способы синхронизации часов. Например, можно установить по опорным часам в начале координат переносные часы, а затем пронести их по решётке и поставить по ним остальные часы. Эта процедура, однако, предполагает передвижение часов. Мы увидим позже, что движущиеся часы обладают другой скоростью хода, если её контролировать с помощью часов решётки, чем часы, оставленные в покое в начале координат. Переносные часы даже перестанут согласоваться с этими последними, когда мы вернём их снова в начало координат! (См. парадокс часов; упражнение 27). Правда, следя за тем, чтобы скорость движения переносных часов составляла лишь весьма малую долю скорости света, мы почти избавимся от этой ошибки, и второй метод синхронизации по своему результату будет очень близок к первому методу, стандартному. Более того, ошибку можно сделать сколь угодно малой, если передвигать переносные часы достаточна медленно.
Использование решётки для измерения всех 4 координат событий
Решётка с синхронизированными часами может использоваться для определения положения в пространстве и времени любого события. За положение события в пространстве принимается положение часов, ближайших к этому событию. Его положение во времени принимается равным времени, которое при этом показывают часы, ближайшие к событию. Итак, координаты события — это набор 4 чисел: 3 из них характеризуют положение в пространстве часов, ближайших к этому событию, а четвёртое равно времени (в метрах), когда по этим часам произошло это событие. Если часы установил предусмотрительный экспериментатор, то это хронографы, и каждый из них может отметить возникновение события (например, приход светового сигнала или частицы). Каждый из них отпечатывает на карточке сущность явления, его время и положение часов. Затем эти карточки можно собрать со всех часов и проанализировать — возможно, на электронной машине.
Шаг решётки зависит от масштабов изучаемых физических явлений
Почему решётка строилась из стержней, каждый из которых был длиной 1 метр? По выданной часами карточке мы не сможем в этом случае установить, произошло ли зафиксированное событие на 0,4 м левее часов или, например, на 0,2 м правее их. Местоположение события будет неопределённым с точностью до заметной доли метра. Время события также будет известно лишь с точностью до заметной доли метра светового времени. Но такой точности вполне достаточно при наблюдении прохождения ракеты. Её куда более чем достаточно, если мы измеряем положение планет на орбитах,— было бы даже разумным увеличить шаг решётки с м до сотен метров. Но ни шаг в 100 м, ни шаг в 1 м не пригодны для решётки, с помощью которой мы изучаем траектории частиц, полученных на мощном ускорителе. Здесь уместнее считать на сантиметры или миллиметры. Итак, положение события в пространстве и во времени можно найти с любой требуемой степенью точности, построив решётку, обладающую достаточно малым шагом.
Определение понятия «наблюдатель»
В теории относительности часто идёт речь о «наблюдателе». Где он расположен? В каком-то одном месте или сразу во всём пространстве? Слово «наблюдатель» — это сокращение, которым обозначается вся система часов-хронографов, связанных с данной инерциальной системой отсчёта. Ни один реальный наблюдатель не справился бы в одиночку с обязанностями того «идеального наблюдателя», которого мы используем при анализе теории относительности. Поэтому лучше представлять себе наблюдателя как человека, совершающего обход всех порученных ему хронографов и собирающего на них свои перфорированные карточки. Таков смысл фразы «наблюдатель обнаруживает то-то и то-то», которой мы будем пользоваться в дальнейшем.
Показания часов характеризуют движение частицы сквозь решётку
Движение частицы сквозь решётку обнаруживается с помощью часов: каждые часы, мимо которыхпролетает частица, отпечатывают как время её пролёта, так и пространственную координату этого события. Как охарактеризовать числами «путь» (мировую линию) частицы? Для этого следует вдоль мировой линии проставить координаты событий. По разностям координат последовательных событий находится скорость частицы. Такая скорость 𝑣 обычно измеряется в метрах в секунду (м/сек). Однако, когда время измеряется в метрах светового времени, скорость должна быть выражена в метрах пути, пройденного за 1 метр времени. Во избежание недоразумений мы будем обозначать скорость, измеренную в м/м, греческой буквой «бета» (β). Световой сигнал проходит 1 м пути за 1 м светового времени, т.е βсвет=1 Скорости частиц, измеренные в м/м, представляют собой отношения их скоростей в м/сек к скорости света; иными словами, β=𝑣/𝑐. Здесь, как и далее, через 𝑐 обозначена скорость света.
Проверка инерциальности системы отсчёта, образованной данной решёткой
По движению пробных частиц сквозь решётку часов, а говоря точнее, по регистрациям совпадений, отпечатанным нашими хронографами, мы можем выяснить, представляет ли собой эта решётка инерциальную систему отсчёта. Если зарегистрировано, что: а) пробная частица (с некоторой заданной точностью) последовательно проходит мимо часов, расположенных на прямой линии; б) скорость β пробной частицы, вычисленная по этим же записям, постоянна (вновь с некоторой заданной степенью точности) и в) такие выводы получаются для стольких мировых линий пробных частиц, сколько их сможет проследить в данной области пространства и времени самый трудолюбивый наблюдатель, то эта решётка часов образует в данной области пространства-времени инерциальную систему отсчёта.
Лабораторная система отсчёта и система ракеты при совпадении 𝑥-осей
Мы снова описали движение пробных частиц относительно конкретной системы отсчёта с целью определить, является ли данная система инерциальной. Одни и те же пробные частицы, а в случае их столкновений одни и те же акты соударения могут быть описаны как по отношению к одной инерциальной системе отсчёта, так и по отношению к другой. Пусть две системы отсчёта реализуются двумя разными решётками из метровых стержней и часов, так что одна система движется относительно другой равномерно, а оси 𝑥 обеих систем совпадают. Назовём одну из этих систем отсчёта лабораторной, а другую, движущуюся относительно первой в положительном направлении оси 𝑥, — системой отсчёта ракеты (рис. 10 и 11). Ракета летит с выключенным двигателем с постоянной скоростью относительно лаборатории. Пусть решётки ракеты и лаборатории перекрываются в том смысле, что имеется область пространства, общая для обеих систем отсчёта (как это описано в разд 3 и показано на рис. 8). В этой общей области пространства-времени движутся пробные частицы. По их движению, зарегистрированному часами данного наблюдателя, этот наблюдатель удостоверяется в том, что его система отсчёта инерциальна; пусть это имеет место для наблюдателей в обеих системах отсчёта.

Рис. 10. Лабораторная система отсчёта и система ракеты. Соответствующие им решётки были наложены друг на друга секунду назад.

Рис. 11. Лабораторная система отсчёта (слева) п система ракеты (справа) —дальнейшая схематизация рис. 10. В обеих системах заштрихованы центральные опорные часы.
Наблюдатели в лаборатории и на ракете фиксируют одно и то же событие
Взорвём хлопушку. Её взрыв будет зарегистрирован ближайшими к нему часами лабораторной решётки; он будет также зарегистрирован ближайшими к месту взрыва часами решётки ракеты. Как связаны между собой записи о координатах взрыва у часов-хронографов в лаборатории и на ракете? Частично на этот вопрос сразу же отвечает принцип относительности: в записях часов в лаборатории и на ракете будет указано одно и то же значение координаты 𝑦. Для доказательства предположим, что часы-хронограф на ракете снабжены кистью, смоченной в краске, и делают отметки на лабораторной решётке при своём движении. Это изображено на рис. 12 для случая, когда 𝑦=1 м. Эти отметки на лабораторной решётке служат для нахождения лабораторной координаты 𝑦, соответствующей 𝑦=1 у часов на ракете. Эти отметки ложатся на лабораторные часы с 𝑦=1, не выше и не ниже их. Ведь если бы краска ложилась на стержни решётки ниже лабораторных часов с 𝑦=1, то оба наблюдателя заключили бы, что часы на ракете с 𝑦=1 прошли «ниже» лабораторных часов с 𝑦=1. Цепочка отметок краской сделала бы этот факт очевидным для всех. Аналогично, если бы эти отметки ложились на стержни выше лабораторных часов с 𝑦=1, то оба наблюдателя заключили бы, что часы на ракете с 𝑦=1 прошли «над» лабораторными часами с 𝑦=1. В обоих случаях имелась бы возможность экспериментально отличить друг от друга эти две системы отсчёта. Но ведь отличить эти системы друг от друга с помощью какого-либо другого эксперимента было невозможно — в принципе относительности содержится утверждение, что такого экспериментально находимого различия между инерциальными системами отсчёта вообще не может быть. Отсюда мы заключаем, что отличить эти две системы отсчёта невозможно и с помощью этого эксперимента. Поэтому координата 𝑦 любого события, и в том числе взрыва, с которого мы начали этот абзац, будет одной и той же как в системе отсчёта ракеты, так и в лабораторной системе.

Рис. 12. Доказательство того, что координата 𝑦 любого события одинакова в лабораторной системе отсчёта и в системе ракеты.
Координата 𝑦 события одинакова как в лабораторной системе отсчёта, так и в системе ракеты
Из аналогичных доводов следует, что и координата 𝑧 любого события одинакова как в системе отсчёта ракеты, так и в лабораторной системе. Заметим, что обе эти координаты события — и 𝑦, и 𝑧 — отсчитываются в направлении, перпендикулярном направлению относительного движения наших систем отсчёта.
Координата 𝑧 события одинакова как в лабораторной системе отсчёта, так и в системе ракеты
Тот факт, что длины, измеренные поперёк направления относительного движения систем отсчёта, одинаковы, сразу же даёт возможность сравнивать ход часов в обеих решётках. Пусть световая вспышка бегает, отражаясь между двумя зеркалами, установленными в системе отсчёта ракеты на опорных часах и на часах, расположенных в точке с координатой 𝑦=1 точно над опорными часами. Такая вспышка будет возвращаться в исходную точку через 2 м светового времени системы ракеты. Траекторию этого светового луча можно проследить и в лабораторной системе вверх до того же самого значения координаты 𝑦 и снова вниз до опорных часов. Учитывая, что скорость света в обеих системах одинакова, можно вычислить лабораторное время, соответствующее времени распространения света по двухметровому замкнутому пути в системе отсчёта ракеты. В следующем параграфе этот расчёт приведёт к заключению об инвариантности интервала.
5. ИНВАРИАНТНОСТЬ ИНТЕРВАЛА
Какая мера характеризует относительное расположение событий 𝐴 и 𝐵 и одинакова во всех инерциальных системах отсчёта?
Расстояние между двумя городскими воротами определяется по значениям разностей координат 𝑥 этих ворот и по значениям разностей их координат 𝑦. Как определить аналогичную физическую величину — пространственно-временной интервал между двумя событиями? Между какими двумя событиями определяется такой интервал?
Пусть событие 𝐴 — акт излучения световой вспышки. Пусть событие 𝐵 — акт приёма этой вспышки после того, как она была отражена другим объектом. Эти два акта можно назвать парой событий. Нас не интересуют сами по себе ни свет, ни отражающий его объект. Однако анализ траектории светового луча в пространстве-времени позволяет легко и быстро найти величину (тот самый интервал), которая связана с этой парой событий и значение которой одинаково во всех инерциальных системах отсчёта.
Событие 𝐴 — акт излучения вспышки
Событие 𝐵 — акт приёма вспышки
Событие 𝐴 — лампа даёт вспышку. Её свет распространяется к отражателю 𝑅 (рис. 13), от которого он снова идёт вниз. Событие 𝐵 — приём вспышки. Рассмотрим теперь подробности согласно рис. 13.

а) Путь светового луча, наблюдаемый в лабораторной системе отсчёта.
б) Путь светового луча, наблюдаемый в системе отсчета ракеты.
в) Путь светового луча, наблюдаемый в системе отсчета сверхракеты.
Рис. 13. Испускание, отражение и приём опорной вспышки (приём происходит в начале координат в системе отсчёта ракеты).
Подробности о координатах событий 𝐴 и 𝐵 в лабораторной системе отсчёта и в системе ракеты
Лампа даёт вспышку в лабораторной системе в нулевой момент времени в начале системы координат 𝑥, 𝑦, 𝑧 (на рисунке заштриховано). Пролёт ракеты мимо этого места приурочен к такому времени, что и для ракеты вспышка имеет место также в начале координат (заштриховано снова) и в нулевой момент. Подытожим данные о координатах события 𝐴 (акт излучения):
𝑥
𝐴
=0,
𝑦
𝐴
=0,
𝑡
𝐴
=0,
(в лабораторной системе),
𝑥
𝐴
́ =0,
𝑦
𝐴
́ =0,
𝑡
𝐴
́ =0,
(в системе ракеты).
Отражатель укреплён на часах ракеты на расстоянии 1 м прямо над началом координат.
В системе ракеты приём вспышки осуществляется в том же месте, где произошло её излучение. Свет вспышки прошёл замкнутый путь длиной 2 м, и на этот путь потребовалось 2 м светового времени. Поэтому координаты события 𝐵 (акт приёма вспышки) в системе отсчёта ракеты равны:
𝑥
𝐵
́ =0,
𝑦
𝐵
́ =0,
𝑧
𝐵
́ =2
м
.
Более содержательны не абсолютные значения координат, а разности координат событий 𝐴 и 𝐵:
Δ
𝑥
́
=
𝑥
𝐵
́ -𝑥
𝐴
́
=
0,
Δ
𝑦
́
=
𝑦
𝐵
́ -𝑦
𝐴
́
=
0,
Δ
𝑡
́
=
𝑡
𝐵
́ -𝑡
𝐴
́
=
2
м
.
В лабораторной системе отсчёта приём вспышки происходит не в начале координат, а на расстоянии Δ𝑥 вправо от него. Если скорость ракеты велика, то велико и расстояние Δ𝑥; если скорость мала, то мало и Δ𝑥. (На рисунке это расстояние равно 1 м, однако дальнейшие расчёты справедливы для любого расстояния). В лабораторной системе отсчёта свет распространяется по гипотенузам двух прямоугольных треугольников, основание каждого из которых равно Δ𝑥/2, а высота 1 м. Полная длина пути поэтому получается равной
2
√
1+(
Δ
𝑥/2)²
Вспомним теперь, что скорость света одинакова как в лабораторной системе отсчёта, так и в системе отсчёта ракеты (что хотя и неправдоподобно, но является законом природы!). Поэтому разность времён акта излучения и акта приёма вспышки в лабораторной системе отсчёта выражается такой же формулой
Δ
𝑡
=
𝑡
𝐵
-
𝑡
𝐴
=
2
√
1+(
Δ
𝑥/2)²
(4)
(в метрах светового времени).
Промежуток времени между событиями 𝐴 и 𝐵 неодинаков для наблюдателей в лаборатории и на ракете
Почему этот промежуток времени превышает 2 м? Дело в том, что гипотенуза прямоугольного треугольника на рис. 13,а больше, чем его высота. Поэтому невозможно избежать заключения о том, что промежуток времени между актами излучения и приёма вспышки неодинаков в двух инерциальных системах отсчёта.
Таблица 5.
Разности координат событий приёма и посылки сигнала
Лабораторная система
отсчёта
Система отсчёта
ракеты
𝑥
приём
-𝑥
излуч
=
Δ
𝑥
𝑥
приём
'-𝑥
излуч
'=
Δ
𝑥'
=0
𝑡приём-𝑡излуч=Δ𝑡=
=2√1+(Δ𝑥/2)²
𝑡
приём
'-𝑡
излуч
'=
Δ
𝑥'
=2
м
В табл. 5 сведены разности как пространственных, так и временной координат событий 𝐴 и 𝐵. Промежуток времени различен в разных инерциальных системах отсчёта; различен и промежуток, разделяющий события в пространстве,— картина аналогична той, когда разности координат Δ𝑥 и Δ𝑦 для двух городских ворот были разными для дневного и ночного землемеров! Но для этих землемеров существовала комбинация координат (квадрат расстояния между воротами), одинаковая для них обоих:
(Расстояние)
²
=
(
Δ
𝑥
)
²
+
(
Δ
𝑦
)
²
=
(
Δ
𝑥'
)
²
+
(
Δ
𝑦'
)
²
.
Есть ли подобная комбинация координат наших двух событий, которая была бы одинаковой в лабораторной системе отсчёта и в системе ракеты? Ответ на этот вопрос: да! Квадрат интервала
(Интервал)
²
=
(
Δ
𝑡
)
²
-
(
Δ
𝑥
)
²
=
(
Δ
𝑡'
)
²
-
(
Δ
𝑥'
)
²
=
(2
м
)
²
(5)
— именно такая величина, как можно проверить путём непосредственной подстановки величин, фигурирующих в табл. 5.
Интервал между между событиями 𝐴 и 𝐵 имеет одну и ту же величину как для наблюдателя в лаборатории, так и на ракете
Взятая нами для исследования двух событий система отсчёта ракеты является довольно-таки специальной, так как и акт излучения, и акт приёма сигнала происходят в ней в одной и той же точке. На рис. 13, в изображён путь отражённого луча в системе отсчёта второй ракеты (система «сверхракеты»), движущейся относительно лабораторной системы отсчёта ещё быстрее, чем первая ракета. В системе этой второй ракеты разность координат 𝑥 двух событий — актов излучения и приёма вспышки (дважды штрихованные величины) 𝑥𝐵ʺ=𝑥𝐴ʺ-Δ𝑥ʺ — отрицательна, ибо акт приёма осуществляется в этой системе отсчёта на отрицательной оси 𝑥. Тем не менее (-Δ𝑥ʺ)²=(Δ𝑥ʺ)² и к тому же можно использовать свойства прямоугольных треугольников на рис. 13, в, из всего этого следует, что полная длина пути светового луча в системе отсчёта второй ракеты даётся выражением 2√1+(Δ𝑥ʺ/2)², которое имеет тот же вид, что и в лабораторной системе. Величина скорости света в системе отсчёта второй ракеты должна быть равна 𝑐, как и в системе первой ракеты. Отсюда найдём время, прошедшее между актами излучения и приёма вспышки:
𝑡
𝐵
ʺ-𝑡
𝐴
ʺ
=
Δ
𝑡ʺ
=
2√
1+(
Δ
𝑥ʺ/2)²
.
Следовательно,
(
Δ
𝑡ʺ)²
-
(
Δ
𝑥ʺ)²
=
(2
м
)
²
,
так что вообще
(
Δ
𝑡)²
-
(
Δ
𝑥)²
=
(
Δ
𝑡')²
-
(
Δ
𝑥')²
=
(
Δ
𝑡ʺ)²
-
(
Δ
𝑥ʺ)²
=
(2
м
)
²
.
(6)
Интервал 𝐴𝐵 имеет одну и ту же величину в системах всех ракет!
Забудем теперь о посланной вспышке, отражателе и о возвращении этой вспышки. Ведь это лишь средства для достижения цели. Они помогли выяснить, какая величина имеет одно и то же значение в различных системах отсчёта. Теперь сосредоточим внимание на этой величине — интервале, оставив в стороне подробности её вывода.
Что одинаково в двух инерциальных системах отсчёта?
Что в них почти одинаково?
Что различной?
Что мы выяснили? Два события, 𝐴 и 𝐵 происходят в одном и том же месте в системе отсчёта ракеты (Δ𝑥'=0), но в разное время (Δ𝑡'=2 м). В лабораторной системе отсчёта эта же пара событий происходит в пространстве на расстоянии Δ𝑥, и, чем быстрее движется ракета, тем больше это расстояние. Этот вывод никого не удивит, и многие с полным правом скажут: «Да это же более чем очевидно!». Удивительно другое. Во-первых, промежуток времени Δ𝑡 между двумя событиями, зарегистрированный в лабораторной системе отсчёта, имеет другую величину, чем зарегистрированный в системе ракеты. Во-вторых, промежуток времени между событиями 𝐴 и 𝐵 по данным, отпечатанным соответствующими двумя хронографами в лаборатории, превышает промежуток времени между теми же двумя событиями, зарегистрированный такими же часами в ракете: Δ𝑡 ≥ Δ𝑡'. В-третьих, пропорция
Δ𝑡
Δ𝑡'
=
⎡
⎢
⎣
1
+
⎛
⎜
⎝
Δ𝑥
2
⎞²
⎟
⎠
⎤½
⎥
⎦
,
в которой оказался увеличенным промежуток времени (см. табл. 5), близка к единице (увеличение очень мало), если мало расстояние, которое прошла ракета в промежутке между событиями 𝐴 и 𝐵. Но если ракета движется очень быстро, разность Δ𝑥 очень велика и пропорция, характеризующая несоответствие двух времён, может быть громадной. В-четвёртых, несмотря на эту только что обнаруженную разницу во времени, зарегистрированном в двух разных системах отсчёта, и несмотря на давно уже известную разницу в пространственном расстоянии между событиями в разных системах отсчёта (Δ𝑥 ≠ Δ𝑥' = 0), существует тем не менее величина, действительно равная в лабораторной системе отсчёта тем же двум метрам промежутка светового времени между событиями 𝐴 и 𝐵, которые были зарегистрированы в системе отсчёта ракеты. Эта величина — интервал
(Интервал)
=
√
(
Δ
𝑡)² - (
Δ
𝑥)²
.
У ракеты может быть очень большая скорость, и тогда Δ𝑥 тоже будет очень большим. Но и Δ𝑡 в этом случае будет очень большим. Более того, величина Δ𝑡 оказывается в точности «подогнанной» к величине Δ𝑥, так что выражение (Δ𝑡)² - (Δ𝑥)² равно (2 м)² вне зависимости от того, чему именно равны порознь Δ𝑥 и Δ𝑡.
Все четыре замечательные идеи частной теории относительности иллюстрируются одной и той же диаграммой
Все перечисленные отношения можно увидеть, взглянув на рис. 13, а. Длина гипотенузы первого прямоугольного треугольника равна Δ𝑡/2 а его основание имеет длину Δ𝑥/2. Утверждение, что выражение (Δ𝑡)² - (Δ𝑥)² обладает универсальной величиной (или, иначе, что (Δ𝑡/2)² - (Δ𝑥/2)² обладает универсальной величиной), значит лишь, что высота этого прямоугольного треугольника строго фиксирована (равна на нашей диаграмме 1 м), с какой бы скоростью ни летела ракета. Но что именно лежало в основе доказательства того, что (Δ𝑡)² - (Δ𝑥)² равняется (2 м)² независимо от скорости полёта ракеты? В основе лежал принцип относительности, согласно которому законы физики одинаковы во всех инерциальных системах отсчёта. Мы воспользовались здесь этим принципом двумя совершенно различными способами. Во-первых, мы вывели из него заключение, что длины, перпендикулярные направлению относительного движения систем, получаются одинаковыми при измерении в этих системах (лабораторной системе и системе отсчёта ракеты). В противном случае одну систему было бы можно отличить от другой по более коротким поперечным масштабам. Во-вторых, из принципа относительности мы заключили, что скорость света должна быть одинаковой как в лабораторной системе отсчёта, так и в системе ракеты (этот вывод подтверждается экспериментом Кеннеди — Торндайка). А если эта скорость одинакова, то из факта большей длины траектории световой вспышки в лабораторной системе (сумма длин гипотенуз двух треугольников), чем в системе отсчёта ракеты, где свет совершает простое движение взад и вперёд (сумма высот двух треугольников: 1 м вверх и столько же вниз), мы непосредственно заключаем, что время между событиями 𝐴 и 𝐵 в лабораторной системе больше, чем в системе отсчёта ракеты.
Короче говоря, один элементарный треугольник на рис. 13, а изображает сразу 4 замечательные идеи, лежащие в основе всей частной теории относительности: инвариантность длин, поперечных движению; инвариантность величины скорости света; зависимость пространственной и временно'й координат от выбора системы отсчёта; инвариантность интервала.
Парадоксально ли различие между промежутками времени, прошедшего в лабораторной системе и в системе отсчёта ракеты?
Итак, в рис. 13, а вкратце содержится вся частная теория относительности в легко запоминающемся виде. Однако проделанный анализ приводит к тому, что на первый взгляд кажется нелепостью. Какой смысл можно вообще усмотреть в том, что промежуток времени между двумя событиями больше в лабораторной системе отсчёта, чем в системе ракеты? Разве мы не приводили уже в качестве довода, что «длины, перпендикулярные направлению относительного движения систем», одинаковы, «в противном случае одну из систем было бы можно отличить от другой по более коротким поперечным масштабам?» Как же быть в этом случае с разными промежутками времени в двух системах отсчёта? Разве это различие не даст возможности физически провести различие между той и другой системами? И разве возможность такого различия не исключена принципом относительности, утверждающим, что одна инерциальная система отсчёта нисколько не хуже другой?
Сравнение относительности времени (Лоренц) с относительностью выбора направления на «север» (Эвклид)

Рис. 14. Удалённость точки 𝐵 от точки 𝐴 по координате «север—юг» («северное склонение 𝐵 относительно 𝐴») зависит от выбора направления на север.
Чтобы ответить на эти вопросы, вернёмся к притче о землемерах. Возьмём точку 𝐵 на рис. 14. Она расположена на 1 м прямо к северу от другой точки 𝐴 согласно построениям ночного землемера (определение направления на север по Полярной звезде). Рассмотрим теперь положение точки 𝐵 с позиций дневного землемера (ориентация на север по магнитной стрелке). Будет ли разность координат Δ𝑦 между 𝐴 и 𝐵 (на языке землемеров — северное склонение) также равна 1 м в дневной системе? Нет, Δ𝑦 здесь меньше, чем 1 м! Почему же? Дело в том, что высота (Δ𝑦) прямоугольного треугольника короче, чем его гипотенуза (1 м). Значит ли это, что правила триангуляции в дневной системе координат отличаются от этих правил в ночной системе координат? Конечно, нет! Точно так же нет дефектов в конструкции и ходе лабораторных часов, на которые можно было бы списать большую длительность промежутка времени 𝐴𝐵. Это «расхождение» в показаниях лабораторных часов и часов на ракете обусловлено лишь самой природой геометрии пространства-времени. Так уж устроен мир! В табл. 6 проведена параллель между геометрией пространства-времени по Лоренцу и эвклидовой геометрией мира землемеров.
Таблица 6.
Различие «северного склонения» (координата 𝑦) точек 𝐴 и 𝐵 в дневной и ночной системах координат и различие времени между событиями 𝐴 и 𝐵 в лабораторной системе отсчёта и системе ракеты. Сравнительный анализ
Вопросы
Ответы студента-геодезиста о различии «северного склонения» между точками 𝐴 и 𝐵 (см. рис. 14)
Ответы студента-физика о различии времени между событиями 𝐴 и 𝐵 (см. рис. 13)
В какой системе отсчёта имеет самый простой вид взаимная удалённость 𝐴 и 𝐵?
В системе координат ночного землемера, сориентированной на Полярную звезду
В системе отсчёта ракеты
Какое обстоятельство упрощает картину в этой системе отсчёта?
Обе точки обладают одинаковым значением координаты 𝑥', т.е. Δ𝑥'=0
Оба события обладают одинаковым значением координаты 𝑥', т.е. Δ𝑥'=0
Почему это обстоятельство упрощает измерение удалённости 𝐴𝐵?
Достаточно единственного метрового стержня, ориентированного на Полярную звезду, чтобы: 1) удостовериться, что координата 𝑥' обеих точек одинакова, и 2) непосредственно измерить «северное склонение» точки 𝐵 относительно точки 𝐴
Достаточно одних часов-хронографа, связанных с системой отсчёта ракеты, чтобы: 1) удостовериться, что координата 𝑥' обоих событий одинакова, и 2) непосредственно измерить запаздывание во времени события 𝐵 относительно события 𝐴
Назовите другую систему, в которой исследуется удалённость 𝐴 и 𝐵
Система координат дневного землемера, сориентированная по магнитному компасу
Лабораторная система отсчёта
Какое усложнение возникает в этой системе при анализе удалённости?
Ни один из метровых стержней, ориентированных по направлению на магнитный полюс, не может сам по себе указать относительное положение точек 𝐴 и 𝐵
Ни одни часы-хронограф в лаборатории не могут в отдельности измерить положение как 𝐴, так и 𝐵
Как преодолевается эта трудность?
Необходимы два ориентированных по направлению на север метровых стержня, один из которых сдвинут на Δ𝑥 м вправо от другого
Необходимы двое таких лабораторных часов, одни из которых сдвинуты на Δ𝑥 м вправо от других
Какие данные фиксирует первый из этих измерительных приборов?
Точку 𝐴 при 𝑦=0
Событие 𝐴 при 𝑡=0
Укажите данные второго измерительного прибора
Точка 𝐵 расположена на Δ𝑦 м к северу
Событие 𝐵 запаздывает на Δ𝑡 сек
Измеряется ли удаление 𝐵 от 𝐴 непосредственно найденной этим путём координатой 𝐵?
Нет. «Северное склонение» меньше, чем расстояние 𝐴𝐵 Точнее: Δ𝑦=√(𝐴𝐵)²-(Δ𝑥)²
Нет. Запаздывание Δ𝑡 больше, чем интервал 𝐴𝐵. Точнее: Δ𝑡=√(𝐴𝐵)²+(Δ𝑥)²
Как же тогда найти удаление 𝐴𝐵. из измерений в этой системе?
По формуле для расстояния: (Расстояние)²=(Δ𝑥)²+(Δ𝑦)². (Проверьте, подставив сюда выражение для Δ𝑦, данное в предыдущем ответе!)
По формуле для интервала: (Интервал)²=(Δ𝑡)²-(Δ𝑥)². (Проверьте, подставив сюда выражение для Δ𝑡, данное в предыдущем ответе!)
Как различаются данные в штрихованной и нештрихованной системах в этих примерах?
Δ𝑦 меньше, чем Δ𝑦' (=𝐴𝐵)
Δ𝑡 больше, чем Δ𝑡' (=𝐴𝐵)
Нет ли в этих выводах чего-нибудь нелепого?
В том смысле, что одинаковые метровые стержни дают неодинаковое «северное склонение»?
В том смысле, что одинаковые часы указывают неодинаковое время?
Да; не доказывает ли это расхождение, что в рассуждения вкрались внутренние противоречия?
Нет. Расстояние 𝐴𝐵 можно измерить одним стержнем, ориентированным «по-ночному». Но нет такого индивидуального метрового стержня, ориентированного «подневному», который дал бы (меньшее) магнитное «северное склонение» 𝐵 относительно 𝐴. Поэтому нельзя сказать, что какой-либо из «дневных» метровых стержней противоречит «ночному» метровому стержню
Нет. Интервал 𝐴𝐵 прямо дают одни часы на ракете. Но нет таких индивидуальных часов, связанных с лабораторией, которые показали бы (большее) запоздание события 𝐵 относительно 𝐴. Поэтому нельзя сказать, что какие-либо из лабораторных часов противоречат часам на ракете
Вызвана ли такая несимметричная разница между значениями координат в штрихованной и нештрихованной системах отсчёта каким либо фундаментальным различием между этими системами?
Из-за Δ𝑦<Δ𝑦'? Нет!
Из-за Δ𝑡>Δ𝑡'? Нет!
Что же тогда ответственно за такую асимметрию?
Просто то стечение обстоятельств, что точка 𝐵 взята на одной прямой север — юг, что и точка 𝐴, при ориентации по Полярной звезде, но не на одной прямой север — юг при ориентации по магнитному компасу
Просто то стечение обстоятельств, что событие 𝐵 произошло в системе отсчёта ракеты в одном месте с 𝐴, но не в одном месте с 𝐴 в лабораторной системе отсчёта
Чем можно здесь проиллюстрировать полное физическое равноправие этих двух систем?
Нужно рассмотреть точку 𝐶 обладающую такой же 𝑥-координатой, что и 𝐴 (т.е. взять 𝐶 на одной линии север — юг с 𝐴 при ориентации по магнитному компасу)
Нужно рассмотреть событие 𝐶, обладающее такой же 𝑥-координатой, что и 𝐴 (т.е. взять 𝐶 в том же месте в лабораторной системе, что и 𝐴, но позднее во времени)
Как будут различаться результаты измерений в штрихованной и нештрихованной системах при таком выборе точки 𝐶?
Δ𝑦 (=𝐴𝐶) будет больше, чем Δ𝑦'
Δ𝑡 (=𝐴𝐶) будет меньше, чем Δ𝑡'
Как вы подытожите это обсуждение?
Нет никакого парадокса в том, что компонента север — юг для 𝐴𝐵 имеет разные значения в двух разных системах координат. Это различие — не следствие неисправности метровых стержней и даже вообще не порок. «Расхождение» в выводах обусловлено внутренней природой эвклидовой геометрии
Нет никакого парадокса в том, что время, прошедшее между 𝐴 и 𝐵, различно в двух разных системах отсчёта. Это различие — не следствие неисправности часов и даже вообще не порок. «Расхождение» в выводах обусловлено внутренней природой геометрии пространства-времени, в котором реализуется вся физика
6. ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ 1). МИРОВЫЕ ЛИНИИ
1) Пространственно-временны'е диаграммы обычно называют диаграммами Минковского.— Прим. перев.
Пространственно-временные диаграммы как удобный способ изображения событий

а) Диаграмма пространства-времени в лабораторной системе отсчёта.
б) Диаграмма пространства-времени в системе отсчёта ракеты.
в) Диаграмма пространства-времени времени в системе отсчета сверхракеты.
Рис. 15. Диаграммы пространства-времени, описывающие излучение опорной вспышки и её приём после отражения. Дуга гиперболы, изображённой на каждой диаграмме, описывается уравнениями
(Интервал)² = 𝑡²-𝑥² = 𝑡'²-𝑥'² = 𝑡ʺ²-𝑥ʺ² .
Удобно рассматривать события предыдущего параграфа (акты излучения и приёма световой вспышки), изображая положение события в пространстве на горизонтальной оси, а время события — на вертикальной оси диаграммы пространства-времени (рис. 15). Свет был излучён лампой-вспышкой, закреплённой на опорных часах первой ракеты. Эта лампа дала вспышку в тот момент, когда часы пролетали мимо опорных часов лаборатории. И те и другие часы в это время показывали нуль времени. Поэтому событие — акт излучения — располагается в начале координат диаграммы пространства-времени, построенной наблюдателем на ракете:
𝑥
излуч
'=0,
𝑡
излуч
'=0.
Это событие располагается также в начале координат диаграммы пространства-времени наблюдателя в лаборатории:
𝑥
излуч
=0,
𝑡
излуч
=0.
Дальнейшая история испущенного светового луча выглядит по-разному на диаграммах пространства-времени лаборатории и обеих ракет. В первой ракете приём отражённого луча происходит в точке 𝑥'=0 на 2м времени позже опорного события
𝑥
приём
'=0,
𝑡
приём
'=2
м
.
как это уже отмечено в табл. 5 и как можно непосредственно увидеть на рис. 15, б. В лабораторной системе отсчёта событие — акт приёма — происходит справа от начала координат:
𝑥
приём
=
Положительная величина,
𝑡
приём
=
√
(2
м
)
²
+(
𝑥
приём
)
²
=
=
Момент времени,
больший 2 м
,
что изображено на рис. 15, а. В системе отсчёта второй ракеты (которая летит быстрее, чем первая!) событие — акт приёма — происходит слева от начала координат (рис. 15, в).
𝑥
приём
ʺ
=
Отрицательная величина,
𝑡
приём
ʺ
=
√
(2
м
)
²
+(
𝑥
приём
ʺ
)
²
=
=
Момент времени,
больший 2 м
(снова!).
Различные точки, помеченные на разных диаграммах пространства-времени как акт приёма, относятся к одному и тому же событию. Событие одно, но его координаты в разных системах отсчёта различны. Что же объединяет между собой эти разные координаты одного и того же события? Все они удовлетворяют уравнению
⎛
⎜
⎜
⎝
Разница
во
времени
⎞²
⎟
⎟
⎠
-
⎛
⎜
⎜
⎝
Расстояние
в
пространстве
⎞²
⎟
⎟
⎠
=
(Интервал)
²
=
=
Постоянная величина.
Но это — уравнение гиперболы. Итак, событие, изображённое на гиперболе 𝑡²-𝑥²=(постоянная величина) диаграммы пространства-времени некой лаборатории или ракеты, будет изображаться также на гиперболе, описываемой тем же уравнением, диаграммы пространства-времени любой другой лаборатории или ракеты.
На диаграмме пространства-времени инвариантный интервал соответствует гиперболе

Рис. 16. Относительное расположение координатных осей, соответствующее выбору направления на север дневного, ночного и некоего третьего землемеров.
Существует ли аналогичная кривая, сопоставляющая разные значения координат, получаемые для одних и тех же ворот дневным и ночным землемерами? Координаты 𝑥 и 𝑦, скажем, ворот 𝐴 относительно городской площади определяются в зависимости от выбора направления на север (рис. 16). Дневной и ночной планы этих ворот изображены на рис. 17, а и б. Сделаем ещё один, третий (отличающийся от двух первых), выбор координатных осей, повёрнутых ещё больше, чем ночные оси относительно дневных. Для землемера, пользующегося этим третьим выбором координатных осей, координата 𝑥ʺ ворот 𝐴 может оказаться отрицательной (рис. 17, в).

а) Чертёж дневного землемера.

б) Чертёж ночного землемера.
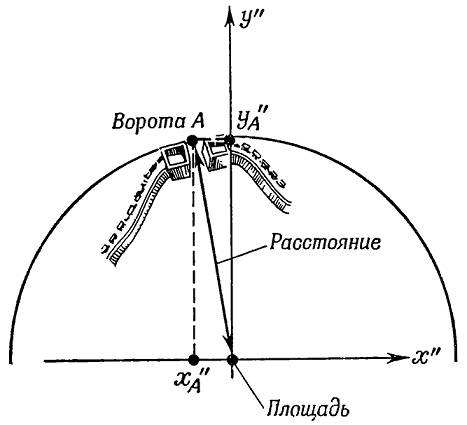
в) Чертёж третьего землемера.
Рис. 17. Координаты ворот 𝐴, измеренные соответственно дневным, ночным и третьим землемерами. Дуга окружности, изображённая на каждой схеме, описывается уравнениями
(Расстояние)
²
=
𝑥²+𝑦²
=
𝑥'²+𝑦ʺ²
=
𝑥'²+𝑦ʺ²
Инвариантное расстояние соответствует окружности на диаграмме 𝑥𝑦
Различные точки, помеченные на разных чертежах как «ворота 𝐴», относятся к одним и тем же воротам. Ворота одни, но их координаты на разных планах различны. Что же объединяет между собой эти разные координаты одних и тех же ворот? То, что все они удовлетворяют условию
⎛
⎜
⎜
⎝
Разность
координат
𝑥
⎞²
⎟
⎟
⎠
+
⎛
⎜
⎜
⎝
Разность
координат
𝑦
⎞²
⎟
⎟
⎠
=
=
(Расстояние)
²
=
Постоянная величина.
Но это — уравнение окружности. Итак, точка, изображённая на окружности 𝑥²+𝑦²=(постоянная величина) в системе координат любого землемера, будет изображаться также на окружности, описываемой тем же уравнением, в системе координат любого другого землемера.
Это — основное различие между школьной эвклидовой геометрией и реальной лоренцевой геометрией пространства-времени. В эвклидовой геометрии инвариантно расстояние между парами точек, ипоэтому для всех землемеров ворота 𝐴 будут изображаться где-либо на окружности (плоскости 𝑥𝑦) с центром в городской площади. В лоренцевой геометрии инвариантен интервал между событиями, и поэтому для всех наблюдателей в лабораториях и ракетах данное событие будет изображаться где-либо на гиперболе (на диаграмме пространства-времени) по отношению к опорному событию.
В эвклидовой геометрии длина (или её квадрат) всегда положительна:
(
Δ
𝑥)²
+
(
Δ
𝑦)²
=
(
Δ
𝑥')²
+
(
Δ
𝑦')²
≥
0.
Напротив, квадрат интервала в лоренцевой геометрии
(
Δ
𝑡)²
-
(
Δ
𝑥)²
=
(
Δ
𝑡')²
-
(
Δ
𝑥')²
может быть положительным, отрицательным или равным нулю в зависимости от того, какая составляющая в нем преобладает — временная или пространственная. Более того, к какому бы из этих типов ни принадлежал интервал в одной системе отсчёта, он останется того же типа и в любой другой системе отсчёта, так как величина интервала одинакова во всех системах. Значит, мы обнаружили, что в природе существует фундаментальный способ классифицировать порядок событий. Мы назовём интервал между двумя событиями временноподобным, светоподобным или пространственноподобным в зависимости от того, положителен, равен нулю или отрицателен его квадрат (см. табл. 7) 1).
1) В отечественной литературе чаще говорят не «светоподобный», а «изотропный», иногда— «нулевой», однако термин «светоподобный» вполне отвечает существу дела, и мы его сохранили в переводе. Довольно употребительный термин «времениподобный», кажущийся на первый взгляд менее двусмысленным, чем «временноподобный», едва ли может быть предпочтён последнему ввиду законов словопостроения русского языка. Отметим, что ряд авторов используют определение квадрата интервала, отличающееся от принятого в этой книге знаком, ввиду чего временноподобный квадрат интервала у них отрицателен, а пространственноподобный — положителен.— Прим. перев.
Таблица 7.
Классификация взаимной упорядоченности пар событий
Характер описания
Величина
квадрата интервала
Наименование
Временна'я часть интервала преобладает по сравнению с пространственной
Положительна
Временноподобный интервал
Временна'я часть интервала равна его пространственной части
Равна нулю
Светоподобный (изотропный) интервал
Пространственная часть интервала преобладает по сравнению с временно'й
Отрицательна
Пространственноподобный интервал
Три типа интервалов между парами событий: временноподобный, светоподобный и пространственноподобный
В зависимости от того, временноподобный он или пространственноподобный, интервал между двумя событиями обозначается по-разному. Временноподобный интервал записывается с помощью греческой буквы «тау» (τ) и называется также инвариантным временноподобным расстоянием или собственным временем (иногда — локальным временем) между двумя событиями:
Δ
τ
=
√
(
Δ
𝑡)²-
Δ
𝑥)²
.
(7)
Собственное время и собственное расстояние
Пространственноподобный интервал обозначается с помощью греческой буквы «сигма» (σ) и называется инвариантным пространственноподобным расстоянием или собственным расстоянием между двумя событиями:
Δ
σ
=
√
(
Δ
𝑥)²-
Δ
𝑡)²
.
(8)
Мировая линия частицы

Рис. 18. Временноподобная мировая линия частицы.
На рис. 18 изображено положение частицы в пространстве в функции времени в предположении, что частица в момент 𝑡=0 находилась в начале координат и затем двигалась вдоль оси 𝑥. Такой график зависимости положения в пространстве от времени на пространственно-временной диаграмме, называется мировой линией частицы. Каждые встречающиеся с частицей часы решётки регистрируют время встречи, так что мировая линия частицы в некотором смысле есть сумма таких отдельных событий-встреч. Никто никогда не наблюдал частиц, движущихся быстрее света. Поэтому любая частица всегда проходит за 1 м светового времени менее 1 м пути. Это значит, что разница во времени между всеми событиями на мировой линии частицы больше, чем расстояние между ними в пространстве, т.е. мировая линия частицы складывается из событий, временноподобных по отношению к исходному событию и по отношению друг к другу. Иначе говоря, мировая линия частицы должна быть временноподобной. Временноподобная мировая линия характеризуется в каждой точке 𝑃 касательной к ней в этой точке, лежащей где-то между мировыми линиями световых лучей, испущенных в той же точке. Эти световые лучи распространяются за 1 м светового времени на 1 м длины. События, лежащие на мировой линии светового луча, одинаково отстоят друг от друга в пространстве и во времени. Поэтому мировая линия светового луча складывается из событий, светоподобных по отношению к исходному событию и друг к другу. Иначе говоря, мировая линия светового луча должна быть светоподобной.
Путь в пространстве обладает длиной
Центральным в эвклидовой геометрии является понятие расстояния. Например, пользуясь гибкой измерительной рулеткой, легко найти расстояние Δ𝑠 вдоль пути, начинающегося на городской площади и идущего по кривой через городские ворота 𝐴 (рис. 19а). Расстояние Δ𝑠 между двумя любыми близкими точками на этом пути (например, теми, что обозначены на рисунке как 3 и 4) можно также вычислить исходя из разностей координат Δ𝑥 и Δ𝑦 этих точек в каждой из систем координат. Ввиду инвариантности расстояния оно будет для этой пары точек одним и тем же в любой из систем координат, хотя сами разности координат Δ𝑥 и Δ𝑦 будут различны в разных системах. Также и расстояния между всеми другими парами соседних точек на этом пути не будут зависеть от выбранной для расчётов системы координат. Значит, это заключение справедливо и в отношении суммы всех отрезков данного пути! Итак, разные землемеры, пользующиеся различными системами координат, найдут, что длина данного пути от определённой начальной точки 𝑂 до определённой конечной точки 𝐵 для всех них одинакова.

Рис. 19а. Расстояние вдоль искривлённого пути, начинающегося на городской площади. Заметим, что полное расстояние вдоль искривлённого пути от точки 𝑂 до точки 𝐵 больше, чем расстояние по прямому пути (ось 𝑦) от точки 𝑂 до точки 𝐵.

Рис. 19б. Собственное время вдоль искривлённой мировой линии на диаграмме пространства-времени. Заметим, что полное собственное время вдоль искривлённой мировой линии от события 𝑂 до события 𝐵 меньше, чем собственное время по прямой оси 𝑡 от события 𝑂 до события 𝐵.
Но от 𝑂 до 𝐵 можно пройти и по совершенно другому пути, например по прямой 𝑂𝐵 (рис. 19а). Этот новый путь, очевидно, обладает другой длиной, чем старый. Такое различие в длинах разных путей между 𝑂 и 𝐵 — настолько общеизвестный факт в эвклидовой геометрии, что не требует никаких комментариев и уж, конечно, не вызывает удивления. В эвклидовой геометрии путь по кривой между заданными двумя точками длиннее, чем прямолинейный путь между этими же двумя точками. Различие же длин для разных путей не приводит ни к каким противоречиям, и никто не станет заявлять, будто измерительная рулетка даёт неверный результат, если её протянуть в соответствии с кривизной пути.
Прямой путь обладает наименьшей длиной
Собственное время играет ту же роль для мировой линии в лоренцевой геометрии, какую играла длина для пути в эвклидовой геометрии. Пусть началом мировой линии служит событие 𝑂 а концом — событие 𝐵. Существует бесконечное множество разных мировых линий, соединяющих события 𝑂 и 𝐵. Соответствующий каждой из них промежуток собственного времени определён вполне однозначно, но различен для разных мировых линий. Удивительно ли это? Если да, то следует подробнее рассмотреть определение собственного времени и методику его измерения.
Протяжённость мировой линии измеряется собственным временем
Рассмотрим частицу, движущуюся от 𝑂 к 𝐵 по искривлённой мировой линии (рис. 19б) 1). В этом случае частица движется реально вдоль оси 𝑥 с переменной скоростью. Пусть эта частица посылает световой сигнал через каждый метр времени по часам, движущимся вместе с частицей. Собственное время Δτ, прошедшее между каждыми двумя последовательными вспышками (например, обозначенными на рисунке через 3 и 4), можно вычислить, исходя из разностей координат Δ𝑥 и Δ𝑡 этих событий, измеренных в некоторой инерциальной системе отсчёта. Ввиду инвариантности этого интервала промежуток собственного времени между двумя данными событиями будет одним и тем же, в какой бы инерциальной системе отсчёта мы его ни вычисляли, хотя сами разности пространственных и временных координат Δ𝑥 и Δ𝑡 будут различны в разных системах отсчёта. Интервалы между всеми другими парами последовательных событий-вспышек на этой мировой линии не будут зависеть от выбранной для вычисления величины интервала системы отсчёта. Значит, это заключение справедливо и в отношении суммы интервалов собственного времени между всеми событиями-вспышками на данной мировой линии! Итак, разные наблюдатели в различных инерциальных системах отсчёта найдут, что промежуток собственного времени между определённым начальным событием 𝑂 и определённым конечным событием 𝐵 вдоль данной мировой линии для всех них одинаков.
1) Конечно, движения вдоль мировой линии реально не происходит, как это и подчеркивается в следующей фразе. Авторы очень удачно охарактеризовали ранее мировые линии на диаграммах Минковского как изображение функциональной зависимости пространственной координаты 𝑥 материального объекта от времени. Поэтому читатель, встречая употребляемое для краткости выражение «движение по мировой линии», должен сопротивляться искушению понимать его буквально.— Прим. перев.
Прямая мировая линия соответствует наибольшему промежутку собственного времени
Но от события 𝑂 до события 𝐵 можно «пройти» и по совершенно другой мировой линии, например по прямой 𝑂𝐵 (рис. 19б). Этой новой мировой линии, очевидно, соответствует другой промежуток собственного времени, чем старой мировой линии. В лоренцевой геометрии искривлённая мировая линия между двумя заданными событиями короче, чем прямая мировая линия между теми же двумя событиями,— короче в смысле соответствующего ей промежутка собственного времени (рис. 20). Расстояние между двумя соседними точками по кривому пути всегда равно или больше разности координат 𝑦 этих точек. Напротив, промежуток собственного времени между двумя соседними событиями по кривой мировой линии всегда равен или меньше соответствующего времени по прямой мировой линии. Фундаментальным способом сравнения различных мировых линий между двумя событиями является определение собственного времени.

а) В эвклидовой геометрии.

б) В лоренцевой геометрии.
Рис. 20. Противоположность между геометриями Эвклида и Лоренца. В лоренцевой геометрии искривлённая мировая линия соответствует движению за меньшее собственное время.
Разный наклон мировой линии в разных её точках (на рис. 19б и 20,б) означает, что движущиеся по ней часы меняют скорость — ускоряются. При ускорении разные часы будут вести себя по-разному, если только эти часы не будут достаточно малыми. Как правило, часы могут выдерживать большие ускорения, лишь если они достаточно компактны. Чем меньше часы, тем большие ускорения они смогут выдерживать и тем резче могут быть изгибы их мировых линий. На всех диаграммах (например, на рис. 19б и 20,б) мы рассматриваем предельный случай бесконечно малых часов.
Теперь мы можем рассматривать такое движение частиц и часов, при котором они испытывают большие ускорения. Рассмотрим, в частности, простой частный случай, изображённый на рис. 19б.
Промежуток собственного времени между событиями 𝑂 и 𝐵 с точки зрения трёх мировых линий
Мировая линия на этом рисунке постепенно меняет свой наклон по мере ускорения п замедления частицы. Будем делать всё короче период ускорения (приложение большой движущей силы!) и период замедления. При этом часть времени, проведённая при равномерном движении с большой скоростью, становится всё продолжительнее. В конце концов мы придём к предельному случаю, когда периоды ускорения и торможения будут слишком короткими для того, чтобы быть различимыми на диаграмме пространства-времени (мировая линия 𝑂𝑄𝐵 на рис. 21). В этом простом предельном случае вся история движения определяется: 1) исходным событием 𝑂, 2) конечным событием 𝐵 и 3) координатой 𝑥 точки поворота 𝑄, расположенной на полпути между 𝑂 и 𝐵. На этом примере особенно просто понять, как величина промежутка собственного времени между 𝑂 и 𝐵 зависит от величины координаты 𝑥 точки поворота, и на этом основании сравнить три мировые линии 𝑂𝑃𝐵, 𝑂𝑄𝐵 и 𝑂𝑅𝐵.

Рис. 21. Сравнение трёх разных мировых линий, связывающих события 𝑂 и 𝐵, Резкие изменения скорости в событиях 𝑄 и 𝑅 изображают предельный случай использования малых («противоударных») часов.
Прямая 𝑂𝑃𝐵 изображает мировую линию неподвижной частицы: 𝑥=0 в течение всего времени. Собственное время, прошедшее от события 𝑂 до события 𝐵 по мировой линии, проходящей через 𝑃, очевидно, равно времени, измеренному в инерциальной системе отсчёта:
τ
𝑂𝑃𝐵
=
10
3
м
светового времени.
Напротив, на мировой линии, соединяющей 𝑂 и 𝐵 через 𝑅, каждая часть — светоподобная, так как для каждого её отрезка разности пространственной и временной координат равны друг другу, и поэтому
τ
𝑂𝑅𝐵
=
⎛
⎜
⎝
Удвоенное собственное
время на отрезке 𝑂𝑅
⎞
⎟
⎠
=
=
2
⎛
⎝
(Время)
²
-
(Расстояние)
²
⎞½
⎠
=
=
0.
Конечно, со скоростью света не могут двигаться никакие часы, и мировая линия 𝑂𝑅𝐵 не может реализоваться в действительности. Тем не менее она представляет собой предельное положение реально осуществимых мировых линий. Иными словами, можно найти такую скорость, которая будет достаточно близкой к скорости света, хотя и меньше её, что путешествие с этой скоростью сначала в одну, а затем в другую сторону вернёт идеальные часы назад в точку 𝑥=0 по прошествии столь короткого промежутка собственного времени, какой нам потребуется.
В отличие от предельного случая линии 𝑂𝑅𝐵 мировая линия 𝑂𝑄𝐵 соответствует промежутку собственного времени:
τ
𝑂𝑄𝐵
=
⎛
⎜
⎝
Удвоенное собственное
время на отрезке 𝑂𝑄
⎞
⎟
⎠
=
=
2
⎡
⎢
⎣
⎛
⎜
⎝
5
3
⎞²
⎟
⎠
-
⎛
⎜
⎝
4
3
⎞²
⎟
⎠
⎤½
⎥
⎦
=
=
2
⎡
⎢
⎣
25-16
9
⎤½
⎥
⎦
=
=
2
м
светового времени.
Этот промежуток собственного времени короче, чем τ𝑂𝑃𝐵=10/3 м по «прямой» мировой линии 𝑂𝑃𝐵!
Как мы видим, собственное время реального физического мира (пространства-времени) существенно отличается от понятия расстояния в школьной эвклидовой геометрии. Самое короткое расстояние — по прямому пути, и поэтому определяют: «Прямая линия есть кратчайший путь между двумя точками». Наоборот, промежуток собственного времени короче для того путешественника, который улетел, ускорившись до огромной скорости, а затем повернул и вернулся назад, чем для человека, остававшегося у себя дома. (См. упражнения 27 и 49, посвящённые парадоксу часов). Короче говоря, собственное время — это подходящее мерило для времени, наблюдаемого частицей, движущейся по мировой линии. Точно так же деления на гибкой рулетке оказываются подходящими для измерения расстояния, пройденного путешественником по криволинейному пути.
7. ПОДРАЗДЕЛЕНИЯ ПРОСТРАНСТВА-ВРЕМЕНИ
Включение координат 𝑦 и 𝑧 в интервал
До сих пор, рассматривая интервал между двумя событиями 𝐴 и 𝐵, мы ограничивались тем случаем, когда координаты 𝑦 и 𝑧 этих событий одинаковы. Тогда расстояние между событиями в пространстве измерялось величиной
Расстояние
=
Δ
𝑥,
а интервал задавался выражением
√
(
Δ
𝑡)²-
(
Δ
𝑥)²
.
Однако ясно, что ориентация осей 𝑥, 𝑦 и 𝑧 может быть выбрана произвольно. При другой ориентации этих осей компонента Δ𝑥 радиуса-вектора между двумя событиями, вообще говоря, окажется совсем другой, чем прежде. Лишь расстояние в пространстве между двумя событиями никак не зависит от выбора ориентации осей и задаётся выражением
(Расстояние)
²
=
(
Δ
𝑥)²
+
(
Δ
𝑦)²
+
(
Δ
𝑧)²
.
Другими словами, это и есть та величина, которую следует взять вместо (Δ𝑥)² в общей формуле для интервала. Итак, общая формула для интервала между событиями
𝐴 с координатами (𝑡, 𝑥, 𝑦, 𝑧)
и
𝐵 с координатами (𝑡+Δ𝑡, 𝑥+Δ𝑥, 𝑦+Δ𝑦, 𝑧+Δ𝑧)
имеет вид
⎛
⎜
⎜
⎝
Интервал
собственного
времени
⎞²
⎟
⎟
⎠
=
(Время)
²
-
(Расстояние)
²
=
=
(
Δ
𝑡)²
-
(
Δ
𝑥)²
-
(
Δ
𝑦)²
-
(
Δ
𝑧)²
(9)
для временноподобного интервала и
⎛
⎜
⎜
⎝
Интервал
собственной
длины
⎞²
⎟
⎟
⎠
=
(Расстояние)
²
-
(Время)
²
=
=
(
Δ
𝑥)²
+
(
Δ
𝑦)²
+
(
Δ
𝑧)²
-
(
Δ
𝑡)²
(10)
для пространственноподобного интервала.
Как понимать эту новую геометрию, основанную на выражении для «интервала собственной длины», в котором три знака «плюс», как и в обычной эвклидовой геометрии, но, кроме того, ещё и один знак «минус»? Следуя Минковскому (1908), можно ввести для измерения времени новую величину 𝑤, задав её как
𝑤
=
√
-1
⋅𝑡
или
𝑤
=
√
-1
⋅
Δ
𝑡
.
(11)
Тогда выражение для интервала собственной длины примет вид
⎛
⎜
⎜
⎝
Интервал
собственной
длины
⎞²
⎟
⎟
⎠
=
(
Δ
𝑥)²
+
(
Δ
𝑦)²
+
(
Δ
𝑧)²
+
(
Δ
𝑤)²
.
Минковский о единстве пространства-времени
Все слагаемые теперь берутся со знаком «плюс». Внешне соответствующая геометрия представляется эвклидовой, хотя и в четырёх, а не в трёх измерениях. Под впечатлением этой формулы Минковский написал ставшее знаменитым изречение: «Отныне пространство и время, взятые по отдельности, обречены влачить лишь призрачное существование, и только единство их обоих сохранит реальность и самостоятельность» 1). В наши дни это единство пространства и времени называют «пространством-временем». Пространство-время — эта та арена, на которой живут, движутся и вообще существуют звезды, атомы и люди. Для разных наблюдателей пространство различно. Время также различно для разных наблюдателей. Но пространство-время одинаково для всех!
1) См. сб. «Принцип относительности», Г. Лоренц, А. Пуанкаре, А. Эйнштейн, Г. Минковский, Сборник работ классиков релятивизма, Л., ОНТИ, 1935.- Прим. перев.
Подход Минковского — залог понимания физического мира. Он концентрирует внимание на величинах, одинаковых во всех системах отсчёта, таких, как интервал. Он выясняет относительный характер величин, зависящих от выбора системы отсчёта, таких, как скорость, энергия, время и расстояние.
Различие между временем и пространством
Но теперь уже понимают, что не следует преувеличивать роли утверждений Минковского. Совершенно справедливо, что время и пространство — неразделимые части единого целого. Однако неверно, что время качественно то же самое, что пространство. Почему же это неверно? Разве время не измеряется в метрах, точно так же как расстояние? Разве координаты 𝑥 и 𝑦 у землемера — не величины одной и той же физической природы? И, по аналогии, разве координаты 𝑥 и 𝑡 на диаграмме пространства-времени не являются также величинами одинаковой природы? Какой же ещё может быть к ним законный подход, кроме равноправного, в формуле √(Δ𝑥)²+(Δ𝑦)²+(Δ𝑧)²-(Δ𝑡)² для пространственноподобного интервала? Равноправный подход — конечно, но одинаковая природа — никак нет! В этой формуле есть знак минус, и его не изгнать оттуда никакими уловками. Знак «минус» отражает разную природу пространства и времени. Перейти к мнимому числу Δ𝑤=√-1⋅Δ𝑡 — вовсе не значит избавиться от этого «минуса». Это случилось бы, если бы величина 𝑤 была реальной, но она мнима. Нет часов, которые показывали бы √-1 секунд или √-1 метров. Реальные часы показывают реальное время, например Δ𝑡=7 сек. Поэтому член -(Δ𝑡)² всегда противоположен по знаку члену (Δ𝑥)²+(Δ𝑦)²+(Δ𝑧)² (расстоянию). Никакими закручиваниями и поворотами никогда не удастся заставить оба знака совпасть друг с другом.
Разница в знаках временного и пространственного членов в выражении для интервала является специфическим свойством лоренцевой геометрии, совершенно новым и не похожим ни на что присущее эвклидовой геометрии. В эвклидовой геометрии расстояние 𝐴𝐵 между двумя точками никак не может быть равно нулю, если только не равны нулю сразу все три величины Δ𝑥, Δ𝑦 и Δ𝑧. Напротив, интервал 𝐴𝐵 между двумя событиями может оказаться равным нулю, даже если разности пространственных и временных координат Δ𝑥, Δ𝑦, Δ𝑧 и Δ𝑡 для 𝐵 и 𝐴 по отдельности велики.
Случай равенства нулю интервала
При каких условиях интервал 𝐴𝐵 равен нулю? Интервал равен нулю, когда разность временных координат для 𝐴 и 𝐵 совпадает по величине с пространственным расстоянием:
Δ
𝑡
=±
√
(
Δ
𝑥)²+(
Δ
𝑦)²+(
Δ
𝑧)²
(12)
Как это условие может быть истолковано физически? Выражение, стоящее справа,— расстояние между двумя точками. При этом свет проходит 1 м расстояния за 1 м светового времени. Поэтому выражение, стоящее справа, представляет собой время, необходимое свету, чтобы покрыть расстояние между 𝐴 и 𝐵. С другой стороны, Δ𝑡 — это то время, которое дано для того, чтобы пройти этот путь. Другими словами, условие (12) выполняется, и интервал 𝐴𝐵 обращается в нуль, если световой сигнал, исходящий из события 𝐴, приходит в пространственную точку события 𝐵 как раз в момент совершения события 𝐵 (либо если сигнал, происходящий из 𝐵, попадает в 𝐴). Интервал между двумя событиями равен нулю, если эти события могут быть связаны между собой одним световым лучом.
Интересно изобразить на соответствующей диаграмме положение всех событий 𝐵, которые могут быть связаны с одним данным событием 𝐴 световым лучом. Пусть событие 𝐴 для простоты произошло в начале координат диаграммы пространства-времени.
Возьмём произвольные координаты 𝑥, 𝑦, 𝑧 события 𝐵. Тогда временна'я координата события 𝐵 может иметь либо величину
𝑡
будущ
=+
√
𝑥²+𝑦²+𝑧²
,
(13)
либо величину
𝑡
прошл
=-
√
𝑥²+𝑦²+𝑧²
,
(14)
Изобразить графически эти формулы проще всего, если ограничиться теми событиями 𝐵, координата 𝑧 которых равна нулю. Тогда следует построить диаграмму пространства-времени с двумя пространственными координатами 𝑥 и 𝑦 и временной координатой 𝑡 (рис. 22). На этой диаграмме любое событие 𝐵, отделённое от 𝐴 нулевым (светоподобным) интервалом, лежит либо на «световом конусе будущего» [знак «плюс» в уравнении (13)], либо на «световом конусе прошлого» [знак «минус» в уравнении (14)] относительно 𝐴.

Рис. 22. Диаграмма пространства-времени, изображающая координаты 𝑥, 𝑦 и 𝑡 событий, для которых 𝑧=0.
Световые конусы разграничивают пространство-время
Рассмотрим на рис. 22 все события, временна'я координата которых превышает на 7 м временну'ю координату вспышки 𝐴. Эти события лежат в плоскости, находящейся на 7 м выше плоскости 𝑥𝑦 и параллельной этой последней. Те из этих событий, которые при этом лежат и на световом конусе с вершиной в 𝐴, образуют окружность. Радиус этой окружности 7 м. Эта окружность (являющаяся окружностью на данной диаграмме для 𝑥, 𝑦, 𝑡, но сферой на полной диаграмме для 𝑥, 𝑦, 𝑧, 𝑡) представляет собой геометрическое место точек распространяющейся энергии излучения, отправленного из 𝐴. В более поздний момент этот импульс распространится на окружность ещё большего радиуса. Итак, световой конус будущего изображает эволюцию расходящегося сферического светового импульса, отправленного из 𝐴. Аналогично световой конус прошлого изображает эволюцию сходящегося импульса излучения, настолько искусно сфокусированного, что он собирается в точку в начале координат в нулевой момент времени.
Световой конус специфичен для лоренцевой геометрии; в эвклидовой геометрии ничего подобного нет. Более того, существование в лоренцевой геометрии светового конуса — факт огромного значения для структуры физического мира. Он приводит к следующему упорядочению всех событий по их причинным связям с любым заданным событием 𝐴 (см. рис. 22).
Подразделение пространства-времени на 5 областей относительно события 𝐴
1. Может ли частица, испущенная в 𝐴, повлиять на то, что должно произойти в 𝐶? Если да, то 𝐶 лежит внутри светового конуса будущего с вершиной в 𝐴.
2. Может ли свет, испущенный в 𝐴, повлиять на то, что должно произойти в 𝐵? Если да, то 𝐵 лежит на световом конусе будущего с вершиной в 𝐴.
3. Может ли быть, что ничто, происходящее в 𝐴, не способно повлиять на то, что происходит в 𝐷? Если да, то 𝐷 лежит вне светового конуса с вершиной в 𝐴.
4. Может ли частица, испущенная в 𝐸, повлиять на то, что происходит в 𝐴? Если да, то 𝐸 лежит внутри светового конуса прошлого с вершиной в 𝐴.
5. Может ли свет, испущенный в 𝐹, повлиять на то, что происходит в 𝐴? Если да, то 𝐹 лежит на световом конусе прошлого с вершиной в 𝐴. Но световой конус с вершиной в событии 𝐴, как и в любом другом событии, существует в пространстве-времени совершенно независимо от того, в каких координатах мы пожелаем его описывать. Поэтому возможности, отмеченные в наших пяти вопросах и касающиеся влияния одного события на другое, не зависят от системы отсчёта, в которой наблюдается эта взаимосвязь между событиями. В этом смысле причинная связь между двумя событиями одинакова в любой системе отсчёта 1).
1) Пространства такого типа носят название частично упорядоченных пространств, так как в них наряду с абсолютными отношениями «раньше» и «позднее» существует и отсутствие определенного отношения между событиями (абсолютно безразличная область). В этой абсолютно безразличной области любое событие может быть «сделано» путем простого выбора системы отсчета более ранним или более поздним (по желанию!), чем опорное событие, лежащее в вершине светового конуса.— Прим. перев.
На рис. 23 (на следующей странице) дана сводка взаимоотношений между выделенным событием 𝐴 и всеми другими событиями в пространстве-времени.
Рис. 23. Наглядное разбиение пространства-времени на 5 областей соответственно классификации событий относительно некоторого опорного события 𝐴.

КУБИК ПРОСТРАНСТВА-ВРЕМЕНИ С ЦЕНТРОМ В СОБЫТИИ 𝐴.
Представлять себе распространённым до бесконечности во всех направлениях в последующих схемах.

АБСОЛЮТНОЕ БУДУЩЕЕ.
События, происходящие позже 𝐴 и отделённые от 𝐴 временноподобным интервалом.

СВЕТОВОЙ КОНУС БУДУЩЕГО.
События, происходящие позже 𝐴 и отделённые от 𝐴 изотропным (светоподобным) интервалом.

«НЕЙТРАЛЬНАЯ» ИЛИ «НЕДОСТИЖИМАЯ» ОБЛАСТЬ («АБСОЛЮТНО БЕЗРАЗЛИЧНАЯ»).
События, отделённые от 𝐴 пространственно подобным интервалом.
Каждое такое событие может быть сделано происходящим либо раньше 𝐴, либо позже 𝐴 посредством выбора подходящей системы координат.

СВЕТОВОЙ КОНУС ПРОШЛОГО.
События, происшедшие раньше 𝐴 и отделённые от 𝐴 изотропным (светоподобным) интервалом.

АБСОЛЮТНОЕ ПРОШЛОЕ.
События, происшедшие раньше А и отделённые от 𝐴 временноподобным интервалом.
ОДИН ИЗ СПОСОБОВ ЧАСТИЧНОГО ОБЪЕДИНЕНИЯ РАСЧЛЕНЁННОЙ КАРТИНЫ.

События, на которые наблюдатель в 𝐴 может активно влиять своими теперешними или будущими действиями.

События, которых уже не может изменить наблюдатель после того, как он оказался в мировой точке 𝐴.
ДРУГОЙ СПОСОБ ЧАСТИЧНОГО ОБЪЕДИНЕНИЯ РАСЧЛЕНЁННОЙ КАРТИНЫ.

События, информацию о которых наблюдатель ещё может узнать, если ничто их не заслонит.

События, участником которых наблюдатель в 𝐴 уже был (активно участвуя в них или просто наблюдая их) или следствия которых и информацию о которых он мог получить раньше.
8. ПРЕОБРАЗОВАНИЕ ЛОРЕНЦА
Движение π-мезона удобнее описывать с помощью координат, а не интервала

Рис. 24. Рождение и распад π-мезона.
На высотах от 10 до 30 км над поверхностью Земли космические лучи постоянно бомбардируют ядра атомов кислорода и азота, вызывая появление заряженных и нейтральных π-мезонов. Проследим движение одного такого π⁺-мезона вниз, к Земле (рис. 24). В связанной с ним системе отсчёта (назовём её «системой ракеты») среднее время жизни мезона равно 2,55×10⁻⁸ сек. Примем в такой системе отсчёта ракеты координаты события — рождения мезона — равными 𝑥'=0, 𝑡'=0 (см. рис. 25, б). Запишем координаты события — распада π-мезона на μ-мезон и нейтрино — в виде
𝑥'=0,
𝑡'=τ
π
.
Как воспримет эти события наблюдатель в лаборатории? Сколько времени проживёт π-мезон с момента своего рождения до смерти по его часам, т.е. чему равен промежуток лабораторного времени 𝑡? Какое расстояние пройдёт π-мезон за период своей жизни, т.е. чему равно лабораторное расстояние 𝑥 от точки его образования в верхних слоях атмосферы до той точки внизу, где он распался? Короче говоря, пусть некоторое событие 𝐸 определяется в системе ракеты заданными значениями координат 𝑥' и 𝑡' относительно начала 𝑂. Как определить тогда координаты 𝑥 и 𝑡 того же самого события относительно того же самого начала в лабораторной системе отсчёта (рис. 25, а)?
Такой вопрос для нас нов. До сих пор мы рассматривали при описании относительного положения событий лишь инвариантный интервал. Величина такого интервала не зависит от выбора системы отсчёта, причём
⎛
⎜
⎜
⎝
Пространствен-
ноподобный
интервал
⎞²
⎟
⎟
⎠
=-
⎛
⎜
⎜
⎝
Времен-
ноподобный
интервал
⎞²
⎟
⎟
⎠
=
=
𝑥²-𝑡²
=
(𝑥')²-(𝑡')²
.
(15)
В разных системах отсчёта координаты события различны
Сосредоточим теперь наше внимание на самих координатах как характеристике расположения события 𝐸 относительно начала 𝑂. Мы сделаем это, заранее признавая, что они зависят от выбора системы отсчёта. В этом отношении положение координат гораздо менее универсально, чем положение инвариантного интервала как меры взаимного разделения событий. Пусть так. Физика должна приладиться к тому, что есть в мире. Описывать удалённость событий друг от друга следует тем методом, который лучше соответствует обстоятельствам. Бывает, что торпедному катеру полезнее указать, что расстояние между носом и кормой атакуемого судна 50 м. Но в другом случае может быть, что ему гораздо важнее указать, что положение носа судна относительно кормы 40 м к северу и 30 м к востоку. В той задаче, которая нас занимает, нам не интересно, что мировая точка распада π-мезона отстоит от мировой точки его образования на величину инвариантного интервала τ, равную около 10⁻⁸ сек. Нам нужно охарактеризовать удалённость этих событий друг от друга самими координатами 𝑥 и 𝑡.

а) Диаграмма пространства-времени лабораторной системы отсчёта.

б) Диаграмма пространства-времени системы отсчёта ракеты.
Рис. 25. Координаты точек рождения (точка 𝑂) и распада (точка 𝐸) π-мезона, изображённые на диаграммах пространства-времени лабораторной системы и системы отсчёта ракеты.
Преобразование Лоренца для координат
Как бы сильно ни различались координаты (𝑥',𝑡') события 𝐸 в системе отсчёта ракеты от его координат (𝑥,𝑡) в лабораторной системе, эти два набора координат связаны друг с другом вполне определённым и простым законом. Этот закон выражается через преобразование Лоренца
𝑥
=
𝑥'
√1-β𝑟²
+
β𝑟𝑡'
√1-β𝑟²
,
𝑡
=
β𝑟𝑥'
√1-β𝑟²
+
𝑡'
√1-β𝑟²
,
(16)
где β𝑟— скорость системы отсчёта ракеты относительно лабораторной системы отсчёта. Ввиду выполнения этого закона говорят, что координаты обеспечивают ковариантное описание взаимной удалённости событий в пространстве-времени в противоположность инвариантному описанию этой удалённости, обеспечиваемому интервалом. Корень «вари» в слове ковариантный»
Определение понятия «ковариантность»
указывает, что координаты изменяются (варьируют) при переходах от одной системы отсчёта к другой. Приставка «ко» означает, что преобразование координат всех событий производится по одному и тому же закону (координированно). Итак, для разных событий различны как координаты 𝑥' и 𝑡', так и координаты 𝑥 и 𝑡, но четвёрка коэффициентов
⎛
⎝
1-β
𝑟
²
⎞-½
⎠
,
β
𝑟
⋅
⎛
⎝
1-β
𝑟
²
⎞-½
⎠
,
β
𝑟
⋅
⎛
⎝
1-β
𝑟
²
⎞-½
⎠
,
⎛
⎝
1-β
𝑟
²
⎞-½
⎠
,
связывающая эти два набора координат, обладает значениями, не зависящими от того, какое событие рассматривается.
В этом разделе мы будем обсуждать вывод формул преобразования Лоренца, их использование и их сходство с известными формулами преобразований эвклидовой геометрии, иллюстрируемыми на примере притчи о землемерах.
Три принципа, на которых основано преобразование Лоренца
Вывод преобразования Лоренца основывается на трех принципах, которые мы уже можем сформулировать:
1) Коэффициенты преобразования не должны зависеть от того, какое событие рассматривается («ковариантность преобразования»).
3) Коэффициенты преобразования должны быть такими, чтобы любой интервал имел одно и то же значение в лабораторной системе и в системе отсчета ракеты.
Эти три принципа легко применить к случаю распада π-мезона. В лабораторной системе отсчета это событие имеет координаты (𝑥,𝑡) относительно события — рождения мезона, и эти координаты должны быть выражены через скорость β𝑟 системы отсчета ракеты, в которой π-мезон покоится. Эту скорость непосредственно даёт отношение координат 𝑥 и 𝑡,
𝑥
𝑡
=
β
𝑟
,
так что
𝑥
=
β
𝑟
𝑡
,
или
𝑥²
=
β
𝑟
²
⋅
𝑡²
.
(17)
Первый этап вывода преобразования Лоренца
Временноподобный интервал, образованный 𝑥 и 𝑡, определяется временем жизни π-мезона в системе отсчёта ракеты (где мезон покоится в точке 𝑥'=0):
𝑡²-𝑥²
=
𝑡'²-𝑥'²
=
𝑡'²-0
=
τ
π
²
.
Подставим в эту формулу β𝑟²𝑡² вместо 𝑥² на основании уравнения (17). Получим
𝑡²
-
β
𝑟
²𝑡²
=
𝑡'²
=
τ
π
²
,
или
𝑡²
=
𝑡²
1-β𝑟²
=
τπ²
1-β𝑟²
,
или
𝑡
=
𝑡'
√1-β𝑟²
=
τπ
√1-β𝑟²
.
(Численный пример: положим β𝑟=¹²/₁₃ скорости света; тогда 1-β𝑟²=1-¹⁴⁴/₁₆₉=²⁵/₁₆₉ и (1-β²)⁻¹/²=¹³/₅=2,6. Следовательно, время жизни π-мезона, измеренное в лаборатории, в 2,6 раза длиннее «собственного времени жизни», т.е. оно в 2,6 раза длиннее, чем время жизни, измеренное в системе отсчёта, связанной с самим мезоном). Расстояние, пройденное π-мезоном, равно времени движения, умноженному на скорость, так что
𝑥
=
β
𝑟
𝑡
=
β𝑟𝑡'
√1-β𝑟²
.
Решение задачи о π-мезоне
Этим расчётом завершается решение поставленной задачи (найти координаты мировой точки распада π-мезона относительно мировой точки его рождения в лабораторной системе координат).
Задача о π-мезоне служила введением к общей задаче — найти координаты данного события в лабораторной системе, если заданы его координаты в системе ракеты. Если мы покажем, что эта задача равнозначна выводу формул преобразования Лоренца, значит, мы пришли к методу вывода этого преобразования, исходя из простейших предположений. На самом деле, мы уже нашли два коэффициента из четырёх в формулах преобразования Лоренца:
𝑡
=
β
𝑟
𝑡
=
𝑡'
√1-β𝑟²
+
𝐴𝑥'
,
𝑥
=
β
𝑟
𝑡
=
β𝑟𝑡'
√1-β𝑟²
+
𝐵𝑥'
.
Что касается остальных двух коэффициентов, временно обозначенных через 𝐴 и 𝐵, то о них мы ничего не узнали просто потому, что π-мезон всё время покоился в точке 𝑥'=0 в системе ракеты. Благодаря этому коэффициенты 𝐴 и 𝐵 могли иметь любые конечные значения при одном и том же решении
Конечный этап вывода преобразования Лоренца
задачи о мезоне. Чтобы найти значения этих коэффициентов, мы перейдём от специального случая (события — распада 𝐸) к более общему случаю — событию, происходящему в точке с произвольными координатами 𝑥' и 𝑡'. Мы вновь потребуем, чтобы величина интервала была одинаковой в лабораторной системе и в системе отсчёта ракеты. Другими словами, потребуем выполнения равенства
𝑡²-𝑥²
=
𝑡'²-𝑥'²
,
или
⎡
⎢
⎣
𝑡'
√1-β𝑟²
+
𝐴𝑥'
⎤²
⎥
⎦
-
⎡
⎢
⎣
β𝑟𝑡'
√1-β𝑟²
+
𝐵𝑥'
⎤²
⎥
⎦
=
𝑡'²-𝑥'²
,
или
𝑡'²
+
2(𝐴-β𝑟𝐵)𝑥'𝑡'
√1-β𝑟²
+
(𝐴²-𝐵²)
𝑥'²
=
𝑡'²
-
𝑥'²
.
(18)
Это равенство не может выполняться для всевозможных 𝑡' и 𝑥', если только коэффициенты 𝐴 и 𝐵 не выбраны вполне определённым образом. Во-первых, эти коэффициенты должны быть такими, чтобы в левой части равенства (18) обратился в нуль множитель при 𝑥'𝑡' (так как в правой части подобного члена нет). Тогда
𝐴
=
β
𝑟
𝐵
.
Во-вторых, множители при (-𝑥'²) в левой и правой частях равенства (18) должны совпадать. Поэтому
𝐵²
-
𝐴²
=
1.
Мы получили два уравнения для двух неизвестных 𝐴 и 𝐵; решая их, найдём
𝐴
=
β𝑟
√1-β𝑟²
и
𝐵
=
1
√1-β𝑟²
Этим вычислением и завершается вывод формул преобразования Лоренца (16).
Роль преобразования Лоренца
Новый — ковариантный — подход имеет дело с компонентами пространственно-временного интервала — координатами 𝑥, 𝑡 (16), а не с величиной самого интервала (15). Язык интервалов подобен универсальному языку: любой интервал одинаков для наблюдателей во всех системах отсчёта. Напротив, компоненты взаимного удаления событий в пространстве-времени, измеренные в одной системе отсчёта,— это весьма частный язык для выражения такого удаления. По своей форме этот язык похож на тот частный язык, с помощью которого та же удалённость описывается в другой системе отсчёта. Ведь в обоих языках фигурируют «пространственные» и «временная компоненты». Но само по себе это обстоятельство ещё ничего не даёт для сравнения информации, которой располагают разные группы наблюдателей. Когда англичанин берёт турецкую газету, ему не легче от знания того, что в турецком языке, как и в английском, есть глаголы и существительные! Ему нужен ещё и словарь. Так вот для перевода на свой язык информации о пространственных и временных координатах событий из других систем отсчёта наблюдателю тоже требуется словарь. Этот словарь — формулы преобразования Лоренца (16).
Аналогия: землемеры пользуются преобразованием эвклидова пространства
Подобный же словарь необходим и при гораздо более обычных обстоятельствах. Дневной землемер, определяющий север по магнитному компасу, может перевести на свой язык измерения северной и восточной координат, сделанные ночным землемером, ориентирующимся по Полярной звезде. Но не потребуется никакого словаря, если они будут сравнивать свои результаты, выраженные на универсальном языке расстояний. Бросается в глаза различие между двумя методами — исходящим из инвариантов (расстояния — универсальный язык) и использующим компоненты (северную и восточную координаты, величины которых, определённые разными наблюдателями, различны). Эту противоположность инвариантных и ковариантных величин иллюстрирует рис. 26.

Рис. 26. Ковариантный подход к геометрии использует компоненты величин, например компоненты вектора 𝑂𝐴. (Напротив, в инвариантном подходе используются длины, например длина 𝑂𝐴. Такие длины имеют численные значения, не зависящие от выбора системы отсчёта. Иначе говоря, любая длина одинакова независимо от того, кто её определяет — землемер, определяющий направление на север по Полярной звезде, или землемер, пользующийся магнитным компасом).
Пусть в одной системе значения компонент равны (𝑥,𝑦)=(7,6), а в другой системе — (𝑥',𝑦')=(2,9). (Эти числа соответствуют нашему чертежу). Очевидно, что значения компонент в двух системах отсчёта различны. В самом деле, они связаны законом «ковариантного преобразования» 𝑥 =
4
5 𝑥' +
3
5 𝑦' , 𝑦 =-
3
5 𝑥' +
4
5 𝑦' ,
который в частном случае вектора 𝑂𝐴 записывается в виде 7 =
4
5 •2 +
3
5 •9 , 6 =-
3
5 •2 +
4
5 •9 ,
Приведённые здесь конкретные численные значения коэффициентов в законе преобразования связаны с тем конкретным поворотом, который изображён на чертеже.
В притче о землемерах студент сделал, как теперь обнаруживается, лишь полдела. Он выяснил, как должен каждый землемер переводить свои результаты на универсальный язык расстояний:
(Расстояние)
²
=
(
Δ
𝑥)²
+
(
Δ
𝑦)²
=
=
(
Δ
𝑥')²
+
(
Δ
𝑦')²
.
Однако он не сформулировал того словаря, который необходим для перевода с дневного на ночной язык и обратно величин компонент. Конечно, выводы студента были ценными, но ведь случается же, когда дневной землемер должен знать не только величину расстояния 𝑂𝐴, но и конкретные координаты (Δ𝑥,Δ𝑦) этого отрезка. При этом может оказаться, что по воле судеб ему недоступно прямое измерение этих компонент. Тогда в его распоряжении будут лишь данные о компонентах (Δ𝑥',Δ𝑦'), полученные при измерении 𝑂𝐴 его коллегой — ночным землемером. Как же ему перевести имеющиеся в его распоряжении числа (Δ𝑥',Δ𝑦') на его «язык» и получить требуемые (Δ𝑥,Δ𝑦)? Каким должен быть словарь? И что должен он знать, чтобы быть в состоянии этот словарь составить? Вот ответ.
Эвклидово преобразование поворота координатных осей
Подобно тому, как для построения формул преобразования Лоренца, переводящих (Δ𝑥',Δ𝑦') в (Δ𝑥,Δ𝑦), необходимо знать относительную скорость движения двух систем отсчёта β𝑟, для перевода компонент (Δ𝑥',Δ𝑦') в (Δ𝑥,Δ𝑦) требуется знать величину наклона 𝑆𝑟 прямой 𝑂𝑦' относительно прямой 𝑂𝑦. В примере, изображённом на рис. 26, наклон оси 𝑂𝑦' к оси 𝑂𝑦 равен 𝑆𝑟=³/₄. Это значит, что при перемещении вверх по оси 𝑦 на 4 единицы необходимо сдвинуться от неё вправо на 3 единицы, чтобы оказаться на оси 𝑦'. Если выразить через величину наклона 𝑆𝑟 формулу преобразования поворота, мы получим
Δ
𝑥
=
Δ𝑥'
√1+𝑆𝑟²
+
𝑆𝑟Δ𝑦'
√1+𝑆𝑟²
,
Δ
𝑦
=-
𝑆𝑟Δ𝑥'
√1+𝑆𝑟²
+
Δ𝑦'
√1+𝑆𝑟²
.
(19)
Доказательство.

Рис. 27. Представление произвольного вектора как геометрической суммы двух векторов, направленных соответственно вдоль осей 𝑦' и 𝑥'. Это представление использовано при выводе уравнений (19) закона преобразования поворота (см. текст).
1. Произвольный вектор (Δ𝑥',Δ𝑦') может рассматриваться (см. рис. 27) как сумма вектора (Δ𝑥',0), направленного вдоль оси 𝑥', и вектора (0,Δ𝑦'), направленного вдоль оси 𝑦'. Для общего доказательства справедливости формул (19) достаточно удостовериться в том, что они верны по отдельности для этих двух векторов.
2. Вектор, направленный вдоль оси 𝑦' и имеющий длину Δ𝑦' обладает относительно осей 𝑥 и 𝑦 компонентами, относящимися друг к другу как 𝑆𝑟 по определению «наклона». Итак,
Δ𝑥
Δ𝑦
=
𝑆
𝑟
,
или
⎛
⎜
⎝
Δ𝑥
Δ𝑦
⎞²
⎟
⎠
=
𝑆
𝑟
²
,
или
(
Δ
𝑥)²
=
𝑆
𝑟
²
⋅
(
Δ
𝑦)²
.
3. Расстояние от начала координат до конца вектора имеет одну и ту же величину в обеих системах координат:
(
Δ
𝑥)²
+
(
Δ
𝑦)²
=
(
Δ
𝑥')²
+
(
Δ
𝑦')²
,
или
𝑆
𝑟
²
(
Δ
𝑦)²
+
(
Δ
𝑦)²
=
0
+
(
Δ
𝑦')²
,
или
(
Δ
𝑦)²
=
(Δ𝑦')²
1+𝑆𝑟²
,
или, наконец,
Δ
𝑦
=
Δ𝑦'
√1+𝑆𝑟²
,
так что
Δ
𝑥
=
𝑆
𝑟
Δ
𝑦
=
𝑆𝑟Δ𝑦'
√1+𝑆𝑟²
.
Сравнивая эти результаты с формулами преобразования поворота (19), мы убеждаемся в правильности коэффициентов при Δ𝑦'.
4. Аналогично рассмотрим вектор, направленный вдоль оси 𝑥' и имеющий компоненты (Δ𝑥',0). Его компоненты вдоль осей 𝑦 и 𝑥 находятся друг к другу в отношении
Δ𝑦
Δ𝑥
=-
𝑆
𝑟
.
Это равенство вместе с фактом инвариантности длины
(
Δ
𝑥)²
+
(
Δ
𝑦)²
=
(
Δ
𝑥')²
+
0
приводит в ходе рассуждений, аналогичных предыдущим, к соотношениям
Δ
𝑥
=
Δ𝑥'
√1+𝑆𝑟²
,
Δ
𝑦
=-
𝑆𝑟Δ𝑥'
√1+𝑆𝑟²
.
Тем самым мы проверили остальные два коэффициента в формулах (19) эвклидова преобразования поворота.
Относительный наклон осей 𝑆𝑟 в геометрии Эвклида аналогичен относительной скорости β𝑟 в геометрии Лоренца
Подводя итоги, можно сказать, что ковариантное преобразование в геометрии Эвклида от (Δ𝑥',Δ𝑦') к (Δ𝑥,Δ𝑦) с очевидностью аналогично преобразованию от (Δ𝑥',Δ𝑡') к (Δ𝑥,Δ𝑡) в лоренцевой геометрии реального физического мира. Величина наклона 𝑆𝑟 осей одной системы координат относительно соответствующих осей другой системы аналогична скорости β𝑟 одной инерциальной системы отсчёта относительно другой. Отношения катетов прямоугольного треугольника к его гипотенузе в эвклидовой геометрии
1
√1+𝑆𝑟²
и
𝑆𝑟
√1+𝑆𝑟²
заменяются в лоренцевой геометрии выражениями
1
√1-β𝑟²
и
β𝑟
√1-β𝑟²
.
Противоположны лишь знаки при 𝑆𝑟 и β𝑟 в знаменателях этих выражений. Знак «минус» в лоренцевой геометрии связан с минусом в выражении для квадрата интервала.
9. ПАРАМЕТР СКОРОСТИ
Аддитивность углов подсказывает возможность определения аддитивного параметра скорости
Всё ли исчерпано? Мы выяснили, как перейти от компонент взаимной удалённости событий, известных в одной системе отсчёта, к аналогичным компонентам в другой системе отсчёта. Короче, мы записали ковариантный закон, связывающий компоненты в разных системах, как для преобразования Лоренца («преобразование в плоскости 𝑥, 𝑡), так и для поворота («преобразование в плоскости 𝑥, 𝑡). В первом случае формулы содержат параметр β𝑟 (относительную скорость систем), а во втором — параметр 𝑆𝑟 (относительный наклон осей). Однако ни один из этих параметров не позволяет ещё получить самое простое описание взаимоотношения рассматриваемых систем координат. Было бы желательно заменить как β𝑟, так и 𝑆𝑟 более естественными параметрами. Оказывается, найти такой более удобный способ описания движения и поворота систем можно. Лучшей характеристикой поворота является угол. Аналогично самой удобной характеристикой движения систем вместо скорости является некоторый параметр скорости θ, который ещё должен быть найден. Лучше всего можно понять смысл и значение этого параметра скорости при описании относительного движения систем отсчёта, если сначала выяснить, почему угол — более удобный параметр, чем наклон при описании поворота.
Ответ таков: потому что углы аддитивны, а наклоны — нет. Что означает это утверждение? Взглянем на рис. 26. Вектор 𝑂𝐴 имеет наклон относительно оси 𝑦'. Этот наклон можно описать величиной 𝑆' (отношением числа единиц длины в направлении оси 𝑥, приходящегося на единицу расстояния в направлении оси 𝑦'). В данном случае мы имеем
𝑆'
=
2
9
.
Вместе с тем вектор 𝑂𝐴 имеет наклон к оси 𝑦, равный
𝑆
=
7
6
,
а ось 𝑦' в свою очередь обладает относительно оси 𝑦 наклоном
𝑆
𝑟
=
3
4
.
Вопрос: выполняется ли следующий закон для наклонов:
⎛
⎜
⎜
⎝
Наклон 𝑂𝐴
относительно
оси 𝑦
⎞
⎟
⎟
⎠
=
⎛
⎜
⎜
⎝
Наклон 𝑂𝐴
относительно
оси 𝑦'
⎞
⎟
⎟
⎠
+
⎛
⎜
⎜
⎝
Наклон 𝑦'
относительно
оси 𝑦
⎞
⎟
⎟
⎠
?
Наклоны в эвклидовой геометрии не аддитивны
Проверка («экспериментальная математика»):
7
6
=
2
9
+
3
4
?
42
36
=
8
36
+
27
36
?
42
=
8
+
27
=
35
?!
Неверно!
Вывод: наклоны не аддитивны! Вопрос: раз наклоны не аддитивны, т.е. 𝑆 не равняется сумме 𝑆' и 𝑆𝑟, то как же найти правильно наклон 𝑆 из наклонов 𝑆' и 𝑆𝑟? Ответ:
(по определению наклона)
⎛
⎜
⎜
⎝
Наклон 𝑂𝐴
относительно
оси 𝑦
⎞
⎟
⎟
⎠
=
𝑆
=
Δ𝑥
Δ𝑦
=
[из (19)]
=
(1+𝑆𝑟²)⁻¹/²Δ𝑥'+𝑆𝑟⋅(1+𝑆𝑟²)⁻¹/²Δ𝑦'
-𝑆𝑟(1+𝑆𝑟²)⁻¹/²Δ𝑥'+(1+𝑆𝑟²)⁻¹/²Δ𝑦'
=
[сокращение числителя и
знаменателя на
(1+𝑆
𝑟
²)⁻¹
/
²
]
=
Δ𝑥'+𝑆𝑟Δ𝑦'
-𝑆𝑟Δ𝑥'+Δ𝑦'
=
(деление числителя и знаменателя на
Δ
𝑦'
)
=
(Δ𝑥'/Δ𝑦')+𝑆𝑟
-𝑆𝑟(Δ𝑥'/Δ𝑦')+1
.
Окончательный вывод:
𝑆
=
𝑆'+𝑆𝑟
1-𝑆'𝑆𝑟
.
(20)
Иными словами, наклоны 𝑆' и 𝑆𝑟 могут считаться аддитивными, лишь если произведением 𝑆'•𝑆𝑟 стоящим в знаменателе, можно пренебречь по сравнению с единицей.
Аддитивны углы наклона

Рис. 28. Угол — удобная мера наклона оси 𝑦' относительно оси 𝑦. Удобство здесь в том. что углы подчиняются простому правилу сложения: θ=θ'+θ𝑟.
Так как наклоны не аддитивны, а значит, неудобны для описания относительного поворота двух систем координат, то как же выбрать лучшую характеристику этого поворота? Ответ: взять угол между осями 𝑦 и 𝑦'. Почему? Потому что углы подчиняются простому закону сложения (рис. 28):
⎛
⎜
⎝
Угол между
𝑂𝐴 и осью 𝑦
⎞
⎟
⎠
=
⎛
⎜
⎝
Угол между
𝑂𝐴 и осью 𝑦'
⎞
⎟
⎠
+
⎛
⎜
⎝
Угол между
осями 𝑦' и 𝑦
⎞
⎟
⎠
,
или
θ
=
θ'
+
θ
𝑟
.
(21)
Благодаря выполнению этого соотношения угол является простейшей характеристикой наклона.
Как связаны между собой новая и старая характеристики наклона — угол θ и наклон 𝑆𝑟 оси 𝑦' относительно оси 𝑦? Ответ:
𝑆
𝑟
=
tg θ
𝑟
(22)
(по тригонометрическому определению функции тангенса; см. рис. 29).
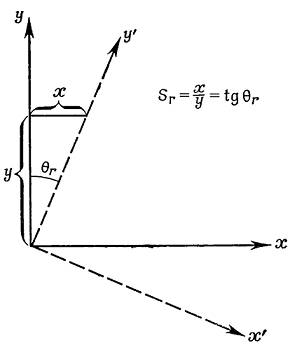
Рис. 29. Связь между взаимным наклоном 𝑆𝑟 осей 𝑦' и 𝑦 двух эвклидовых систем координат и углом θ𝑟 между этими осями.
Закон сложения величин наклона в эвклидовой геометрии
Вопрос: как можно расшифровать закон сложения величин наклона, если исходить из того, что эти величины суть тангенсы углов? Ответ:
tg θ
=
tg (θ'+θ
𝑟
)
=
⎛
⎜
⎝
аддитивность
углов
⎞
⎟
⎠
=
tg θ'+tg θ𝑟
1-tg θ'•tg θ𝑟
,
(тригонометрия)
(23)
или
𝑆
=
𝑆'+𝑆𝑟
1-𝑆'•𝑆𝑟
•
⎛
⎜
⎝
тангенсы заменены
на величины наклонов
⎞
⎟
⎠
Сравнивая сложный закон сложения тангенсов (величин наклона) с простым законом сложения углов (θ=θ'+θ𝑟), мы убеждаемся в том, что угол — простейшая характеристика поворота.
Закон сложения скоростей

Рис. 30. Мировая линия пули, изображённая на диаграмме пространства-времени системы отсчёта ракеты. Пуля была выпущена вперёд по движению ракеты со скоростью β'=Δ𝑥'/Δ𝑡' в системе отсчёта ракеты.
Что же будет простейшей характеристикой движения? Во всяком случае, не сама скорость, так как она не подчиняется простому закону сложения. Определим этот закон сложения скоростей. Пусть в системе отсчёта ракеты будет в направлении вперёд по её движению выстрелена пуля со скоростью β' в этой системе (рис. 30):
β'
=
Число метров,
пройденных в
направлении оси 𝑥'
за каждый
⎛
⎜
⎜
⎜
⎝
Метр времени 𝑡',
прошедший
по часам
на ракете
⎞
⎟
⎟
⎟
⎠
=
Δ𝑥'
Δ𝑡'
.
Относительно лаборатории ракета движется со скоростью β𝑟. Чему равна скорость β пули относительно лаборатории, измеренная по решётке часов лабораторной системы отсчёта? Ответ: эта скорость равна
β
=
⎛
⎜
⎜
⎜
⎝
Число метров,
пройденных в
направлении оси 𝑥
за каждый
⎞
⎟
⎟
⎟
⎠
⎛
⎜
⎜
⎜
⎝
Метр времени 𝑡,
прошедший
по часам
в лаборатории
⎞
⎟
⎟
⎟
⎠
=
Δ𝑥
Δ𝑡
=
[преобразование Лоренца; формулы (16)]
=
(1-β𝑟²)⁻¹/²Δ𝑥'+β𝑟(1-β𝑟²)⁻¹/²•Δ𝑡'
β𝑟(1-β𝑟²)⁻¹/²Δ𝑥'+(1-β𝑟²)⁻¹/²•Δ𝑡'
=
[в числителе и знаменателе произведено
сокращение на множитель
(1-β
𝑟
²)⁻¹
/
²
]
=
Δ𝑥'+β𝑟Δ𝑡'
β𝑟Δ𝑥'+Δ𝑡'
=
числитель и знаменатель
разделены на
Δ
𝑡'
)
=
(Δ𝑥'/Δ𝑡')+β𝑟
β𝑟(Δ𝑥'/Δ𝑡')+1
.
Окончательно
β
=
β'+β𝑟
1+β'β𝑟
(24)
(закон сложения скоростей). Иными словами, скорости не аддитивны. Лишь в предельном случае, когда скорости малы, две скорости β' и β𝑟 могут рассматриваться как аддитивные (с определённой степенью точности), если в знаменателе закона (24) произведением β'β𝑟 можно пренебречь по сравнению с единицей (с той же самой степенью точности, например 1:10 или 1:10⁶). Пример неаддитивности скоростей: пусть в момент выстрела ракета обладает скоростью, равной ¾ скорости света; пусть пуля движется относительно ракеты со скоростью, равной ¾ скорости света. Чему будет равна скорость пули относительно лаборатории? Ответ: не ¾+¾=1,5 скорости света, а
β
=
¾+¾
1+(¾)•(¾)
=
³/₂
²⁵/₁₆
=
24
25
=
0,96
(в метрах лабораторного расстояния за метр светового времени по лабораторным часам). Таким образом, релятивистский закон сложения скоростей (24) гарантирует, что никакой объект не может быть приведён в движение со скоростью света.
Определим параметр скорости таким образом, чтобы он был аддитивным!
Выяснив, что скорость сама по себе не аддитивна, мы предлагаем найти новую меру движения —«параметр скорости» θ, который должен быть аддитивным, т.е.
⎛
⎜
⎜
⎜
⎝
Параметр
скорости пули
относительно
лаборатории
⎞
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎝
Параметр
скорости пули
относительно
ракеты
⎞
⎟
⎟
⎟
⎠
+
⎛
⎜
⎜
⎜
⎝
Параметр
скорости ракеты
относительно
лаборатории
⎞
⎟
⎟
⎟
⎠
или
θ
=
θ'
+
θ
𝑟
.
(25)
Смысл этого параметра θ будет совершенно иным, чем смысл угла, описывающего поворот. Ни ка какой диаграмме параметр скорости нельзя изобразить в виде обычного угла, и вот по какой простой причине. Расстояния между точками на листе бумаги подчиняются законам эвклидовой геометрии. Напротив, интервалы между событиями в физическом мире определяются лоренцевой геометрией пространства-времени. Но если невозможно запечатлеть движущиеся пули и идущие часы на листе бумаги, то это никоим образом не лишает реальности указанные функционирующие объекты. Так и невозможность изобразить на листе бумаги аддитивность параметра скорости θ не сможет нас смутить, но скорее заставит взглянуть на действительный мир быстрых частиц и физики высокой энергии с тем, чтобы увидеть там активное проявление закона сложения параметра скорости. Этот закон сложения параметра скорости, θ=θ'+θ𝑟, во всех отношениях столь же реален, как и закон сложения углов поворота.
Скорость равна тангенсу гиперболическому от параметра скорости
Как же связаны между собой скорость β и параметр скорости θ? Соответствующая формула аналогична формуле, выражающей связь между наклоном и углом наклона (через тангенс угла), и имеет вид
β
=
th θ
.
(26)
Обозначение th означает «тангенс гиперболический». Функция гиперболического тангенса, как и гиперболических синуса и косинуса (sh θ и ch θ), причём th θ=sh θ/ch θ, обычны в математическом анализе. Таблицы всех этих трёх функций можно найти в любом хорошем математическом справочнике. Их формальное определение дано в табл. 8. Тем не менее нам нет необходимости обращаться к этой таблице и к справочникам; ведь всё, что нам требуется знать о функции th θ, можно без труда получить уже из её определения. А определяется она следующими двумя свойствами:
а) Эта функция должна правильно описывать закон сложения скоростей. Тогда из соотношения
β
=
β'+β𝑟
1+β'β𝑟
и требования аддитивности θ=θ'+θ𝑟 мы получаем закон сложения
th θ
=
th(θ'+θ
𝑟
)
=
th θ+th θ𝑟
1+th θ'•th θ𝑟
(27)
[см. определение (26)].
б) При малых скоростях параметр θ должен переходить в обычную характеристику движения — скорость β. Это требование означает, что функция th θ должна становиться сколь угодно близка к θ при стремлении θ к нулю. Вспомним, что обычный тангенс обычного угла стремится по величине к этому углу в пределе малых углов, если углы измеряются в радианах. Если измерять углы в градусах, то следует ввести поправочный множитель π/180°. Здесь подобным же образом было бы можно измерять параметр скорости и в единицах, аналогичных градусам и минутам, но проще всего те единицы, при которых
th θ
—⟶
малые θ
θ.
Назовём эти единицы «гиперболическими радианами»; они безразмерны.
Как можно найти связь между параметром скорости и скоростью из свойств (а) (аддитивность) и (б) (равенство th θ=θ для малых значений параметра скорости)?
Построение таблицы для тангенса гиперболического
Ответ. 1) Начнём со столь малого параметра скорости θ, что его th θ может быть приравнен θ с требуемой степенью точности. Примем, например,
th 0,01
=
0,01
в качестве первого шага для построения таблицы тангенса гиперболического.
2) Следующий шаг состоит в использовании закона сложения (27):
th 0,02
=
th (0,01+0,01)
=
=
th 0,01+th 0,01
1+th 0,01⋅th 0,01
=
0,01+0,01
1+0,0001
.
(28)
3) На этом этапе следует условиться о том, с какой степенью точности мы будем брать численные значения. Почему бы, например, не принять th 0,02 равным 0,02 точно так же, как мы приняли th 0,01 равным th 0,01? Однако в знаменателе формулы (28) стоит слагаемое 0,0001! Его наличие означает, что число 0,02 отличается от величины th 0,02 приблизительно на 1:10⁴. Условимся же теперь вычислять все значения th θ с точностью до 1:10⁴. Поэтому нам потребуется учесть поправку 0,0001, стоящую в знаменателе. Но если нам понадобилось учитывать такую поправку при вычислении th 0,02, почему бы не учесть её и в th 0,01? Потому что там она была бы ещё меньше. Иными словами, разница между th 0,01 и 0,01 равна величине, которой можно пренебречь, если условиться брать результаты с точностью лишь до 1:10⁴. С этой точностью мы получим в конце концов
th 0,02
=
0,020000
1,0001
=
0,019998
.
4) Найдём теперь значение th 0,04:
th 0,04
=
th (0,02+0,02)
=
=
th 0,02+th 0,02
1+th 0,02⋅th 0,02
=
2•0,019998
1+(0,019998)²
=
=
0,039980
.
Поправка в знаменателе изменяет теперь численную величину результата примерно на 4:10⁴. Тем не менее этот результат верен с точностью около 1:10⁴. Он получен на основании точной формулы (27) в применении к значениям гиперболического тангенса, которые сами были верны с точностью 1:10⁴.
5) Дальнейшие шаги при построении таблицы значений гиперболического тангенса аналогичны предыдущим. Так, зная th 0,04 и th 0,01, мы можем вычислить th 0,05=(th 0,04+0,01). Мы получим далее th 0,1; th 0,2 и th 0,4, а затем th 0,5=(th 0,4+0,1). Аналогично мы вычислим th 1, th 2 и все прочие значения th θ, которые нам потребуются. Так мы получим результаты, подытоженные на рис. 31.

Рис. 31. Связь между параметром скорости θ и самой скоростью β=th θ, получаемая непосредственно из закона сложения th(θ₁+θ₂) =
θ₁+θ₂
1+θ₁•θ₂
как это описано в тексте. Например, пусть пуля выпускается со скоростью β'=0,75 из ракеты, движущейся со скоростью β𝑟=0,75. Требуется найти скорость пули β относительно лабораторной системы. Мы знаем, что аддитивны не скорости, а параметры скорости. По графику для точки 𝐴 находим θ'=θ𝑟=0,973. Сложение даёт θ=θ'+θ𝑟=1,946. Для этого значения параметра скорости находим по графику точку 𝐵 и величину скорости β=0,96. Тот же результат получен другим способом в тексте (стр. 68).
Различие между параметром скорости и обычным углом
Из рис. 31 сразу же видны два свойства параметра скорости, никак не связанные с конкретным выбором чисел. Во-первых, наклон кривой функции th θ относительно θ стремится к единице при малых θ. Это — новое выражение того факта, что скорость β=th θ и параметр скорости θ стремятся друг к другу при стремлении θ→0. Во-вторых, когда параметр скорости стремится к бесконечно большим положительным (или отрицательным) значениям, то скорость β=th θ стремится к плюс (или минус) единице. Другими словами, допустимы любые значения параметра скорости на всём интервале значений от θ→-∞ и до θ→+∞. Различие между «гиперболическими углами» или параметром скорости, область изменения которого неограниченна, и обычными углами очевидно. Обычный угол не приводит ни к чему новому, когда он превысит конечный интервал от 0 до 2π радиан.
Параметр скорости и постоянство скорости света
Как связаны представления о параметре скорости и о законе сложения скоростей с тем элементарным физическим опытным фактом, который привёл физику к пространственно-временной точке зрения? Вот самая непосредственная из возможных связей. Из результатов наблюдений и всего того, что уже в 1905 г. было известно об электромагнитных волнах, Эйнштейн был вынужден заключить, что скорость света одинакова во всех инерциальных системах отсчёта. Это же можно сказать иначе, переводя на язык мысленных опытов: фотон, выстреленный со скоростью света из быстро движущейся ракеты, движется относительно лаборатории со скоростью, равной всё той же скорости света.
На языке параметра скорости можно сказать, что ракета обладает конечным параметром скорости θ𝑟, тогда как величина параметра скорости фотона (β=1) бесконечна (θ'=∞; см. асимптотическую часть кривой в верхней правой части рис. 31). Прибавьте к бесконечности конечное число, и вы получите снова бесконечность в качестве суммы θ=θ'+θ𝑟. Поэтому скорость фотона в лабораторной системе отсчёта равна β=th θ=th ∞=1, т.е. это снова скорость света. Мы замкнули круг, вновь вернувшись к идее, лежащей в основании теории относительности: скорость света имеет одну и ту же величину во всех системах отсчёта.
Простота описания движения с помощью параметра скорости
Мы пришли к заключению, что естественной характеристикой движения является параметр скорости, подчиняющийся простому закону сложения: θ=θ'+θ𝑟. Но почему же наша интуиция не подсказала нам сразу идеи введения этого параметра? Почему гиперболические углы не знакомы всякому школьнику так же хорошо, как обычные углы? Ответ ка это прост. Обыденный опыт сталкивает нас со всякими углами — и большими, и малыми. Поэтому не найдётся простачка, который стал бы, складывая наклоны 𝑆'=1 (угол в 45°) и 𝑆𝑟=1 (ещё раз 45°), утверждать, что он получит наклон, равный 𝑆=𝑆'+𝑆𝑟=2 (т.е. угол в 63°26', что неверно!). Все знают, что правильный путь — это складывать углы (сумма в нашем примере равна 45°+ 45°=90°, чему соответствует наклон 𝑆=∞). Но обыденный опыт не сталкивает нас со скоростями, близкими к скорости света. Автомобили, реальные ракеты и реальные пули движутся со скоростями, крайне малыми по сравнению со скоростью света. Поэтому и потребовалось долгое время, пока люди не узнали истинной физики пространства-времени. Но теперь, наконец, мы поняли разницу природы законасложения скоростей [громоздкое уравнение (24)] и закона сложения параметров скорости [простое уравнение (21): θ=θ'+θ𝑟]. Более того, те наблюдения, которые прежде обескураживали (например, равенство величины скорости света во всех системах отсчёта), стали описываться очень просто на языке параметра скорости. К тому же этот параметр, как и всё, что входит вместе с ним в пространственно-временную структуру физики, совершенно необходим. Если вы хотите описать природу физического мира такой, какая она на самом деле у этого четырёхмерного мира, то у вас нет никакого другого выбора, кроме описанных выше идей. Эта железная необходимость становится всё очевиднее по мере того, как в обиход нашей цивилизации, нашей индустрии входят электронные и ядерные установки, а вместе с ними — сверхбыстрые частицы.
Обходного пути нет! Параметр скорости — такой же простой способ для описания скорости движения, как обычный угол — для описания наклона. Но, согласившись с этим выводом, какую выгоду извлечём мы, пытаясь упростить формулы преобразования Лоренца?
У прощение эвклидова преобразования поворота путём введения угла
Для того чтобы сориентироваться в этом вопросе, рассмотрим сначала аналогичную задачу в эвклидовой геометрии на плоскости 𝑥𝑦. Станет ли формула (19), выражающая одну систему координат через другую,
Δ
𝑥
=
(1+𝑆
𝑟
²)⁻¹
/
²
Δ
𝑥'
+
𝑆
𝑟
•
(1+𝑆
𝑟
²)⁻¹
/
²
Δ
𝑦'
,
Δ
𝑦
=-
𝑆
𝑟
(1+𝑆
𝑟
²)⁻¹
/
²
Δ
𝑥'
+
(1+𝑆
𝑟
²)⁻¹
/
²
Δ
𝑦'
,
менее сложной, если выразить относительный наклон 𝑆𝑟 осей 𝑦 и 𝑦' через обычный угол θ𝑟? Ответ: коэффициенты в преобразовании поворота принимают вид
(1+𝑆
𝑟
²)⁻¹
/
²
=
(1+tg²θ
𝑟
)⁻¹
/
²
=
=
⎛
⎜
⎝
cos²θ𝑟+sin²θ𝑟
cos²θ𝑟
⎞
⎟
⎠
⁻¹/²
=
⎛
⎜
⎝
1
cos²θ𝑟
⎞
⎟
⎠
⁻¹/²
=
cos θ
𝑟
.
и
𝑆
𝑟
(1+𝑆
𝑟
²)⁻¹
/
²
=
tg θ
𝑟
•
cos θ
𝑟
=
=
sin θ𝑟
cos θ𝑟
=
sin θ
𝑟
.
Поэтому формулы преобразования переходят в
Δ
𝑥
=
Δ
𝑥'
•
cos θ
𝑟
+
Δ
𝑦'
•
sin θ
𝑟
,
Δ
𝑦
=-
Δ
𝑥'
•
sin θ
𝑟
+
Δ
𝑦'
•
cos θ
𝑟
,
(29)
и мы можем заключить, что связь между старыми и новыми координатами приобретает наипростейший вид, если коэффициенты в ковариантных преобразованиях выразить через «тригонометрические», или «круговые», функции угла поворота.
Упрощение формул преобразования Лоренца путём введения параметра скорости
Обратимся теперь к формулам преобразования Лоренца, записанным через относительную скорость:
Δ
𝑥
=
(1-β
𝑟
²)⁻¹
/
²
Δ
𝑥'
+
β
𝑟
(1-β
𝑟
²)⁻¹
/
²
Δ
𝑡'
,
Δ
𝑡
=
β
𝑟
(1-β
𝑟
²)⁻¹
/
²
Δ
𝑥'
+
(1-β
𝑟
²)⁻¹
/
²
Δ
𝑡'
.
Как станет выглядеть эта пара уравнений, если мы выразим в ней скорость β𝑟 через «улучшенную» характеристику движения θ𝑟? Ответ таков. Вспомним, что скорость и параметр скорости связаны между собой соотношением
β
𝑟
=
th θ
𝑟
.
Отметим, что коэффициенты в формулах преобразования Лоренца зависят от β𝑟 и тем самым от θ𝑟. Эти коэффициенты равны
(1-β
𝑟
²)⁻¹
/
²
=
(1-th²θ
𝑟
)⁻¹
/
²
(30)
и
β
𝑟
(1-β
𝑟
²)⁻¹
/
²
=
th θ
𝑟
•
(1-th²θ
𝑟
)⁻¹
/
²
.
(31)
Полученные выражения на первый взгляд довольно сложны. Тем не менее они вполне определённы. Мы знаем, как найти величину th θ𝑟 для любого заданного значения θ𝑟 (см. рис. 31 и сопровождающие его рассуждения). Знание величины th θ𝑟 позволяет нам вычислить выражения (30) и (31) с любой желаемой степенью точности для любого наперёд заданного значения параметра скорости. Эти две функции θ𝑟 настолько важны, что каждая из них получила своё собственное название в теории гиперболических функций. Если мы примем стандартные названия для этих функций, то это никоим образом не повлияет на наши возможности определять величины этих функций в любом интересующем нас случае без использования каких-либо руководств или справочников, своими собственными силами. Поэтому мы примем и будем в дальнейшем употреблять следующие стандартные названия:
(1-th²θ
𝑟
)⁻¹
/
²
=
ch θ
𝑟
=
=
(Косинус гиперболический
θ
𝑟
),
th θ
𝑟
•
(1-th²θ
𝑟
)⁻¹
/
²
=
sh θ
𝑟
=
=
(Синус гиперболический
θ
𝑟
),
Это названия, и не более чем названия! Используя их, мы найдём, что формулы преобразования Лоренца принимают вид
Δ
𝑥
=
Δ
𝑥'
•
ch θ
𝑟
+
Δ
𝑡'
•
sh θ
𝑟
,
Δ
𝑡
=
Δ
𝑥'
•
sh θ
𝑟
+
Δ
𝑡'
•
ch θ
𝑟
.
(32)
Преобразование Лоренца, выраженное через параметр скорости
Отсюда мы заключаем, что связь между старыми и новыми координатами приобретает наиболее простой вид, когда коэффициенты преобразования выражаются как гиперболические функции параметра относительного движения θ𝑟 систем отсчёта. Более того, будучи выражены с помощью гиперболических синуса и косинуса, формулы преобразования Лоренца ещё больше, чем ранее, напоминают стандартный тригонометрический вид (29) формул преобразования поворота.
Как можно лучше уяснить себе и прочувствовать свойства фигурирующих в преобразовании Лоренца гиперболических функций? Два самых интересных и существенных их свойства вытекают непосредственно из определений (30) и (31). Во-первых, отношение
sh θ𝑟
cs θ𝑟
=
th θ
𝑟
(33)
совершенно аналогично соответствующему отношению для тригонометрических функций. Во-вторых, разность квадратов двух гиперболических функций равна
ch²θ
𝑟
-
sh²θ
𝑟
=
1
1-th²θ𝑟
-
th²θ𝑟
1-th²θ𝑟
=
=
1-th²θ𝑟
1-th²θ𝑟
=
1.
(34)
Сопоставьте эту формулу с аналогичным соотношением для тригонометрических функций:
cos²(угол)
+
sin²(угол)
=
1.
(35)
Сравнение тригонометрических и гиперболических функций1)
1 Авторы здесь и в других местах вместо термина «тригонометрический» говорят «круговой». Действительно, тригонометрические функции, как это видно из дальнейшего обсуждения, тесно связаны с простейшей кривой второго порядка — окружностью, тогда как гиперболические функции связаны со свойствами другой кривой второго порядка, гиперболы. Поэтому между ними много общего. Однако в переводе мы пользуемся более принятым в отечественной литературе термином «тригонометрический».— Прим. перев.
Уравнения (34) и (35) допускают простую геометрическую интерпретацию. Отложим на рис. 32 по вертикальной оси функцию «косинус», а по горизонтальной оси — функцию «синус» (одного и того же аргумента). Уравнение (35) тогда описывает окружность единичного радиуса, и поэтому тригонометрические функции можно называть «круговыми». Напротив, уравнение (34) описывает при аналогичном построении гиперболу (рис. 33), и поэтому мы говорим о «гиперболических функциях». Знак «плюс» в соотношении cos²α+sin²α=1 происходит от того, что для получения квадрата длины вектора нужно сложить его 𝑥- и 𝑦- компоненты, возведённые в квадрат. Почему же в соотношении ch²α-sh²α=1 фигурирует знак «минус»? Потому, что квадрат пространственно-временного интервала определяется как разность квадратов удалённостей событий во времени и в пространстве.

Рис. 32. Тригонометрические функции: график связи между косинусом и синусом — окружность. Пример: (3/5)²+(4/5)²=1
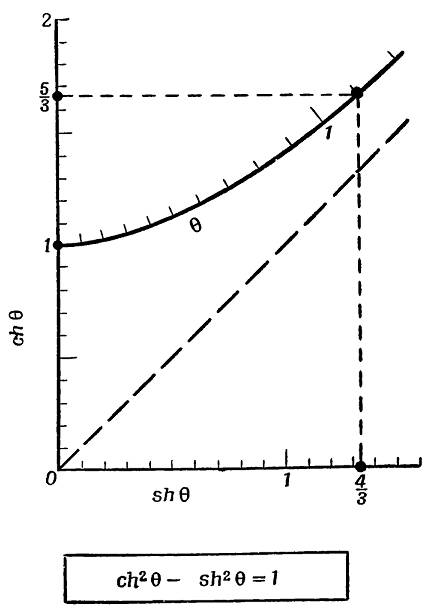
Рис. 33. Гиперболические функции: график связи между гиперболическими косинусом и синусом — гипербола. Пример: (5/3)²-(4/3)²=1
Проверка того факта, что преобразование поворота в эвклидовой геометрии оставляет неизменной длину
Разные знаки в соотношениях cos²α+sin²α=1 и ch²θ-sh²θ=1 связаны с различием между понятиями длины в эвклидовой геометрии и интервала в лоренцевой геометрии. Рассмотрим по очереди более подробно и ту и другую геометрии с этой точки зрения. Удостоверимся вновь в том факте, что в эвклидовой геометрии ковариантное преобразование координат (29), выраженное теперь не через величину наклона, а через тригонометрические функции, обеспечивает выполнение инвариантности длины. Для этого вычислим в штрихованных координатах квадрат длины:
(Длина)
²
=
(
Δ
𝑥)²
+
(
Δ
𝑦)²
=
=
(
Δ
𝑥'
cos θ
𝑟
+
Δ
𝑦'
sin θ
𝑟
)²
+
(-
Δ
𝑥'
sin θ
𝑟
+
Δ
𝑦'
cos θ
𝑟
)²
=
=
(
Δ
𝑥')²
cos²θ
𝑟
+
2(
Δ
𝑥')(
Δ
𝑦')cos θ
𝑟
sin θ
𝑟
+
(
Δ
𝑦')²
sin²θ
𝑟
+
+
(
Δ
𝑥')²
sin²θ
𝑟
-
2(
Δ
𝑥')(
Δ
𝑦')sin θ
𝑟
cos θ
𝑟
+
(
Δ
𝑦')²
cos²θ
𝑟
=
=
[(
Δ
𝑥')²
+
(
Δ
𝑦')²]
⋅
(sin²θ
𝑟
+
cos²θ
𝑟
)
=
=
(
Δ
𝑥')²
+
(
Δ
𝑦')²
(подчёркнутые члены сокращаются).
Тем самым мы провели инвариантность выражения для длины. Отметим, что соотношение
cos²θ
𝑟
+
sin²θ
𝑟
=
1
играет важную роль, связывая понятия ковариантности (преобразование координат, сводящееся к изменению ориентаций координатных осей) и инвариантности (неизменность длины при переходах между системами координат).
Проверка того факта, что преобразование Лоренца оставляет неизменным интервал
Ясно, что связь между ковариантностью и инвариантностью в лоренцевой геометрии основывается на соотношении
ch²θ
𝑟
-
sh²θ
𝑟
=
1.
Это видно из вычисления квадрата интервала (как пространственноподобного, так и временноподобного) в штрихованных координатах:
⎛
⎜
⎜
⎝
Интервал
собственной
длины
⎞²
⎟
⎟
⎠
=-
⎛
⎜
⎜
⎝
Интервал
собственного
времени
⎞²
⎟
⎟
⎠
=
=
⎛
⎜
⎝
Удалённость
в пространстве
⎞²
⎟
⎠
-
⎛
⎜
⎝
Удалённость
во времени
⎞²
⎟
⎠
=
=
(
Δ
𝑥)²
-
(
Δ
𝑡)²
=
=
(
Δ
𝑥'
ch θ
𝑟
+
Δ
𝑡'
sh θ
𝑟
)²
-
(
Δ
𝑥'
sh θ
𝑟
+
Δ
𝑡'
cos θ
𝑟
)²
=
=
(
Δ
𝑥')²
ch²θ
𝑟
+
2(
Δ
𝑥')(
Δ
𝑦')ch θ
𝑟
sh θ
𝑟
+
(
Δ
𝑡')²
sh²θ
𝑟
-
-[
(
Δ
𝑥')²
sh²θ
𝑟
-
2(
Δ
𝑥')(
Δ
𝑦')sh θ
𝑟
ch θ
𝑟
+
(
Δ
𝑡')²
ch²θ
𝑟
]=
=
[(
Δ
𝑥')²
-
(
Δ
𝑡')²]
⋅
(ch²θ
𝑟
-
sh²θ
𝑟
)
=
=
(
Δ
𝑥')²
-
(
Δ
𝑡')²
.
Так мы вновь проверили (простейшим возможным способом) тот факт, что преобразование Лоренца оставляет неизменным выражение для интервала.
Обратное преобразование Лоренца
Как мы уже вполне убедились, преобразование Лоренца служит для перевода информации с языка системы координат ракеты (𝑥', 𝑡') на язык лабораторной системы координат (𝑥, 𝑡). Кроме того, этот «словарь» во всех отношениях согласуется с универсальным языком интервалов (непротиворечивость ковариантного и инвариантного описаний в физике пространства-времени). Но мы нуждаемся в большем — ведь турецко-английский словарь можно купить в одном переплёте с англо-турецким. Так где же этот второй «словарь теории относительности»? Как совершить обратный переход от 𝑥 и 𝑡 к 𝑥' и 𝑡'? Если первый словарь соответствовал формулам
𝑥
=
𝑥'ch θ
𝑟
+
𝑡'sh θ
𝑟
,
𝑡
=
𝑥'sh θ
𝑟
+
𝑡'ch θ
𝑟
,
(36)
то какие формулы будут служить для обратного перехода от лабораторных к ракетным данным? Ответ: преобразование Лоренца, обратное преобразованию (36), задаётся формулами
𝑥'
=
𝑥ch θ
𝑟
-
𝑡sh θ
𝑟
,
𝑡'
=-
𝑥sh θ
𝑟
-
𝑡ch θ
𝑟
.
(37)
Доказательство. Подставьте последние выражения для 𝑥' и 𝑡' в формулы (36) и покажите, что получаются тождества (т.е. если перевести английское слово на турецкий язык, а затем снова на английский, то мы снова придём к исходному слову, если только каждый из словарей действительно является обратным по отношению к другому!).
В табл. 8 формальные определения гиперболических функций и некоторые соотношения для них записаны параллельно аналогичным определениям и соотношениям для тригонометрических функций. Здесь через 𝑒 обозначено основание натуральных логарифмов, численно равное 2,718281…, а через 𝑖 обозначен квадратный корень из минус единицы (мнимая единица), так что 𝑖²=-1. Обычные правила сложения и умножения экспонент справедливы и для экспонент, содержащих 𝑖. Угол θ берётся в обычных или гиперболических радианах, но не в градусах. Выражения типа 4! обозначают факториал; так, «четыре факториал» =4!=4×3×2×1=24. Чтобы разобраться в этих соотношениях, получите равенства 7—13 из определений 1—6 на обеих сторонах таблицы и качественно покажите, как из них вытекают графики на рис. 32 и 33. Особо отметьте различия в знаках в левой и правой сторонах таблицы.
Таблица 8.
Тригонометрические и гиперболические функции
ОПРЕДЕЛЕНИЯ
Тригонометрические функции
Гиперболические функции
1.
sin θ
=
𝑒𝑖θ-𝑒-𝑖θ
2𝑖
1.
sh θ
=
𝑒θ-𝑒-θ
2
2.
cos θ
=
𝑒𝑖θ+𝑒-𝑖θ
2𝑖
2.
ch θ
=
𝑒θ+𝑒-θ
2
3.
tg θ
=
sin θ
cos θ
3.
th θ
=
sh θ
ch θ
4.
sin θ
=
θ
-
θ³
3!
+
θ⁵
5!
-
θ⁷
7!
+…
4.
sh θ
=
θ
+
θ³
3!
+
θ⁵
5!
+
θ⁷
7!
+…
5.
cos θ
=
1
-
θ²
2!
+
θ⁴
4!
-
θ⁶
6!
+…
5.
ch θ
=
1
+
θ²
2!
+
θ⁴
4!
+
θ⁶
6!
+…
6.
tg θ
=
θ
+
θ³
3
+
2
15
θ⁵+…
6.
th θ
=
θ
-
θ³
3
+
2
15
θ⁵-…
СООТНОШЕНИЯ
7.
sin(-θ)
=-
sin(θ)
7.
sh(-θ)
=-
sh(θ)
8.
cos(-θ)
=
cos(θ)
8.
ch(-θ)
=
ch(θ)
9.
tg(-θ)
=-
tg(θ)
9.
th(-θ)
=-
th(θ)
10.
cos²θ
+
sin²θ
=1
10.
ch²θ
+
sh²θ
=1
11.
sin(θ₁+θ₂)
=
sin θ₁
cos θ₂
+
+
cos θ₁
sin θ₂
11.
sh(θ₁+θ₂)
=
sh θ₁
ch θ₂
+
+
ch θ₁
sh θ₂
12.
cos(θ₁+θ₂)
=
cos θ₁
cos θ₂
-
-
sin θ₁
sin θ₂
12.
ch(θ₁+θ₂)
=
ch θ₁
ch θ₂
-
-
sh θ₁
sh θ₂
13.
tg(θ₁+θ₂)
=
tg θ₁+tg θ₂
1-tg θ₁tg θ₂
13.
th(θ₁+θ₂)
=
th θ₁+th θ₂
1-th θ₁th θ₂
СПОСОБЫ БЫСТРОЙ ОЦЕНКИ ДЛЯ ПРОСТЫХ СМЕРТНЫХ
При малых
θ
При малых
θ
sin θ≈θ
sh θ≈θ
tg θ≈θ
th θ≈θ
Пример
:
θ=0,1
Пример
:
θ=0,1
Быстрая оценка:
Быстрая оценка:
sin θ≈0,1
sh θ≈0,1
tg θ≈0,1
th θ≈0,1
Точные значения:
Точные значения:
sin θ=0,0998
sh θ=0,1002
tg θ=0,1003
th θ=0,0997
При больших
θ
sh θ≈𝑒
θ
/2
ch θ≈𝑒
θ
/2
Пример
:
θ=3, 𝑒
θ
≈20.
Быстрая оценка:
sh θ≈10
th θ≈10
Точные значения:
sh θ=10,018
th θ=10,068
Упражнения к главе 1
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Можно без труда проанализировать важные направления современных исследований, если опираться на теорию относительности. Такой анализ решающим образом зависит от физической интуиции, которая развивается на основе опыта. Опыт же не может быть теперь приобретён в лаборатории, так как даже простые эксперименты по теории относительности очень сложны и дороги ввиду громадной величины скорости света. Альтернативой этим простым экспериментам должны послужить следующие упражнения, в которых обсуждаются разнообразные следствия структуры пространства-времени. Эта структура вновь и вновь проявляется, когда мы обсуждаем разные вопросы:
парадоксы;
загадки;
выводы соотношений;
практические приложения;
оценки эффектов;
их точный расчёт;
трудности интерпретации.
Эта глава содержит все необходимые формальные данные для того, чтобы найти ответ в каждом упражнении, однако лучший путь развития интуиции (практического понимания явлений) — это работа без поспешности. Поэтому вы убедитесь, что лучше всего продолжать возвращаться к этим упражнениям, даже когда эта книга будет для вас пройденным этапом. Те, кто хочет пройти основной материал за возможно кратчайшее время, могут ограничиться упражнениями, названия которых напечатаны курсивом в помещённом ниже списке.
Математические преобразования при решении этих упражнений очень кратки, и лишь немногие расчёты займут в записи более пяти строк. Но с другой стороны, упражнения потребуют времени на «разжёвывание». Меньше всего времени отнимут упражнения, не помеченные звёздочкой; труднее упражнения с одной звёздочкой; упражнения же, помеченные двумя звёздочками, предназначены для студентов старших курсов и аспирантов.
Основное правило Уилера. Никогда не начинай вычислений, пока не знаешь ответа. Каждому вычислению предпосылай оценочный расчёт; привлеки простые физические соображения (симметрию! инвариантность! сохранение!) до того, как начинать подробный вывод; продумай возможные ответы на каждую загадку. Будь смелее, ведь никому нет дела до того, что именно ты предположил. Поэтому делай предположения быстро, интуитивно. Удачные предположения укрепляют эту интуицию. Ошибочные предположения дают полезную встряску. Во всяком случае жизнь как практическая проверка пространственно-временны'х идей оказывается наиболее забавной шуткой, хотя и достаточно продолжительной!
A. Интервал пространства-времени (разд. 5—7)
1. Пространство и время—подробный пример
2. Практическая синхронизация часов
3. Соотношения между событиями
4. Одновременность
5. Временно'й порядок событий
6*. Расширяющаяся Вселенная
7. Собственное время и связь
8. Время на сбор информации и на принятие решения
Б. Преобразование Лоренца (разд. 8 и 9)
9. Лоренцево сокращение — подробный пример
10. Замедление хода часов
11. Относительная синхронизация часов
12. Эвклидовы аналогии
13. Лоренцево сокращение. II
14. Замедление хода часов. II
15. Формулы преобразования Лоренца со временем в секундах
16*. Вывод формул преобразования Лоренца
17*. Собственная длина и собственное время
18*. Плоскость обоюдного согласия
19*. Преобразование углов
20*. Преобразование скорости вдоль оси 𝑦
21**. Преобразование направлений скоростей
22**. Эффект «прожектора»
B. Загадки и парадоксы
23. Парадокс эйнштейновского поезда — подробный пример
24. Загадка Эйнштейна
25*. Парадокс шеста и сарая
26**. Война в космосе
27*. Парадокс часов
28*. Предметы, движущиеся быстрее света
Г. Основания теории
29. Синхронизация движущимися часами — подробный пример
30. Конструкция часов и замедление их хода
31. Инерциальные системы отсчёта, связанные с Землёй
32*. Размеры инерциальной системы
33*. Опыт Майкельсона — Морли
34*. Эксперимент Кеннеди — Торндайка
35*. Эксперимент Дикке
36*. Долой теорию относительности!
Д. Приближение малых скоростей
37. Эвклидова аналогия — подробный пример
38. Преобразование Галилея
39*. Пределы применимости преобразования Галилея
40*. Столкновения в теории Ньютона и в теории относительности. Область, в которой обе теории совпадают друг с другом с точностью до 1%
41*. Примеры предельных переходов к механике Ньютона
Е. Физика пространства-времени. Новые факты
42. Замедление времени для μ-мезона — подробный пример
43. Замедление времени для π⁺-мезона
44*. Аберрация света звёзд
45. Опыт Физо
46. Черенковское излучение
47*. Искривление лучей света звёзд Солнцем
Ж. Геометрическое истолкование
48. Геометрическое истолкование
49. Парадокс часов. II — подробный пример
З. Винегрет
50. Сокращение или поворот?
51**. Парадокс часов. III
52*. Наклонный стержень
53*. Парадокс метрового стержня
54**. Тонкий человек на решётке
А. ИНТЕРВАЛ ПРОСТРАНСТВА-ВРЕМЕНИ (РАЗД. 5-7)
1. Пространство и время — подробный пример
Два события происходят в лабораторной системе отсчёта в одном и том же месте, но отстоят во времени на 3 сек.
а) Чему равно расстояние в пространстве между этими событиями в системе отсчёта ракеты, если промежуток времени между событиями равен в ней 5 сек?
б) Чему равна скорость β𝑟 ракеты относительно лабораторной системы отсчёта?
Решение
а) Интервал пространства времени между этими двумя событиями имеет одну и ту же величину в обеих системах отсчёта:
(
Δ
𝑡)²
-
(
Δ
𝑥)²
=
(
Δ
𝑡')²
-
(
Δ
𝑥')²
.
Запишем содержание задачи так:
Δ𝑥 = 0,
Δ𝑡 = 3(сек) × 𝑐 (м/сек) = 9⋅10⁸ м,
Δ𝑥' требуется определить,
Δ𝑡' = 5(сек) × 𝑐 (м/сек) = 15⋅10⁸ м,
Подставим эти данные в выражения для интервала:
81⋅10¹⁶
-
0
=
225⋅10¹⁶
-
(
Δ
𝑥')²
.
Решаем полученное уравнение:
(
Δ
𝑥')²
=
144⋅10¹⁶
м
²
,
или
Δ
𝑥'
=
12⋅10⁸
м
.
б) В лабораторной системе отсчёта оба события произошли в одном и том же месте. В системе отсчёта ракеты это «место» лаборатории сдвинулось на 12⋅10⁸ м за 5 сек (или за 15⋅10⁸ м светового времени). Поэтому относительная скорость двух систем отсчёта равна
Δ𝑥'
Δ𝑡'
=
12⋅10⁸
15⋅10⁸
=
4
5
.
2. Практическая синхронизация часов
Вы — наблюдатель, находящийся в покое вблизи часов с пространственными координатами 𝑥=6 м, 𝑦=8 м, 𝑧=0 м в лабораторной системе отсчёта. Вы хотите синхронизировать свои часы с часами, находящимися в начале координат, используя опорный сигнал. Подробно опишите количественно, как вы сделаете это. ▼
3. Соотношения между событиями

Рис. 34. Как связаны между собой события 𝐴, 𝐵 и 𝐶?
На рис. 34 изображены на диаграмме пространства-времени лабораторной системы отсчёта события 𝐴, 𝐵 и 𝐶. Ответьте на следующие вопросы, касающиеся пары событий 𝐴 и 𝐵:
а) Какой интервал лежит между этими событиями — временноподобный, светоподобный или пространственноподобный?
б) Чему равно собственное время (или собственное расстояние) между этими событиями?
в) Могло ли одно из этих событий быть причиной другого?
Ответьте на такие же вопросы о паре событий 𝐴 и 𝐶.
Ответьте на такие же вопросы о паре событий 𝐶 и 𝐵. ▼
4. Одновременность
«𝐴 сталкивается с 𝐵; одновременно на расстоянии миллиона миль от них 𝐶 сталкивается с 𝐷». Выразите одной или двумя фразами, как требует частная теория относительности переформулировать или охарактеризовать это утверждение. ▼
5. Временно'й порядок событий
«Событие 𝐺 произошло до события 𝐻». Покажите, что порядок во времени этих двух событий в лабораторной системе отсчёта будет тем же, что и в системе отсчёта ракеты, тогда и только тогда, когда события будут разделены временноподобным или светоподобным интервалом. ▼
6*. Расширяющаяся Вселенная
а) Гигантская бомба разрывается в окружающем её пустом пространстве. По какому закону будут двигаться друг относительно друга её осколки? Как может быть обнаружено их относительное движение? Обсуждение: Представим себе, что каждый осколок снабжён источником света, посылающим сигналы через известные равные друг другу промежутки времени Δτ в его системе отсчёта (собственное время!). Зная эти интервалы между вспышками, каким путём может наблюдатель определить на одном осколке относительную скорость движения β любого другого осколка? Предположим, что он может при этом пользоваться: 1) известным значением интервала собственного времени Δτ между вспышками и 2) измеряемым им временем Δ𝑡приём между приходом к нему последовательных сигналов. (Замечание. Последнее не равно промежутку времени Δ𝑡 между последовательными вспышками на удаляющемся передатчике в системе отсчёта этого наблюдателя. См. рис. 35). Предлагается выразить β через Δτ и Δ𝑡приём. Как будет зависеть измеряемая скорость удаления от расстояния между осколком, на котором находится наблюдатель, и другим осколком? (Замечание. В каждый данный момент в каждой данной системе отсчёта осколки, очевидно, улетят от места взрыва на расстояния, прямо пропорциональные их скоростям в этой системе отсчёта!)

Рис. 35. Вычисление времени Δ𝑡приём, прошедшего между поступлением двух последовательных сигналов от удаляющегося излучателя к наблюдателю.
б) Как можно заключить по наблюдению света, испускаемого звёздами, что Вселенная расширяется? Обсуждение: В раскалённых звёздах атомы испускают свет различных характерных для этих атомов частот («спектральные линии»). Мы можем измерять на Земле наблюдаемый период колебаний для каждой спектральной линии приходящего от звёзд света. По расположению этих спектральных линий мы можем установить, с излучением какого элемента мы имеем дело. Атомы этого же элемента можно возбуждать в лабораторных условиях, где они в состоянии покоя излучают свет, спектральные линии которого характеризуются собственным периодом, и мы можем его измерить. Используйте теперь результаты части (а) этого упражнения и опишите, как сравнение наблюдаемого периода колебаний для спектральных линий приходящего от звёзд света с собственным периодом колебаний для спектральных линий света, излучаемого покоящимися атомами в лаборатории, даёт величину скорости удаления звёзд, излучающих свет. Это наблюдаемое изменение периода, обусловленное движением источника, называется допплеровским смещением (эффектом Допплера). (Более подробное описание его см. в упражнении 75 гл. 2 и последующих упражнениях). Если началом Вселенной был гигантский взрыв, как должны быть связаны друг с другом наблюдаемые скорости разбегания различных звёзд, находящихся на разных расстояниях? Здесь следует пренебречь замедлением скоростей за время разбегания (под действием гравитационного притяжения и пр.), однако мы рассмотрим такое замедление при более полном анализе (упражнение 80). ▼
7. Собственное время и связь
Пусть Солнце испустило световую вспышку, которая была поглощена Луной. Собственное время между моментами испускания и поглощения этой вспышки равно нулю,— верно или ложно это утверждение? Будет ли равно нулю собственное время между двумя событиями (излучением и поглощением), если вспышка подвергалась отражению зеркалами на Луне, прежде чем была поглощена? (Внимание!) Пусть световая вспышка была излучена на Земле и распространяется в воздухе по прямой до другого места на Земле, где она поглощается. (Скорость света в воздухе немного меньше, чем 𝑐) Будет ли равен нулю промежуток собственного времени между излучением и поглощением этой вспышки? ▼
8. Время на сбор информации и на принятие решения
При описании событий мы использовали сеть часов-хронографов. Расположение события отождествляется с расположением ближайших к событию часов, а время события — с тем временем, которое зафиксировали эти часы. Предмет физики — изучение взаимных отношений между событиями. Если аналитико-координационный центр расположен в начале координат сети часов, чему будет равно (в его системе отсчёта) время запаздывания между получением данных для анализа и регистрацией данных на часах нарасстоянии 𝑅 от центра? Пусть часы с координатами 𝑥=6⋅10⁹ м, 𝑦=8⋅10⁹ м и 𝑧=0 м регистрируют прохождение метеорита в момент 41⋅10⁹ м времени. Часы с координатами 𝑥=3⋅10⁹ м, 𝑦=4⋅10⁹ м и 𝑧=0 м регистрируют прохождение этого же метеорита в момент 47⋅10⁹ м времени. Наблюдателю в аналитико-координационном центре для принятия мер защиты требуется 3 секунды. Если приведённые выше данные передаются ему световыми сигналами и анализируются сразу же при получении, успеет ли наблюдатель принять меры защиты? ▼
Б. ПРЕОБРАЗОВАНИЕ ЛОРЕНЦА (РАЗД. 8 И 9)
9. Лоренцево сокращение — подробный пример
Пусть ракета снабжена метровым стержнем, который наблюдается в лабораторной системе отсчёта (лабораторной системе стержней и часов). В чём будет состоять отличие заключений наблюдателя в лаборатории относительно длины метрового стержня от того, что предсказывала дорелятивистская физика? Мы разобьём этот обширный вопрос на четыре части.
а) Как поставленный здесь вопрос о длине может быть переформулирован в вопрос о разделении двух событий? Замечание. Оба конца метрового стержня прочерчивают в пространстве-времени свои мировые линии. Однако каждая мировая линия — это последовательность бесконечного числа событий. Как же разумным образом выбрать именно ту пару событий, которая даёт необходимую информацию о наблюдаемой длине метрового стержня?
Решение. Выберем эти два заслуживающих внимания события таким образом. 𝐴: Один конец метрового стержня пролетает мимо некоторых лабораторных часов в тот момент, когда они показывают полдень. 𝐵: Другой конец метрового стержня пролетает мимо других лабораторных часов, когда они тоже показывают полдень. Обсуждение. Положения концов движущегося метрового стержня необходимо измерять в один и тот же момент времени в лабораторной системе отсчёта. В противном случае мы не смогли бы разумно определить ту пару точек в лаборатории, длину расстояния между которыми мы измеряем. Итак, оба события должны быть одновременными в лабораторной системе отсчёта (Δ𝑡=0). Они могут быть одновременными, а могут и не быть в системе отсчёта ракеты (Δ𝑡' может равняться или не равняться нулю) — это там несущественно! Ведь в системе отсчёта ракеты метровый стержень неподвижен, и там положение его концов можно определять в любое время.
б) Пусть метровый стержень ориентирован вдоль оси 𝑥 (направления движения) ракеты, так что в системе отсчёта ракеты расстояние между его концами равно Δ𝑥'=1 м. Чему будет равна его наблюдаемая длина в лабораторной системе отсчёта?
Решение. Искомая длина —это разделение в пространстве пары событий 𝐴 и 𝐵 в лабораторной системе отсчёта:
Δ
𝑥
=
Δ𝑥'
ch θ𝑟
=
Δ
𝑥'
⋅
√
1-β
𝑟
²
.
(38)
Эта длина меньше 1 м. Такое укорачивание называется лоренцевым сокращением. Обсуждение. Преобразование Лоренца (37) связывает между собой разности координат событий в лабораторной системе отсчёта и в системе ракеты:
Δ
𝑥'
=
Δ
𝑥 ch θ
𝑟
-
Δ
𝑡 sh θ
𝑟
,
Δ
𝑡'
=
-
Δ
𝑥 sh θ
𝑟
+
Δ
𝑡 ch θ
𝑟
,
Δ
𝑦'
=
Δ
𝑦,
Δ
𝑧'
=
Δ
𝑧.
(39)
Наши события одновременны в лабораторной системе отсчёта (Δ𝑡=0). Отсюда Δ𝑥'=Δ𝑥 ch θ𝑟, что и даёт приведённый ответ. Заметим, что Δ𝑡' не равняется нулю, т.е. события 𝐴 и 𝐵 не одновременны, если их рассматривать в системе отсчёта ракеты. Эта разница во времени между двумя событиями на концах метрового стержня не вызывает недоумения у работников на ракете относительно значения длины их метрового стержня: для них он покоится, и длина его 1 м. Их не удивляет и тот факт, что наблюдатели в лаборатории регистрируют укорочение этой длины («лоренцево сокращение»). Они скажут: «А почему бы и нет? Ведь наблюдатели в лаборатории измеряют положения концов метрового стержня во времена 𝑡𝐴' и 𝑡𝐵', а мы знаем, что эти времена различны. Интересно, как бы им удалось при этом заключить, что длина равна 1 м?»
в) Пусть метровый стержень направлен вдоль оси 𝑦 (перпендикулярно направлению движения) в системе отсчёта ракеты, так что расстояние между его концами в этой системе равно Δ𝑦'=1 м. Чему равна длина стержня, наблюдаемая в лабораторной системе отсчёта?
Решение. Длина есть величина пространственного удаления друг от друга двух событий (𝐴 и 𝐵) лабораторной системе; при этом
Δ
𝑦
=
Δ
𝑦'
.
Эта длина равна 1 м. В направлениях, перпендикулярных движению, размеры тел не сокращаются. Обсуждение. Отметим, что оба события теперь одновременны не только в лабораторной системе отсчёта (Δ𝑡=0), но и в системе отсчёта ракеты (Δ𝑡'=0), согласно соотношениям (39). Для работников на ракете поэтому нет ничего странного в том, что наблюдатели в лаборатории будут согласны с ними относительно длины метрового стержня.
г) Вернёмся ещё раз к вопросу (б). Как можно принять тот вывод, что метровый стержень, летящий с ракетой, представляется короче одного метра длины в лаборатории находящимся там наблюдателям? Если бы этот вывод был верен, не получили бы мы возможности различать по физическим законам систему отсчёта ракеты (в которой метровые стержни сохраняют свою стандартную длину) от лабораторной системы отсчёта (где те же самые стержни регистрируются как укороченные)? Но если это так, то не разрушает ли логика рассуждений теории относительности того принципа, который лежит в её же основе? Этот принцип утверждает, что между двумя инерциальными системами отсчёта нельзя провести никаких различий на основании физических наблюдений в этих системах? Но разве мы не обнаружили в высшей степени замечательное физическое различие между такими двумя системами?

Рис. 36. Поле, простирающееся на большее расстояние в направлении 𝑥, чем в направлении 𝑥'.
Решение. Да, различие между размерами предметов в направлении оси 𝑥, зарегистрированными в этих двух системах отсчёта, существует. Однако физика явлений в обеих системах ничем не отличается. Метровый стержень, покоящийся относительно ракеты и направленный по её движению, оказывается короче длины 1 м в лаборатории. Но и метровый стержень, покоящийся в лаборатории и параллельный направлению движения, окажется укороченным при его измерении работниками на ракете. «Что за нелепица! — возразите вы.— Мне стоит только привлечь элементарную логику, и вся эта релятивистская бессмыслица рухнет. Вы говорите, что метровый стержень на ракете может при измерении из лаборатории оказаться длиной всего в полметра, но тогда вы должны согласиться, что длина в полметра в лаборатории регистрируется на ракете как полный метр. Итак, размеры тел в системе отсчёта ракеты больше, чем их размеры в лабораторной системе (в направлении движения). Значит, там различна сама физика — почему бы ей не быть разной в двух разных системах отсчёта. И я без труда определю, в какой системе отсчёта нахожусь — в лабораторной системе или в системе ракеты. А принцип относительности?! Это же просто выдумка!» Мы ответим на это возражение так. Вероятно, каждый из нас при первом знакомстве с идеями Эйнштейна и Лоренца находит их обескураживающими; ведь мы так мало имели дела с предметами, двигающимися по-настоящему быстро. Может быть, принцип относительности покажется вам немного уютнее, если вы познакомитесь с его аналогом в эвклидовой геометрии. Конечно, между формулами (Δ𝐿)²=(Δ𝑥)²+(Δ𝑦)² в эвклидовой геометрии и (Δτ)²=(Δ𝑡)²-(Δ𝑥)² в лоренцевой геометрии есть некоторая разница. Но ясно, что вас больше волнует вопрос о том, могут ли расстояния в одной системе отличаться от расстояний в другой, чем то, меньше ли расстояния в новой системе, чем в старой (лоренцево сокращение в лоренцевой геометрии), или то, больше ли они в новой системе, чем в старой (возрастание длин в эвклидовой геометрии). Взглянем же на рис. 36. Там изображено поле, протяжённость которого в направлении оси 𝑥 явно превышает протяжённость в направлении оси 𝑥':
Δ
𝑥
=
Δ𝑥'
cos θ𝑟
.
(40)

Рис. 37. Другое поле, простирающееся на большее расстояние в направлении 𝑥' чем в направлении 𝑥.
С другой стороны, взглянем на рис. 37 (в упражнении 48 вы найдёте пространственно-временные аналоги рис. 36 и 37). Здесь изображено другое поле, которое простирается в направлении оси 𝑥 на то же расстояние Δ𝑥. Однако его протяжённость в направлении оси 𝑥' больше, чем Δ𝑥:
Δ
𝑥'
=
Δ𝑥
cos θ𝑟
.
(41)
Вы безусловно согласитесь с этими выводами. У вас даже не зародится сомнения, будто формулы (40) и (41) противоречат друг другу. Ведь вы понимаете, что величина Δ𝑥 в этих формулах каждый раз относится к другому измерению другого поля. Может быть, теперь вы будете готовы поверить, что длина метрового стержня, покоящегося относительно ракеты, будет зарегистрирована в лаборатории как отрезок меньше одного метра длины, тогда как метровый стержень, покоящийся в лаборатории, окажется короче одного метра при измерении с ракеты? Вы скажете: «Я согласен теперь, что в ваших утверждениях нет логических противоречий. Но, может быть, вы не остановитесь на том, что сказали, и по-настоящему докажете мне справедливость сказанного только что, а именно что метровый стержень, покоящийся в лабораторной системе, будет короче одного метра с точки зрения системы отсчёта ракеты». Ответ таков: разрешим формулы преобразования Лоренца (39) относительно координат лабораторной системы отсчёта, выразив их через координаты в системе ракеты. Иначе говоря, поменяем местами штрихованные и нештрихованные координаты в этих формулах и заменим знак скорости на обратный. Или же просто перейдём к уравнениям (36), обратным по отношению к (39). В любом случае запишем соотношения
Δ
𝑥
=
Δ
𝑥' ch θ
𝑟
-
Δ
𝑡' sh θ
𝑟
,
Δ
𝑡
=
-
Δ
𝑥' sh θ
𝑟
+
Δ
𝑡' ch θ
𝑟
,
Δ
𝑦
=
Δ
𝑦',
Δ
𝑧
=
Δ
𝑧'.
(42)
Новый метровый стержень покоится в лабораторной системе отсчёта. Если смотреть из системы отсчёта ракеты, он находится в движении. Поэтому при определении его длины в системе отсчёта ракеты мы должны исходить из двух отправных точек в этой системе, а именно из положений концов нашего метрового стержня в один и тот же момент времени в системе отсчёта ракеты. Итак, Δ𝑡'=0. Первое из соотношений (42) сразу же даёт
Δ
𝑥'
=
Δ𝑥
ch θ𝑟
=
Δ
𝑥
⋅
√
1-β
𝑟
²
.
(43)
Длина, зарегистрированная в системе отсчёта ракеты, короче одного метра, если метровый стержень покоится относительно лаборатории, что и требовалось доказать.
10. Замедление хода часов
Пусть часы движутся вместе с ракетой (рис. 38) и наблюдаются из лабораторной системы отсчёта (лабораторная решётка стержней и часов). В чём будет состоять отличие заключений наблюдателя в лаборатории относительно времени, показываемого движущимися часами, от того, что предсказывала дорелятивистская физика? Разобьём этот вопрос на 4 части.

Рис. 38. Способ сравнивать показания одних часов на ракете с показаниями нескольких лабораторных часов.
а) Как этот вопрос о ходе времени может быть переформулирован в вопрос о разделении двух событий?
б) Пусть между двумя событиями, выбранными в части (а), часы на ракете отсчитали 1 м светового времени, т.е. в системе отсчёта ракеты зарегистрирован интервал времени Δ𝑡'=1 м. Покажите, что соответствующий промежуток времени, зарегистрированный в лабораторной системе отсчёта, определяется соотношением
Δ
𝑡
=
Δ
𝑡'
⋅
ch
θ
𝑟
=
Δ𝑡'
√1-β𝑟²
.
(44)
Этот промежуток времени превышает 1 м светового времени. Такое удлинение называется замедлением хода часов (замедлением времени).
в) Как можно согласиться с выводом, полученным в части (б), о том, что 1 м времени, прошедший в системе отсчёта ракеты, оказывается больше, чем 1 м времени для наблюдателя в лаборатории? Не позволит ли этот вывод различать, исходя из физических законов, систему отсчёта ракеты (в которой часы идут с их стандартной скоростью) и лабораторную систему отсчёта (где те же самые часы отстают)? Не будет ли, таким образом, этот вывод противоречить принципу относительности (разд. 3), на котором основана вся теория относительности?
г) Пойдём ещё дальше и покажем, что 1 м времени, прошедший по часам, покоящимся в лабораторной системе отсчёта (Δ𝑡=1 м), будет зарегистрирован как интервал времени больше одного метра наблюдателями в системе отсчёта ракеты согласно формуле
Δ
𝑡'
=
Δ
𝑡
ch
θ
𝑟
=
Δ𝑡
√1-β𝑟²
.
(45)
Каким образом этот вывод подтверждает симметрию между обеими системами отсчёта (ракеты и лаборатории), требуемую принципом относительности? ▼
11. Относительная синхронизация часов
а) Покажите, что если два события происходят одновременно и в одном и том же месте в лабораторной системе отсчёта, они будут одновременными в системе отсчёта любой ракеты. Покажите, что если два события происходят одновременно, но не в одной и той же точке на оси 𝑥 в лабораторной системе отсчёта, они не будут наблюдаться как одновременные ни в одной системе отсчёта ракеты. Тот факт, что движущиеся относительно друг друга наблюдатели не всегда будут соглашаться друг с другом, одновременны или нет два события, носит название относительности одновременности.
б) Два события происходят одновременно и имеют одно и то же значение координаты 𝑥 в лабораторной системе отсчёта, но разница в значениях координат 𝑦 и 𝑧 для них равна Δ𝑦 и Δ𝑧. Покажите, что эти два события будут одновременными и в системе отсчёта ракеты.
в) Пользуясь формулами преобразования Лоренца, покажите, что в момент 𝑡=0 в лабораторной системе отсчёта часы в системе отсчёта ракеты на положительной части оси 𝑥 оказываются позади лабораторных часов, а на отрицательной части оси 𝑥 — впереди лабораторных часов, причём разница во времени, показываемом часами в лабораторной системе отсчёта и системе ракеты, возрастает по мере удаления от начала координат по закону
𝑡'
=-
𝑥sh θ
𝑟
=
-𝑥
β𝑟
√1-β𝑟²
.
(46)
г) Пользуясь формулами преобразования Лоренца, покажите, что в момент 𝑡'=0 в системе отсчёта ракеты часы в лабораторной системе отсчёта на положительной части оси 𝑥 оказываются впереди часов ракеты, а на отрицательной части оси 𝑥 — позади часов ракеты, причём разница во времени, показываемом часами в системе отсчёта ракеты и в лабораторной системе, возрастает по мере удаления от начала координат по закону
𝑡'
=+
𝑥'sh θ
𝑟
=
+𝑥'
β𝑟
√1-β𝑟²
.
(47)
Тот факт, что никто из двух наблюдателей, движущихся относительно друг друга, не согласится, что время опорного события и времена, когда все часы в системе отсчёта другого наблюдателя показывают нулевой момент, одновременны, носит название относительной синхронизации часов.
д) Казалось бы, что разные знаки в законах (46) и (47) приводят к асимметрии между системами отсчёта, позволяющей провести различие между этими системами, что противоречило бы принципу относительности. Покажите, что если наблюдатель в каждой системе отсчёта ориентирует положительное направление своей оси 𝑥 в направлении движения другой системы относительно него, то все физические измерения, связанные с синхронизацией часов, дадут в каждой системе совершенно тождественные результаты. Иначе говоря, системы отсчёта нельзя различить с помощью и этого метода. Разница в знаках в приведённых выше уравнениях вызвана произвольным (и асимметричным) выбором общего для обеих осей 𝑥 положительного направления.
е) Полученные выводы иногда выражаются в виде утверждения, что «наблюдатель на ракете обнаруживает рассинхронизированность разных лабораторных часов между собой». Объясните, в чём ошибочность этой формулировки. Покажите, что для необходимых при этом измерений недостаточно одного-единственного наблюдателя на ракете. Как выразить полученные выше выводы безупречно корректно, чётко и ясно (хотя бы это оказалось значительно длиннее!)? ▼
12. Эвклидовы аналогии
а) Пусть в плоскости 𝑥𝑦 эвклидовой системы координат лежит прямой стержень. Начертите диаграмму, изображающую этот стержень в плоскости 𝑥𝑦; постройте проекции стержня на оси 𝑥, 𝑦 и 𝑥', 𝑦'. Разберите аналогию между различием в значениях 𝑥-компонент длины стержня, измеренных в двух повёрнутых относительно друг друга эвклидовых системах координат, и различием в длине движущегося стержня, наблюдаемого в лабораторной системе отсчёта, и покоящегося в системе ракеты стержня.
б) Разберите аналогию между замедлением времени и изменением длины 𝑦-компоненты стержня при переходе между повёрнутыми друг относительно друга эвклидовыми системами координат [см. часть (а)]. Назовите инварианты геометрии Эвклида и геометрии Лоренца.
в) Разберите аналогию между относительной синхронизацией часов и случаем двух повёрнутых друг относительно друга эвклидовых систем координат, когда точки на положительной части оси 𝑥 в одной системе координат будут иметь, скажем, отрицательные значения координаты 𝑦 в другой системе (и тем более отрицательные, чем дальше мы будем уходить от начала координат). ▼
13. Лоренцево сокращение. II
Пусть метровый стержень, покоящийся в системе отсчёта ракеты, направлен вдоль оси 𝑥'. Покажите, что наблюдатель в лабораторной системе заключит, что стержень претерпел лоренцево сокращение, если измерит время, за которое этот стержень пролетает мимо одних из часов лабораторной системы, и умножит его на величину относительной скорости движения систем. ▼
14. Замедление хода часов. II
Два события происходят в одном и том же месте, но в разные моменты времени в системе отсчёта ракеты. Покажите, что наблюдатель в лабораторной системе заключит, что промежуток времени между этими двумя событиями будет больше в его системе, если измерит расстояние между событиями в лабораторной системе и разделит его на величину относительной скорости движения систем. ▼
15. Формулы преобразования Лоренца со временем в секундах
Пусть время измеряется в секундах (пометим это индексом: 𝑡сек), а 𝑣𝑟 — относительная скорость лабораторной системы отсчёта и системы ракеты, выраженная в м/сек. Покажите, что формулы преобразования Лоренца принимают тогда вид
𝑥'
=
𝑥 ch θ
𝑟
-
𝑐𝑡
сек
sh θ
𝑟
=
𝑥-𝑣𝑟𝑡сек
√1-(𝑣𝑟²/𝑐²)
,
𝑡
сек
-
𝑣
𝑟
𝑥
𝑡
сек
'
=-
𝑡
sh θ
𝑟
+
𝑡
сек
ch θ
𝑟
=
𝑐²
,
𝑐
√
1-(𝑣
𝑟
²/𝑐²)
(48)
где
𝑣𝑟
𝑐
=
th θ
𝑟
.
Запишите в тех же обозначениях и обратное преобразование Лоренца. ▼
16*. Вывод формул преобразования Лоренца
Воспользуйтесь следующим новым методом (принадлежащим Эйнштейну) для вывода формул преобразования Лоренца. Пусть ракета равномерно движется со скоростью β𝑟 в направлении оси 𝑥 в лабораторной системе отсчёта. Координаты 𝑥', 𝑦', 𝑧', 𝑡' произвольного события (например, взрыва) в системе отсчёта ракеты взаимно однозначно связаны с координатами 𝑥, 𝑦, 𝑧, 𝑡 этого же события, измеренными в лабораторной системе. При этом 𝑦=𝑦' и 𝑧=𝑧' (расстояния в направлениях, перпендикулярных движению, совпадают в обеих системах). Что же касается связи между 𝑥, 𝑡 и 𝑥', 𝑡' то предположим существование линейной зависимости
𝑥
=
𝑎𝑥'
+
𝑏𝑡'
,
𝑡
=
𝑒𝑥'
+
𝑓𝑡'
.
Здесь четвёрка коэффициентов 𝑎, 𝑏, 𝑒 и 𝑓 1) неизвестна, 2) не зависит ни от 𝑥, 𝑡, ни от 𝑥', 𝑡' 3) зависит лишь от относительной скорости β𝑟 движения этих двух систем отсчёта.
Найдите отношения 𝑏/𝑎, 𝑒/𝑎, 𝑓/𝑎 как функции скорости β𝑟, исходя лишь из следующих трёх предположений: 1) световая вспышка, происшедшая в 𝑥=0, 𝑡=0 (𝑥'=0, 𝑡'=0) распространяется вправо со скоростью света в обеих системах отсчёта (𝑥=𝑡, 𝑥'=𝑡') 2) световая вспышка, происшедшая в 𝑥=0, 𝑡=0 (𝑥'=0, 𝑡'=0), распространяется влево со скоростью света в обеих системах отсчёта (𝑥=-𝑡, 𝑥'=-𝑡') 3) точка 𝑥'=0 обладает в лабораторной системе отсчёта скоростью β𝑟.
Теперь используйте четвёртое предположение — инвариантность интервала (разд. 5): 4) 𝑡²-𝑥²=(𝑡')²-(𝑥')² и найдите с его помощью величину постоянной 𝑎, а тем самым значения всех 4 коэффициентов 𝑎, 𝑏, 𝑒 и 𝑓. Согласуются ли полученные таким путём результаты с лоренцевыми значениями коэффициентов преобразования? ▼
17*. Собственная длина и собственное время
а) Пусть два события 𝑃 и 𝑄 разделены пространственноподобным интервалом. Покажите, что можно найти такую систему отсчёта ракеты, в которой оба события произошли одновременно. Покажите также, что в этой системе отсчёта ракеты расстояние между данными событиями равно собственному расстоянию а между ними. (Один из путей: предположим, что такая система отсчёта действительно существует, а затем с помощью формул преобразования Лоренца покажем, что относительная скорость этой системы меньше скорости света (β𝑟<1), что и оправдывает сделанное предположение).
б) Пусть два события 𝑃 и 𝑅 разделены временноподобным интервалом. Покажите, что можно найти такую систему отсчёта ракеты, в которой оба события произошли в одном и том же месте. Покажите также, что в этой системе отсчёта ракеты промежуток времени между данными событиями равен промежутку собственного времени τ между ними. ▼
18*. Плоскость обоюдного согласия
В каждый момент имеется лишь одна плоскость, на которой показания часов лаборатории и ракеты совпадают. Покажите, что скорость движения этой плоскости в лабораторной системе отсчёта равна th (θ𝑟/2), где θ𝑟 — параметр относительной скорости лабораторной системы отсчёта и системы ракеты. ▼
19*. Преобразование углов
Метровый стержень покоится в системе отсчёта ракеты под углом φ' с осью 𝑥. Под каким углом φ ориентирован тот же метровый стержень к оси 𝑥 лабораторной системы отсчёта? Чему равна длина этого стержня, наблюдаемая в лабораторной системе отсчёта? Предположим теперь, что направления электрических силовых линий вокруг точечного заряда преобразуются так же, как направление метрового стержня, направленного вдоль той же линии. Качественно изобразите электрические силовые линии изолированного точечного положительного заряда, покоящегося в системе отсчёта ракеты, если их рассматривать: а) в системе отсчёта ракеты и б) в лабораторной системе отсчёта. Какие отсюда можно получить выводы о силах, действующих в лабораторной системе отсчёта на покоящиеся в этой системе пробные заряды, окружающие наш движущийся заряд? ▼
20*. Преобразование скорости вдоль оси 𝑦
Пусть частица движется с постоянной скоростью β𝑦'=Δ𝑦'/Δ𝑡' в направлении оси 𝑦' в системе отсчёта ракеты. Преобразуйте компоненты её смещения 𝑦 и 𝑡 пользуясь формулами преобразования Лоренца. Покажите, что 𝑥- и 𝑦- компоненты скорости этой частицы выражаются в лабораторной системе отсчёта как
β
𝑥
=
th θ
𝑟
,
β
𝑦
=
β𝑦'
ch θ𝑟
.
(49)
▼
21**. Преобразование направлений скоростей
Пусть частица движется со скоростью β' в плоскости 𝑥'𝑦' в системе отсчёта ракеты, и направление её движения образует угол φ' с осью 𝑥'. Найти угол, который образует направление скорости этой частицы с осью 𝑥 в лабораторной системе отсчёта. (Совет: преобразовать не скорости, а смещения). Почему получаемый угол будет иным, чем найденный в упражнении 19? Сравните эти результаты в предположении, что скорость ракеты относительно лабораторной системы отсчёта весьма велика. ▼
22**. Эффект «прожектора»
Световая вспышка испущена под углом φ' к оси 𝑥' в системе отсчёта ракеты. Показать, что угол φ направления распространения этой вспышки по отношению к оси 𝑥 в лабораторной системе отсчёта даётся уравнением
cos φ
=
cos φ'+β𝑟
1+β𝑟cos φ'
.
(50)
Показать, что этот результат можно получить из решения предыдущего упражнения, положив в нем скорость β' равной единице. Рассмотрите затем частицу, покоящуюся в системе отсчёта ракеты и равномерно излучающую свет во всех направлениях. Рассмотрите те 50% света, которые эта частица излучает в переднюю полусферу в системе отсчёта ракеты. Примите также, что ракета движется относительно лабораторной системы отсчёта весьма быстро. Требуется показать, что в лабораторной системе отсчёта этот свет сконцентрируется в узкий конус, направленный вперёд по движению, с осью, совпадающей с направлением движения частицы. Это явление называется эффектом «прожектора». ▼
В. ЗАГАДКИ И ПАРАДОКСЫ
23. Парадокс эйнштейновского поезда — подробный пример
Пусть на поезде, движущемся со скоростью β𝑟, близкой к единице, едут три человека (𝐴, 𝑂 и 𝐵). 𝐴 едет в голове поезда, 𝑂 в середине, а 𝐵 — в хвосте (рис. 39). На земле около железнодорожного пути стоит четвёртый человек, 𝑂'. В тот самый момент, когда 𝑂 проезжает мимо 𝑂', сигналы ламп вспышек от 𝐴 и 𝐵 достигают 𝑂 и 𝑂'. Кто первым послал сигнал? Пользуясь только тем фактом, что скорость света конечна и не зависит от скорости движения его источника, покажите, что 𝑂 и 𝑂' ответят на этот вопрос по-разному. Найдя качественное решение задачи, вычислите количественно разницу между моментами времени, когда послали сигналы 𝐴 и 𝐵, наблюдаемую в системе отсчёта поезда (Δ𝑡𝐵𝐴) и в системе отсчёта 𝑂' (Δ𝑡𝐵𝐴'); пользуясь преобразованием Лоренца или другим путём.

Рис. 39. Кто подал сигнал первым — путешественник 𝐴 или путешественник 𝐵?
Решение. Наблюдатели 𝐴 и 𝐵 покоятся относительно наблюдателя 𝑂. К тому же они находятся на равных расстояниях от 𝑂, что последний может не спеша проверить, пользуясь своей линейкой. Следовательно, сигналам от 𝐴 и от 𝐵 требуется одно и то же время, чтобы достигнуть 𝑂. Эти сигналы принимаются наблюдателем 𝑂. одновременно. Поэтому наблюдатель 𝑂 заключает, что наблюдатели 𝐴 и 𝐵 послали свои сигналы в один и тот же момент: Δ𝑡𝐵𝐴=0.
Наблюдатель 𝑂', стоящий рядом с железнодорожными путями, делает совершенно иные выводы. Его рассуждения таковы: «Две вспышки пришли ко мне, когда середина поезда проходила мимо меня. Значит, обе эти вспышки должны быть испущены до того, как середина поезда поравнялась со мной. А до этого момента наблюдатель 𝐴 был ко мне ближе, чем наблюдатель 𝐵. Поэтому свет от 𝐵 должен был пройти до меня более длинный путь и затратить на это большее время, чем свет от 𝐴. Но оба сигнала поступили ко мне одновременно. Следовательно, наблюдатель 𝐵 должен был послать свой сигнал раньше, чем наблюдатель 𝐴» (Δ𝑡𝐵𝐴=𝑡𝐵'-𝑡𝐴'). Итак, наблюдатель 𝑂', стоящий рядом с железнодорожными путями, делает заключение, что сначала послал свои сигнал 𝐵, а потом уже', 𝐴 тогда как едущий на поезде наблюдатель 𝑂 заключает, что оба наблюдателя, 𝐴 и 𝐵, послали сигналы в одно и то же время.
Чему равен промежуток времени между посылкой сигналов наблюдателями 𝐴 и 𝐵? В нештрихованной системе отсчёта (поезд) эти сигналы были отправлены одновременно, так что Δ𝑡=0. Расстояние между точками посылки сигналов равно Δ𝑥=Δ𝑥𝐵𝐴=𝑥𝐵-𝑥𝐴=𝐿, где 𝐿 — длина поезда. Поэтому в штрихованной системе отсчёта (движущейся вправо по отношению к нештрихованной системе, то есть поезду, как это бывает обычно при использовании штрихованных и нештрихованных обозначений) промежуток времени между посылкой сигналов 𝐴 и 𝐵 можно найти по формулам преобразования Лоренца:
Δ
𝑡'
=-
Δ
𝑥 sh θ
𝑟
+
Δ
𝑡 ch θ
𝑟
,
Δ
𝑡'
=-
𝐿 sh θ
𝑟
=-
𝐿β𝑟
√1-β𝑟²
.
Знак «минус» показывает, что наблюдатель 𝐵, находящийся на положительной части оси 𝑥', отправил свой сигнал раньше по «ракетному» времени (более отрицательное время!), чем наблюдатель 𝐴.
24. Загадка Эйнштейна
Когда Эйнштейн был ребёнком, он ломал голову над такой загадкой: пусть бегун смотрит на себя в зеркало, которое он держит перед собой в вытянутой руке; если он бежит почти со скоростью света, сможет ли он увидеть себя в зеркале? Разберите этот вопрос в рамках теории относительности. ▼
25*. Парадокс шеста и сарая
Взволнованный студент пишет: «Теория относительности — наверняка недоразумение. Возьмём шест длиной 20 м и будем двигать его в направлении его длины с такой скоростью, чтобы в лабораторной системе отсчёта он оказался длиной всего 10 м. Тогда в некоторый момент этот шест можно целиком спрятать в сарае, длина которого также 10 м (рис. 40). Но рассмотрите то же самое в системе отсчёта бегуна с шестом. Для него наполовину сократившимся в длину оказывается сарай. Как же можно спрятать 20-метровый шест в 5-метровом сарае?! Разве этот невероятный вывод не доказывает, что в основе теории относительности где-то есть противоречие?»

Рис. 40. Бегун быстро мчится с «20-метровым шестом», помещающимся в «10-метровом сарае». В следующее мгновенье он выскочит в заднюю дверь, сделанную из бумаги.
Напишите ответ взволнованному студенту, ясно и подробно объяснив в нем, как шест и сарай должны без противоречий рассматриваться в теории относительности. (Развенчайте парадокс, начертив две. диаграммы пространства-времени, соблюдая масштабы, одну на «плоскости» 𝑥𝑡, а другую — на «плоскости» 𝑥'𝑡'. Примите, что в начале координат обеих диаграмм «событие» 𝑄 совпадает с 𝐴. На обеих диаграммах проведите мировые линии точек 𝐴, 𝐵, 𝑃 и 𝑄. Следите за соблюдением масштабов! На обеих диаграммах пометьте время (в метрах) совпадения 𝑄 и 𝐵, 𝑃 и 𝐵. Для определения этого времени воспользуйтесь формулами преобразования Лоренца или иными методами). ▼
26*. Война в космосе

Рис. 41. Два ракетных корабля пролетают мимо друг друга с огромными скоростями.
Две ракеты, обладающие равными длинами покоя, проходят мимо друг друга с релятивистским скоростями на встречных курсах. Наблюдатель 𝑂 располагает в хвостовой части своей ракеты орудием, ствол которого направлен поперёк относительного движения ракет. В тот момент, когда точка 𝑎 и 𝑎' поравнялись друг с другом, она стреляет из своего орудия (рис. 42). В системе отсчёта 𝑂 лоренцеву сокращению подвергается пролетающая мимо ракета, так что наблюдатель 𝑂 ожидает, что его снаряд не попадает в неё. Но в системе отсчёта другого наблюдателя 𝑂' лоренцевски сокращённой представляется ракета 𝑂. Поэтому в тот момент, когда точки 𝑎 и 𝑎' поравнялись друг с другом, наблюдатель 𝑂' отмечает картину (рис. 43). Попадает ли на самом деле снаряд в ракету или пролетит мимо? Дайте подробный ответ, укажите некорректности в постановке задачи и ошибку в одной из диаграмм.

Рис. 42. Наблюдатель в системе 𝑂 ожидает, что снаряд, выпущенный, когда точки 𝑎 и 𝑎' совпадали, не попадёт в другой корабль.

Рис. 43. Наблюдатель в системе 𝑂' ожидает, что снаряд, выпущенный, когда точки 𝑎 и 𝑎' совпадали, попадёт в другой корабль. ▼
27*. Парадокс часов 1)
1) Ряд статей, в которых разбирается парадокс часов, вместе с упоминаниями о многих других публикациях см. в сборнике Special Relativity Theory, Selected Reprints, published for the American Association of Physics Teachers by the American Institute of Physics, 335 East 45th Street, New York 17, New York, 1963. [Парадокс часов часто называют «парадоксом близнецов».— Прим. перев.]
(Первый вариант: см. также упражнения 49, 51 и 81).
Близнецы Пётр и Павел расстались в тот день, когда им исполнилось по 21 году. Пётр отправился в направлении оси 𝑥 на 7 лет своего времени (2,2⋅10⁸ сек, или 6,6⋅10¹⁶ м времени) со скоростью 24/25 = 0,96 скорости света, после чего сменил скорость на обратную и за 7 лет вернулся назад, тогда как Павел оставался на Земле, а) В каком возрасте вернулся Пётр? б) Начертите диаграмму пространства-времени, изображающую движение Петра. Укажите на ней 𝑥- и 𝑡-координаты точек поворота и встречи. Для простоты прибегните к идеализации, приняв Землю за инерциальную систему отсчёта, к которой и приурочьте вашу диаграмму, выбрав за начало координат событие отлёта Петра, в) Сколько лет было Павлу в момент встречи? ▼
28*. Предметы, движущиеся быстрее света 2)
2) См. Milton A. Rothman, Things that go Faster than Light, Scientific American, 203, 142 (July, 1960).
Формулы преобразования Лоренца теряют смысл, если принять величину относительной скорости движения двух систем отсчёта больше скорости света. Считается, что вследствие этого масса, энергия и информация (сообщения) не могут передаваться от точки к точке быстрее света. Проверьте этот вывод на следующих примерах.

Рис. 44. Может ли точка пересечения 𝐴 двигаться со скоростью, превышающей скорость света?
а) Парадокс ножниц. Очень длинный прямой стержень, наклонённый под углом φ к оси 𝑥, движется вниз с постоянной скоростью (рис. 44). Найдите скорость β𝐴, с которой движется точка пересечения 𝐴 нижней грани стержня и оси 𝑥. Может ли эта скорость превзойти скорость света? Можно ли использовать движение точки 𝐴 для передачи сообщения из начала координат наблюдателю, расположенному далеко на оси 𝑥?
б) Предположим, что тот же стержень первоначально покоился, а точка пересечения 𝐴 совпадала с началом координат. Затем та область стержня, которая находилась в начале координат, подвергалась удару молотом, пославшему её вниз. Точка пересечения двинулась вправо. Можно ли было использовать такое движение точки пересечения для передачи сообщения со скоростью, превышающей скорость света?
в) Будем быстро вращать мощный прожектор таким образом, чтобы его луч двигался в одной плоскости. Пусть в этой же плоскости на равных расстояниях от прожектора, но вдали друг от друга находятся два наблюдателя — 𝐴 и 𝐵. Как далеко они должны расположиться от прожектора, чтобы его луч пробегал от 𝐴 до 𝐵 быстрее, чем мог бы пройти световой сигнал от 𝐴 до 𝐵? Перед тем как занять свои места, наблюдатели получили следующие инструкции:
Инструкция для 𝐴: Увидев луч прожектора, немедленно выстрелить в 𝐵.
Инструкция для 𝐵: Увидев луч прожектора, немедленно пригнуться, чтобы избежать пули, посланной 𝐴.
Не передаётся ли при таких обстоятельствах предупреждение от 𝐴 к 𝐵 со скоростью, большей скорости света?
г) В некоторых руководствах к осциллографам пишется, что скорость луча на экране превышает скорость света. Возможно ли это? ▼
Г. ОСНОВАНИЯ ТЕОРИИ
29. Синхронизация движущимися часами — подробный пример
Мистер Энгельсберг не признаёт нашего метода синхронизации часов световыми сигналами (разд. 4). Он заявляет: «Я могу синхронизировать свои часы тем способом, какой мне понравится». Прав ли он? Мистер Энгельсберг хочет синхронизировать пару тождественных часов (назовём их Биг Бен и Литтл Бен), расположенных в миллионе миль друг от друга (чуть больше, чем в 1,5⋅10⁹ м), относительная скорость которых равна нулю. Он берёт для этого третьи часы той же конструкции, что двое первых, и заставляет их двигаться с постоянной скоростью между ними. При прохождении мимо Биг Бена эти часы устанавливаются на то время, которое он показывает в этот момент. Когда движущиеся часы проходят мимо Литтл Бена, этот последний ставится по времени, которое показывают движущиеся часы. «Вот теперь Биг Бен и Литтл Бен синхронизированы»,— объявляет мистер Энгельсберг. Прав ли он? Насколько именно рассинхронизированы при этом Биг Бен и Литтл Бен, если это проверить по решётке часов, покоящейся относительно их и синхронизированной обычным методом световых сигналов? Подсчитайте величину рассинхронизированности, если мистер Энгельсберг пользуется третьими часами, движущимися со скоростью сто тысяч миль в час (4,5⋅10⁴ м/сек). Есть ли какая-нибудь причина (не считая субъективного предпочтения), почему никто из нас не пользуется методом синхронизации, предлагаемым мистером Энгельсбергом?
Решение. Проведём сначала количественный расчёт. Для наблюдения за движущимися (третьими) часами можно воспользоваться решёткой часов, покоящейся относительно Биг Бена и Литтл Бена, которую мы синхронизировали стандартным методом световых сигналов. Относительно этой решётки третьи часы движутся со скоростью 𝑣=4,5⋅10⁴ м/сек, т.е.
β
=
𝑣
𝑐
=
4,5⋅10⁴ м/сек
3⋅10⁸ м/сек
=
1,5⋅10⁴
м
Длины за 1 м светового времени.
При такой скорости третьи часы покрывают расстояние между Биг Беном и Литтл Беном за срок Δ𝑡=10¹³ м светового времени. Сравнивая показания стрелок движущихся часов и часов решётки, мимо которых они поочерёдно проходят, мы сталкиваемся с эффектом замедления времени (упражнение 10. По отношению к часам решётки движущиеся часы будут идти медленнее в (√1-β²)⁻¹ раз. Поэтому эти движущиеся (третьи) часы зарегистрируют в качестве срока путешествия от Биг Бена до Литтл Бена время
Δ
𝑡'
=
Δ
𝑡
√
1-β²
=
Δ
𝑡
⋅
(1-2,25⋅10⁻⁸)¹
/
².
Воспользуемся разложением для бинома
(1-δ)¹
/
²
=
1
-
δ
2
-
δ²
8
-…
≈
1
-
δ
2
,
(так как величина δ мала) и получим приближённый ответ
Δ
𝑡'
=
Δ
𝑡
-
1
2
⋅2,25⋅10⁻⁸
Δ
𝑡
,
или
Δ
𝑡'
-
Δ
𝑡
=-
1,12⋅10⁻⁸
⋅
10¹³
=-
1,12⋅10⁵
м
=
=-
0,4⋅10⁻³
сек
.
(51)
Поставим стрелки Литтл Бена по движущимся часам, а затем сверим их с соседними часами решётки. Литтл Бен будет отставать от часов решётки на 0,4 миллисекунд (мсек).
Промежуток времени для движущихся часов, равный Δ𝑡' на пути между Биг Беном и Литтл Беном, можно определить и более непосредственным путём. Часы движутся по прямой. Интервал прошедшего времени, зарегистрированный ими на соответствующей мировой линии, равен поэтому собственной длине этой мировой линии между данными двумя событиями, т.е. он равен интервалу между прохождениями мимо Биг Бена и Литтл Бена:
Δ𝑡'=Δ(собственное время)=(Интервал)=
=√(Δ𝑡)²-(Δ𝑥)².
Вычисленная отсюда величина расхождения показаний лабораторных и движущихся часов в полном соответствии с результатом (51) равна
Δ
𝑡'
-
Δ
𝑡
=
√
(
Δ
𝑡)²-(
Δ
𝑥)²
-
Δ
𝑡
.
Обратимся теперь к вопросу о пригодности метода движущихся часов для процедуры синхронизации. Мистер Энгельсберг волен определять синхронизацию как ему будет угодно. Однако, используя метод движущихся часов для синхронизации Биг Бена и Литтл Бена, он натолкнётся на следующие трудности: 1) Время, которое будет поставлено на лабораторных часах при такой синхронизации, окажется зависящим от скорости движущихся часов. Возьмём, например, часы, летящие в десять раз быстрее, чем в разобранном выше случае. Тогда расхождение между Литтл Беном и соседними с ним часами решётки составит уже не 0,4, а 40 мсек. Два Литтл Бена, стоящие рядом друг с другом, будут показывать разное время, если их синхронизировать с Биг Беном с помощью разных часов (движущихся с различными скоростями)! 2) Даже если условиться всегда использовать движущиеся часы, летящие с некоторой данной скоростью, результат синхронизации при таком методе будет зависеть от пути движущихся часов. Чем длиннее будет путь, пройденный движущимися часами с постоянной скоростью, тем больше будут отставать часы Литтл Бен по сравнению с соседними часами решётки. 3) Если движущиеся часы вернутся к Биг Бену, совершив путешествие по замкнутому маршруту, они окажутся рассинхронизированными с Биг Беном по возвращении! (См. парадокс часов; упражнение 27). Метод синхронизации мистера Энгельсберга приводит и к другим неприятностям, но уже приведённых вполне достаточно, чтобы показать его непригодность для составления простого описания явлений, протекающих в пространстве-времени.
30. Конструкция часов и замедление их хода
При описании явления замедления времени (хода часов) в упражнении 10 мы не делали различия между пружинными часами, часами на кварцевом кристалле, биологическими часами (старение), атомными часами, радиоактивными часами или часами, в которых периодический процесс состоит в последовательном отражении светового импульса между двумя параллельными зеркалами. Предположим, что все эти часы отрегулированы таким образом, что идут совершенно одинаково, покоясь в системе отсчёта ракеты. Покажите, что явления замедления хода этих часов (упражнение 10) протекают совершенно одинаково, вне зависимости от их внутреннего механизма, когда они пролетают мимо стандартных часов, покоящихся в лабораторной системе отсчёта. (Обсуждение. Как получилось, что мы до сих пор ни разу не обратили внимания на конструкцию часов? Нужно ли в действительности вводить в рассмотрение какой-либо конкретный механизм часов, если рассматриваются световые сигналы, путешествующие взад и вперёд между часами в целях синхронизации? Требуется ли вообще что-либо ещё, кроме начальной световой вспышки (например, от электрической искры) и полупрозрачных посеребрённых зеркал, установленных в точках наблюдения (рис. 45), для того чтобы получить стандартные отрезки времени?)

Рис. 45. Измерение времени без помощи часов. Пунктирной прямой обозначена мировая линия полупрозрачного зеркала. ▼
31. Инерциальные системы отсчёта, связанные с Землёй
Система отсчёта будет инерциальной в некоторой области пространства и времени, если первоначально покоившаяся пробная частица будет сохранять своё состояние покоя с некоторой данной степенью точности во всей этой области пространства-времени. Как было показано, свободно падающий вблизи Земли космический корабль эффективно является инерциальной системой отсчёта на протяжении периода времени в несколько секунд. Многие опыты, касающиеся быстро движущихся частиц и собственно света, проводятся в лабораториях, жёстко связанных с Землёй, а не находящихся в состоянии свободного падения! В таких связанных с Землёй лабораториях действует сила тяжести. Но тем не менее для проведения некоторых опытов требуется так мало времени, что пробная частица, высвобождаемая в начале опыта, не успевает до его конца пройти в своём падении сколько-нибудь значительный путь. Поэтому для многих экспериментальных целей жёстко связанная с Землёй лаборатория с достаточной степенью точности может быть принята за инерциальную систему отсчёта.
а) Пусть элементарная частица, движущаяся со скоростью, равной 0,96 скорости света, проходит через кубическую искровую камеру, сторона которой равна 1 м. Какое расстояние прошла бы в своём падении под действием гравитационного поля Земли за это время отдельная пробная частица, первоначально находившаяся в покое? Сравните полученную длину с поперечником атомного ядра (несколько превышающего 10⁻¹⁵ м). Подытожьте результат, указав размеры пространственно-временной области, в которой жёстко связанную с Землёй лабораторию можно идеализированно считать инерциальной, и приведя взятую степень точности. Какими размерами должна обладать искровая камера, чтобы, пока элементарная частица со скоростью 0,96 скорости света пересекает её, отдельная пробная частица могла пройти в своём падении из состояния покоя заметное расстояние?
б) В опыте Майкельсона — Морли (упражнение 33) луч света претерпевает отражения между парами зеркал, удалённых друг от друга на 2 м, так что луч проходит в целом путь, равный 22 м. Какое расстояние пройдёт в своём падении из состояния покоя в гравитационном поле Земли пробная частица за то время, пока данный фотон проходит через установку Майкельсона — Морли? С какой степенью точности является инерциальной жёстко связанная с Землёй система отсчёта в той области пространства-времени, где проводится опыт Майкельсона — Морли? ▼
32.* Размеры инерциальной системы
Насколько велика может быть данная область пространства (Δ𝑥=Δ𝑦=Δ𝑧=𝐿 в метрах), насколько долго её можно исследовать (Δ𝑡 в метрах!) и насколько близко она может быть расположена к центру гравитационного притяжения, чтобы ещё нельзя было заметить существенного отличия е этой области от идеальной инерциальной системы отсчёта?
а) Отличие первого рода: относительное ускорение перпендикулярно направлению притяжения.

Рис. 46. Освобождённые на одинаковой высоте (лежащие на одной горизонтали) грузы приближаются друг к другу в процессе падения. (Масштабы не выдержаны).
1) Частный случай. Два массивных шарика высвобождаются в состоянии покоя; оба находятся на высоте 250 м над поверхностью Земли; расстояние между ними -25 м (рис. 46). Покажите, что расстояние между ними уменьшится примерно на 10⁻³ м, прежде чем они упадут на Землю. (Воспользуйтесь методом подобных треугольников или каким-нибудь близким методом. Этот пример обсуждался нами на стр. 19). Время падения с высоты 250 м с ускорением 9,8 м/сек² равно приблизительно 7 сек, или 21⋅10⁸ м светового времени. Итак, падающий железнодорожный вагон может рассматриваться как инерциальная система отсчёта при условиях, что:
Условия
,
соответствующие тому
,
что отличие от идеальной инерциальной системы отсчёта ненаблюдаемо
ε
(
наименьшее отличие
,
доступное обнаружению при помощи данных приборов)
ε≥1⋅10⁻³
м
𝑟
(
расстояние от центра Земли
)
Δ
𝑥
(
расстояние по горизонтали
)
Δ
𝑦
и
Δ
𝑧
(
протяжённость области в двух других направлениях
)
Δ
𝑡
(
время наблюдения
)
𝑟≥𝑟₀=6,4⋅10⁶
м
Δ
𝑥=𝐿≤25
м
При обсуждении взяты равными нулю; мы их приравняем нулю и здесь, так как в дальнейшем они не рассматриваются [часть (в)]
Δ
𝑡≤21⋅10⁸
м
(7
сек
)
2) Более общий случай. Пробная частица 𝐵 отстоит на расстоянии Δ𝑥 от пробной частицы 𝐴. Обе они находятся на одинаковом расстоянии 𝑟 от центра притяжения и рассматриваются в течение времени Δ𝑡. Обозначим через 𝑎 общую величину ускорения этих частиц под действием притягивающего центра (в м/сек²), а через 𝑎*=𝑎/𝑐² — величину того же ускорения, измеренную в метрах расстояния за квадратный метр времени. Показать, что ускорение частицы 𝐵 относительно 𝐴, (Δ𝑎𝑥)* (в метрах расстояния на квадратный метр времени), даётся формулой
(
Δ
𝑎
𝑥
)*
=-
Δ𝑥
𝑟
𝑎*
.
(52)
(Считать входящие в рассмотрение углы настолько малыми, что их синусы и тангенсы можно приравнять друг другу).
б) Отличие второго рода: относительное ускорение параллельно направлению притяжения.
1) Общий случай. Пробная частица 𝐵 отстоит на расстоянии Δ𝑧 от пробной частицы 𝐴, и на одной прямой с ними на расстоянии 𝑟 находится притягивающий центр. Таким образом, частица 𝐵 находится дальше от центра, чем 𝐴, и на неё действует меньшая сила. Поэтому 𝐵 отстаёт в своём падении от 𝐴, а наблюдатель, расположенный на 𝐴, найдёт, что на 𝐵 действует ускорение в положительном направлении оси 𝑧. Показать, что это относительное ускорение (выраженное в метрах расстояния за квадратный метр времени) равно
(
Δ
𝑎
𝑧
)*
=
+2
Δ𝑧
𝑟
𝑎*
.
(53)
(Совет: воспользуйтесь тем фактом, что величина 𝑎* убывает обратно пропорционально квадрату расстояния по закону всемирного тяготения Ньютона: 𝑎*=const/𝑟². Возьмите разность сил на расстояниях 𝑟 и 𝑟+Δ𝑧 Воспользуйтесь чрезвычайной малостью Δ𝑧 (каких-нибудь несколько метров) до сравнению с 𝑟 (тысячи километров) и упростите результат).

Рис. 47. Освобождённые на одной вертикали, но на разных высотах грузы удаляются друг от друга в процессе падения. (Масштабы не выдержаны).
2) Частный случай (см. стр. 17). Пусть одна пробная частица находится на высоте 250 м над поверхностью Земли, а другая — на высоте 275 м. Насколько увеличится разность высот (25 м) этих частиц за те (приблизительно) 7 сек, пока они не упадут на Землю? [Наводящий вопрос: во сколько раз различаются численные значения для Δ𝑎𝑧 в (б1) и для Δ𝑎𝑥 в (а2)?] Дополните (или, если угодно, пересмотрите) на основании этого результата таблицу на стр. 99.
в) Случай, когда исследуемая область далека от центра Земли.
Агентство космических исследований расширяет опыты над пробными частицами и космическими лучами. Исследовательская группа приходит к заключению, что использовавшаяся в прежних исследованиях область недостаточно обширна для проведения новых программ, а время 7 сек недостаточно велико. Руководство утверждает их заявку на размеры области Δ𝑥=200 м, Δ𝑦=200 м, Δ𝑧=100 м и время 100 сек с тем же допуском, что и раньше (ε=1⋅10⁻³ м =1 мм). На расстояние скольких земных радиусов от центра Земли нужно забросить с помощью ракет оборудование, чтобы отклонение системы отсчёта от идеально инерциальной было менее приемлемого нижнего предела? (Некоторые возможные попутные вопросы: как изменяется в зависимости от расстояния 𝑟 от центра Земли величина 𝑎*? Как зависят от 𝑟 величины (Δ𝑎𝑥)* и (Δ𝑎𝑧)*? Как зависят Δ𝑥 и Δ𝑧 от (Δ𝑎𝑥)*, (Δ𝑎𝑧)* и от времени Δ𝑡?) ▼
33*. Опыт Майкельсона — Морли 1)
1 A.A. Michelson, E.W. Morley, American Journal Of Science, 34, 333 (1887). Логическое место этого опыта в теории относительности разобрано в статье: Н. P. Robertson, Reviews of Modern Physics, 21, 378 (1949). (См. историю опыта Майкельсона— Морли в книге: Б. Джефф, Майкельсон и скорость света, ИЛ, М., 1963.— Прим. перев.)
а) Пусть самолёт движется относительно воздуха со скоростью 𝑐 (не скорость света!) из пункта 𝐴 в пункт 𝐵. В направлении от 𝐵 к 𝐴 дует со скоростью 𝑣 сильный ветер. Показать, что время полёта по замкнутому маршруту от 𝐴 до 𝐵 и обратно до 𝐴 превышает в этом случае время такого же полёта по замкнутому маршруту в условиях безветрия в 1/[1-(𝑣²/𝑐²)] раз. Парадокс: Казалось бы, ветер должен был бы ускорять полёт в одну сторону и замедлять — в другую в равной мере. Почему же тогда время полёта по замкнутому маршруту различно в зависимости от того, дует ветер или нет? Дайте этому простое физическое объяснение. Что произойдёт в том случае, когда скорость ветра близка к скорости самолёта?
б) Пусть теперь тот же самолёт летит по замкнутому маршруту между 𝐴 и 𝐶. Расстояние между этими пунктами то же, что между 𝐴 и 𝐵, но направление 𝐴𝐶 перпендикулярно направлению 𝐴𝐵, так что при полёте между 𝐴 и 𝐶 самолёт движется поперёк ветра. Показать, что время полёта по замкнутому маршруту между 𝐴 и 𝐶 превышает в этом случае время такого же полёта по замкнутому маршруту в условиях безветрия в 1/[1-(𝑣²/𝑐²)] раз.
в) Пусть из пункта 𝐴 одновременно с одинаковой скоростью относительно воздуха вылетают два самолёта. Один летит из 𝐴 в 𝐵 и назад в 𝐴 сначала против ветра, а затем по ветру (скорость ветра равна 𝑣). Другой самолёт летит из 𝐴 в 𝐶 и назад в 𝐴 всё время поперёк ветра. Какой из них вернётся первым в 𝐴 и чему будет равен промежуток времени между моментами их возвращения? Покажите с помощью формулы разложения бинома, что при 𝑣≪𝑐 этот промежуток времени можно приближённо выразить как
Δ
𝑡
=
𝐿
2𝑐
𝑣²
𝑐²
где 𝐿 — длина пути по замкнутому маршруту между 𝐴 и 𝐵 (и между 𝐴 и 𝐶).
г) Пусть на Южном полюсе находится Центр снабжения исследовательских станций, расположенных на окружности радиуса 300 км с центром в полюсе. Каждый понедельник множество грузовых самолётов одновременно вылетает из Центра и летит по радиусам во всех направлениях на одной и той же высоте. Каждый самолёт сбрасывает над своей станцией грузы и сразу же направляется обратно на базу. На холме, с которого удобно обозревать Центр снабжения, стоит распорядитель с секундомером в руках. Он обнаруживает, что не все самолёты возвращаются на базу одновременно. Его ставит в тупик такой разнобой, ибо по точным промерам он знает, что: 1) расстояния от базы до всех станций одинаковы, 2) каждый самолёт его эскадрильи летит относительно воздуха с одной и той же скоростью, а именно 300 км/час, и 3) путь каждого самолёта относительно поверхности Земли представляет собой прямую, соединяющую Центр со станцией (как туда, так и обратно). В конце концов наш распорядитель решает, что разброс во времени возвращения самолётов связан с ветром, дующим на той высоте, где летят самолёты. По своему секундомеру он обнаруживает, что интервал времени между моментами возвращения первого и последнего самолётов равен 4 сек. Чему равна тогда скорость, с которой дует ветер на той высоте, где летят самолёты? И что может сказать распорядитель о направлении этого ветра?
д) В своём знаменитом опыте Майкельсон и Морли пытались обнаружить так называемый эфирный ветер — эффект движения Земли относительно эфира, причём в этом последнем свет, как считалось, распространяется со скоростью 𝑐. Они произвели сравнение интервалов времени, за которые свет проходит замкнутые пути («туда и обратно») параллельно направлению движения Земли вокруг Солнца и перпендикулярно этому направлению. В их опыте свет многократно отражался между почти параллельными зеркалами [что соответствовало многократным полётам самолётов взад и вперёд в примере (в)]. Таким способом удалось добиться, чтобы полная длина замкнутого пути распространения света составила 22 м. Если эфир неподвижен относительно Солнца, а Земля движется по своей орбите со скоростью 30⋅10³ м/сек, то чему будет приблизительно равна разница во времени возвращения световых импульсов, испущенных одновременно, но распространявшихся по двум взаимно перпендикулярным путям? Эта разница оказывается недоступной прямому измерению ввиду своей малости даже для современных приборов, и поэтому предсказания гипотезы эфирного ветра проверялись с помощью следующего косвенного метода.

Рис. 48. Схема интерферометра Майкельсона — Морли, установленного на вращающейся мраморной плите.
е) Конструкция собственно интерферометра Майкельсона — Морли схематически представлена на рис. 48. Почти монохроматический свет (содержащий лишь одну частоту) входит в прибор через линзу 𝑎. Часть его отражается полупрозрачным посеребрённым зеркалом 𝑏, а часть продолжает распространяться до зеркала 𝑑. Оба получившихся луча многократно отражаются взад и вперёд, пока они не доходят соответственно до зеркал 𝑒 и 𝑒₁, которые направляют их назад, и оба луча в конце концов снова попадают на зеркало 𝑏. На этом последнем зеркале часть каждого луча вместе с частью другого, объединяясь, направляется в телескоп 𝑓. Прозрачная стеклянная пластина 𝑐, размеры которой совпадают с размерами полупрозрачного зеркала 𝑏, включена для того, чтобы каждый луч прошёл одно и то же число раз (а именно три) сквозь данную толщу стекла на своём пути к телескопу 𝑓.
Предположим, что длины взаимно перпендикулярных путей в точности одинаковы, а вся установка покоится относительно эфира. Тогда монохроматический свет, разделённый зеркалом 𝑏 на два луча, при некоторой разности фаз между ними вернётся к зеркалу 𝑏 с той же самой разностью фаз. В этом случае световые волны, входящие в телескоп 𝑓, будут складываться, и поле зрения мы увидим ярко освещённым. Если бы, напротив, один из лучей отстал во времени на величину, соответствующую половине периода колебаний этого света, то он пришёл бы вновь к зеркалу 𝑏 на эти полпериода позже другого луча; волны, входящие в телескоп, вычитались бы друг из друга, и поле зрения оказалось бы тёмным. Если бы относительное запаздывание луча составило целый период, то поле зрения в телескопе снова было бы ярко освещено, и так далее. Чему равен промежуток времени, соответствующий одному периоду колебаний световой волны? Майкельсон и Морли пользовались спектральной линией натрия с длиной волны 5890 ангстрем (Å) (Å=10⁻¹⁰ м). Ввиду равенств νλ=𝑐 и ν=1/𝑇 видно, что период для этой спектральной линии натрия равен примерно 2⋅10⁻¹⁵ сек.
Но ведь невозможно «выключить» предполагаемый эфирный ветер, отъюстировать установку и после этого вновь «включить» этот эфирный ветер. Вместо этого Майкельсон и Морли пустили свой интерферометр плавать в бассейне, наполненном ртутью, и медленно вращали его вокруг центра, как грампластинку, непрерывно наблюдая яркость поля зрения телескопа (рис. 48). В этом случае, если свет на каком-то пути тратит больше времени при некоторой данной ориентации установки, то при её повороте на 90° такой же задержке во времени подвергнется свет, идущий по другому пути. Значит, полное изменение запаздывания света, когда он распространяется по двум разным путям, должно быть при повороте интерферометра вдвое больше того, что мы вычислили бы с помощью формулы в примере (в).
Усовершенствовав свой метод, Майкельсон и Морли сумели доказать, что изменение времени распространения света по двум путям при повороте установки соответствовало менее чем ¹/₁₀₀ сдвига от одного потемнения поля зрения телескопа до следующего потемнения. Покажите, что этот вывод свидетельствует о том, что движение эфира у поверхности Земли (если оно вообще имеет место) происходит со скоростью менее ¹/₆ скорости движения Земли по её орбите. Для того чтобы исключить возможность такого совпадения, что в этот момент эфир «дул» относительно Солнца с той же скоростью, с какой движется по своей орбите Земля, они повторяли свой опыт каждые три месяца — и каждый раз с отрицательным результатом.
ж) Опровергает ли сам по себе опыт Майкельсона — Морли теорию распространения света в эфире? Можно ли так видоизменить эту теорию, чтобы она пришла в согласие с результатами этого опыта? Как это сделать? Какой новый опыт можно было бы привлечь для проверки такой модифицированной теории? ▼
34*. Эксперимент Кеннеди — Торндайка 1)
1) Сообщение об оригинальной постановке эксперимента можно найти в статье R. J. Кеnnedy, Е.М. Thorndike, Physical Review, 42, 400 (1932). Место эксперимента в логической структуре теории относительности проанализировано в работе Н. P. Rоbеrtsоn, Reviews of Modern Physics, 21, 378 (1949).
Целью постановки опыта Майкельсона — Морли было обнаружение любого возможного движения Земли относительно гипотетической жидкости, эфира,— той среды, в которой свет, как предполагалось, распространяется со специфической для него скоростью 𝑐. Но такого относительного движения Земли и эфира обнаружить не удалось. Результаты этого опыта отчасти сыграли впоследствии свою роль в ниспровержении понятия эфира. Согласно современным взглядам, для распространения света вообще не требуется никакой среды.
Какое значение имеет отрицательный результат опыта Майкельсона — Морли для нас, людей, не признающих теории эфира как среды, в которой распространяется свет? Просто-напросто: 1) Скорость света по замкнутому пути, измеренная на Земле, одинакова во всех направлениях, т.е. скорость света изотропна. 2) Скорость света изотропна не только тогда, когда Земля при движении вокруг Солнца летит в одном каком-то направлении, например, в январе (назовём этот случай движения «лабораторной системой отсчёта»), но и когда Земля движется в противоположном направлении в июле (уйдя вокруг Солнца в противоположную часть своей орбиты; назовём Землю в этот период её движения «системой отсчёта ракеты»). 3) Обобщение этого вывода на любые пары инерциальных систем, находящихся в движении относительно друг друга, приводит к утверждению, что скорость света на замкнутом пути изотропна как в лабораторной системе отсчёта, так и в системе ракеты.
Полученный вывод оставляет без ответа один важный вопрос, а именно: обладает ли скорость света, распространяющегося по замкнутому пути, которая изотропна как в лабораторной системе, так и в системе отсчёта ракеты, ещё и одинаковым численным значением в обеих этих системах отсчёта? Предположение о том, что эта скорость численно одна и та же во всех инерциальных системах отсчёта, является центральным фактом при доказательстве инвариантности интервала (разд. 5). Но верно ли это предположение?
а) Эксперимент для проверки предположения о равенстве скорости света, распространяющегося по замкнутому пути, в двух движущихся относительно друг друга инерциальных системах отсчёта был предпринят в 1932 г. Роем Дж. Кеннеди и Эдуардом М. Торндайком. В этом эксперименте был применён интерферометр, плечи которого были не равны друг другу (рис. 49). Допустим, что разность длин плеч этого интерферометра равна Δ𝑙 Покажите, что световой импульс, поступающий в установку, затрачивает для обхода замкнутого пути по длинному плечу на 2Δ𝑙/𝑐 больше времени, чем для обхода замкнутого пути по короткому плечу. Использованная Кеннеди и Торндайком разность длин Δ𝑙 равнялась приблизительно 16 см. Чему равна приблизительно разность во времени, за которое свет завершает обход двух неодинаковых замкнутых путей в этом интерферометре?

Рис. 49. Схематическое изображение установки, использованной в эксперименте Кеннеди — Торндайка.
Детали этого интерферометра помечены теми же буквами, что и соответствующие детали интерферометра Майкельсона — Морли в упражнении 33. Экспериментаторы остановились на больших размерах плеч прибора с тем, чтобы обеспечить его оптическую и механическую стабильность. Интерферометр смонтирован на плите из кварца, который почти не изменяет своих размеров при колебаниях температуры. Кроме того, он помещён в вакуумную камеру, так что колебания атмосферного давления не отражаются на длине оптического пути в плечах интерферометра (разным значениям давления воздуха соответствует несколько различная величина скорости света!). Вакуумная камера окружена камерой, наполненной водой, температура которой поддерживалась постоянной с точностью до ±0,001°C. Вся эта установка была помещена в небольшой тёмной комнате (не изображённой на рисунке), где температура поддерживалась постоянной с точностью до нескольких сотых градуса. Эта тёмная комната в свою очередь была окружена большей тёмной комнатой, где температура поддерживалась постоянной с точностью до нескольких десятых градуса. Размеры всей установки в целом можно охарактеризовать тем, что разность длин двух плеч интерферометра (то есть отрезков 𝑏𝑒 и 𝑏𝑒₁ равна 16 см.
б) Кеннеди и Торндайк в действительности использовали не импульс света, а непрерывный монохроматический свет, колебания волн которого обладали периодом 𝑇=1,820⋅10⁻¹⁵ сек (λ=5461 Å), излучавшийся атомами ртути. Определите, сколькими периодами позже «приходил к финишу» свет по длинному плечу интерферометра, чем по короткому плечу? (Разность периодов обозначим через 𝑛). Если это число периодов оказывалось целым, то суперпозиция лучей, приходящих по обоим плечам, приводила к сложению волн, и экспериментаторы видели ярко освещённое поле зрения телескопа. Наоборот, если это число периодов оказывалось полуцелым, то волны, приходящие по обоим плечам, взаимно вычитались, гасились, и экспериментаторы видели тёмное поле зрения телескопа.
в) Но Земля всё время движется по своей орбите вокруг Солнца. Каждые шесть месяцев её скорость движения относительно неподвижных звёзд изменяет свой знак. Будет ли и в такой новой системе отсчёта скорость распространения света по замкнутому пути иметь ту же самую численную величину 𝑐, что и в исходной системе отсчёта? Ответ на вопрос (б), касающийся этой исходной системы отсчёта, можно переписать в виде
𝑐
=
2
𝑛
Δ𝑙
𝑇
.
(54)
Здесь Δ𝑙 — разность длин плеч интерферометра, 𝑇 — величина периода волн, испускаемых светящимися атомами, а 𝑛 — число периодов, на которое различаются моменты возвращения света по длинному и короткому путям. Предположим теперь, что в ходе обращения Земли вокруг Солнца в поле зрения нашего телескопа не обнаруживается изменения яркости (например, перехода от света к темноте). Это значит, что наблюдаемая величина 𝑛 неизменна. Что можно было бы заключить из этого гипотетического результата о численном значении 𝑐 скорости света? Укажите, какие стандарты длины и времени были привлечены для вывода этого результата (54). Наибольшей стабильностью в сохранении своих размеров из всех известных материалов обладает кварц. Самый надёжный механизм для измерения времени, который мы можем построить на Земле,— это атомные стандарты времени.
г) Для того чтобы осуществить эксперимент, описанный в предыдущих пунктах, Кеннеди и Торндайк должны были обеспечить безупречную работу своего интерферометра в течение полугода непрерывных наблюдений яркости поля зрения телескопа. Но столь длительные непрерывные наблюдения были невозможны, так что на самом деле продолжительность их наблюдений колебалась от восьми дней до одного месяца. С интервалами в три месяца имело место по нескольку таких периодов наблюдения. Данные, полученные по этим наблюдениям, дали возможность Кеннеди и Торндайку установить, что за срок непрерывных наблюдений в течение 6 месяцев число периодов 𝑛 относительного отставания одного луча от другого смогло бы составить лишь менее чем 3/1000 одного периода. Возьмите дифференциал выражения (54) для того, чтобы определить наибольшее относительное изменение скорости света по замкнутому пути в двух разных системах отсчёта, которое могло бы согласоваться с данной оценкой изменения 𝑑𝑐/𝑐 (здесь первая система отсчёта —«лабораторная», и вторая, система отсчёта ракеты,— просто сама наша планета, взятая в два момента, разделённые шестью месяцами времени; относительная скорость движения этих двух систем равна удвоенной скорости движения Земли по её орбите — 2⋅30 км/сек).
Историческая справка. Во времена, когда в 1887 г. был проделан опыт Майкельсона — Морли, никто ещё не был готов к восприятию той идеи, что законы физики (не исключая и самой величины скорости света) одинаковы во всех инерциальных системах отсчёта. С точки зрения стандартного в наши дни эйнштейновского подхода просто очевидно, что и опыт Майкельсона — Морли, и эксперимент Кеннеди — Торндайка должны были привести к негативному результату. Но когда Кеннеди и Торндайк предприняли в 1932 г. свои измерения, кроме теории Эйнштейна продолжали ещё обсуждаться две её альтернативы — назовём их теориями 𝐴 и 𝐵. В этих обеих неэйнштейновских теориях принимались старые представления о некотором абсолютном пространстве, или «эфире», в котором свет распространяется со скоростью 𝑐. И теория 𝐴, и теория 𝐵 объясняли отсутствие сдвига интерференционных полос в опыте Майкельсона — Морли, утверждая, что всё, что движется со скоростью 𝑣 относительно «абсолютного пространства», сокращает свою пространственную длину в направлении движения до величины, равной этой старой длине, помноженной на √1-(𝑣²/𝑐²) («гипотеза сокращения Лоренца — Фитцджеральда»). Разница между этими двумя теориями состояла в подходе к влиянию «движения сквозь абсолютное пространство» на скорость хода часов. Теория 𝐴 отвергала возможность такого эффекта, а согласно теории 𝐵, величина 1 секунды на стандартных часах, движущихся через абсолютное пространство со скоростью 𝑣, должна была становиться равной √1-(𝑣²/𝑐²) секунды. В теории 𝐵 величина отношения Δ𝑙/𝑇 не должна была зависеть от скорости движения часов, и она предсказывала негативный результат эксперимента Кеннеди — Торндайка, что он и дал в действительности («сложное объяснение простого эффекта»). Согласно теории 𝐴, отношение Δ𝑙/𝑇 в выражении (54) должно было умножиться на величину √1-(𝑣₁²/𝑐²) в то время года, когда «скорость Земли относительно абсолютного пространства» равна 𝑣₁ и на величину √1-(𝑣₂²/𝑐²) в то время года, когда эта скорость равна 𝑣₂. Поэтому интерференционные полосы должны были бы сдвигаться между двумя моментами года (соответствующими скоростям 𝑣₁=𝑣орбит+𝑣Солнце и 𝑣₂=𝑣орбит-𝑣Солнце если бы только по чистой случайности Солнце не было «в покое относительно абсолютного пространства»— случайности настолько маловероятной, что её невозможно было бы рассматривать как причину наблюдаемого негативного результата эксперимента. Итак, эксперимент Кеннеди — Торндайка заставил отвергнуть теорию 𝐴 (признававшую лишь сокращение длин), но оставил допустимой теорию 𝐵 (сокращение длин плюс замедление времени), равно как и намного более простую теорию Эйнштейна, утверждающую равноправность всех инерциальных систем отсчёта.
«Степень чувствительности» эксперимента Кеннеди — Торндайка зависит от того, о какой теории идёт речь. С точки зрения теории 𝐴 наблюдения могут обнаружить «скорость Солнца относительно абсолютного пространства», если она не менее 15 км/сек (именно так оценивали чувствительность своего опыта сами Кеннеди и Торндайк в своей статье). С точки зрения же теории Эйнштейна эти наблюдения показали, что скорость распространения света по замкнутому пути имеет одинаковую численную величину (с ошибкой около 2 м/сек) в двух инерциальных системах отсчёта, скорость относительного движения которых составляет 60 км/сек. ▼
35*. Эксперимент Дикке 1)
1) См. R. Н. Diсkе, The Eotvos Experiment, Scientific American, 205, 84 (December 1961), а также P. G. Rоll, R. Кrоtkоv, R. H. Diсke, Annals of Physics, 26, 442 (1964). Первая из этих статей представляет собой популярный обзор, написанный ещё в начале проведения эксперимента. Вторая статья сообщает окончательные результаты эксперимента и тем более интересна, что в ней описаны те тонкие предосторожности, которые потребовалось предпринять для обеспечения исчерпывающего учёта всех привходящих влияний, могущих подействовать на течение опыта.
а) Высота пизанской «Падающей башни» составляет около 55 м. Галилей пишет: «Скорости падения в воздухе шаров из золота, свинца, меди, порфира и прочих тяжёлых веществ различаются настолько мало, что при падении с высоты 100 локтей (около 46 м) шар из золота наверняка не обгонит шара из меди более чем на 4 пальца. Проведя это наблюдение, я пришёл к выводу, что в среде, где исключено всякое сопротивление, все тела падали бы с одинаковой скоростью» 2). Приняв «4 пальца» равными 7 см, найдите наибольшее относительное различие ускорения силы тяжести Δ𝑔/𝑔 для шаров из золота и меди, соответствующее результатам опытов Галилея. Результат новейшего эксперимента Дикке: это отношение не превышает 3⋅10⁻¹¹. Приняв, что это отношение даётся таким новейшим результатом, вычислите, насколько разойдутся при своём падении с вершины 46-метровой вышки в вакууме одновременно брошенные два таких шара, когда первый из них достигнет поверхности Земли. С какой высоты при тех же условиях нужно было бы сбросить шары из разных веществ, чтобы при падении в вакууме в однородном гравитационном поле с напряжённостью 10 м/сек² они разошлись один от другого на расстояние в 1 мм? Сравните эту высоту с расстоянием между Землёй и Луной (3,8⋅10⁸ м), и вы увидите, почему эксперимент Дикке не мог состоять в сбрасывании шаров!
2) Галилео Галилей, Диалоги о двух новых науках. Соч., т. I, ГТТИ, М.— Л.„ 1934.
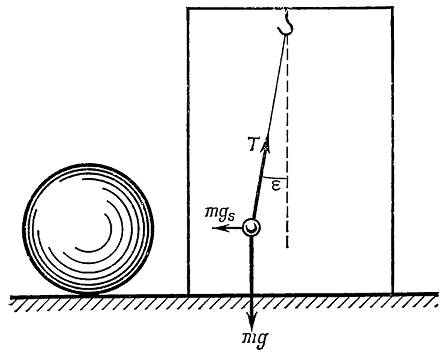
Рис. 50. Массивный шар, помещённый вблизи груза, вызывает статическое отклонение отвеса от вертикали.
б) Гиря отвеса массы 𝑚 подвешена на конце длинной нити, закреплённой на потолке герметически закрытой комнаты (рис. 50). Шар очень большой массы, помещённый сбоку от этой комнаты, действует на груз с силой гравитационного происхождения 𝑚𝑔𝑠 направленной по горизонтали. Здесь 𝑔𝑠=𝐺𝑀/𝑅², 𝑀 — масса шара, а 𝑅 — расстояние между грузом отвеса и центром шара. Эта горизонтальная сила вызывает статическое отклонение нити отвеса от вертикали на малый угол ε. (Аналогичный пример из практики: на севере Индии масса Гималайских гор приводит к небольшому отклонению линии отвеса, что затрудняет прецизионные геодезические промеры). Переместим теперь массивный шар так, чтобы он оказался у противоположной стены комнаты (рис. 51), и тогда статическое отклонение нити подвеса от вертикали, сохранив ту же величину угла, изменит своё направление на противоположное. Но ведь угол ε чрезвычайно мал (массив Гималаев вызывает отклонение нити подвеса всего на 5 дуговых секунд, т.е. на 0,0014°!). Однако, если всё время перемещать массивный шар вокруг герметически закрытой комнаты, наблюдатель в комнате сможет измерить обусловленное им гравитационное поле — для этого ему нужно со всё большей и большей степенью точности измерять полный угол, на который изменяется отклонение нити подвеса, 2ε=2 sin ε. Выведите уравнение, необходимое для вычисления величины 𝑔𝑠 с помощью этого угла.

Рис. 51. Расположение шара по другую сторону отвеса приводит к статическому отклонению его от вертикали в противоположном направлении.
в) Мы, жители Земли, располагаем огромным шаром, эффективно совершающим ежедневный обход вокруг нас каждый день. Этот шар — самое массивное тело Солнечной системы — само Солнце! Чему равняется гравитационное ускорение 𝑔𝑠=𝐺𝑀/𝑅², обусловленное Солнцем в окрестностях Земли? (Некоторые из постоянных, которые вам понадобятся при вычислении, можно найти в конце этой книги).
г) Необходимо учесть ещё одно ускорение, которое, однако, не будет фигурировать при окончательном сравнении величины гравитационного ускорения 𝑔𝑠 для различных веществ. Таким дополнительным ускорением будет центробежное ускорение, вызванное движением Земли вокруг Солнца. Когда ваш автомобиль поворачивает, то вас прижимает к той его стороне, которая является внешней относительно направления поворота. Эта отбрасывающая сила, именуемая центробежной фиктивной силой или центробежной силой инерции, обусловлена ускорением вашей системы отсчёта (автомобиля) относительно центра дуги поворота. Величина этой центробежной силы инерции равна 𝑚𝑣²/𝑟, где 𝑣 — скорость движения автомобиля, а 𝑟 — радиус дуги поворота. Наша Земля движется вокруг Солнца по приблизительно круговой орбите. Сила гравитационного притяжения Солнца 𝑚𝑔𝑠 действует на груз отвеса в направлении к Солнцу, центробежная же сила инерции 𝑚𝑣²/𝑅 стремится отбросить груз в сторону от Солнца. Сравните величину «центробежного ускорения» 𝑣²/𝑅 в окрестностях Земли с вычисленной вами в пункте (в) величиной гравитационного притяжения 𝑔𝑠, имеющего противоположное направление. Чему равно результирующее ускорение (в направлении к Солнцу или от него), действующее на частицу, летящую вместе с Землёй, если его наблюдать в (ускоренно движущейся) системе отсчёта Земли?

а) Предполагаемый эффект утром.

б) Предполагаемый эффект вечером.
Рис. 52. Схематическое изображение эксперимента Дикке.
Различие величин гравитационного ускорения золота и алюминия, вызванного Солнцем, привело бы к изменению знака результирующего закручивающего момента от утра к вечеру. Большой алюминиевый шар обладает такой же массой, как и маленький шар из золота, имеющего более высокую плотность.
д) Какова цель проведённого обсуждения? На груз отвеса, расположенный поблизостиот поверхности Земли, действуют гравитационное ускорение 𝑔𝑠 направленное к Солнцу, и равное ему по абсолютной величине, но противоположное по направлению центробежное ускорение 𝑣²/𝑅 (от Солнца). В результате в ускоренно движущейся системе отсчёта Земли действующая на груз результирующая сила, в целом обусловленная существованием Солнца, оказывается равной нулю. Но именно так мы и строили с самого начала инерциальную систему (разд. 2), положив, что эта система отсчёта находится в состоянии свободного падения к центру гравитационного притяжения. Покоящаяся на земной поверхности частица находится в состоянии свободного падения относительно Солнца, и поэтому результирующая сила, действующая на неё со стороны последнего, просто равна нулю. Какое же тогда может иметь отношение всё это к установлению равенства гравитационного ускорения, действующего на частицы различного состава, т.е. к предмету эксперимента Дикке? Ответ. Наша цель — обнаружить разницу (если таковая имеется) в гравитационном ускорении 𝑔𝑠, действующем со стороны Солнца на различные вещества. Предполагается, что центробежное ускорение 𝑣²/𝑅 при движении вокруг Солнца по данной круговой орбите одно и то же для всех веществ и поэтому выйдет из игры при сравнении их ускорений. Рассмотрим крутильные весы, подвешенные за центр масс на кварцевой нити (рис. 52, а). На концах лёгкого стержня длины 𝑙 две равные массы из разных веществ (например, из алюминия и из золота). Предположим теперь, что величина гравитационного ускорения 𝑔₁, действующего на золото со стороны Солнца, несколько превышает ускорение 𝑔₂, действующее на алюминий со стороны Солнца. Тогда влияние Солнца выразится в форме слабого результирующего закручивающего момента, действующего на крутильные весы. Покажите, что в случае расположения Солнца, изображённого на рис. 52, а, этот закручивающий момент действует против часовой стрелки, если смотреть сверху. Покажите также, что его абсолютная величина даётся выражением
⎛
⎜
⎝
Закручивающий
момент
⎞
⎟
⎠
=
𝑚𝑔₁
𝑙
2
-
𝑚𝑔₂
𝑙
2
=
=
𝑚(𝑔₁-𝑔₂)
𝑙
2
=
𝑚𝑔
𝑠
Δ𝑔
𝑔𝑠
𝑙
2
.
(55)
Предположим, что отношение Δ𝑔/𝑔𝑠 равно максимальной величине (3⋅10⁻¹¹), не противоречащей результатам последних экспериментов, длина 𝑙 равна 0,06 м, а масса каждого груза составляет по 0,03 кг. Чему равна тогда величина результирующего закручивающего момента? Сравните эту величину с тем закручивающим моментом, который даёт бактерия (масса 10⁻¹⁵ кг), если её посадить на конец метрового стержня, уравновешенного относительно его середины в гравитационном поле Земли.
е) С Земли мы видим, как Солнце движется по небу. По прошествии 12 час расположение Солнца станет таким, как это изображено на рис. 52, б. Покажите, что в этой новой конфигурации результирующий закручивающий момент будет иметь то же численное значение, которое вы вычислили раньше, но направлен он будет теперь уже по часовой стрелке, если смотреть сверху, т.е. прямо противоположно случаю, рассмотренному в пункте (д)! Такое изменение закручивающего момента, происходящее каждые 12 час, делает возможным зарегистрировать, пользуясь крутильными весами, малую разность Δ𝑔=𝑔₁-𝑔₂ ускорений, которым подвергаются золотой и алюминиевый образцы. Так как крутильные весы подвергаются различным вибрациям, вызванным флуктуациями, движением транспорта, движениями земной коры и пр., необходимо учитывать лишь те отклонения, которые происходят в фазе с изменением положения Солнца.
ж) Действующий на стержень закручивающий момент приводит к повороту кварцевой нити на угол θ рад по формуле
Закручивающий момент = 𝑘θ
где 𝑘 — константа жёсткости нити по отношению к закручиванию. Показать, что максимальный размах поворотов крутильных весов за время одного поворота Земли вокруг оси выражается формулой
θ
полн
=
𝑚𝑔𝑠 𝑙
𝑘
Δ𝑔
𝑔
.
з) Реальный вариант крутильных весов Дикке состоит из золотого и алюминиевого грузов массой по 0,030 кг, укреплённых на концах спицы длиной 6⋅10⁻² м. Эта спица подвешивалась в вакууме на кварцевой нити, константа жёсткости которой по отношению к кручению равна 2⋅10⁻⁸ ньютон⋅м/радиан (н⋅м/рад). Статистическая обработка данных по угловым смещениям таких крутильных весов за продолжительные интервалы времени привела к заключению, что отношение Δ𝑔/𝑔 для пары золото — алюминий менее чем 3⋅10⁻¹¹. Какому среднему максимальному размаху поворотов за время одного обращения Земли вокруг оси соответствует эта величина? Случайные движения (флуктуации) крутильных весов, т.е. шумы, обладают намного большей амплитудой, и поэтому требуется статистическая обработка данных с помощью электронной вычислительной машины. ▼
36*. Долой теорию относительности!
Мистер Большой Скептик — человек образованный, логически мыслящий и даже окончивший школу. Но он выдвигает ряд возражений против теории относительности. Дайте же ответ на каждое возражение так, чтобы камня на камне от него не оставить, но при этом не критикуя его! Если хотите, составьте просто связный единый рассказ о том, как и почему физик приходит к релятивистскому миросозерцанию, и ответьте в этом рассказе на все возражения мистера Большого Скептика.
а) «Наблюдатель 𝐴 говорит, что часы отстают у наблюдателя 𝐵, тогда как 𝐵 говорит, что часы отстают у 𝐴. В этом — нарушение логики. Поэтому от теории относительности следует отказаться».
б) «Наблюдатель 𝐴 говорит, что метровые стержни наблюдателя 𝐵 укоротились, тогда как 𝐵 говорит, что укоротились метровые стержни наблюдателя 𝐴. В этом — нарушение логики. Поэтому от теории относительности следует отказаться».
в) «Теория относительности не допускает даже однозначного определения пространственных и временной координат. Поэтому всё, что утверждается в ней о скоростях (а значит, и о движении вообще), лишено смысла».
г) «В теории относительности постулируется, что свет распространяется с универсальной скоростью, не зависящей от того, в какой системе отсчёта мы исследуем его распространение. Этот постулат никак не может быть верным. Всякий здравомыслящий человек знает, что, полетев с большой скоростью в сторону, куда от него удаляется световой импульс, он тем самым снизит скорость удаления этого импульса от себя. Значит, свет не может обладать одной и той же скоростью для наблюдателей, движущихся друг относительно друга. Такое опровержение основного постулата подрывает в корне всю теорию относительности».
д) «Нет ни единого опытного подтверждения результатов теории относительности».
е) «Теория относительности не может предложить никакого способа описывать событие, не привлекая координат, и никакого способа говорить о координатах, не связывая себя с той или иной конкретной системой отсчёта. Но ведь физические события существуют независимо от какого бы то ни было выбора систем координат или выбора систем отсчёта. Таким образом, теория относительности со своими координатами и системами отсчёта не может дать полноценного описания этих событий».
ж) «Теория относительности говорит лишь о том, как мы наблюдаем события, а не о том, что реально происходит. Значит, это не научная теория, так как наука имеет своим предметом объективную реальность». ▼
Д. ПРИБЛИЖЕНИЕ МАЛЫХ СКОРОСТЕЙ
37. Эвклидова аналогия — подробный пример
Пусть угол между соответствующими осями двух повёрнутых друг относительно друга эвклидовых (декартовых) систем, θ𝑟, весьма мал. Пользуясь приведёнными в табл. 8 разложениями в ряды, найдите приближённый вид формул преобразования, связывающих значения координат некоторой данной точки в этих двух системах. Пренебрегите степенями θ𝑟 выше первой.
Решение. При малых θ𝑟 табл. 8 даёт
sin θ
𝑟
≈
θ
𝑟
,
cos θ
𝑟
≈
1,
Поэтому формулы преобразования в эвклидовой геометрии, обратные формулам (29), приобретают вид
𝑥'
=
𝑥 cos θ
𝑟
-
𝑦 sin θ
𝑟
≈
𝑥-θ
𝑟
𝑦
,
𝑦'
=
𝑥 sin θ
𝑟
+
𝑦 cos θ
𝑟
≈
θ
𝑟
𝑥+𝑦
.
(56)
Эти приближённые формулы преобразования могут быть сделаны сколь угодно точными, для чего достаточно взять соответственно малый угол θ𝑟.
38. Преобразование Галилея
Предположим, что величина β𝑟 весьма мала. Тогда β𝑟=th θ𝑟≈θ𝑟. Пользуясь приведёнными в табл. 8 разложениями в ряды и пренебрегая степенями θ𝑟 выше первой, покажите, что формулы преобразования Лоренца принимают вид (β𝑟≪1)
𝑥'
=
𝑥-β
𝑟
𝑡
(57)
и
𝑡'
=-
β
𝑟
𝑥+𝑡
.
(58)
Теперь, исходя из обыденных нерелятивистских ньютоновских соображений, выведите формулы преобразования, связывающие между собой две системы отсчёта. Это преобразование называется преобразованием Галилея и выражается формулами
𝑥'
=
𝑥-𝑣
𝑟
𝑡
сек
(59)
(собственно преобразование Галилея) и
𝑡
сек
'
=
𝑡
сек
.
(60)
Здесь 𝑣𝑟 — скорость относительного движения двух систем отсчёта, выраженная в метрах в секунду.
Может показаться, что формулы (57) и (58) и формулы (59) и (60) полностью противоречат друг другу. Справедливо ли это первое впечатление, а если нет, то почему? [Обсуждение. Почему в преобразовании Галилея (59) скорость 𝑣𝑟 заменяет величину β𝑟 из формулы (57)? Какой вид принимает формула (58), если подставить в неё величины 𝑣𝑟 и 𝑡сек? Как соотносятся друг с другом обыденные скорости и скорость света?] ▼
39*. Пределы применимости преобразования Галилея
Перейдите к более точному приближению в записи формул преобразования Лоренца при малых относительных скоростях, сохранив члены порядка θ𝑟², но продолжая пренебрегать членами более высоких порядков. (Это —«второе приближение по θ𝑟». Обратите внимание на то, что, согласно табл. 8, разложение th θ𝑟 даже во втором порядке по θ𝑟 даёт β𝑟≈θ𝑟). Покажите, что и в этом улучшенном втором приближении коэффициенты при 𝑥 и 𝑡 согласуются с соответствующими коэффициентами в формулах (57) и (58) с точностью, превышающей 1%, если скорости β𝑟 ниже чем ¹/₇.
Если гоночный автомобиль может при постоянном ускорении с места набрать за 7 сек скорость 60 миль/час (около 27 м/сек), то за сколько дней (приблизительно) он достигнет при том же ускорении скорости β=1/7? За сколько дней можно достичь этой скорости при наивысшем ускорении, переносимом человеческим организмом в течение длительных периодов времени (около 7 𝑔, т.е. при семикратном ускорении свободного падения)? ▼
40*. Столкновения в теории Ньютона и в теории относительности. Область, в которой обе теории совпадают друг с другом с точностью до 1 %

Рис. 53. Изображение симметричного упругого рассеяния в лабораторной системе отсчёта. (Обратите внимание на разную штриховку кадров в лабораторной системе отсчёта и системе отсчёта ракеты!).
Пусть протон 𝐴 подвергается упругому столкновению с протоном 𝐵, первоначально находившимся в покое. Результат такого столкновения невозможно предсказать, так как мы не указали, насколько протоны сблизились при столкновении (а от этого зависит исход). При большинстве столкновений протон 𝐴 отклонится от первоначального пути лишь на малый угол α𝐴, а протон 𝐵 при этом ощутит лишь слабый толчок в сторону под углом α𝐵 (относительно направления движения протона 𝐴), близким к 90°. Но может произойти и очень тесное сближение протонов, когда почти вся энергия передаётся протону 𝐵, и он вылетает под весьма малым углом α𝐵 к направлению «вперёд» (первоначальному пути 𝐴). Промежуточными случаями по отношению к этим двум крайностям являются происходящие время от времени столкновения с «симметричным рассеянием», когда обе (тождественные) частицы разлетаются с одинаковыми скоростями в направлениях, образующих равные углы, α𝐴=α𝐵=α/2, с направлением «вперёд» (рис. 53). Вопрос: чему равен угол отклонения частиц при симметричном рассеянии? Обсуждение. По механике Ньютона полный угол разлёта одинаковых частиц равен 90° при всяком упругом столкновении (будь то симметричное рассеяние или нет!). То, что этот угол при столкновениях быстрых частиц оказывается менее 90°, есть одно из самых интересных и доказательных предсказаний теории относительности. На рис. 54б дана фотография «медленного» столкновения, при котором, в согласии с теорией Ньютона, угол разлёта равен 90°. Напротив, на рис. 54а представлен случай «быстрого» столкновения, при котором угол разлёта частиц явно меньше 90°. Этот факт означает, что отличие угла разлёта от 90° даёт хороший критерий отклонения законов движения от ньютоновских. Рассмотрим, например, такой вопрос: ниже какого значения должна быть скорость частицы в подобном опыте по рассеянию, для того чтобы величина угла разлёта частиц отклонялась от 90° менее чем на ¹/₁₀₀ радиана? Решение этой задачи значительно упрощается, если подойти к случаю описанного выше симметричного рассеяния, выбрав систему отсчёта таким образом, чтобы можно было максимально воспользоваться соображениями симметрии. Сядем для этого в ракету и полетим направо как раз с такой скоростью, которая равна компоненте «вперёд» скорости каждой из частиц после рассеяния. Тогда при наблюдении с этой ракеты частицы 𝐴 и 𝐵 не будут испытывать движения в направлении движения ракеты после столкновения. Что же касается боковых компонент скорости частиц 𝐴 и 𝐵 (в направлениях вверх и вниз), то заметим, что эти скорости были равны по абсолютной величине и противоположны по направлению в лабораторной системе отсчёта. Но ведь такая симметрия скоростей не может измениться, если мы наблюдаем теперь столкновение с ракеты, летящей вправо. Поэтому и при наблюдении в системе отсчёта ракеты скорости частиц 𝐴 и 𝐵 после столкновения будут равны по абсолютной величине и противоположны по знаку. Это тот вывод № 1, которым мы обязаны соображениям симметрии. Вывод № 2 из соображений симметрии также может быть получен при анализе столкновения в системе отсчёта ракеты. Он гласит, что в этой системе до столкновения скорости частиц 𝐴 и 𝐵 также были равны по абсолютной величине и противоположны по направлению. Почему? Какое противоречие ожидало бы нас, если бы эти скорости не были равными? — Да просто нарушилась бы сама симметрия, что легко усмотреть из следующего.

Рис. 54а. Сделанная в камере Вильсона фотография релятивистского и почти симметричного рассеяния, когда первоначально один электрон двигался, а другой покоился.
Начальная скорость первого электрона около β=0,97. Угол между треками разлетающихся электронов много меньше, чем предсказывавшиеся ньютоновской механикой 90°. Искривление треков электронов как заряженных частиц вызвано присутствием магнитного поля, с помощью которого определялись импульсы электронов.

Рис. 546. Фотография нерелятивистского симметричного упругого рассеяния, когда первоначально один протон двигался, а другой покоился. Начальная скорость первого протона около β=0,1. Угол между треками разлетающихся протонов равен 90° в согласии с ньютоновской механикой.
Схема скоростей в системе отсчёта ракеты после столкновения характеризуется симметрией между правым и левым направлениями. Иными словами, глядя на частицы, разлетающиеся после столкновения, невозможно сказать, из каких направлений пришли эти частицы в точку соударения. С равным успехом частица 𝐴 могла прийти слева, а 𝐵 — справа, или частица 𝐴 — справа, а 𝐵 — слева (например, наблюдатель мог обойти арену и посмотреть с другой стороны). Но ведь участвующие в столкновении частицы тождественны друг другу, и ничего не должно измениться, если их взаимно переименовать.

Рис. 55. Изображение симметричного упругого рассеяния в системе отсчёта ракеты (ср. с рис. 53). Была выбрана скорость ракеты, при которой горизонтальные компоненты скоростей частиц после столкновения равны нулю.
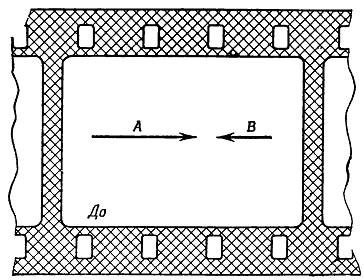
Рис. 56. Так рассеяние изображалось бы в системе отсчёта ракеты, если бы частицы 𝐴 и 𝐵 до рассеяния обладали неравными скоростями. (Ошибочное предположение).

Рис. 57. Рисунок 56 (в системе отсчёта ракеты), если его рассматривать на просвет.

Рис. 58. Рисунок 57 (в системе отсчёта ракеты), если поменять местами обозначения 𝐴 и 𝐵 для тождественных частиц.
Заметим теперь, что на рис. 56 и 58 мы имеем две разные начальные ситуации, приведшие к одному и тому же исходу (см. рис. 53). Более того, эти начальные ситуации отличаются друг от друга лишь тем, что путём некоторого увеличения скорости ракеты, с которой проводятся наблюдения, ситуация на рис. 56 переходит в ситуацию на рис. 58. Но результат столкновения, начальная ситуация которого изображена на рис. 56, уже не будет сохранять вида результата столкновения, начавшегося, как на рис. 58, если мы так ускорим движение наблюдателя. Значит, в нашем первоначальном предположении, что рис. 56 и рис. 58 различны, содержится противоречие, и, чтобы его избежать, необходимо признать, что в системе отсчёта ракеты частицы 𝐴 и 𝐵 имели до столкновения одинаковые скорости, как это и изображено на рис. 55.
Но скорости частиц 𝐴 и 𝐵 были попарно равны не только до (и после) столкновения,— величина скорости каждой из них при столкновении вообще не изменилась. Если бы это было не так, то возникла бы следующая трудность. (Третье использование соображений симметрии — теперь уже не симметрии в пространстве, а симметрии во времени!) Снимем кинофильм об этом столкновении частиц, проявим его и отпечатаем, а затем просмотрим в обратном направлении. Если прежде частицы теряли скорость при столкновении, то теперь они будут приобретать её. Такое различие двух направлений течения времени — типичный признак так называемых необратимых процессов, например: 1) переноса тепла от нагретого объекта к охлаждённому; 2) старения живого организма; 3) разбивания яйца или 4) неупругого столкновения. Но ведь мы ограничивались здесь рассмотрением лишь упругих столкновений! Значит, мы должны говорить теперь только о таких процессах, которые являются обратимыми, а обратимость определяется следующим образом:
Обратимым называется такой процесс, в ходе которого оба направления времени невозможно отличить друг от друга, если рассматривать кинохронику этого процесса, пропуская фильм через проектор в любом направлении.
Так как столкновение двух протонов является упругим, все четыре скорости, изображённые на рис. 59, одинаковы.

Рис. 59. Завершение анализа, основанного на соображениях симметрии. В системе отсчёта ракеты, где горизонтальные компоненты скоростей частиц после столкновения равны нулю, абсолютные значения всех скоростей как до, так и после столкновения одинаковы.
Эти выводы весьма просты и ёмки. Всё рассуждение, приводящее к данному заключению, тоже может быть выражено просто и ёмко — тремя словами; «из соображений симметрии». Опираясь подобным образом на соображения симметрии, мы упрощаем исследование громадного множества физических задач.
Пока что наши рассуждения, основывавшиеся на соображениях симметрии, в равной мере относились как к ньютоновской, так и к релятивистской механике. Различия проявляются, когда мы переходим от полностью завершённой диаграммы в системе отсчёта ракеты к исходной диаграмме в лабораторной системе отсчёта. В механике Ньютона сложение скоростей осуществляется по векторному правилу. Поэтому, чтобы найти скорости частиц 𝐴 и 𝐵 в лабораторной системе отсчёта после столкновения, нам оставалось лишь добавить к горизонтальной компоненте их скоростей скорость движения ракеты β𝑟 (см. рис. 60). Тогда очевидно, что угол разлёта частиц в механике Ньютона всегда равен 90° — независимо от их скоростей. Но в теории относительности это не так!

Рис. 60. Исследование скоростей частиц в лабораторной системе отсчёта после столкновения в ньютоновской (нерелятивистской) теории.
Покажите, что налетающий протон может обладать скоростями вплоть до β=²/₇, и тем не менее угол между скоростями 𝑣𝐴 и 𝑣𝐵 при симметричном рассеянии будет отличаться от 90° (своего значения в теории Ньютона) не более чем на 0,01 рад. Иными словами, покажите, что ньютоновская механика с хорошей точностью описывает столкновение частицы, летящей со скоростью (²/₇)𝑐, с покоящейся частицей (или столкновение двух частиц, летящих со скоростями (²/₇)𝑐 каждая). При этом вам могут пригодиться выводы из упражнения 20. ▼
41*. Примеры предельных переходов к механике Ньютона
Примем в качестве приблизительного верхнего предела применимости механики Ньютона скорость частиц β=¹/₇ (см. упражнение 39). Заполните клетки в нижеследующей таблице по аналогии с верхней графой, которую мы уже заполнили.
Пример движения
β
Корректно ли в этом примере использование механики Ньютона
?
Спутник, обращающийся вокруг Земли со скоростью 30 000
км/час
1/36 000
Да, так как
β<1/7
Земля, обращающаяся вокруг Солнца по орбите со скоростью 30
км/сек
Электрон, обращающийся вокруг протона (атом водорода) по орбите с минимальным радиусом. (Указание. Скорость электрона при его движении на основной орбите атома с атомным номером 𝑍, где 𝑍 — число протонов в ядре, выведена для случая малых скоростей в упражнении 101 гл. 2 и равна
𝑣
=
𝑍
137
⋅
𝑐;
для водорода 𝑍=1).
Электрон на основной орбите атома золота
𝑍=79
Электрон, движущийся с кинетической энергией 5000
эв
. (
Указание
: 1 эв =
1,6⋅10⁻¹⁹
дж
. Проведите оценку, исходя из ньютоновского выражения для кинетической энергии).
Протон или нейтрон, движущийся с кинетической энергией 10
Мэв
(миллионов электронвольт) в атомном ядре
▼
Е. ФИЗИКА ПРОСТРАНСТВА-ВРЕМЕНИ. НОВЫЕ ФАКТЫ
42. Замедление времени для μ-мезона — подробный пример
Мю-мезоны (μ-мезоны) — элементарные частицы, образующиеся при некоторых ядерных реакциях. Если взять некоторое число этих мезонов, то через 1,5 микросекунды (мксек) (время измеряется в той системе отсчёта, в которой μ-мезоны покоятся) половина из них распадается на другие элементарные частицы. Половина оставшихся μ-мезонов распадается в следующие 1,5 мксек и т.д.
а) Рассмотрим (μ-мезоны, образовавшиеся при бомбардировке атомных ядер атмосферных газов космическими лучами на высоте 60 км над поверхностью Земли. Пусть эти μ-мезоны летят вертикально вниз со скоростью, близкой к скорости света. Приблизительно за сколько времени они достигнут поверхности Земли (время измеряется наблюдателем, покоящимся относительно Земли)? В случае если бы не происходило замедления хода времени, какая (приблизительно) часть общего числа мезонов, образовавшихся на высоте 60 км, достигла бы поверхности Земли, ещё не претерпев распада?
б) Представим довольно сложную ситуацию, имеющую место при реальных экспериментах, в виде идеализированной схемы, в общем ей равнозначной. Пусть все мезоны образуются на одной и той же высоте (60 км); пусть все они обладают одинаковой скоростью; пусть они летят вертикально вниз; наконец, пусть ¹/₈ от их общего числа достигает уровня моря, не успев распасться. Вопрос: что может быть причиной такого большого расхождения между предсказанием в п. (а) и приведёнными данными наблюдений? Насколько отличается при этом скорость данных μ-мезонов от скорости света? 1)
1) Существует кинофильм, посвящённый этому эксперименту. См. статью «Измерение релятивистского эффекта замедления хода времени с помощью μ-мезонов», David Н. Frisch, James Н. Smith, American Journal of Physics, 31, 342 (May, 1963). Оригинальный эксперимент был описан в статье В. Rossi, D. В. Hall, Physical Review, 59, 223 (1941).
Решение: Рассматриваемые μ-мезоны летят со скоростью, близкой к скорости света. Поэтому они проходят 60 км примерно за
60⋅10³ м
3⋅10⁸ м/сек
=
2⋅10⁻⁴
сек
.
«Половинное время жизни» (период полураспада) μ-мезонов в той системе отсчёта, где они покоятся, равно 1,6⋅10⁻⁶ сек. Если бы замедления хода времени не было, время полёта мезонов до поверхности Земли равнялось бы 2⋅10⁻⁴/1,6⋅10⁻⁶=133 периодам полураспада. По прошествии каждого периода полураспада число μ-мезонов уменьшается вдвое, так что после 133 периодов должна была бы остаться «в живых» лишь
1
2
×
1
2
×
1
2
×
1
2
…
=
⎛
⎜
⎝
1
2
⎞¹³³
⎟
⎠
≈
10⁻⁴⁰
часть их первоначального числа. На самом же деле осталось ¹/₈=(¹/₂)³, как показал эксперимент в п. (б). Значит, в системе отсчёта ракеты, в которой μ-мезоны покоятся, прошло время, равное лишь 3 периодам полураспада:
Δ
𝑡'
=
3⋅
(
1,5⋅10⁻⁶
сек
)
⋅
(
3⋅10⁸
м/сек
)
=
=
1,35⋅10³
м
.
Путь, пройденный мезоном в системе, связанной с ним самим, естественно, равен нулю:
Δ𝑥'=0.
Поэтому интервал собственного времени между событием «образование мезонов» и событием «достижение ими поверхности Земли» равен
Δ
τ
=
√
(
Δ
𝑡')²-(
Δ
𝑥')²
=
1,35⋅10³
м
.
Но численное значение этого интервала одинаково как в лабораторной системе отсчёта, так и в системе самих мезонов; поэтому
Δ
τ
=
√
(
Δ
𝑡)²-(
Δ
𝑥)²
=
1,35⋅10³
м
или
⎡
⎢
⎣
⎛
⎜
⎝
Δ𝑥
β
⎞²
⎟
⎠
-
(
Δ
𝑥)²
⎤½
⎥
⎦
=
1,35⋅10³
м
.
(61)
Нам известен тот путь, который прошли мезоны в лабораторной системе отсчёта: Δ𝑥=6⋅10⁴ м. Тогда мы можем найти и скорость β по формуле (61). Возводя обе части этой формулы в квадрат и деля их на (Δ𝑥)², получим
1
β²
-1
=
⎛
⎜
⎝
1,35⋅10³
6⋅10⁴
⎞²
⎟
⎠
,
или
1-β²
β²
=
5,06⋅10⁻⁴
.
Очевидно, что β мало отличается от единицы. Поэтому примем
1-β²
=
(1+β)
(1-β)
≈
2(1-β)
,
откуда
1-β²
β²
≈
2(1-β)
β²
≈
2(1-β)
≈
5⋅10⁻⁴
или
1-β
≈
2,5⋅10⁻⁴
Эта малая величина, стоящая в правой стороне полученного равенства, и определяет отличие скорости μ-мезонов от скорости света.
43. Замедление времени для π⁺-мезона
Как видно из нижеследующей таблицы, в лабораторных условиях гораздо проще исследовать распад π⁺-мезонов, чем μ-мезонов:
Частица
Период полураспада
(
измеренный в системе покоя частицы
)
«
Характерная длина
» (
период полураспада, умноженный на скорость света
)
μ
-мезон
1,5⋅10⁻⁶
сек
450
м
(масса в 207 раз превышает массу электрона)
π
-мезон
18⋅10⁻⁹
сек
5,4
м
(масса в 273 раза превышает массу электрона)
Из данного числа π⁺-мезонов половина распадётся на другие элементарные частицы за 18 наносекунд [1 нсек = 10⁻⁹ сек] (если измерять время в той системе отсчёта, где π⁺-мезоны покоятся). Половина оставшихся распадётся за следующие 18 нсек и т.д. В Пенсильванско-Принстонском протонном синхротроне π⁺-мезоны получают, обстреливая пучком протонов алюминиевую мишень, помещённую внутри ускорителя. Мезоны вылетают тогда из мишени со скоростью, приближающейся к скорости света. Если бы замедления хода времени не было и не было также отсева мезонов из получающегося пучка за счёт столкновений, то чему было бы равно наибольшее расстояние от мишени, на котором половина мезонов оставалась бы ещё не распавшейся? Интересующие нас в данном эксперименте π⁺-мезоны обладают параметром скорости, соответствующим
ch θ
=
1
√1-β²
=
15.
Во сколько раз предсказываемое таким образом расстояние от мишени, на которое мезоны успевают улететь за время полураспада, увеличивается за счёт замедления хода времени, т.е. во сколько раз эффект замедления времени позволяет увеличить расстояние между регистрирующей аппаратурой и мишенью? ▼
44*. Аберрация света звёзд

Наблюдатель, быстро движущийся в один из дней года в некотором данном направлении вместе с планетой, должен, чтобы увидеть четыре далёкие звезды, направить свои телескопы так, как показано на рисунке.

Наблюдатель, быстро движущийся через полгода в противоположном направлении.
Рис. 61. Аберрация света звёзд. На обеих схемах представлена ситуация, наблюдаемая в той системе отсчёта, где Солнце покоится.
Угловое расстояние между одной далёкой звездой (𝐵) и другими далёкими звёздами (𝐴, 𝐶) меняется в зависимости от времени года, так как в течение 6 месяцев Земля изменяет свою скорость на 2⋅30 км/сек = 60 км/сек. Показать, что этот угол аберрации, обозначаемый через φ (по отношению к углам, которые регистрировал бы наблюдатель на Солнце), определяется равенством sin φ=β Здесь β — скорость движения Земли по орбите вокруг Солнца. Хотя эффект аберрации света звёзд и поддаётся экспериментальному обнаружению, угол аберрации φ настолько мал, что наблюдения не смогли до настоящего времени дать здесь решающего подтверждения приведённой выше релятивистской формулы, так как теория Ньютона даёт очень близкое предсказание, а именно tg φ=β. ▼
45. Опыт Физо
Распространение света сквозь прозрачную материальную среду происходит медленнее, чем через вакуум. Обозначим скорость света в среде через β' (β'<1). Рассмотрим идеализированный случай, когда скорость β' не зависит от длины волны. Поместим среду в ракету, летящую со скоростью β𝑟 вправо относительно лабораторной системы отсчёта, и направим в эту среду пучок света, распространяющийся также вправо. Исходя из закона сложения скоростей, найдём величину скорости света β в лабораторной системе отсчёта. Требуется показать, что при малых относительных скоростях ракеты и лабораторной системы отсчёта скорость света в лабораторной системе приближённо даётся выражением
β
≈
β'
+
β[1-(β')²]
.
(62)
Это выражение для скорости было проверено Физо, который воспользовался водой, текущей в противоположных направлениях в двух плечах интерферометра, подобного (но не тождественного) интерферометру Майкельсона и Морли (см. упражнение 33) 1).
1) H. Fizeau, Comptes Rendus, 33, 349 (1851) В этой статье (на французском языке) дано превосходное обсуждение некоторых центральных вопросов теории относительности, и притом более чем за 50 лет до первой работы Эйнштейна. ▼
46. Черенковское излучение 2)
2) Это весьма важное как с принципиальной, так и прикладной точек зрения излучение было открыто П. А. Черенковым в 1934 г., когда он был аспирантом С. И. Вавилова и работал в лаборатории последнего; ввиду важной роли самого С. И. Вавилова в открытии черенковского излучения оно иногда называется излучением Вавилова — Черенкова. Теоретически оно было впервые истолковано и детально изучено И. Е. Таммом и И. М. Франком в 1937 г. В 1958 г. П. А. Черенков, И. Е. Тамм и И. М. Франк были удостоены Нобелевской премии по физике за открытие и исследование черенковского излучения.— Прим. перев.

Рис. 62. Нахождение черенковского угла φ.
Никто и никогда не наблюдал того, чтобы частицы двигались быстрее скорости света в вакууме. Однако в материальной среде наблюдалось движение частиц со скоростями, превышающими скорость света в этой среде. Когда заряженная частица движется в среде со скоростью, превышающей скорость света в этой среде, она создаёт когерентное световое излучение в форме конуса, ось которого совпадает с направлением движения частицы. (Вспомните подобные волны, образуемые моторным катером, мчащимся по спокойной воде!) Это излучение называется черенковским. Пусть β — скорость движения частицы в материальной среде, а β' — скорость света в этой среде. Приняв эти обозначения, воспользуйтесь рис 62 и покажите, что половинный угол раствора конуса света φ даётся выражением
cos φ
=
β'
β
.
(63)
В качестве среды возьмите оргстекло люсит, в котором β'=²/₃ Чему должна быть равна та минимальная скорость заряженной частицы, при которой она ещё производит черенковское излучение, двигаясь в люсите? Чему равен максимальный угол ₃, под которым может происходить черенковское излучение в люсите? Измерение этого угла — хороший способ определения скорости частицы 3)
3) Подробности об экспериментальном применении черенковского излучения см. в гл. 7 сборника Techniques of High Energy Physics, ed. David M. Ritson, Interscience Publishers, New York, 1961.

Рис. 63. Черенковское излучение, генерируемое пучком электронов, движущихся в воздухе при энергии 700 Мэв.
Пучок электронов намного уже, чем круг черенковского излучения, видимый на экране. Пучок генерируется слева внизу линейным ускорителем электронов Станфордского университета и выходит в воздух из вакуумной камеры через тонкую алюминиевую фольгу. Сам пучок становится видимым, как это показано на фотографии, благодаря возбуждению и ионизации молекул газов, вызываемым им при прохождении в воздухе. Наряду с таким возбуждением молекул электроны дают черенковское излучение, сосредоточенное в узком конусе, направленном по их движению. Конус света, излучённый электронами в начале пучка (его левая часть), даёт на экране светлое кольцо, образующее внешнюю часть освещённого круга. Подлетая ближе к экрану, электроны продолжают генерировать черенковское излучение всё под тем же углом, так что кольцо становится всё уже, и в целом мы имеем систему налагающихся концентрических колец света. Эти кольца от всех электронов в пучке сливаются в один сплошной круг света. Черенковский угол φ для электронов в начале пучка (наиболее удалённых от экрана) равен половине угла, под которым виден этот освещённый круг из закрытого фольгой окошечка вакуумной камеры, откуда поступают электроны. Скорость β электронов с энергией 700 Мэв отличается от единицы (скорости света) менее чем на 1/1 000 000, как это видно из формул гл. 2. Поэтому мы можем с хорошей точностью положить β. Скорость света в воздухе β' можно вычислить из величины наблюдаемого коэффициента преломления света в воздухе: 𝑛=1/β'=1,00029. Тогда черенковский угол определяется из формулы cos φ = β'/β ≈ β' = 1/𝑛 = 1/1,00029 .
Для малых углов φ можно применить разложение cos φ ≈ 1-φ²/2 = (1+2,9⋅10⁻⁴)⁻¹ = 1-2,9⋅10⁻⁴ .
Отсюда получим теоретическое значение черенковского угла φтеор = 2,4⋅10⁻¹ рад.
Расстояние от окошечка в вакуумной камере до экрана приблизительно равно 12 м, а радиус светового круга составляет около 26,5 см, так что наблюдаемый черенковский угол равен φэксп = 26,5/1200 = 2,2⋅10⁻¹ рад
в хорошем согласии с предсказанием теории.
▼
47*. Искривление лучей света звёзд Солнцем
Оцените степень отклонения лучей света звёзд Солнцем, исходя из простейших соображений. Обсуждение. Рассмотрим сначала упрощённый пример. Кабина лифта ширины 𝐿 начинает свободно падать из состояния покоя вблизи поверхности Земли. В момент начала падения от одной стены кабины в горизонтальном направлении к другой стене направляется узкий луч света. Свободно падающая кабина лифта реализует инерциальную систему отсчёта. Следовательно, световой луч пересечёт кабину по линии, представляющей собой прямую относительно кабины. Но относительно Земли световой луч будет падать, так как падает кабина. Значит, световой луч должен падать в гравитационном поле. Другой пример: луч света от звезды, проходя по касательной мимо земной поверхности, должен подвергнуться гравитационному отклонению (независимо и в дополнение к явлению рефракции в атмосфере). Однако срок, за который луч пробегает мимо Земли, настолько краток, что этоотклонение крайне незначительно и не могло быть до сих пор обнаружено в земных условиях. Но вблизи поверхности Солнца ускорение силы тяжести много больше, чем на Земле, и достигает 275 м/сек². К тому же свет тратит много больше времени при прохождении мимо Солнца ввиду его огромного диаметра — 1,4⋅10⁹ м. Исходя из этого диаметра и из величины скорости света, определите «эффективное время падения» луча. Пользуясь полученным временем падения, вычислите полную скорость по направлению к Солнцу, приобретённую лучом за весь период гравитационного взаимодействия. [Максимальное ускорение, действующее в течение этого «эффективного времени», даёт тот же суммарный эффект (проверьте это вычислениями!), что и реально действующее ускорение, переменное по абсолютной величине и по направлению в течение всего периода прохождения луча в гравитационном поле Солнца.] Сравнивая эту поперечную скорость с продольной для светового луча, определите угол его отклонения. Строгий расчёт в частной теории относительности приводит к тому же результату. Однако общая теория относительности, созданная Эйнштейном в 1915 г., предсказала не учитывавшийся прежде эффект, связанный с изменением длин в поле тяготения и приводящий к подобию (дополнительного) преломления света в этом поле, что удваивает величину предсказанного отклонения лучей. [Наблюдаемая величина отклонения: во время солнечного затмения 1947 г.— (9,8±1,3)⋅10⁻⁶ рад; 1952 г.— (8,2±0,5)⋅10⁻⁶ рад.] ▼
Ж. ГЕОМЕТРИЧЕСКОЕ ИСТОЛКОВАНИЕ
48. Геометрическое истолкование
Постройте геометрическое истолкование преобразования Лоренца по следующей схеме:
а) Покажите, что на лабораторной диаграмме пространства-времени мировая линия начала пространственной системы координат системы отсчёта ракеты изображается прямой 𝑡' на рис. 64. Это — геометрическое место всех событий, происходящих в начале пространственных координат системы отсчёта ракеты, т.е. это ось 𝑡' системы отсчёта ракеты. Покажите, что геометрическое место событий, происходящих в точке 𝑥'=1 м в системе отсчёта ракеты,— это прямая, параллельная оси 𝑡' на рис. 64; аналогичные заключения следуют о точках 𝑥'=2, 3, 4 и т.д. метров.

Рис. 64. Положение на диаграмме пространства-времени в лабораторной системе отсчёта оси времени системы отсчёта ракеты.
б) Покажите, что наклон оси 𝑡' по отношению к оси 𝑡 на рис. 64 определяется выражением
Число метров
пройденного пути
Число метров
прошедшего времени
=
β
𝑟
=
th θ
𝑟
.
Как меняется этот наклон β𝑟 в следующих двух случаях:
1) когда ракета движется очень медленно;
2) когда ракета летит со скоростью, очень близкой к скорости света?
в) Сделаем теперь решающий шаг! Как провести в диаграмме пространства-времени лабораторной системы отсчёта ось 𝑥' ракеты? Принцип относительности утверждает, что измеряемое значение скорости света должно быть одинаково в обеих системах отсчёта. На рис. 65 пунктиром проведена мировая линия вспышки света. Покажите, что на основании принципа относительности ось 𝑥' системы отсчёта ракеты должна подниматься вправо с тем же наклоном, с каким ось 𝑡' системы отсчёта ракеты отклоняется вправо же. Покажите, что геометрические места событий, происходящих в моменты времени 𝑡'=1, 2, 3 и т.д. метров в системе отсчёта ракеты, являются прямыми, лежащими параллельно оси 𝑥'.

Рис.65. Положение на диаграмме пространства-времени в лабораторной системе отсчёта пространственной оси системы отсчёта ракеты.

Рис. 66. Градуирование пространственной и временной осей системы отсчёта ракеты.
г) Проградуируйте оси координат системы отсчёта ракеты! Проведите гиперболу 𝑡²-𝑥²=1 (рис. 66). В той точке, где эта гипербола пересекает ось 𝑡 лабораторной системы отсчёта (где 𝑥=0), мы имеем момент времени 𝑡=1. Однако интервал 𝑡²-𝑥² инвариантен, так что при этом мы получим также (𝑡')²-(𝑥')²=1 Следовательно, в точке пересечения гиперболой оси 𝑡' системы отсчёта ракеты (где 𝑥'=0) мы имеем момент времени 𝑡'=1. Из соображений симметрии и ввиду линейности уравнений преобразования отрезок оси 𝑡' от точки 𝑡'=0 до точки 𝑡'=1 можно использовать в качестве единицы масштаба, откладываемого как вдоль оси 𝑡', так и вдоль оси 𝑥'. Тем самым схема построения завершена. Реализуйте её!
д) Покажите, что если два события одновременны в лабораторной системе отсчёта, они будут лежать на прямой, параллельной оси 𝑥 лабораторной системы на диаграмме пространства-времени (рис. 67). Покажите, что, если два события одновременны в системе отсчёта ракеты, они будут лежать на прямой, параллельной оси 𝑥 системы ракеты на диаграмме пространства-времени. Поэтому два наблюдателя не обязательно считают одновременными одни и те же пары событий. Это и есть относительная синхронизация часов.

Рис. 67. Эффект замедления хода времени.
е) Используя линии одновременности на рис. 67, покажите, что для наблюдателя в системе отсчёта ракеты часы, расположенные в начале лабораторной системы пространственных координат, ещё не показывают 1 м времени, когда 𝑡'=1 м (т.е. лабораторные часы отстают). Вместе с тем для наблюдателя в лабораторной системе отсчёта часы, расположенные в начале лабораторной системы пространственных координат, уже показывают больше 1 м времени (т.е. отстают часы на ракете). Это и есть замедление хода времени.
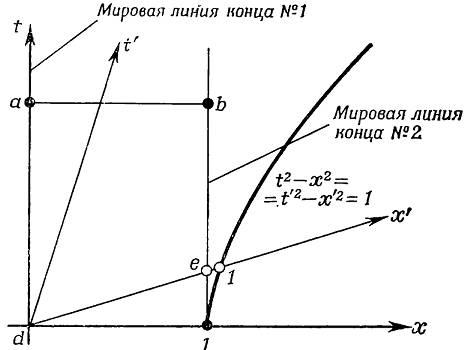
Рис. 68. Метровый стержень, покоящийся в лабораторной системе отсчёта, подвергается лоренцеву сокращению при наблюдении из системы отсчёта ракеты.
ж) Пусть метровый стержень покоится в лабораторной системе отсчёта, причём одним концом упирается в начало её пространственных координат (рис. 68). Если измерять его длину в лабораторной системе отсчёта, то мы получим результат типа 𝑎𝑏 на рис. 68. Измеряя его длину в системе отсчёта ракеты (т.е. регистрируя положения его концов «в один и тот же момент времени»), мы получим результат типа 𝑑𝑒 на том же рисунке. Покажите, что эти результаты измерений дают наблюдаемый эффект лоренцева сокращения в системе отсчёта ракеты. Переходя к рис. 69, покажите, что метровый стержень, покоящийся в системе отсчёта ракеты и упирающийся одним концом в начало её пространственных координат, подвергается лоренцеву сокращению при наблюдении из лабораторной системы отсчёта.

Рис. 69. Метровый стержень, покоящийся в системе отсчёта ракеты, подвергается лоренцеву сокращению при наблюдении из лабораторной системы отсчёта.
з) Нарисуйте диаграммы пространства-времени, иллюстрирующие относительность одновременности, замедление хода времени и лоренцево сокращение длин для тех предельных случаев, когда скорость ракеты относительно лабораторной системы отсчёта очень мала или очень велика.
и) Вернёмся к рис. 22 (стр. 54), где на диаграмме пространства-времени описано движение частиц и световых вспышек в двух измерениях. Покажите, что «плоскость одновременности» системы отсчёта ракеты наклонена относительно «плоскости одновременности» лабораторной системы отсчёта. Разберитесь, какую роль играет этот наклон для факта относительности одновременности событий, происходящих в разных точках оси 𝑥 диаграммы пространства-времени лабораторной системы отсчёта и для факта относительности одновременности событий, происходящих в разных точках оси 𝑦 диаграммы пространства-времени лабораторной системы.
к) Рассмотрите системы отсчёта ракеты, движущейся в отрицательном направлении оси 𝑥 лабораторной системы отсчёта. Проверьте выводы из диаграммы на рис. 70, в частности обратный знак для эффекта относительной синхронизации часов, но один и тот же характер эффекта замедления хода времени (по сравнению со случаем ракеты, движущейся в положительном направлении оси 𝑥).

Рис. 70. Положение пространственной и временной осей системы отсчёта ракеты, движущейся в отрицательном направлении оси 𝑥 лабораторной системы отсчёта. ▼
49. Парадокс часов. II — подробный пример 1)
1) Е. Lowry, American Journal of Physics, 31, 59 (1963).
Вернувшись из своего 14-летнего путешествия, Пётр (см. упражнение 27) ещё достаточно, молод для того, чтобы взяться за изучение теории относительности. Но чем больше он ей занимается, тем сильнее запутывается. Поскольку как он, так и его брат Павел находились в относительном движении друг относительно друга, то оба должны наблюдать замедление хода часов друг друга. Будучи вложено в уста Павла, это простое утверждение позволяет без труда понять, почему часы Петра, как и процесс старения организма Петра, шли замедленно, так что Пётр оказался моложе своего брата-близнеца после возвращения. Но ведь если это утверждение справедливо,— рассуждает Пётр,— то почему не я, когда я провожу исследование, обнаруживаю, что часы Павла идут замедленно? Как же это он смог постареть сильнее, чем я? Вопрос: как разрешить затруднения Петра?
Решение. По мере того как Пётр, обуреваемый сомнениями, всё глубже изучал теорию, он обнаруживал, что такие слова, как «наблюдатель» и «наблюдаемый интервал времени», не сводятся к тем простым понятиям, к которым он сводил их первоначально. Он не думал раньше о том, как он мог бы непосредственно день за днём контролировать процесс старения Павла, остававшегося на Земле, используя для этого радиопередачи или иные способы. Пётр обнаружил, что, хотя эта процедура и выполнима, её анализ отнюдь не прост. Он обнаружил, что в теории относительности «наблюдателя» следует понимать как целую систему стержней и хронометров, движущуюся с постоянной скоростью — в данном случае с той же, с какой сам Пётр удаляется от Земли (β𝑟=24/25=0,96). Эта непрерывная цепочка часов («часы Петра и система отсчёта Петра») всё время пролетает мимо Земли. Каждые часы, пролетая мимо Павла, регистрируют: 1) показания часов Павла и 2) свои собственные показания и положение. Когда мы говорим скороговоркой, что «Пётр наблюдает Павла», это значит, что Пётр собирает когда-то позднее все эти зарегистрированные данные.
«Ну, и что же? — спрашивает сам себя Пётр на этом этапе.— Я так или иначе знаю, что показания часов Павла изменяются между каждыми двумя последующими регистрациями только на √1-β𝑟=7/25 той величины, на которую изменяются показания моих часов. Значит, именно Павел должен был оказаться моложе в конце путешествия, а не я. Но вы посмотрите только, как он поседел! Значит, я в чём-то ошибаюсь...».
Мысленно перебирая вновь этапы своего путешествия, Пётр не мог не вспомнить того момента, когда он перестал удаляться от Земли и когда началось его возвращение. «Я остановился; я начал двигаться назад, но...— внезапно спросил он сам себя,— но моя инерциальная система отсчёта?! Как могла полететь назад инерциальная система?» И он начал придирчиво разбираться в этом вопросе. Для него стала ясной необходимость признать, что использовавшаяся в первой части его путешествия система отсчёта (и, в частности, его сетка часов, регистрировавшая информацию в течение всех семи лет удаления от Земли) должна была продолжать своё стремительное движение, подобно потоку машин на автостраде, когда всего один автомобиль разворачивается и направляется назад. При возвращении домой Петра сопровождал другой поток часов — вторая инерциальная система отсчёта. Все семь лет обратного пути рядом с ним летели одни и те же часы этого второго потока. Когда эти часы приняли эстафету, на них было поставлено время (7 лет), которое показывали улетевшие часы. И они показали 14 лет в тот момент, когда Пётр вновь встретил Павла.
Возвращавшаяся цепочка часов пролетала мимо Земли все эти семь лет. Одни за другими они регистрировали свои собственные показания и показания часов Павла. Отпечатанные этими последними часами регистрационные карточки ложились всё более и более высокой кучей у ног Павла. И на протяжении всех этих семи лет возвращения карточки показывали, что часы Павла регистрируют лишь 7/25 проходящего времени. А 7/25 от семи лет — это 1,96 года.

Рис. 71. Как Пётр проводит учёт процесса старения Павла.
В период удаления Петра (отрезок 𝑂𝑇 на диаграмме) его часы показали, что прошло семь лет. Его сопровождала цепочка синхронизированных часов, каждые из которых дали сигнал конца седьмого года полёта в соответствующем пункте «линии одновременности» 𝐴𝑇, отметив это на своей регистрационной карточке. Те часы системы отсчёта Петра, которые дали этот сигнал в мировой точке 𝐴, зафиксировали, что там часы Павла показали лишь 1,96 года («замедление хода часов, наблюдаемое из движущейся системы отсчёта») На обратном пути Петра сопровождала другая цепочка синхронизированных часов («вторая инерциальная система отсчёта»). Каждые из них на линии одновременности 𝐵𝑇 показывали время 7 лет. Те часы, которые двигались вместе с Петром, отсчитали на мировой линии 𝑇𝐶 ещё семь лет, так что последний год был четырнадцатым годом путешествия Петра, в конце которого он встретился с Павлом в мировой точке 𝐶. На участке 𝐵𝐶, когда часы в связанной с Петром системе отсчёта показали, что прошло 7 лет, Павел снова состарился лишь на 1,96 года (снова «замедление хода часов, наблюдаемое из движущейся системы отсчёта»). Но учёт, проделанный до сих пор из двух инерциальных систем Петра, ещё не полон. Ни в одной из этих систем не учтён отрезок 𝐴𝐵, также соответствующий прошедшему времени. Этот отрезок составляет 46,08 года («поправка на изменение линии одновременности» для двух систем отсчёта Петра — удаляющейся и возращающейся вместе с ним). Итак, замедление хода часов Павла, наблюдаемое двумя системами хронографов Петра, никак не помешает Петру вернуться к Павлу более молодым, чем окажется этот последний.
«Что за чертовщина в этих рассуждениях? — возопил тут Пётр.— Теперь получается, что Павел должен был постареть на 1,96 года за время моего путешествия туда и на 1,96 года за время моего путешествия обратно, т.е. в общем на 3,92 года. И при этом я знаю, что я постарел на 14 лет, и я знаю, что он постарел ещё больше на самом деле! Что же я упустил из виду?» При этом он нарисовал диаграмму пространства-времени (рис. 71), и вот тут-то разрешилось его противоречие — он заметил, что до сих пор не учитывал отрезка времени 𝐴𝐵. Пётр обнаружил, что учёт этого времени соответствует поправке, необходимой при переходе между системами одновременности в удаляющейся и возвращающейся системах отсчёта. Отдельный расчёт, базирующийся на выводах из упражнения 11, даёт для этого отрезка времени значение в 46,08 года. Такую поправку следует добавить к времени, прошедшему у Павла, которое было измерено двумя последовательными системами хронографов Петра. Тогда Пётр смог окончательно вычислить возраст Павла (включая 21 год — возраст последнего к началу путешествия):
21+1,96+46,08+1,96
=
71 год.
Сам же он мог радоваться своей относительной молодости:
21+14
=
35 лет.
(без поправки на то время, которое понадобилось ему, чтобы разобраться в теории относительности!).
Приведённые рассуждения не претендуют на то, чтобы их считали простейшим способом вычисления возраста близнецов. Проще всего — это вернуться к рассуждениям Павла, изложенным в упражнении 27. В них достаточно рассматривать одну-единственную инерциальную систему отсчёта, а именно ту, в начале пространственных координат которой расположен Павел. Новые рассуждения иллюстрируют лишь, как любой корректный путь расчёта приводит к одному и тому же корректному результату.
3. ВИНЕГРЕТ
50. Сокращение или поворот 1)?
1) Более подробный анализ этой проблемы, а также ссылки на литературу можно найти в книге Edwin F. Taylor, Introductory Mechanics, John Wiley and Sons, New York, 1963, p. 346.
Рассмотрим куб, покоящийся в системе отсчёта ракеты, каждое ребро которого в этой системе имеет длину 1 м. В лабораторной системе отсчёта этот куб подвергается лоренцеву сокращению, как показано на рис. 72. Обнаружить такое лоренцево сокращение можно, например, определяя положение четырёх часов, которые покоятся в лабораторной системе отсчёта и синхронизированы в ней, причём четыре угла куба, 𝐸, 𝐹, 𝐺 и 𝐻 совпадают с соответствующими часами, когда все четверо часов показывают одно и то же время. При этом процесс наблюдения не осложняется учётом времени, которое требуется свету, чтобы пройти пути от разных углов куба. Рассмотрим теперь другой способ наблюдения!
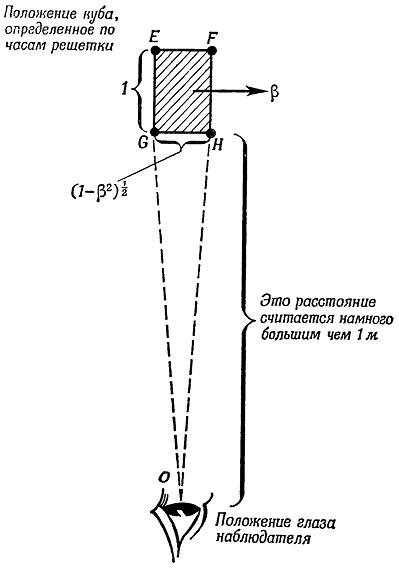
Рис. 72. Положение глаза наблюдателя, визуально исследующего пролетающий мимо него «куб».
Встанем в лабораторной системе отсчёта и будем смотреть на куб одним глазом в то время, когда куб пролетает перед нами (рис. 72). Что мы видим в каждый данный момент времени? — Тот свет, который приходит в наш глаз в этот момент, даже если этот свет вышел из разных углов куба в разное время. Значит, то, что человек наблюдает визуально, может быть совсем иным, чем то, что он наблюдает с помощью часовой сети. Если мы смотрим на куб снизу, то расстояние 𝐺𝑂 равно расстоянию 𝐻𝑂, так что свет, одновременно вышедший из точек 𝐺 и 𝐻, одновременно достигнет и глаза 𝑂. Поэтому, глядя на куб снизу, мы увидим лоренцево сокращение дна куба.
а) Свет из точки 𝐸, приходящий в 𝑂 одновременно со светом из 𝐺, должен быть испущен из 𝐸 раньше, чем свет из 𝐺. Насколько раньше? Какой путь пройдёт куб за это время? Чему равно расстояние 𝑥 на рис. 73?

Рис. 73. Что видит наблюдатель, смотря снизу вверх.
б) Предположим, что некто решил истолковать видимую проекцию куба на рис. 73 как его поворот, а не лоренцево сокращение. Найдите выражение, описывающее угол такого кажущегося поворота φ не подвергнутого сокращению куба на рис. 74. Исследуйте это выражение в двух предельных случаях: β→0 и β→1.

Рис. 74. Как этот наблюдатель может истолковать свои визуальные наблюдения (проекцию рис. 73).
в) Соответствует ли выражение «на самом деле» реальному положению вещей в следующих высказываниях:
1) Наблюдатель в системе отсчёта ракеты говорит: «Мой куб на самом деле не подвергся ни повороту, ни сокращению».
2) Наблюдатель, пользующийся часовой сеткой лабораторной системы отсчёта, говорит: «Этот куб на самом деле подвергся лоренцеву сокращению, а не повороту».
3) Зритель, визуально проводящий наблюдения в лабораторной системе отсчёта, утверждает: «Куб на самом деле повернулся, а не претерпел лоренцево сокращение».
Как сформулировать в одной или двух фразах корректное высказывание, которое показало бы каждому из этих наблюдателей, что его партнёры должны были прийти к иным заключениям, чем он? ▼
51**. Парадокс часов. III
Можно ли улететь в место, удалённое на 7000 световых лет, и вернуться назад, постарев не более чем на 40 лет? «Да!»— к такому выводу пришёл инженер в правлении некой большой авиационной фирмы в своём последнем отчёте. Он рассмотрел путешественника, подвергающегося постоянному ускорению 1 𝑔 (или такому же торможению, в зависимости от этапа полёта; см. диаграмму пространства-времени на рис. 75). Верен ли его вывод при сделанных им предположениях? (Ради простоты, ограничьтесь анализом первого этапа путешествия, когда действует двигатель 𝐴, т.е. первыми десятью годами во времени астронавта, а затем удвойте пройденное при этом расстояние, чтобы узнать, какой путь проделан до самой дальней точки, достигнутой в путешествии).

Рис. 75. Мировая линия ракеты, движущейся по замкнутому пути с постоянным ускорением или торможением.
а) Ускорение не равно 𝑔=9,8 м/сек² относительно лабораторной системы отсчёта. Если бы оно было таким, то во сколько раз быстрее света двигался бы космический корабль к концу десятилетнего полёта? (1 год = 31,6⋅10⁶ сек). Если мы определяем ускорение не по отношению к лабораторной системе отсчёта, то по отношению к чему же мы его определяем? Обсуждение. Взглянем на медицинские весы, на которых стоит астронавт. Двигатели корабля пусть будут давать такую тягу, чтобы весы всё время показывали правильный вес. При этих условиях астронавт всё время подвергался ускорению 𝑔=9,8 м/сек² по отношению к такому космическому кораблю, который: 1) был бы мгновенно сопутствующим первому, так чтобы их скорости в этот момент совпадали, однако 2) не подвергался бы ускорению и поэтому 3) мог бы быть принят за инерциальную (мгновенную) систему отсчёта, ускорение относительно которой равняется 𝑔 (Начиная с этого места, мы переходим от 𝑔, выраженного в м/сек², к 𝑔*=𝑔/𝑐², выраженному в метрах пути за квадрат метров времени).

Рис. 76. Регистрация ускоренного движения ракеты в лабораторной системе отсчёта.
б) Какую скорость разовьёт космический корабль за данный промежуток времени? Но мы сразу же подвергнем этот вопрос критике и перефразируем его. Дело в том, что скорость β — недостаточно простая для исследования величина. Простым является параметр скорости θ, и его простота состоит в аддитивности. Смысл же аддитивности в том, что, если параметр скорости космического корабля на рис. 76 относительно воображаемой мгновенно сопутствующей инерциальной системы отсчёта меняется от 0 до 𝑑θ за время 𝑑τ по часам астронавта, то параметр скорости этого корабля по отношению к лабораторной системе отсчёта за тот же промежуток времени по часам астронавта изменится от своего первоначального значения θ до значения θ+𝑑θ. Свяжем теперь величину 𝑑θ с ускорением 𝑔* в мгновенно сопутствующей инерциальной системе отсчёта. В этой системе
𝑔*
𝑑τ
=
𝑑β
th 𝑑θ
≈
𝑑θ
,
так что
𝑑θ
=
𝑔*
𝑑τ
.
(64)
По прошествии каждого интервала времени 𝑑τ по часам астронавта происходит соответствующее увеличение параметра скорости космического корабля на 𝑑θ=𝑔*𝑑τ. Полная величина параметра скорости космического корабля в лабораторной системе отсчёта просто-напросто равна сумме всех этих последовательных увеличений параметра скорости. Пусть вначале космический корабль покоился. Тогда его параметр скорости линейно возрастал пропорционально величине истёкшего времени по часам астронавта согласно уравнению
θ
=
𝑔*τ
.
(65)
Так определяется параметр скорости θ космического корабля в лабораторной системе отсчёта в любой момент времени 𝑥 в системе отсчёта астронавта.
в) Какое расстояние в лабораторной системе отсчёта 𝑥 покрывает космический корабль за данный промежуток времени τ в системе отсчёта астронавта? В каждый момент скорость космического корабля в лабораторной системе отсчёта связана с его параметром скорости уравнением 𝑑𝑥/𝑑𝑡=th θ, так что расстояние 𝑑𝑥, пройденное за лабораторное время 𝑑𝑡 равно
𝑑𝑥=th θ 𝑑𝑡.
Вспомним, что соответствующие промежутки времени по часам астронавта 𝑑𝑥 представляются как более длинные промежутки 𝑑𝑡 в лабораторной системе отсчёта (замедление хода времени), и между ними существует связь
𝑑𝑡=ch θ 𝑑τ.
Отсюда расстояние в лабораторной системе отсчёта 𝑑𝑥, пройденное за время 𝑑τ по часам астронавта, равно
𝑑𝑥
=
th θ
ch θ
𝑑τ
=
sh θ
𝑑τ
.
Подставляя сюда выражение θ=𝑔*τ из пункта (б), найдём
𝑑𝑥
=
sh(𝑔*τ)
𝑑τ
.
Просуммируем (проинтегрируем) все эти малые перемещения 𝑑𝑥, начиная с момента «нуль» во времени астронавта и до конечного момента по этому времени; мы получим
𝑥
=
1
𝑔*
[ch(𝑔*τ)-1]
.
(66)
Так выражается расстояние 𝑥 в лабораторной системе отсчёта, покрытое космическим кораблём за любое данное время τ в системе отсчёта астронавта.
г) Переведём 𝑔* (в м/м²) в 𝑔=𝑔*𝑐² (в м/сек²) и τ (в м) в τсек=τ/𝑐 (в сек) в формуле (66). Выясним, был ли прав инженер, заключив в своём отчёте о возможности полёта, упомянутого в начале этого упражнения (1 год 31,6⋅10⁶ сек). ▼
52*. Наклонный стержень

Рис. 77а. Метровый стержень движется перпендикулярно самому себе (наблюдение в лабораторной системе отсчёта).

Рис. 77б. Движение метрового стержня, наблюдаемое в системе отсчёта ракеты.
Метровый стержень, параллельный оси 𝑥, движется в положительном направлении оси 𝑦 в лабораторной системе отсчёта со скоростью β𝑦. В системе отсчёта ракеты этот стержень несколько наклонён вверх в положительном направлении оси 𝑥'. Объясните, почему это так, причём сначала не пользуясь уравнениями. Пусть центр метрового стержня проходит через точку 𝑥=𝑦=𝑥'=𝑦'=0 в момент 𝑡=𝑡'=0, как это изображено на рис. 77а и 776. Вычислите затем величину угла θ', образованного метровым стержнем и осью 𝑥' в системе отсчёта ракеты. Обсуждение. Где и когда пересекает правый конец метрового стержня ось 𝑥 с точки зрения лабораторной системы отсчёта? Где и когда пересекает правый конец метрового стержня эту ось с точки зрения системы отсчёта ракеты? Экспериментально наблюдаемая томасовская прецессия электрона в атоме (см. упражнение 103) может быть объяснена тем же самым путём, что и явление наклона метрового стержня. ▼
53*. Парадокс метрового стержня 1)
1) См. R. Shaw, American Journal of Physics, 30, 72 (1962).
Замечание. До того как приступать к упражнению 53, следует разобраться в упражнении 52.
Метровый стержень, параллельный оси 𝑥 лабораторной системы отсчёта, движется в ней по направлению к началу координат со скоростью β𝑟. Очень тонкая пластинка, параллельная плоскости 𝑥𝑦 в лабораторной системе отсчёта, движется в ней вверх в направлении оси 𝑦 со скоростью β𝑦. В пластинке имеется круглое отверстие диаметром 1 м, в центре которого проходит ось 𝑦. Центр метрового стержня оказывается в начале пространственных координат лабораторной системы отсчёта в тот момент, когда движущаяся вверх пластинка достигает плоскости 𝑦=0. Так как метровый стержень претерпел лоренцево сокращение в лабораторной системе отсчёта, то он без труда проходит сквозь отверстие в пластинке. Поэтому в ходе движения метрового стержня и пластинки между ними не произойдёт соударения. Однако кто-нибудь может выдвинуть возражение против этого вывода и аргументировать его следующим образом: в системе отсчёта ракеты, где метровый стержень покоится, он не подвергнут сокращению, но зато в этой системе лоренцево сокращение испытывает отверстие в пластине. Поэтому невозможно, чтобы сохраняющий свою полную длину метровый стержень прошёл через сжавшееся отверстие в пластинке. Таким образом, соударение между метровым стержнем и пластинкой неизбежно. Разрешите этот парадокс, используя ответ, полученный в предыдущем упражнении. Ответьте без всяких оговорок на вопрос: произойдёт соударение метрового стержня с пластинкой или нет?

Рис. 78. Сможет ли метровый стержень пройти без соударения сквозь отверстие диаметром 1 м?
▼
54**. Тонкий человек на решётке 1)
1) W. Rindler, American Journal of Physics, 29, 365 (1961).
Некто имеет обыкновение ходить крайне быстро — настолько быстро, что релятивистское сокращение длин делает его очень тонким. Когда он идёт по улице, ему нужно пройти по канализационной решётке. Человек, стоящий рядом с решёткой, не сомневается, что быстро идущий тонкий человек провалится в отверстие решётки. Однако с точки зрения быстрого ходока он сам обладает обычными размерами, а релятивистское сокращение претерпевает решётка. Для него отверстия в решётке много уже, чем для спокойно стоящего человека, и, конечно, он не думает о возможности провалиться. Кто же здесь прав? Ответ связан с относительностью свойства жёсткости.
Идеализируем эту задачу: пусть метровый стержень скользит вдоль самого себя по гладкому столу. Пусть на пути этого стержня имеется отверстие шириной 1 м. Если лоренцево сокращение уменьшает длины в 10 раз, то в системе отсчёта стола (лаборатория) стержень имеет в длину 10 см и явно провалится в метровое отверстие. Предположим, что в лабораторной системе отсчёта метровый стержень движется настолько быстро, что в ходе падения в отверстие сохраняет горизонтальную ориентацию (наклона в лабораторной системе нет). Запишите в лабораторной системе отсчёта уравнение движения нижнего края метрового стержня, приняв, что 𝑡=𝑡'=0 в тот момент, когда задний конец метрового стержня пересекает край отверстия, вступая в него. При малых значениях вертикальной составляющей скорости стержень будет падать с обычным ускорением 𝑔. В системе отсчёта метрового стержня (ракеты) этот стержень имеет длину 1 м, тогда как отверстие подверглось лоренцеву сокращению в 10 раз. Теперь ширина отверстия 10 см, и стержень никак не может упасть в него. Произведите преобразование, переведя уравнения движения из лабораторной системы в систему отсчёта ракеты, и покажите, что стержень «перегнётся» в этой последней системе через край отверстия, иначе говоря, он не будет жёстким (твёрдым). Упадёт ли в конце концов стержень в отверстие в обеих системах отсчёта? Будет ли стержень на самом деле твёрдым или деформируемым в ходе этого опыта? Можно ли найти какие-либо физические характеристики этого стержня (например, степень его гибкости или сжимаемости), исходя из того описания его движения, которое даёт нам теория относительности? ▼
54а. Измерение скорости стандартного объекта одиночным наблюдателем — подробный пример 1)
1 Упражнение добавлено переводчиком - Прим. ред.
Построение системы отсчёта при помощи решётки с часами — почти всегда умозрительная операция. Более того, мы вынуждены описывать множество объектов и происходящие с ними процессы, не приходя с этими объектами в прямой контакт. Так, например, астрономические наблюдения дают информацию о чрезвычайно далёких звёздах и галактиках, которые не только нам никогда не удастся посетить (см. упражнение 104), но даже луч радиолокатора, посланный из Солнечной системы, не смог бы вернуться к нам за исторически разумные сроки, отразившись от этих удалённых объектов (мы уже не говорим об интенсивности отражённого луча). Всё человечество в астрономических масштабах — это одна мировая линия (двойная планетная система Земля — Луна не более чем типографская точка, если изобразить на листе бумаги Солнечную систему). Поэтому рассмотрим такого одиночного наблюдателя, получающего всю возможную информацию из внешнего мира через приходящий к нему, независимо от его воли, свет — через световой конус прошлого . Понятие одновременности для такого наблюдателя представляет лишь академический интерес, гораздо важнее для него понятие «одновременно наблюдаемого». Один из кинематических эффектов, проявляющихся при наблюдениях с помощью светового конуса прошлого, рассмотрен в упражнении 50. Здесь мы рассмотрим вопрос о том, чему равна «одновременно наблюдаемая» скорость объекта, летящего вдоль луча зрения наблюдателя.
Пусть стандартный предмет (например, пятикопеечная монета) равномерно и прямолинейно движется вдоль луча зрения наблюдателя. Сначала предмет летит на наблюдателя; в момент встречи наблюдатель может быстро пригнуться 2), чтобы пропустить предмет; затем предмет удаляется от наблюдателя. Так как размеры предмета стандартные, наблюдатель может по углу зрения, под которым виден предмет, определить расстояние до него. По изменению этого «одновременно наблюдаемого» расстояния со временем можно определить «одновременно наблюдаемую» скорость движения объекта.
2) Для человечества «пригнуться» было бы затруднительно.
а) Требуется показать, что эта скорость равна
β
до
=
β
1-β
до встречи объекта с наблюдателем и
β
после
=
β
1+β
после встречи. Здесь β — обычная скорость объекта, выраженная в единицах скорости света (так как движение происходит по лучу зрения, достаточно ограничиться её абсолютной величиной), а β —«одновременно наблюдаемая» скорость. Попутно следует обосновать возможность находить расстояние до объекта по угловым размерам.
б) Требуется наглядно показать, рассматривая движение предмета с околосветовой скоростью (в обычном смысле), почему возникает асимметрия в «одновременно наблюдаемой» скорости между случаями до и после встречи. Нельзя ли в качестве объекта взять сам свет?
Решение.

Рис. 78а.
а) Так как «одновременно наблюдаемую» скорость предмета требуется выразить через обычную скорость β, предполагается, что мы знаем больше, чем наш наблюдатель, и стоим, так сказать, над ним. Поэтому мы можем изобразить рассматриваемую ситуацию на диаграмме пространства-времени (рис. 78а), где наблюдатель покоится,— его мировая линия совпадает с осью времени. Наблюдения проводятся регулярно, через каждые Δ𝑡 метров светового времени (таким образом, речь идёт не о периодически вспыхивающем объекте, как в упражнении 6, а о постоянно светящемся). Объект движется по лучу зрения (ось 𝑥), и наблюдатель видит лишь его поперечное сечение, а так как лоренцево сокращение происходит в направлении движения объекта, видимое сечение не зависит от скорости движения. Поэтому, зная абсолютный поперечник объекта, наблюдатель по его угловым размерам без труда определит расстояние: оно равно отношению линейных размеров объекта к его угловым размерам, выраженным в радианах. Чему же соответствует это расстояние на диаграмме пространства-времени? По методу определения оно должно совпадать с расстоянием от наблюдателя до другого такого же стандартного объекта, который покоился бы относительно наблюдателя и находился в том месте, где пролетал движущийся объект в момент, когда он излучил принятый при измерении углов свет. Поперечные сечения обоих объектов, очевидно, совпадают. Иначе говоря, мировые линии вспомогательного покоящегося объекта и основного движущегося объекта должны пересекаться в мировой точке испускания светового луча, по которому производилось измерение расстояния. Итак, искомое расстояние должно быть равно расстоянию до определённого таким образом вспомогательного объекта (ведь он всё время покоится!). Это расстояние по построению равно координате 𝑥 мировой точки испускания «измерительного» луча. Проведём вычисления отдельно для наблюдений до встречи с движущимся объектом и после этой встречи.
1) До встречи. Рассматривается левая ветвь светового конуса прошлого. Её уравнение на плоскости 𝑡, 𝑥 имеет вид
𝑡
=
𝑥
+
𝑛
Δ
𝑡
.
Здесь 𝑛=-1, -2, -3, … и уравнение описывает световой луч, проходящий через точку 𝑛Δ𝑡 на оси 𝑡. В свою очередь мировая линия движущегося объекта описывается уравнением
𝑡
=
𝑥
β
.
Исключая из этих двух уравнений 𝑡, найдём
𝑥
β
=
𝑥
+
𝑛
Δ
𝑡
.
Поскольку теперь 𝑥 полностью определяется выбором числа 𝑛 (обычная скорость β и периодичность наблюдений Δ𝑡 считаются уже заданными), естественно принять 𝑥=𝑥𝑛. Тогда
𝑥
𝑛
⎛
⎜
⎝
1
β
-
1
⎞
⎟
⎠
=
𝑛
Δ
𝑡
или
𝑥
𝑛
=
β
1-β
Δ
𝑡𝑛
.
Отсюда
Δ
𝑥
=
𝑥
𝑛+1
-
𝑥
𝑛
=
β
1-β
Δ
𝑡
,
и искомая «одновременно наблюдаемая» скорость до встречи равна
β
до
=
Δ𝑥
Δ𝑡
=
β
1-β
,
что и требовалось получить.
2) После встречи. В этом случае берётся правая ветвь светового конуса прошлого, уравнение которой записывается в виде
𝑡
=-
𝑥
+
𝑛
Δ
𝑡
,
Подставляя сюда 𝑡 из уравнения мировой линии стандартного объекта, получим
𝑥𝑛
β
=-
𝑥
+
𝑛
Δ
𝑡
откуда
𝑥
𝑛
=
β
1+β
Δ
𝑡𝑛
и
β
после
=
Δ𝑥
Δ𝑡
=
β
1+β
,
т.е. искомая «одновременно наблюдаемая» скорость после встречи. Так как β<1, то очевидно, что βпосле<β<βдо.
б) Исследуем поведение «одновременно наблюдаемых» скоростей при β→1:
β
до
→∞
,
β
после
→
1
2
.

Рис. 78б.

Рис. 78в.
На рис. 78б показано наблюдение объекта, движущегося практически со скоростью света. Мы видим, что свет приходит к наблюдателю вместе с объектом, т.е., с точки зрения одиночного наблюдателя, объект «мгновенно» пришёл из точки своего «рождения». При удалении объекта свет от него продолжает всё время поступать к наблюдателю, так как скорость распространения света не зависит от скорости движения его источника. При этом, конечно, мы не учитываем тонкостей, связанных с интенсивностью света, о которых говорилось в упражнении 22. Детализируя рис. 78б (см. рис. 78в), нетрудно получить непосредственно предельное значение «одновременно наблюдаемой» скорости после встречи. Вспомним, что эта скорость определяется как отношение изменения 𝑥-координаты точки излучения света объектом к соответствующему изменению 𝑡-координаты точки приёма этого света (момент измерения):
β
после
=
𝑂𝑇
Δ𝑡
(см. обозначения на рис. 78в). Теперь Δ𝑡=𝑂𝑃=𝑃𝑈. Так как в пределе скорость объекта принимается равной скорости света (β=1), то
𝑂𝑅
=
β
Δ
𝑡
=
Δ
𝑡
;
отсюда и из подобия треугольников 𝑂𝑇𝑆, 𝑂𝑅𝑄, 𝑂𝑆𝑃 и 𝑂𝑄𝑈 следует
β
после
=
𝑂𝑇
Δ𝑡
=
𝑂𝑇
𝑂𝑅
=
𝑂𝑆
𝑂𝑄
=
𝑂𝑃
𝑂𝑈
=
1
2
что уже было получено выше. Такой пример движения объекта с около-световой скоростью, как и всякий гротеск, делает очевидными специфические заключения: в данном случае это вывод о неодинаковом впечатлении наблюдателя о скорости приближающегося и удаляющегося объекта.
Казалось бы, в данном пределе наилучшим «объектом» был бы сам свет; это, однако, не так. Прежде всего, свет не может сам «светиться», т.е. улетающий от нас фотон в принципе не может (если он не рассеивается на некой среде) испускать фотоны в сторону или назад (см. упражнение 68), так что «одновременно наблюдаемой» скорости уходящего от нас света попросту не существует. Что же касается такой скорости приходящего к нам света, то она неинтересна, так как равна бесконечности для одиночного наблюдателя не по каким-либо физическим причинам, а по самому своему определению! Кроме того, свет нельзя назвать «стандартным объектом», так как для него нет такого понятия, как видимый поперечник, и поэтому бессмысленно определять «расстояние» до него с помощью угловых измерений.
2. ИМПУЛЬС И ЭНЕРГИЯ
10. ВВЕДЕНИЕ. ИМПУЛЬС И ЭНЕРГИЯ, ВЫРАЖЕННЫЕ В ЕДИНИЦАХ МАССЫ
Физика изучает материю, её движение и те силы, которые вызывают это движение. Как связаны между собой сила и движение? В этом кратком вступлении нет нужды заниматься систематизацией сил — электрических, магнитных и прочих. Напротив, стоящая перед нами задача является ещё более насущной. Как можно вообще узнать, действует ли какая бы то ни было сила на частицу? А если сила на неё действует, то чем в поведении мировой линии этой частицы характеризуется наличие силы? И наконец, как можно измерить величину такой силы по изменениям энергии и импульса частицы?
Изменение импульса одного объекта как признак его взаимодействия с другим объектом
Чтобы разобраться в сущности понятия «силы», попытайтесь представить себе, как можно было бы обойтись без него! Наиболее очевидное применение «силы» состоит в том, чтобы объяснить, почему частица ускоряет или замедляет своё движение. Пробная частица в отсутствие действующих на неё сил просто по определению не ускоряется и не замедляется. По отношению к инерциальной системе отсчёта она сохраняет своё состояние покоя или движения с постоянной скоростью. Она «прочерчивает» прямую мировую линию. На рис. 79 такая мировая линия изображена для частного случая частицы, движущейся в направлении оси 𝑥. Напротив, на рис. 80 дана мировая линия частицы, которая, очевидно, изменяет свою скорость и поэтому должна быть подвержена действию силы. Никто и никогда не наблюдал, чтобы изменение скорости происходило без определённой причины, и обычно это — столкновение с соседними частицами либо сила, обусловленная удалённой частицей. Поэтому силу можно охарактеризовать как форму взаимодействия (рис. 81). Эта мысль подкрепляется ещё более следующими двумя соображениями: 1) Если присутствие 𝐴 вызывает изменение скорости 𝐵, то присутствие 𝐵 также вызывает изменение скорости 𝐴. 2) Когда взаимодействие прекращается, а частицы удаляются друг от друга, происшедшее изменение импульса одной из них равно по модулю и противоположно по направлению изменению импульса другой. Поэтому вместо того, чтобы говорить о силах, действующих между частицами, мы можем говорить об изменении их импульсов. И уж явно усложнённым подходом был бы учёт сразу и импульса, и силы в рамках теории относительности. Поэтому мы будем говорить лишь об одном импульсе.
Рис. 79. Мировая линия частицы, на которую не действует никаких сил.

Рис. 80. Мировая линия частицы, на которую действует сила.

Рис. 81. Мировые линии двух взаимодействующих частиц.
Как следует определить импульс? Первые исследователи, развивавшие ньютоновскую механику, определяли импульс как произведение массы частицы на её скорость. Определённый таким образом импульс хорош тем, что сохраняется при соударениях частиц малой энергии. Однако опыт показал, что импульс, определённый по ньютоновскому рецепту как произведение массы на скорость, не сохраняется, когда сталкивающиеся частицы обладают большими скоростями. Итак, перед нами стоит выбор — отказаться либо от ньютоновского определения импульса, либо от закона сохранения этой величины. Закон сохранения импульса стал для нас настолько существенным, что мы примем за фундаментальный именно его. Мы будем исходить из закона сохранения импульса, а уж отсюда выводить выражение для импульса, определённого как векторная величина, сохраняющаяся во всех системах отсчёта.
Импульс определяется так, чтобы он сохранялся
Требование, чтобы импульс сохранялся во всех системах отсчёта, будет использовано в этой главе трижды, и всякий раз обращение к нему будет производить революцию в нашем понимании природы. В следующем параграфе это требование будет использовано при анализе в двух измерениях лобового упругого столкновения шаров, и в результате мы выведем релятивистское выражение для импульса частицы. В разд. 12 мы выведем релятивистское выражение для энергии частицы, исходя из требования сохранения при столкновении частиц в одномерном случае. В разд. 13 мы применим требование сохранения к случаю неупругого столкновения частиц для того, чтобы вывести закон эквивалентности энергии и массы покоя. Может возникнуть вопрос: как же закон сохранения импульса может представлять какую-либо ценность, если и импульс, и энергия определены именно так, чтобы они сохранялись? Этот вопрос приводит нас к самой сущности физических законов и физической теории 1). Чтобы на него ответить, рассмотрим объект, который, катаясь, подобно бильярдному шару, сталкивается с различными телами. Рассматривая первые столкновения, мы найдём (или определим) с помощью закона сохранения неизвестные импульсы отдельных объектов. Но при последующих столкновениях положение изменится. Ведь мы уже будем знать значения импульса участвующих в этих столкновениях тел! И теперь закон сохранения импульса будет выполняться уже не по определению, а в силу глубинных законов природы. Все физические законы и физические теории обладают именно этим глубоким и тонким свойством, а именно они одновременно и дают нам определение требующихся понятий, и позволяют нам сделать выводы, следующие из их использования. И наоборот, если у нас нет объектов, которыми занимается теория, для которых выводится закон или формулируется принцип, то само их отсутствие лишает нас возможности применять или даже формулировать физические понятия. Как безнадёжно устарел лозунг старой теории: «Не начинай исследования, не сформулировав понятий!». Истинно творческая сущность любого продвижения вперёд в человеческом познании состоит в том, что теория, понятие, закон и метод измерения, навеки неотъемлемые друг от друга, возникают в неразрывном единстве друг с другом.
1) См. Henri Poincaré, The Foundations of Science, translated by G. B. Halsted, Science Press, Lancaster, Pennsylvania, 1946, p. 310, 333.
Многочисленные примеры подтверждают, что законы сохранения — это не порочный круг утверждений
Таким образом, физика даёт способ установить гармонию в опытных фактах. Для того чтобы установить закон сохранения, недостаточно какого-то одного эксперимента. Их должно быть по меньшей мере два; в первом мы находим определение сохраняющейся величины, а второй проверяет, действительно ли эта величина сохраняется. В этой главе мы займёмся экспериментами первого типа, т.е. необходимыми для формулирования определений величин. Проверка же работы этих определений — процесс, протекающий ежедневно и ежечасно в ходе постоянного развития экспериментальной физики.
В механике Ньютона импульс частицы определяется как произведение массы на скорость. В гл. 1 мы измеряли скорость β в метрах расстояния, пройденного за метр светового времени. При таком определении скорости ньютоновское выражение для импульса имеет вид игр. Здесь не утверждается ничего нового об импульсе (и это не релятивистское выражение для импульса!), лишь подчёркивается, что время измеряется в метрах. Но когда время измеряется в метрах, импульс имеет размерность массы. Для того чтобы перейти к обычным единицам (например, кг⋅м/сек), требуется лишь домножить этот импульс на коэффициент перевода 𝑐 (скорость света), чтобы перейти от β к 𝑣, так что
⎛
⎜
⎝
Ньютоновский импульс
в обычных единицах
⎞
⎟
⎠
=
𝑚β𝑐
=
𝑚𝑣
.
Импульс и энергию удобнее всего выражать в единицах массы
Подобным же образом в ньютоновской механике кинетическая энергия частицы определяется как произведение массы на квадрат скорости, разделенное на два. Взяв скорость β, измеряемую в м/м, получим ньютоновское выражение для кинетической энергии в виде ½𝑚β². Здесь не утверждается ничего нового об энергии (и это не релятивистское выражение для энергии!), лишь подчеркивается, что время измеряется в метрах. Но когда время измеряется в метрах, энергия имеет размерность массы; и энергия, и импульс обладают одной и той же размерностью. Для того чтобы перейти к обычным единицам (например, джоулям), требуется лишь домножить эту энергию на коэффициент перевода 𝑐² (квадрат скорости света), чтобы перейти от β² к 𝑧, так что
⎛
⎜
⎜
⎝
Ньютоновская
кинетическая энергия
в обычных единицах
⎞
⎟
⎟
⎠
=
1
2
𝑚β²𝑐²
=
1
2
𝑚𝑣²
.
Мы будем обозначать импульс (𝑝) и кинетическую энергию (𝑇), выраженные в единицах массы, без дополнительных значков. Итак, в ньютоновском пределе малых скоростей
𝑝
=
𝑚β
⎫
⎪
⎬
⎪
⎭
⎛
⎜
⎝
малые скорости,
размерность массы
⎞
⎟.
⎠
𝑇
=
1
2
𝑚β²
(67)
При этом мы снабдим обозначения для импульса и энергии в обычных единицах индексом «обычн», подчёркнуто громоздким, чтобы вызвать неприязнь к использованию обычных единиц. Тогда в ньютоновском пределе малых скоростей
𝑝
обычн
=
𝑚𝑣
⎫
⎪
⎬
⎪
⎭
⎛
⎜
⎝
малые скорости,
обычные единицы
⎞
⎟.
⎠
𝑇
обычн
=
1
2
𝑚𝑣²
(68)
В этой главе мы выведем релятивистские выражения для энергии и импульса в единицах массы. Энергия и импульс, выраженные в единицах массы, могут быть просто переведены в величины обычной размерности путём умножения соответственно на 𝑐 и 𝑐². Эти результаты подытожены (в обеих системах единиц) на внутренней стороне обложки книги.
11. ИМПУЛЬС
Из соображений симметрии следует, что импульс параллелен скорости
Много ли можно узнать об импульсе, не обращаясь к эксперименту, а просто из сведений, которыми мы располагаем о структуре пространства-времени? В частности, если вообще существует для каждой частицы такая векторная величина, которую мы называем «импульс», причём сумма этих величин для всех частиц при взаимодействиях последних сохраняется, то как должен импульс любой частицы зависеть от её скорости? Так как импульс — величина векторная, нам следует прежде всего выяснить направление этого вектора для данной частицы и уже затем найти зависимость его модуля от её скорости. Начнём с обоснования того, что вектор импульса частицы ориентирован по направлению её движения. Этот вывод можно получить из соображений симметрии — мощного метода физического анализа — следующим образом. В инерциальной системе отсчёта пространство одинаково во всех направлениях, так что мы называем его изотропным. Раз это так, то одним-единственным направлением, связанным с движением прямолинейно летящей частицы, может быть лишь то направление, в котором происходит это движение. Если бы вектор импульса частицы не был направлен в точности по её движению, а составлял, скажем, угол 30° с направлением движения частицы, то существовало бы громадное множество векторов, все повёрнутые на 30° по отношению к направлению движения и совершенно равноправные, каждый из которых мог бы изображать импульс. Но ведь пространство изотропно! Поэтому мы не могли бы предпочесть ни одного из этих векторов остальным. Но, однако, мы предположили, что импульс определяется однозначно как по своему модулю, так и по направлению, если задана скорость. Значит, мы столкнулись с противоречием, от которого можно избавиться, лишь приняв, что вектор импульса должен лежать вдоль направления движения частицы. Но это значит, что можно выбрать его как параллельным, так и антипараллельным этому направлению, и мы произвольно выбираем направление вектора импульса, совпадающее с направлением скорости частицы 1). Итак, можно окончательно сказать, что вектор импульса частицы совпадает по направлению с её скоростью.
1) Мы могли бы, конечно, выбрать направление вектора импульса частицы противоположным (антипараллельным) направлению ее движения. Такой выбор соответствовал бы симметрии данной задачи и не приводил бы ни к каким физическим противоречиям, если его распространить на все частицы. В таком случае импульсы отдельных частиц и полный импульс системы обладали бы направлениями, противоположными направлениям соответствующих импульсов, определенных выше. Однако по традиции мы ориентируем вектор импульса частицы в том же направлении, какое имеет ее скорость.
Нахождение зависимости импульса от скорости на основании закона сохранения импульса
Итак, мы знаем уже, как направлен вектор импульса частицы. Вторым этапом исследования будет определение абсолютной величины (модуля) этого вектора. Это можно сделать, потребовав, чтобы полный импульс сохранялся при упругих столкновениях. Вместе со свойством инвариантности интервала в лоренцевой геометрии это требование окажется достаточным для того, чтобы показать, что ньютоновское выражение для импульса
𝑝
=
𝑚β
(=𝑚 th θ)
=
𝑚⋅
⎛
⎜
⎝
Смещение за
единицу времени
⎞
⎟
⎠
должно быть заменено релятивистской формулой
𝑝
=
𝑚 sh θ
=
𝑚β
√1-β²
=
=
𝑚⋅
⎛
⎜
⎝
Смещение за
единицу собственного времени
⎞
⎟
⎠
(69)
Если скорость β мала (т.е. мал параметр θ), точное релятивистское выражение (69) приближённо совпадает с ньютоновским выражением.
При соответствующем выборе системы отсчёта полный импульс до столкновения равен нулю

Рис. 82. Скользящее упругое столкновение, наблюдаемое в системе отсчёта, которая движется таким образом, что оба шара имеют до столкновения одинаковые скорости, но движутся во взаимно противоположных направлениях.
Рассуждения, приведённые в тексте, показывают, что после упругого столкновения оба шара движутся вновь с их первоначальными скоростями, а направления их движения снова взаимно противоположны, если их наблюдать в той же системе отсчёта.
Возьмём в качестве сталкивающихся объектов два одинаковых шара 𝐴 и 𝐵 и предположим, что между ними происходит не лобовое (редкое) столкновение, а скользящее (типичное). Всегда можно найти систему отсчёта, движущуюся с такой скоростью, что скорости шаров до столкновения равны и противоположны по направлению (рис. 82). В этой системе отсчёта полный импульс двух одинаковых шаров равен нулю.
Заключение о равенстве нулю полного импульса следует из таких соображений симметрии: допустим, что полный импульс в этой симметричной по скоростям системе отсчёта отличен от нуля. Тогда, как мы сейчас увидим, возникает противоречие. Если другие два шара начинают двигаться в точности так же, как 𝐴 и 𝐵 на рис. 82, причём они отличаются лишь тем, что на место шара 𝐴 помещён шар 𝐵, а на место 𝐵 — 𝐴, ситуация не может измениться. Поэтому полный импульс должен остаться тем же самым как по величине, так и по направлению, что и полный импульс системы на рис. 82 (мы не изобразили его там, потому что на самом деле он равен нулю!). Но ведь изображение нового столкновения можно получить, если рассматривать рис. 82, повернув книгу вверх ногами (поворот на 180° в её собственной плоскости). А это приводит к изменению направления полного импульса на обратное. Следовательно, полный вектор импульса не должен изменяться при повороте на 180°! Это противоречие исчезает, лишь если полный вектор импульса по модулю равен нулю. Итак, до столкновения две тождественные частицы обладают равными и противоположно направленными импульсами.
Что же произойдёт после столкновения? Шары должны и тогда двигаться во взаимно противоположных направлениях с равными скоростями. Если бы это было не так, то сумма их импульсов не была бы равна нулю и полный импульс не сохранялся бы при соударении в нарушение принятого требования. Ограничимся (лишь временно) анализом соударений, являющихся упругими по следующему определению. Если просматривать кинофильм, изображающий процесс столкновения, в обратном порядке, то в этом процессе не произойдёт никаких изменений, кроме того, что частица 𝐴 стала двигаться теперь справа налево, а частица 𝐵 — слева направо, тогда как раньше всё было наоборот, В этом смысле упругое соударение — это такое соударение, которое обратимо. Если изображённое на рис. 82 соударение является в этом смысле упругим, то каждый шар изменяет лишь направление своего движения, но не абсолютную величину скорости (не считая момента удара), и в результате эффект соударения сводится к простому повороту векторов скорости обеих частиц. В этой системе отсчёта можно выбрать направления осей 𝑥 и 𝑦 таким образом, что 𝑥-компоненты скоростей обеих частиц не изменятся при столкновении, тогда как их 𝑦-компоненты просто изменят знак.
Описание столкновения в трех разных системах отсчета

Рис. 83. То же столкновение, что на рис. 82, но наблюдаемое в системе отсчёта ракеты.
Нас интересует анализ 𝑦-компоненты полного импульса и сохранение этой компоненты при таком столкновении. Для этого проще всего рассмотреть столкновение в такой системе отсчета, где шар 𝐴 движется только в направлении оси 𝑦. Это система отсчета ракеты, летящей вправо по отношению к системе, в которой изображен рис. 82, со скоростью, равной 𝑥-компоненте скорости шара 𝐴. Наблюдаемое в такой системе отсчета столкновение изображено на рис. 83. Имеется также система отсчета, в которой шар 𝐵 движется только в направлении оси 𝑦. Это лабораторная система отсчета, движущаяся влево по отношению к системе, в которой изображен рис. 82, со скоростью, равной 𝑥-компоненте скорости шара 𝐵. Наблюдаемое в такой системе отсчета столкновение изображено на рис. 84.

Рис. 84. То же столкновение, что на рис. 82, но наблюдаемое в лабораторной системе отсчёта.
Мы стремимся узнать всё, что только можно, об импульсе частицы (скорость которой может быть очень близка к скорости света), исходя из данных ньютоновской физики об импульсе частицы с очень малой скоростью. Для этих целей анализ скользящего соударения подходит идеально. Мы можем подобрать такое столкновение, при котором частица-мишень обладает сколь угодно малой скоростью не только до соударения, но и после него (частица 𝐵 на рис. 84). Тогда импульс частицы-мишени может быть получен по ньютоновской формуле 𝑝=𝑚β как до, так и после соударения. Исходя из этого, легко определить изменение импульса медленной частицы (𝐵) в процессе соударения, что позволит нам найти изменение импульса и даже самый импульс быстрой частицы (𝐴). Исходя из симметрии схемы столкновения, очевидно, что приобретённый частицей 𝐵 импульс вдвое превышает величину её импульса до соударения, так что
1
2
⋅
⎛
⎜
⎝
Изменение
импульса 𝐵
⎞
⎟
⎠
=
𝑚
𝑑𝑦
𝑑𝑡
.
Импульс пропорционален величине перемещения частицы за единицу собственного времени
Частица 𝐴 передаёт часть импульса частице 𝐵, но не за счёт изменения абсолютной величины своего импульса, а за счёт изменения направления своего вектора импульса. Иными словами, переданный импульс составляет меньшую и известную нам сторону треугольника импульсов. Другие две (равные друг другу) стороны этого треугольника являются бóльшими и неизвестны нам. Однако мы знаем, чему равны как длинные, так и короткая стороны подобного треугольника — треугольника перемещений. Из пропорциональности соответствующих сторон подобных треугольников мы сразу же получаем (см. рис. 85) выражение для импульса быстро движущейся частицы 𝐴:
𝒑=𝑚
𝑑𝒓
𝑑τ
=𝑚
⎛
⎜
⎝
Перемещение за единицу
собственного времени
⎞
⎟
⎠
.
(70)
Компоненты этого вектора по отдельности 1) равны:
𝑝
𝑥
=
𝑚
𝑑𝑥
𝑑τ
,
𝑝
𝑦
=
𝑚
𝑑𝑦
𝑑τ
,
𝑝
𝑧
=
𝑚
𝑑𝑧
𝑑τ
(71)
в лабораторной системе отсчёта.
1) Почему не 𝑝𝑥 а 𝑝𝑥? В четырёхмерной геометрии пространства-времени в отличие от эвклидовой геометрии пространства существенно расположение индекса (см. подробности относительно стандартных обозначений в примечании на стр. 157).
В системе отсчёта ракеты компоненты импульса даются выражениями, аналогичными формулам (71) с той лишь разницей, что в них фигурируют 𝑑𝑥', 𝑑𝑦' и 𝑑𝑧' — компоненты перемещения, измеренные в системе отсчёта ракеты. Интервал собственного времени 𝑑τ' между двумя близкими событиями на мировой линии частицы обладает одним и тем же значением при вычислении исходя из данных, полученных на ракете, и при вычислении на основании лабораторных измерений («инвариантность интервала»). Поэтому излишне различать 𝑑τ и 𝑑τ'. Кроме того, величина 𝑑𝑦' (в системе отсчёта ракеты) равна величине 𝑑𝑦 (в лабораторной системе отсчёта), а также 𝑑𝑧=𝑑𝑧' Следовательно, компоненты импульса
𝑝
𝑦
=
𝑚
𝑑𝑦
𝑑τ
и
𝑝
𝑧
=
𝑚
𝑑𝑧
𝑑τ
,
перпендикулярные к направлению движения ракеты относительно лабораторной системы отсчёта, не зависят от скорости этого движения.
Импульс аналогичен перемещению в том отношении, что поперечные компоненты этих обоих векторов не зависят от скорости движения наблюдателя. Такая аналогия этих двух векторов имеет очень простую причину: импульс получается из перемещения (Δ𝑥, Δ𝑦, Δ𝑧) путём умножения на величину 𝑚/Δτ, одинаковую во всех инерциальных системах отсчёта!
Массу наиболее целесообразно определять как не зависящий от скорости коэффициент в выражении для импульса
Из исследования импульса, проделанного на рис. 85, ясно, что величина 𝑚 — это масса в том смысле, в каком её понимают в ньютоновской механике. Поэтому 𝑚 есть величина постоянная, одинаковая для всех скоростей, всех положений и всех моментов времени. Всё различие между релятивистской формулой для импульса (например, 𝑚⋅𝑑𝑥/𝑑τ) и соответствующей ньютоновской формулой (𝑚⋅𝑑𝑥/𝑑𝑡) сводится поэтому к различию между собственным и лабораторным временем, а не к различию в 𝑚 при этих двух описаниях природы. В некоторых прежних изложениях теории относительности ньютоновское выражение для импульса (𝑚⋅𝑑𝑥/𝑑𝑡) исправлялось не путём простой замены 𝑑𝑡 на 𝑑τ, принятой сейчас, а путём введения «массы движения», зависящей от скорости таким образом, чтобы можно было продолжать пользоваться формулами типа Ньютона, например:
𝑝
𝑥
⎛
⎜
⎝
релятивистская
величина
⎞
⎟
⎠
=
𝑚
движения
⋅
𝑑𝑥
𝑑τ
.
Эта масса движения должна тогда быть равна
𝑚
движения
=
𝑚
𝑑𝑡
𝑑τ
=
𝑚
√1-β²
.
(72)
Такое обозначение ещё можно иногда встретить. Однако в физических рассуждениях полезнее всего использовать величины, одинаковые во всех системах отсчёта, такие, как 𝑚 и 𝑑τ. Этот факт сейчас получает всё более широкое признание. Поэтому мы будем обычно понимать под термином «масса» не зависящую от скорости величину 𝑚.

Рис. 85. Вывод релятивистского выражения для импульса из закона сохранения импульса в случае скользящего соударения.
Частица 𝐵 движется настолько медленно, что ньютоновское выражение для импульса представляет собой сколь угодно хорошее приближение для её импульса: (Импульс)=𝑚⋅Δ𝑦𝐵/Δ𝑡𝐵 Здесь Δ𝑡𝐵 — время, за которое частица 𝐵 пролетает расстояние Δ𝑦𝐵 от нижней границы рисунка до точки соударения. Это лабораторное время по своей величине сколь угодно близко к собственному времени полёта Δτ𝐵 по той же причине, а именно потому, что скорость 𝐵 может быть выбрана сколь угодно малой. (Пример: при β=0,01 относительное различие величин Δτ и Δ𝑡 составляет 5⋅10⁻⁵). Поэтому импульс 𝐵 можно записать как 𝑚⋅Δ𝑦𝐵/Δτ𝐵. Зная величину импульса 𝐵, можно найти величину импульса 𝑝𝐴 частицы 𝐴, сравнивая изображённые здесь диаграммы для импульса и для перемещения 𝐴 (правило подобных треугольников). Для частицы 𝐴 𝑦-компонента перемещения может быть сделана равной 𝑦-компоненте перемещения частицы 𝐵 (симметричное расположение «пола» и «потолка», о которые ударяются соответственно 𝐴 и 𝐵): Δ𝑦𝐴=Δ𝑦𝐵=Δ𝑦. Промежуток собственного времени между моментами соударения и удара об пол (потолок) также один и тот же для 𝐴 и 𝐵: Δτ𝐴=Δτ𝐵.
Доказательство 1) Движение частицы 𝐴 в системе отсчёта ракеты совпадает с движением частицы 𝐵 в лабораторной системе отсчёта (ср. рис. 83 и 84). Поэтому собственные времена полёта равны одно другому: (Δτ𝐴)система ракеты = (Δτ𝐵)лабораторная система.
2) Но собственное время между двумя событиями (столкновение и удар) одинаково во всех системах отсчёта, т.е. (Δτ𝐴)лабораторная ракеты = (Δτ𝐴)система ракеты.
3) Следовательно, (Δτ𝐴)лабораторная ракеты = (Δτ𝐵)лабораторная система.
что и требовалось доказать. Конечно, лабораторные часы показывают совершенно разные продолжительности полётов частиц 𝐴 и 𝐵, если 𝐴 обладает скоростью, близкой к скорости света: (Δ𝑡𝐴)²лабораторная ракеты = = (Δτ𝐴)²лабораторная ракеты + (Δ𝑥𝐴)²лабораторная ракеты ≫ ≫ (Δτ𝐴)²лабораторная ракеты = = (Δτ𝐵)²лабораторная ракеты = (Δ𝑡𝐵)²лабораторная ракеты .
Поэтому импульс частицы 𝐴 в конце концов выражается непосредственно через величины, которые относятся лишь к движению 𝐴: 𝒑𝐴 = 𝑚
Δ𝒓𝐴
Δτ𝐴 .
Переходя от конечных разностей к производным и вспоминая, что импульс и перемещение обладают одним и тем же направлением, получим 𝒑 = 𝑚
𝑑𝒓
𝑑τ .
Это и есть релятивистская формула для импульса, справедливая для частицы, обладающей сколь угодно высокой энергией.
Релятивистский импульс сводится к ньютоновскому в пределе малых скоростей
Насколько велико различие между релятивистским и ньютоновским выражениями для импульса? Релятивистское выражение для импульса должно сводиться к ньютоновскому, когда скорости частиц малы. Такие медленные частицы проходят путь, много меньший одного метра за один метр времени (𝑑𝑟/𝑑𝑡). Тогда собственное время √(𝑑𝑡)²-(𝑑𝑟)²=√1-β²⋅𝑑𝑡 при любом перемещении медленной частицы очень мало отличается от координатного времени 𝑑𝑡:
𝑑τ
≈
𝑑𝑡
(для медленной частицы),
причём для β=0,01 это равенство справедливо с точностью до 5 : 100 000 и стремится к тождественному совпадению при β→0. При этом релятивистское выражение для импульса 𝒑=𝑚⋅𝑑𝒓/𝑑τ совпадает с ньютоновским выражением 𝒑=𝑚⋅𝑑𝒓/𝑑𝑡 величина 𝑚 одна и та же (инвариант 𝑚!).
В некоторых случаях удобнее выражать импульс через параметр скорости частицы θ, а иногда через её скорость β=th θ. Тогда
𝑝
=
𝑚
𝑑𝑟
𝑑τ
=
𝑚
𝑑𝑟
√(𝑑𝑡)²-(𝑑𝑟)²
=
=
𝑚⋅𝑑𝑟/𝑑𝑡
=
⎡
⎢
⎣
1
-
⎛
⎜
⎝
𝑑𝑟
⎞
⎟
⎠
²
⎤
⎥
⎦
½
𝑑𝑡
=
𝑚β
√1-β²
=
𝑚 th θ
√1-th²θ
=
=
𝑚 th θ
=
⎧
⎪
⎩
ch²θ
-
sh²θ
⎫
⎪
⎭
½
ch²θ
ch²θ
𝑚 th θ ch θ
√ch²θ-sh²θ
=
𝑚 sh θ
,
так что
𝑝
=
𝑚 sh θ
=
𝑚β
√1-β²
⎛
⎜
⎜
⎝
релятивистский
импульс,
размерность массы
⎞
⎟
⎟
⎠
(73)
Другой вид имеет ньютоновское выражение для импульса:
𝑝
=
𝑚β
=
𝑚 th θ
⎛
⎜
⎜
⎝
ньютоновский
импульс,
размерность массы
⎞
⎟
⎟
⎠
(74)
Эти два выражения для импульса различаются множителем
𝑑𝑡
𝑑τ
=
ch θ
1
√1-β²
,
который определяет отношение между лабораторным временем и собственным временем, регистрируемым часами, летящими вместе с частицей. Этот множитель совпадает с коэффициентом в формуле замедления хода времени (см. упражнение 10). Присутствие такого множителя в релятивистской формуле для импульса показывает, что частица способна нести с собой в процессах столкновений сколь угодно большой импульс, если только она движется со скоростью, близкой к скорости света. Этого никак нельзя было ожидать, опираясь на неверную в этом случае ньютоновскую формулу для импульса 𝑝=𝑚β, где 𝑚 — постоянная, а β не может превышать единицы.
Таким образом, выражение для импульса быстро движущихся частиц существенно отличается от предсказываемого теорией Ньютона. Однако процедура определения массы некоторой новой частицы, принявшей участие в процессе столкновения, в принципе одна и та же как в релятивистской, так и в ньютоновской механике. Её суть может быть выражена по-разному: 1) как принцип действия и противодействия; 2) как принцип, связывающий отдачу ружья с импульсом пули; 3) как закон сохранения импульса.
Определение массы неизвестной частицы по упругому столкновению её со стандартной частицей

Рис. 86. Скорости до и после лобового упругого столкновения, наблюдаемые в той системе отсчёта, где полный импульс равен нулю.
Рассмотрим специально лобовое упругое столкновение: 1) стандартной частицы массы 𝑚₁ (пусть величина этой массы произвольно устанавливается Международным комитетом мер и весов) и 2) исследуемой частицы, обладающей пока неизвестной массой 𝑚₂ величину которой нам нужно определить. Говоря, что столкновение является лобовым и упругим, мы имеем в виду существование такой системы отсчёта, в которой зарегистрированные до и после соударения данные о скоростях частиц обнаруживают симметрию, изображённую на рис. 86. Эта симметрия состоит в том, что полный импульс меняет свой знак на обратный в результате соударения. Но ведь полный импульс при соударении сохраняется! Значит, этот полный импульс должен быть равен нулю. Итак, импульсы наших двух частиц после столкновения должны удовлетворять условию
𝑚₁
⎛
⎜
⎝
𝑑𝑥
𝑑τ
⎞
⎟
⎠₁
+
𝑚₂
⎛
⎜
⎝
𝑑𝑥
𝑑τ
⎞
⎟
⎠₂
=
0.
Из этого соотношения можно получить выражение неизвестной массы в единицах известной массы стандартной частицы:
𝑚₂
𝑚₁
=
(-𝑑𝑥/𝑑τ)₁
(𝑑𝑥/𝑑τ)₂
=
=
-Δ𝑥₁
√(Δ𝑡₁)²-(Δ𝑥₁)²
×
√(Δ𝑡₂)²-(Δ𝑥₂)²
Δ𝑥₂
.
(75)
Здесь Δ𝑥₁ и Δ𝑥₂ — расстояния, пройденные каждой из двух частиц из точки соударения до точек наблюдения, а Δ𝑡₁ и Δ𝑡₂ — соответствующие времена движения. В случае упругого столкновения нерелятивистских частиц правая сторона равенства (75) принимает ньютоновский вид
𝑚₂
𝑚₁
=-
β₂
β₁
=
-Δ𝑥₁/Δ𝑡₁
Δ𝑥₂/Δ𝑡₂
⎛
⎜
⎝
ньютоновский
предел
⎞
⎟
⎠
.
(76)
Простота релятивистского определения импульса не может быть вполне оценена, пока импульс не рассматривается как пространственная часть 4-вектора энергии-импульса. И только тогда становится ясно, что баланс энергии в процессах столкновения может служить косвенной проверкой закона сохранения импульса, так что к бесчисленному множеству непосредственных экспериментальных способов проверки закона сохранения импульса добавляется ещё этот косвенный способ.
12. 4-ВЕКТОР ЭНЕРГИИ-ИМПУЛЬСА
Для того чтобы представить себе импульс и энергию как части более обширного единого целого, полезно вспомнить, как пространство и время объединяются, становясь частями также более обширного единого целого. Рассмотрим переход частицы из мировой точки (события) 𝐴 в пространстве-времени в соседнюю мировую точку 𝐵. Идея объединения пространства и времени состоит в том, чтобы рассматривать 4-вектор, соединяющий 𝐴 и 𝐵 1). Компоненты этого 4-вектора (смещения 𝑑𝑥, 𝑑𝑦, 𝑑𝑧 и 𝑑𝑡) имеют разные значения в зависимости от того, в какой системе отсчёта рассматривается этот 4-вектор. Несмотря на произвольный способ описания 4-вектора 𝐴𝐵, который мы выберем, этот 4-вектор оказывается вполне строго определён. Не только интервал имеет одну и ту же величину во всех системах отсчёта! Что ещё более важно, расположение самих событий 𝐴 и 𝐵, а значит, и положение 4-вектора 𝐴𝐵 в пространстве-времени определяются так же строго, как положение двух городских ворот, независимо от того, какие координаты мы используем, и даже независимо от того, используем ли мы вообще какие бы то ни было координаты.
1) В 1872 г. в своей лекции в ознаменование вступления в должность профессора Эрлангенского университета Феликс Клейн провозгласил новую точку зрения на геометрию, что оказало решающее влияние на современную геометрию. Ключевой пункт его идеи состоял в проведении различия между геометриями разного рода, исходя из законов преобразования компонент величин. Например, можно с полной ясностью увидеть различие между эвклидовой геометрией и лоренцевой геометрией реального физического мира на основании используемого ныне определения вектора:
4-вектор определяется заданием в каждой инерциальной системе отсчёта четырёх чисел (различных в разных системах!), причём эти числа преобразуются при переходах между системами отсчёта по формулам преобразования Лоренца (32).
3-вектор определяется заданием в каждой эвклидовой системе координат трёх чисел (компонент, различных в разных системах координат!), причём эти числа преобразуются при переходах между системами координат по соответствующим формулам преобразования поворота геометрии Эвклида (29).
Зная, что некоторая величина — вектор, и зная значения её компонент лишь в одной системе отсчёта, можно сразу же найти значения её компонент в любой другой системе отсчёта, используя соответствующий 3- или 4-мерный закон преобразования компонент.
Энергия как четвёртая компонента 4-вектора энергии-импульса
Мы ожидаем, что подобным же образом можно будет понять смысл импульса и энергии частицы на любом заданном этапе её истории, понять их как компоненты и не более как компоненты 4-вектора, существующего независимо от всякого выбора координат. Более того, связь такого «4-вектора энергии-импульса» с 4-вектором смещения 𝐴𝐵 не будет ни косвенной, ни далёкой. Разве может быть что-либо более последовательным и прямым, чем следующая цепочка рассуждений:
1) Берётся 4-вектор смещения 𝐴𝐵 с компонентами
𝑑𝑡
,
𝑑𝑥
,
𝑑𝑦
,
𝑑𝑧
(см. рис. 87).

Рис. 87. 4-вектор перемещения 𝐴𝐵, соединяющий события 𝐴 и 𝐵 на мировой линии частицы. Он изображён здесь для частного случая, когда 𝑦- и 𝑧- компоненты перемещения 𝑑𝑦 и 𝑑𝑧 одновременно равны нулю.
2) С помощью 4-вектора 𝐴𝐵 строится единичный касательный вектор путём деления его на интервал собственного времени
𝑑τ
=
√
(𝑑𝑡)²-(𝑑𝑥)²-(𝑑𝑦)²-(𝑑𝑧)²
,
взятый между мировыми точками 𝐴 и 𝐵 компоненты этого касательного вектора
𝑑𝑡
𝑑τ
𝑑𝑥
𝑑τ
,
𝑑𝑦
𝑑τ
,
𝑑𝑧
𝑑τ
изображены на рис. 88.
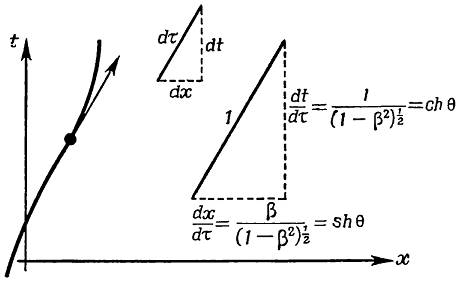
Рис. 88. Единичный касательный вектор к мировой линии частицы, полученный делением 4-вектора перемещения 𝐴𝐵 (рис. 87) на инвариантный интервал собственного времени 𝑑τ. Временная и пространственная компоненты единичного вектора касательной равны
𝑑𝑡
𝑑τ =
𝑑𝑡
√(𝑑𝑡)²-(𝑑𝑥)² =
1
√1-(𝑑𝑥/𝑑𝑡)² =
1
√1-β² = = 1 = 1 = √1-th²θ
⎛
⎜
⎝ ch²θ - sh²θ
⎞
⎟
⎠
½
ch²θ ch²θ =
ch θ
√ch²θ-sh²θ = ch θ
и
𝑑𝑥
𝑑τ =
𝑑𝑥
√(𝑑𝑡)²-(𝑑𝑥)² =
𝑑𝑡/𝑑𝑥
√1-(𝑑𝑥/𝑑𝑡)² =
β
√1-β² = = th θ = th θ = √1-th²θ
⎛
⎜
⎝ ch²θ - sh²θ
⎞
⎟
⎠
½
ch²θ ch²θ =
th θ ch θ
√ch²θ-sh²θ = sh θ .
(В приведённом здесь частном случае полная пространственная компонента перемещения 𝑑𝑟 равна 𝑥-компоненте перемещения 𝑑𝑥. В более общем случае пространственная часть перемещения имеет вид 𝑑𝑟=√(𝑑𝑥)²+(𝑑𝑦)²+(𝑑𝑧)², и тогда она даёт пространственную компоненту единичного вектора касательной, равную
𝑑𝑟
𝑑τ =
β
√1-β² sh θ .
⎞
⎟
⎠
3) 4-вектор энергии-импульса получается при умножении этого единичного вектора на постоянную 𝑚; его компоненты равны
𝐸
=
𝑝
𝑡
=
𝑚
𝑑𝑡
𝑑τ
,
𝑝
𝑥
=
𝑚
𝑑 𝑥
𝑑τ
,
𝑝
𝑦
=
𝑚
𝑑 𝑦
𝑑τ
,
𝑝
𝑧
=
𝑚
𝑑 𝑧
𝑑τ
(77)
(см. рис. 89).
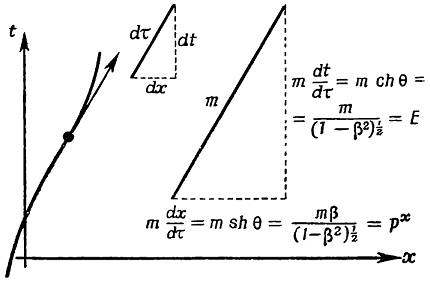
Рис. 89. 4-вектор энергии-импульса, полученный при умножении единичного вектора касательной (рис. 88) на постоянную массу 𝑚 частицы. Временная компонента его называется «релятивистской энергией» и обозначается через 𝐸.
Подробности хода этих рассуждений и различные формы записи пространственных и временных компонент всех этих трёх 4-векторов приведены на рисунках. Не может быть никакого сомнения в том, что 4-вектор (𝑑𝑡, 𝑑𝑥, 𝑑𝑦, 𝑑𝑧) остаётся 4-вектором после деления его на величину 𝑑τ и умножения на величину 𝑚, которые обе остаются одинаковыми во всех системах отсчёта.
Сохранение энергии 𝐸 в одной системе отсчёта следует из сохранения импульса во всех системах отсчёта
Этим и исчерпывается краткое введение во взаимосвязь между импульсом и энергией. Перейдём теперь к важному вопросу: почему временну'ю компоненту получившегося 4-вектора можно называть энергией? Причины две. Во-первых, потому что эта компонента имеет правильную размерность — она выражается в единицах массы. Во-вторых, и это важнее всего, потому что полная величина этой компоненты сохраняется при всех столкновениях. Доказательство того, что сумма значений 𝐸 для всех частиц подчиняется закону сохранения, базируется на простом соображении: если три компоненты какого-либо 4-вектора сохраняются во всех системах отсчёта, то четвёртая компонента также должна сохраняться (см. табл. 9). Мы знаем, что три (пространственные) компоненты полного импульса физической системы сохраняются во всех системах отсчёта. Поэтому полная временная компонента его тоже сохраняется. Подробности этого доказательства см. ниже.
Формулы преобразования Лоренца для элементов смещения при переходе между лабораторной системой отсчёта и системой ракеты можно записать в виде (37):
𝑑𝑡'
=-
𝑑𝑥 sh θ
𝑟
+
𝑑𝑡 ch θ
𝑟
,
𝑑𝑦'
=
𝑑𝑦
,
𝑑𝑥'
=
𝑑𝑥 ch θ
𝑟
-
𝑑𝑡 sh θ
𝑟
,
𝑑𝑧'
=
𝑑𝑧
.
Эти равенства не нарушатся, если их разделить с обеих сторон на инвариантный интервал 𝑑τ=𝑑τ' и умножить на инвариантную массу 𝑚:
𝑚
𝑑𝑡'
𝑑τ'
=-
𝑚
𝑑𝑥
𝑑τ
sh θ
𝑟
+
𝑚
𝑑𝑡
𝑑τ
ch θ
𝑟
,
𝑚
𝑑𝑦'
𝑑τ'
=
𝑚
𝑑𝑦
𝑑τ
,
𝑚
𝑑𝑥'
𝑑τ'
=
𝑚
𝑑𝑥
𝑑τ
ch θ
𝑟
-
𝑚
𝑑𝑡
𝑑τ
sh θ
𝑟
,
𝑚
𝑑𝑧'
𝑑τ'
=
𝑚
𝑑𝑧
𝑑τ
,
Но 𝑚⋅𝑑𝑥/𝑑τ, 𝑚⋅𝑑𝑦/𝑑τ и 𝑚⋅𝑑𝑧/𝑑τ — компоненты релятивистского импульса, а 𝑚⋅𝑑𝑡/𝑑τ — временна'я компонента нового 4-вектора, т.е. та самая величина, которую мы решили назвать «релятивистской энергией 𝐸». Мы пришли, таким образом, к следующим важным соотношениям, связывающим импульс и новую величину 𝐸 в одной системе отсчёта с импульсом и 𝐸' — в другой инерциальной системе отсчёта:
𝐸'
=-
𝑝
𝑥
sh θ
𝑟
+
𝐸 ch θ
𝑟
,
𝑝'
𝑦
=
𝑝
𝑦
,
𝑝'
𝑥
=
𝑝
𝑥
ch θ
𝑟
-
𝐸 sh θ
𝑟
,
𝑝'
𝑧
=
𝑝
𝑧
.
(78)
Преобразования Лоренца для энергии и импульса
Рассмотрим теперь столкновение двух частиц; пусть 𝑝₁𝑥 и 𝑝₂𝑥 будут соответственно 𝑥-компонентами импульса этих частиц до столкновения, измеренными в лабораторной системе отсчёта, а 𝐸₁ и 𝐸₂ — их «релятивистскими энергиями» в этой же системе. Пусть аналогично 𝑝₁'𝑥 и 𝑝₂'𝑥 будут 𝑥-компонентами импульса этих частиц до столкновения, измеренными в системе отсчёта ракеты. Для того чтобы записать 𝑥-компоненту полного импульса в системе отсчёта ракеты до столкновения, следует сложить друг с другом два выражения 𝑥-компоненты импульса (для каждой частицы), фигурирующие как второе уравнение в системе (78):
(𝑝₁'
𝑥
+
𝑝₂'
𝑥
)
=
(𝑝₁
𝑥
+
𝑝₂
𝑥
)
ch
θ
𝑟
-
(𝐸₁
+
𝐸₂)
sh
θ
𝑟
.
Таблица 9.
Неизменность импульса в двух системах отсчёта гарантирует неизменность энергии в обеих системах
**
СВЯЗЬ С ОБСУЖДЕНИЕМ СОХРАНЕНИЯ ИМПУЛЬСА И ЭНЕРГИИ

Равенство нулю 𝑥-компоненты вектора в одной системе отсчёта никак не облегчает исследование поведения 𝑡-компоненты этого вектора. Здесь изображены три вектора, обладающие разными абсолютными величинами (и один из них вообще равен нулю), которые все кажутся одинаковыми для исследователя, знающего лишь величину их 𝑥-компонент.
**
Закон сохранения импульса утверждает, что полная сумма импульсов после столкновения равна полной сумме импульсов до столкновения. Или, что то же самое, имеется определённая величина — изменение полного импульса при столкновении, о которой мы знаем, что она равна нулю. Но это ещё не всё. Нам нужна вся информация о полном 4-векторе (равном изменению полного 4-вектора энергии-импульса при столкновении). Рассматривая одну только пространственную компоненту (или, на нашей диаграмме, удостоверившись только в равенстве нулю 𝑥-компоненты этого 4-вектора), мы никак не можем здесь показать, что равна нулю и временная компонента (иначе говоря, что равно нулю изменение энергии).

Взглянуть на этот же вектор из другой системы отсчёта — значит сразу же обнаружить разницу между векторами, казавшимися одинаковыми в прежней системе отсчёта. Допустим, что, как мы знаем, пространственная компонента некоторого 4-вектора равна нулю в двух разных системах отсчёта. Тогда можно быть уверенным, что этот 4-вектор вообще равен нулю (случай, изображённый справа).
**
Равенство нулю пространственной компоненты («импульсной компоненты») определённого 4-вектора (который и есть разность полных 4-векторов энергии-импульса до и после столкновения) в двух различных системах отсчёта гарантирует, что все компоненты этого 4-вектора вообще равны нулю. Значит, из того факта, что импульс сохраняется как в лабораторной системе отсчёта, так и в системе отсчёта ракеты, можно заключить, что и энергия сохраняется в обеих системах.
Такое же уравнение можно записать для этих частиц и после столкновения (две отдельные частицы после упругого столкновения; одна объединённая частица при неупругом ударе и много частиц, если неупругий удар сопровождался дроблением). Можно следующим образом сопоставить эти уравнения до и после столкновения:
До столкновения
: полная
𝑥
-компонента импульса, наблюдаемая в системе отсчёта ракеты
=
До столкновения
: полная
𝑥
-компонента импульса, наблюдаемая в лабораторной системе отсчёта
ch θ
𝑟
-
До столкновения
: полная релятивистская энергия, наблюдаемая в лабораторной системе отсчёта
sh θ
𝑟
(79)
↑
↑
↑
1-й этап
: эти члены равны друг другу ввиду закона сохранения импульса!
2-й этап
: эти члены равны друг другу ввиду закона сохранения импульса!
Вывод
: эти члены равны друг другу, что доказывает сохранение релятивистской энергии!
↓
↓
↓
После столкновения
: полная
𝑥
-компонента импульса, наблюдаемая в системе отсчёта ракеты
=
После столкновения
: полная
𝑥
-компонента импульса, наблюдаемая в лабораторной системе отсчёта
ch θ
𝑟
-
После столкновения
: полная релятивистская энергия, наблюдаемая в лабораторной системе отсчёта
sh θ
𝑟
(80)
Второй раз в этой главе мы потребуем, чтобы импульс сохранялся при столкновениях как в лабораторной системе отсчёта, так и в системе отсчёта ракеты. Ввиду этого требования каждая из скобок, обозначающая импульс в уравнении (79), будет равна соответствующей скобке, обозначающей импульс в уравнении (80). Если справедливы оба уравнения, причём соответствующие скобки для импульсов равны друг другу, то скобки, обозначающие энергию, также должны быть равны. Поэтому в лабораторной системе отсчёта полная релятивистская энергия одинакова до и после столкновения: полная релятивистская энергия при столкновениях сохраняется.
Свойства полной релятивистской энергии
Из этих рассуждений мы получаем три вывода. Во-первых, мы можем сопоставить каждой частице массы 𝑚 «релятивистскую энергию»
𝐸
=
𝑚
𝑑𝑡
𝑑τ
.
Во-вторых, если имеется несколько свободно движущихся частиц, то релятивистская энергия этой системы равна сумме релятивистских энергий отдельных частиц. В-третьих, когда эти частицы разлетаются друг от друга после соударений и энергии отдельных частиц изменяются, полная релятивистская энергия системы остаётся той же, какой она была до столкновения (сохранение релятивистской энергии).
Свойство аддитивности, когда энергия системы свободных частиц равна сумме энергий отдельных частиц системы, знакомо нам на примере импульса, когда полный импульс физической системы складывается из импульсов входящих в неё частиц. Факт такой аддитивности говорит о том, что для нахождения энергии системы частиц достаточно вычислить энергии всех входящих в неё частиц по отдельности.
Другие способы выражать энергию
Выражение для релятивистской энергии частицы может быть записано множеством способов, причём целесообразность использования каждого из них зависит от обстоятельств. Так, согласно рис. 89, мы получим
𝐸
=
𝑚
𝑑𝑡
𝑑τ
=
𝑚
√1-β²
=
𝑚 ch θ
.
(81)
Какие можно сделать заключения о связи между релятивистской энергией 𝐸 и скоростью из этого соотношения? Какие заключения можно сделать отсюда о связи между 𝐸 и энергией в ньютоновской теории? Между энергией и импульсом? При очень малых скоростях β можно разложить выражение для релятивистской энергии в ряд по степеням β, пользуясь формулой бинома или каким-либо другим методом:
𝐸
=
𝑚
√1-β²
=
𝑚⋅(1-β²)⁻¹
/
²
=
=
𝑚
⎛
⎜
⎝
1
+
β²
2
+
3
8
β²
+
…
⎞
⎟
⎠
.
Если скорость β достаточно мала, в этом разложении можно ограничиться с любой желаемой степенью точности первыми двумя членами:
𝐸
≈
𝑚
⎛
⎜
⎝
1
+
β²
2
⎞
⎟
⎠
=
𝑚
+
𝑚β²
2
⎛
⎜
⎝
малые
скорости
⎞
⎟
⎠
.
(82)
Но здесь ½𝑚β² — обычное ньютоновское выражение для кинетической энергии, взятое в единицах массы. Значит, релятивистская энергия имеет отношение к кинетической энергии частицы, хотя она (величина 𝐸) и не равна этой кинетической энергии ввиду наличия добавочного члена 𝑚. Этот добавочный член сохраняется, даже если частица находится в состоянии покоя, т.е. вообще лишена кинетической энергии. Поэтому член 𝑚 называют энергией покоя 𝐸покоя частицы,
𝐸
покоя
=
𝑚
⎛
⎜
⎝
энергия покоя в
единицах массы
⎞
⎟
⎠
(83)
Выражение для энергии покоя частицы в обычных единицах 𝐸покоя обычн можно получить из выражения для энергии покоя в единицах массы, умножая последнее на множитель перевода 𝑐². Мы приходим тогда к знаменитому выражению
𝐸
покоя обычн
=
𝑚𝑐²
⎛
⎜
⎝
энергия покоя в
обычных единицах
⎞
⎟
⎠
(84)
Включение энергии покоя существенно для выполнения закона сохранения
Невозможно удовлетворить требованию сохранения импульса и энергии во всех инерциальных системах отсчёта, если не учитывать во всех системах энергию покоя в составе полной энергии. Этот урок, преподнесённый нам физикой пространства-времени, никак не предполагался в ньютоновской физике. Механика Ньютона не знает выражения для энергии покоя частицы, хотя, правда, в ней допускается добавление к энергии частицы любой постоянной добавочной энергии без нарушения законов, описывающих движение этой частицы. Предельное значение релятивистского выражения для энергии в случае малых скоростей можно рассматривать как нахождение величины этой ранее произвольной постоянной.
Релятивистское выражение для кинетической энергии
Можно считать, что релятивистская энергия частицы в любой системе отсчёта складывается из двух частей: энергии покоя частицы 𝑚 плюс дополнительной энергии, которой обладает частица благодаря своему движению. Этот добавок и есть кинетическая энергия частицы. Тогда релятивистское выражение для кинетической энергии имеет вид
𝑇
=
𝐸-𝐸
покоя
=
𝑚 ch θ
-
𝑚
=
𝑚(ch θ-1)
=
=
𝑚
⎛
⎜
⎝
1
√1-β²
-1
⎞
⎟
⎠
⎛
⎜
⎝
кинетическая энергия
в единицах массы
⎞
⎟
⎠
(85)
Это выражение для релятивистской кинетической энергии справедливо для частиц, движущихся с любыми скоростями. Напротив, ньютоновская формула для кинетической энергии ½𝑚β² верна лишь для медленных частиц.
При возрастании скорости и её стремлении к скорости света энергия возрастает безгранично. Поэтому, если бы мы даже располагали неограниченными энергетическими ресурсами, нам всё равно не удалось бы разогнать частицу до скорости света. Таблица 10 иллюстрирует это быстрое возрастание энергии, необходимой для ускорения частицы по мере приближения её скорости к скорости света.
Таблица 10.
Энергия, которую должен получить атом водорода (
𝑚=1,67⋅10⁻²⁷
кг
) для того, чтобы приобрести скорость, близкую к скорости света
β
Расстояние
,
пройденное световой вспышкой от линии старта при состязании света и частицы за время
,
пока частица не отстанет на 1 см
𝐸обычн
𝑚𝑐²
𝑇обычн
𝑚𝑐²
𝑇обычн
джоули
Обыденный эквивалент этой энергии
0,5
2
см
1,15
0,15
2⋅10⁻¹¹
-
0,99
2
м
7,1
6,1
10⁻⁹
-
0,99999
1
км
222
221
3⋅10⁻⁸
Кинетическая энергия одной крупинки поваренной соли, упавшей с высоты 1 см
0,999
…
99 (13 девяток)
10
¹¹
м
1
)
2,2⋅10⁶
~2,2⋅10⁶
3⋅10⁻⁴
Кинетическая энергия одной крупной дробинки, упавшей с высоты 1 см
0,9999
…
99 (18 девяток)
10
¹⁶
м
2
)
7,1⋅10⁸
~7,1⋅10⁸
10⁻¹
Кинетическая энергия одной крупной дробинки, упавшей из окна третьего этажа
0,9999
…
999 (28 девяток)
10
²⁶
м
3
)
7,1⋅10¹³
7,1⋅10¹³
10⁴
Кинетическая энергия мотоцикла, движущегося со скоростью 40 км/час
1) Около ²/₃ расстояния от Солнца до Земли.
2) Около одного светового года.
3) Приблизительное расстояние до самой далёкой сфотографированной в настоящее время галактики.

Рис. 90. 4-вектор энергии-импульса.
Энергию как временну'ю компоненту 4-вектора энергии-импульса или как сторону треугольника на рис. 90, направленную вдоль оси времени, можно вычислить по методам, обычно применяемым для нахождения сторон любого треугольника. В двух основных методах используются пропорциональность и теорема Пифагора. Чтобы найти энергию как функцию скорости, мы пользовались подобием треугольника 𝑚𝐸𝑝 и треугольника 𝑑τ 𝑑𝑡 𝑑𝑥 (см. рис. 87). Из пропорциональности их сторон мы нашли соотношение
𝐸
𝑚
=
𝑑𝑡
𝑑τ
=
1
√1-β²
.
Теперь же нас интересует зависимость энергии от импульса. Чтобы найти её, достаточно проанализировать один лишь треугольник 𝑚𝐸𝑝, но при этом необходимо иметь в виду, что для него справедлива не эвклидова, а лоренцева геометрия. Квадрат гипотенузы определяется тогда не как сумма, а как разность квадратов катетов, так что
𝑚²
=
𝐸²
-
𝑝²
(в единицах массы).
(82)
Масса как абсолютная величина 4-вектора энергии-импульса
Но так определяется квадрат «длины» 4-вектора энергии-импульса 1). Эта формула совершенно аналогична выражению для квадрата четырёхмерного пространственно-временно'го интервала между соседними мировыми точками на мировой линии частицы
(𝑑τ)²
=
(𝑑𝑡)²
-
(𝑑𝑟)²
.
1) По ряду причин удобно выражать квадрат абсолютной величины 4-вектора через все четыре компоненты этого вектора, однако при этом следует быть несколько более внимательным, чем при записи квадрата 3-мерного вектора в эвклидовом пространстве. В этой книге, как и в большей части современной литературы, 4-векторы записываются через их компоненты с верхними индексами (контравариантные компоненты): 𝑝 𝑡 = 𝐸 = 𝑚
𝑑𝑡
𝑑τ , 𝑝 𝑥 = 𝑚
𝑑𝑥
𝑑τ , 𝑝 𝑦 = 𝑚
𝑑𝑦
𝑑τ , 𝑝 𝑧 = 𝑚
𝑑𝑧
𝑑τ .
В другом представлении используются нижние индексы (ковариантные компоненты), однако все пространственные компоненты при этом меняют знак: 𝑝 𝑡 = 𝑚
𝑑𝑡
𝑑τ , 𝑝 𝑥 =- 𝑚
𝑑𝑥
𝑑τ , 𝑝 𝑦 =- 𝑚
𝑑𝑦
𝑑τ , 𝑝 𝑧 =- 𝑚
𝑑𝑧
𝑑τ .
Эти два альтернативных представления, использующие контравариантные и ковариантные компоненты (верхние и нижние индексы), применимы не только к 𝑝, но и к другим 4-векторам, например к радиусу-вектору 𝑅, соединяющему начало координат некоторой инерциальной системы отсчета с каким-либо данным событием (мировой точкой), так что 𝑅𝑡 = 𝑡 , 𝑅𝑥 = 𝑥 , 𝑅𝑦 = 𝑦 , 𝑅𝑧 = 𝑧
и 𝑅𝑡 = 𝑡 , 𝑅𝑥 =- 𝑥 , 𝑅𝑦 =- 𝑦 , 𝑅𝑧 =- 𝑧 .
В этих обозначениях инвариантный квадрат интервала для события, отделенного от начала временноподобным интервалом, имеет стандартный вид τ² = 𝑅𝑡𝑅𝑡 + 𝑅𝑥𝑅𝑥 + 𝑅𝑦𝑅𝑦 + 𝑅𝑧𝑅𝑧 = = 𝑡² - 𝑥² - 𝑦² - 𝑧² .
Если же интервал является пространственноподобным, его квадрат следует записывать как σ² =-( 𝑅𝑡𝑅𝑡 + 𝑅𝑥𝑅𝑥 + 𝑅𝑦𝑅𝑦 + 𝑅𝑧𝑅𝑧 )= =- 𝑡² + 𝑥² + 𝑦² + 𝑧² .
4-вектор энергии-импульса является временноподобным 4-вектором по весьма простой причине: ведь две последовательные мировые точки на мировой линии одной и той же частицы разделены временноподобным интервалом. Поэтому квадрат абсолютной величины этого вектора следует вычислять по формуле, аналогичной формуле для τ², т. е.
⎛
⎜
⎜
⎝
Квадрат
абсолютной
величины
⎞
⎟
⎟
⎠ = 𝑝 𝑡 𝑝 𝑡 + 𝑝 𝑥 𝑝 𝑥 + 𝑝 𝑦 𝑝 𝑦 + 𝑝 𝑧 𝑝 𝑧 = =
𝑚²[(𝑑𝑡)²-(𝑑𝑥)²-(𝑑𝑦)²-(𝑑𝑧)²]
𝑑τ² = 𝑚² .
В геометрии Эвклида, где векторы обладают лишь пространственными компонентами, такое различие между верхними и нижними индексами несущественно, и там часто используются лишь нижние индексы, причем в эвклидовой геометрии знак пространственных контравариантных и ковариантных компонент берется один и тот же. Однако в геометрии пространства-времени, где существует разница в знаке пространственных компонент, взятых с верхними или с нижними индексами, необходимо явно учитывать контравариантность и ковариантность компонент. Кроме того, обычно удобнее работать с контравариантными компонентами 4-векторов (верхние индексы!), так как именно эти компоненты часто бывают непосредственно связаны с координатами мировых точек, дифференциалы радиусов-векторов которых являются контравариантными по определению в произвольных системах координат (не только в декартовых).
[В оригинале книги это примечание имело несколько иной вид, а именно авторы приняли, что при переходе от контравариантных к ковариантным компонентам изменяют знак не пространственные, а временная компонента 4-векторов, что позволяет проще увязать изложение с эвклидовой геометрией для 3-мерных векторов. Однако в современной литературе, особенно по общей теории относительности, преобладает противоположный выбор сигнатуры, так что многие авторы перешли к принятой нами здесь записи компонент векторов и в частной теории относительности, например Л. Д. Ландау и Е. М. Лифшиц в последнем издании (1967 г.) «Теории поля». Для того чтобы стандартизировать изложение, переводчику пришлось несколько изменить данное примечание, сохранив общий стиль авторов. Следует отметить, что здесь, как и в других частях книги, они предполагают, что используются лишь декартовы системы координат; если бы мы не ограничивались здесь декартовыми координатами (перейдя, например, к сферическим координатам), нам пришлось бы явно проводить различие между ковариантными и контравариантными компонентами векторов уже в 3-мерном эвклидовом пространстве. Тогда радиус-вектор не был бы истинным вектором: свойствами вектора обладали бы лишь его бесконечно малые приращения.— Прим. перев.]
В обеих формулах слагаемые, стоящие справа, зависят от состояния движения частицы или той системы отсчёта, в которой производится наблюдение. Иными словами, отдельные компоненты 4-вектора энергии-импульса (энергия частицы 𝐸 и её импульс 𝑝) обладают разными значениями в лабораторной системе отсчёта и в системе отсчёта ракеты. Левые части каждого из этих соотношений (масса покоя 𝑚 и интервал τ), напротив, одинаковы во всех системах отсчёта.
Явное выражение для энергии через импульс можно получить из формулы (86), разрешая её относительно 𝐸:
𝐸
=
√
𝑚²+𝑝²
.
(87)
Это выражение справедливо в равной мере как при больших, так и при малых импульсах, причём его можно упростить для обоих предельных случаев.
Выражение энергии через импульс: ньютоновский и ультрарелятивистский предельные случаи
Когда импульс 𝑝 мал по сравнению с 𝑚 (т.е. когда скорость β весьма мала по сравнению с единицей —«нерелятивистский предел»), выражение (87) можно разложить, пользуясь формулой для бинома или каким-либо иным способом, и получить
𝐸=𝑚
⎡
⎢
⎣
1+
⎛
⎜
⎝
𝑝
𝑚
⎞²
⎟
⎠
⎤½
⎥
⎦
=𝑚+
𝑝²
2𝑚
+
𝑝⁴
8𝑚³
+…
(малые
𝑝
).
При достаточно малых значениях импульса 𝑝 этот ряд можно с любой степенью точности приравнять его первым двум членам
𝐸≈𝑚
𝑝²
2𝑚
(малые
𝑝
).
(88)
Первое слагаемое имеет здесь смысл энергии покоя, а второе представляет собой ньютоновское выражение для кинетической энергии частицы с импульсом 𝑝.
Если же импульс 𝑝 очень велик по сравнению с 𝑚 («ультрарелятивистский предел»), то точное выражение (87) снова может быть разложено в степенной ряд, на этот раз в виде
𝐸=𝑝
⎡
⎢
⎣
1+
⎛
⎜
⎝
𝑚
𝑝
⎞²
⎟
⎠
⎤½
⎥
⎦
=𝑝+
𝑚²
2𝑝
+
𝑚⁴
8𝑝³
+…
(большие
𝑝
).
Если импульс достаточно велик, этот ряд можно с любой желаемой степенью точности приравнять его первому слагаемому:
𝐸≈𝑝
(ультрарелятивистский предел).
(89)
В этом предельном случае масса покоя не играет роли во взаимной связи импульса и энергии.
Правдоподобно ли, что катеты 𝐸 и 𝑝 треугольника на рис. 90 могут неограниченно возрастать, в то время как гипотенуза 𝑚 остаётся постоянной и оказывается меньше любого из катетов? Возможно ли, чтобы в прямоугольном треугольнике гипотенуза сохраняла постоянную длину, в то время как катеты неограниченно удлинялись? Такое поведение длин гипотенузы и катетов в корне противоречит законам эвклидовой геометрии. Однако рассматриваемая нами геометрия не является эвклидовой, а в лоренцевой геометрии пространства-времени квадрат гипотенузы равен разности квадратов катетов. Поэтому сочетание не изменяющейся в длине гипотенузы с неограниченно растущими и в пределе равными друг другу катетами, 𝐸 и 𝑝, отнюдь не парадоксально.
Импульс как мера скорости переноса массы-энергии
Можно и иначе убедиться в том, что энергия должна приближаться по величине к импульсу, когда каждая из этих величин становится много больше, чем масса покоя. В самом общем случае, без каких бы то ни было приближений, из формул
𝑝
=
𝑚β
√1-β²
и
𝐸
=
𝑚
√1-β²
следует результат
𝑝
=
β𝐸
(для всех скоростей).
(90)
Из этого равенства следует, что импульс 𝑝 неограниченно приближается по своей величине к энергии 𝐸, когда скорость становится сколь угодно близкой к скорости света.
Существует очень наглядная интерпретация равенства (90). Здесь 𝐸 описывает массу-энергию частицы, а β — скорость, с которой движется эта масса-энергия. Поэтому их произведение, импульс 𝑝, является мерой скорости переноса массы-энергии. Любопытно, что множитель, описывающий в этой формуле массу-энергию [величина 𝐸 в равенстве (90)], не равен той массе 𝑚, появления которой можно было бы ожидать из теории Ньютона. За перенос массы-энергии ответственна не одна лишь масса покоя, но сумма массы покоя с массовым эквивалентом кинетической энергии, иными словами, полная масса-энергия 𝐸.

Рис. 91. Решать, какая из релятивистских формул удобна для анализа экспериментальных данных, следует исходя из величин, измеряемых на опыте:
а) Скорость определяется по времени полёта, энергия — из закона сохранения, применённого к предыдущим или последующим столкновениям.
б) Полезна при анализе столкновений, когда нас не интересует скорость, а внимание сосредоточено на проверке или применении законов сохранения.
в) Скорость определяется по времени полёта, импульс — по искривлению трека частицы в магнитном поле.
г) Для нахождения 𝑝, или β, или 𝐸, когда две из величин известны; 𝑚 не представляет интереса.
Масса покоя непосредственно не представлена в равенстве 𝑝=β𝐸. Мы помещаем это равенство поэтому в центр рис. 91 и размещаем вокруг него прочие ключевые формулы, связывающие энергию, импульс и скорость. Связи между каждой из них обладают своими специфическими областями применения, как это указано в подписи к рисунку.
Мы ничего не говорили в нашем исследовании импульса и энергии о внутренней структуре (если таковая имеется) объекта — носителя этих характеристик. Этот объект может быть ракетой, сложной органической молекулой, элементарной частицей или даже фотоном — элементарным квантом света. Во всех случаях движение такого объекта совершается со скоростью, меньшей скорости света, за исключением, конечно, самого света. Для света, распространяющегося в вакууме, скорость β в точности равна единице. В этом случае формулы
𝑝
=
𝑚β
√1-β²
и
𝐸
=
𝑚
√1-β²
с очевидностью теряют всякий смысл, но зато равенство (90) приобретает исключительную простоту.
𝑝
=
𝐸
⎛
⎜
⎜
⎝
для любого вида энергии,
распространяющегося
со скоростью света
⎞
⎟
⎟
⎠
(91)
Кроме того, из соотношения 𝑚²=𝐸²-𝑝² мы видим, что в этом случае масса покоя равна нулю. Следовательно, любой объект, переносящий энергию по прямолинейному пути со скоростью света, характеризуется нулевой массой покоя. В настоящее время известны лишь три механизма переноса энергии со скоростью света — электромагнитное излучение, гравитационное излучение и нейтрино, причём экспериментально из них наблюдались пока лишь первый и последний 1).
1) По поводу обнаружения нейтрино см. С.L. Соwan, F. Rеinеs, F.В. Наrrisоn, Н.W. Кrusе, A.D. Мс Guirе, Science, 124, 103 (1956).
Относительно реализуемых в настоящее время попыток обнаружить гравитационное излучение, приходящее от космических источников, см. J. Webеr, Gravitational Waves, in Gravitation and Relativity, ed. H.-Y. Chiu and W.F. Hoffman, New York, 1964. [Имеется русский перевод: сб. «Гравитация и относительность», изд-во «Мир», М., 1965, стр. 179.— Прим. перев.]
Любой сгусток энергии, движущийся со скоростью света, имеет нулевую массу покоя
Равенство 𝑝=𝐸 выполняется со стопроцентной точностью лишь для излучения с нулевой массой покоя, но оно является сколь угодно точным приближением для любой частицы, если её энергия достаточно велика по сравнению с массой покоя частицы. Поэтому в таком ультрарелятивистском пределе частица с массой покоя 𝑚 ведёт себя практически так же, как фотон, с точки зрения законов сохранения энергии и импульса
13. ЭКВИВАЛЕНТНОСТЬ ЭНЕРГИИ И МАССЫ ПОКОЯ
Масса покоя конечного состояния системы при неупругом соударении больше, чем масса покоя начального состояния
Полный импульс всех частиц системы сохраняется при столкновении; сохраняется и их полная энергия (сумма энергий покоя и кинетических энергий). Этим принципом мы руководствовались, изучая столкновения частиц. Но будет ли верным придерживаться этого принципа, перейдя от упругих столкновений к неупругим? Пусть пластилиновый шарик с большой скоростью налетает на другой пластилиновый шарик, покоящийся на поверхности катка. При столкновении они слипаются и вместе скользят по льду. Мы с готовностью примем, что к такому столкновению применим закон сохранения импульса, но есть ли основания думать, что здесь имеет смысл применять и закон сохранения энергии? При таком столкновении часть энергии превратится в теплоту, а другая часть первоначальной энергии превратится во вращательную энергию крутящейся вокруг своего центра масс гантели, образованной слипшимися шариками. Как описать адекватно этот более сложный случай, если при характеристике системы мы ограничимся лишь двумя величинами, 𝐸 и 𝑝, связанными между собой элементарной формулой 𝐸²-𝑝²=𝑚²?
Ответ: следует признать, что масса покоя конечного состояния системы превышает сумму масс покоя объектов до столкновения. Это — новое утверждение физики пространства-времени, которого не знала и о котором вообще не могла догадываться ньютоновская механика. Возрастание массы покоя измеряет как раз ту энергию, которая перешла в теплоту и в энергию вращения, а также в прочие формы внутреннего возбуждения конечного состояния системы. Если не учитывать того изменения массы покоя, которое происходит при многих столкновениях, мы столкнёмся с кажущимися нарушениями закона сохранения энергии, либо закона сохранения импульса, либо обоих этих законов.
Как производить учёт этого изменения массы покоя? В примере с двумя пластилиновыми шарами следует применить:
1) закон сохранения энергии
𝐸конечная = 𝐸начальная = 𝐸₁ + 𝑚₂ ;
2) закон сохранения импульса
𝑝конечный = 𝑝начальный = 𝑝₁ + 𝑝₂ = 𝑝₁
и 3) соотношение
(𝑚конечная)² = (𝐸конечная)² - (𝑝конечный)² .
Мы получим тогда
(
𝑚
конечная
)
²
=
(
𝐸₁
+
𝑚₂
)
²
-
𝑝₁²
=
=
𝐸₁²
+
2𝐸₁𝑚₂
+
𝑚₂²
-
𝑝₁²
=
=(
𝐸₁²
-
𝑝₁²
)+
2𝐸₁𝑚₂
+
𝑚₂²
=
=
𝑚₁²
+2(
𝑚₁
+
𝑇₁
)
𝑚₂
+
𝑚₂²
=
=
(𝑚₁+𝑚₂)²
+
2𝑇₁𝑚₂
.
(92)
Законы сохранения справедливы во всех случаях столкновений — упругих, неупругих и сверхупругих
Очевидно, что масса покоя объединившихся шаров больше, чем сумма масс покоя первоначальных объектов 1 и 2. Кроме того, эта добавочная масса покоя тем больше, чем больше кинетическая энергия соударения 𝑇. Из этого примера мы заключаем, что законы сохранения энергии и импульса в равной мере справедливы (и равно полезны) как при упругих, так и при неупругих столкновениях.
Как же реализуется это неожиданное «бесплатное приложение» к законам сохранения? Что оно говорит нам об эквивалентности энергии и массы покоя? Эти вопросы требуют более детального обсуждения.
«Энергия сохраняется в каждой системе отсчета, если импульс сохраняется как в лабораторной системе отсчета, так и в системе ракеты». При доказательстве этой теоремы на основании уравнений (79) и (80) не имело значения, один ли объект получался в результате столкновения, или разлетались тысячи осколков, или между двумя частицами происходило упругое соударение. Физика знает множество реакций, при которых изменяется число частиц. Одной из самых драматических является рождение пары электронов, один из которых имеет отрицательный, а другой — положительный заряд (электрон и позитрон), когда в пустом пространстве сталкиваются два носителя энергии, например при столкновении двух электронов:
𝑒⁻
(быстрый)
+
𝑒⁺
(покоящийся)
=
𝑒⁻
+
𝑒⁻
+
𝑒⁻
+
𝑒⁺
.
Такой процесс называется неупругим, так как кинетическая энергия превращается в массу покоя. Существуют также сверхупругие процессы, при которых часть массы покоя объекта (законсервированная внутренняя энергия) превращается в энергию кинетическую:
⎛
⎜
⎝
Медленный
электрон
⎞
⎟
⎠
+
⎛
⎜
⎜
⎜
⎝
Атом, содержащий
энергию
внутреннего
возбуждения
⎞
⎟
⎟
⎟
⎠
=
=
⎛
⎜
⎝
«Разрядившийся»
атом
⎞
⎟
⎠
+
⎛
⎜
⎝
Быстрый
электрон
⎞
⎟
⎠
.
Наконец, происходят процессы распада, когда одна частица превращается в две частицы с меньшей суммарной массой покоя:
𝐾⁺
→
π⁺
+
π⁰
;
положительный 𝐾-мезон (масса 967 масс электрона) распадается за 10⁻⁸ сек на положительный пи-мезон (масса 273 массы электрона) и нейтральный пи-мезон (масса 264 массы электрона).
Все усложнения, происходящие в теории вследствие изменения числа частиц, никоим образом не сказываются на справедливости законов сохранения импульса и энергии. К счастью, продукты реакции и частицы, вступающие в реакции, вместе с их энергиями и импульсами, могут быть определены и исследованы независимо от того, является ли упругой или неупругой реакция, которая только что произошла с ними или которая должна вскоре произойти. Каждая частица всегда несёт с собой свой 4-вектор энергии-импульса. При этом она не знает о том, предстоит ли ей испытать упругое или неупругое столкновение. Она неизбежно должна всегда располагать всей бухгалтерией, необходимой для возможного упругого столкновения. Поэтому независимо от того, предстоит ли упругое или неупругое столкновение, до этого столкновения импульс и энергия каждой частицы являются вполне определёнными. Следовательно, определёнными являются и полные импульс и энергия всей системы до столкновения. Подобным же образом известны полные импульс и энергия и после столкновения. Поэтому можно говорить об изменении (если таковое происходит) полных энергии и импульса в ходе столкновения. Это изменение при упругом столкновении равно нулю. Изменение энергии отсутствует также и в неупругих столкновениях ввиду того, что изменение полного импульса равно нулю как в лабораторной системе отсчёта, так и в системе ракеты; порука тому — наши прежние рассуждения [см. уравнения (79) и (80)]. Мы никогда не имели никаких серьёзных оснований для сомнения в том, что импульс, а значит, и энергия сохраняются в неупругих соударениях.
Что можно сказать теперь о подтверждении законов сохранения импульса и энергии в неупругих процессах данными наблюдений? Импульс и энергия были определены таким образом, чтобы они сохранялись при простейших упругих столкновениях. Поэтому уже невозможно изменить их определения с тем, чтобы привести в соответствие с более широким кругом процессов столкновения. Значит, либо измеренные в любых экспериментах изменения импульса и энергии равны нулю, и тогда законы сохранения импульса и энергии образуют фундаментальный принцип, либо изменение импульса и энергии отлично от нуля, и в этом случае данные опыта привели бы к революции, опрокинув принципы теории относительности. Результаты наблюдений показывают, что изменение равно нулю. Такая проверка повторяется ежедневно и ежечасно в ходе постоянной регистрации столкновений частиц высоких энергий в лабораториях всего мира.
Мы располагаем бесчисленными данными наблюдений, подтверждающими выполнение законов сохранения
Анализ экспериментов по проверке законов сохранения и обсуждение нашего опыта в их истолковании см. в упражнениях 90—100.
Энергия, высвобождающаяся при сгорании угля или газа, при взрыве динамита, представляется нам в масштабах повседневного опыта громадной. Однако, если перевести её величину на язык эквивалентной массы, мы обнаруживаем, что перешедшая в энергию часть массы не составляет и 10⁻⁹ от полной величины массы покоя (см., например, упражнение 63), а такое изменение массы слишком мало для того, чтобы его можно было обнаружить с помощью приборов, которыми мы сейчас располагаем. Поэтому в поисках той области, где было бы возможно досконально проверить законы сохранения, мы вынуждены обращаться к миру физики элементарных частиц и к миру ядерной физики.
Таблица 11.
Сколько проверок геометрии Эвклида и геометрии Лоренца производится каждый год?
Проверки эвклидовой геометрии
Проверки лоренцевой геометрии
42 000
геодезистов (согласно статистическим данным США за 1963 г.), каждый из которых производит по 20 съёмок в год, определяя при каждой по
𝑛
вершин ограничивающего многоугольника, измеряя внутренний угол при каждой вершине, складывая углы и сравнивая полученную сумму с величиной (
𝑛-2
)
⋅180°
, предсказываемой эвклидовой геометрией
50 ускорителей элементарных частиц (ориентировочно), дающих частицы с энергией выше 100
Мэв
, каждый из которых работает по 100 дней в году и каждый регистрирует по 200 столкновений в день, в которых должны были бы чувствоваться отклонения от релятивистских законов сохранения
Результат
:
800 000
проверок в год, каждая с относительной точностью
1⋅10⁻⁴
или выше
Результат
:
1 000 000
проверок в год, каждая с относительной точностью
1⋅10⁻⁴
или выше
В ядерной физике многие объекты исследования живут лишь очень короткое время. Нелегко точно определить значения масс таких короткоживущих частиц с помощью обычных масс-спектрометров. Вместо этого их массы определяются с помощью законов сохранения импульса и энергии, применяемых к процессам столкновений или превращений частиц, массы одной или более из которых нам уже известны. Уже при таких расчётах можно проверять законы сохранения, так как интересующая нас частица часто образуется в ходе нескольких различных реакций. Однако для того, чтобы непосредственно проверить равенство энергии, выделяющейся при превращениях, и энергии, вычисляемой по изменению величины массы покоя, лучше обратиться к миру ядерной физики. Там величина массы определяется непосредственно и с высокой степенью точности как для стабильных ядер, так и для некоторых нестабильных.
Ядерная физика предоставляет особенно благоприятные возможности для точной проверки законов сохранения
Возможности точного сравнения величины выделяющейся энергии и изменения массы наиболее благоприятны в случае лёгких ядер, так как при этом изменение массы в ходе рядовой ядерной реакции составляет более значительную часть полной массы и, следовательно, может быть более точно определено, чем в случае тяжёлых ядер. Мы рассмотрим поэтому реакцию между двумя самыми лёгкими атомными ядрами,— ту реакцию, которая к тому же имеет громадное значение в наш ядерный век:
⎛
⎜
⎝
Быстрый
дейтрон
⎞
⎟
⎠
+
⎛
⎜
⎝
Покоящийся
дейтрон
⎞
⎟
⎠
↗
↘
⎛
⎜
⎜
⎜
⎝
Протон
с очень
высокой
энергией
⎞
⎟
⎟
⎟
⎠
+
⎛
⎜
⎜
⎜
⎝
Ядро
трития с
высокой
энергией
⎞
⎟
⎟
⎟
⎠
⎛
⎜
⎜
⎜
⎝
Нейтрон
с очень
высокой
энергией
⎞
⎟
⎟
⎟
⎠
+
⎛
⎜
⎜
⎜
⎝
Ядро
гелия-3 с
высокой
энергией
⎞
⎟
⎟
⎟
⎠
или
𝙷²
(быстрый)
+
𝙷²
↗
↘
𝙷¹
+
𝙷³
𝑛
+
𝙷𝚎³
(93)
Обе альтернативные реакции, описываемые схемой (93), происходят со сравнимыми частотами при взрыве водородной бомбы (или «термоядерного оружия»). Они приводят к высвобождению значительной энергии, что характерно для устройств, использующих дейтерий («тяжёлый водород» 𝙷²). Кинетическая энергия продуктов такой термоядерной реакции в сотни раз превышает кинетическую энергию первоначальных дейтронов.
Масса ядра трития, определённая из законов сохранения, согласуется с его массой, измеренной с помощью спектрометра
Реакция, приводящая к возникновению ядра трития [первая из двух альтернативных реакций (93)], служит наиболее точным самостоятельным методом проверки законов сохранения, какой только возможно найти в физике вообще. Реализация этого метода возможна потому, что с помощью масс-спектрометра удаётся независимым образом точно определять массы покоя всех частиц, принимающих участие в этой реакции (дейтрона, протона и ядра трития).
Но массу покоя нейтрона невозможно определить независимым образом столь же точно. Поэтому мы не концентрируем внимания на второй реакции (93), приводящей к образованию нейтрона. Она непригодна для проведения наиболее точных проверок эквивалентности массы и энергии. Нейтрон — нестабильная частица (со средним временем жизни около 17 мин), а что важнее всего, он безразличен к воздействию электрического и магнитного полей в масс-спектрометре (электрически нейтрален!). Такая безразличность является препятствием для прецизионного независимого определения массы нейтрона.
Допустим, что мы сосредоточили бы здесь своё внимание не на ядре трития, а на нейтроне. На что могли бы мы надеяться, не располагая независимо определённым точным значением массы нейтрона? Нам пришлось бы отказаться от попыток проверки законов сохранения, и вместо этого мы могли бы использовать законы сохранения для определения массы нейтрона с относительной точностью около 10⁻⁵. Что же может гарантировать нам, что законы сохранения дают в применении ко второй реакции средство для надёжного определения массы нейтрона? Дело в том, что законы сохранения, если применить их к первой реакции, дают такое значение массы ядра трития, что оно согласуется с данными масс-спектрометрии даже лучше, чем до 10⁻⁵ своей величины. (См. на стр. 166—167 «Анализ реакции 𝙷²+𝙷²→𝙷¹+𝙷³»). Как эта последняя проверка законов сохранения, обладающая наивысшей точностью, так и множество других экспериментов в прочих областях физики, проводимых с несколько меньшей прецизионностью, убедительно говорят о полноценности принципа сохранения.
Необходимо сделать оговорку о тех единицах, в которых проведены расчёты на стр. 166—167. В принципе было бы естественно выразить все значения энергии и импульса в килограммах по аналогии с предыдущими расчётами в этой главе. Однако для этого пришлось бы перевести все величины, измеренные с помощью масс-спектрометра, из «атомных единиц массы» (АЕМ — новая шкала, выбранная в 1961 г., когда перешли от 𝙾¹⁶=16,000 к 𝙲¹²=12,000) в килограммы, одновременно переведя значения кинетической энергии, измеряемые физиками-ядерщиками в электронвольтах, в килограммы. Удобнее выражать энергию в единицах АЕМ, избегая расчётов, в ходе которых АЕМ переводятся в килограммы. К тому же все используемые нами формулы справедливы при любом выборе единиц для массы-энергии, лишь бы только эти единицы последовательно использовались от начала и до конца. Но тогда будет нужно перейти от электронвольт к АЕМ. Как это сделать? К счастью, для этого нет необходимости знать число килограммов, содержащихся в 1 АЕМ, или, что то же, не надо знать, сколько атомов содержится в одном грамм-атоме (число Авогадро 𝑁=(6,02252±0,00028)⋅10²³). Та неопределённость, с которой в настоящее время известна эта величина (10⁻⁵), повлияла бы на все наши выводы, если бы мы захотели совершить переход к килограммам. Множитель перехода от электронвольт к АЕМ вычислен на стр. 168.
АНАЛИЗ 1) РЕАКЦИИ 𝙷² (БЫСТРЫЙ) +𝙷²→𝙷¹+𝙷³
1) Приведённые здесь экспериментальные данные были опубликованы в статье Е.N. Strait, D.М. Van Patter, W.W. Buechner, A. Sperduto, Physical Review, 81, 747 (1951). Авторы выражают признательность Бюхнеру и Спердуто за дополнительную информацию и за обсуждение последовательной интерпретации этих данных.
Законы сохранения импульса и энергии:
𝐸₂
+
𝑚₂
=
𝐸
₁
+
𝐸
₃
(сохранение энергии),
(94)
𝑝₂
𝑥
+
0
=
0
+
𝑝
₃
𝑥
⎛
⎜
⎜
⎝
сохранение
компоненты 𝑥
импульса
⎞
⎟
⎟
⎠
(95)
0
+
0
=
𝑝
₁
𝑦
+
𝑝
₃
𝑦
⎛
⎜
⎜
⎝
сохранение
компоненты 𝑦
импульса
⎞
⎟
⎟
⎠
(96)
0
+
0
=
0
+
𝑝
₃
𝑦
⎛
⎜
⎜
⎝
сохранение
компоненты 𝑧
импульса
⎞
⎟
⎟
⎠
(97)
Нижние индексы указывают здесь массовое число изотопа, а черта над символом означает, что эта величина взята после реакции.
Любое из четырёх уравнений (94) — (97) может рассматриваться как независимый источник информации о ядре трития — либо относительно его энергии, либо о соответствующей компоненте его импульса. Но нас интересует не вся совокупность этой информации — мы хотим найти одну простую характеристику ядра трития, не совпадающую ни с одной из этих четырёх величин, а именно его массу покоя. К счастью, эта масса покоя определяется как абсолютная величина 4-вектора энергии-импульса:
𝑚₃²
=
𝐸
₃²
-
(
𝑝
₃
𝑥
)²
-
(
𝑝
₃
𝑦
)²
-
(
𝑝
₃
𝑧
)²
.
(98)
Подставим в эту формулу величины компонент из уравнений (94)—(97); мы получим тогда
𝑚₃²
=(
𝐸₂
+
𝑚₂
-
𝐸
₁
)²-(
𝑝₂
𝑥
+0-0)²-(0+0-
𝑝
₁
𝑦
)²-
-(0+0-0)²
=
=
[
𝐸
₁²-0-(
𝑝
₁
𝑦
)²-0]
+
[𝐸₂²-(𝑝₂
𝑥
)²-0-0]
+
+
𝑚₂²
-
2𝑚₂
𝐸
₁
+
2𝑚₂
𝐸
₂
-
2𝐸₂
𝐸
₁
=
=
[𝑚₁²]
+
[𝑚₂²]
+
+
𝑚₂²
-
2𝑚₂
𝐸
₁
+
2𝑚₂
𝐸
₂
-
2𝐸₂
𝐸
₁
=
=
𝑚₁²
+2
(𝑚₂+𝐸₂)
(𝑚₂-
𝐸
₁)
,
𝑚₃²
=
𝑚₁²
+2(
𝑚₂
+
𝑚₂
+
𝑇₂
)(
𝑚₂
-
𝑚₁
-
𝑇
₁
).
(99)
Мы воспользовались здесь соотношениями вида 𝐸=𝑚+𝑇, связывающими кинетическую и полную энергии.

Рис. 92. Доказательство того, что протоны (𝙷¹), образуемые в реакции 𝙷² (1,808 Мэв) + 𝙷² (покоящийся) → → 𝙷¹ (очень быстрый) + 𝙷³ (быстрый)
под углом 90° к направлению движения первоначального дейтрона (𝙷²), обладают энергией 3,467 Мэв. (Значение 3,467 Мэв было получено при сравнении приведённых здесь результатов с данными ряда аналогичных промеров). Число протонов, вылетающих с энергиями в интервале от 𝐸-0,1 Мэв до 𝐸+0,1 Мэв, изображено как функция 𝐸. Разброс энергий вызван конечной толщиной мишени; конечной шириной щели, выделявшей пучок; неоднородностями магнитного поля и т.д. Экспериментальная кривая взята из D.М. Van Patter, W.W. Вueсhner, Physical Review, 87, 51 (1952).
Нам известны значения всех величин в правой части уравнения (99). Таким образом, с помощью этого уравнения можно предвычислить величину массы ядра трития 𝑚₃. Численные значения масс, фигурирующих в правой части уравнения (99), находятся из опытов с масс-спектрометром и выражаются в «атомных единицах массы», АЕМ, где за основу взята масса изотопа углерода 𝙲, принятая за 12,0000…АЕМ. Эти массы равны
𝑚₂
=
2,0141019±0,0000003
АЕМ;
(100)
𝑚₁
=
1,0078252±0,0000003
АЕМ.
(101)
Кинетические энергии были измерены в опытах с ядерными реакциями (см. рис. 92):
⎛
⎜
⎝
Кинетическая энергия
первоначального дейтрона
⎞
⎟
⎠
=
𝑇
₂
=
=(
1,808±0,002
Мэв
)×
×(
1,073562⋅10⁻³
АЕМ/
Мэв
)=
=
0,001941±0,000002
АЕМ
(102)
(вывод множителя перехода от единиц Мэв к атомным единицам массы см. стр. 168);
⎛
⎜
⎝
Кинетическая энергия
полученного дейтрона
⎞
⎟
⎠
=
𝑇
₁
=
=(
3,467±0,0035
Мэв
)×
×(
1,073562⋅10⁻³
АЕМ/
Мэв
)=
=
0,003722±0,000004
АЕМ.
(103)
Подставим эти значения в равенство (99), используя лишь шесть значащих цифр соответственно точности измерений кинетической энергии. Два члена в правой части этого равенства оказываются равны
𝑚₁²
=
1,015712
АЕМ
²
2(2𝑚₂+𝑇₂)
(𝑚₂-𝑚₁-
𝑇
₁)
=
8,080881±0,00003
АЕМ
²
⎛
⎜
⎝
Сумма этих
членов
⎞
⎟
⎠
=
𝑚₃²
=
9,096593±0,00003
АЕМ
²
.
Квадратный корень этой величины и есть масса ядра трития, предсказываемая при анализе данной ядерной реакции:
𝑚₃
=
3,016056±0,000015
АЕМ.
(104)
Сравним это значение массы ядра трития со значением, измеренным с помощью масс-спектрометра 1):
𝑚₃
=
3,0160494±0,0000007
АЕМ.
(105)
Относительная разница между этими двумя результатами составляет около 2⋅10⁻⁶ и меньше, чем величина ошибки в результате, полученном при анализе опыта по ядерным реакциям. Такое точное предсказание величины массы ядра трития, исходя из релятивистских законов сохранения, представляет собой отличное подтверждение справедливости этих законов сохранения.
1) Приведённые ниже спектрометрические величины для масс были определены по работе F. Еverling, L.А. König, J.Н.Е. Мattauch, А. Н. Wapstra, Nuclear Phys., 25, 177 (1961). Вместо этого можно было бы взять значения масс из стандартных таблиц масс ядер, однако значения масс, приведённые в этих таблицах, представляют собой «наилучший компромисс» между разного рода данными, включая не только результаты опытов по масс-спектрометрии, но анализ ядерных реакций, подобных рассматриваемой здесь нами. При составлении стандартных таблиц анализ данных, полученных при экспериментальном исследовании ядерных реакций, производится на основании релятивистских законов сохранения. Поэтому значения масс, взятые из стандартных таблиц, не могут служить для независимой проверки этих законов сохранения, которая нас здесь интересует. Это побуждает нас ограничиться пока масс-спектрометрическими значениями масс ядер. Когда же данный анализ и прочие исследования подтвердят законы сохранения, мы предпочтём основываться на данных стандартных таблиц, при составлении которых эти законы были использованы для определения наиболее надёжных значений масс, исходя из всевозможных доступных данных. В качестве стандартной таблицы можно указать: L.А. König, J.Н.Е. Мattauch, А.Н. Wарstra, Nuclear Phys., 31, 18 (1962).
Множитель перехода от электронвольт к атомным единицам массы (АЕМ)
Искомый множитель перехода использован при вычислениях, проведённых на стр. 166—167, для перевода величин наблюдаемых кинетических энергий дейтрона и ядра трития из электронвольт в АЕМ, что потребовалось в целях окончательной проверки законов сохранения.
Один электронвольт есть то количество энергии, которое необходимо, чтобы перенести одну частицу с элементарным зарядом 𝑒 через разность потенциалов 1 вольт
Что такое 1 АЕМ? Возьмём 12 г 𝙲¹², разделим на 𝑁 и получим величину массы одного атома 𝙲¹²; по определению она равна 12 АЕМ. Следовательно, 1 AEM = 1/𝑁 г
↓
↓
Умножение на
𝑁
Умножение на
𝑁
↓
↓
𝑁 электронвольт есть та энергия, которая необходима, чтобы перенести 𝑁 элементарных зарядов через разность потенциалов 1 вольт
𝑁 атомных единиц массы, выраженных в единицах массы, эквиваленты 1 г или 0,001 кг
↓
↓
т.е. та энергия, которая необходима, чтобы перенести 1 моль электричества через разность потенциалов 1 вольт
а выраженные в единицах энергии эквиваленты 𝑚𝑐²=(0,001 кг) ⋅[(2,997925±0,000003)⋅10⁸ м/сек]²
↓
↓
или та энергия, которая необходима, чтобы перенести количество электричества, равное фарадееву электрохимическому эквиваленту (96487,0±1,6 кулон), через разность потенциалов 1 вольт: 96487,0±1,6 джоулей
т.е. эквивалентны (8,987554±0,000009)⋅10¹³ джоулей
↓
↓
Это 𝑁 электронвольт
Это 𝑁 атомных единиц массы
↘
↙
следовательно, 1 электронвольт эквивалентен
96487,0±1,6
(8,987554±0,000009)⋅10¹³
или (1,073562±0,000017)⋅10⁻⁹ АЕМ (относительная ошибка равна 1,6⋅10⁻⁵)
↓
т.е. 1 АЕМ эквивалентна (0,931478±0,000015)⋅10³ Мэв
В этих вычислениях масса ядра трития выступает как вывод, полученный при анализе законов сохранения, сопоставленный и подтверждённый методами масс-спектроскопии. Этот пример подтверждения физики пространства-времени впечатляет, и после него невозможно уже сомневаться в том, что энергия массы покоя способна превращаться в кинетическую энергию.
Тем не менее всё ещё может быть непонятным, как это такой простой принцип смог породить столь сложное равенство, как (99), которое мы применили для вывода массы ядра трития. Почему мы не взяли просто определённые спектрометрическим путём массы реагентов, такие же массы продуктов реакции и не сравнили их с балансом кинетической энергии при этом превращении? Что могло бы быть проще этого?!
Реагенты:
𝙷²
2.0141019
АЕМ
𝙷²
2.0141019
АЕМ
Сумма:
4,0282038
АЕМ
Продукты реакции:
𝙷¹
1,0078252
АЕМ
𝙷³
3,0160494
АЕМ
Сумма:
4,0238746
АЕМ
Разность:
0,0043292
АЕМ
Энергетический эквивалент:
4,0322546
Мэв
Трудность возникает лишь на следующем этапе, когда требуется определить из наблюдений полный выход кинетической энергии. Кинетическая энергия дейтрона, находившегося до реакции в движении, известна и равна 1,808 Мэв, тогда как кинетическая энергия протона после реакции равна 3,467 Мэв.
Однако при этом затруднительно измерять кинетическую энергию получающегося ядра трития, и эта энергия не измерялась. Но если неизвестна кинетическая энергия одного из продуктов реакции, то это значит, что не проводилось непосредственного измерения полного выхода кинетической энергии. Как же можно тогда сопоставить выход энергии при реакции с изменением масс покоя реагентов? Сводится ли на самом деле такое сравнение к какому-то непосредственному сопоставлению двух энергий? — Нет.
Измеряются кинетические энергии не всех частиц. Простое сравнение энергий невозможно
Можно составить ложное представление о происходящих явлениях, если думать, что они исчерпываются энергетическими переходами. При геодезической съёмке возможна столь же ошибочная концепция. Так, земельный план является многоугольником хитрой формы, наложенным на поверхность, которая не является плоской. Требуется найти длину прямолинейной границы 𝐴, а землемер измерил лишь разность координат по линии север — юг для 𝐴 и 𝐵. Если его воображение неспособно на большее, то он встанет в тупик! Подобным же образом безнадёжно определять массу ядра трития из приведённых выше данных для дейтрон-дейтронной реакции, основываясь лишь на энергиях. Необходимо учесть также баланс импульсов.
Определение массы ядра трития аналогично определению длины наклонной стороны многоугольника

Рис. 93. Определение массы ядра трития с помощью законов сохранения, рассматриваемое как геометрическая задача. Учтите: точки 𝑂, 𝐵, 𝐶 лежат в плоскости чертежа; точка 𝐴 лежит выше плоскости чертежа (𝑦-компонента импульса).
Массу ядра трития находят, пользуясь законами сохранения, подобно тому как землемер находит длину стороны многоугольника из ряда измерений на этом многоугольнике, пользуясь эвклидовой геометрией (рис. 93). Между этими двумя случаями имеется лишь одно существенное различие — в физике необходимо исходить из лоренцевой геометрии. Поэтому мы получим
(
𝑚₃
)
²
=
(
𝐸
-компонента
𝐴𝐵
)
²
-
(
𝑝
-компонента
𝐴𝐵
)
²
.
Энергетическая и импульсная компоненты стороны 𝐴𝐵 в этой формуле определяются по энергетическим и импульсным компонентам других трёх сторон многоугольника, т.е. по данным о других трёх частицах. Как найти значения 𝐸 и 𝑝 для одной из этих частиц, например для налетающего дейтрона? Ответ: с помощью процедуры, изображённой на рис. 94 и не похожей на обычно используемую при съёмках земельных планов! Предположим, что от землемера требовалось бы использовать метод, аналогичный применённому в опыте с реакцией 𝙷²+𝙷²→𝙷¹+𝙷³. Сделать это он мог бы, лишь воспользовавшись следующей необычной процедурой для нахождения компонент граничной прямой 𝐶𝐵 в направлениях север — юг и восток — запад (см. рис. 94, переводя его с языка физики частиц на язык геодезии!): 1) Измерение длины прямой 𝐶𝐵. 2) и 3) Измерение компоненты этого отрезка в направлении север — юг. 4) Использование теоремы Пифагора для нахождения компоненты отрезка 𝐶𝐵 в направлении восток — запад.

Рис. 94. Экспериментальное определение энергии и импульса как компонент 4-вектора энергии-импульса в опыте по соударению дейтронов, 𝙷²+𝙷²→𝙷¹+𝙷³. (Обозначение концов вектора через 𝐵 и 𝐶 — использование тех же обозначений, что и на рис. 93).
а — масса покоя (определённая с помощью масс-спектрометра);
б — кинетическая энергия (определяемая разностью потенциалов, через которую пропущены бомбардирующие дейтроны);
в — сумма энергии покоя и кинетической энергии (из соотношения 𝐸=𝑚+𝑇);
г — импульс (из соотношения 𝑝²=𝐸²-𝑚²).
Теперь мы разобрали, как определяются компоненты векторов энергии-импульса дейтрона-мишени (на рис. 93 отрезок 𝑂𝐶), налетающего дейтрона (𝐶𝐵) и выбитого протона (𝑂𝐴). Компоненты неизвестной четвёртой стороны многоугольника (отрезок 𝐴𝐵, соответствующий ядру трития) могут быть тогда найдены путём простого комбинирования трёх других известных 4-векторов — вычисления, начинающегося магической формулой «применим законы сохранения импульса и энергии»:
𝑝
₃
𝑘
=
𝑝₂
𝑘
+
𝑝₀
𝑘
-
𝑝
₁
𝑘
(𝑘=𝑥,𝑦,𝑧,𝑡)
.
Индексом «нуль» обозначен первоначально покоившийся дейтрон. «Длина» искомой четвёртой стороны многоугольника сразу же даёт требуемую массу
(𝑚₃)²
=
(
𝑝
₃
𝑡
)²
-
(
𝑝
₃
𝑥
)²
-
(
𝑝
₃
𝑦
)²
-
(
𝑝
₃
𝑧
)²
.
Использование законов сохранения всегда связано с многоугольником, построенным из 4-векторов
Проделанный анализ показывает, что определение массы ядра трития, исходя из реакции 𝙷²+𝙷²→𝙷¹+𝙷³, имеет в высшей степени геометрический характер. Этим примером иллюстрируется общий принцип: используя законы сохранения энергии и импульса, мы всегда говорим о многоугольнике, построенном в пространстве-времени из 4-векторов. Если не считать различия между геометриями Лоренца и Эвклида, расчёты здесь не отличаются от проводимых в геодезии, тригонометрии или любых других исследованиях треугольников и многоугольников. Из этого сравнения физики элементарных частиц и геодезии, как ни из какого иного подхода, следует полный охват ситуаций, с которыми можно столкнуться при анализе экспериментов. Нет ни одной задачи из области столкновений частиц, реакций между ними и процессов их превращений, которая не имела бы своего аналога в элементарной геометрии. В табл. 12 подобраны и обсуждены некоторые примеры таких задач и их соответствующих аналогов.
Таблица 12.
Нахождение массы, энергии или другой физической величины с помощью законов сохранения аналогично нахождению длины одной из сторон многоугольника, угла или другой геометрической величины с помощью теорем эвклидовой геометрии
Физика частицАналог в геометрии Эвклидапроцессзадача 𝐴 (быстрая) + 𝐵 (мишень) → 𝐶 (наблюдаемая) + 𝐷 (ненаблюдаемая)
Известны: 𝑚𝐴, 𝑚𝐵, 𝑚𝐶
Измеряются: 𝐸𝐴, 𝐸𝐶 и направление 𝑝𝐶 относительно 𝑝𝐴
Вычисляются: неизвестная масса 𝑚𝐷
Даны (для неправильного четырехугольника, стороны которого не компланарны): длины трёх сторон, компоненты этих трёх сторон в направлении север — юг и угол между двумя из этих сторон с точки зрения наблюдателя, который смотрит вдоль третьей стороны
Найти: длину четвёртой стороны
Фотон (с импульсом 𝑝)+ Электрон (покоящийся) → Электрон (движущийся) + Фотон (с импульсом 𝑝)
Даны: масса покоя электрона, начальный импульс (или энергия, 𝐸=𝑝) фотона и направление вылета конечного фотона
Вычислить: импульс (или энергию 𝐸=𝑝) этого фотона («эффект Комптона», см. упражнение 70)
Даны (для неправильного четырехугольника, стороны которого не компланарны): длины всех четырёх сторон, компоненты двух сторон в направлении север — юг (аналог «энергии фотона и электрона до столкновения»!) и угол между двумя из сторон («фотон до и после рассеяния») с точки зрения наблюдателя, смотрящего вдоль третьей стороны («электрон-мишень»)
Найти: компоненту одной неизвестной стороны в направлении восток — запад
₉₄𝙿𝚞²³⁹ (покоящийся) → ₅₆𝙱𝚊¹⁴⁴+₃₈𝚂𝚛⁹⁵ (спонтанный распад ядра плутония на два фрагмента)
Измеряются: скорости тяжёлого и лёгкого фрагментов в опытах по времени полёта, а также масса 𝙿𝚞²³⁹ с помощью масс-спектрометра
Найти: массы покоя обоих фрагментов
Даны: большая сторона треугольника («масса покоя плутония») и два прилежащих угла («параметры скорости θ, связанные со скоростью по формуле (β=th θ»)
Найти: две другие стороны
Тот же процесс, что в предыдущем примере
Даны: данные измерений предыдущего примера
Найти: кинетическую энергию, высвободившуюся при распаде
Даны: данные предыдущего примера
Найти: разность между большей стороной и суммой двух других сторон треугольника
(μ (покоящийся мю-мезон) → 𝑒 (быстрый электрон) + ν (нейтрино; скорость света)
(Мю-мезон спонтанно распадается за ~10⁻⁶ сек)
Известны: масса покоя электрона
Измеряются: кинетическая энергия электрона, порождённого при этом превращении
Найти: массу покоя мю-мезона
Известны: две меньшие стороны треугольника («масса покоя электрона 𝑚 и масса покоя нейтрино 0») и один угол («параметр скорости θ электрона, найденный по его энергии, 𝐸=𝑚 ch θ»)
Найти: большую сторону треугольника
Здесь так же невозможно дать рецепты для анализа всех типов столкновений и превращений, которые могут иметь место в физике и происходят на самом деле, как было бы нелепо пытаться в кратком учебнике по основам эвклидовой геометрии перечислить и решить всё множество задач, которые могут быть поставлены там. Сущность типичной задачи можно сформулировать, обобщая аналогии табл. 12. Пусть даны такие-то и такие-то стороны многоугольника, а также такие-то и такие-то проекции их на направления север — юг, восток — запад и верх — низ, а также такие-то и такие-то углы. Требуется определить такие-то и такие-то длины («массы покоя»), проекции («энергии или импульсы») или углы («скорости относительно других частиц или относительно лаборатории»). Углубляться в разнообразные вычисления, необходимые для решения таких задач,— вовсе не значит прояснить основные идеи. В физике частиц эти «идеи» сводятся в конце концов к двум очень простым свойствам геометрии пространства-времени: 1) векторная сумма 4-векторов энергии-импульса всех участвующих в реакции частиц равна нулю (если брать 4-векторы продуктов реакции с обратным знаком) и 2) инвариантная абсолютная величинакаждого 4-вектора равна массе покоя соответствующей частицы.
Применение законов сохранения к исследованию столкновений и превращений.
Известные и неизвестные величины
Применение этих идей регулируется стандартными правилами алгебры. 1) Чтобы найти 𝑛 различных неизвестных, нужно иметь 𝑛 независимых уравнений, в которых все прочие величины известны. 2) Если мы располагаем лишь 𝑛-𝑟 независимыми уравнениями, то 𝑟 неизвестных величин останутся неопределенными. (Примером служит столкновение дейтрона заданной энергии с покоящимся дейтроном, приводящее к образованию ядра трития и протона. Если бы даже были заданы массы покоя всех четырех частиц, было бы всё равно невозможно предсказать исход этой реакции. Причина проста: протон может вылететь в любом из бесчисленного множества направлений, в каком ему заблагорассудится. В этой задаче угол вылета протона является неопределенным. Если задать этот угол как одно из условий задачи (в нашем примере θ = 90°), то можно вычислить энергию. Наоборот, задавая энергию, можно предсказать величину угла вылета протона). 3) Если мы имеем 𝑛+𝑠 независимых уравнений для нахождения 𝑠 неизвестных, то нам достаточно для этого ограничиться первыми 𝑛 уравнениями. Остальные 𝑠 уравнений будут служить для проверки точности измерений или выполнения физических законов. Используя эти принципы, часто берут в качестве основных величин значения компонент 𝐸, 𝑝 𝑥, 𝑝 𝑦 и 𝑝 𝑧 различных частиц как для удобства их учета, так и ради систематического контроля числа известных и неизвестных величин.
Примером подсчета числа известных и неизвестных служит реакция: (Дейтрон) + (Дейтрон) (Протон) + (Ядро трития), используемая для нахождения массы ядра трития. Этот пример проанализирован в табл. 13.
Таблица 13.
Учёт известных и неизвестных величин, 𝙷²+𝙷²→𝙷¹+𝙷³ характеризующих реакцию
Комментарий.
Как и в тексте, здесь принято, что отсутствуют масс-спектрографические данные о массе 𝙷³ в тот момент, когда эта масса определяется из баланса импульса и энергии в данной реакции. В таблице измеряемые величины обозначены через «ДА», те же, которые не измерены,— через «НЕТ».
Каждая из четырёх частиц характеризуется пятью символами (четыре компоненты энергии-импульса и масса покоя), так что в целом мы имеем 20 величин. Из них известны 10 (помеченные в таблице через «ДА») и 10 неизвестны. Для определения этих десяти неизвестных мы имеем ровно десять уравнений. Поэтому не удивительно, что информацию, содержащуюся в этих 10 уравнениях, можно скомбинировать таким образом, что получается одно уравнение (99), выражающее искомую массу ядра трития через измеряемые величины.
𝐸=𝑝 𝑡 𝑝 𝑥 𝑝 𝑦 𝑝 𝑧 Инвариантная абсолютная величина 4-вектора
Реагенты (все компоненты 4-вектора энергии-импульса проставить в таблице с положительным знаком) 𝙷² (мишень) НЕТ (измеряется 𝑚₂, а не не посредственно 𝐸₂) ДА (нуль!) ДА (нуль) ДА (нуль)
𝑚₂ - ДА, ур. (100) (спектрометр) 𝙷² (быстрый) НЕТ (измеряется 𝐾𝐸, см. ниже) НЕТ ДА (нуль) ДА (нуль)
𝑚₂*=𝑚₂ - ДА (спектрометр)
Продукты реакции (все компоненты проставить в таблице с обратным знаком) 𝙷¹ (измерено) НЕТ (измеряется 𝐾𝐸, см. ниже) ДА (нуль) НЕТ ДА (нуль)
𝑚₁ - ДА, ур. (101) (спектрометр) 𝙷³ (не измерено) НЕТ НЕТ НЕТ НЕТ
𝑚₃ - «НЕТ»,ур. (105) (требуется найти)
Сумма, дающая изменение полного 4-вектора энергии-импульса системы, должна быть нулю, чтобы 4-векторы образовали замкнутый четырехугольник («закон сохранения») 0 ур. (94) 0 ур. (95) 0 ур. (96) 0 ур. (97) ПОЛУЧАЮТСЯ ЧЕТЫРЕ УРАВНЕНИЯ
Дополнительная информация. ПОЛУЧАЕТСЯ ЕЩЁ ШЕСТЬ УРАВНЕНИЙ:
𝐸₂*-𝑚₂*=1,808 Мэв (кинетическая энергия налетающего дейтрона), уравнение (102).
𝐸₂-𝑚₂=0 (кинетическая энергия дейтрона-мишени, принимаемого покоящимся).
𝐸₁-𝑚₁=3,467 Мэв (кинетическая энергия полученного протона), уравнение (103).
𝐸₃²-𝑝₃²=𝑚₃² (4-вектор энергии-импульса полученного ядра трития), уравнение (98).
𝐸₁²-𝑝₁²=𝑚₁² (4-вектор энергии-импульса энергии-импульса полученного протона).
(𝐸₂*)² - (𝑝₂*)² = (𝑚₂*)² = 𝑚₂² (4-вектор энергии-импульса налетающего дейтрона).
«Масса покоя может быть превращена в энергию, а энергия может быть превращена в массу покоя»,— так можно не совсем точно подытожить некоторые следствия двух фундаментальных и уже строгих принципов: 1) полный 4-вектор энергии-импульса системы не изменяется в ходе реакции и 2) инвариантная абсолютная величина 4-вектора энергии-импульса любой данной частицы равна массе покоя этой частицы. Какую разумную информацию о физических законах можно извлечь из этих основных принципов? К каким затруднениям приводит иногда использование слишком нестрогой формулировки «принципа эквивалентности массы и энергии»? Некоторые ответы на эти вопросы даны в табл. 14.
Таблица 14.
Плюсы и минусы понятия массы
❔
Одинакова ли величина массы покоя во всех инерциальных системах отсчёта?
✔
Да. В одной системе отсчёта она выражается через энергию 𝐸 и импульс 𝑝 как 𝑚²=𝐸²-𝑝², а в другой системе — как 𝑚²=(𝐸')²-(𝑝')². Поэтому масса покоя является инвариантом
❔
Одинакова ли величина энергии во всех инерциальных системах отсчёта?
✔
Нет. Энергия выражается как 𝐸=√𝑚²+𝑝² либо как 𝐸=𝑚 ch θ=𝑚/√1-β², либо как 𝐸= (Масса покоя) + (Кинетическая энергия) = 𝑚+𝑇, и её величина зависит от выбора системы отсчёта, в которой рассматривается частица (или система частиц). Эта величина минимальна в той системе отсчёта, где импульс частицы (системы частиц) равен нулю (в случае системы частиц равен нулю полный импульс). Лишь в этой системе отсчёта энергия равна массе покоя
❔
Равна ли нулю энергия объекта с нулевой массой покоя? (Фотон: квант света, рентгеновские лучи, гамма-излучение).
✔
Нет. Энергия равна тогда 𝐸=√0²+𝑝²=𝑝 (в обычных единицах 𝐸обычн=𝑐𝑝обычн). Формально можно сказать иначе, что вся энергия представлена в виде кинетической энергии (в этом специальном случае нулевой массы покоя 𝑇=𝑝 и вообще отсутствует форма энергии покоя. Итак, 𝐸=(Масса покоя)+(Кинетическая энергия)=0+𝑇=𝑇=𝑝 (лишь в случае нулевой массы покоя!)
❔
Означает ли инвариантность массы покоя, что эта масса не может изменяться при столкновениях?
✔
Нет. Масса покоя часто изменяется при неупругих соударениях. Пример 1: столкновение двух пластилиновых шаров — нагревание и увеличение вследствие этого массы после столкновения. Пример 2: столкновение двух электронов (𝑒⁻) достаточной энергии порождает новую пару, состоящую из одного обычного электрона и одного положительного электрона (позитрона) (𝑒⁺): 𝑒⁻ (быстрый) + 𝑒⁻ (покоящийся) → 𝑒⁺ + 3𝑒⁻
❔
Как величина может быть инвариантной и тем не менее изменяться в результате столкновения?
✔
Инвариантность означает «неизменность величины, определяемой в различных инерциальных системах отсчёта», а не «неизменность при столкновениях или при воздействии внешних сил»
❔
Изменяется ли масса покоя при всяком неупругом столкновении?
✔
Нет. Пример: в столкновении 𝑒⁻ (быстрый) + 𝑒⁻ (покоящийся) → → 2
⎛
⎜
⎜
⎝
Электроны с
умеренной
скоростью
⎞
⎟
⎟
⎠ + +
⎛
⎜
⎜
⎝
Электромагнитная энергия,
или фотоны, порождённые
в процессе столкновения
⎞
⎟
⎟
⎠
массы покоя электронов остались после столкновения такими же, какими они были до этого
❔
Изменяется ли когда-нибудь масса покоя при упругих столкновениях?
✔
Нет — по определению упругого столкновения! Пример: 𝑒⁻ (быстрый) + 𝑒⁻ (покоящийся) → → 2
⎛
⎜
⎜
⎝
Электроны с
умеренной
скоростью
⎞
⎟
⎟
⎠ + +
⎛
⎜
⎝
Никакого излучения
⎞
⎟
⎠
❔
Дана система, состоящая из нескольких (𝑛) свободно движущихся частиц. Равна ли масса покоя такой системы сумме масс покоя отдельных входящих в неё частиц? Пример: ящик с нагретым газом.
✔
Нет. Масса покоя 𝑀 системы превышает сумму масс покоя частиц, если только все частицы по чистой случайности не движутся с одной и той же скоростью в одну сторону. Аддитивной является не масса покоя, а энергия и импульс: 𝐸системы =
𝑛
∑
𝑖=1 = 𝐸𝑖 , 𝑝системы𝑥 =
𝑛
∑
𝑖=1 = (𝑝𝑥)𝑖 .
На основании этих сумм может быть вычислена и масса покоя системы: 𝑀² = (𝐸сис)² - (𝑝сис𝑥)² - (𝑝сис𝑦)² - (𝑝сис𝑧)² .
❔
Упрощается ли это соотношение, когда полный импульс системы равен нулю?
Пример 1. Ящик с нагретым газом покоится в лаборатории
Пример 2. Любая система свободно движущихся частиц, рассматриваемая в инерциальной системе отсчёта, выбранной таким образом, чтобы полный импульс оказался равным нулю
✔
Да. В этом случае масса покоя системы выражается в виде суммы энергий отдельных частиц: 𝑀 = 𝐸системы =
𝑛
∑
𝑖=1 𝐸𝑖 .
Более того, энергия каждой частицы всегда может быть выражена как сумма энергии покоя и кинетической энергии: 𝐸𝑖 = 𝑀𝑖 + 𝑇𝑖 , 𝑖=1, 2, …, 𝑛 .
Итак, масса покоя системы превосходит сумму масс покоя входящих в неё отдельных частиц на величину, равную полной кинетической энергии всех этих частиц (взятую в системе отсчёта, где полный импульс равен нулю!): 𝑀 =
𝑛
∑
𝑖=1 𝑚𝑖 +
𝑛
∑
𝑖=1 𝑇𝑖
❔
Обладает ли хоть каким-нибудь значением для эксперимента понятие «массы покоя физической системы»?
✔
Да. Масса покоя системы определяет её инертность, т.е. сопротивление ускорению, вызываемому силой, действующей на систему в целом. (Пример. Ящик с нагретым газом в принципе больше сопротивляется ускорению, чем этот же ящик, если газ в нем охладить). Масса покоя системы определяет также то гравитационное притяжение, с которым эта система действует на пробные частицы. (Пример 1. Горячая звезда, содержащая определённые количества атомов данных типов, в принципе сильнее притягивает свои планеты, чем такая же комбинация атомов, если их охладить. Пример 2. Облако электромагнитного излучения состоит из фотонов, масса покоя каждого из которых равна нулю, а «кинетическая энергия» положительна. Поэтому масса покоя облака излучения положительна. Облако оказывает гравитационное притяжение на удалённый объект, например Солнце, и в свою очередь подвержено гравитационному притяжению со стороны Солнца).

Рис. 95. Полная кинетическая энергия, сумма масс покоя отдельных частиц и масса покоя системы как функции времени, в течение которого взрывается ядерное устройство и остывают продукты взрыва.
❔
В космическом пространстве взрывается 20-мегатонная водородная бомба. Переводится ли при этом 0,93 кг массы в энергию?
[Δ𝑚= Δ𝐸/𝑐²= (20⋅10⁶ т)⋅(10⁶ г/т)⋅(10³ кал/г — эквивалент тринитротолуола)⋅(4,18 дж/кал)/𝑐²=(8,36⋅10¹⁶ дж)/(9⋅10¹⁶ м²/сек²)=0,93 кг]
✔
И да, и нет: необходима более корректная постановка вопроса. Масса покоя системы расширяющегося газа, осколков и излучения сохраняет ту же величину, какая была до взрыва,— масса покоя системы 𝑀 не изменяется. Однако произошло превращение водорода в гелий, а также произошли и другие ядерные превращения. В результате произошла «перекачка» величин между различными частями в формуле массы покоя системы: 𝑀 = ∑ 𝑚𝑖 + ∑ 𝑇𝑖
Первый член справа — сумма масс покоя отдельных составных частей системы — уменьшился на 0,93 кг.
⎛
⎝ ∑ 𝑚𝑖
⎞
⎠
конечн =
⎛
⎝ ∑ 𝑚𝑖
⎞
⎠
начальн -0,93 кг.
Второй член — сумма кинетических энергий, включая «кинетическую энергию» появившихся фотонов и нейтрино, — увеличился на столько же:
⎛
⎝ ∑ 𝑇𝑖
⎞
⎠
конечн =
⎛
⎝ ∑ 𝑇𝑖
⎞
⎠
начальн +0,93 кг. ⬆ первоначальное содержание тепловой
энергии в бомбе, практически равное нулю
по сравнению с 0,93 кг
Таким образом, часть массы покоя составных частей системы превратилась в энергию, но масса покоя системы в целом не изменилась
❔
Пусть ядерный взрыв будет произведён в подземной полости, а затем его продукты будут охлаждены, собраны и взвешены. Окажется ли тогда их масса меньше, чем масса первоначального ядерного устройства?
✔
Да. Решающим является здесь период ожидания, за который теплота и излучение успеют удалиться, так что продукты взрыва снова будут содержать такое же количество теплоты, какое было сначала в бомбе. Тогда в выражении для массы покоя системы 𝑀 = ∑ 𝑚𝑖 + ∑ 𝑇𝑖
второй член, величина которого резко возросла в момент взрыва, но понизилась за время охлаждения, в конечном итоге, после взрыва и последующего охлаждения, окажется прежним. Напротив, сумма масс покоя ∑𝑚𝑖 всё время уменьшалась, а вместе с ней уменьшилась и величина массы 𝑀 того, что мы взвешиваем (после периода охлаждения); см. рис. 95
❔
Означает ли эйнштейновское утверждение об эквивалентности массы и энергии, что энергия — это то же самое, что масса?
✔
Нет. Величина энергии зависит от того, в какой инерциальной системе отсчёта мы рассматриваем частицу (или систему частиц). Величина же массы покоя не зависит от выбора инерциальной системы отсчёта. Энергия — всего лишь временная компонента 4-вектора, тогда как масса определяется как полная абсолютная величина этого 4-вектора (см. также упражнение 67). Временна'я компонента 4-вектора совпадает с его абсолютной величиной лишь в том частном случае, когда пространственные компоненты этого 4-вектора равны нулю, т.е. когда равен нулю импульс частицы (или полный импульс системы частиц). Лишь тогда величина энергии совпадает с величиной массы покоя
❔
Если говорить без всякого крючкотворства, является ли равенство 𝐸обычн=𝑚𝑐² именно тем, что на самом деле существенно в законе эквивалентности массы и энергии?
✔
Исторически — да, в наше время — нет! В прежние времена не признавали, что и джоули и килограммы — это две единицы, различные лишь вследствие исторической случайности, но измеряющие одну и ту же величину — массу-энергию. Подобным же образом одну и ту же массу-энергию можно измерять и в других разных единицах — в эргах и в граммах. Множитель перехода 𝑐², подобно множителю перехода от секунд к метрам или от миль к футам, в наше время можно рассматривать, если угодно, как условность, но не как новую принципиальную величину
❔
Если основным во взаимосвязи массы и энергии является не множитель 𝑐², что же тогда будет там основным?
✔
Различие между массой и энергией в том, что масса характеризует абсолютную величину 4-вектора, а энергия — временную компоненту этого же 4-вектора. Все соображения, подчёркивающие это различие, идут на пользу пониманию взаимосвязи массы и энергии. Любая расплывчатость в терминологии, затушёвывающая это различие, является потенциальным источником ошибок и недоразумении
❔
Масса покоя 𝑀 системы свободно движущихся частиц определяется не как сумма масс покоя 𝑚𝑖 отдельных частиц системы, но как сумма их энергий 𝐸𝑖 (при этом—только в той системе отсчёта, где полный импульс системы равен нулю). Почему бы тогда не дать величинам 𝐸𝑖 новое название, а именно не назвать их «релятивистскими массами» отдельных частиц? При таком обозначении (𝑚𝑖)релят = 𝐸𝑖 =
⎧
⎪
⎪
⎨
⎪
⎪
⎩ = 𝑚𝑖+𝑇𝑖 , = √𝑚𝑖²+𝑝𝑖², =
𝑚𝑖
√1-β𝑖² ,
и можно записать 𝑀 =
𝑛
∑
𝑖=1 (𝑚𝑖)релят
✔
Понятие «релятивистской массы» (массы движения) приводит к недоразумениям, и мы его здесь не используем. 1) Оно применяет термин «масса», принадлежащий абсолютной величине 4-вектора, к совершенно другому понятию — временной компоненте 4-вектора. 2) При его использовании казалось бы, что увеличение энергии частицы при росте её скорости или импульса связано с какими-то изменениями во внутренней структуре этой частицы. На самом же деле увеличение энергии с ростом скорости заложено в геометрических свойствах самого пространства (преобразование Лоренца!)
❔
Может ли это различие между массой и энергией быть проиллюстрировано на какой-то простой диаграмме?

Рис. 96. 4-вектор энергии-импульса одной и той же частицы в трёх различных системах отсчёта.
✔
Да! На рис. 96. 4-вектор энергии-импульса одной и той же частицы изображён в разных системах отсчёта. Энергия в разных системах различна, но масса покоя (абсолютная величина 4-вектора) имеет во всех системах одно и то же значение 𝑚. (Кажущееся различие между значениями 𝑚 в трёх изображённых здесь системах вызвано тем, что мы пытались изобразить лоренцеву геометрию на эвклидовой плоскости. В лоренцевой геометрии квадрат гипотенузы равен разности квадратов катетов 𝐸' и 𝑝' или 𝐸ʺ и 𝑝ʺ)
❔
Существует ли столь же простая диаграмма, иллюстрирующая превращение части массы покоя ядра плутония в энергию в процессе деления?

Рис. 97. Сумма масс покоя продуктов деления ядра плутония меньше, чем масса покоя исходного ядра.
✔
Да, см. рис. 97. Векторная сумма двух временноподобных 4-векторов есть 4-вектор с абсолютной величиной 𝑀 (масса покоя 𝙿𝚞²³⁹ до деления), превышающей сумму абсолютных величин 𝑚₁ и 𝑚₂ обоих 4-векторов-слагаемых (масс покоя продуктов деления). В противоположность эвклидовой геометрии, где длина третьей стороны треугольника всегда меньше суммы длин двух других сторон, здесь 𝑀>𝑚₁+𝑚₂
Упражнения к главе 2
Скорость частицы β и параметр скорости θ почти никогда не используются при решении задач, касающихся импульса и энергии частиц, движущихся с релятивистскими скоростями. С одной стороны, величиной β неудобно пользоваться, так как она входит в выражения для импульса и энергии под знаком квадратного корня: √1-β². С другой стороны, и это существеннее, очень малое изменение скорости β может соответствовать огромному изменению импульса и энергии, если частица двигалась со скоростью, близкой к скорости света. Если, например, частица первоначально двигалась со скоростью β=0,99, а затем её скорость увеличилась на 0,01, то это соответствует увеличению импульса и энергии этой частицы в бесконечное число раз. Обычно в задачах, касающихся быстро движущихся частиц, пользуются их кинетической энергией или полной энергией. Тогда импульс каждой частицы можно найти по формулам (85) и (86):
𝐸²
-
𝑝²
=
𝑚²
,
𝑇
=
𝐸
-
𝑚
.
При этом удобнее всего вообще не говорить о скорости и не пользоваться формулами, содержащими скорость или параметр скорости.
Если же требуется явно выразить величину скорости, её можно найти из соотношения
β
=
th θ
=
sh θ
ch θ
=
𝑚 sh θ
𝑚 ch θ
=
𝑝
𝐸
.
(106)
В таких случаях часто бывает достаточно (например, в упражнении 55) найти величину разности 1-β скорости света и скорости частицы р. Подставляя 𝑝=β𝐸 в уравнение
𝐸²
-
𝑝²
=
𝑚²
,
получим
𝑚²
𝐸²
=
1-β²
=
(1-β)
(1+β)
.
При скорости β, очень близкой к единице, 1+β≈2, и тогда
1-β
≈
𝑚²
2𝐸²
,
β≈1
.
(107)
В задачах на столкновения (упражнение 90 и последующие) удобно поставить чёрточки над величинами, взятыми «после столкновения» (например, 𝑝, 𝐸).
Число звёздочек при номерах упражнений соответствует возрастанию трудности этих упражнений.
Номера в скобках, стоящие после названия упражнений, указывают, какие упражнения необходимо решить, прежде чем приступать к данному
A. Общие задачи
55.
Быстрые электроны
56*.
Космические лучи
57.
Границы ньютоновской механики
58*.
Релятивистская ракета
59*.
Парадокс центра масс
60*.
Второй вывод релятивистского выражения для импульса
61*.
Второй вывод релятивистского выражения для энергии
Б. Эквивалентность энергии и массы покоя
62.
Задачи на пересчёт
63.
Релятивистская химия
64**.
Релятивистский осциллятор
65**.
Импульс без массы?
B. Фотоны
66.
Частицы нулевой массы покоя
67.
Эйнштейновский вывод принципа эквивалентности энергии и массы покоя — подробный пример
68*.
Устойчивость фотона (66)
69*.
Давление света (66)
70*.
Эффект Комптона (66)
71**.
Измерение энергии фотона
72**.
Энергия и частота фотона (66)
73*.
Гравитационное красное смещение (66)
74*.
Плотность спутника Сириуса (73)
Г. Допплеровское смещение
75.
Формулы Допплера (66, 22)
76.
Распад π⁰-мезона; подробный пример
77.
Полёт неоновой лампочки (75)
78.
Физик и светофор (75)
79.
Допплеровское смещение на краю диска Солнца (73, 75)
80.
Расширяющаяся Вселенная (75)
81*.
Анализ парадокса часов с помощью эффекта Допплера (75)
82*.
«Не превышайте скорости» (75)
83*.
Допплеровское уширение спектральных линий (75)
84*.
Изменение энергии фотона вследствие отдачи излучателя (83)
85*.
Эффект Мёссбауэра (84)
86**.
Резонансное рассеяние (85)
87**.
Измерение допплеровского смещения по резонансному рассеянию (86)
88**.
Проверка эффекта гравитационного красного смещения с помощью эффекта Мёссбауэра (73, 87)
89**.
Проверка парадокса часов с помощью эффекта Мёссбауэра (87)
Д. Столкновения
90.
Симметричное упругое столкновение
91.
Давид и Голиаф — подробный пример
92.
Абсолютно неупругое столкновение
93*.
Порождение частиц протонами
94*.
Порождение частиц электронами
95*.
Фоторождение пары одиночным фотоном (66, 93)
96**.
Фоторождение пары двумя фотонами (95)
97**.
Аннигиляция электрон-позитронной пары
98*.
Проверка принципа относительности (97)
99*.
Отождествление частиц по трекам в пузырьковой камере
100*.
Накопительные кольца и встречные пучки (93)
Е. Атомная физика
101*.
Де Бройль и Бор (72)
102*.
Ви'дение посредством электронов (101)
103**.
Прецессия Томаса (52, 101)
Ж. Межзвёздные полёты
104*.
Трудности межзвёздных полётов (58)
А. ОБЩИЕ ЗАДАЧИ
55. Быстрые электроны
Станфордский линейный ускоритель сконструирован для ускорения электронов вплоть до кинетической энергии 40 Бэв (40 миллиардов электронвольт; 1 эв = 1,6⋅10⁻¹⁹ дж) для экспериментов с элементарными частицами. Ускоритель имеет в длину 10 000 фут (приблизительно 3000 м) и напоминает по виду трубу; электроны ускоряются в нем электромагнитными волнами, генерирующимися в огромных «радиолампах»— клистронах.
а) С точки зрения лабораторной системы отсчёта возрастание энергии электрона на каждом метре пути, пройденного в трубе ускорителя, приблизительно одинаково. Чему равна энергия, которую каждый электрон приобретает на 1 м пути (в Мэв); Допустим, что справедливо ньютоновское выражение для кинетической энергии. Какой путь должен был бы проделать электрон в трубе ускорителя, чтобы его скорость сравнялась со скоростью света? (Ответ на этот вопрос был предвосхищен в тексте, см. стр. 27).
б) На самом же деле, конечно, даже электроны с энергией 40 Бэв, выходящие из ускорителя, обладают скоростью β, меньшей, чем скорость света. Чему равна разность 1-β между скоростью света и скоростью этих электронов? Устроим состязания на скорость полёта между электронами с энергией 40 Бэв и световой вспышкой в эвакуированной трубе длиной 1000 км. Насколько свет опередит электроны в конце дистанции? Выразите ответ в миллиметрах.
в) Чему равна длина трубы «3 000 м» (длина ускорителя), если её измерять в системе отсчёта ракеты, движущейся вместе с электронами энергии 40 Бэв, которые даёт ускоритель? ▼
56*. Космические лучи
а) В космических лучах наблюдалась (косвенными методами) по меньшей мере одна частица, энергия которой была оценена в 16 дж (1,0⋅10²⁰ эв) 1). Если носителем этой энергии был протон (𝑚𝑐²≈1 Бэв), то сколько времени потребовалось бы ему, чтобы пересечь нашу Галактику (диаметром 10⁵ световых лет), если измерять время по часам, летящим вместе с этим протоном? Ответ выразите в секундах (1 год ≈ 32⋅10⁶ сек). (В системе отсчёта Земли такой протон, движущийся почти со скоростью света, совершит этот перелёт немногим более чем за 10⁵ лет!)
1) Jonh Linsley, Physical Review Letters, 10, 146 (1963).
б) Во сколько раз энергия частицы должна превышать её энергию покоя, чтобы диаметр нашей Галактики в результате лоренцева сокращения оказался равным диаметру этой частицы (около 1 ферми, что равно 10⁻¹⁵ м)? Какое количество массы потребовалось бы превратить в энергию, чтобы придать требуемую скорость протону? ▼
57. Границы ньютоновской механики
а) Один электронвольт (1 эв) равен тому изменению, которое претерпевает кинетическая энергия частицы, несущей единичный элементарный заряд, когда она проходит через разность потенциалов 1 в. 1 эв =1,60⋅10⁻¹⁹ дж. Чему равны энергии покоя электрона и протона (их массы указаны в конце книги), выраженные в миллионах электронвольт (Мэв)?
б) Кинетическая энергия частицы, движущейся с данной скоростью β, даётся выражением ½ 𝑚β² неточно. Относительная ошибка,
⎛
⎜
⎜
⎜
⎝
Релятивистское
выражение для
кинетической
энергии
⎞
⎟
⎟
⎟
⎠
-
⎛
⎜
⎜
⎜
⎝
Ньютоновское
выражение для
кинетической
энергии
⎞
⎟
⎟
⎟
⎠
,
⎛
⎜
⎝
Ньютоновское выражение
для кинетической энергии
⎞
⎟
⎠
равна 1 % при достижении ньютоновской кинетической энергией величины, составляющей определённую часть энергии покоя. Чему равна эта часть? [Можно ограничиться приблизительным ответом, полученным из анализа следующего члена разложения по формуле бинома (или в степенной ряд) точной формулы для энергии как функции скорости β, либо из других чётко сформулированных рассуждений.] Назовём этот случай (когда ошибка составляет 1 %) совершенно произвольно «границей ньютоновской механики». При какой кинетической энергии достигает этой границы протон (выразите энергию в Мэв)? При какой — электрон? ▼
58*. Релятивистская ракета
Какие ограничения накладывает теория относительности на лётные качества и скорость ракеты? Будем схематически представлять действие двигателя как последовательные выбросы одинаковых шариков, имеющих одну и ту же массу покоя 𝑚. Каждый выброс тогда можно рассматривать как «неупругое столкновение наоборот». Пусть каждый выброс осуществляется на ракете одним и тем же способом. Тогда разумно предположить, что скорость удаления одинакова для любого шарика, если её рассматривать в инерциальной системе отсчёта, в которой ракета покоится (она изображена на рис. 98 в «лабораторной системе отсчёта», связанной с ракетой до выброса). Назовём эту скорость удаления шарика скоростью выброса βвыбр.

Рис. 98. Исследование движения релятивистской ракеты.
а) Используя обозначения рис. 98, запишите уравнения сохранения импульса и сохранения энергии. Не забудьте учесть начальную энергию покоя 𝑀₁ но не считайте, что масса покоя сохраняется — ведь речь идёт о «неупругом столкновении наоборот»! Исключите из этих уравнений 𝑚 и найдите таким образом приращение 𝑑θ,
𝑑θ
=
β
выбр
⎛
⎜
⎝
𝑀₁-𝑀₂
𝑀₂
⎞
⎟
⎠
,
где βвыбр — скорость выброса относительно первоначальной системы ракеты. Так как 𝑀₂-𝑀₁=𝑑𝑀 — изменение массы ракеты, то
𝑑θ
=-
β
выбр
𝑑𝑀
𝑀
,
где 𝑀 — масса ракеты в любой данный момент времени. Если мы рассмотрим теперь новую систему отсчёта («систему ракеты»), в которой ракета покоится, выброс следующей порции массы со скоростью βвыбр в этой системе приведёт к дальнейшему изменению параметра скорости на 𝑑θ. Однако, согласно уравнению (25), новое значение параметра скорости ракеты в первоначальной системе отсчёта равно просто сумме всех изменений параметра скорости (сами скорости не аддитивны, но параметры скорости аддитивны). К тому же массы покоя (и изменения массы покоя) инвариантны, одинаковы во всех системах отсчёта. Поэтому окончательное значение параметра скорости в первоначальной системе отсчёта может быть получено путём суммирования (интегрирования) приращений параметра скорости:
θ
∫
0
𝑑θ
=-
β
выбр
𝑀
∫
𝑀₁
𝑑𝑀
𝑀
.
Интеграл справа равен натуральному логарифму, так что
θ
=
β
выбр
⋅ln
𝑀₁
𝑀
(релятивистская ракета),
(108)
⎛
⎜
⎜
⎜
⎜
⎝
Величина параметра
скорости, достигнутая
после сжигания
любой данной
массы горючего
⎞
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎝
Скорость
выброса
продуктов
сгорания
⎞
⎟
⎟
⎟
⎠
⋅ln
⎛
⎜
⎜
⎝
Начальная
масса покоя
ракеты
⎞
⎟
⎟
⎠
⎛
⎜
⎜
⎝
Конечная
масса покоя
ракеты
⎞
⎟
⎟
⎠
Это и есть уравнение движения релятивистской ракеты.
б) Нерелятивистской называется такая ракета, которая движется со скоростью, много меньшей скорости света. Покажите, что приведённое выше уравнение движения релятивистской ракеты в нерелятивистском пределе принимает вид обычного уравнения движения нерелятивистской ракеты:
𝑣
=
𝑣
выбр
⋅ln
𝑀₁
𝑀
(нерелятивистская ракета),
(109)
в) Покажите, исходя из основных законов сохранения, что масса покоя в случае релятивистской ракеты не сохраняется. Куда же она девается? Покажите, что масса покоя (приближённо) сохраняется в предельном случае нерелятивистской ракеты.
г) Покажите, что скорость релятивистской ракеты может приближаться сколь угодно близко к скорости света, но не превосходить её.
д) Рассмотрите частный случай, когда скорость выброса очень велика. Покажите, что при βвыбр, стремящейся к скорости света (т.е. при очень больших θвыбр), необходимая для достижения данного значения параметра скорости ракеты выбрасываемая масса покоя стремится к нулю. Из этого следует что использование света для создания тяги ракеты соответствует полному переводу массы покоя топлива в энергию излучения; уравнение движения тогда принимает вид
θ
=
ln
𝑀₁
𝑀
⎛
⎜
⎝
для ракеты с
фотонными двигателями
⎞
⎟
⎠
(110)
е) Иногда высказывают следующее обобщающее заключение: «Наиболее экономична ракета с фотонной тягой». Покажите, что это утверждение и верно, и ошибочно одновременно. Обсуждение. Найдите «коэффициент полезного действия» для двигателей, тягу которых создают световые вспышки. Насколько экономично продолжать ускорять «шлак» (использованные элементы) вместе с полезным грузом? Существует ли хоть один тип взаимодействия элементарных частиц, при котором вообще не остаётся «шлака» и образуется лишь свет (т.е. гамма-лучи)? См. стр. 162 и упражнение 97.
ж) Чему равно наименьшее отношение масс (отношение начальной массы к конечной, когда горючее исчерпано) для идеальной ракеты, в которой масса полностью превращается в свет, при котором ракета ускоряется из состояния покоя до такой скорости, при которой течение времени замедляется в десять раз? Чему равно это отношение масс в случае наибольшей скорости выброса, достижимой в ракетах с химическими двигателями (около 4000 м/сек)? Замечание. В технической литературе часто говорится об «удельном импульсе» (обозначаемом через 𝐼) ракетного горючего; например, 𝐼=260 сек для керосина с жидким кислородом и 350 сек для жидкого водорода с жидким кислородом. Умножьте эти величины на 9,8 м/сек², чтобы перейти к физическим единицам (скорости выброса в м/сек или к импульсу в кг⋅м/сек, сообщаемому ракете каждым килограммом отработавшего топлива). Последний способ выражения через импульс в противоположность использованию единиц времени применим и на Луне, где 𝑔≈(1/6)*9,8 м/сек², и на Земле, где 𝑔=9,8 м/сек². ▼
59*. Парадокс центра масс
Пусть в системе отсчёта ракеты вдоль оси 𝑥 в состоянии покоя закреплена длинная труба. С двух противоположных концов в неё одновременно и с одинаковой скоростью (с точки зрения системы отсчёта ракеты) выстреливаются два одинаковых пушечных ядра. Эти ядра упруго сталкиваются в середине трубы и разлетаются вновь к её концам. До того как ядра достигают этих концов, их наглухо закрывают, и в дальнейшем ядра всё время движутся взад и вперёд в трубе без трения.

Рис. 99. Пушечные ядра, летящие навстречу друг другу.
а) Опишите движение центра масс этих двух ядер в системе отсчёта ракеты.
б) Одновременно ли производятся в лабораторной системе отсчёта выстрелы, посредством которых ядра вводятся в трубу? Опишите движение центра масс ядер в лабораторной системе отсчёта. При этом удобно воспользоваться диаграммой пространства-времени. Инвариантно ли положение центра масс в теории относительности?
в) Предположим теперь, что в системе отсчёта ракеты труба не закреплена, а лежит на абсолютно гладкой поверхности. Рассмотрите движение центра масс трубы в обеих системах отсчёта. Как движется в каждой из систем отсчёта центр масс системы, включающей трубу плюс оба пушечных ядра? ▼
60*. Второй вывод релятивистского выражения для импульса
а) На рис. 85 в системе отсчёта ракеты между моментами столкновения двух шаров и попадания шара 𝐴 в верхнюю стенку проходит интервал времени Δ𝑡'. В лабораторной системе отсчёта этот промежуток времени равен Δ𝑡. Пользуясь формулами преобразования Лоренца, найдите связь между этими двумя промежутками времени, Δ𝑡' и Δ𝑡. Найдите связь между значениями 𝑦-компоненты скорости шара 𝐴 в обеих системах (см. упражнение 20).Приняв за β скорость шара 𝐴 в системе отсчёта ракеты, покажите, что 𝑦-компонента скорости шара 𝐴 в лабораторной системе отсчёта β𝐴𝑦,лаб определяется выражением
β
𝐴
𝑦
,
лаб
=
β
ch θ𝑟
.

Рис. 100. Компоненты скорости шаров 𝐴 и 𝐵 в лабораторной системе отсчёта до столкновения.
б) Проанализируйте теперь это столкновение в лабораторной системе отсчёта. На основании его симметрии в лабораторной системе и в системе отсчёта ракеты проверьте правильность данных о компонентах скоростей, приведённых на рис. 100. Вспомните, что импульс частицы должен быть направлен вдоль её движения (разд. 11). Поэтому треугольник векторов скорости шара 𝐴 до и после столкновения подобен треугольнику векторов импульса шара 𝐴 до и после столкновения (рис. 101). Предположим, что шар 𝐵 в лабораторной системе отсчёта движется настолько медленно, что его импульс можно определять по ньютоновской формуле 𝑚β. Потребуем теперь, чтобы изменение импульса шара 𝐴 в процессе столкновения было равно по величине и противоположно по направлению изменению импульса шара 𝐵. Пропорциональность соответственных сторон подобных треугольников даёт равенство:
⎛
⎜
⎜
⎝
Горизонтальный
пунктирный отрезок
на диаграмме импульса
⎞
⎟
⎟
⎠
⎛
⎜
⎜
⎝
Вертикальный
пунктирный отрезок
на диаграмме импульса
⎞
⎟
⎟
⎠
=
⎛
⎜
⎜
⎝
Горизонтальный
пунктирный отрезок
на диаграмме скорости
⎞
⎟
⎟
⎠
⎛
⎜
⎜
⎝
Вертикальный
пунктирный отрезок
на диаграмме скорости
⎞
⎟
⎟
⎠
.

Рис. 101. Диаграммы скорости и импульса шара 𝐴 в лабораторной системе отсчёта.
Покажите, что отсюда следует выражение
𝑝
𝑥
=
𝑚 sh θ
𝑟
для 𝑥-компоненты импульса быстро движущегося шара 𝐴.
в) В пределе малых 𝑦-компонент скоростей величина 𝑝 𝑥 становится равной полному импульсу 𝑝 шара 𝐴, а параметр относительной скорости θ𝑟 становится равным параметру θ шара 𝐴. Отсюда следует выражение для релятивистского импульса частицы
𝑝
=
𝑚 sh θ
.
▼
61*. Второй вывод релятивистского выражения для энергии

Рис. 102. Анализ упругого лобового столкновения частиц разных масс в ньютоновской механике. Скорости частиц до и после соударения в лабораторной системе отсчёта (верхний рисунок) и в системе отсчёта ракеты (нижний рисунок), найденные по ньютоновскому закону сложения скоростей.
а) Сохранение ньютоновского импульса. Рассмотрим лобовое упругое соударение частиц различных масс покоя (𝑚₁ и 𝑚₂). Частица 1 отскакивает от частицы 2, потеряв часть своей скорости и передав часть импульса частице 2. Рассмотрите это столкновение с ньютоновских позиций. Основываясь на рис. 102, покажите, что в лабораторной системе отсчёта из ньютоновского закона сохранения импульса следует уравнение
𝑚₁β₁
+
𝑚₂β₂
=
𝑚₁
β
₁
+
𝑚₂
β
₂
,
в котором величина β₁ отрицательна в случае указанных на этом рисунке направлений движения. Чёрточки над буквами означают, что соответствующие величины взяты после соударения. Рассмотрим теперь этот же процесс в системе отсчёта ракеты. При малой относительной скорости движения ракеты β𝑟 скорость каждой частицы в системе отсчёта ракеты находится путём простого вычитания β𝑟 из скорости этой частицы в лабораторной системе отсчёта. Примените ньютоновский закон сохранения импульса к столкновению с точки зрения системы отсчёта ракеты. Покажите, что если ньютоновский импульс сохраняется в лабораторной системе отсчёта, он будет автоматически сохраняться и в системе отсчёта ракеты, движущейся с малой скоростью относительно лабораторной системы отсчёта.

Рис. 103. Анализ упругого лобового столкновения частиц разных масс в релятивистской механике. Скорости частиц до и после соударения в лабораторной системе отсчёта (верхний рисунок) и в системе отсчёта ракеты (нижний рисунок), найденные по релятивистскому закону сложения параметров скорости.
б) Из сохранения релятивистского импульса следует сохранение релятивистской энергии. Рассмотрим теперь то же столкновение с релятивистской точки зрения. Покажите, что закон сохранения релятивистского импульса в лабораторной системе отсчёта выражается уравнением
𝑚₁ sh θ₁
+
𝑚₂ sh θ₂
=
𝑚₁ sh
θ
₁
+
𝑚₂ sh
θ
₂
.
(111)
При этом массы обеих частиц остаются неизменными, так как столкновение является упругим. В случае указанных на рис. 103 направлений движения величина θ₁ отрицательна. В релятивистской механике скорости частиц в системе отсчёта ракеты могут быть найдены путём вычитания параметра относительной скорости θ𝑟 из параметра скорости этих частиц в лабораторной системе отсчёта (см. стр. 69). Примените закон сохранения импульса к этому столкновению, рассматриваемому в системе отсчёта ракеты. Используйте данные табл. 8 (стр. 77—78) для того, чтобы преобразовать все гиперболические синусы, зависящие от разностей параметров скорости. В полученном уравнении перегруппируйте члены, объединяя те из них, которые содержат ch θ𝑟 или sh θ𝑟:
(Скобка № 1)
⋅
ch θ
𝑟
-
(Скобка № 2)
⋅
sh θ
𝑟
=
0.
(112)
Величины, стоящие в скобках, уже не зависят от параметра относительной скорости θ𝑟. Если теперь потребовать, чтобы импульс сохранялся в системе отсчёта любой ракеты, то полученное уравнение должно выполняться при всех значениях параметра относительной скорости θ𝑟. Мы можем взять систему ракеты с любым значением параметра скорости — от нуля (когда ch θ𝑟=1 и sh θ𝑟=0) и до бесконечности (когда ch θ𝑟 равняется sh θ𝑟). Но полученное уравнение может выполняться при всех значениях θ𝑟 в указанных пределах, лишь если каждая из скобок по отдельности равна нулю. Покажите, что скобка № 1 равняется нулю, если импульс сохраняется в лабораторной системе отсчёта. Покажите, что скобка № 2 равняется нулю, если
𝑚₁ ch θ₁
+
𝑚₂ ch θ₂
=
𝑚₁ ch
θ
₁
+
𝑚₂ ch
θ
₂
.
(113)
Уравнение (112) выражает закон сохранения импульса в системе отсчёта ракеты. Очевидно, что импульс сохраняется в системах отсчёта всех возможных ракет тогда и только тогда, когда в лабораторной системе одновременно выполняются уравнения (111) и (113). Уравнение (111) выражает закон сохранения импульса в лабораторной системе отсчёта. Какой же закон сохранения выражает уравнение (113)? Выясните смысл величины 𝑚 ch θ и назовите новый закон сохранения.
в) Останется ли справедливым приведённый вывод, если обозначить массы покоя частиц после столкновения через 𝑚₁ и 𝑚₂ и допустить, что они отличны от масс покоя частиц до столкновения? Будет ли оставаться верным закон сохранения релятивистской энергии и в этом случае? Сохраняется ли при таких столкновениях релятивистская кинетическая энергия? ▼
Б. ЭКВИВАЛЕНТНОСТЬ ЭНЕРГИИ И МАССЫ ПОКОЯ
62. Задачи на пересчёт
а) Сколько массы излучает 100-ваттная электрическая лампочка (в форме теплоты и света) в течение года?
б) В Соединённых Штатах в год вырабатывается около 10¹² квт⋅час электроэнергии. Чему равен массовый эквивалент этой энергии? В самом ли деле это количество массы превращается в энергию в процессе генерирования электроэнергии? Может быть, превращается меньшее или большее количество массы? Мотивируйте свой ответ.
в) Когда студент изо всех сил крутит педали велосипеда, он производит ½ лошадиной силы полезной мощности (1 л.с. = 746 вт). Коэффициент полезного действия человеческого организма составляет около 25%; это значит, что 75% пищи сгорает, превращаясь в теплоту, и лишь 25% пищи при сгорании переводится в полезную работу. Сколько времени должен ехать студент на велосипеде, чтобы потерять 1 кг массы за счёт её превращения в энергию? Почему же для уменьшения веса полезна физкультура?
г) На квадратный метр поверхности, перпендикулярной направлению солнечных лучей, вблизи Земли, но вне её атмосферы, от Солнца приходит около 1,4 квт световой энергии. (Эти 1,4 квт/м² носят название солнечной постоянной). Какое количество массы излучает Солнце в форме света в одну секунду? Сколько массы с Солнца поступает в форме света на Землю в год?
д) Два товарных поезда, каждый массой 10⁶ кг, движутся друг другу навстречу по одному и тому же пути с одинаковыми скоростями 45 м/сек (примерно 160 км/час). При столкновении они останавливаются. Масса покоя поездов в сумме с массами покоя рельсов и насыпи сразу же после столкновения возрастает; сколько микрограмм составляет это возрастание? Пренебрегите потерями энергии в форме звука и света. ▼
63. Релятивистская химия
При соединении 1 кг водорода 8 кг кислорода выделяется около 10⁸ дж энергии. Очень хорошие химические весы могут обнаружить относительное изменение массы, равное 10⁻⁷. Во сколько раз такая чувствительность больше (или меньше) необходимой для обнаружения относительного изменения массы в данной реакции? ▼
64**. Релятивистский осциллятор

Рис. 104. Электрон в качестве колеблющегося груза в релятивистском осцилляторе.
Для того чтобы проверить законы теории относительности, некий инженер решил построить осциллятор с очень лёгким колеблющимся грузом, способным очень быстро двигаться взад и вперёд. Самым лёгким из известных грузов с ненулевой массой покоя является электрон. Инженер взял кубический ящик из металла, каждое ребро которого равно 1 м, и слегка его подогрел, чтобы из стенок «испарилось» небольшое число электронов (рис. 104). Поперёк ящика в середине его помещена электрически изолированная от стенок металлическая сетка, к которой от генератора подведено высокое положительное напряжение. Ручку регулятора напряжения можно поворачивать, чтобы менять постоянную разность потенциалов 𝑉₀ между стенками ящика и сеткой.
Вакуумный насос выкачивает воздух из ящика, чтобы электроны могли свободно двигаться внутри него, не сталкиваясь с молекулами воздуха. Пусть испарившийся с внутренней части стенки ящика электрон первоначально обладает весьма малой скоростью (примем эту начальную скорость равной нулю). Положительно заряженная сетка притягивает этот электрон; он ускоряется в её направлении, проходит сквозь отверстие в ней, замедляется по мере удаления от неё, так как его тормозит притяжение сетки, на мгновение останавливается и снова летит к сетке. В результате он колеблется взад и вперёд между стенками ящика.
а) Насколько малым может быть сделан период колебаний электрона 𝑇 (время одного замкнутого колебательного движения туда и обратно между стенками)? Конструировавший эту установку инженер утверждает, что при соответствующем повороте ручки регулятора напряжения можно получить по желанию сколь угодно высокую частоту колебаний ν=1/𝑇 Прав ли он?
б) Когда напряжение достаточно мало, электрон остаётся нерелятивистским, и его движение можно описывать законами ньютоновской механики. Во сколько раз при этом увеличивается частота колебаний электрона при удвоении напряжения на сетке? (Обсуждение. Во сколько раз различается до и после удвоения напряжения ньютоновская кинетическая энергия электрона в соответствующих точках его траектории? Во сколько раз изменяется при этом его скорость?)
в) Как выглядит окончательная формула для частоты ν как функции напряжения в нерелятивистском случае?
г) Чему равна частота в крайнем улътрарелятивистском случае, когда электрон бо'льшую часть своего времени движется... (конец фразы не будем договаривать!)... ?
д) Начертите на одном и том же графике две зависимости частоты ν от напряжения на сетке 𝑉₀: 1) нерелятивистскую кривую из пункта (в), проведённую жирно там, где ей можно пользоваться с уверенностью, и пунктиром в других местах; 2) ультрарелятивистское значение из пункта (г). По этому графику количественно определите, при каком напряжении поведение электрона переходит из нерелятивистского в релятивистское. По возможности дайте простое объяснение того, как ваши выводы учитывают порядок величины (т.е. отбрасывают множители типа 2, π и т.д.). ▼
65**. Импульс без массы?

Рис. 105. Перенос массы, не сопровождаемый переносом частиц или излучения.
На рис. 105 изображён миниатюрный мотор, установленный на платформе и питаемый от аккумулятора, поставленного на него. С помощью ремённой передачи мотор приводит во вращение колёсико с лопатками, «гребущее» по воде. Устройство с гребным колёсиком смонтировано на той же платформе, что и мотор. Мощность мотора равна 𝑑𝐸/𝑑𝑡.
а) Какое количество массы переносится в секунду с одного конца платформы на другой от мотора к гребному колесу?
б) Масса переносится на расстояние 𝑥 со скоростью, найденной вами в пункте (а). Какой импульс связан с этим переносом массы? Так как этот импульс мал, применимы ньютоновские представления об импульсе.
в) Пусть платформа первоначально покоится и стоит на горизонтальной поверхности стола на колёсах, лишённых трения. Платформа начнёт двигаться! В каком направлении? Что произойдёт с этим движением, когда истощится заряд аккумулятора? Насколько продвинется платформа за это время?
г) Покажите, что наблюдатель на платформе наблюдал бы перенос энергии лишь ремённой передачей; наблюдатель на столе наблюдал бы перенос энергии отчасти ремённой передачей, а отчасти самой платформой; наблюдатель же, движущийся по ремённой передаче в одну сторону, наблюдал бы перенос энергии отчасти ремённой передачей (отрезком ремня, движущимся в сторону, противоположную ему), а отчасти платформой. Очевидно, что не всегда можно сделать заключение, удовлетворяющее всех наблюдателей, о путях, по которым энергия передаётся с одного места на другое, или о скорости, с которой эта энергия переносится! ▼
В. ФОТОНЫ
66. Частицы нулевой массы покоя
На чём основывается вывод важного соотношения 𝐸²-𝑝²=𝑚²? Получите из него соотношение между энергией и импульсом, справедливое для случая нулевой массы покоя (фотоны, гравитоны, нейтрино). Что можно заключить из этого соотношения относительно наклона мировой линии такой частицы (а следовательно, о её скорости)? Как зависят ваши результаты от равенства sh θ и ch θ друг другу в случае больших θ, если их рассматривать как предельный случай? Существует ли для частиц с нулевой массой покоя «сопутствующая система отсчёта» («система покоя»)? ▼
67. Эйнштейновский вывод принципа эквивалентности энергии и массы покоя — подробный пример
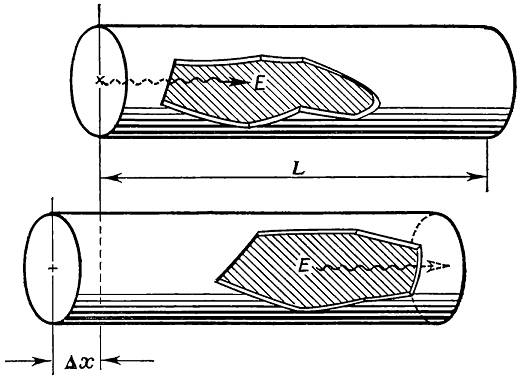
Рис. 106. Перенос массы излучением.
Задача. Исходя из того, что свет переносит энергию и оказывает давление на тела, показать, что его энергия эквивалентна массе, и тем самым, обобщая, доказать, что всякая энергия эквивалентна массе. Комментарий. Эквивалентность энергии и массы является настолько фундаментальным следствием теории, что Эйнштейн, получив это следствие собственно из теории относительности, сразу же продолжил свои рассуждения и нашёл альтернативный подход, приводящий к тому же выводу, но опирающийся на элементарную физику 1). Он рассмотрел первоначально покоившийся закрытый ящик массы 𝑀 (рис. 106). Из его левой стенки вправо излучается направленный сгусток электромагнитной энергии, проходящий через весь ящик длины 𝐿 и поглощающийся в противоположном его конце. Это излучение переносит энергию 𝐸. Но оно несёт также импульс - это видно из следующих соображений. Излучение оказывает давление на левую стенку ящика, когда оно покидает её. В результате ящик испытывает толчок влево и приобретает импульс -𝑝. Но ведь импульс системы в целом первоначально был равен нулю, значит излучение несёт импульс 𝑝 противоположный импульсу, полученному ящиком. Как воспользоваться этими данными о переносе энергии и импульса излучением для нахождения массового эквивалента этого излучения? Эйнштейн получил ответ, исходя из того, что центр масс системы не двигался до того, как начался процесс переноса, и поэтому не мог начать двигаться во время его протекания. Но очевидно, что масса ящика передвинулась влево. Значит, излучение должно перемещать массу вправо. Это были общие идеи, которыми руководствовался Эйнштейн, детали же состояли в следующем.
1) A. Einstein, Annalen der Physik, 20, 627 (1906).
Из теории относительности Эйнштейн знал, что импульс 𝑝 направленного пучка излучения равен его энергии 𝐸 (как 𝑝 так и 𝐸 измеряются в единицах массы; см. разд. 10). Однако, чтобы освободить рассуждения от всякого прямого использования принципа относительности, он получил соотношение 𝑝=𝐸 из следующих элементарных соображений. Давление, оказываемое на идеальный излучатель или поглотитель со стороны пучка, равно плотности энергии в этом пучке. Это известно как из теории электромагнитного излучения Максвелла, так и из непосредственных измерений давления, оказываемого светом на подвешенное в вакууме зеркальце. Такие измерения были впервые успешно произведены Е. Ф. Николсом и Дж. Ф. Халлом около 1901—1903 гг. 1). В настоящее время эти эксперименты были настолько упрощены, а их чувствительность так повышена, что они могут производиться в учебной лаборатории 2).
⎛
⎜
⎜
⎜
⎜
⎝
Плотность энергии
излучениях
в единицах энергии,
содержащаяся
в единице объёма
⎞
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
Давление, оказываемое
направленным
излучением на
идеальный излучатель
или поглотитель в
единицах силы на
единицу площади
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
.
1) П.Н. Лебедев произвёл прецизионные опыты по измерению давления света в 19000 г. (см. П.Н. Лебедев, Избранные сочинения, М.- Л., 1949). - Прим. перев.
2) См. R. Pollock, American Journal of Physics, 31, 901 (1963). Метод Поллока измерения давления света состоит в использовании явления резонанса для усиления слабых эффектов, так что их величина достигает легко поддающихся измерению значений. Поллок разработал этот эксперимент в сотрудничестве с той же самой группой первокурсников, с которой авторы этой книги имели удовольствие выработать это изложение теории относительности. Авторы особенно признательны Марку Вассерману, члену этой группы, сделавшему ряд полезных замечаний по поводу некоторых дальнейших схем.
Взяв этот вывод, умножим обе стороны равенства на величину площади 𝐴 излучающей стенки и длину 𝑙 сгустка радиации (которая должна быть по крайней мере короче длины 𝐿 ящика). Заметим, что 𝑙 равняется времени действия давления излучения, умноженному на скорость света. Поэтому наш множитель имеет вид
⎛
⎜
⎜
⎝
Объём,
занятый сгустком
энергии излучения
⎞
⎟
⎟
⎠
=
⎛
⎜
⎝
Площадь излучающей
поверхности
⎞
⎟
⎠
×
×
⎛
⎜
⎜
⎝
Время действия
давления
на поверхность
⎞
⎟
⎟
⎠
×
⎛
⎜
⎝
Скорость
света
⎞
⎟
⎠
.
Перемножая соответственные стороны двух последних равенств, найдём
⎛
⎜
⎜
⎝
Энергия,
переносимая
излучением
⎞
⎟
⎟
⎠
=
⎛
⎜
⎜
⎝
Сила, действующая
со стороны
излучения на стенку
⎞
⎟
⎟
⎠
×
×
⎛
⎜
⎝
Время действия
силы
⎞
⎟
⎠
×
⎛
⎜
⎝
Скорость
света
⎞
⎟
⎠
=
=
⎛
⎜
⎜
⎜
⎜
⎝
Импульс, переданный
излучением стенке, т.е.
величина импульса,
переносимого самим
излучением
⎞
⎟
⎟
⎟
⎟
⎠
×
⎛
⎜
⎝
Скорость
света
⎞
⎟
⎠
.
То же самое в единицах массы:
𝐸
=
⎛
⎜
⎜
⎜
⎝
Энергия
направленного
сгустка
излучения
⎞
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎝
Импульс
направленного
сгустка
излучения
⎞
⎟
⎟
⎟
⎠
=
𝑝
.
(114)
Итак, излучение переносит импульс и энергию вправо, тогда как ящик переносит импульс и массу влево. Но центр масс этой системы (ящик + излучение) не может двигаться. Значит, излучение должно переносить вправо не только энергию, но и массу. Чему равна эта масса? Чтобы ответить на этот вопрос, сначала зададимся другими вопросами:
а) Чему равна скорость ящика в то время, когда в нем распространяется излучение?
б) Когда излучение поглощается в противоположном конце ящика, вся система снова приходит в состояние покоя. На какое расстояние сдвинется ящик за время распространения излучения?
в) Потребуем теперь, чтобы центр масс системы сохранял положение одно и то же как до, так и после распространения излучения. Чему на основании этих соображений равен массовый эквивалент энергии, перенесённой из одного конца ящика в другой?
Ответы. а) В период, пока излучение распространяется, импульс ящика должен быть равен по абсолютной величине и противоположен по направлению импульсу 𝑝 излучения. Ящик движется с очень малой скоростью β, так что для нахождения его импульса достаточно применить ньютоновскую формулу 𝑀β:
𝑀β
=-
𝑝
=-
𝐸
.
Отсюда находим величину скорости ящика:
β
=-
𝐸
𝑀
.
б) Время распространения фотона практически равно 𝑡=𝐿 метрам светового времени. За этот срок ящик проходит расстояние
Δ
𝑥
=
β𝑡
=-
𝐸𝐿
𝑀
.
в) Если бы излучение не несло с собой массы и ящик был единственным объектом, наделённым массой, то этот сдвиг Δ𝑥 представлял бы собой полное перемещение центра масс системы влево. Но Эйнштейн утверждал, что если центр масс изолированной системы первоначально покоился, то он не может прийти в движение или изменить своё положение. Поэтому, заключил Эйнштейн, должно произойти уравновешивающее смещение части масс системы. Этот перенос массы вправо можно понять лишь как новое свойство самого излучения. Значит, в то время, как ящик двигался влево, излучение должно было перенести вправо некоторую массу 𝑚, величина которой пока неизвестна, но такова, что обеспечивает неподвижность центра масс системы в целом. Длина пути переноса равна полной длине ящика 𝐿 минус то расстояние Δ𝑥, на которое ящик сдвинулся за это время влево. Однако величина Δ𝑥 меньше, чем 𝐿, в пропорции 𝐸/𝑀. Это отношение может быть сделано сколь угодно малым при любой данной величине перенесённой энергии излучения 𝐸, если взять ящик достаточно большой массы 𝑀. Поэтому мы имеем право принять пройденное излучением расстояние равным самой величине 𝐿. Итак, со сколь угодно высокой степенью точности условие неподвижности центра масс можно записать в виде
𝑀
Δ
𝑥
+
𝑚𝐿
=
0
.
Отсюда, подставляя величину Δ𝑥, найденную в пункте (б), определим значение массы 𝑚:
𝑚
=-
Δ𝑥𝑀
𝐿
=-
⎛
⎜
⎝
-
𝐸𝐿
𝑀
⎞
⎟
⎠
⋅
𝑀
𝐿
.
Окончательно:
𝑚
=
𝐸
.
Мы пришли к выводу, что процесс излучения, распространения и поглощения энергии 𝐸 эквивалентен переносу массы 𝑚=𝐸 из одного конца ящика в другой его конец. Элементарность этого вывода и фундаментальность результата делают приведённые рассуждения одними из самых интересных в физике.
Обсуждение. Существование масс-эквивалента для энергии излучения влечёт за собой существование масс-эквивалента тепловой энергии и, далее, всех прочих форм энергии, как показывает следующее рассуждение. Та энергия, которая была излучена из левой стенки ящика, могла до этого существовать там в форме тепловой энергии. Эта тепловая энергия могла перевести рядовой атом поверхности стенки в возбуждённое состояние, а затем этот атом мог вернуться с этого более высокого энергетического уровня на более низкий и в результате излучить разность энергий этих уровней в виде радиации. Этот поток энергии затем пересекает ящик, поглощается и в конце концов снова принимает форму тепловой энергии. Каким бы ни был механизм излучения и поглощения света в деталях, конечным результатом явится перенос тепловой энергии из одного конца ящика в другой его конец. Говорить, что масса должна была переместиться из конца в конец ящика при соответствующем распространении в нем излучения, значит поэтому утверждать, что масса перемещается при изменении места локализации тепловой энергии. Тепловая энергия, в свою очередь, может быть получена из химической энергии, или из энергии ядерных превращений, или из электрической энергии. Более того, образовавшаяся в правом конце ящика тепловая энергия может быть вновь превращена в любую из этих форм энергии. Поэтому все эти формы энергии, равно как и вообще все прочие её формы, эквивалентны при их переносе перемещению количества массы
𝑚
=
𝐸
.
Как можно подтвердить ещё идею переноса массы сгустком излучения? Мы уже знаем, что масса покоя фотона равна нулю вследствие соотношения
(Масса покоя)
²
=
(Энергия)
²
-
(Импульс)
²
=
0

Рис. 107. Излучение приводит к переносу массы покоя из точки в точку, несмотря на то что масса покоя самого излучения равна нулю!
(вернитесь к анализу в этом упражнении, а также в предыдущем; см., кроме того, разд. 12). Далее, то, что верно для индивидуального фотона, остаётся верным и для сгустка излучения, состоящего из множества фотонов: энергия и импульс по абсолютной величине равны друг другу, так что масса покоя излучения с необходимостью равна нулю. Нет ли противоречия в самой основе наших рассуждений, когда мы говорим, что масса покоя сгустка равна нулю, и тут же добавляем, что этот сгусток с энергией 𝐸 переносит массу 𝑚=𝐸 из одного места в другое? Источником трудности является смешение двух совершенно различных понятий: 1) энергии — временной компоненты 4-вектора энергии-импульса и 2) массы покоя — абсолютной величины этого вектора. Когда система делится на две части (распространяющееся вправо излучение и получивший отдачу влево ящик), компоненты 4-векторов энергии-импульса излучения и ящика в сумме тождественно равны соответствующим компонентам первоначального 4-вектора энергии-импульса системы до генерации излучения (рис. 107). Но при этом абсолютные величины 4-векторов (а масса покоя и есть абсолютная величина!) не аддитивны. Работая в эвклидовой геометрии, никто ведь не требует, чтобы длина одной стороны треугольника была равна сумме длин двух других его сторон. То же самое верно и в лоренцевой геометрии. Масса покоя системы (𝑀) не может приниматься равной сумме масс покоя излучения (равной нулю) и ящика, получившего отдачу (меньшей, чем 𝑀). Но компоненты 4-векторов энергии-импульса аддитивны, например
⎛
⎜
⎝
Энергия
системы
⎞
⎟
⎠
=
⎛
⎜
⎝
Энергия
излучения
⎞
⎟
⎠
+
⎛
⎜
⎜
⎝
Энергия ящика,
получившего
отдачу
⎞
⎟
⎟
⎠
.
Мы видим отсюда, что энергия ящика, получившего отдачу, равна 𝑀-𝐸. Уменьшилась не только энергия ящика, когда излучение отделилось от его стенки, уменьшилась также его масса покоя (см. укоротившуюся длину 4-вектора на диаграмме). Значит, излучение унесло часть массы покоя стенки ящика, хотя само это излучение и не имеет массы покоя. Результат,
⎛
⎜
⎝
Масса покоя
системы
⎞
⎟
⎠
≠
⎛
⎜
⎝
Масса покоя
излучения
(нуль)
⎞
⎟
⎠
+
⎛
⎜
⎜
⎜
⎝
Масса покоя
ящика,
получившего
отдачу
⎞
⎟
⎟
⎟
⎠
,
в геометрии пространства-времени настолько же естествен, как и неравенство 5≠3+4 в эвклидовой геометрии.
Как же обстоит дело с гравитационным притяжением, действующим со стороны нашей системы на некий пробный объект? Конечно, перераспределение масс, когда излучение распространяется слева направо, приводит к изменению такого притяжения. Но пусть пробный объект находится от системы на расстоянии 𝑟, столь значительном, что подобное перераспределение пренебрежимо мало влияет на характер притяжения. Иными словами, пусть притяжение пробного объекта единичной массы определяется только той полной массой системы 𝑀, которая фигурирует в ньютоновской формуле тяготения:
⎛
⎜
⎝
Сила, действующая
на единичную массу
⎞
⎟
⎠
=
𝐺𝑀
𝑟²
.
Если так, то не ощутит ли наш удалённый приёмник мгновенного уменьшения силы гравитационного притяжения в тот момент, когда излучение распространяется через ящик? Разве масса покоя излучения не равна нулю, тогда как масса покоя ящика, испытавшего отдачу, стала меньше первоначальной массы покоя 𝑀 системы? Не стала ли, таким образом, полная тяготеющая масса меньше, чем вначале, вследствие протекающего процесса переноса? Нет! Масса покоя системы — и мы повторим это — не равна сумме масс покоя её отдельных частей. Вместо этого она равна абсолютной величине полного 4-вектора энергии-импульса системы. Но ни полный импульс системы (равный в нашем случае нулю!), ни её полная энергия ни в какой момент времени не изменяются: ведь наша система изолирована. Поэтому не меняется и абсолютная величина 𝑀 полного 4-вектора энергии-импульса (рис. 107). А это в конце концов значит, что не изменяется и гравитационное притяжение.
Во всём этом анализе была, однако, одна небольшая подтасовка: ящик в действительности не может двигаться как твёрдое тело. Если бы он мог так двигаться, то информация об отделении излучения от левой стенки могла бы быть получена по наблюдению движения противоположной — правой — стенки задолго до прихода к ней самого излучения, т.е. эта информация была бы передана с большей скоростью, чем распространяется свет! На самом же деле толчок отдачи, вызванный генерацией излучения, распространяется по боковым стенкам ящика в виде волны колебания, т.е. со скоростью звука, и эта волна достигает противоположного конца намного позднее, чем туда приходит излучение. Тем временем акт поглощения излучения в правом конце ящика возбуждает другую волну колебания, которая движется назад по боковым стенкам ящика. Добавить к нашей задаче исследование колебаний ящика значило бы усложнить анализ, но не изменить сколько-нибудь существенно полученные выше выводы.
68*. Устойчивость фотона
Покажите, что изолированный фотон не может раздробиться на два фотона, распространяющихся в направлениях, не совпадающих с направлением распространения первоначального фотона. (Указание. Используйте законы сохранения импульса и энергии и тот факт, что третья сторона треугольника короче, чем сумма двух других сторон. О каком треугольнике идёт речь?) ▼
69*. Давление света
а) Вычислите полную силу, с которой действует луч одноваттного фонарика.
б) Основываясь на значении солнечной постоянной (1,4 квт/м²; см. упражнение 62), вычислите величину давления солнечного света на спутник Земли. Рассмотрите как отражающие, так и поглощающие поверхности, а также «реальные» поверхности (с частичным поглощением). Почему несуществен цвет падающего света?
в) Частицы, размеры которых меньше некоторых критических, могут быть вытолкнуты из солнечной системы давлением солнечного света. Критические размеры определяются равенством выталкивающей силы и силы гравитационного притяжения частиц Солнцем. Оцените эти размеры, сделав все необходимые предположения. Перечислите в своём ответе сделанные предположения. Зависят ли полученные критические размеры от расстояния частиц от Солнца? ▼
70*. Эффект Комптона

Рис. 108. Комптоновское рассеяние фотона на электроне.

Рис. 109. Диаграмма сохранения импульса при комптоновском рассеянии. Вспомните закон косинусов: 𝑃² = 𝑝² + 𝑝² - 2𝑝𝑝 cos φ .
В 1923 г. Артур Комптон показал, что рассеянные на свободных электронах рентгеновские лучи (фотоны) имеют после рассеяния меньшую энергию, чем до рассеяния 1). Этот эксперимент расценивается многими как самое ценное достижение физического опыта 20-х годов. Рассмотрим столкновение фотона с энергией 𝐸ф и электрона, который первоначально покоился; определим энергию фотона после рассеяния под углом φ к направлению своего падения. Угол φ носит название угла рассеяния. Мы примем следующие обозначения:
1) A. H. Compton, Physical Review, 22, 411 (1923).
До рассеяния
После рассеяния
Электрон
𝐸, 𝑃
𝐸
,
𝑃
Фотон
𝐸
ф
,
𝑝
𝐸
ф
,
𝑝
Не пользуйтесь в своих рассуждениях ни ℎ, ни ν, ни β, ни θ, ни λ, а только одними законами сохранения импульса и энергии да уравнениями
𝐸²
-
𝑃²
=
𝑚²
для электрона,
𝐸
ф
²
-
𝑝²
=
0
для фотона.
Начертите график выраженной в единицах энергии покоя электрона энергии рассеянного фотона в функции угла рассеяния φ для того случая, когда энергия падающего фотона вдвое превышает энергию покоя электрона (2⋅0,511 Мэв).

Рис. 110. Результаты эксперимента Комптона, в котором фотоны рассеивались на электронах в графитовой мишени.
При расположении детектора на всех углах, кроме φ=0, наблюдаются фотоны, рассеянные с потерей энергии (электроны испытывают отдачу), наряду с теми фотонами, которые почти или вообще не потеряли энергии (отдачу испытывает система электрон + атом как целое)
Собственно, опыты Комптона показали, что некоторые фотоны рассеиваются без заметного изменения энергии (рис. 110). Это были фотоны, рассеивавшиеся на электронах, связь которых в атоме оказалась настолько крепкой, что отдача передавалась атому как целому. Покажите, что для фотонов, рассеивающихся на крепко связанных в атомах средней массы [например, 10⋅2000⋅(масса электрона)] электронах, изменение энергии пренебрежимо мало. ▼
71*. Измерение энергии фотона

Рис. 111. Измерение энергии фотона.
Пусть некий данный радиоактивный источник испускает фотоны высокой энергии (рентгеновские лучи), характерной для соответствующих радиоактивных ядер. Поэтому точные измерения энергии часто могут быть использованы для выяснения состава даже мельчайшего образца. В установке, схема которой дана на рис. 111, регистрируются лишь такие события, когда срабатывание счётчика 𝐴 (попадание в него электрона) сопровождается срабатыванием счётчика 𝐵 (попадание рассеянного фотона). Чему равна энергия падающих фотонов, детектируемыхтаким способом (в единицах энергии покоя электрона)? ▼
72*. Энергия и частота фотона
В 1900 г. Макс Планк открыл, что свет частоты ν (число колебаний в секунду) с необходимостью следует признать состоящим из квантов (выражение Планка) или фотонов (более позднее выражение Эйнштейна), каждый из которых обладает энергией 𝐸=ℎν/𝑐² (выраженной здесь в единицах массы), где ℎ — универсальный коэффициент пропорциональности, именуемый постоянной Планка. Но как может быть правильной формула Планка, если, как мы теперь знаем, не только 𝐸, но и ν зависит от выбора системы отсчёта, в которой мы наблюдаем свет?
а) Как изменяется энергия фотона при преобразовании Лоренца? Возьмём фотон с энергией 𝐸 (и импульсом 𝑝=𝐸, движущийся в положительном направлении оси х в лабораторной системе отсчёта. Требуется с помощью закона преобразования 4-вектора энергии-импульса найти выражение для энергии 𝐸' этого фотона в системе отсчёта ракеты через одни только величины 𝐸 и θ𝑟.
б) Определите, как изменяется частота света ν при преобразовании Лоренца. Говоря конкретнее, пусть отрезок синусоиды («серия вспышек») света распространяется в положительном направлении оси 𝑥 так что в течение одного метра светового времени мимо начала лабораторной системы отсчёта проходит ν/𝑐 горбов волны. Имеется в виду, что нулевой или «опорный» горб (или вспышка) проходит мимо начала в нулевой момент времени и что начало системы отсчёта ракеты совпадает с началом лабораторной системы в этот же момент. Требуется показать, что координата 𝑥 горба № 𝑛 связана с моментом наблюдения (в метрах) соотношением
𝑛
=
ν
𝑐
(𝑡-𝑥)
.
На том же основании в системе отсчёта ракеты получается соотношение
𝑛
=
ν'
𝑐
(𝑡'-𝑥')
.
Выразите последнюю формулу через лабораторные координаты, пользуясь преобразованием Лоренца (введя параметр относительной скорости θ𝑟). Насколько можно, упростите полученное выражение, пользуясь формулой
ch θ
±
sh θ
=
𝑒
±θ
из табл. 8, где 𝑒 — основание натуральных логарифмов: 𝑒=2,718281… Сравните полученное выражение для 𝑛 с формулой для 𝑛 в лабораторной системе отсчёта и, пользуясь тем, что обе формулы зависят от 𝑥 и 𝑡, найдите простое выражение для ν' через ν и θ𝑟.
в) Сравните выводы, полученные вами в пунктах (а) и (б). Покажите, что в случае света, распространяющегося в направлении относительного движения двух систем отсчёта, преобразование энергии фотона при переходе между этими системами совпадает с аналогичным преобразованием частоты световой волны. Этот вывод справедлив для произвольного направления распространения света (см. упражнение 75). Итак, если мы связали фотоны со световой волной в одной системе отсчёта, эта связь сохранится во всех других системах. Из теории относительности не следует определённого численного значения постоянной Планка ℎ в формуле, связывающей энергию (в единицах массы) и частоту; 𝐸=(ℎ/𝑐²) ν. Из опыта следует, что постоянная Планка ℎ равна 6,63⋅10⁻³⁴ дж⋅сек 1). Покажите, что, если энергия измеряется в обычных единицах, связь между энергией и частотой принимает вид
𝐸
обычн
=
ℎν
(энергия в обычных единицах).
(115)
1) Более привычны единицы — грамм, сантиметр и секунда, в которых 𝑐=3⋅10¹⁰ см/сек, ℎ=6,63⋅10⁻²⁷ эрг⋅сек, а 𝑔=980 см/сек². — Прим. перев.
г) Покажите, что формула, описывающая эффект Комптона (упражнение 70), принимает при этом вид
ν
=
ν
.
1
+
ℎν
(1-cos φ)
𝑚𝑐²
(116)
Идея о том, что рассеянная (переизлучённая) волна обладает пониженной частотой, когда электрон получает электрический удар от поля волны фотона, встречала сильное сопротивление в 20-х годах нашего века. ▼
73*. Гравитационное красное смещение
Следующие две задачи предполагают некоторое знакомство с определёнными элементарными фактами теории тяготения:
I. Очень малый объект (либо сферически симметричный объект произвольного радиуса) с массой 𝑚₁ притягивает объект с массой 𝑚₂ (также малый либо сферически симметричный) с силой 𝐹=𝐺𝑚₁𝑚₂/𝑟². Здесь 𝑟 — расстояние между центрами этих объектов, а 𝐺 - ньютоновская гравитационная постоянная:
𝐺
=
6,67⋅10⁻¹¹
м
³
/
сек
²⋅
кг
=
6,67⋅10⁻⁸
см
³
/
сек
²⋅
г
.
II. Работа, необходимая для перенесения пробной частицы единичной массы из точки 𝑟 в точку 𝑟+𝑑𝑟 против сил гравитационного притяжения, вызываемых наличием закреплённой массы 𝑚, равна
𝐺𝑚
=
𝑑𝑟
𝑟²
.
Переходя от обычных единиц энергии к единицам размерности массы, запишем эту работу как
𝑑𝑊
=
𝐺𝑚
𝑐²
⋅
𝑑𝑟
𝑟²
=
𝑚*
⋅
𝑑𝑟
𝑟²
(117)
(работа, отнесённая к единице массы пробной частицы).
III. В этой формуле первый сомножитель, 𝑚*=𝐺𝑚/𝑐², имеет очевидный смысл — это масса притягивающего центра, выраженная не в килограммах, а в метрах. Например, масса Земли (𝑚=5,983⋅10²⁴ кг) равна в единицах длины 𝑚Земля*=4,44⋅10⁻³ м тогда как масса Солнца (𝑚=1,987⋅10³⁰ кг) равна 𝑚Солнце*=1,47⋅10³ м.
IV. Пусть пробная частица находится сначала на расстоянии 𝑟 от притягивающего центра, а затем уносится на бесконечность. Необходимая для этого работа равна
𝑊
=
𝑚*
𝑟
(118)
из расчёта на единицу массы, содержащейся в пробной частице.
а) Какая часть вашей энергии покоя перейдёт в потенциальную энергию, если вы подниметесь на высоту памятника Вашингтону (555 фут, или 170 м)? Пусть
𝑔*
=
𝐺𝑚З
𝑐²
⋅
1
𝑟З²
=
𝑚З*
𝑟З²
есть ускорение силы тяжести на поверхности Земли (радиус 𝑟З), выраженное в м/м².
б) Какая часть вашей энергии покоя перейдёт в потенциальную энергию, когда вы подниметесь за пределы действия гравитационного поля Земли? Допустим, что, кроме Земли, во Вселенной ничего нет. Зависит ли доля энергии, теряемой в пункте (а) или (б), от вашей первоначальной массы?
в) Используйте результат, полученный в пункте (а), для нахождения относительного изменения энергии фотона, поднимающегося вертикально на высоту 𝑧 в однородном гравитационном поле 𝑔*. Масса покоя фотона равна нулю, и формально можно сказать, что фотон обладает кинетической энергией 𝐸=𝑇. Поэтому фотон располагает лишь одним источником, а именно своей кинетической энергией, за счёт которого он может компенсировать возрастание потенциальной энергии при подъёме в гравитационном поле. Световая волна с частотой ν состоит из фотонов энергии 𝐸=ℎν/𝑐² (см. упражнение 72). Требуется показать, что относительная потеря энергии фотонами, поднимающимися в гравитационном поле, соответствует следующему относительному изменению их частоты:
Δν
ν
=-
𝑔*𝑧
(однородное гравитационное поле).
г) Вывод, полученный в пункте (б), используйте для нахождения величины относительной потери энергии фотоном при его удалении на бесконечность. (Применение этого вывода является хорошим приближением с точностью до 1%, если сама величина относительной потери энергии не превышает 2%). Пусть, например, фотон испускается из какой-то точки на поверхности астрономического объекта массы 𝑀 (кг) или 𝑀* (м) и радиуса 𝑟. Исходя из величины относительной потери энергии, покажите, что относительное изменение частоты определяется формулой
Δν
ν
=-
𝑀*
𝑟
.
(119)
Такое уменьшение частоты называется гравитационным красным смещением, потому что в видимом свете смещение состоит в сдвиге линий к низкочастотному (красному) концу спектра. Найдите величину относительного гравитационного красного смещения для света, испускаемого с поверхности Земли, и для света, испускаемого с поверхности Солнца. ▼
74*. Плотность спутника Сириуса
Сириус (Альфа созвездия Большого Пса) — самая яркая звезда неба. Сириус и его маленький спутник обращаются один вокруг другого. Анализируя это обращение с помощью ньютоновской механики, астрономы смогли определить, что масса спутника Сириуса приблизительно равна массе нашего Солнца (𝑚≈2⋅10³⁰ кг, 𝑚*≈1,5⋅10³ м).
Излучение спутника Сириуса было исследовано спектроскопически. Отождествлённые по своему взаимному расположению спектральные линии некоторого химического элемента оказались сдвинутыми по своей частоте на 7⋅10⁻⁴ от величины частоты тех же спектральных линий того же элемента в лаборатории. (Эти опытные данные верны с точностью до первой значащей цифры). Интерпретируя это красное смещение как гравитационное (см. формулу в конце упражнения 73), найдите среднюю плотность спутника Сириуса в граммах на кубический сантиметр. Этот тип звёзд носит название белых карликов. ▼
Г. ДОППЛЕРОВСКОЕ СМЕЩЕНИЕ
75. Формулы Допплера
Пусть фотон движется в лабораторной системе отсчёта в плоскости 𝑥𝑦 в направлении, образующем угол φ с осью 𝑥, так что он обладает компонентами импульса 𝑝 𝑥=𝑝 cos φ, 𝑝 𝑦=𝑝 sin φ и 𝑝 𝑧=0.
а) Используйте формулы преобразования Лоренца для 4-вектора энергии-импульса и соотношение 𝐸²-𝑝²=0, справедливое для фотона, чтобы показать, что в системе отсчёта ракеты фотон обладает энергией 𝐸',
𝐸'
=
𝐸 ch θ
𝑟
⋅
(1-β
𝑟
cos φ)
,
(120)
и движется в направлении, образующем с осью 𝑥' угол φ', причём
cos φ'
=
cos φ-β𝑟
1-β𝑟 cos φ
.
(121)
б) Найдите обратные уравнения, выражающие 𝐸 и cos φ через 𝐸', cos φ' и β𝑟. Сравните эти обратные уравнения с полученными в упражнении 22 («эффект прожектора»).
в) Если частота света в лабораторной системе отсчёта равна ν, то чему равна частота этого света ν' в системе отсчёта ракеты? Такое различие частот, обусловленное относительным движением, носит название релятивистского эффекта Допплера (упражнение 6). Позволяют ли полученные уравнения определить, в какой системе отсчёта покоится источник фотонов? ▼
76. Распад π⁰-мезона; подробный пример
Нейтральный пи-мезон (π⁰-мезон), движущийся в лабораторной системе отсчёта в направлении оси 𝑥 и обладающий кинетической энергией, равной его энергии покоя, распадается на два фотона. В системе отсчёта ракеты, где мезон покоится, эти фотоны разлетаются в положительном и отрицательном направлениях оси 𝑦'. Определите энергии фотонов в системе отсчёта ракеты (в единицах энергии покоя мезона) и энергии и направления вылета фотонов в лабораторной системе отсчёта.
Решение. В системе отсчёта ракеты π⁰-мезон до своего распада покоился (импульс равен нулю). Он никак не мог распасться на один фотон, не нарушив сохранения импульса. При распаде на два фотона импульс сохранится, если: а) фотоны разлетаются в противоположных направлениях в той системе отсчёта, где мезон до своего распада покоился, и б) импульсы этих фотонов в такой системе равны по абсолютной величине, так что фотоны обладают одинаковыми энергиями (для фотонов 𝐸'=𝑝'). Таким образом, в системе отсчёта ракеты задача имеет следующее решение: каждый фотон уносит половину энергии покоя мезона, 𝐸'=𝑚/2. Кроме того, эти фотоны по условию должны разлетаться в положительном и отрицательном направлениях оси 𝑦' (φ=±90°, так что cos '=0).
Энергия и направление вылета каждого из фотонов в лабораторной системе отсчёта могут быть найдены по формулам, полученным в упражнении 75:
𝐸
=
𝐸' ch θ
𝑟
⋅
(1+β
𝑟
cos φ')
,
cos φ
=
cos φ'+β𝑟
1+β𝑟 cos φ'
.
Прежде всего необходимо найти величины θ𝑟, и β𝑟. Согласно условию задачи, кинетическая энергия мезона в лабораторной системе отсчёта до его распада была равна массе покоя; тогда
𝐸
π
≡
𝑚 ch θ
𝑟
≡
𝑇
+
𝑚
=
2𝑚
,
откуда
ch θ
𝑟
=
1
√1-β𝑟²
=
2
,
так что
β
𝑟
=
√3
2
.
Подставьте теперь эти данные и величину 𝐸'=𝑚/2 в уравнения преобразования, и вы получите
𝐸
=
𝑚
,
cos φ
=
β
𝑟
=
√3
2
,
так что φ=30°. Величину энергии можно было бы найти непосредственно по симметрии распада и по равенству полной энергии мезона до распада 2𝑚. Выводы подытожены на рис. 112. Проверьте, что в лабораторной системе отсчёта импульс сохраняется, как и энергия.

Рис. 112. Решение задачи о распаде π⁰-мезона.
77. Полёт неоновой лампочки
Неоновая лампочка, которая в своей системе покоя изотропно во всех направлениях излучает красный свет, приближается к наблюдателю с очень большого расстояния, двигаясь со скоростью, близкой к скорости света, по прямолинейному пути, отстоящему от наблюдателя на расстоянии 𝑙 по перпендикуляру. С течением времени изменяются как цвет излучения, так и число фотонов, приходящих к наблюдателю от лампочки. Качественно опишите эти изменения на различных этапах движения. Рассмотрите как эффект Допплера, так и «эффект прожектора» (упражнения 75 и 22). ▼
78. Физик и светофор
Физика задержали за то, что он поехал на красный свет. На суде он заявил, что приближался к перекрёстку на скорости, при которой красный свет казался ему зелёным. Судья, получивший в своё время физическое образование, обвинил тогда физика в превышении предельной скорости и присудил его к уплате одного доллара за превышение местного предела скорости 20 миль/час на каждую милю в час. Чему равна сумма штрафа? Примите длину волны зелёного света равной 5300 Å (1 Å=10⁻¹⁰ м), а длину волны красного света — 6500 Å. Учтите, что свет распространялся в отрицательном направлении оси 𝑥 (φ=φ'=π). ▼
79. Допплеровское смещение на краю диска Солнца
Солнце совершает один оборот вокруг своей оси за 24,7 суток. Радиус Солнца составляет около 7,0⋅10⁸ м. Вычислите величину допплеровского смещения, которое должно наблюдаться для света с длиной волны 5000 Å (1 Å=10⁻¹⁰ м) на одном из краёв диска Солнца вблизи его экватора. Происходит ли это смещение в стороны красного или синего конца видимого спектра? Сравните величину смещения Допплера с величиной гравитационного красного смещения для поверхности Солнца (упражнение 73). ▼
80. Расширяющаяся Вселенная. (Вспомните упражнение 6)
а) Производится спектрометрическое исследование света, приходящего от далёкой галактики. Спектральную линию с длиной волны 7300 Å удаётся отождествить (по её положению в общей картине линий) со спектральной линией водорода, обладающей для излучения водорода в условиях лаборатории длиной волны 4870 Å. Если изменение длины волны обусловлено эффектом Допплера, то с какой скоростью должна двигаться относительно Земли исследуемая галактика? Заметьте, что свет распространяется в направлении, противоположном направлению движения галактики (φ=φ'=π).
б) Полученные независимым путём данные говорят о том, что исследуемая галактика находится от нас на расстоянии 5 миллиардов световых лет. Оцените время, прошедшее с момента, когда эта галактика отделилась от нашей Галактики (Млечного Пути), приняв для простоты, что в прошлом скорость удаления была всегда постоянной (не замедлялась под действием взаимного притяжения галактик). Астроном Эдвин Хаббл обнаружил в 1929 г. 1), что это время (обратная которому величина носит название постоянной Хаббла, так что его можно называть хаббловским временем) приблизительно одинаково для всех галактик, расстояния до которых и скорости которых удалось измерить. Отсюда возникло представление о расширяющейся Вселенной 2). Приведёт ли к увеличению или уменьшению в оценке времени, прошедшего с начала расширения, учёт влияния тяготения в прошлом, приводящий к замедлению этого расширения?
1) Е. Hubble, Proс. U. S. National Acad. Sci., 15, 168 (1929).
2) Дальнейшие подробности см., например, в книге Hermann Bondi, Cosmology, Cambridge University Press, Second Edition, 1960. [Теоретически возможность расширяющейся модели Вселенной была предсказана еще в 1921 г. А. А. Фридманом; см. его работы, перепечатанные в Успехах физических наук, 86, № 3 (1963).— Прим. перев.]
▼
81*. Анализ парадокса часов с помощью эффекта Допплера 3)
3) Е. Feenberg, American Journal of Physics, 27, 190 (1959).
Проблема парадокса часов (см. упражнения 27 и 49) может быть изящно разрешена с помощью учёта эффекта Допплера. Вспомним, что Павел оставался на Земле, тогда как Пётр летал с огромной скоростью β𝑟 до далёкой звезды и обратно на Землю. Пусть они оба наблюдали удалённую переменную звезду, яркость которой попеременно ослабевает и увеличивается с частотой ν в системе отсчёта Земли (ν' в системе отсчёта ракеты). Предположим, что расстояние до этой переменной звезды намного превышает длину пути Петра, а направление на неё в системе отсчёта Земли перпендикулярно направлению движения Петра. Оба наблюдателя зарегистрируют одно и то же общее число пульсаций переменной в течение всего путешествия Петра от его вылета до возвращения. Исходя из этого факта и из формулы для допплеровского смещения (упражнение 75)
ν'
=
ν ch θ
𝑟
⋅
(1-β
𝑟
cos φ)
(122)
при данном угле наблюдения φ= 90° в лабораторной системе отсчёта, проверьте утверждение, что к концу путешествия, описанного в упражнении 27, Пётр постареет всего на 14 лет, тогда как Павел — на все 50. ▼
82*. «Не превышайте скорости»
На автостраде установлен стационарный радиолокатор, сдвиг частоты луча которого, отражённого от едущей навстречу ему машины, используется для измерения скорости её. Одна из таких установок, используемых полицией в штате Нью-Джерси, работает на частоте 2455 Мгц. Насколько сдвигается частота отражённого луча, если приближающаяся к радиолокатору машина имеет скорость 80 миль/час (1 миля/час = 0,447 м/сек). (Произведите приближённый расчёт, предполагая, что автомашина служит источником той же частоты, какой обладает излучение, падающее на неё в её системе покоя. Для того чтобы решить эту задачу, необходимо произвести два преобразования: от системы отсчёта автострады к системе отсчёта машины, а затем от системы отсчёта машины вновь к системе отсчёта автострады). Допустим, что радиолокационная установка способна различать скорости, разность между которыми составляет не менее 10 миль/час. Какое относительное изменение частоты может зарегистрировать эта установка? ▼
83*. Допплеровское уширение спектральных линий
Средняя кинетическая энергия атома газа при температуре 𝑇°𝐊 (шкала Кельвина) равна ³/₂⋅𝑘𝑇 (Константа 𝑘 называется постоянной Больцмана и равна 1,38⋅10⁻²³ дж/град). Определите относительное изменение частоты, обусловленное допплеровским смещением, которое будет наблюдаться в излучении атомов газа при температуре 𝑇. Используйте в качестве приближения для малых скоростей ньютонову механику. Будет ли наблюдаемая частота больше или меньше вследствие эффекта Допплера? Это явление — причина того, почему любая данная спектральная линия газа, возбуждённого электрическим разрядом, состоит из узкой полосы частот вокруг некоторой центральной частоты. Оно называется допплеровским уширением спектральных линий. ▼
84*. Изменение энергии фотона вследствие отдачи излучателя
а) Свободная частица, первоначально покоившаяся и обладавшая массой покоя 𝑚, излучает фотон с энергией 𝐸. Эта частица (её масса покоя стала равна 𝑚) испытывает отдачу, и её параметр скорости становится равен θ (рис. 113).

Рис. 113. Отдача, испытываемая частицей при испускании фотона.
Сформулируйте законы сохранения таким образом, чтобы в них не фигурировала ни скорость, ни параметр скорости. Рассмотрите тот случай, когда относительное изменение массы покоя в процессе излучения намного меньше единицы. Покажите, что энергия фотона равна 𝐸₀=𝑚-𝑚. Покажите также, что в общем случае
𝐸
=
𝐸₀
⎛
⎜
⎝
1
-
𝐸₀
2𝑚
⎞
⎟
⎠
или
𝐸-𝐸₀
𝐸₀
=
Δ𝐸
𝐸₀
=-
𝐸₀
2𝑚
.
(123)
б) Покажите, что такое изменение энергии в области видимого света (𝐸₀,обычн ≈3 эв), излучаемого атомами газа (𝑚𝑐≈10⋅10⁹ эв), намного меньше, чем обусловленное эффектом Допплера, вследствие теплового движения атомов (упражнение 83) даже при таких низких температурах, как комнатные (𝑘𝑇≈1/40 эв). ▼
85*. Эффект Мёссбауэра
а) Свободный атом железа 𝙵𝚎⁵⁷, образовавшийся в так называемом «возбуждённом состоянии» при радиоактивном распаде кобальта 𝙲𝚘⁵⁷, при переходе в «нормальное состояние» атома 𝙵𝚎⁵⁷ излучает из ядра гамма-квант (фотон высокой энергии) с энергией 14,4 кэв. Чему будет равно относительное изменение энергии гамма-кванта, вызванное эффектом отдачи атома? Масса атома 𝙵𝚎⁵⁷ составляет около 57 масс протона.
б) В 1958 г. 29-летний P. Л. Мёссбауэр сделал важное открытие, что не все излучаемые гамма-кванты испытывают такой сдвиг частоты 1). Исходя из квантовой механики, он доказал теоретически, подтвердив свой вывод экспериментальной проверкой, что когда атомы железа включены в твёрдое тело (поскольку атомы железа образовались при радиоактивном распаде атомов кобальта, первоначально включённых в это твёрдое тело), значительная часть этих атомов железа не испытывает отдачи, свойственной свободным атомам в момент излучения. Напротив, они ведут себя так, как если бы их жёстко связали с покоящимся твёрдым телом. Импульс отдачи передаётся при этом всему телу как целому. Но масса тела превышает массу отдельного атома на много порядков (степеней 10), и в этом случае мы имеем явление, названное процессом без отдачи. (Излучение фотонов ядрами атомов, связанных в твёрдом теле, не сопровождающееся эффектом отдачи, напоминает один из фактов, обнаруженных Комптоном, а именно что некоторые из фотонов, рассеянных крепко связанными в атоме электронами, приобретают очень малое изменение энергии, так как атом испытывает отдачу как единое целое; см. упражнение 70). Для гамма-лучей, испускаемых в процессах без отдачи, в упражнении 84 в качестве 𝑚 следует взять массу всего куска металла, в которой заключены атомы железа. Если эту массу принять равной 1 г, чему будет равен относительный сдвиг частоты гамма-кванта в процессе «без отдачи»?
1) За это открытие немецкий учёный был удостоен Нобелевской премии 1961 г.; подробности см. в статье S. DeBenedetti, The Mössbauer Effect, Scientific American, 202, 72 (April, 1960).

Рис. 114. Естественная ширина линии для фотона, испущенного ядром 𝙵𝚎⁵⁷.
в) Испущенные возбуждёнными ядрами 𝙵𝚎⁵⁷ гамма-лучи не состоят из квантов, несущих в точности одну и ту же энергию; их энергии сосредоточены в узком диапазоне (это же касается и их частот), обусловливающем естественную ширину линии. Практически из тысячи или более фотонов можно выделить несколько классов. Любой данный фотон принадлежит к тому или другому классу в зависимости от того, в каком из многих равных по ширине интервалов лежит его частота. Число фотонов в каждом классе как функция частоты изображается графически и образует колоколообразную кривую (рис. 114). Ширина этой кривой на высоте половины её максимума обозначается через Δν. Для гамма-квантов, излучаемых 𝙵𝚎⁵⁷ и обладающих энергией 14,4 кэв, отношение Δν/ν₀ весьма мало и равно 3⋅10⁻¹³. Чему равна естественная ширина линии Δν излучения ядер 𝙵𝚎⁵⁷ в герцах? Сравните естественную относительную ширину линии с относительным сдвигом частоты, вызываемым отдачей свободного атома железа. Сравните её также с относительным сдвигом частоты гамма-лучей в процессе без отдачи.
Открытие Мёссбауэром процессов «без отдачи» сделало, таким образом, возможным распоряжаться источниками излучения, частота которых имеет фантастически узкий разброс порядка 3⋅10⁻¹³. В одном из следующих упражнений (в 87) говорится о применении для регулируемого изменения относительной эффективной частоты источника излучения, приёмника или обоих вместе на величины порядка 10⁻¹³, вызванные движением (допплеровское смещение). Какие применения может найти излучение строго определённой частоты? Их множество. Эффект Мёссбауэра является, например, основой важных новых методов в физике твёрдого тела, молекулярной физике и биофизике. Можно обнаружить изменения естественной частоты излучения ядер 𝙵𝚎⁵⁷, обусловленные влиянием других соседних атомов или внешними магнитными полями, и изучить таким образом взаимодействие между атомами железа и окружающим его веществом кристалла (пример: различие частот излучения 𝙵𝚎⁵⁷ в железном образце и в кристаллической решётке карбида железа); изучить взаимодействие между атомом железа в молекуле с остальной частью последней (пример: сдвиг частоты 𝙵𝚎⁵⁷ для атомов железа, связанных в молекулах гемоглобина). ▼
86**. Резонансное рассеяние
Ядра железа 𝙵𝚎⁵⁷ в основном (нормальном) состоянии поглощают гамма-лучи с резонансной энергией 14,4 кэв значительно сильнее, чем гамма-лучи с несколько иными энергиями. Поглощаемая при этом энергия переходит во внутреннюю энергию ядер, переводя 𝙵𝚎⁵⁷ в «возбуждённое состояние». По истечении некоторого времени такие возбуждённые ядра вновь излучают гамма-лучи в некотором случайном направлении и вновь возвращаются в основное состояние. Итак, гамма-лучи, поглотившись из первоначального направленного пучка, испускаются вновь во всех направлениях. Поэтому число гамма-квантов, прошедших сквозь тонкую пластинку, содержащую 𝙵𝚎⁵⁷, будет при резонансной энергии 14,4 кэв меньше, чем при любых соседних значениях энергии. Такой процесс называют резонансным рассеянием. Покажите, что при попадании гамма-кванта с резонансной энергией 𝐸₀ в первоначально покоившийся свободный атом железа этот гамма-квант не может быть поглощён его ядром, так как тогда не могут выполняться одновременно закон сохранения импульса и закон сохранения энергии. Покажите, что оба закона сохранения выполняются, если атом железа принадлежит кристаллу с массой 1 г и поглощает резонансный гамма-квант в ходе процесса без отдачи, когда импульс падающего гамма-кванта распределяется по всему кристаллу. («Выполняются»? Для импульса — да, для энергии — нет. Однако относительное несоответствие энергий, эквивалентное относительному несоответствию частот, меньше 3⋅10⁻¹³, т.е. достаточно мало, чтобы ядро атома железа «не заметило» этого несоответствия и поэтому поглотило падающий гамма-квант). ▼
87**. Измерение допплеровского смещения по резонансному рассеянию

Рис. 115. Резонансное рассеяние фотонов.
В экспериментальной установке, изображённой на рис. 115, источник, содержащий возбуждённые ядра 𝙵𝚎⁵⁷, испускает (наряду с прочими формами излучения) гамма-кванты с энергией 𝐸₀ без отдачи. Поглотитель, содержащий ядра 𝙵𝚎⁵⁷ в основном состоянии, поглощает часть этих гамма-квантов также в процессе без отдачи, вновь испуская их затем во всех направлениях. Поэтому счётчик гамма-лучей, расположенный, как это изображено на рисунке, зарегистрирует уменьшение потока гамма-квантов в случае поглотителя, содержащего 𝙵𝚎⁵⁷ в основном состоянии, по сравнению со случаем поглотителя без таких ядер 𝙵𝚎⁵⁷ Пусть теперь источник движется в сторону поглотителя со скоростью β. Какой должна быть его скорость, чтобы на поглотитель попадали гамма-лучи с частотой, относительный сдвиг которой равен 3⋅10⁻¹³, что соответствует широте резонансной линии? Выразите ответ в см/сек. Увеличится или уменьшится число зарегистрированных счётчиком гамма-квантов при этих условиях? Что произойдёт с этим числом, если источник будет удаляться от поглотителя с той же скоростью? Сделайте примерный чертёж зависимости числа зарегистрированных гамма-квантов от скорости источника. Позволяет ли этот метод измерять абсолютную скорость источника в нарушение принципа относительности? ▼
88**. Проверка эффекта гравитационного красного смещения с помощью эффекта Мёссбауэра
Гамма-квант с энергией 14,4 кэв, испущенный ядром 𝙵𝚎⁵⁷ без отдачи, летит вертикально вверх в однородном гравитационном поле. Чему будет равно относительное уменьшение энергии этого фотона при подъёме его на высоту 𝑧 (упражнение 73)? С какой скоростью и в каком направлении должен двигаться расположенный на такой высоте поглотитель, содержащий 𝙵𝚎⁵⁷, чтобы этот гамма-квант мог быть рассеян им без отдачи? Вычислите, чему равна такая скорость при высоте 22,5 м. Постройте чертёж зависимости числа зарегистрированных в единицу времени гамма-квантов от скорости движения поглотителя в двух предположениях: а) существования гравитационного красного смещения и б) отсутствия гравитационного красного смещения. В эксперименте, произведённом Паундом и Ребкой 1), из очень большого числа показаний счётчика фотонов был получен после статистического анализа результат: относительный сдвиг частоты при данных условиях Δν/ν₀=(2,56±0,26)⋅10⁻¹⁵.
1) R. V. Роund, G. A. Rеbka, Physical Review Letters, 4, 337(1960).
▼
89**. Проверка парадокса часов с помощью эффекта Мёссбауэра
История с Петром, оставившим своего брата-близнеца Павла в земной лаборатории, улетевшим с огромной скоростью и обнаружившим по возвращении, что Павел стал старше его, так противоречит нашему житейскому опыту, что для нас будет полной неожиданностью узнать, что такой опыт уже проделан, а предсказания теории полностью подтвердились! Чалмерс Шервин заметил, что в качестве близнецов можно взять два одинаковых атома железа с тем же успехом, как два живых существа 2). Пусть один из этих атомов всё время покоится, а другой движется по замкнутому пути, совершая, возможно, несколько кругов. Относительное различие в старении атомов-близнецов будет одним и тем же после миллиона кругов, как и после одного круга, но тогда его будет легче измерить. Как же заставить второй атом проделать множество круговых путешествий? Включим его в горячий кусок железа, где он будет колебаться взад и вперёд вокруг положения равновесия (тепловое возбуждение!). Как теперь измерить разницу в темпах старения? В истории с Петром и Павлом можно считать число праздничных хлопушек, которые каждый из них взрывал в свои дни рождения в период, пока они были разлучены друг с другом. В эксперименте с атомами железа сравнивается не число вспышек хлопушек между моментами расставания и встречи, а частота фотонов, испущенных в процессах без отдачи, т.е. фактически число «тик-так», сосчитанных двумя тождественными ядерными часами в течение одной лабораторной секунды. Иными словами, сравнивались эффективные частоты ВНУТРЕННИХ ядерных колебаний (не путать с колебаниями взад и вперёд атома железа как целого!) для наблюдаемых в лаборатории: а) покоящегося ядра железа и б) ядра железа в горячем образце.
2) Chalmers Shеrwin, Physical Review, 120, 17 (1960).
Покоящееся ядро железа получить трудно. Поэтому в реальном эксперименте сравнивались эффективные внутренние ядерные частоты, не для (а) и (б), а для (б) и (б'): двух кристаллов железа при разных температурах 𝑇 и 𝑇+Δ𝑇. Паунд и Ребка 1), произведя измерения, нашли, что более тёплый образец (Δ𝑇=1°𝐊) обладает относительным изменением эффективной частоты
1) R. V. Роund, G. A. Rеbka, Physical Review Letters, 4, 274 (1960).
Δν
ν
=
(-2,09±0,24)
⋅
10⁻¹⁵
(меньшее число колебаний; меньшее число «тик-так»; меньшее число дней рождения; замедление старения!).
Чтобы было проще понять этот эксперимент, возвратимся к идее покоящегося атома железа и атома-близнеца, подвергнутого тепловому возбуждению при температуре 𝑇. Предскажите относительное уменьшение числа внутренних колебаний в горячем образце за лабораторную секунду и сравните предсказание с данными опыта.

Рис. 116. Сравнение хода покоящихся ядерных часов с ходом ядерных часов, совершающих тепловое движение.
Обсуждение. На рис. 116 дано сравнение числа эффективных «тик-так» двух «внутренних ядерных часов» за интервал лабораторного времени 𝑑𝑡. Имейте в виду, что скорость атомов при тепловом возбуждении составляет около 10⁻⁵ от скорости света. Как можно приближённо представить коэффициент расхождения частот 1-√1-β²? Насколько уменьшается число «тик-так» горячего атома по сравнению с холодным, приходящееся на интервал лабораторного времени 𝑑𝑡? Покажите, что накапливающийся дефект числа «тик-так» для горячего атома составляет в 1 сек
ν₀
⎛
⎜
⎝
β²
2
⎞
⎟
⎠
средн
(1
сек
)
,
где через (β²)средн обозначена «средняя квадратичная величина скорости атома» (в единицах скорости света). Заметьте, что средняя кинетическая энергия теплового возбуждения горячего атома железа (масса 𝑚𝙵𝚎=57𝑚протон) Даётся классической кинетической теорией газов в виде
1
2
𝑚
𝙵𝚎
(β²)
средн
²
=
3
2
𝑘𝑇
.
Здесь 𝑘 — постоянная Больцмана — множитель перехода между двумя единицами энергии, градусами и джоулями (или градусами и эргами); 𝑘=1,38⋅10⁻²³ дж/град (𝑘=1,38⋅10⁻¹⁶ эрг/град). Как согласуется результат эксперимента Паунда и Ребки с результатом вашего исчисления? ▼
Д. СТОЛКНОВЕНИЯ
90. Симметричное упругое столкновение
При упругом столкновении частицы с массой 𝑚 и кинетической энергией 𝑇 с частицей той же массы, находившейся в состоянии покоя, направления скоростей частиц после столкновения образуют разные углы с первоначальным направлением движения первой частицы, если энергии частиц после рассеяния различны. Однако ньютоновская механика предсказывает, что угол α между векторами скорости частиц после рассеяния всегда равен 90°. Иное предсказание делает механика теории относительности: согласно ей этот угол должен быть меньше 90° (см. упражнение 40). Вопрос: насколько меньше 90° должен быть угол α в простейшем случае симметричного упругого столкновения, когда частицы после рассеяния обладают одинаковыми энергиями и разлетаются под одинаковыми углами к первоначальному направлению движения первой частицы (рис. 117)? Определите угол, исходя лишь из законов сохранения импульса и энергии в релятивистской форме.
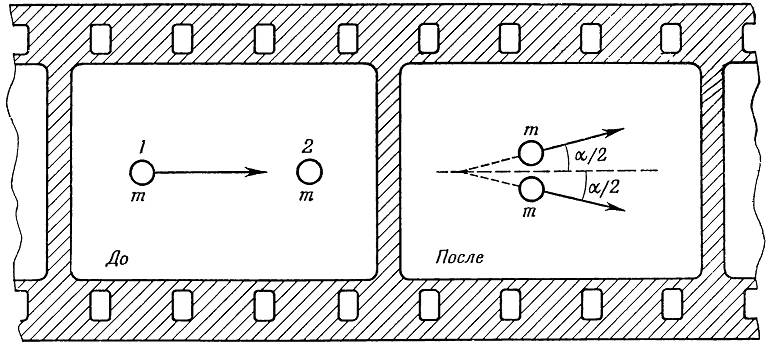
Рис. 117. Симметричное упругое столкновение тождественных частиц.
Обсуждение. Чему равна полная энергия системы до столкновения? Какой должна быть поэтому полная энергия каждой из двух частиц после столкновения? Чему должен быть поэтому равен импульс частицы? (См. введение к упражнениям на стр. 179, где сказано о взаимосвязи между импульсом и энергией и о том, почему следует избегать всякого упоминания или использования скорости в задачах, относящихся лишь к импульсу и энергии). Каков был начальный импульс системы? Покажите, что искомый угол определяется выражением
cos²
α
2
=
𝑇+2𝑚
𝑇+4𝑚
.
Отсюда с помощью тригонометрического тождества
cos²
α
2
=
1
2
(1+cos α)
получите выражение
cos α
=
𝑇
𝑇+4𝑚
.
(124)
Чему равен полный угол α: 1) для ньютоновского упругого столкновения при малой скорости и 2) для ультрарелятивистского столкновения с очень большой величиной 𝑇? ▼
91. Давид и Голиаф — подробный пример
Какой минимальной кинетической энергией должен обладать электрон для того, чтобы передать половину своей кинетической энергии первоначально покоившемуся протону при упругом лобовом соударении? Проведите свои вычисления таким образом, чтобы в конце концов прийти к одному-единственному уравнению, решая которое можно (и должно) определить одну безразмерную неизвестную величину 𝑇𝑒/𝑚𝑝, где 𝑇𝑒 — кинетическая энергия налетающего электрона, а 𝑚𝑝 — масса покоя протона. Определите величину 𝑇𝑒,обычн в Мэв, приближённо принимая 𝑚𝑝 𝑐²≈1000 Мэв. (Если вы будете решать это уравнение приближённо, дайте оценку погрешности).
Решение. Эта задача сводится к алгебраическим преобразованиям, и главное в ней — избежать ненужных алгебраических преобразований! Столкновение предполагается упругим, так что электрон и протон не уничтожаются в результате его и не возникает никакого излучения. В этом случае закон сохранения энергии сводится к сохранению кинетической энергии. Обозначим через 𝑇𝑒 кинетическую энергию налетающего электрона. В условии сказано, что после столкновения протон обладает половиной энергии налетающего электрона: 𝑇𝑝=𝑇𝑒/2. Поэтому и электрон уносит также половину своей первоначальной кинетической энергии: 𝑇𝑒=𝑇𝑒/2.
Столкновение является лобовым, так что все движения происходят вдоль оси 𝑥, а импульсы складываются как скаляры с учётом лишь их знаков. Электрон отскочит от протона, и поэтому его импульс после столкновения будет отрицательным. Из закона сохранения импульса следует
𝑝
𝑒
=
𝑝
𝑝
-
𝑝
𝑒
.
Чтобы связать импульс с энергией, воспользуемся общейформулой
𝐸²
-
𝑝²
=
𝑚²
,
откуда
𝑝²
=
𝐸²
-
𝑚²
=
(𝑇+𝑚)²
-
𝑚²
=
=
𝑇²
+
2𝑚𝑇
+
𝑚²
-
𝑚²
=
𝑇²
+
2𝑚𝑇
,
подчёркнутые члены взаимно уничтожаются, так что
𝑝
=
√
𝑇²+2𝑚𝑇
.
Поэтому закон сохранения импульса можно переписать в виде
√
𝑇
𝑒
²+2𝑚
𝑒
𝑇
𝑒
=
⎛
⎝
𝑇
𝑝
²
+
2𝑚
𝑝
𝑇
𝑝
⎞½
⎠
-
⎛
⎝
𝑇
𝑒
²
+
2𝑚
𝑒
𝑇
𝑒
⎞½
⎠
.
Подставляя сюда следствие закона сохранения энергии
𝑇
𝑝
=
𝑇
𝑒
=
𝑇𝑒
2
,
получаем
√
𝑇
𝑒
²+2𝑚
𝑒
𝑇
𝑒
=
⎛
⎜
⎝
𝑇𝑒²
4
+
𝑚
𝑝
𝑇
𝑒
⎞½
⎟
⎠
-
⎛
⎜
⎝
𝑇𝑒²
4
+
𝑚
𝑒
𝑇
𝑒
⎞½
⎟
⎠
.
Деление этого соотношения с обеих сторон на √𝑇𝑒𝑚𝑝 даёт
⎛
⎜
⎝
𝑇𝑒
𝑚𝑝
+
2𝑚𝑒
𝑚𝑝
⎞½
⎟
⎠
=
⎛
⎜
⎝
𝑇𝑒
4𝑚𝑝
+
1
⎞½
⎟
⎠
-
⎛
⎜
⎝
𝑇𝑒
4𝑚𝑝
+
𝑚𝑒
𝑚𝑝
⎞½
⎟
⎠
.
Как и требовали условия задачи, в этом уравнении имеется лишь одна неизвестная величина 𝑇𝑒/𝑚𝑝. Мы решим его приближённо, исходя из того факта, что масса покоя электрона приблизительно в 2000 раз меньше массы покоя протона, т.е. 𝑚𝑒/𝑚𝑝≪1. Пренебрежём этим отношением в только что полученном выражении и найдём
⎛
⎜
⎝
𝑇𝑒
𝑚𝑝
⎞½
⎟
⎠
≈
⎛
⎜
⎝
𝑇𝑒
4𝑚𝑝
+
1
⎞½
⎟
⎠
-
1
2
⎛
⎜
⎝
𝑇𝑒
𝑚𝑝
⎞½
⎟
⎠
,
3
2
⎛
⎜
⎝
𝑇𝑒
𝑚𝑝
⎞½
⎟
⎠
≈
⎛
⎜
⎝
𝑇𝑒
4𝑚𝑝
+
1
⎞½
⎟
⎠
.
Возводя обе стороны в квадрат, найдём
9
4
𝑇𝑒
𝑚𝑝
≈
𝑇𝑒
4𝑚𝑝
+
1
,
𝑇𝑒
𝑚𝑝
≈
1
2
.
Правильный ответ может отличаться от этого на часть или кратное величины 𝑚𝑒/𝑚𝑝=1/2000. Умножая решение с обеих сторон на 𝑚𝑝 𝑐², получим
𝑇
𝑒,
обычн
=
𝑇
𝑒
𝑐²
=
𝑚𝑝 𝑐²
2
=
1000 Мэв
2
=
500
Мэв
.
92. Абсолютно неупругое столкновение

Рис. 118. 4-вектор энергии-импульса составной частицы после абсолютно неупругого соударения.
На первоначально покоившуюся свободную частицу массы 𝑚₁ налетает вторая частица с кинетической энергией 𝑇 и другой массой покоя 𝑚₁. При столкновении частицы слипаются и в дальнейшем движутся вместе. Чему равна масса покоя 𝑚 составной частицы после столкновения? При каких условиях масса покоя составной частицы сводится к ньютоновской величине 𝑚=𝑚₁+𝑚₂? Какой может быть с точки зрения этих условий максимальная величина кинетической энергии 𝑇 налетающей частицы, когда ньютоновский подход приблизительно справедлив? Обсуждение. Чему равен импульс системы до столкновения? Чему равен он после столкновения? Какие величины, изображённые на рис. 118, известны, а какие требуется определить, если дан импульс системы? Применима ли теорема Пифагора к «гипотенузе» этого «треугольника»? ▼
93*. Порождение частиц протонами
Ускорители для получения частиц высоких энергий строятся, в частности, для того, чтобы создавать в больших количествах для исследовательских целей некоторые из частиц с коротким временем жизни, которые в обычных условиях попадают в лаборатории лишь случайно как результат воздействия космических лучей. В процессе их порождения часть кинетической энергии частиц высокой энергии, полученных в ускорителе, превращается в массу покоя этих новых частиц. В 1955 г. Сегре с сотрудниками получил в Калифорнийском университете, Беркли, антипротоны (частицы той же массы, что протоны, но с отрицательным зарядом), бомбардируя пучком протонов покоящуюся мишень, содержащую водород (протоны) 1). Ряд законов сохранения, действующих в физике элементарных частиц (сохранение заряда, сохранение числа барионов — тяжёлых частиц), требует одновременного создания вместе с антипротоном и обычного протона. Таким образом,налетающий протон и протон мишени должны сохраниться после столкновения, но плюс к этому возникает протон-антипротонная пара. Вопрос: чему равна та минимальная кинетическая энергия налетающего протона, которая способна вызвать образование пары? Эту минимальную кинетическую энергию называют пороговой энергией.
1) O. Chamberlain, E. Segrè, C. Wiegand, T. Ypsilantis, Phisical Review, 100, 947, (1955).

Рис. 119. Ошибочная диаграмма порогового порождения протон-антипротонной пары в лабораторной системе отсчёта.
а) Первый (некорректный) подход. Проанализируем столкновение, изображённое на рис. 119, когда вся кинетическая энергия налетающего протона превращается в массу покоя, и все четыре присутствующие в конце процесса частицы покоятся. Удовлетворяет ли эта реакция одновременно закону сохранения энергии и закону сохранения импульса?

Рис. 120. Правильная диаграмма порогового порождения протон-антипротонной пары в системе отсчёта ракеты.
б) Второй подход . Найдите систему отсчёта, в которой все четыре частицы конечного состояния могут покоиться, но процесс совместим с законом сохранения импульса. Обсуждение. Система отсчёта, в которой полный импульс равен нулю, называется системой центра масс 1). В системе центра масс столкновение протекает так, как это изображено на рис. 120. Полная энергия сталкивающихся протонов может быть взята меньшей в том случае, когда все четыре частицы конечного состояния покоятся, чем когда эти четыре частицы разлетаются друг от друга. Почему? (Рассмотрите столкновение в системе центра масс. Пренебрегите электрическим взаимодействием между частицами, так как его роль ничтожно мала при интересующих нас здесь высоких энергиях).
1) Авторы употребляют здесь изобретённый ими термин система центра импульса, что конечно, соответствует их стремлению развить новую терминологию и связано с отказом пользоваться понятием «масса покоя», однако едва ли он сможет укорениться. Вероятно, было бы лучше говорить о системе нулевого импульса; в переводе был восстановлен традиционный термин «система центра масс».— Прим. перев.

Рис. 121. Правильная диаграмма порогового порождения протон-антипротонной пары в системе отсчёта ракеты.
в) Третий подход. Из анализа второго подхода мы узнали, что наиболее эффективный перевод кинетической энергии в массу покоя, совместимый с законом сохранения импульса, имеет место, когда образующиеся частицы не разлетаются друг от друга. Значит, в лабораторной системе отсчёта все они будут двигаться вместе с одной и той же скоростью (рис. 121). Исходя теперь из этой схемы и пользуясь лишь законами сохранения импульса и энергии, выраженными в лабораторной системе отсчёта, определите пороговую кинетическую энергию 𝑇порог порождения протон-антипротонной пары. Выразите свой результат в единицах энергии покоя протона и в Бэв.
г) Чему равна энергия каждой частицы после столкновения?
д) Покажите, что пороговая энергия, найденная в пункте (в), может быть получена из результатов упражнения 92. Примите, что каждая из начальных частиц в этом упражнении обладает массой протона и что конечная масса 𝑚 равна учетверённой массе протона.
е) Почему протон-антипротонные пары могут порождаться при более низкой пороговой энергии налетающего протона, если вместо водорода в качестве мишени использовать тяжёлые ядра? ▼
94*. Порождение частиц электронами
Какова пороговая кинетическая энергия 𝑇порог налетающего электрона для процесса
(Быстрый) электрон
+
(Покоящийся) протон
→
→
Электрон
+
Антипротон
+
Два протона?
▼
95*. Фоторождение па'ры одиночным фотоном
а) Гамма-квант (фотон высокой энергии, масса покоя равна нулю) может обладать энергией, превышающей энергию покоя электрон-позитронной пары. (Вспомним, что позитрон обладает той же массой покоя, что и электрон, но положительным зарядом). Тем не менее процесс
(Гамма-квант высокой энергии)
→
→
(Электрон)
+
(Позитрон)
не может протекать в отсутствие дополнительного вещества или излучения. Докажите, что этот процесс несовместим с законами сохранения импульса и энергии, записанными в лабораторной системе отсчёта. Рассмотрите самый общий случай, когда траектории образующихся (предположительно) электрона и позитрона не образуют одинаковых углов с продолжением траектории первоначального гамма-кванта. Повторите доказательство (тогда оно станет максимально убедительным) в системе центра масс предполагаемой пары (т.е. в системе отсчёта, где полный импульс двух образующихся частиц равен нулю).
б) В присутствии дополнительного вещества гамма-квант способен породить пару электрон — позитрон. Чему равна пороговая энергия 𝑇порог, при которой гамма-квант оказывается способен вызвать часто наблюдаемый процесс
(Гамма-квант)
+
(Покоящийся электрон)
→
→
(Позитрон)
+
2 (электрона)
?
Энергия покоя электрона, как и позитрона, составляет около половины мегаэлектронвольт. ▼
96**. Фото рождение па'ры двумя фотонами
Два гамма-кванта разных энергий сталкиваются в вакууме и исчезают, порождая электрон-позитронную пару. В каком диапазоне энергий гамма-квантов и в каком диапазоне углов между направлениями их первоначального распространения может реализоваться такая реакция? ▼
97**. Аннигиляция электрон-позитронной пары
Позитрон 𝑒⁺ с кинетической энергией 𝑇 аннигилирует на мишени, содержащей практически покоящиеся в лабораторной системе отсчёта электроны 𝑒⁻
𝑒⁺
(быстрый)
+
𝑒⁻
(покоящийся)
→
Излучение.
а) В системе отсчёта центра масс (где полный импульс первоначальных частиц равен нулю) покажите, что при такой аннигиляции с необходимостью образуются как минимум два гамма-кванта (а не один).
б) Выведите формулу для энергии одного из образующихся гамма-квантов в лабораторной системе отсчёта как функции угла между направлением вылета этого гамма-кванта и направлением движения позитрона до его аннигиляции. Пусть в вашей формуле никак не фигурирует скорость или параметр скорости — оба они в этой задаче излишни.
в) Чему равны максимальная и минимальная энергии гамма-кванта, возможные в лабораторной системе отсчёта?
г) С помощью простого приближённого метода выразите результат пункта (в) в предельных случаях: 1) очень малых 𝑇 и 2) очень больших 𝑇. ▼
98*. Проверка принципа относительности

Рис. 122. Схема постановки эксперимента для проверки принципа относительности.
а) В установке, изображённой на рис. 122, регистрируются лишь те события, при которых счётчики гамма-лучей 𝐴 и 𝐵, расположенные на одинаковых расстояниях от мишени, одновременно реагируют на гамма-кванты, т.е. включены в «схему совпадений». Чему равны энергия и скорость налетающего позитрона, регистрируемого таким способом?
б) Принцип относительности (разд. 3) утверждает, что скорость света одинакова во всех инерциальных системах отсчёта независимо от движения источника этого света. Напротив, много лет назад В. Ритц пытался доказать, что свет, излучаемый источником вперёд по направлению его движения, распространяется быстрее, чем свет, излучённый против его движения. Если бы описанная выше установка срабатывала и в отсутствие совпадения, как было бы можно использовать измерение времени, прошедшего между попаданием гамма-квантов в счётчики 𝐴 и 𝐵, для выяснения того, какая из гипотез о поведении скорости света правильна? Результаты такого опыта изображены на рис. 123 1).
1) D. Sadeh, Phisical Review Letters, 10, 271 (April, 1693).

Рис. 123. Результаты эксперимента по проверке постоянства скорости света, выполненного Д. Саде.
Промежуток времени между регистрациями фотонов счётчиками 𝐴 и 𝐵 был измерен для множества пар таких событий. Промежутки различной длительности автоматически отводились в разные «каналы» многоканальной электронной вычислительной машины. В результате на горизонтальной оси (названной «номер канала») откладывалась относительная мера времени между попаданиями гамма-квантов в счётчики 𝐴 и 𝐵. На вертикальной оси откладывались количества пар гамма-квантов, соответствующих данному промежутку времени, разделявшему моменты их регистрации. Нижняя кривая изображает результаты эксперимента на установке, подобной изображённой на рис. 122, где на лету аннигилировали позитроны заданной энергии. Верхняя кривая была получена при перенесении счётчика 𝐴 в положение, составляющее 180° относительно счётчика 𝐵. В этом случае регистрировались только те пары гамма-квантов, для которых позитрон перед аннигиляцией останавливался (при этом лабораторная система отсчёта являлась системой центра масс, в которой фотоны испускаются в двух взаимно противоположных направлениях!). Вершины верхней и нижней кривой соответствуют одному и тому же промежутку времени, откуда видно, что свет (гамма-кванты) распространяется от мишени до счётчика 𝐴 с одинаковой скоростью независимо от того, двигался или покоился испустивший его позитрон. Если бы скорость гамма-кванта складывалась со скоростью летящего позитрона, вершина нижней кривой совпадала бы с левой пунктирной линией.
▼
99*. Отождествление частиц по трекам в пузырьковой камере

Рис. 124. На снимке в пузырьковой камере заснят распад четырёх различных π⁺-мезонов. Из книги R. D. Hill, Tracking Down Particles, W. A. Benjamin, New York, 1963.
Движущиеся заряженные частицы могут оставлять наблюдаемые визуально следы в камере Вильсона, пузырьковой камере и искровой камере, так как заряд частицы взаимодействует на расстоянии с электронами в атомах, вызывая образование ионов. Эти ионы детектируются различными способами в указанных трёх видах камер. Пузырьковые камеры заполняются жидким водородом, готовым закипеть (перегретым водородом). Возникающие при прохождении заряженных частиц высокой энергии ионы играют роль точек образования пузырьков («центров закипания»). На рис. 124 изображена картина, заснятая в пузырьковой камере. Там видно четыре разных π⁺-мезона, проникающих в камеру, которые все останавливаются в жидком водороде. Сначала происходит реакция распада π⁺-мезона на μ⁺-мезон, трек которого виден на снимке, и на нейтральную частицу, не оставляющую следа. Затем каждый μ⁺-мезон останавливается и распадается на положительный электрон (позитрон, 𝑒⁺) и две нейтральные частицы. Спиральный трек одного из позитронов, движущихся в наложенном извне магнитном поле, занимает центр фотографии.
Сосредоточим внимание на первой реакции,
π⁺
(покоящийся)
→
μ⁺
+
𝑥
,
где 𝑥 — неизвестная нейтральная частица. По радиусу кривизны трека μ⁺-мезона в магнитном поле можно найти импульс этого мезона, оказывающийся равным 𝑝μ=58,2 𝑚𝑒 в единицах массы покоя электрона.
а) Пользуясь законами сохранения, найдите массу покоя нейтральной частицы (𝑚π⁺=273,2 𝑚𝑒 и 𝑚μ⁺=206,8 𝑚𝑒).
б) Что это за нейтральная частица? Обсуждение. Самой лёгкой из известных частиц с ненулевой массой покоя является электрон. Приближённый расчёт в (а) приводит к предположению, что масса покоя частицы 𝑥 равна нулю. Может быть, это фотон? Такая возможность исключается другим законом сохранения — для момента импульса. Существовавший сначала π⁺-мезон обладал моментом импульса, равным нулю. Если потребовать выполнения закона сохранения момента импульса, то следует заключить что суммарный момент частиц — продуктов реакции — равен нулю. Возникший μ⁺-мезон имеет спиновый момент импульса, равный ½ℏ=½⋅ℎ/(2π) где ℎ — постоянная Планка. Мы знаем к тому же, что спиновый момент импульса фотона равен ℏ Невозможно, чтобы два момента, соответственно равные ½ℏ и ℏ, при какой-либо их ориентации в сумме дали полный момент импульса равный нулю. Значит, частица 𝑥 не может быть фотоном. Определите, чему равен её спиновый момент импульса? Мы называем частицу 𝑥 нейтрино. Здесь вы определили два основных свойства нейтрино, даже вообще не увидев его наблюдаемых следов! ▼
100*. Накопительные кольца и встречные пучки

Рис. 125. Пристонско-станфордский эксперимент по встречным электронным пучкам.
Электроны инжектировались в каждое кольцо примерно по 10 мин. Когда оба кольца были таким образом заполнены, линейный ускоритель был отключён, и в течение 30 мин снимались данные. Потери энергии электронами, излучавшими из-за ускоренного движения по круговым орбитам, компенсировались радиоволновым методом в резонаторах радиочастотной «подкачки».
Насколько «энергичнее» окажется столкновение, если два соударяющиеся электрона движутся навстречу друг другу, по сравнению со столкновением, когда один электрон налетает на другой электрон, который покоится? Обсуждение. Когда движущаяся частица налетает на покоящуюся, то энергия, которая может пойти на порождение новых частиц, на нагрев или на иные взаимодействия, меньше, чем начальная энергия (сумма энергий покоя и кинетических энергий обеих начальных частиц). См. по этому поводу упражнение 93. Причина состоит в том, что система частиц после реакции в целом сохраняет движение «вперёд» (закон сохранения импульса!), соответствующая которому кинетическая энергия не может пойти ни на придание этим частицам скорости относительно друг друга, ни на порождение новых частиц. Поэтому значительная часть энергии, сообщаемой частицам в ускорителях, не может быть использована для изучения взаимодействий и «выбрасывается» в форме кинетической энергии продуктов столкновения. Но в системе центра масс (определённой как система отсчёта, в которой полный импульс системы взаимодействующих частиц равен нулю) равенство полного импульса нулю имеет место как до, так и после столкновения. Поэтому в системе центра масс участвующая во взаимодействии энергия равна всей полной энергии первоначальных частиц. Можно ли как-то достигнуть того, чтобы лабораторная система отсчёта стала одновременно системой центра масс? Одним из способов является постройка двух ускорителей элементарных частиц, создающих два пучка частиц, направленных «в лоб» один другому. Если энергии и массы покоя частиц в обоих пучках одинаковы, то наша лабораторная система отсчёта будет и системой центра масс, и тогда при каждом столкновении вся энергия сможет быть реализована в столкновении для взаимодействия. Но проще и дешевле можно добиться того же результата, используя всего один ускоритель плюс накопительные кольца, в которых частицы сохраняются после того, как они достигнут своей максимальной энергии (рис. 125). Магнитное поле удерживает частицы (в данном случае — электроны) на круговых орбитах. Пучок частиц впрыскивается из ускорителя таким образом, чтобы в обоих кольцах направление циркуляции частиц было взаимно противоположным. Между частицами из двух пучков происходят столкновения в точке 𝐴, где пучки пересекаются (поэтому говорят о встречных пучках). Одним из преимуществ накопительных колец является сохранение в пучках тех электронов, которые не провзаимодействовали при одной встрече, но могут принять участие в столкновении при одной из последующих.
В каждом из колец «законсервированы» электроны с кинетической энергией 500 Мэв. Чему равна в лабораторной системе отсчёта полная величина энергии, которая может реализоваться во взаимодействии? Чему должна была бы быть равна кинетическая энергия электрона, налетающего на покоящийся электрон, из которой для взаимодействия можно было бы получить такую же энергию? (Когда пишутся эти строки, наибольшая энергия, которую может сообщить электрону одиночный ускоритель, равна 6 Бэв). Какой кинетической энергией должны обладать протоны, «консервируемые» в накопительных кольцах, чтобы они дали эквивалент полезной энергии протона 1000 Бэв, налетающего на покоящийся протон? (Когда пишутся эти строки, наибольшая энергия, которую может сообщить протону одиночный ускоритель, равна 35 Бэв). 1)
1) Новейший ускоритель протонов в Серпухове под Москвой даёт протоны с энергией 76 Бэв.- Прим. перев.
▼
Е. АТОМНАЯ ФИЗИКА
101*. Де Бройль и Бор
Покажите, что результаты упражнения 72 приводят к соотношению 𝑝=ℎ/λ𝑐 для импульса фотона, выраженного в единицах массы. Рассмотрите следующий интуитивный довод (основанный на удивительном выводе де Бройля 2), который был неполным, но исторически важным, так как привёл к весьма плодотворным исследованиям, а в конце концов — и к окончательному выводу и последующему развитию квантовой механики). Предположим, что длина волны λ=ℎ/𝑝𝑐 может ассоциироваться и с частицей ненулевой массы покоя, например с электроном. Пусть этот электрон движется по круговой орбите вокруг неподвижного ядра. Для того чтобы волна, описывающая электрон, была везде однозначной, необходимо потребовать равенства длины орбиты 2π𝑟 некоторому целому числу 𝑛 длин волн λ, умещающихся на протяжении этой орбиты. Покажите, что отсюда следует соотношение
2) Louis de Broglie, Comptes Rendus (Paris), 177, 507 (1923).
𝑟𝑝
обычн
=
𝑛ℎ
2π
=
𝑚ℏ
(
𝑛=1, 2, 3,
)
,
(125)
где 𝑝обычн — величина импульса электрона в обычных единицах. Какая величина момента импульса электрона, находящегося на такой орбите, следует из соотношения (125)? В пределе малых скоростей ньютоновская механика говорит, что радиус орбиты даётся соотношением
𝑟
=
(4πε₀)𝑛²ℎ²
4π²𝑍𝑒²𝑚
(126а)
(𝑒 в кулонах, 4πε₀=1,113⋅10⁻¹⁰ (кулон⋅сек)²/кг⋅м³; ℎ, 𝑚 и 𝑝 в системе СИ — кг, м, сек), или
𝑟
=
𝑛²ℏ²
𝑍𝑒²𝑚
(126б)
(𝑒 в CGSE; ℏ, 𝑚 и 𝑟 в системе CGS — г, см, сек), где 𝑍 — атомный номер ядра (число протонов в нем), 𝑚 — масса и 𝑒 — заряд электрона. Это формула радиуса орбит атома Бора. Покажите, что скорость электрона на орбите равна (в приближении малых скоростей)
β
=
α𝑍
𝑛
,
(127)
где
α
=
𝑒²
=
1
(4πε₀)
ℎ
⋅
𝑐
137
2π
— безразмерная постоянная, называемая постоянной тонкой структуры. [Эта формула верна, когда 𝑒 выражается в кулонах, 4πε₀=1,113⋅10⁻¹⁰ (кулон⋅сек)²/кг⋅м³, ℎ и 𝑐 — в кг, м, сек. Если её выразить в системе г, см, сек, причём 𝑒 взять в единицах CGSE, то α=𝑒²/ℏ𝑐=1/137). Полученное выражение для β использовалось в упражнении 41. ▼
102*. Ви'дение посредством электронов
Из общих принципов физической оптики следует невозможность получить изображение таких деталей объекта, которые меньше длины волны света, с помощью которого получают это изображение. Предположим, что это утверждение верно и в применении к волнам вещества, обсуждавшимся в предыдущем упражнении. Через какую разность потенциалов должны быть пропущены (ускорены) электроны, чтобы с их помощью было можно получить изображение бактерии (размером около 1 мк, т.е. 10⁻⁶ м) в электронном микроскопе? Какой энергией (в Мэв) должны обладать электроны, чтобы с их помощью можно было исследовать структуру протонов и нейтронов (диаметр которых равен около 1 ферми, т.е. 10⁻¹⁵ м)? ▼
103**. Прецессия Томаса

Рис. 126. Ньютоновская механика утверждает, что при обороте электрона вокруг ядра ориентация его спина не изменится.
Представьте себе электрон как отрицательно заряженный шарик, вращающийся вокруг своей оси, подобно гироскопу. Эта грубая классическая модель не соответствует действительности, но приемлема для некоторых целей, например для следующей. Ньютоновская механика предсказывает, что электрон в атоме должен вращаться по некоторой орбите вокруг ядра и сохранять при этом неизменным направление оси своего вращения относительно инерциальных систем отсчёта точно так же, как это происходит с гироскопом, перемещаемым по окружности.
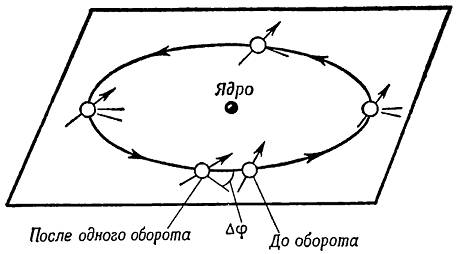
Рис. 127. Теория относительности предсказывает прецессию оси вращения электрона на угол, обозначенный здесь через Δφ, за один оборот вокруг ядра.
Однако, как открыл в 1927 г. Л. X. Томас 1), теория относительности удивительным образом утверждает, что если электрон вращается вокруг ядра, вектор его спина направлен по-разному после каждого оборота. Такая прецессия, названная прецессией Томаса, приводит к наблюдаемому эффекту в спектральных линиях излучения некоторых атомов. Объяснение этой прецессии связано с эффектом наклонного метрового стержня (упражнение 52) и основывается на относительности одновременности. Проанализируйте эффект прецессии Томаса для электрона по следующей схеме (или другим способом).
1) L. H. Thomas, Philosophical Magazine, (7) 3, 1 (1927).

Рис. 128. Правильный многоугольник как приближённое описание ньютоновской круговой орбиты электрона в атоме.
Что заставляет ось вращения электрона принимать новое направление после того, как электрон опишет полный круг? Двигаясь по окружности, электрон испытывает ускорение, направленное к её центру. Но, к сожалению, частная теория относительности неспособна описывать действие ускорения на ориентацию векторов. Поэтому мы поступим так, как это часто делается в физике: если данная проблема не поддаётся непосредственному решению, следует найти более простую, но аналогичную ей задачу, решить которую мы сумеем! В данном случае приближённо представим круговой путь классического электрона как правильный многоугольник с 𝑛 сторонами. Для того чтобы совершить один полный оборот по орбите, электрон должен пройти теперь по ряду прямолинейных отрезков, испытав между ними 𝑛 резких изменений направления движения, каждый раз на угол α=2π/𝑛. План штурма задачи: исследовать, как изменится направление спина электрона при прохождении одного из таких углов [пункты от (а) до (в)]; затем устремить число сторон 𝑛 к бесконечности так, чтобы угол α, на который всякий раз меняется направление движения электрона, стремился к нулю, пока не получится в качестве предельного случая классическая круговая орбита [пункты от (г) до (д)].

Рис. 129. Частный случай изменения ориентации оси вращения электрона при изменении направления его движения.
а) На рис. 129 электрон изображён до (𝐴) и после (𝐵) того, как он изменил направление своего движения на угол α. Жирная черта, пересекающая в каждом случае электрон,— проекция направления спина на плоскость орбиты (плоскость 𝑥𝑦). На рисунке представлен тот частный случай, когда эта проекция была направлена вдоль оси 𝑥 до изменения электроном его направления движения. Когда же произошло это изменение направления движения электрона как целого, ориентация спина должна была также измениться на некоторый малый угол 𝑑φ, и это изменение нельзя понять в рамках механики Ньютона! Чем оно вызвано? Его причиной является относительность одновременности.

Рис. 130. Заменим одиночный электрон, огибающий угол, двумя электронами, 𝐴 и 𝐵, движущимися по пересекающим прямым путям. Потребуем, чтобы ориентация спина у 𝐴 и у 𝐵 была одинаковой в системе отсчёта, где 𝐴 покоится.
Огибая угол, электрон испытывает сильное и резкое ускорение. К счастью, мы можем анализировать по отдельности шарики 𝐴 и 𝐵, движущиеся с одинаковыми по модулю скоростями в направлениях, образующих в лабораторной системе отсчёта угол α, как это изображено на рис. 130. Ни один из этих шариков пусть не ускоряется, но в момент их встречи наблюдатели, движущиеся вместе с ними, могут зарегистрировать одинаковое направление осей вращения шариков 𝐴 и 𝐵. Рисунок в системе отсчёта ракеты изображает относительную ориентацию спинов в той системе отсчёта, где шарик 𝐴 покоится. Именно в этой системе отсчёта ракеты наблюдатель на 𝐴 производит сравнение ориентаций векторов спина. (Вопрос: какой наблюдатель проводит сравнение — 𝐴 или 𝐵? В том случае, когда угол α весьма мал, наблюдатель 𝐴 и наблюдатель 𝐵 будут почти покоиться друг относительно друга, так что в пределе всё равно, кто из них производит сравнение!) Так как мы заменяем одиночный шарик, огибающий угол, двумя шариками 𝐴 и 𝐵, мы требуем, чтобы в системе отсчёта ракеты проекции спина для 𝐴 и для 𝐵 были взаимно параллельны. Главное здесь в том, что хотя эти проекции и параллельны в системе отсчёта ракеты, они не параллельны в лабораторной системе отсчёта. В результате направление вектора спина электрона изменяется, когда электрон огибает угол, при наблюдении в лабораторной системе отсчёта.
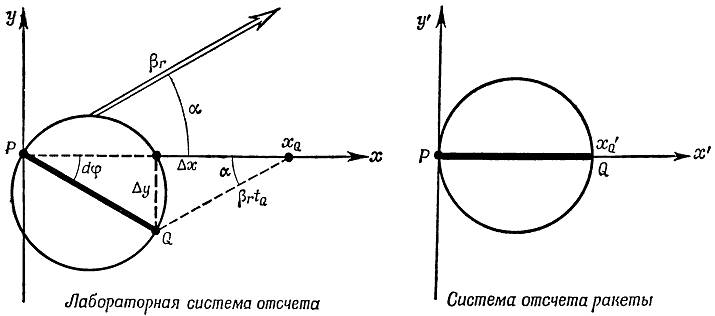
Рис. 131. Исследование ориентации оси вращения шарика 𝐵 в лабораторной системе отсчёта и в системе отсчёта ракеты; схема начерчена для того, чтобы получить ответы на вопросы: где и когда точка 𝑄 пересекает ось 𝑥? Где вследствие этого расположена точка 𝑄 в момент времени 𝑡=0 в лабораторной системе отсчёта?
На рис. 131 в крупном масштабе изображён шарик 𝐵. Обозначим, согласно этой схеме, концы проекции спиновой оси через 𝑃 и 𝑄. Выберем начала координат в лабораторной системе отсчёта и в системе отсчёта ракеты так, чтобы в момент 𝑡=𝑡'=0 эти начала совпадали с точкой 𝑃. Тогда в системе отсчёта ракеты точка 𝑄 пересечёт ось 𝑥 в этот же момент 𝑡'=𝑡𝑄'=0. Но в лабораторной системе отсчёта это будет не так! На рис. 131 показан электрон 𝐵 в момент времени 𝑡=0 в лабораторной системе отсчёта. Пусть 𝑥𝑄 и 𝑡𝑄 будут соответственно другой точкой и более поздним моментом времени в лабораторной системе отсчёта, при которых точка 𝑄 пересекает ось 𝑥. Пользуясь формулами преобразования Лоренца и полагая 𝑡𝑄=0, покажите, что
𝑥
𝑄
=
𝑥
𝑄
'
ch θ
𝑟
,
𝑡
𝑄
=
𝑡
𝑄
'
sh θ
𝑟
.
(128)
Вопрос: где находилась точка 𝑄 в момент времени 𝑡=0 в лабораторной системе отсчёта? К моменту 𝑡𝑄 точка 𝑄 прошла расстояние β𝑟 𝑡𝑄, как это показано на рисунке. Покажите, исходя из него, что за это время координаты 𝑥 и 𝑦 точки 𝑄 изменились на величины
Δ
𝑥
=
β
𝑟
𝑡
𝑄
cos α
=
β
𝑟
𝑥
𝑄
'
sh θ
𝑟
cos α
,
Δ
𝑦
=
β
𝑟
𝑡
𝑄
sin α
=
β
𝑟
𝑥
𝑄
'
sh θ
𝑟
sin α
,
(129)
где на последнем этапе были использованы соотношения (128). Это значит, что в момент 𝑡=0 лабораторной системы отсчёта точка 𝑃 была (по определению) в начале координат, а точка 𝑄 имела координаты 𝑥𝑄-Δ𝑥 и -Δ𝑦. Поэтому угол наклона 𝑑φ отрезка 𝑃𝑄 к горизонтали, найденный в лабораторной системе отсчёта в момент 𝑡=0, т.е. изменение ориентации вектора спина после того, как электрон обогнул угол, даётся выражением
tg 𝑑φ
=
-Δ𝑦
𝑥𝑄-Δ𝑥
.
(130)
Подставляя сюда 𝑥𝑄, Δ𝑥 и Δ𝑦 из соотношений (128) и (129) и производя упрощения, найдём
tg 𝑑φ
=
-β𝑟²sin α
1-β𝑟²cos α
.
В атоме β𝑟≤𝑍/137 (см. упражнение 101), так что при малых 𝑍 β𝑟≪1. Поэтому
tg 𝑑φ
≈
𝑑φ
≈
-β
𝑟
²sin α
.
Это и есть тот угол, на который спиновая ось электрона поворачивается при огибании электроном угла α в том частном случае, когда проекция этой оси на плоскость орбиты электрона направлена первоначально вдоль его движения.

Рис. 132. Частный случай, когда электрон не изменяет ориентации своей оси при изменении направления движения.
б) Возьмём другой частный случай, на этот раз когда проекция оси вращения параллельна оси 𝑥 (𝑥𝑦 — плоскость орбиты). Покажите, что теперь наблюдатели в лабораторной системе отсчёта и в системе отсчёта ракеты будут согласны между собой в том, что точки 𝑃 и 𝑄 пересекают ось 𝑦 одновременно. Поэтому в данном случае при огибании электроном угла в лабораторной системе отсчёта будет отсутствовать поворот оси вращения электрона.

Рис. 133. Общий случай изменения ориентации оси вращения электрона, когда последний меняет направление своего движения.
в) В процессе движения электрона по орбите проекция его оси вращения на плоскость 𝑥𝑦 (рис. 127) будет иногда параллельна направлению его движения (случай (а)), а иногда — перпендикулярна этому направлению (случай (б)). В общем случае она будет составлять некоторый угол φ с направлением движения электрона, меняющийся на 𝑑φ, когда электрон огибает угол. Чему может быть равна величина этого изменения, 𝑑φ? При φ=0 [случай (а)] 𝑑φ=-β𝑟²sin α; при φ=90° [случай (б)] 𝑑φ=0. В общем случае изменение должно лежать между нулём и -β𝑟²sin α. Исходя из рис. 133, проведём следующие рассуждения, чтобы показать, что при малых α и β𝑟² искомое изменение равно -β𝑟²sin α cos²φ. Дополним первоначальную линию 𝑃𝑄 её горизонтальной и вертикальной составляющими 𝑃𝑅 и 𝑄𝑅. Из пунктов (а) и (б) мы знаем, что вертикальный отрезок 𝑄𝑅 не подвергнется повороту, когда электрон обогнёт угол, тогда как горизонтальный отрезок 𝑃𝑅 повернётся по часовой стрелке на угол β𝑟²sin α. Покажите, что при малых углах α это приводит к неизменности 𝑥-компоненты 𝑃𝑄 и уменьшению 𝑦-компоненты на величину (𝐿 cos φ)⋅(β𝑟²sin α). Поэтому тангенс нового угла φ+𝑑φ равен
tg(φ+𝑑φ)
≈
𝐿 sin φ-(𝐿 cos φ)(β𝑟²sin α)
𝐿 cos φ
=
=
tg φ
-
β
𝑟
²sin α
.
(131)
Требуется найти tg 𝑑φ≈𝑑φ; согласно табл. 8,
tg 𝑑φ
=
tg[(φ+𝑑φ)-φ]
=
tg(φ+𝑑φ)-tg φ
1+tg(φ+𝑑φ)⋅tg φ
.
Используя равенство (131), получим
tg 𝑑φ
=
tg φ-β𝑟²sin α-tg φ
1+(tg φ-β𝑟²sin α) tg φ
=
=
-β𝑟²sin α
1+tg²φ-β𝑟²sin α tg φ
.
При очень малых α можно пренебречь последним слагаемым в знаменателе, где останется тогда сумма
1+tg²φ
=
1+
sin²φ
cos²φ
=
cos²φ+sin²φ
cos²φ
=
1
cos²φ
,
так что
tg 𝑑φ
≈
𝑑φ
=-
β
𝑟
²sin α
cos²φ
.
(132)
Это и есть тот угол, на который поворачивается (прецессирует) ось вращения электрона, когда последний огибает угол, изменяя направление своего движения на α, в общем случае ориентации проекции этой оси вращения на плоскость орбиты под углом φ к направлению движения электрона.
г) Из уравнения (132) видно, на какой угол 𝑑φ поворачивается вектор спина электрона, когда электрон изменяет направление своего движения на α, один раз огибая угол. Чему будет тогда равен полный угол прецессии Δφ при обходе электроном всей замкнутой орбиты? (См. рис. 127 и 128). В замкнутой орбите содержится 𝑛 поворотов, каждый из которых происходит на угол α=2π/𝑛. При больших 𝑛 (малых α) sin α≈α так что полный угол прецессии спина при одном обороте электрона вокруг ядра составляет
Δ
φ
≈-
β
𝑟
²(𝑛α)
〈cos²φ〉
ср
≈-
β
𝑟
²
〈cos²φ〉
ср
.
Чему равен множитель 〈cos²φ〉ср? Предположим, что полный угол прецессии Δφ за один оборот является малым (скорость β𝑟 мала!). Тогда при обходе электроном его орбиты угол φ между переменным направлением движения и проекцией оси вращения на плоскость орбиты пробежит все значения от 0 до 2π. Покажите, что в этом случае
〈cos²φ〉
ср
=
1
2π
2π
∫
0
cos²φ
𝑑φ
=
1
2
.
Поэтому полный угол прецессии спина электрона за один полный оборот по орбите равен
Δ
φ
=-
πβ
𝑟
²
(угол прецессии за один оборот).
(133)
д) Электрон, двигающийся со скоростью β=β𝑟, за один полный оборот по орбите прецессирует на угол Δφ=-πβ𝑟²=-πβ². Покажите, что электрону требуется совершить 2π/Δφ=2/β² оборотов вокруг ядра, чтобы прецессия возвратила его в прежнее положение (прецессия на 2π рад). Примем теперь боровскую частоту обращения электрона вокруг ядра за ν𝐵 Покажите, что частота прецессии Томаса ν𝑇 (частота прецессии спина электрона) выражается через боровскую частоту как
ν𝑇
ν𝐵
≈
1
2
β²
(частота прецессии Томаса).
(134)
Мы знаем из упражнения 101, что скорость движения электрона на орбите в элементарной теории Бора равна
β
=
α𝑍
𝑛
=
𝑍
137𝑛
.
Здесь 𝑍 — число элементарных зарядов в ядре, а 𝑛 — номер энергетического уровня электрона, причём низший (основной) уровень соответствует 𝑛=1. Отсюда следует, что частота прецессии Томаса для электрона в атоме определяется выражением
ν𝑇
ν𝐵
≈
1
2
⎛
⎜
⎝
𝑇
137𝑛
⎞²
⎟
⎠
(частота прецессии Томаса).
(135)
(Замечание. В некоторых атомах имеет место дополнительная прецессия спина электрона, обусловленная моментом силы, возникающим при взаимодействии магнитного момента электрона с магнитным полем ядра. Для электрона находящегося на внутренней орбите атома водорода, такая магнитная прецессия имеет обратное направление и вдвое превышает по абсолютной величине прецессию Томаса. Поэтому полный эффект состоит в прецессии с вдвое меньшей частотой по сравнению с тем, что предсказывает один лишь учёт магнитного взаимодействия без анализа эффектов частной теории относительности).
Ж. МЕЖЗВЁЗДНЫЕ ПОЛЁТЫ
104*. Трудности межзвёздных полётов 1)
1) См. Edward Purcell, in Interstellar Communication, ed. A.G.W. Cameron, Benjamin, New York, 1963. [Русский перевод: Межзвёздная связь, изд-во «Мир», М., 1966.]
Игнорируя полностью все технические затруднения, рассмотрим лишь те трудности полётов в межзвёздные просторы, которые вызываются самой теорией относительности. Пусть имеется (в 1989 г.?) ракетный двигатель, обладающий ничтожной массой. В нем можно регулировать соединение материи и антиматерии, поступающей из баков, причём возникают одни лишь фотоны, и двигатель направляет всё это излучение в нужную сторону. Этот двигатель ускоряет космический корабль, величина массы всех конструкций которого, включая защиту, ничтожно мала. Условия контракта таковы: нужно ускорить полезный груз до скорости, при которой коэффициент замедления времени равен 10, произвести торможение для посещения планет около далёкой звезды (предполагается, что она покоится относительно нашего Солнца), а затем вернуться на Землю с такой же скоростью. Полезный груз, включая пассажиров, который требуется доставить по замкнутому маршруту, равен 100 т (100⋅10³ кг).
а) Воспользуйтесь результатами упражнения 58 для определения полной массы топлива, необходимого для путешествия по замкнутому маршруту. (Но не учетверённой величины массы того топлива, которое необходимо для единичного акта ускорения ракеты из состояния покоя до её максимальной скорости!)
б) Чему равно расстояние (в световых годах) до самой далёкой звезды, которой можно достигнуть за время жизни астронавта (предполагаемая продолжительность жизни человека в 1989 г. 100 лет)? (Для простоты пренебрегите временем работы двигателей ракеты по сравнению со значительно более длительным сроком полёта с постоянной скоростью). Какой (приблизительно) промежуток времени пройдёт на Земле в течение этого полёта?
в) Приняв плотность межзвёздной среды равной одному атому водорода на кубический сантиметр, укажите, чему равна кинетическая энергия этих атомов (в Бэв) в системе отсчёта ракеты, движущейся с максимальной скоростью? Сколько таких частиц будет попадать на 1 м лобовой поверхности ракеты в секунду и насколько велико это число по сравнению с мощностью пучка протонов высокой энергии от ускорителя (около 10¹² протонов в секунду, каждый с энергией порядка 10 Бэв)? Для защиты работников от чрезмерного облучения на таком ускорителе устанавливают щит из железобетона толщиной 3—4 м. Оцените теперь возможности межзвёздных космических путешествий! ▼
3. ФИЗИКА ИСКРИВЛЁННОГО ПРОСТРАНСТВА-ВРЕМЕНИ
Только исторический подход освобождает дух от засилья прошлого; он поддерживает его самостоятельность и стремится лишь внести ясность.
Бенедетто Кроче
Для того чтобы понять нынешнее значение физики пространства-времени, едва ли не лучше всего вспомнить, как она выковывалась тружениками науки в прошлом. Рассказ о том, как она продвигалась вперёд, постоянно проводя разведку боем, никак нельзя полностью вместить в несколько десятков страниц; но вместе с тем нельзя и обойти несколько великих имён и поворотных пунктов, предопределивших её развитие. Приступая к рассказу о её истории, мы надеемся разобраться — по крайней мере в общих чертах — во взаимоотношении физики локальных лоренцевых систем отсчёта и физики в более обширных областях пространства-времени, таких, как околоземное космическое пространство или солнечная система в целом.
Изменение духа физики при расширении пространственно-временных масштабов.
Галилей и Ньютон считали, что движение можно адекватно описать в жёсткой эвклидовой системе отсчёта, распространённой на всё пространство и сохраняющейся неизменной во все времена. Такая система остаётся вне изменений, происходящих с веществом и с энергией. В этом идеальном пространстве Галилея и Ньютона действует таинственная сила тяготения, контрабандой занесённая из мира физики, чуждое влияние, не описываемое геометрией. Напротив, Эйнштейн утверждает, что нет никакого таинственного тяготения — налицо лишь структура самого пространства-времени.
Эйнштейн против Ньютона — множество инерциальных систем отсчёта, каждая из которых локальна, против единой глобальной системы
Он говорит: сядьте в космический корабль, и вы убедитесь, что там нет тяжести. Локально физика лишена тяготения (разд. 2 гл. 1). Все свободные частицы движутся прямолинейно с постоянными скоростями, и в инерциальной системе отсчёта физика проста. Однако такие системы инерциальны лишь в ограниченной области пространства-времени, и этот факт мы подчёркивали, постоянно называя инерциальные системы отсчёта локальными. Трудности возникают, когда мы описываем связь между направлением движения частицы, наблюдаемым из двух соседних локальных систем отсчёта. Согласно Эйнштейну, все различия в направлениях в данной системе и соседней локальной системе отсчёта характеризуются «кривизной пространства-времени». Факт существования этой кривизны делает невозможным описание движения в единой идеальной эвклидовой системе отсчёта, охватывающей пространство. Геометрия проста лишь в областях, достаточно малых для того, чтобы они казались плоскими. Короче говоря, Эйнштейн пользуется множеством локальных областей, в каждой из которых геометрия лоренцева («частная теория относительности»), и законы тяготения проистекают от неидеального соответствия между одной локальной областью и соседней с ней (гравитация как кривизна пространства-времени —«общая теория относительности»). У Ньютона была единая глобальная система отсчёта, но в этой системе нет ни одного спутника, на котором отсутствовала бы тяжесть, и ни одна частица не может двигаться там прямолинейно и равномерно.
Как развивались воззрения Галилея, Ньютона и Эйнштейна? И в чём, собственно, смысл странного выражения «кривизна пространства-времени»?
Общеизвестно глубочайшее противоречие между результатами опытов Галилея по свободному падению и утверждением Аристотеля о том, что «нисходящее движение масс золота, или свинца, или любых иных весомых тел происходит тем быстрее, чем больше их вес». За несколько лет до опытов Галилея Молетти в Падуе утверждал, что свинцовые и деревянные грузы падают одинаково быстро, но этого утверждения было недостаточно, чтобы опровергнуть взгляд Аристотеля. Для окончательного доказательства потребовалось вмешательство Галилея. Неясно, бросал ли Галилей свинцовые и деревянные грузы с «Падающей башни» в Пизе, но он определённо провёл более убедительные эксперименты с потенциально более высокой степенью точности, чем опыт с «Падающей башни» 1).
1) Подробности см. в книге Галлилео Галлилея «Диалоги о двух науках», впервые опубликованной в марте 1638 г. [Русский перевод: Галлилей, Диалоги о двух новых науках, ОНТИ, М., 1937.]

ГАЛИЛЕО ГАЛИЛЕЙ
Пиза, 14 февраля 1564 г. — Арчетри, близ Флоренции, 8 января 1642 г.
«Мой портрет уже закончен, сходство очень хорошее, рука отличного мастера». 22 сентября 1635 г.
* * *
«Если кто-либо и когда-либо мог претендовать на то, чтобы быть выделенным из числа других людей за свой разум, так это Птоломей и Коперник, заслуга которых в том, что они дальше всех заглянули в Систему Мира и наиболее глубоко её исследовали».
* * *
«Дорогой мой Кеплер, что мы сделаем со всем с этим? Будем ли смеяться или плакать?»
* * *
«Когда же я перестану удивляться?»
Кто, вступая на путь первооткрывателя закона ускоренного падения, мог обойти исследование полёта снаряда? Изучая этот полёт и стремясь описать его простейшим образом, Галилей должен был прийти к мысли о сложении движений — движения по вертикали с постоянным направленным вниз ускорением и горизонтального движения с постоянной скоростью (равномерного переноса). Отсюда оставался всего лишь шаг до принципа относительности в первой из его известных формулировок. Вот что говорят действующие лица в книге Галилея 2):
2) Книга Галилео Галилея «Диалоги о двух главнейших системах мира — птоломеевой и коперниканской» впервые опубликована в феврале 1632 г. [Русский перевод: Галилей, Диалоги о двух главнейших системах мира, Гостехиздат, М., 1947.] Сочинения Галилея, как и сочинения Данте, по своей силе и насыщенности — сокровища человеческой мысли, и учащиеся средних школ Италии изучают их как часть великого литературного наследия.
Галилей: первая из известных формулировок принципа относительности
Сальвиати, Запритесь с кем-нибудь из друзей в кают-компании под палубой большого корабля, взяв с собой мух, бабочек и других небольших летающих животных. Возьмите и большой сосуд с водой, в котором плавают рыбы. Подвесьте бутыль, из которой капля по капле вытекает вода в широкий сосуд внизу. Пока ваше судно стоит на месте, внимательно наблюдайте, как насекомые летают по помещению с одинаковыми скоростями во все стороны. Рыбы плавают как угодно, не предпочитая какого-либо особого направления. Капли падают в сосуд под бутылью. Если же вы бросите что-нибудь вашему другу, то вы приложите одинаковое усилие, в каком бы направлении ни бросали, если расстояния одинаковы. Прыгая обеими ногами сразу, вы будете пролетать одинаковые расстояния в любом направлении. Тщательно пронаблюдав всё это (хотя вы и не сомневались, что всё будет происходить именно так, пока корабль стоит на месте), отдайте команду, чтобы корабль начал двигаться с любой скоростью, лишь бы его движение было равномерным и не подвергалось каким бы то ни было возмущениям. Ни в одном из указанных процессов вы не обнаружите ни малейшего изменения и не сможете ни по одному из них узнать, движется ли ваш корабль или стоит на месте. Прыгая, вы будете пролетать над полом те же расстояния, что раньше, и ваши прыжки в сторону кормы не окажутся длиннее прыжков в сторону носа корабля несмотря на то, что, пока вы находились в воздухе, пол под вами двигался в направлении, противоположном вашему. Для того чтобы перебросить какой-нибудь предмет вашему другу, вам не понадобится затратить большее усилие, если ваш друг стоит ближе к носу корабля, а не к корме, когда вы расположились против него. Капли будут продолжать падать в стоящий внизу сосуд, не отклоняясь к корме, хотя, пока они летят в воздухе, судно успевает передвинуться на несколько пядей. Рыбы будут плавать в воде в своём сосуде с одинаковой лёгкостью во все стороны и в равной мере хватать приманку, в какой бы угол сосуда мы её ни поместили. Наконец, бабочки и мухи будут совершать полёты равно во всех направлениях, и вы никогда не обнаружите, что они скопились у кормы, как бы устав поспевать за ходом корабля, от которого они были отделены, находясь длительное время в воздухе...
Сагредо. Хотя мне и не приходилось в моих странствиях проводить таких наблюдений, я убеждён, что всё будет происходить именно так, как вы описали. Для меня служит подтверждением то, что я, помнится, сидя в своей каюте, часто не мог понять, идёт наш корабль или стоит на месте; случалось, я думал, что он идёт в одну сторону, тогда как мы двигались в противоположную...
Принцип относительности Галилея в этой первоначальной формулировке хотя и прост, но не настолько, насколько мог бы быть. В чём состоит его простота? Физические процессы выглядят одинаково в равномерно движущемся корабле и в корабле, стоящем на месте. Равномерное относительное движение кораблей не сказывается на законах движения, описываемых в каждом из них. В каждом корабле мы видим, что изолированное тело совершает равномерное прямолинейное движение в горизонтальном направлении и подвержено равноускоренному движению в вертикальном направлении. Ядро, падающее вертикально вниз на одном корабле, при наблюдении с другого корабля описывает параболическую кривую; ядро, падающее вертикально вниз на этом втором корабле, также описывает параболическую кривую, если его наблюдать с первого корабля. Простота принципа относительности Галилея кроется во взаимной эквивалентности двух находящихся на Земле систем отсчёта и в симметрии между ними. В каком же смысле эта простота не так велика, как она могла бы быть?
Распространение рассуждений Галилея с обычного корабля на космический
Системы отсчёта в определении Галилея ещё не являются инерциальными. Чтобы получить последние, требуется лишь небольшая замена понятий — переход от морского корабля к космическому. Тогда совершенно одинаковыми становятся все направления — вверх и вниз, на восток и на запад, на север и на юг. Тело, не подвергающееся воздействию сил, не испытывает ускорения,, и его движение будет равномерным как с точки зрения одного космического» корабля, так и другого. Сегодня под галилеевым принципом относительности понимают именно это тождество выражений закона свободного движения во всех инерциальных системах отсчёта.
Как бы Галилей ни изощрял свою фантазию, он не мог в 1632 г. предложить своим читателям поместиться в космическом корабле.

Рис. 134. Майор Эдвард Уайт не испытывает никакого ускорения относительно космического корабля, в котором находится майор Джеймс Макдивитт, кроме тех моментов, когда он выбрасывает струю кислорода из двигателя, находящегося в его правой руке. В 100 милях внизу видна Калифорния. Полёт космического корабля «Джемини 3»— 7 июня 1965 г.
И всё же он смог бы описать ту большую простоту физических явлений, которая проявляется при наблюдении с таких преимущественных позиций. Бутыли, капли воды и все прочие пробные объекты сохраняют состояние покоя или движения с постоянной скоростью. Отсутствие ускорения всех соседних объектов относительно космического корабля было бы понятно Галилеям всех эпох. Кто выразил яснее, чем Галилей, совпадение величины ускорения всех соседних объектов относительно Земли? И разве смог бы удивить Галилея тот факт, что астронавт может парить рядом со своим космическим кораблём (рис. 134)?
Исследования последнего времени придали новый драматизм галилеевскому принципу универсальности свободного падения, не изменив самого принципа. Ролл, Кротков и Дикке 1) доказали равенство величины ускорения для алюминия и золота с относительной точностью 10⁻¹¹.
1) P. G. Rоll, R. Кrоtkоv, R. H. Diсke, Annals of Physics, 26, 442 (1964).
«Наделённый сознанием» космический корабль. Что управляет его сознанием?

Рис. 135. «Наделённый сознанием» космический корабль. Любое нарушение его свободного движения, например встреча с газовым облаком слева, связано с изменением скорости. Парящий в середине космического корабля маленький спутник — «сознание» — защищён от столкновения с газовым облаком. Он продолжает своё движение по прежнему. Наблюдая это «сознание» с помощью чувствительных датчиков (схематически изображённых здесь в виде контактных переключателей), космический корабль получает информацию о том, что он движется иначе, чем требует этого внутренний спутник Потревоженный переключатель приводит в действие противоположную ему корректирующую ракету как раз на тот срок, в течение которого она приводит движение корабля в согласие с его «сознанием»
Мартин Шварцшильд предложил конструкцию «наделённого сознанием» космического корабля, обеспечивающую одинаковый характер его движения как при наличии сопротивления со стороны разрежённых газов или солнечного ветра, так и при движении в абсолютном вакууме. Роль «сознания» выполняет второй корабль (спутник), парящий внутри первого, большего корабля (рис. 135). Пока космический корабль совершает свободное движение, спутник не испытывает ускорения относительно него, но когда такое ускорение возникает, вся ответственность за появление ускорения лежит на космическом корабле, и последний с помощью небольших ракет кратковременно ускоряется, делает рывок и вновь приводится в соответствие со своим внутренним «сознанием». Хотя на корабль может влиять сопротивление внешней среды, оно преодолевается мощностью ракет. Космический корабль тогда сохраняет такое движение, какое имело бы место при одновременном отсутствии как внешнего сопротивления, так и влияния двигателей.

ИСААК НЬЮТОН
Булстпорп
,
25 декабря 1642 г
. —
Кенсингтон
(
Лондон
),
20 марта 1727 г
.
«Бестрепетный ума посланец одинокий,
Скиталец вечный в странных океанах дум».
Водсворт
.
* * *
«Не знаю, каким представляет себе меня мир, но самому себе я кажусь просто ребёнком, который играет на морском берегу и забавляется, отыскивая лучше обкатанные камешки или более красивые, чем обычно, ракушки, в то время как великий океан истины лежит передо мной, ещё девственно непознанный».
Ньютон
.
* * *
«Почему я называю его волшебником? — Потому, что он видел во Вселенной и всем, что в ней есть, загадку — секрет, который можно прочесть, если старательно поразмыслить над некоторыми фактами, некоторыми таинственными ключами, которые даёт нам Бог к разгадке мира, дозволив братству посвящённых поиск некоего философического сокровища. Он верил, что найти эти ключи к истине можно отчасти в свидетельстве небес и строении элементов (что и приводит к ложной мысли, будто он был натурфилософом-экспериментатором), но отчасти и в известных писаниях и традициях, пришедших к нам от собратьев по неразрывной цепи, начиная с первого таинственного откровения в Вавилоне. Он видел во Вселенной зашифрованное послание Всемогущего, подобное той криптограмме, в которой он сообщал Лейбницу своё открытие математического анализа. И он верил, что только сама мысль и концентрация ума смогут раскрыть эту загадку для посвящённых».
Кейнс
.
Когда космический корабль со своим «сознанием» выходит в пустоту, он летит по идеальному пути без помощи ракет и чувствительных датчиков. Посмотрите, какая замечательная гармония! Внутренний спутник не видит внешнего мира. Он не осязает, не чувствует, не видит корабля, окружающего его со всех сторон. И тем не менее он добросовестно идёт в пространстве-времени тем же путём, что и корабль. Более того, его абсолютная добросовестность не зависит от того, из чего он сделан, будь то алюминий или золото. Откуда же такие «сознания», независимо от своего химического состава и конструкции вообще, черпают все данные о верном пути? Где источник, управляющий массой в её движении?
«Там же, где масса,— локально»,— отвечает Эйнштейн. «Источник действует на расстоянии»,— отвечает Ньютон.
Эйнштейн утверждает, что спутник получает информацию самым простым из возможных способом. Он реагирует на структуру пространства-времени в непосредственной близости от него самого. Он движется по прямой в своей локальной инерциальной системе отсчёта. Невозможно вообразить более простого и более прямолинейного движения.
Ньютон утверждает, что информацию о том, как ему двигаться, спутник получает на расстоянии, через «силу тяготения». Двигаться — но относительно чего? Относительно идеальной, богом данной и неизменной эвклидовой системы отсчёта, заполняющей всё пространство и охватывающей все времена! Ньютон говорит, что спутник двигался бы по идеальной прямой в этой глобальной системе отсчёта, если бы его не отклоняла Земля. Но как увидеть эту идеальную прямую? Какая жалость — не существует ничего, абсолютно ничего, что двигалось бы когда-нибудь по этой идеальной прямой. Эта прямая — плод чистейшего воображения. И тем не менее, как утверждает Ньютон, её определение просто: спутник любой природы, двигающийся с любой скоростью, отклоняется от этой идеальной прямой с одним и тем же ускорением (рис. 136).
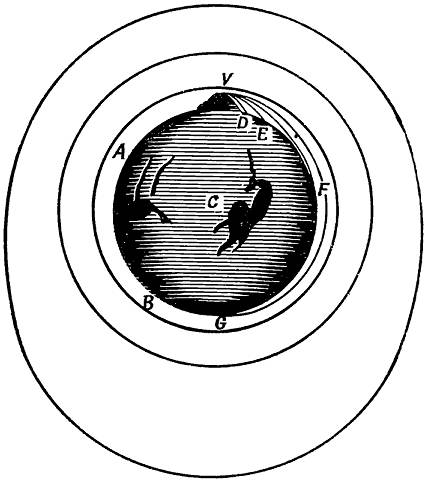
Рис. 136. В ньютоновской механике разные частицы, движущиеся с различными скоростями, отклоняются от идеально прямого пути с одним и тем же ускорением. В этом смысле не существует принципиального различия между падением снаряда и движением спутника. На этом рисунке Ньютона, опубликованном в 1686 г., пушка достаточно большой мощности, установленная на вершине горы, горизонтально выпускает свои снаряды. Самый мощный выстрел запускает тогда на орбиту спутник. Две внешние кривые изображают другие возможные орбиты спутников.
Нигде, кроме книги А. Койре [Alexander Коуré, A Documentary History of the Problem of Fall from Kepler to Newton, Transactions of the American Philosophical Society, 45, part 4 (1955)], не рассказано с таким стремлением к замечательной документальности, как Ньютон лишь постепенно пришёл к решению задачи о свободном падении. Рисунок взят из книги Ньютона, Newton’s Principia Philosophiae Naturalis Principia Mathematica. Joseph Streater, London, July 5, 1686; моттовский перевод её на английский язык, пересмотренный и отредактированный Флорианом Каджори, был опубликован в двух томах (University of California Press, Berkeley, 1962). [Перевод на русский язык см. в Собрании трудов акад. А. Н. Крылова, т. 7, Изд-во АН СССР, М.— Л., 1936; И. Ньютон, Математические начала натуральной философии.— Прим. перев.]
Физика проста, лишь если её рассматривать локально
Эйнштейн говорит: Взгляните в лицо фактам. Никакого фона в виде идеальной эвклидовой системы отсчёта, охватывающей всё пространство, не существует. И её незачем постулировать, ведь, согласно самому Ньютону, никакая частица, включая даже луч света, никогда не двигается по прямой линии в этой идеальной системе отсчёта. Зачем же говорить, что пространство-время эвклидово в больших масштабах, если ничто не подтверждает эту гипотезу непосредственно? Пытаться установить всеобъемлющую эвклидову систему отсчёта и относить к ней движение — это ложный путь в физике. Не пытайтесь описывать движение относительно удалённых объектов. физика проста, лишь если её рассматривать локально. А локально и мировая линия спутника уже не менее пряма, чем любая другая мировая линия. Забудем все эти разговоры об «отклонении» и «силе тяготения». Вот я внутри космического корабля или парю рядом с ним снаружи. Ощущаю ли я хоть что-нибудь вроде «силы тяготения»? Отнюдь нет. «Ощущает» ли такую силу космический корабль? Нет. Зачем же тогда говорить о ней? Примем же, что космический корабль и я движемся оба в некоторой области пространства-времени в отсутствие любых сил. Примем, что движение в этой области уже само по себе идеально прямолинейно.
Как можно выразить прямолинейность этого движения? Построим локальную решётку метровых стержней и часов — локальную инерциальную систему отсчёта, называемую также лоренцевой системой отсчёта (разд. 2). Как узнать, инерциальна ли эта система отсчёта? Проследите движение каждой частицы, каждого луча света, проверьте, что все они движутся прямолинейно и равномерно в этой системе. Убедившись таким образом в инерциальности системы отсчёта, заметьте, что и космический корабль движется также с постоянной скоростью и по прямой (либо покоится) относительно этой локальной инерциальной системы отсчёта. «Двигайся по прямой в своей локальной инерциальной системе отсчёта»,— какой другой приказ массе от «источника», управляющего её движением, мог бы быть проще? Должен ли спутник, прежде чем узнать, как ему двигаться, выяснить расположение Земли, Луны и Солнца? Вовсе нет. Со всех сторон окружённый чёрными стенами космического корабля, он должен лишь чувствовать локальную структуру пространства-времени там, где он находится, для того чтобы следовать верному пути.
Великолепно! И просто к тому же! Но не слишком ли прост взгляд Эйнштейна на движение? Мы начали с того, что заинтересовались движением космического корабля вокруг Земли и «в гравитации». А в конце концов мы, кажется, стали говорить только о движении космического корабля (или спутника) относительно строго локальной инерциальной системы отсчёта, о тривиально простом прямолинейном движении. Можно ли здесь усмотреть хоть следы «гравитации»? Нет. Это и есть великое открытие Эйнштейна: пространство-время всегда и всюду локально эвклидово 1). Исследуя движение одной отдельно взятой частицы, невозможно обнаружить никаких признаков существования гравитации.
1) Здесь авторы часто называют пространство-время для простоты «эвклидовым». Читателя должен иметь в виду, что речь идёт на самом деле о псевдоэвклидовости, т.е. что геометрия пространства-времени (локально) лоренцева (по терминологии авторов).— Прим. перев.
Критерием наличия гравитации является относительное движение двух частиц, но не движение одной частицы
Для адекватного измерения гравитационного воздействия необходимо наблюдать относительное ускорение двух частиц, лишь незначительно удалённых друг от друга. Насколько же удалённых? Это зависит от степени чувствительности измерительных приборов. Два массивных шарика, удалённых друг от друга по горизонтали на 25 м, будучи брошены с высоты 250 м с нулевой относительной скоростью, ударяются о землю спустя 7 сек (21⋅10 м светового времени), и расстояние между ними в этот момент будет меньше начального на 10⁻³ м (см. разд. 2 и рис. 5, расчёты в упражнении 32). Два массивных шарика, удалённых друг от друга по вертикали на 25 м, будучи брошены с высоты 250 м с нулевой относительной начальной скоростью, за те же 7 сек удалятся друг от друга на 2⋅10⁻³ м (рис. 6). Если наши измерительные приборы не способны обнаружить такие малые относительные смещения, можно считать, что массивные шарики двигались в одной и той же инерциальной системе отсчёта, где гравитация никак себя не проявляет. Более чувствительные измерительные приборы отметят «приливное воздействие» тяготения — всё ускоряющееся сокращение удалений в направлениях, параллельных поверхности Земли, и ускоряющееся увеличение вертикальных удалений. Каждый маленький массивный шарик будет продолжать двигаться по прямой в своей собственной локальной инерциальной системе отсчёта, но теперь уже, при повышенной степени точности, область применимости одной инерциальной системы отсчёта не простирается столь далеко, чтобы адекватно описывать движение другого груза. «Тяжесть» проявляет себя в расхождениях на миллиметр-другой.
Пока что гравитация рассматривалась как явление локальное. Мы даже не упоминали ни о расстоянии грузиков от центра Земли, ни об ускорении относительно этого центра! Единственным ускорением, которое принималось во внимание, было ускорение соседних частиц друг относительно друга («приливные ускорения»— то же, что относительные ускорения, описанные на стр. 17). Эти относительные ускорения удваиваются при удвоении удалений. Истинная мера «приливного воздействия» имеет поэтому характер «ускорения на единицу взаимного удаления». Пусть ускорение измеряется в метрах пути на квадрат метров светового времени, т.е. в единицах м/м² или 1/м. Тогда мерой приливного воздействия (различного в разных направлениях) будет величина размерности ускорение/удаление или 1/м². В нашем примере в горизонтальных направлениях (𝑥 и 𝑦) эта величина равна
-0,001 м
(21⋅10⁸ м)²
⋅
1
25 м
=-
9⋅10⁻²⁴
м
⁻²
,
а в вертикальном направлении (𝑧) она вдвое больше и имеет противоположный знак: +18⋅10⁻²⁴ м⁻². Это приливное воздействие мало, но это реальный и наблюдаемый эффект. Кроме того, это локально определённая величина, а Эйнштейн как раз говорил, что мы должны сконцентрировать своё внимание на локально определённых величинах, если хотим найти простое описание природы.
Эйнштейн говорит к тому же, что это «приливное воздействие» не требует для своего объяснения какой-то таинственной силы тяготения, распространяющейся через пространство-время и дополняющей структуру последнего. Напротив, «приливное воздействие» может и должно быть описано на языке геометрии самого пространства-времени как кривизна пространства-времени. Хотя Эйнштейн говорил о 4-мерном пространстве-времени, его понятие кривизны можно проиллюстрировать с помощью 2-мерной геометрии на поверхности сферы (рис. 137).

Рис. 137. Путешественники 𝐴 и 𝐵, начав двигаться параллельно друг другу и не отклоняясь ни влево, ни вправо, обнаруживают тем не менее, что приближаются друг к другу, пройдя некоторое расстояние. Истолкование 1: действует какая-то таинственная сила «тяготения». Истолкование 2: движение происходит на искривлённой поверхности.
Притча о двух путешественниках
Первый путешественник 𝐴 стоит на экваторе, готовый отправиться прямо на север. Его приятель 𝐵, стоявший плечом к плечу с 𝐴, поворачивается на 90° и направляется прямо на восток, проходит расстояние (Δ𝑥)₀=10 км по экватору, снова поворачивается на 90° и останавливается лицом к северу. После этого оба, и 𝐴, и 𝐴, начинают идти к северу и проходят по 200 км (рис. 137). Сначала их пути строго параллельны; более того, оба путешественника уверены, что каждый из них абсолютно точно выдерживает взятое им направление. Они не отклоняются ни вправо, ни влево. И тем не менее судья, посланный измерить расстояние между ними после того, как они прошли по 200 км, обнаруживает, что оно стало меньше первоначальных 10 км. Почему? Мы это прекрасно знаем: дело в том, что поверхность Земли искривлённая. Путешественники встретятся в конце концов на Северном полюсе. Обозначим широту через φ (φ=0°, cos φ=1 на экваторе, φ=90°, cos φ=0 на Северном полюсе). Тогда удаление одного путешественника от другого на некоторой промежуточной широте равно 10 км⋅cos φ. Для близких к экватору широт достаточно взять первые два члена разложения функции косинуса по степеням угла φ. Тогда мы получим для расстояния между путешественниками выражение Δ𝑥 = (Δ𝑥)₀ ⋅
⎛
⎜
⎝ 1 -
φ²
2
⎞
⎟
⎠ .
При этом угол φ определяется как отношение длины дуги 𝑠, пройденной с юга на север, к радиусу 𝑅 земного шара: φ=𝑠/𝑅. Таким образом, уменьшение первоначального расстояния (Δ𝑥)₀ определяется выражением (Δ𝑥)₀ - (Δ𝑥) = (Δ𝑥)₀ ⋅
φ²
2 = (Δ𝑥)₀ ⋅
𝑠²
2𝑅² .
Если сначала это расстояние было равно (Δ𝑥)₀=10 км, длина 𝑠=200 км, а радиус 𝑅=6371 км, то сокращение расстояния должно составить 0,005 км, или 5 м. Эта величина производит впечатление, однако не своим численным значением (что значат 5 м по сравнению с 10 000 м?), а принципиальным фактом существования такого расхождения. Ведь никакого расхождения не было бы, если бы охваченная движением путешественников область 10 км⋅200 км была плоской. Существование этого расхождения — самое непосредственное свидетельство того, что используемая при описании 2-мерной поверхности земного шара геометрия должна быть геометрией искривлённого пространства.
Измерение кривизны по изменению удаления друг от друга двух первоначально параллельных идеальных линий1)
1) Здесь большей частью под «идеальными линиями» и «мировыми линиями» авторы понимают не любые мировые линии, а экстремальные, т.е. геодезические линии. - Прим. перев.
Как же можно адекватно описать и количественно измерить эту кривизну? Как можно прийти к числу, не зависящему от длины пути и расстояния между путешественниками,— к числу, описывающему саму локальную кривизну, а не путешественников? Заметим сначала, что расстояние между 𝐴 и 𝐵 уменьшается в ускоряющемся темпе, так что целесообразно говорить именно об этом ускорении. Как можно оценить его величину? Воспользуемся тем фактом, что относительное ускорение есть скорость изменения относительной скорости, а относительная скорость в свою очередь есть скорость изменения расстояния. Поэтому начнём именно с расстояния (удаления) Δ𝑥 = (Δ𝑥)₀ - (Δ𝑥)₀
𝑠²
2𝑅² .
Пройдём дополнительно ещё небольшой путь, так что вместо 𝑠 получим 𝑠+𝑑𝑠, где величина 𝑑𝑠 весьма мала по сравнению с другими интересующими нас величинами. В результате такого дополнительного сдвига расстояние сокращается до величины (Δ𝑥)нов = (Δ𝑥)₀ - (Δ𝑥)₀
(𝑠+𝑑𝑠)²
2𝑅² .
Имея в виду, что квадратом малой величины 𝑑𝑠 можно пренебречь, получим (Δ𝑥)нов = (Δ𝑥)₀ - (Δ𝑥)₀
(𝑠²+2𝑠 𝑑𝑠)
2𝑅² .
Возьмём разность между новым и старым удалением, разделим её на дополнительный путь 𝑑𝑠 и найдём тем самым скорость изменения удаления — «скорость удаления»:
⎛
⎜
⎝
Изменение
удаления
⎞
⎟
⎠
⎛
⎜
⎝
«Скорость
удаления»
⎞
⎟
⎠ = =
⎛
⎜
⎜
⎝
Дополнительный
путь, пройденный
путешественниками
⎞
⎟
⎟
⎠ =
(Δ𝑥)нов-Δ𝑥
𝑑𝑠 =- (Δ𝑥)₀
𝑠
𝑅² . (136)
Скорость удаления равна нулю, когда 𝐴 и 𝐵 начинали свой путь от экватора (𝑠=0), и причина этого была проста — пути 𝐴 и 𝐵 были тогда в точности параллельными. Но чем дальше к северу они продвигались, т.е. чем больше становилась величина 𝑠 в уравнении (136), тем быстрее начинали приближаться друг к другу 𝐴 и 𝐵. Такое «ускорение удаления» измеряется отношением
⎛
⎜
⎝
Скорость
удаления
⎞
⎟
⎠
⎛
⎜
⎝
«Ускорение
удаления»
⎞
⎟
⎠ = =
⎛
⎜
⎜
⎝
Расстояние от места,
где скорость удаления
была равна нулю
⎞
⎟
⎟
⎠ -(Δ𝑥)₀ 𝑠 = 𝑅² =- (Δ𝑥)₀ . 𝑠 𝑅² (137)
Если бы наши путешественники начали свой путь при вдвое большем расстоянии друг от друга, чем в этом примере [(Δ𝑥)₀], то «ускорение удаления» возросло бы в два раза согласно уравнению (137). Другими словами, истинная мера кривизны поверхности земного шара определяется не самим «ускорением удаления», но «ускорением удаления на единицу первоначального удаления»:
⎛
⎜
⎝
Мера
кривизны
⎞
⎟
⎠ =
⎛
⎜
⎝
«Ускорение
удаления»
⎞
⎟
⎠
⎛
⎜
⎝
Первоначальное
удаление
⎞
⎟
⎠ = =
-(Δ)₀/𝑅²
(Δ)₀ =-
1
𝑅² .
Хотя эта величина и мала, но она доступна измерению — она равна — 1/(6,371⋅10⁶ м)² = 2,5⋅10⁻¹⁴ м⁻². Как это похоже на «приливное воздействие» (стр. 239)! Даже размерность одна и та же! Эта аналогия геометрического понятия «кривизны» и гравитационного понятия «приливного воздействия» и предвосхищает эйнштейновское геометрическое истолкование гравитации.
Приливное относительное ускорение в физике тяготения истолковывается как кривизна пространства-времени (геометрия)
Начав так добросовестно двигаться параллельно друг другу и не отклоняясь ни влево, ни вправо, наши путешественники обнаружили по нарушению постоянства расстояния между ними, что они теперьпонемногу сближаются друг с другом. Они приписывают это явление существованию некой таинственной «силы тяжести», искривляющей их пути. Они исследуют природу этой «силы тяжести». Повторяя свое путешествие на велосипедах, мотоциклах, легковых автомобилях, грузовиках, они всякий раз обнаруживают одно и то же сокращение первоначального расстояния между друг другом. Им знакомо уравнение Ньютона (Сила) = (Масса) ⋅ (Ускорение) .
По совпадению относительных ускорений для всех видов транспорта они заключают, что сила, обусловленная «тяготением», должна быть прямо пропорциональна массе экипажа.
Но другие исследователи включаются в обсуждение, заранее предупредив, что они проявят гораздо больше осторожности. Они говорят, что гравитационную силу следует записать как произведение:
⎛
⎜
⎝
Сила
тяжести
⎞
⎟
⎠ =
⎛
⎜
⎜
⎜
⎝
Гравитационная
масса объекта
подвергающегося
воздействию
⎞
⎟
⎟
⎟
⎠ ⋅
⎛
⎜
⎜
⎝
Напряженность
гравитационного
поля
⎞
⎟
⎟
⎠ .
Они подставляют эту силу в ньютоновское уравнение движения, всячески подчеркивая, что фигурирующая там масса — это «инертная масса» подвергающегося воздействию объекта. И они приходят к уравнению
⎛
⎜
⎜
⎝
Инертная масса объекта
подвергающегося
воздействию
⎞
⎟
⎟
⎠ ⋅
⎛
⎜
⎝
Ускорение
⎞
⎟
⎠ = =
⎛
⎜
⎜
⎜
⎝
Гравитационная
масса объекта
подвергающегося
воздействию
⎞
⎟
⎟
⎟
⎠ ⋅
⎛
⎜
⎜
⎝
Напряженность
гравитационного
поля
⎞
⎟
⎟
⎠
или (Ускорение) =
(Гравитационная масса)
(Инертная масса) × ×
⎛
⎜
⎝
Напряжённость гравитационного
поля
⎞
⎟
⎠ .
Эти исследователи говорят: «Посмотрите, вы получили одинаковое ускорение для всякого вида транспорта, с которым работали. Это означает, что отношение гравитационной и инертной масс одинаково для всех объектов. Вы сделали великое открытие, касающееся массы».
Всё это время с высоты на них глядел космический путешественник. Он видел все эти автопробеги, следил за множеством измерений сокращения расстояния и слушал по своей системе дальней связи все солидные дискуссии о «гравитации». Он улыбался. Он ведь знал, что речь-то шла не о «гравитации», а о геометрии искривлённого пространства, и все разговоры о равенстве «гравитационной массы» и «инертной массы» — сплошной туман. Ничего, кроме понятия кривизны, не требуется для описания всё увеличивающейся скорости, с которой приближаются друг к другу 𝐴 и 𝐵.
Если Землю окружить цепочкой пробных частиц, то их ускорение в направлении Земли следует понимать как интегральный эффект относительных ускорений всех соседних частиц по направлению друг к другу
Эйнштейн тоже улыбался. Он сказал нам, что ничего, кроме кривизны пространства-времени, не требуется для описания того изменения на один-два миллиметра расстояния между двумя грузиками, расположенными первоначально вокруг Земли с интервалом 25 м и предоставленных самим себе с нулевыми относительными скоростями. Более того, эта кривизна полностью характеризует гравитацию. «Что за нелепое утверждение! — такова бывает первая реакция.— Как могут ничтожные и медленные изменения расстояний между соседними шариками привести к пониманию тех громадных скоростей, с которыми падающие массы ударяются о Землю?» Ответ прост: глобальная структура пространства-времени складывается из множества пригнанных друг к другу локальных инерциальных систем отсчёта. Можно считать, что в начале каждой из этих локальных лоренцевых систем находится по одному из массивных шариков. При одновременном сближении всех соседних грузиков («кривизна») сжимается и общая структура пространства-времени — она стягивается ближе к Земле (рис. 138). Так суммарный эффект множества локальных проявлений кривизны принимает вид гравитации, возбуждаемой в больших масштабах Землёй как целым.

Рис. 138. Локальные кривизны складываются и дают эффект тяготения на больших протяжениях. В инерциальной системе отсчёта, связанной с грузом 𝐴, другой груз 𝐵 за срок 7 сек сокращает первоначальное расстояние до 𝐴 (25 м) на 1 мм (локальная кривизна пространства вблизи 𝐴𝐵). Аналогичное сокращение происходит во всех соседних парах грузов. В результате вся образуемая ими окружность стягивается за 7 сек в отношении 1 мм/25 м = 1/25 000 по сравнению с её первоначальными размерами (относительное изменение длины). Расстояние до центра Земли уменьшается с той же быстротой, т.е. на величину
1
25 000 ⋅ 6 371 000 м = 250 м .
Этот, очевидно, крупномасштабный эффект обусловлен, по толкованию Эйнштейна, сложением множества эффектов мелкого масштаба — изменений локальных размеров, связанных с кривизной пространства (невозможность для 𝐵 оставаться в состоянии покоя с точки зрения инерциальной системы отсчёта, связанной с 𝐵).
Эйнштейн: Все качества гравитации происходят исключительно из локальных эффектов, из локальной кривизны пространства-времени
Короче говоря, для описания движения в любой локальной инерциальной системе отсчёта используется лоренцева геометрия («частная теория относительности»). Относительно такой локальной инерциальной системы отсчёта любая близкая к ней электрически нейтральная пробная частица движется по прямой и с постоянной скоростью. Движение немного более удалённых частиц наблюдается происходящим с изменяющимися скоростями или направлениями их мировых линий в пространстве-времени. Такие изменения описываются как «приливные воздействия тяготения». Их понимают как проявления локальной кривизны пространства-времени. С точки зрения изучающего локальную физику, гравитация вовсе не проявляет себя в движении одной пробной частицы, но лишь в изменении взаимного удаления двух или более близких друг к другу пробных частиц. Однако эти изменения локального значения складываются в эффект глобальной структуры пространства-времени, обыденные проявления которой истолковывают как «гравитацию».

АЛЬБЕРТ ЭЙНШТЕЙН
Ульм
,
Германия
,
14 марта 1879 г
. —
Принстон
,
США
,
18 апреля 1965 г
.
«Ньютон сам лучше знал слабые места своих умственных построений, чем поколения, наследовавшие ему. Это восхищало меня всегда».
* * *
«Только гений Римана, одинокий и непостижимый, уже в середине прошлого века достиг нового понимания пространства, и это была концепция пространства, лишённого жёсткости, способность которого участвовать в физических явлениях была признана возможной».
* * *
«Все эти попытки происходили из веры в то, что сущее должно обладать вполне гармоничной структурой. Сегодня мы имеем менее, чем когда-либо, оснований позволить увести себя от этой замечательной веры» 1).
1) Эти три цитаты взяты из книги Albert Einstein, Essays in Science, Philosophical Library, New York, 1934.
Напротив, Ньютон предполагал, что существует одна идеальная всеобщая система отсчёта:
«Абсолютное пространство в силу своей природы, безотносительно к чему-либо внешнему, остаётся всегда одинаковым и неподвижным».
«Абсолютное, истинное или математическое время само по себе и в силу своей внутренней природы течёт одинаково, безотносительно к чему-либо внешнему...» 1).
1) Isaac Nеwtоn, Mathematical Principles of Natural Philosophy and His System of the World, Vol. 2, translated by Andrew Motte in 1729, revised and annotated by Florian Cajori, University of California Press, Berkeley, 1947, p. 6.
Ньютон считает, что массивный шарик или космический корабль действительно ускорены относительно этой идеальной системы отсчёта. Производящая ускорение «сила» таинственным образом действует через пространство и возбуждается удалёнными объектами. С точки зрения Ньютона, тот факт, что человек, помещённый в космический корабль, не замечает ни ускорения, ни самой силы, является просто реализующейся в природе случайностью. Эту случайность можно истолковать как «нечаянное» равенство «гравитационной массы» и «инертной массы», либо как-нибудь иначе.
Мужество и трезвость взглядов Ньютона: делать доступное; оставлять попытки более глубокого понимания будущим поколениям
В беседах с одним из авторов этой книги в давно прошедшие годы Эйнштейн выражал своё глубочайшее уважение к Ньютону и, в частности, восхищение его мужеством. Он подчёркивал, что Ньютон даже лучше, чем его критики в XVII столетии, понимал трудности, связанные с идеями абсолютного пространства и абсолютного времени. Однако постулирование этих понятий было в то время единственным практически осуществимым способом продвинуться в описании движения. В результате Ньютон разделил проблему движения на две части: 1) пространство и время и их смысл — представления, вызывавшие затруднения, разъяснить которые было суждено лишь через 230 лет, и 2) законы ускорения относительно такого идеализированного пространства-времени — те законы, которые и дал Ньютон миру.
Nature and Nature’s laws lay hid in night:
God said, Let Newton be! and all was light.
Pope
[Природа и её Закон — весь мир во мрак одет. Да будет Ньютон! — Бог сказал, и вот повсюду свет.]
Эйнштейновское предвидение: физический мир описывается чисто геометрически
Мы находим теперь, что эйнштейновский взгляд на природу пространства и времени приводит к новому пониманию гравитации как чисто геометрического явления. Эйнштейн умер, завещая миру своё ещё не подтверждённое предвидение, что не только гравитация, но и весь физический мир вообще может быть полностью описан на языке одной лишь геометрии. Может быть, стоило бы в заключительном диалоге бросить общий взгляд на физику и задаться вопросом: какие её разделы допускают простое описание на языке геометрии пространства-времени, а какие всё ещё далеки от подобного понимания?
Таблица 15.
Схема подхода к физике с точки зрения пространства-времени
❔
Как движется свободная электрически нейтральная частица?
✔
Такая частица следует наиболее прямой возможной линии в пространстве-времени, на языке геометрии — геодезической линии
❔
Сколько компонент у 4-вектора энергии-импульса этой частицы?
✔
Четыре
❔
Являются ли все компоненты независимыми?
✔
Нет, они связаны между собой соотношением 𝐸² - (𝑝 𝑥)² - (𝑝 𝑦)² - (𝑝 𝑧)² = 𝑚²
❔
Как электромагнитное силовое поле влияет на движение электрически заряженной частицы?
✔
В любой данной точке действительная мировая линия такой частицы систематически отклоняется («искривляется») от той идеальной геодезической мировой линии, которая проходит через эту точку в том же направлении. На языке обыденной физики это значит, что заряженная частица испытывает ускорение относительно идеальной нейтральной пробной частицы
❔
Как можно количественно измерить напряжённость электромагнитного поля в данной области пространства-времени?
✔
По кривизне мировой линии любой заряженной частицы, проходящей через эту область во временноподобном направлении относительно идеальной геодезической, проходящей через ту же точку в том же направлении. Можно во всех деталях измерить напряжённость электромагнитного поля — как его направленность, так и абсолютную величину в данном месте (локально), измеряя кривизны трёх мировых линий заряженных частиц, проходящих через данную область
❔
Чему равно число независимых компонент напряжённости электромагнитного поля в точке?
✔
Шести. Для наблюдателя в данной инерциальной системе отсчёта электромагнитное поле разлагается на отдельные электрическое и магнитное поля (напряжённости каждого из которых имеют по три компоненты). Если в данной инерциальной системе отсчёта заряженная частица мгновенно покоится, её ускорение определяется одним лишь электрическим полем (измеренным в этой системе). Если же частица движется, то магнитное поле даёт вклад в её ускорение («магнитная сила»)
❔
Как влияет гравитационное поле на движение одной частицы? (Речь идёт о корректно определённом гравитационном поле, т.е. взятом в локальной инерциальной системе отсчёта, в отличие от обыденного или кажущегося гравитационного поля, ощущаемого, например, на поверхности Земли, не являющейся инерциальной системой отсчёта и не подверженной свободному падению)
✔
Никак, потому что при этом отсчёт ведётся от мировой линии самой частицы! (Или от мировой линии идеальной пробной частицы, пробегающей по тому же пути в пространстве-времени)
❔
Как влияет гравитационное поле на относительное движение двух пробных частиц? (Для простоты примите, что их мировые линии первоначально параллельны и разделены малым, но отличным от нуля интервалом). Это влияние лучше описывать выражением «приливное поле», чем неопределённым выражением «гравитационное поле»—«приливное» потому, что относительное ускорение частиц воды на противоположных сторонах земного шара, вызываемое Луной, приводит к явлению прилива
✔
Взаимное удаление двух пробных частиц систематически изменяется со временем, начиная с момента первоначальной параллельности мировых линий («девиация геодезических»)
❔
Чем оправдано большее внимание к приливной силе, влияние которой практически пренебрежимо мало (например, на спутник или на систему спутников), а не к обыденному или кажущемуся гравитационному полю, удерживающему спутники на орбитах?
✔
Дело в том, что, как выяснилось, проще всего физика поддаётся локальному анализу, т.е. анализу относительно локальной инерциальной системы отсчёта. Локально, для человека на спутнике, кажущееся гравитационное поле отсутствует. Этого человека интересует лишь расстояние до соседних спутников его системы. Это расстояние постепенно изменяется под действием приливных сил в этой окрестности (сил, вызванных здесь Землёй и, в меньшей степени, Луной и Солнцем)
❔
Как можно количественно измерить приливное поле в данной окрестности в пространстве-времени, т.е., говоря на языке геометрии искривлённого пространства Римана (1854) или общей теории относительности Эйнштейна (1916), измерить в этой окрестности «кривизну пространства-времени»?
✔
По девиации геодезических для двух мировых линий. Приливное поле, или кривизна, может быть всесторонне измерено как в отношении своих свойств направленности, так и по абсолютной величине в данной области путём измерения девиаций геодезических для пар мировых линий соответствующего числа пробных частиц, находящихся в этой области
❔
К чему все эти разговоры о «кривизне пространства-времени»? Разве недостаточно просто регистрировать фактические данные о приливных воздействиях, воздерживаясь от этой геометрической интерпретации?
✔
Почему в обыденной жизни всегда было бы нужно давать геометрическое истолкование угла в 90° с помощью треугольника, стороны которого относятся как 3:4:5? Почему не проще собрать попросту миллионы разрозненных фактов о всевозможных измерениях? Ответ (как на эти вопросы, так и на исходные вопросы слева): дело в том, что геометрическая интерпретация более экономична и глубока при анализе фактов, а в случае гравитации мы имеем простое истолкование наблюдательных данных на языке геометрии искривлённого пространства-времени. При этом уже не требуется предполагать, что мир состоит из пространства-времени и некоторой таинственной магической «физической» силы тяготения, чуждой пространству-времени и добавляемой к нему
❔
Допустим, что можно оправдать геометрическое описание тяготения. Но как тогда быть с электромагнетизмом? Ведь в конце концов это привычное нам поле имеет другой характер, чем гравитационное. Кроме того, не исчерпываются ли возможности геометрии описанием тяготения? Не следует ли теперь истолковывать электромагнетизм как нечто негеометрическое, т.е. как нечто чуждое, таинственное и «физическое», добавляемое к пространству-времени? И если одно поле (электромагнитное) описывается как негеометрическое, то почему такое внимание уделяется описанию физики тяготения на языке чистой геометрии?
✔
Для многих обыденных целей удобно мыслить электромагнетизм как некое чуждое и «физическое» поле, претерпевающее свою специфическую динамическую эволюцию на фоне идеального плоского пространства-времени. Даже в обыденных исследованиях гравитационных эффектов (не очень массивные тела, испытывающие слабые ускорения) часто упрощённо представляют гравитацию как «физическое» поле, действующее через плоское фоновое пространство-время и погружённое в него. Но, поскольку речь идёт о принципиальной стороне дела, следует помнить, что как электромагнитное, так и гравитационное поле (лучше говорить: приливное поле) можно понимать как проявления кривизны пространства-времени. При таком описании природы термин «приливное поле» в некоторой точке — всего лишь синоним кривизны пространства-времени в этой точке. Электромагнитное поле в некоторой точке связано с изменением кривизны в окрестностях этой точки
❔
На исследовании каких явлений мы концентрировали пока своё внимание?
✔
На действии поля на частицу (или на движение любого локализованного сгустка массы-энергии, например облака излучения)
❔
Какой другой аспект необходимо учесть для полного охвата физики поля?
✔
Действие частицы (или любого локализованного сгустка массы-энергии) на поле
❔
Существуют ли альтернативные и в основном эквивалентные способы описания такого действия частицы на поле?
✔
Да. Описание 1: действие частицы на поле означает изменение ею структуры пространства-времени, но лишь в её непосредственной окрестности; это воздействие распространяется от точки к точке в окружающем пространстве-времени. Описание 2: игнорируя детали этого процесса распространения, необходимо учитывать лишь то воздействие, которое производится на расстоянии частицей при резких последовательных изменениях её скорости (точка зрения «действия на расстоянии», дальнодействие)
❔
Какие эффекты производит в данной системе отсчёта частица, покоящаяся в этой системе?
✔
Электрическое поле, пропорциональное её заряду и обратно пропорциональное квадрату расстояния; магнитное поле отсутствует; приливное поле, пропорциональное массе и обратно пропорциональное кубу расстояния, и больше никаких других компонент приливного поля
❔
Какие эффекты производит в данной системе отсчёта частица, равномерно движущаяся этой системе?
✔
Кроме электрического, ещё и магнитное поле; не только приливное поле, свойственное покоящейся в частице, но и дополнительные приливные поля
❔
Какие эффекты производит мгновенно ускоренная частица на расстоянии, превышающем время (в метрах), в течение которого имело место ускорение?
✔
Электрическое и магнитное поля, пропорциональные заряду частицы и eё ускорению и обратно пропорциональные первой степени расстояния («электромагнитные волны»), распространяющиеся на это расстояние со стандартной скоростью (свет!). Приливные поля, по величине пропорциональные массе и ускорению частицы и обратно пропорциональные первой степени расстояния от неё. Распространяются на это расстояние со скоростью света («гравитационные волны»; ещё не наблюдались; приёмные устройства конструируются)
❔
Знаем ли мы внутреннюю структуру элементарных частиц, производящих эти электромагнитные и гравитационные эффекты на расстоянии?
✔
Адекватное описание внутренней структуры элементарных частиц (электронов, мезонов, протонов и пр.) отсутствует. Мы не знаем его, несмотря на: 1) построение ускорителей чрезвычайно высокой энергии и связанное с этим постоянное накопление громадного числа интересных количественных данных о массах и превращениях «элементарных» частиц и 2) происходящие время от времени открытия удивительных и прекрасных закономерностей, связывающих эти данные
❔
Какой смысл может иметь обсуждение движения и взаимодействий элементарных частиц, если мы не знаем их структуры?
✔
Размеры этих частиц очень малы по сравнению с расстояниями между частицами в атоме (сопоставьте их с расстоянием от радиопередатчика до радиоприёмника!) Поэтому детали внутреннего строения в значительной степени несущественны, так же как детали внутреннего строения Земли в значительной степени несущественны для определения той силы, с которой она притягивает к себе Луну
❔
Как мы, при всём нашем незнании строения элементарных частиц, подходим к ним в настоящее время?
✔
Их рассматривают как странные и неоднородные объекты, погружённые в пространство-время
❔
Но как же можно придерживаться идеалов чисто геометрического описания природы, если частицы — это чуждые объекты, погружённые в пространство-время, а не объекты, слагающиеся из пространства-времени?
✔
Лучшие из современных представлений не утверждают, что частицы не построены из пространства-времени. Скорее признаётся, что наши познания о них недостаточны даже для того, чтобы разумно обсуждать этот вопрос. На данном этапе разумно рассматривать частицы, как если бы они были чуждыми объектами, чтобы иметь возможность разбираться в структуре мира и подходить к частицам с практических, рабочих позиций. Такая рабочая процедура не исключает когда-то в будущем возможность описать частицы на языке геометрии, как сейчас описывают «глаз» тайфуна на языке аэродинамики, а воронку водоворота — на языке гидродинамики
❔
Необходимо ли для объяснения мира повседневной физики привлекать в дополнение к частицам (строение которых может быть, а может и не быть геометрическим) и к электромагнитным и гравитационным полям (о которых мы знаем, как подходить к ним с геометрических позиций) ещё и какие-либо другие фундаментальные понятия?
✔
Только одно понятие — квантовый принцип, центральный для всей физики
❔
Можно ли привести простой пример проблемы, решаемой этим квантовым принципом?
✔
Задача о том, как свободная частица (находящаяся в существенно плоской области пространства-времени) движется из точки 𝐴 в точку 𝐵 по прямой линии: 1) Как эта частица «пробует» приемлемые альтернативные пути, которые она могла бы избрать. 2) Расплывание «прямой» линии, ведущей из 𝐴 в 𝐵 в результате этого процесса «распробования», происходящего непрерывно. 3) Как яснее определить и измерить действительное физическое распространение этого рода по так называемому «классическому» или идеальному пути из 𝐴 в 𝐵
❔
Сдерживают ли «квантовые силы» атом как единое целое? Связывают ли они атомы друг с другом (химия!)? Являются ли они причиной электропроводности и упругости твёрдых тел?
✔
Нет! Такой вещи, как «квантовая сила», не существует. Единственными силами, обусловливающими структуру атомов, молекул и твёрдых тел, являются электрические силы. Для того чтобы объяснить весь мир повседневной физики (за исключением тяготения), требуется лишь существование: 1) этих сил, 2) элементарных частиц и 3) квантового принципа, управляющего движением частиц под действием этих сил
❔
Имеется ли другой пример, иллюстрирующий объяснение фундаментальных процессов квантовой физикой?
✔
Электрон движется по круговой орбите вокруг протона, который тяжелее его в 1836 раз, и удерживается на этой орбите электрическим притяжением со стороны протона. 1) Почему относительная величина расплывания орбиты мала, если эта орбита велика? 2) Почему способность частицы «распробовать» пространство вокруг орбиты делает физически невозможным существование любых орбит, кроме тех, на протяжении которых укладывается целое число длин волн («квантовое число», «квантовое условие», см. упражнение 101)? 3) Насколько велика относительная размытость или неопределённость положения в пространстве для орбиты с малым квантовым числом? 4) Величина специфической энергии, или «квантовый уровень», связанный с этими «квантовыми состояниями движения». 5) Величина энергии, выделяемая при «переходах» электрона с одного такого уровня на другой
❔
Если вся физика подчиняется квантовому принципу (точная формулировка которого здесь не приводится), то какой смысл при каких бы то ни было обстоятельствах может иметь использование языка «классической» (неквантовой) физики для описания движения? Как можно рассматривать «положение в пространстве» и его изменение от одного «момента» к другому вдоль «мировой линии» частицы, если неизбежно существует квантовое размазывание или неопределённость того пути, которым следует частица в пространстве-времени?
✔
Чем больше орбита, тем меньше относительная величина размазывания («большей» названа орбита с большим «квантовым числом»). И вообще хотя предсказания квантовой физики сильно отличаются по своему характеру («вероятности», «квантовые состояния») от предсказаний классической физики («когда» и «где»), тем не менее они по своим практическим следствиям становятся всё ближе и ближе к предсказаниям классической механики в предельном случае больших квантовых чисел (принцип соответствия Нильса Бора между классической и квантовой физикой)
❔
Если ограничиться рассмотрением тех условий, при которых квантовые неопределённости координат практически несущественны и применимы классические (неквантовые) представления («предельный случай принципа соответствия»), на самом ли деле много в этих условиях физических явлений, которые мы можем объяснить?
✔
Громадное количество! Механика точек и твёрдых тел, небесная механика и феноменологическая гравитация, динамика упругих сред, аэро- и гидродинамика с теорией звука, термодинамика, теория электричества и магнетизма, геометрическая и физическая оптика
❔
Какие разделы физики можно сверх этого успешно проанализировать, приняв на вооружение квантовый принцип, но ограничиваясь электромагнитными и гравитационными силами и теми случаями, когда расстояния между частицами велики по сравнению с размерами этих частиц (отказ от учёта идей физики элементарных частиц)?
✔
Вся атомная физика: энергетические уровни всех атомов; их размеры; испускание света при переходах атомных электронов из одного состояния в другое; эффекты бомбардировки атомов светом или частицами. Все основные закономерности химии: столкновения между атомами; сила связи атомов в молекулах; форма и размеры молекул; основные и возбуждённые состояния молекул; сопротивление молекул деформациям; механизм химических реакций; механизмы аккумуляции и переноса энергии молекулами. Все основные закономерности физики твёрдого тела: кристаллические структуры; теплота образования; упругость; тепло- и электропроводность; сверхпроводимость; коэффициент поглощения света; магнитные свойства; дислокации и прочность материалов; экситоны, фононы, плазмоны, магноны и прочие агенты, аккумулирующие и переносящие энергию на микроскопическом уровне в твёрдых телах. Статистическая механика теплового равновесия для твёрдых тел, жидкостей, газов и их систем; их фазы. Сверхтекучесть. Скорости протекания реакций
❔
Какая проблема из всего множества вопросов физики твёрдого тела нуждается в дальнейшей экспериментальной и теоретической разработке?
✔
Атом или молекула, входящие в состав твёрдого тела, переведены в возбуждённое энергетическое состояние путём поглощения пришедшего извне света. Каков механизм, с помощью которого происходит разрядка этой концентрации энергии, когда последняя распространяется по твёрдому телу в виде теплоты или колебаний решётки («фононов»)?
❔
Можно ли до биться, успехов в исследовании систем, расстояние между элементарными частицами в которых не очень велико по сравнению с размерами частиц?
✔
Да, в ядерной физике. В ядре расстояния между элементарными частицами составляют величины порядка 10⁻¹³ см, тогда как установлено, что эффективные размеры нейтрона и протона имеют порядок 10⁻¹⁴ см. Мы располагаем богатейшими данными об энергетических уровнях ядер, о размерах ядер, о несферичности атомных ядер, о радиоактивности ядер, о делении ядер и о ядерных превращениях, вызываемых их бомбардировкой. Многие стороны этих эффектов удаётся точно предсказывать, несмотря на тот факт, что неизвестна природа основных сил, действующих в ядре (это ни электрические, ни гравитационные, но некие «ядерные силы» короткого радиуса действия, убывающие с расстоянием много быстрее, чем обратный квадрат). Другие экспериментальные факты менее понятны или вообще не интерпретированы
❔
Какая из множества проблем ядерной физики представляется созревшей для дальнейшего экспериментального и теоретического исследования в настоящее время?
✔
Механизм деления ядер и, в частности, механизм того, как при делении ядер урана или других тяжёлых ядер иногда образуются наряду с двумя много более массивными осколками также ядра гелия или тяжёлого водорода
❔
Существует ли простой критерий, позволяющий в конкретных условиях указать, какое из взаимодействий является более важным: 1) внутренние взаимодействия, обусловливающие структуру элементарных частиц; 2) ядерное; 3) электромагнитное; 4) гравитационное взаимодействие?
✔
Да. Критерий — количество энергии, связанное с каждым из этих взаимодействий
❔
Каковы сравнительные значения этих четырёх видов энергии для железного шара радиусом 1 м?
✔
1) Внутренняя энергия элементарных частиц (определяемая массами покоя входящих в шар нейтронов и протонов): 3,3⋅10⁴ кг. 2) Ядерная энергия (определяемая изменением массы при объединении нейтронов и протонов и образовании 𝙵𝚎⁵⁶): 3,1⋅10² кг. 3) Электрическая энергия (определяемая энергией связи электронов в атомах железа и энергией связи атомов железа в кристаллической решётке металлического железа; вся эта энергия даётся в переводе в единицы массы): около 2⋅10⁻² кг. 4) Гравитационная энергия (энергия, требующаяся для удаления атомов железа на бесконечность против сил тяготения, переведённая в единицы массы): около 2⋅10⁻¹⁹ кг
❔
Какой из этих четырёх видов энергии возрастает быстрее всего при увеличении числа частиц?
✔
Гравитационная энергия, ибо каждая частица гравитационно взаимодействует с любой другой частицей
❔
Существуют ли условия, при которых соотношение между этими четырьмя видами энергии радикально изменяются?
✔
Да, в достаточно массивной звезде (если звезда холодная, то при массе, примерно равной массе Солнца, т.е. 2⋅10³⁰ кг; если горячая, то при большей массе, когда плотность оказывается ниже и гравитационные силы должны действовать на больших расстояниях)
❔
Могут ли силы гравитационного притяжения в достаточно массивном или достаточно плотном (или и массивном и плотном одновременно) астрономическом объекте возобладать над силами, обусловливающими внутреннюю структуру элементарных частиц, и вызвать исчезновение этих частиц?
✔
Мы не знаем ответа на этот вопрос, хотя он и возбуждает большой интерес и в настоящее время интенсивно исследуется как «гравитационный коллапс». Внимание было привлечено к этому гипотетическому механизму в январе 1963 г., когда был открыт так называемый «квазизвёздный объект» — часть некой галактики, отстоящей от нас на расстоянии 2⋅10⁹ световых лет,— выделяющей за короткий по астрономическим масштабам промежуток времени в 10⁶ лет или менее энергию (около 10⁵⁴ дж), эквивалентную той, которая выделилась бы при полном превращении в энергию массы около 10⁷ солнц. Сейчас открыты и продолжают открываться многочисленные другие квазизвёздные источники (это название теперь сокращённо произносится как «квазар»)
❔
Существуют ли какие-либо другие условия, при которых можно ожидать эффектов, аналогичных гравитационному коллапсу, с исчезновением элементарных частиц, или обратных процессов, при которых давление падает и происходит расширение?
✔
Эти условия существовали на ранних этапах расширения Вселенной и должны существовать на поздних этапах, когда Вселенная будет снова сжиматься
❔
Что подтверждает представления о расширении Вселенной?
✔
Разбегание галактик: галактики, находящиеся на вдвое большем расстоянии, убегают вдвое быстрее и т.д., как если бы они вылетели из общего центра с разными скоростями около 14⋅10⁹ лет назад
❔
Какая сила доминирует в больших масштабах в динамике Вселенной?
✔
Гравитация (кривизна пространства-времени)
4. Решения упражнений
РЕШЕНИЯ УПРАЖНЕНИЙ К ГЛАВЕ 1
1. Пространство и время — подробный пример
Решение дано в тексте.
2. Практическая синхронизация часов
Установите стрелки часов в положение, соответствующее √6²+8²+0²=10 м светового времени. Нажмите кнопку пуска часов в момент прихода опорного сигнала. ▲
3. Соотношения между событиями
Ответы на вопросы а), б) и в) согласно рис. 34. Для событий 𝐴 и 𝐵: а) временноподобный интервал; б) 4 м собственного времени; в) да; для событий 𝐴 и 𝐶: а) пространственноподобный интервал; б) 4 м собственного расстояния; в) нет; для событий 𝐶 и 𝐵: а) светоподобный интервал; б) нуль; в) да, так как эти события можно связать одним световым лучом. ▲
4. Одновременность
Слово «одновременность» пригодно для описания соотношения между событием «𝐴 сталкивается с 𝐵» и событием «𝐶 сталкивается с 𝐷» лишь в конкретной инерциальной системе отсчёта. Чтобы охарактеризовать соотношение между этими двумя событиями независимо от какого бы то ни было выбора системы отсчёта, следует сказать: событие «𝐴 сталкивается с 𝐵» отделено от события «𝐶 сталкивается с 𝐷» пространственноподобным интервалом в миллион миль. ▲
5. Временно'й порядок событий
Случай светоподобного интервала. Если световой луч может непосредственно пройти от события 𝐺 к событию 𝐻, то эти события связаны между собой светоподобным интервалом,— это чисто физическое утверждение, никак не связанное с выбором инерциальной системы отсчёта. Но это значит, что событие 𝐺 предшествует 𝐻 в любой инерциальной системе, что и требовалось доказать.
Случай временноподобного интервала. Событие 𝐻 расположено внутри светового конуса будущего с вершиной в событии 𝐺 в некоторой инерциальной системе отсчёта. Поэтому из 𝐺 в 𝐻 может попасть частица, движущаяся равномерно со скоростью, меньшей скорости света с точки зрения данной системы отсчёта. Но тот факт, что частица может непосредственно перейти из 𝐺 в 𝐻, никак не связан с конкретным выбором инерциальной системы. Поэтому событие 𝐺 предшествует событию 𝐻 в любой инерциальной системе, что и требовалось доказать.
Случай пространственноподобного интервала. Эта возможность исключается; интервал между двумя рассматриваемыми здесь событиями может быть лишь светоподобным или временноподобным, и не иначе. Поэтому теперь требуется доказать, что два события, разделённые пространственноподобным интервалом, не имеют универсального порядка во времени,— такой порядок во времени существует лишь для пар событий, интервалы между которыми являются светоподобными или временноподобными. Рассмотрим для примера в лабораторной системе отсчёта два события, разности координат которых равны 𝑥𝐻-𝑥𝐺=900 м и 𝑡𝐻-𝑡𝐺=540 м. Тогда пространственноподобный интервал между ними составляет
⎛
⎝
(
900
м
)
²
-
(
540
м
)
²
⎞½
⎠
=
720
м
Если рассматривать эти же события в системе отсчёта, быстро движущейся вправо, то они окажутся ближе друг к другу во времени, но величина интервала останется без изменения. В какой бы системе отсчёта ни проводились измерения, разности координат будут оставаться на гиперболе
(𝑥
𝐻
-𝑥
𝐺
)²
-
(𝑡
𝐻
-𝑡
𝐺
)²
=
(720
м
)²
(рис. 139). Когда новая система отсчёта достигнет достаточно большой скорости относительно лабораторной системы (такова, например, система 𝐽), то событие 𝐻 станет наблюдаться до события 𝐺. Такая ситуация имеет место для любой пары событий, разделённых пространственноподобным интервалом, и её можно описать с помощью гиперболы, подобной гиперболе на рис. 139. Короче говоря, если события 𝐺 и 𝐻 разделены пространственноподобным интервалом, то при выборе системы наблюдателя, движущейся достаточно быстро вправо или влево относительно лабораторной системы отсчёта, можно «сделать» событие 𝐺 сколь угодно более ранним или сколь угодно более поздним по сравнению с событием 𝐻.

Рис. 139. Иллюстрация того, как выбор системы отсчёта сказывается на величине разностей пространственных и временных координат двух событий 𝐺 и 𝐻. Через 𝐿 обозначена лабораторная система отсчёта; система 𝐴 «медленно» движется вправо относительно лабораторной системы отсчёта; последовательность 𝐵, 𝐶, 𝐷, … изображает системы отсчёта, движущиеся со всё большими и большими скоростями вправо относительно лабораторной системы. Система 𝐽 такая, в которой разности координат вновь оказываютсяцелочисленными. ▲
6. Расширяющаяся Вселенная
а) Средний чертёж на рис. 35 даёт для собственного времени, прошедшего между двумя вспышками, выражение
Δ
τ
=
√
(
Δ
𝑡)²-(
Δ
𝑥)²
=
√
(
Δ
𝑡)²-(β
Δ
𝑡)²
=
Δ
𝑡
√
1-β²
.
Из правого чертежа на том же рисунке следует выражение для времени, прошедшего между приёмом двух последовательных сигналов:
Δ
𝑡
приём
=
Δ
𝑡
+
β
Δ
𝑡
=
Δ
𝑡
(1+β)
.
Исключим из первого уравнения Δ𝑡 с помощью второго и найдём скорость удаления осколков β:
β
=
(Δ𝑡приём)²-(Δτ)²
(Δ𝑡приём)²+(Δτ)²
.
Расстояние между осколком, на котором летит наблюдатель, и другим осколком бомбы, который он наблюдает, равняется времени, прошедшему с момента взрыва, умноженному на скорость удаления этих осколков друг от друга.
б) Пользуясь предыдущей формулой, определите скорость удаления звезды. Приравняйте Δτ собственному периоду световой волны, а Δ𝑡приём — наблюдаемому периоду для света, приходящего от удалённого источника. Если Вселенная когда-то (𝑡=0) взорвалась, а её первоначальный объём был ничтожно мал, то теперь, в более поздний момент времени 𝑇, расстояние до каждой звезды (или галактики) будет равно β𝑇 (для вдвое быстрее удаляющейся галактики и расстояние будет вдвое большим). Расстояние же до галактики в тот более ранний момент, когда она испустила принятый нами теперь свет, было равно β𝑇/(1+β). Коэффициент красного смещения Δ𝑡приём/Δτ превосходит 3 для самых быстро удаляющихся известных нам сейчас источников (так называемых квазаров — квазизвёздных объектов), однако расстояния до них неизвестны. В настоящее время мы умеем определять независимыми способами расстояния лишь для источников, удаляющихся от нас со скоростями β=0,2 и меньшими. Исходя из этих расстояний и наблюдаемого красного смещения, можно определить 𝑇 равным от 10¹⁰ до 1,4⋅10¹⁰ лет. ▲
7. Собственное время и связь
Ответ на первый вопрос: утверждение верно. На второй вопрос: нет, собственное время положительно. Одним из доказательств этого служит тот факт, что при отражении света вспышки между зеркалами на Луне можно добиться совпадения момента поглощения этого света с моментом прихода в эту точку частицы, испущенной с поверхности Солнца при вспышке. Собственное же время между событиями испускания и прихода к цели частицы с необходимостью больше нуля. Ответ на третий вопрос: нет, собственное время больше нуля. ▲
8. Время на сбор информации и на принятие решения
Время запаздывания равно 𝑅 м светового времени, так как для связи использовались непосредственно передаваемые световые сигналы. Все другие средства связи дают большие времена запаздывания. В распоряжении наблюдателя будет 3,4 сек для принятия защитных мер, т.е. на 0,4 сек больше, чем необходимые ему 3 сек. ▲
9. Лоренцево сокращение — подробный пример.
Решение дано в тексте.
10. Замедление хода часов
а) Можно, например, воспользоваться событиями, состоящими в пробивании отметок стрелкой часов на ракете в бумажных экранах, как это показано на рис. 38.
б) По определению Δ𝑥'=0. Подставляя эту величину в уравнение (42), получим (44).
в) Принцип относительности не нарушается ввиду симметрии между системами отсчёта. Отдельные покоящиеся в лаборатории часы отстают с точки зрения системы отсчёта ракеты, если их сравнивать последовательно со встречающимися им часами, покоящимися в системе ракеты [см. часть г)]. Нелишне также вспомнить анализ части г) в предыдущем упражнении.
г) По определению Δ𝑥=0. Подставляя эту величину в уравнение (39), получим (45). ▲
11. Относительная синхронизация часов
а), б) и в) При Δ𝑥=0 и Δ𝑡=0 формулы преобразования Лоренца дают Δ𝑡'=0 в системе отсчёта любой ракеты. Это верно вне зависимости от того, равны ли нулю Δ𝑦 и Δ𝑧 или не равны (вопрос б)). Если же Δ𝑡=0, а Δ𝑥≠0, тогда
Δ
𝑡'
=-
Δ
𝑥
sh
θ
𝑟
≠
0
.
Уравнение (46) получается при использовании соответствующих условий (𝑡=0) в уравнениях (37).
г) Чтобы вывести (47), подставим 𝑡'=0 в уравнения (36).
д) Если выбрать в системе ракеты положительное направление оси 𝑥' в направлении относительного движения лабораторной системы, то знак в уравнении (47) изменится на обратный, и это уравнение примет тот же вид, что уравнение (46).
е) Чтобы произвести измерения в нескольких разных местах в системе отсчёта ракеты при 𝑡'=0 (т.е. одновременно в этой системе), необходимо воспользоваться несколькими часами-хронографами. Лучше было бы употребить выражение: «Пусть часы-хронографы на ракете будут расположены так, чтобы каждые из лабораторных часов были рядом с ними в начальный момент ракетного времени (𝑡'=0), и пусть они сфотографируют в этот момент циферблаты лабораторных часов. Тогда на этих фотографиях не все лабораторные часы будут показывать время 𝑡=0». ▲
12.Эвклидовы аналогии

Рис. 140.
а) и б) См. рис. 140. Аналогия проявляется, когда мы сравниваем координаты 𝑥 эвклидовой системы и лоренцевой системы, а также координаты 𝑦 эвклидовой системы и 𝑡 лоренцевой системы. При этом на рис. 140 расстояние 𝑥𝐴' меньше, чем расстояние 𝑥𝐴, что соответствует различию наблюдаемых длин одного и того же движущегося стержня в системах отсчёта ракеты и лаборатории. Подобным же образом, замедление хода часов аналогично различию между значениями координат 𝑦𝐴' и 𝑦𝐴 в двух эвклидовых системах. В эвклидовой геометрии инвариантом является длина стержня, получаемая из значений координат его концов в любой системе. В лоренцевой геометрии инвариант — это интервал между двумя событиями, получаемый из результатов наблюдений в любой инерциальной системе отсчёта.

Рис. 141.
в) См. рис. 141. Точки, для которых 𝑦'=0, не все имеют координату 𝑦=0. Подобным же образом, не все события, происшедшие при 𝑡'=0, будут иметь координату 𝑡=0. ▲
13. Лоренцево сокращение. II
Сосредоточим своё внимание на следующих двух событиях: прохождении концов метрового стержня через начало пространственных координат лабораторной системы. В системе отсчёта ракеты эти события разделены расстоянием минус один метр (минус потому, что лаборатория в системе отсчёта ракеты движется в отрицательном направлении оси 𝑥) и временем, равным (1 м)/(относительная скорость):
Δ
𝑥'
=-
1
м
.
Δ
𝑡'
=
1 м
β𝑟
.
В лабораторной системе оба события происходят в одном и том же месте, но разделены отрезком времени Δ𝑡 который по условию задачи следует положить равным 𝐿/(относительная скорость), где 𝐿 —«длина» метрового стержня, измеренная таким путём в лабораторной системе отсчёта. Подставляя эти величины в формулы преобразования Лоренца (16), выразим Δ𝑡 через относительную скорость:
Δ
𝑡
=
𝐿
β𝑟
=
β𝑟(-1 м)+(1 м)/β𝑟
√1-β𝑟²
.
Отсюда
𝐿
=
√
1-β
𝑟
²
м
,
что и соответствует лоренцеву сокращению, наблюдаемому в лабораторной системе [формула (38)]. ▲
14. Замедление хода часов. II
Согласно условию задачи, Δ𝑥'=0, а Δ𝑡'≠0. Расстояние между двумя событиями в лабораторной системе отсчёта можно вычислить по формуле преобразования Лоренца
Δ
𝑥
=
0
+
Δ
𝑡'
sh
θ
𝑟
.
От нас требуется «измерить» время, прошедшее между этими событиями в лабораторной системе, разделив полученное выше расстояние на скорость движения обеих систем друг относительно друга:
Δ
𝑡
=
Δ𝑥
β𝑟
=
Δ𝑥
th θ𝑟
=
Δ
𝑡'
ch
θ
𝑟
Это и есть формула, описывающая замедление хода часов (44). ▲
15. Формулы преобразования Лоренца со временем в секундах
Просто подставим в формулы (37) 𝑡=𝑡сек/𝑐 и β𝑟=𝑣𝑟/𝑐. Обратные преобразования [(36) или (16)] примут тогда вид
𝑥
=
𝑥'
ch
θ
𝑟
+
𝑐𝑡
сек
'
sh
θ
𝑟
𝑥'+𝑣𝑟 𝑡сек'
√1-(𝑣𝑟/𝑐)²
,
𝑡
сек
'
+
𝑣
𝑟
𝑥'
𝑡
сек
=
𝑥'
sh
θ
𝑟
+
𝑡
сек
'
ch
θ
𝑟
=
𝑐²
,
𝑐
√
1-(𝑣
𝑟
/𝑐)²
▲
16. Вывод формул преобразования Лоренца
Из первого предположения следует условие 𝑎+𝑏=𝑒+𝑓, из второго — условие 𝑏-𝑎=𝑒-𝑓, а третье предположение даёт β𝑟=𝑏/𝑓. В совокупности из полученных трёх условий найдём 𝑓/𝑎=1, 𝑏/𝑎=𝑒/𝑎=β𝑟. Подставляя эти значения коэффициентов в исходные формулы для 𝑥 и 𝑡, запишите условие инвариантности интервала. Отсюда следует 𝑎=(1-β𝑟²)⁻¹/². Полученные формулы преобразования совпадают с (16). ▲
17. Собственная длина и собственное время
а) Направьте ось 𝑥' вдоль линии, соединяющей рассматриваемые события в лабораторной системе отсчёта. Сделайте предположение, что существует такая система отсчёта ракеты, в которой оба события происходят одновременно. Тогда преобразование Лоренца даёт
Δ
𝑡'
=
0
=-
Δ
𝑥
sh
θ
𝑟
+
Δ
𝑡
ch
θ
𝑟
,
откуда
sh θ𝑟
ch θ𝑟
=
th
θ
𝑟
=
β
𝑟
=
Δ𝑡
Δ𝑥
<
1.
Так как отношение Δ𝑡/Δ𝑥 меньше единицы, относительная скорость наших систем также меньше единицы, что подтверждает правильность предположения о существовании данной системы отсчёта ракеты. Из факта инвариантности интервала следует
(
Δ
𝑥)²
-
(
Δ
𝑡)²
=
(
Δ
𝑥')²
-
0²
=
(
Δ
σ)²
,
так что расстояние между событиями в системе отсчёта ракеты равно собственному расстоянию между этими событиями.
б) Снова направьте ось 𝑥 вдоль линии, соединяющей рассматриваемые события в лабораторной системе отсчёта. Сделайте теперь предположение. что существует такая система отсчёта ракеты, в которой оба события происходят в одном и том же месте. Тогда
Δ
𝑥'
=
0
=
Δ
𝑥
ch
θ
𝑟
-
Δ
𝑡
sh
θ
𝑟
,
откуда
th
θ
𝑟
=
β
𝑟
=
Δ𝑥
Δ𝑡
<
1,
что подтверждает правильность предположения о существовании данной системы отсчёта ракеты. Заметьте, что отношение Δ𝑥/Δ𝑡 есть просто та скорость, какой должен обладать в лабораторной системе наблюдатель на ракете, переносящийся от события к событию. Часть а) этого упражнения не содержит такой возможности. Из факта инвариантности интервала следует
(
Δ
𝑡)²
-
(
Δ
𝑥)²
=
(
Δ
𝑡')²
-
0²
=
(
Δ
τ)²
,
так что промежуток времени между этими событиями в данной системе отсчёта ракеты равен интервалу собственного времени между ними. ▲
18. Плоскость обоюдного согласия
Эту задачу можно решить двумя способами: во-первых, путём краткого рассуждения и, во-вторых, путём длинных математических преобразований (!). Рассуждения сводятся к следующему. Плоскость, на которой показания часов лаборатории и ракеты совпадают, должна быть перпендикулярна направлению относительного движения этих систем отсчёта, так как видеть сразу и лабораторные, и ракетные часы синхронизированными друг с другом можно лишь в такой плоскости [см. часть б) упражнения 11]. Однако лабораторная система отсчёта и система ракеты во всех отношениях взаимно равнозначны. Поэтому скорость «плоскости согласия» должна быть одинакова как с точки зрения системы отсчёта ракеты, так и с точки зрения лабораторной системы (разным может быть лишь её направление). Какая промежуточная скорость будет сохранять своё численное значение при переходе от первой системы отсчёта ко второй? Во всяком случае, не β/2. Предмет, движущийся в лабораторной системе со скоростью β/2, будет обладать в системе отсчёта ракеты скоростью, не равной - β/2 (ведь скорости не просто складываются). Однако предмет, движущийся в лабораторной системе так, что его параметр скорости равен θ𝑟/2, будет обладать в системе отсчёта ракеты параметром скорости - θ𝑟/2 (параметры скорости аддитивны). Поэтому скорость движения «плоскости согласия» должна быть равна в лабораторной системе отсчёта β=th ½θ𝑟, если, конечно, такая плоскость существует.
Математические преобразования, дающие тот же результат, состоят в следующем. Положите в преобразованиях Лоренца (36) 𝑡=𝑡'. Исключите затем из них 𝑥 и найдите, чему равно отношение 𝑥/𝑡 — скорость движения плоскости, на которой времена одинаковы. Вы получите (см. табл. 8):
2
sh²
θ
𝑟
𝑥
=
ch
θ
𝑟
-1
=
2
=
th
θ
𝑟
.
𝑡
sh
θ
𝑟
2
sh
θ
𝑟
sh
θ
𝑟
2
2
2
▲
19. Преобразование углов
Обозначим через Δ𝑥' проекцию метрового стержня на ось 𝑥' в системе отсчёта ракеты, а через Δ𝑦' — аналогичную проекцию на ось 𝑦'. Значит, тангенс угла φ' равен tg φ'=Δ𝑥'/Δ𝑦'. В лабораторной системе отсчёта 𝑦-проекция будет оставаться равной прежней 𝑦-проекции в системе ракеты, но 𝑥проекция подвергнется лоренцеву сокращению, согласно выводам упражнения 9. Мы получим
Δ
𝑦
=
Δ
𝑦'
,
где
Δ
𝑦
=
(1
м
)
sin φ'
,
и
Δ
𝑥
=
Δ
𝑥'
√
1-β
𝑟
²
,
где
Δ
𝑥'
=
(1
м
)
cos φ'
,
Отсюда легко вычислить величину тангенса искомого угла в лабораторной системе отсчёта
tg φ
=
Δ𝑦
Δ𝑥
=
tg φ'
√1-β𝑟²
.
Длина метрового стержня, измеренная в лабораторной системе отсчёта, равна
𝐿
=
√
(
Δ
𝑥)²+(
Δ
𝑦)²
.
Подставляя сюда полученные выше значения Δ𝑥 и Δ𝑦, найдём
𝐿
=
√
1-β
𝑟
²
cos²φ'
м
.

Рис. 142. Электрические силовые линии заряженной частицы в системе отсчёта ракеты.

Рис. 143. Электрические силовые линии заряженной частицы в лабораторной системе отсчёта.
Мысленно заменяя электрические силовые линии метровыми стержнями, можно выяснить, как выглядит электрическое поле вблизи заряженной частицы, покоящейся в системе отсчёта ракеты (на рис. 142 изображена картина, наблюдаемая в системе ракеты, а на рис. 143 — картина, наблюдаемая в лабораторной системе отсчёта). Мы считаем, что электрическая сила, действующая на пробный заряд, покоящийся в лабораторной системе отсчёта, пропорциональна плотности электрических силовых линий в том месте, где он находится. Следовательно, на пробные заряды, расположенные вдоль пути движения быстрой заряженной частицы (например, в точке 𝐴 на рис. 143), будет действовать сила, меньшая, чем если бы частица покоилась. В свою очередь на пробные заряды, расположенные в стороне от пути движения быстрой заряженной частицы, будет действовать в момент их наибольшего сближения (например, в точке 𝐵 на рис. 143) сила, превышающая ту, которая действовала бы, если бы частица — источник поля — покоилась. На этом и на подобных ему релятивистских эффектах основывается анализ электрического и магнитного полей в превосходной книге Парселла, выпущенной в издательстве Мак-Гроу Хилл. ▲
20. Преобразование скорости вдоль оси 𝑦
Из условия задачи мы знаем, что для любой пары событий на мировой линии частицы Δ𝑥'=0. Тогда из формул преобразования Лоренца
Δ
𝑦
=
Δ
𝑦'
,
Δ
𝑥
=
Δ
𝑡'
sh
θ
𝑟
,
Δ
𝑡
=
Δ
𝑡'
ch
θ
𝑟
,
откуда можно вычислить компоненты скорости в лабораторной системе отсчёта:
β
𝑦
=
Δ𝑦
Δ𝑡
=
Δ𝑦'
Δ𝑡' ch θ𝑟
=
β𝑦'
ch θ𝑟
,
β
𝑥
=
Δ𝑥
Δ𝑡
=
th
θ
𝑟
.
▲
21. Преобразование направлений скоростей
В системе отсчёта ракеты разности координат даются соотношениями
Δ
𝑦'
=
β'
sin φ'
⋅
Δ
𝑡'
и
Δ
𝑥'
=
β'
cos φ'
⋅
Δ
𝑡'
.
Найдём значения смещений Δ𝑦 и Δ𝑥 в лабораторной системе отсчёта, пользуясь формулами преобразования Лоренца (42), откуда угол между вектором скорости частицы и направлением относительного движения в лабораторной системе отсчёта оказывается равен
β'
sin
φ'
tg φ
=
Δ
𝑦
=
ch θ
𝑟
.
Δ
𝑥
β' cos φ'+β
𝑟
Отличие полученного угла от угла, найденного в упражнении 19, вытекает из того, что теперь мы рассматривали преобразование скорости — величины, включающей время. В последнем уравнении угол φ стремится к нулю при β𝑟→1, тогда как, напротив, в упражнении 19 мы нашли, что угол наклона метрового стержня по отношению к направлению относительного движения систем стремится к 90°, когда β𝑟→1. ▲
22. Эффект «прожектора» 1)
1) Здесь речь идёт о том пучке лучей, который испущен при единичной мгновенной вспышке. Если бы «прожектор» действовал непрерывно в течение всего времени, его луч, напротив, расширился бы вокруг оси, совпадающей с направлением движения (вперёд или назад—несущественно), концентрируясь с точки зрения неподвижного наблюдателя в перпендикулярном движению «прожектора» направлении (например, на летящем вместе с ним экране). См. в связи с этим упражнение 19. Я благодарен П. И. Филиппову, заметившему этот эффект и обратившему на него моё внимание.—Прим. перев.
В системе отсчёта ракеты проекция на ось 𝑥 пути, пройденного светом вспышки, равна Δ𝑥'=cos φ'⋅Δ𝑡'.
Чтобы найти Δ𝑥 и Δ𝑡 в лабораторной системе отсчёта, воспользуемся формулами преобразования Лоренца (42). Скорость распространения света вспышки β равна единице как в системе отсчёта ракеты, так и в лабораторной системе. Поэтому косинус угла между направлением луча и осью 𝑥 в лабораторной системе даётся выражением
Δ𝑥
Δ𝑡
=
cos φ
=
cos φ'+β𝑟
β𝑟 cos φ'+1
.
Это выражение совпадает с полученным в упражнении 21 в случае, когда β'=1, как можно показать на основании тригонометрических тождеств. Лучи, распространяющиеся в переднее полушарие в системе отсчёта ракеты, обладают углами, меньшими, чем φ'=90°. Из только что полученного выражения следует величина максимального угла для таких лучей в лабораторной системе отсчёта: cos φ=β𝑟 при φ'=90°.
Весь свет, испущенный лампой в её системе покоя в переднее полушарие, собирается в направленном вперёд конусе с таким углом раствора относительно направления движения лампы, если наблюдение проводится из лабораторной системы отсчёта. ▲
23. Парадокс эйнштейновского поезда — подробный пример
Решение дано в тексте.
24. Загадка Эйнштейна
Да, он увидит себя в зеркале. В его системе отсчёта, как и в любой другой инерциальной системе, свет обладает одной и той же скоростью. Своё изображение в зеркале он будет видеть точно таким же, как и при любой другой постоянной скорости движения относительно земли. ▲
25. Парадокс шеста и сарая

Рис. 144. Пространственно-временная диаграмма в системе отсчёта сарая.

Рис. 145. Пространственно-временная диаграмма в системе отсчёта бегуна.
Разрешение этого «парадокса» состоит в том, что в системе отсчёта бегуна передний конец шеста покидает сарай прежде, чем задний конец шеста входит в сарай. Поэтому с точки зрения бегуна шест вообще ни в какой момент времени не находится в сарае целиком. Последовательность событий можно подробнее проиллюстрировать двумя диаграммами пространства-времени (рис. 144 и 145), численные значения длин и моментов времени на которых можно получить из следующих соображений. Так как множитель, описывающий лоренцево сокращение, по условию задачи равен 2, то (см. упражнение 9)
ch θ
𝑟
=
2
.
Поэтому из тождества
ch²θ
-
sh²θ
=
1
следует, что
sh θ
𝑟
=
√
3
.
Отсюда относительная скорость двух систем отсчёта равна
β
𝑟
=
th θ
𝑟
=
√3
2
.
Чтобы найти численные значения, приведённые на рис. 144 и 145, достаточно воспользоваться этими данными, а также тем, что длина шеста в системе отсчёта бегуна равна 20 м, а в лабораторной системе 10 м. ▲
26. Война в космосе
Камень преткновения состоял в понятии одновременности —«в тот момент, когда» (см. также упражнение 11). Точки 𝑎 и 𝑎' могут поравняться друг с другом только в другом месте вдоль траектории относительного движения ракет, а не в точке, где производится выстрел из орудия. Поэтому момент, когда точки 𝑎 и 𝑎' поравнялись друг с другом, может совпадать с моментом выстрела лишь в какой-то одной из двух систем отсчёта. По условию задачи такая одновременность имеет место в системе 𝑂, так что рис. 42 правилен по определению. Но рис. 43 неверен: к тому времени, когда в системе 𝑂' поравняются точки 𝑎 и 𝑎', выстрел уже будет произведена Неверна и подпись под рис. 43: снаряд пролетит мимо ракеты с точки зрения обеих систем отсчёта. ▲
27. Парадокс часов
а) Возраст отправившегося в путешествие Петра будет при его возвращении равен (в годах): 21 (возраст на старте) + 7 (время, проведённое на удаляющейся от Павла ракете 𝐴) + 7 (время, проведённое на приближающейся к Павлу ракете 𝐵), т.е. всего 35 лет.
б) См. рис. 146.

Рис. 146.
в) Исходя из величины относительной скорости, равной 24/25, найдём значение гиперболического косинуса от параметра скорости
ch θ
𝑟
=
√
1-β
𝑟
²
=
25
7
.
Точка, в которой Пётр изменил свою скорость на обратную, имеет в системе отсчёта ракеты 𝐴 координату 𝑥'=0, так как Пётр всё время был в начале координат этой системы; время же, соответствующее этому моменту, равно в системе отсчёта ракеты 𝑡'=7 лет. Из формулы преобразования Лоренца для времени найдём, что момент изменения направления скорости в лабораторной системе отсчёта соответствует
𝑡
=
𝑥' sh
θ
𝑟
+
𝑡' ch
θ
𝑟
=
0+7
⋅
25
7
лет
.
Промежуток времени между расставанием и встречей в лабораторной системе отсчёта вдвое превышает это 𝑟, так что к моменту встречи Павлу исполнится 21 + 25 + 25 = 71 год, и он будет более чем в два раза старше, чем Пётр-путешественник! ▲
28. Предметы, движущиеся быстрее света
а) Когда стержень проходит в своём движении вниз расстояние Δ𝑦=β𝑦Δ𝑡, точка 𝐴 продвигается вдоль оси 𝑥 на расстояние Δ𝑥, даваемое выражением
Δ𝑦
Δ𝑥
=
tg φ
,
т.е.
Δ
𝑥
=
Δ𝑦
tg φ
=
β𝑦
tg φ
Δ
𝑡'
.
Поэтому скорость движения точки пересечения 𝐴 равна
β
𝐴
=
Δ𝑥
Δ𝑡
=
β𝑦
tg φ
.
Для любой величины β𝑦 можно подобрать такой достаточно маленький, но всё же отличный от нуля угол φ, что β𝐴 будет больше единицы, т.е. будет превышать скорость света. Но такое перемещение точки пересечения ни в коей мере не влечёт за собой передачи информации вдоль оси 𝑥 точно так же, как не происходит переноса информации между двумя будильниками, заранее поставленными на определённые моменты времени и зазвеневшими поэтому в разных точках пространства с таким интервалом времени между звонками, что свет не мог бы связать эти два события. В настоящем же примере нужно было предварительно в течение длительного срока ускорять длинный прямой стержень, пока он не приобрёл бы своей конечной скорости, а наблюдатель в начале координат не имеет никакого шанса передать только что появившуюся у него информацию другому наблюдателю, находящемуся далеко от него вдоль оси 𝑥, с помощью мчащейся точки пересечения. В части б) этого упражнения рассмотрена безуспешная попытка передать такую вновь полученную информацию со сверхсветовой скоростью.
б) В этом случае точка пересечения сможет перемещаться вправо не быстрее, чем со скоростью распространения в стержне акустических волн, т.е. со скоростью, во много раз меньшей, чем скорость света.
в) Обозначим угловую скорость вращения прожектора через ω (в радианах в секунду). Условие того, что скорость поворота луча превышает 𝑐, имеет вид
ω𝑟
>
𝑐
или
𝑟
>
𝑐/ω
.
Указанное в условии предупреждение вовсе не передаётся от 𝐴 к 𝐵, совершенно так же, как оно не передавалось бы в случае, если будильники поставлены на очень близкие друг к другу моменты времени.
г) Да, скорость луча на экране может превышать скорость света, как и скорость вращения луча прожектора в части в) этого упражнения могла быть больше 𝑐. ▲
29. Синхронизация движущимися часами — подробный пример
Решение дано в тексте.
30. Конструкция часов и замедление их хода
В основе всех рассуждений лежит допущение, что невозможно определить абсолютную скорость движения инерциальной системы отсчёта исходя из вида физических законов, записанных в этой системе, и из входящих в них численных значений констант. Принцип работы любых реальных часов использует скорость протекания тех или иных физических процессов. Возьмём в одной инерциальной системе покоящиеся часы различных конструкций и сравним их ход; затем проделаем это для такого же набора часов, покоящихся в другой инерциальной системе. Если относительный ход часов разных конструкций будет меняться от одной инерциальной системы к другой, то это позволило бы найти абсолютное различие между разными инерциальными системами. Такое неодинаковое поведение разных физических процессов при переходах между системами отсчёта противоречило бы принципу относительности, и поэтому мы должны признать, что это невозможно. Взяв в исходной инерциальной системе часы, прокалиброванные в метрах светового времени, и осторожно ускорив их так, чтобы они в конце концов стали покоиться в другой инерциальной системе отсчёта, движущейся равномерно и прямолинейно относительно первой, мы (как следует предположить) получим в этой второй системе часы, правильно прокалиброванные в метрах светового времени. ▲
31. Инерциальные системы отсчёта, связанные с Землёй
а) Путь по вертикали 𝑧, пройденный за время 𝑡сек при свободном падении первоначально покоившейся частицей, находится из формулы
𝑧
=
1
2
𝑔𝑡
сек
²
Здесь 𝑔≈10 м/сек² —«гравитационное ускорение» (ускорение силы тяжести) вблизи поверхности Земли. В нашем случае время падения лишь немного превышает 1 метр светового времени, т.е. около 3,3⋅10⁻⁹ сек. Отсюда
𝑧
≈
10
2
⋅
(3,3⋅10⁻⁹)²
≈
5⋅10⁻¹⁷
м
.
Это на два порядка меньше размеров атомного ядра! Итак, пространственно-временная область размерами (1 м × 1 м × 1 м пространстве) × 1 м во времени является инерциальной с точностью до 5⋅10⁻¹⁷ м. Пусть, например, пройденное при падении расстояние измеряется интерференционными методами при помощи видимого света. Тогда минимальное обнаружимое смещение при падении примерно равно длине световой волны — около 5000 Å (5⋅10⁻⁷ м). Чтобы частица при своём падении пролетела такой путь, требуется
⎛
⎜
⎝
(Путь)⋅2
𝑔
⎞½
⎟
⎠
=
3⋅10⁻⁴
сек
=
=
10⁵
м
светового времени.
За такой срок частица, летящая с околосветовой скоростью, прошла бы в искровой камере приблизительно 𝐿=10⁵ м =100 км!
б) За 22 м светового времени (т.е. 73⋅10⁻⁹ сек =73 нсек) частица пройдёт при падении из состояния покоя путь 𝑧, приблизительно равный
𝑧
=
10
2
⋅
(73⋅10⁻⁹)²
≈
2,5⋅10⁻¹⁴
м
,
что примерно втрое превышает диаметр нуклона. С такой точностью является инерциальной связанная с Землёй система отсчёта в опыте Майкельсона — Морли. ▲
32. Размеры инерциальной системы
a1) На рис. 46 являются подобными два треугольника с острым углом θ соответственно при вершинах в точке 𝐵 и в центре Земли. Меньшая сторона первого из них равна ε/2, а второго 25/2 м. Записывая формулу пропорциональности соответствующих сторон подобных треугольников, получим
ε/2
250 м
=
(25 м)/2
6,4⋅10⁶ м
,
откуда ε≈10⁻³ м, что и следовало доказать.
а2) Замените на рис. 46 пометку «25 м» на Δ𝑥, а 𝑟𝑒 - на 𝑟. Пусть ускорение, действующее по направлению от точки 𝐵 к центру Земли, равно 𝑎*. Тогда проекция этого ускорения на ось 𝑥, параллельную поверхности Земли, составляет 𝑎* sin θ. Относительное ускорение (Δ𝑎𝑥)* двух частиц (первая падает из точки 𝐵, а вторая - из 𝐴) вдвое превышает эту величину и имеет обратный ей знак:
(
Δ
𝑎
𝑥
)*
=-
2𝑎*
sin θ
.
Из правого треугольника, острый угол θ которого помещён в центре Земли, найдём
sin θ
=
Δ𝑥
2𝑟
,
так что окончательно
(
Δ
𝑎
𝑥
)*
=-
2𝑎*
Δ𝑥
2𝑟
=-
Δ𝑥
𝑟
𝑎*
,
что и требовалось получить.
б1) Воспользуемся данным в тексте советом; тогда
𝑎*
⎪
⎪𝑟
=
const
𝑟²
;
𝑎*
⎪
⎪𝑟+Δ𝑧
=
const
(𝑟+Δ𝑧)²
=
const
𝑟²
⎛
⎜
⎝
1+
Δ𝑧
𝑟
⎞⁻²
⎟
⎠
=
=
const
𝑟²
⎡
⎢
⎣
1-2
Δ𝑧
𝑟
+3
⎛
⎜
⎝
Δ𝑧
𝑟
⎞²
⎟
⎠
-
…
⎤
⎥
⎦
,
где взята формула бинома Ньютона. Учтём, что Δ𝑧 много меньше, чем 𝑟, и пренебрежём поэтому всеми членами разложения, за исключением первых двух. Вычитая теперь величину 𝑎* в точке 𝑟 из 𝑎* в точке 𝑟+Δ𝑧, получим
Δ
𝑎*
≈-
2
𝑎*
𝑟
Δ
𝑧
.
Знак «минус» означает, что ускорение будет тем меньше, чем больше высота. Две частицы, начавшие падение из состояния покоя в точках, лежащих одна над другой (на одной вертикали), подвергаются действию относительного ускорения, и расстояние между ними будет возрастать. Такое относительное ускорение (Δ𝑎𝑧)* положительно и по абсолютной величине равно Δ𝑎*:
(
Δ
𝑎
𝑧
)*
≈+
2
𝑎*
𝑟
Δ
𝑧
.
что и требовалось доказать.
б2) Расстояние, пройденное из состояния покоя под действием постоянного ускорения, пропорционально этому ускорению. Сравнивая между собой уравнения (52) и (53), следует заключить, что ускорение одной частицы относительно другой теперь будет вдвое больше, чем в части а), и к тому же противоположного знака. Значит, вместо уменьшения расстояния на 10⁻³ м [часть а)] мы должны иметь теперь увеличение расстояния на 2⋅10⁻³ м. Поэтому таблицу на стр. 99 следует пересмотреть следующим образом. В первом столбце запишите ε≥2⋅10⁻³ м; в третьем столбце Δ𝑥=0; в четвёртом столбце Δ𝑦 и Δ𝑧≤25 м. Если бы мы в первом столбце ничего не изменили, то в четвёртом столбце нам пришлось бы записать: Δ𝑦≤25 м, Δ𝑧≤12,5 м.
в) Следуя данным здесь советам, найдём
𝑎*
~
1
/
𝑟²
,
(
Δ
𝑎
𝑥
)*
~
Δ
𝑥
/
𝑟³
,
ε
~
(
Δ
𝑎
𝑥
)*
(
Δ
𝑡)²
,
ε
~
Δ
𝑥
(
Δ
𝑡)²
/
𝑟³
.
Если здесь оставить ε прежним, то следует увеличить Δ𝑥 в 8 раз, Δ𝑡 в 14 раз, т.е. (Δ𝑡)² в 200 раз. Поэтому числитель в последней дроби увеличится в 1600 раз, и если мы хотим во всех случаях сохранить одно и то же значение ε, то нужно, чтобы 𝑟³ также возросло в 1600 раз:
𝑟³
≈
1600
𝑟
𝑒
³
.
Отсюда найдём
𝑟
≈
12
𝑟
𝑒
.
▲
33. Опыт Майкельсона — Морли
а) При полёте против ветра самолёт движется относительно Земли со скоростью 𝑐-𝑣. Поэтому он проходит отрезок 𝐴𝐵 за время 𝑡₁=𝑑/(𝑐-𝑣), где 𝑑 - длина отрезка 𝐴𝐵.
При полёте с попутным ветром самолёт имеет относительно Земли скорость 𝑐+𝑣, и срок обратного полёта оказывается равен 𝑡₂=𝑑/(𝑐+𝑣).
Полное время полёта по замкнутому маршруту равно
𝑡₁
+
𝑡₂
=
2𝑑/𝑐
1-(𝑣/𝑐)²
.
Но 2𝑑/𝑐 - время такого полёта в отсутствие ветра. Значит, время, необходимое для перелёта по замкнутому маршруту между 𝐴 и наветренным пунктом 𝐵, превышает время для такого же перелёта в условиях штиля в 1/[1-(𝑣/𝑐)²] раз, что и требовалось показать.
Полёт против ветра требует большей затраты времени, чем полёт по ветру. Поэтому средняя скорость относительно Земли при полёте по замкнутому маршруту должна быть меньше, когда дует ветер, чем при штиле. Это особенно ясно в предельном случае, когда скорость ветра 𝑣 приближается к величине скорости самолёта относительно воздуха 𝑐. При этом самолёт может вернуться из 𝐵 в 𝐴 за короткий срок
𝑑
𝑐+𝑣
≈
𝑑
2𝑣
,
но зато ему необходимо очень большое время, чтобы долететь против ветра из 𝐴 в 𝐵 вначале.
б) Чтобы ветер его не сносил в сторону, самолёт должен развить скорость против ветра, равную относительно воздуха скорости самого ветра, т.е. 𝑣. Абсолютная же величина скорости самолёта относительно воздуха равна 𝑐. Применяя теорему Пифагора к треугольнику скоростей, обнаружим, что скорость самолёта поперёк ветра (равная его скорости относительно Земли) составляет √𝑐²-𝑣². Чтобы покрыть с такой скоростью полный путь 2𝑑 (полёт по замкнутому маршруту), требуется время
2𝑑
√𝑐²-𝑣²
=
2𝑑/𝑐
√1-(𝑣/𝑐)²
,
в 1/√1-(𝑣/𝑐)² раз превышающее срок полёта по замкнутому маршруту 2𝑑/𝑐 при штиле.
в) Примем длину пути по замкнутому маршруту равной 𝐿=2𝑑. Тогда разность времён таких полётов в двух взаимно перпендикулярных направлениях получится, если вычесть из выражения, найденного в части а) этого упражнения, выражение, найденное в части б):
Δ
𝑡
=
𝐿/𝑐
1-(𝑣/𝑐)²
-
𝐿/𝑐
√1-(𝑣/𝑐)²
.
Разлагая по формуле бинома Ньютона выражения в скобках, найдём
Δ
𝑡
=
𝐿
𝑐
⎧
⎨
⎩
⎡
⎢
⎣
1
+
⎛
⎜
⎝
𝑣
𝑐
⎞²
⎟
⎠
+
⎛
⎜
⎝
𝑣
𝑐
⎞⁴
⎟
⎠
+…
⎤
⎥
⎦
-
-
⎡
⎢
⎣
1
+
1
2
⎛
⎜
⎝
𝑣
𝑐
⎞²
⎟
⎠
+
3
8
⎛
⎜
⎝
𝑣
𝑐
⎞⁴
⎟
⎠
+…
⎤
⎥
⎦
⎫
⎬
⎭
.
При 𝑣/𝑐≪1 величина Δ𝑡 достаточно точно выражается одним членом низшей степени по 𝑣/𝑐:
Δ
𝑡
≈
𝐿
2𝑐
⎛
⎜
⎝
𝑣
𝑐
⎞²
⎟
⎠
.
Это и требовалось доказать. Первым вернётся в 𝐴 самолёт, летавший поперёк ветра.
г) Разрешая последнее уравнение относительно 𝑣 и подставляя численные значения из условия задачи, получим 𝑣=14 км/час. Направление ветра ориентировано вдоль маршрута того самолёта, который вернулся последним. Однако данные условия задачи не позволяют определить, в каком из двух направлений, параллельных этому маршруту, собственно дует ветер.
д) Подставляя в формулу, полученную в части в) этого упражнения, величины
𝐿
=
22
м
,
𝑣
=
30⋅10³
м
/
сек
,
𝑐
=
3⋅10⁸
м
/
сек
,
найдём
Δ
𝑡
=
11
3
⋅
10⁻¹⁶
сек
.
е) Полагая Δ𝑡≤10⁻²
𝑇
=
2⋅10⁻¹⁷
сек
=
𝐿
𝑐
⎛
⎜
⎝
𝑣
𝑐
⎞²
⎟
⎠
(обратите внимание на то, что множитель 1/2 в выражении для Δ𝑡 в части в) сокращается) и подставляя сюда данные задачи, получим
𝑣
≤
5⋅10³
м
=
1
6
𝑣
𝑒
.
ж) Нет, сам по себе опыт Майкельсона не служит опровержением теории распространения света в эфире. Например, могло бы случиться, что Земля увлекает эфир за собой, так что экспериментальная установка покоится относительно находящегося около поверхности Земли эфира. Для проверки этого предположения некоторые исследователи предлагали (и провели такой эксперимент!) разместить приборы на вершине горы; для этого можно было бы использовать и спутники. Для того чтобы специалисты, работающие в соответствующей области науки, отреклись от какой-либо тщательно разработанной теории, требуется опровергнуть её целым рядом всесторонне поставленных опытов, и опыт Майкельсона — Морли оказался первым ударом, нанесённым теории светового эфира, от которого она уже никогда полностью не оправилась. ▲
34. Эксперимент Кеннеди — Торндайка
а) За время Δ𝑡 (в секундах) свет проходит расстояние 𝑐Δ𝑡 метров. В данном случае его следует приравнять разности длин двух замкнутых путей 2Δ𝑙, так что Δ𝑡=2Δ𝑙/𝑐. Так как Δ𝑙=16⋅10⁻² м, эта разность времён составляет Δ𝑡≈10⁻⁹ сек=1 нсек.
б) 𝑛=Δ𝑡/𝑇≈10⁻⁹/(2⋅10⁻¹⁵)=5⋅10⁵ периодов. Величину 𝑛 можно найти также из формулы
𝑛
=
2Δ𝑙
𝑐𝑇
.
в) Предположим, что число 𝑛 не изменяется (не наблюдается перехода от света к темноте в поле зрения телескопа). Тогда должна быть постоянна и скорость 𝑐, так как отношение Δ𝑙/𝑇 не изменяется. Здесь стандартом длины (предполагается, что она не изменяется) служат размеры кварцевой плиты, на которой смонтирован интерферометр, тогда как постоянные интервалы времени задаются периодом света, излучаемого атомами.
г) Взяв приращение для выражения (54) в предположении постоянства Δ𝑙/𝑇, получим
𝑑𝑐
=-
2
𝑑𝑛
𝑛²
Δ𝑙
𝑇
или
𝑑𝑐
𝑐
=-
𝑑𝑛
𝑛
.
Подставляя сюда условия задачи и вычисленную выше величину 𝑛=5⋅10⁵, получим при 𝑑𝑛≤3/1000
⎪
⎪
⎪
𝑑𝑐
𝑐
⎪
⎪
⎪
≤
3
1000
⋅
1
5⋅10⁵
=
3
5
⋅
10⁻⁸
,
или
𝑑𝑐
≤
3
5
⋅
10⁻⁸
⋅
3
⋅
10⁸
≈
2
м
/
сек
,
в качестве того наибольшего изменения скорости света, которое ещё не могло быть обнаружено в этом чрезвычайно тонком эксперименте (эта величина приведена в табл. 4 на стр. 26). ▲
35. Эксперимент Дикке
а) Пусть шар из меди падает с ускорением 𝑔₁, а шар из золота — с ускорением 𝑔₂=𝑔₁+Δ𝑔, лишь немного превышающим предыдущее. Их разность Δ𝑔 обусловлена сопротивлением воздуха и возрастает к концу падения. Мы, однако, упростим рассуждения, предположив, что Δ𝑔 равняется некоторой средней величине в течение всего процесса падения. Тогда пути, пройденные шарами за одно и то же время падения 𝑡, равны
𝑠₂
=
1
2
(𝑔₁+
Δ
𝑔)
𝑡²
и
𝑠₁
=
1
2
𝑔₁
𝑡²
.
Их разность составляет
𝑠₂
-
𝑠₁
=
Δ
𝑠
=
1
2
Δ
𝑔
⋅
𝑡²
.
Разделив левую и правую стороны этого равенства на соответствующие стороны уравнения движения шара из меди, найдём
Δ𝑠
𝑠₁
=
Δ𝑔
𝑔₁
.
Измерения Галилея дали численные значения 𝑠₁=46 м и Δ𝑠=7⋅10⁻² м, т.е.
Δ𝑔
𝑔₁
=
7⋅10⁻²/46
≈
10⁻³
.
Таково наибольшее значение относительного различия ускорения силы тяжести для разных объектов, не противоречащее наблюдениям Галилея. Примем теперь это отношение равным наибольшей величине, не противоречащей новейшему эксперименту Дикке:
Δ𝑔
𝑔
≤
3⋅10⁻¹¹
(по Роллу, Кроткову и Дикке).
Тогда при падении с той же высоты 46 м один шар опередил бы другой не более чем на отрезок
Δ
𝑠
=
𝑠₁
Δ𝑔
𝑔₁
=
46⋅3⋅10⁻¹¹
м
=
1,5⋅10⁻⁹
м
,
что примерно в десять раз меньше характерных размеров атома. Если бы мы потребовали, чтобы разность Δ𝑠 равнялась целому миллиметру, т.е. 10⁻³ м, то шары пришлось бы сбросить в постоянном гравитационном поле с высоты 𝑠₁ равной
𝑠₁
=
Δ𝑠
Δ𝑔/𝑔₁
=
10⁻³
3⋅10⁻¹¹
=
1
3
⋅
10⁸
м
,
что составляет около одной десятой расстояния от Земли до Луны (3,8⋅10⁸ м). Излишне говорить, что гравитационное поле Земли не постоянно (не однородно) на таком протяжении.
б) Условия равновесия состоят в равенстве нулю как результирующей горизонтальной компоненты силы, так и её результирующей вертикальной компоненты. Из рис. 50 и 51 видно, что эти условия выполняются, если
𝑇 sin ε
=
𝑚𝑔
𝑠
,
𝑇 cos ε
=
𝑚𝑔
.
Взяв отношения соответствующих сторон этих равенств, получим
tg ε
≈
ε
≈
𝑔𝑠
𝑔
,
откуда
𝑔
𝑠
≈
𝑔ε
.
в) Подставляя значения постоянных, данные в конце этой книги, и взяв в качестве 𝑀 массу Солнца, найдём
𝑔
𝑠
=
𝐺𝑀
𝑅²
=
5,94⋅10⁻³
м
/
сек
²
.
г) Подставляя значения постоянных, найдём
𝑣²
𝑅²
=
5,94⋅10⁻³
м
/
сек
²
.
В ускоренной системе отсчёта, связанной с Землёй, это «центробежное ускорение», увлекающее предметы от Солнца, уравновешивается центростремительным ускорением силы тяжести, величина которого вычислена в части в). Полная величина ускорения, наблюдаемая в ускоренной системе отсчёта Земли, равна нулю.
д) Формула (55) непосредственно следует из определения закручивающего момента и из ситуации, изображённой на рис. 52. Подставим 𝑔𝑠=6⋅10⁻³ м/сек² [см. часть в) этого упражнения] и получим величину полного закручивающего момента со стороны гравитационного поля Солнца:
⎛
⎜
⎝
Закручивающий
момент
⎞
⎟
⎠
=
(0,03
кг
)
⋅
(6⋅10⁻³
м
/
сек
²)
×
×
(3⋅10⁻¹¹)
⋅
(0,03
м
)
=
1,6⋅10⁻¹⁶
кг
⋅
м
²
/
сек
²
.
Если поместить на конец метрового стержня одну бактерию (с массой около 10⁻¹⁵ кг), то это даст закручивающий момент, примерно равный
(10⁻⁵
кг
)
(10
м
/
сек
²)
(1/2
м
)
≈
5⋅10⁻¹⁵
кг
⋅
м
/
сек
²
,
что почти в тридцать раз превышает самое большое значение закручивающего момента, какое только может дать притяжение Солнца в крутильных весах Дикке!
е) Ответ очевиден из рис. 52.
ж) Приравняйте 𝑘θ закручивающему моменту, данному уравнением (55), и вы получите искомый результат.
з) θполн=1,6⋅10⁻⁸ рад. ▲
36. Долой теорию относительности!
а) См., что получено в упражнении 10 относительно замедления хода часов.
б) См. упражнение 9 (Лоренцево сокращение — подробный пример).
в) Один из основных выводов частной теории относительности состоит в том, что пространственные координаты событий неодинаковы в системе отсчёта ракеты и в лабораторной системе отсчёта, а также что промежуток времени между событиями может быть различен с точки зрения двух инерциальных систем, движущихся друг относительно друга равномерно и прямолинейно. То, что теория отражает эти факты, существующие в природе, совсем даже не плохо. Просто так устроен наш мир! Если нам требуется привязать наблюдательные данные к конкретной системе отсчёта, то теория относительности даёт возможность найти значения координат в этой системе, если уже известны их значения в какой-то другой системе отсчёта. Теория относительности указывает, как связаны между собой значения скоростей одних и тех же частиц с точки зрения различных взаимно перекрывающихся систем отсчёта. Подводя итог, можно перечислить заслуги теории относительности:
1) Она вскрывает тот факт, что сами по себе отдельно взятые пространственные и временная координаты зависят от такого чисто случайного обстоятельства, как выбор системы отсчёта.
2) Она указывает, как связать значения координат, скоростей, ускорений и сил, наблюдаемые в одной системе отсчёта, с соответствующими значениями этих же величин, наблюдаемыми в другой инерциальной системе отсчёта, перекрывающейся с предыдущей.
3) Мы обязаны ей языком инвариантов —«универсальным языком», на котором взаимосвязь между событиями может быть описана независимо от их пространственных и временных координат одинаково для любой системы отсчёта. Дальнейшие подробности об этом см. в части е) этого упражнения.
г) Постоянство скорости света, её одинаковая величина во всех инерциальных системах отсчёта, конечно же, противоречит представлениям здравого смысла, возникшего из повседневного опыта, который связан с измерением малых скоростей. Но ведь всё-таки самые тщательные эксперименты заставили нас в конце концов признать правильность этого кажущегося нелепым факта! Например, опыт Майкельсона — Морли (упражнение 33) и позднейшие постановки этого опыта показали, что скорость света изотропна — одинакова во всех направлениях — во всех инерциальных системах. Более того, экспериментом Кеннеди — Торндайка (упражнение 34) было доказано, что и численное значение этой скорости одинаково во всех системах отсчёта, движущихся равномерно и прямолинейно относительно друг друга. Запроектированные теперь ещё более тщательные измерения смогут проверить этот факт со значительно возросшей степенью точности (см. текст на стр. 25—27).
д) Утверждение мистера Большого Скептика заставляет нас провести разделение всех предсказаний теории относительности на те, которые получили непосредственное подтверждение, и те, которые были подтверждены косвенно или ещё не были проверены. Вот список некоторых из этих предсказаний:
1) Лоренцево сокращение масштабов (упражнение 9). Наблюдаемую величину ионизации воздуха при распространении в нем частиц, обладающих релятивистскими скоростями, можно удовлетворительно объяснить, если учесть лоренцево сокращение для электрических силовых линий, исходящих из этих частиц (упражнение 19). Приводимое ниже объяснение принадлежит перу Е. Дж. Уильямса [первоначальный чёткий анализ см., в частности, на стр. 331 в статье, опубликованной в Proceedings of the Royal Society, серия A, 130, 328 (1931), а более детальный разбор и дальнейшие ссылки можно найти в том же журнале, том 139, 163 (1933)]:
Если бы лоренцево сокращение не сжимало электрические силовые линии в тонкий концентрированный пучок, плоскость которого перпендикулярна направлению движения, то заряженная частица не смогла бы вырывать электроны из атомов, находящихся так далеко от её траектории, и производимая ею ионизация была бы много слабее, чем это наблюдается в действительности. Рассмотрим атом азота, находящийся на наблюдаемом расстоянии 1/3 мм (около 3⋅10⁻⁴ м) от траектории движения заряженной частицы. Если бы лоренцева сокращения не происходило, то силовые линии электрического поля частицы «обметали» бы атом азота также на протяжении, грубо говоря, 3⋅10⁻⁴ м пути частицы, и это заняло бы время (при β=1) порядка (3⋅10⁻⁴ м)/(3⋅10⁸ м/сек)=10⁻¹² сек. Такой интервал времени действия электрических сил слишком велик для того, чтобы возбудить атом. В самом деле, уподобим атом маятнику. Медленно сместим точку подвеса маятника сначала в одну, а затем в противоположную сторону (такое смещение аналогично воздействию на атом электрического поля). Произведённое возмущение не возбудит колебаний маятника, так как эффективное время действия перемещающей силы на точку подвеса 𝑇силы намного превышает характерное (резонансное) время колебаний 𝑇колеб маятника. Для атома это характерное время равно 10⁻¹⁶ сек, и если эффективное время действия электрических сил не будет сравнимым с ним, то не произойдёт ни возбуждения, ни ионизации атома. Так как заряженная частица, являющаяся источником возмущающей силы, уже движется практически со скоростью света, отсутствуют резервные возможности сократить эффективное время её действия на атом азота и сделать его меньше 10⁻¹² сек, что требовалось бы для объяснения наблюдаемой ионизации. Вот здесь-то и спасает дело лоренцево сокращение. Благодаря ему эффективная толщина пучка силовых линий, действующего на атом азота, сокращается с 3⋅10⁻⁴ до 3⋅10⁻⁴√1-β² м, и эффективное время действия сил становится равным не 10⁻¹², а 10⁻¹²√1-β² сек. Если заряженная частица имеет скорость β=1-10⁻⁹, то √1-β²≈(2⋅10⁻⁹)¹/²≈5⋅10⁻⁵, и эффективное время действия сил составит всего ~0,5⋅10⁻¹⁶ сек — величина эта достаточно мала, чтобы произошла ионизация атома азота, хотя он и удалён на миллионы атомных поперечников от линии движения заряженной частицы.
2) Замедление хода часов (упражнение 10). Подтверждается в опытах со сверхбыстрыми элементарными частицами (упражнения 42 и 43).
3) Относительность одновременности (упражнение 11). Подтверждается косвенно (явление «томасовской прецессии», упражнение 103, где анализ основывается на выводах упражнения 52).
4) Парадокс часов (упражнение 27). Для случая часов бытовой конструкции, побывавших в космическом полёте, проверка ещё не произведена. Подтверждается со значительной степенью точности в случае, когда в качестве часов используются ядра атомов железа (упражнение 89).
Самым убедительным и чувствительным методом проверки специфических предсказаний частной теории относительности оказалось использование столкновений сверхбыстрых частиц, энергетического баланса при ядерных превращениях и порождения пар элементарных частиц. Эти вопросы обсуждаются в тексте гл. 2 и в упражнениях к этой главе.
е) Что скажет вам шофёр, если вы станете указывать ему в качестве данных о городах, в которые нужно заехать, их широту и долготу? Всё, что ему нужно узнать, сводится к расстояниям до этих городов. Так же обстоит дело и в пространстве-времени: вполне можно обойтись без координат, указав лишь интервалы между всеми событиями. Эти интервалы никак не зависят от выбора координат, и тем не менее в них содержится вся действительно нужная информация.
ж) Наблюдения связывают нас с физической реальностью; характеризуя их результаты, мы характеризуем и саму «реальность». ▲
37. Эвклидова аналогия — подробный пример
Решение дано в тексте.
38. Преобразование Галилея
Формулы (57) и (58) получаются из формул (37), если в них подставить выражения из строк 4 и 5 правого столбца табл. 8. В ньютоновской механике не делается различия между величинами момента времени для одного и того же события, измеренными разными движущимися относительно друг друга наблюдателями. Иначе говоря, в ньютоновской механике полагают 𝑡'=𝑡. Здесь можно перейти к времени, измеренному в секундах, и тогда 𝑡сек'=𝑡сек. Ради простоты момент совпадения начал лабораторной системы и системы отсчёта ракеты полагают равным нулю (𝑡=0). В лабораторной системе на оси 𝑥 положение начала отсчёта ракеты описывается функцией времени 𝑣𝑟 𝑡ceк. Утверждается, что координата 𝑥 события в системе отсчёта ракеты равна разности соответствующей координаты события и координаты точки начала отсчёта ракеты, взятых в лабораторной системе. Следовательно, имеет место формула
𝑥'
=
𝑥
-
𝑣
𝑟
𝑡
сек
.
Формулы (57) и (59) практически совпадают — разница состоит лишь в выборе единиц измерения времени. Заметим, что
β
𝑟
𝑡
=
𝑣𝑟
𝑐
𝑡
=
𝑣
𝑟
𝑡
𝑐
=
𝑣
𝑟
𝑡
сек
.
Подставляя это равенство, приведём формулу (57) к виду (59). Однако формулы (58) и (60) нельзя привести к одному и тому же виду одной лишь заменой единиц измерения! Запишите формулу (58) так, чтобы в неё входили 𝑣𝑟 и 𝑡сек. Для этого достаточно разделить обе её стороны на 𝑐 и учесть, что 𝑡/𝑐=𝑡сек :
𝑡
сек
'
=-
𝑣𝑟
𝑐
⋅
𝑥
𝑐
+
𝑡
сек
=
𝑡
сек
-
𝑥
𝑣𝑟
𝑐²
.
(58')
Формула (58') отличается от формулы (60) в тексте членом 𝑥𝑣𝑟/𝑐², которым можно в большинстве случаев пренебречь, так как обычно скорость 𝑣𝑟 намного меньше, чем скорость света 𝑐. Пример. Наибольшая скорость, с которой летал человек, достигается на искусственных спутниках Земли и примерно равна 30 000 км/час или 8000 м/сек. Наибольшее расстояние между космонавтом в спутнике и наблюдателем на Земле имеет место, когда наблюдатель находится на стороне Земли, противоположной положению спутника в этот момент. Тогда расстояние между ними примерно равно диаметру Земли — около 13⋅10⁶ м. Таким образом, наибольшее значение члена 𝑥𝑣𝑟/𝑐², достигнутое до сих пор с участием наблюдателей, равно
(13⋅10⁶
м
)
(8⋅10³ м/сек)
(3⋅10⁸ м/сек)²
=
10⁻⁶
сек
.
Конечно, такой интервал времени доступен измерению современными средствами, но его едва ли понадобится измерять в ходе анализа экспериментов на спутниках хотя бы уже потому, что космонавт обычно поддерживает связь с наземным наблюдателем на обращённой к нему стороне планеты! 1)
1) После выхода в свет американских изданий книги Тейлора и Уилера и их сборника решений к упражнениям соотечественники авторов уже успели побывать на Луне. Взяв с форзаца книги величину расстояния от Земли до Луны и учтя, что первая космическая скорость на Луне составляет всего около 1700 м/сек, читатель найдёт, что член 𝑥𝑣𝑟/𝑐 в формуле (58') и в данном случае остаётся меньше 10⁻⁵ сек, когда астронавты кружат по окололунной орбите. Первую космическую скорость для Луны можно получить, приравняв друг другу центростремительную силу лунного притяжения и центробежную силу, действующую при движении по круговой орбите:
𝑣²
𝑅 = 𝐺
𝑀
𝑅²
(здесь уже произведено сокращение на величину массы космического корабля); в качестве 𝑅 следует положить величину радиуса Луны, 𝑅=1740 км=1,74⋅10⁶ м; масса Луны равна 𝑀=7,3⋅10²² кг. Конечно, наибольшей скорости космический корабль достигает на обратном пути к Земле, при вхождении в её атмосферу, но тогда слишком мала величина 𝑥. — Прим. перев. ▲
39. Пределы применимости преобразования Галилея
Найдём из табл. 8 приближённые выражения функций sh θ и ch θ с точностью до членов второго порядка:
sh θ
≈
θ
,
ch θ
≈
1
+
θ
2
(в первом случае поправка второго порядка просто равна нулю!). Вид формул (37) с точностью до членов второго порядка малости можно получить, имея в виду, что даже в этом приближении θ𝑟≈β𝑟. Тогда в этом втором приближении будем иметь
𝑥'
=
𝑥
⎛
⎜
⎝
1
+
β𝑟²
2
⎞
⎟
⎠
-
β
𝑟
𝑟
,
𝑡'
=-
β
𝑟
𝑟
+
𝑡
⎛
⎜
⎝
1
+
β𝑟²
2
⎞
⎟
⎠
.
Коэффициенты, входящие в эти уравнения, отличаются от коэффициентов в формулах (57) и (58) менее чем на 1%, если принять
β𝑟²
2
<
10⁻²
или
β
𝑟
²
<
1
50
,
откуда приближённо получим
β
𝑟
<
1
7
,
что и требовалось получить.
При старте с места гоночный автомобиль развивает ускорение 𝑎=𝑣/𝑡=4 м/сек². Если поддерживать такое ускорение постоянным, то скорости 𝑣=(1/7)⋅3⋅10⁸ м/сек можно достигнуть за срок примерно в 𝑡=𝑣/𝑎=10⁷ сек, т.е. около 4 месяцев. Даже с ускорением 7𝑔≈70 м/сек² для достижения этой скорости потребовалось бы около недели! ▲
40. Столкновения в теории Ньютона и в теории относительности
В системе отсчёта ракеты частицы после столкновения разлетаются вдоль оси 𝑦 со скоростями ±β𝑟. В упражнении 20 было показано [формула (49)], что 𝑥- и 𝑦- компоненты скоростей этих частиц в лабораторной системе отсчёта будут равны
β
𝑥
=
th
θ
𝑟
=
β
𝑟
,
β
𝑦
=
β𝑦'
ch θ𝑟
=±
β𝑟
ch θ𝑟
.
Тангенс угла 𝑎/2, образованного осью 𝑥 и любым из этих двух векторов скорости в лабораторной системе отсчёта (см. рис. 53), даётся формулой
tg
α
2
=
β𝑦
β𝑥
=
1
ch θ𝑟
=
√
1-β
𝑟
²
.

Рис. 147.
Требуется найти величину малого угла δ/2 (рис. 147), который составляет разность между π/4 радиан и α/2, откуда получается сам угол δ как отклонение полного угла α, образованного векторами скорости в лабораторной системе отсчёта, от прямого, т.е. от π/2=90°. Из формулы 13 в табл. 8 найдём
tg
π
-
tg
α
tg
δ
=
tg
⎛
⎜
⎝
π
-
α
⎞
⎟
⎠
=
4
2
.
2
4
2
1
+
tg
π
⋅
tg
α
4
2
Воспользовавшись полученным выше выражением для tg α/2 и приняв во внимание, что tg π/4=1, а также что для малых δ справедливо приближённое равенство tg δ/2≈δ/2, мы придём к формуле
δ
2
=
1-√1-β𝑟²
1+√1-β𝑟²
≈
1-(1-β𝑟²/2)
1-(1-β𝑟²/2)
=
β𝑟²/2
2-β𝑟²/2
≈
β𝑟²
4
;
δ
=
β𝑟²
2
,
где выражение √1-β𝑟² было подвергнуто разложению по правилу бинома Ньютона, в котором мы оставили лишь два первых слагаемых. От нас требовалось выяснить, при каких β𝑟 угол δ не превышает 10⁻² рад. Очевидно, это условие принимает вид
β
𝑟
²
<
1
50
или
β
𝑟
<
1
7
.
Когда симметричные относительно друг друга скорости сталкивающихся и разлетающихся частиц в системе отсчёта ракеты будут меньше этой величины, угол между векторами скорости разлетающихся частиц в лабораторной системе будет отличаться от прямого менее чем на 10⁻² рад. В лабораторной системе отсчёта, где одна из частиц первоначально покоилась, скорость налетающей частицы поэтому должна быть меньше, чем 2β 𝑟<2/7. ▲
41. Примеры предельных переходов к механике Ньютона
Пример
движения
β
Корректно ли в этом примере
использование механики Ньютона
?
См. в тексте
(стр.
118
)
1/37200
Да, потому что
β<1/7
10⁻⁴
Да
1/137
Да
79/137
Нет
4/30
Да, на пределе
10
⁻²
Да
▲
42. Замедление времени для μ-мезона — подробный пример
Решение дано в тексте.
43. Замедление времени для π⁺-мезона
Если бы замедления времени не происходило, то из условий задачи следовало бы, что на расстоянии 5,4 м от мишени оставалась бы нераспавшейся половина мезонов. В упражнении 10 [см. формулу (44)] было выяснено, что множитель, характеризующий замедление времени, — это ch θ𝑟. Следовательно, с точки зрения лабораторной системы отсчёта в рассматриваемом опыте π-мезоны будут «жить» в течение срока, в 15 раз превышающего их «собственное время жизни»— то, которое наблюдается в системе отсчёта ракеты, где они покоятся. В лаборатории те же мезоны летят с околосветовыми скоростями, и поэтому они смогут пролететь около 15 «характерных расстояний» (см. таблицу в тексте), т.е. приблизительно 80 м, прежде чем их количество в пучке вследствие распада снизится вдвое по сравнению с первоначальным. ▲
44. Аберрация света звёзд
Ориентируем ось 𝑥 в направлении относительного движения. В покоящейся по отношению к Солнцу лабораторной системе отсчёта свет, приходящий от далёких звёзд 𝐵 и 𝐷, будет иметь компоненты скорости β𝑦=±1 и β𝑥=0. В системе отсчёта ракеты (Земли) скорость распространения этого света также равна единице, но теперь 𝑥-компонента его скорости будет равна -β𝑟, т.е. относительной скорости движения двух рассматриваемых систем отсчёта мимо друг друга. Синус угла φ равняется 𝑥-компоненте скорости, разделённой на абсолютную величину скорости:
sin φ
=
β𝑟
1
=
β
𝑟
.
Этот вывод находится в согласии с результатами, полученными в упражнении 22. ▲
45. Опыт Физо
Закон сложения скоростей (24) даёт
β
=(
β'
+
β
𝑟
)(
1
+
β'β
𝑟
)⁻¹
.
При малых β𝑟 это выражение можно разложить по формуле бинома Ньютона, ограничиваясь лишь членами первой степени по β𝑟:
(
1
+
β'β
𝑟
)⁻¹
≈
1
-
β'β
𝑟
.
Используя это разложение в предыдущей формуле и вновь отбрасывая в окончательном результате члены, в которых β𝑟 возводится в степень выше первой, получим требуемый ответ — формулу (62). ▲
46. Черенковское излучение
Формула (63) непосредственно следует из построения на рис. 62. Чтобы испускать черенковское излучение в некоторой среде, частица должна в ней двигаться по крайней мере не медленнее, чем распространяется световой импульс в этой среде. Это видно из формулы (63): косинус угла φ никак не может быть больше единицы. Поэтому в люсите частица, для того чтобы давать черенковское излучение, должна двигаться по крайней мере со скоростью, равной 2/3 скорости света в пустоте. С другой стороны, угол φ в данном веществе будет максимален, когда его косинус имеет наименьшее значение, т.е. при наибольшем значении скорости частиц β. Ясно, что β не может превышать единицу, так что в люсите величина косинуса φ, равная 2/(3β) всегда больше или равна 2/3. Соответствующий этому максимальный угол составляет 0,841 рад, или 48°,2. ▲
47. Искривление лучей света звёзд Солнцем
Путь, равный диаметру Солнца, световой сигнал проходит за время, равное 1,4⋅10⁹ м, или 4,7 сек; это и есть «эффективное время падения» светового луча, проходящего вплотную к поверхности Солнца. Полная скорость падения равна этому времени, умноженному на ускорение силы тяжести у поверхности Солнца (275 м/сек²), так что составляет приблизительно 1300 м/сек, или 4,3⋅10⁻⁶ м пути за 1 м светового времени. Угол отклонения луча, если он малый, можно приблизительно определить как отношение полученной скорости падения к полной скорости света, т.е. к единице. Итак, мы предсказали, что угол, на который отклоняется световой луч, равен 4,3⋅10⁻⁶ рад. Общая теория относительности предсказывает вдвое больший эффект, что хорошо согласуется с данными наблюдений, приведёнными в конце упражнения. ▲
48. Геометрическое истолкование
Упражнение построено так, что каждый шаг рассуждения мал, и читатель постепенно подводится к решению; поэтому едва ли было бы целесообразно давать здесь более детальный анализ. Но в последней части упражнения [часть к)] полезно отметить, что степень рассинхронизированности часов лабораторной системы отсчёта и часов системы ракеты определяется величиной sh θ𝑟 [см. формулу (46)], которая меняет свой знак при изменении знака относительной скорости (а тем самым и параметра относительной скорости). Напротив, степень замедления времени определяется величиной sh θ𝑟 [см. формулу (44)], не меняющей знака при изменении знака скорости. ▲
49. Парадокс часов. II — подробный пример
Решение дано в тексте.
50. Сокращение или поворот?
а) Свет, который приходит в наш глаз в данный момент, происходит от двух событий, по-разномуудалённых от глаза. Поэтому события должны были произойти в разные моменты времени, и это — главное. В данном случае свет должен был выйти из точки 𝐸 на 1 м времени раньше, чем из точки 𝐺, чтобы оба луча одновременно достигли наблюдателя. За этот срок куб, покоящийся в системе отсчёта ракеты, пройдёт относительно наблюдателя путь 𝑥, равный произведению β на 1 м.
б) Интересно, что, наблюдая в этих условиях маленькие объекты одним глазом, можно истолковать увиденное как поворот пролетающего мимо объекта. Так, например, если бы куб был повёрнут, как на рис. 74, можно было бы видеть часть его боковой стороны и укороченную нижнюю, т.е. получился бы тот же эффект, который в предыдущем случае теория относительности объясняла соответственно конечностью скорости распространения света и лоренцевым сокращением. Из рисунка видно, что угол φ такого кажущегося поворота даётся выражением
sin φ
=
β
.
В пределе при β→0 угол кажущегося поворота также стремится к нулю, и получается результат наблюдения, следующий из теории Ньютона. В пределе при β→1 объект представляется повернувшимся на 90° — вам кажется, что он летит, повернувшись к вам своей боковой стороной!
в) Ответы разным наблюдателям:
1) Наблюдателю в системе отсчёта ракеты: «Когда объект покоится в данной системе отсчёта, метод, с помощью которого вы его наблюдаете, не играет роли, так как разное время распространения света от разных частей объекта не приводит к искажению наблюдаемой картины».
2) Наблюдателю, использующему часовую сетку лабораторной системы: «Ваша система часов позволяет вам определять, в какое время происходят далёкие друг от друга события, и корректно фиксировать их одновременность. Однако эта точная бухгалтерия всё же не даёт вам исключительных прав решать, что же произошло «на самом деле», и навешивать ярлык «невсамделишного» на результаты, полученные наблюдателем в системе отсчёта ракеты или сильно удалённым зрителем, проводящим визуальные наблюдения».
3) Зрителю, визуально проводящему наблюдения в лабораторной системе отсчёта: «Если вы понимаете, к чему приводит задержка во времени прихода сигналов от разных точек объекта, то вам должно быть ясно, что зрительное впечатление поворота объекта никак не противоречит результатам наблюдений, проведённых любым из ваших коллег».
Выражение «на самом деле» здесь не может иметь единого значения, независимого от системы отсчёта наблюдателя и от его измерительной методики. Все методы измерения «правильные», но одни оказываются полезнее других, так как дают основу для интуиции и позволяют предсказать результаты того или иного конкретного опыта. ▲
51. Парадокс часов. III
Из этого упражнения уже чуть было не получился «подробный пример»!
а) Если бы была правильной ньютонова механика, то, подвергаясь в течение 10 лет ускорению 1𝑔, вы приобрели бы в конце концов скорость, равную
𝑣
=
𝑎𝑡
=
𝑔𝑡
≈
(10
м
/
сек
²)
(10⋅3⋅10⁷
сек
)
=
=
3⋅10⁹
м
/
сек
,
т.е. вдесятеро превышающую скорость света! Альтернатива этому противоречащему физическим законам выводу дана в тексте упражнения.
б) Решение дано в тексте.
в) Уравнение (66) проще всего проверить, продифференцировав его и сравнив результат с предыдущим уравнением. Продифференцировать гиперболический косинус проще всего, представив его через экспоненты, а результат дифференцирования выразив снова через гиперболическую функцию — на этот раз синус (см. табл. 8).
г) Проделав в уравнении (66) предложенные подстановки, получим
𝑥
=
𝑐²
𝑔
⎡
⎢
⎣
ch
⎛
⎜
⎝
𝑔τсек
𝑐
⎞
⎟
⎠
-1
⎤
⎥
⎦
.
Здесь следует взять в качестве 𝑔≈10 м/сек² и вспомнить, что 10 лет — это приблизительно 3⋅10⁸ сек. Воспользовавшись приближёнными формулами из табл. 8, найдём
𝑥
≈
9⋅10¹⁶
10
⎡
⎢
⎣
ch
⎛
⎜
⎝
10⋅3⋅10⁸
3⋅10⁸
⎞
⎟
⎠
-1
⎤
⎥
⎦
≈
9⋅10¹⁵
𝑒¹⁰
2
м
≈
≈
10²⁰
м
≈
10⁴
световых лет.
Такое расстояние покрывается за время действия двигателя 𝐴 если же его удвоить, то мы получим расстояние до самой дальней точки пути — 20 000 световых лет. ▲
52. Наклонный стержень
Решение этого упражнения основывается на относительности одновременности (см. упражнение 11). В лабораторной системе отсчёта все точки стержня пересекают ось 𝑥 одновременно при 𝑡=0. Но картина, наблюдаемая в системе отсчёта ракеты, будет другой! Когда в лабораторной системе 𝑡=0, часы системы отсчёта ракеты будут показывать на положительной части оси 𝑥' моменты времени, меньшие нуля [часть в) упражнения 11]. Это значит, что к моменту 𝑡'=0 по часам системы отсчёта ракеты правый конец стержня уже пересечёт ось 𝑥. Но середина стержня проходит через начало координат ракеты в момент 𝑡'=0, так что в системе отсчёта ракеты метровый стержень будет наблюдаться несколько повёрнутым правым концом вверх (см. рис. 77б). Перейдём к количественному выражению эффекта. В лабораторной системе отсчёта правый конец стержня пересекает ось 𝑥 в момент 𝑡=0 и в точке 𝑥=1/2 м. Координаты того же события в системе отсчёта ракеты следуют из формул преобразования Лоренца:
𝑥'
=
𝑥 ch θ
𝑟
=
1
2
ch θ
𝑟
м
,
𝑡'
=-
𝑥 sh θ
𝑟
=-
1
2
sh θ
𝑟
м
.
Требуется найти положение правого конца стержня не в отрицательный момент времени 𝑡'=-𝑥 sh θ𝑟, а в момент 𝑡'=0, т.е. на 𝑥 sh θ𝑟=½⋅sh θ𝑟 м светового времени позже. Какое положение по истечении этого срока займёт правый конец стержня? Значения компонент скорости конца метрового стержня можно определить по формуле, полученной в упражнении 20 [формула (49), в которой следует поменять местами штрихованную и нештрихованную скорости и изменить знак параметра скорости на обратный]:
β
𝑦'
=
β𝑦
ch θ𝑟
,
β
𝑥'
=-
th θ
𝑟
.
Тогда в момент 𝑡'=0 правый конец метрового стержня окажется в точке с координатами
𝑦'
=
β
𝑦'
𝑡'
=
β𝑦
ch θ𝑟
1
2
sh θ
𝑟
м
=
1
2
β
𝑦
th θ
𝑟
м
и
𝑥'
=
1
2
ch θ
𝑟
-
th θ
𝑟
ch θ𝑟
2
=
1
2
⎛
⎜
⎝
ch θ
𝑟
-
sh²θ𝑟
ch θ𝑟
⎞
⎟
⎠
=
1
2 ch θ𝑟
.
В тот же момент (𝑡'=0) середина метрового стержня совмещается с началом координат системы отсчёта ракеты. Поэтому угол φ, образованный стержнем и осью 𝑥 системы отсчёта ракеты, определяется выражением
tg φ
=
𝑦'
𝑥'
β
𝑦
sh θ
𝑟
.
▲
53. Парадокс метрового стержня
Соударения не произойдёт. Конечно, в системе отсчёта ракеты стержень не подвергается лоренцеву сокращению, но ведь там движущаяся вверх пластинка наклонена — её правый край приподнят. В сущности можно рассматривать рис. 77 как изображение отверстия в пластинке! Правый край этого отверстия вплотную проскальзывает перед самым «носом» горизонтального метрового стержня, а левый край отверстия — сразу вслед за «хвостом» метрового стержня. Так метровый стержень при всей своей стандартной длине точь-в-точь «помещается» в подвергнувшемся сокращению отверстии, повёрнутом под углом. ▲
54. Тонкий человек на решётке
Вот ключ к решению этого упражнения. На свете не существует таких вещей, как «жёсткий» метровый стержень или «жёсткий» мост. Пусть длинный мост имеет опоры только на своих концах. Быстро уберём из-под него правую опору, и правый конец моста сразу же начнёт падать. Но середина моста ещё не начнёт! Ведь она не «знает» ещё об исчезновении правой опоры. Стоящий посередине моста человек ощущает под своими ногами его металл таким же устойчивым, как прежде. Падение начнётся здесь с определённым опозданием, и время задержки определяется сроком, за который упругое колебание проходит через металл от правого конца моста до места, где стоит человек. Аналогично обстоит дело и с метровым стержнем. Конечно, его жёсткость можно повысить, делая его из улучшенных материалов,— при этом увеличится скорость распространения в нем упругих колебаний, так что сократится время задержки, после которого середина стержня начнёт падать. Но возможности улучшения материала стержня не беспредельны: скорость распространения упругих волн никогда не может превысить скорости света. Время задержки не может стать меньше времени распространения света.
Вера в существование абсолютно жёстких предметов — вредное заблуждение, и отказ от него позволяет разобраться, например, в такой, казалось бы, парадоксальной ситуации. Пусть метровый стержень сначала покоится, лёжа на узкой полке в ракете, а затем полка резко откидывается вниз и стержень начинает падать с ускорением силы тяжести. В системе ракеты стержень падает «синхронно» на всём своём протяжении, но в лабораторной системе это будет не так: там ракета мчится вправо — параллельно ориентации полки — с огромной скоростью. Поэтому в лабораторной системе отсчёта сначала начинает падать правый конец метрового стержня, когда левый его конец всё ещё продолжает лежать на полке. В этой системе наблюдается, что стержень искривлён (и он искривлён там на самом деле), что, конечно, не противоречит релятивистски сформулированному понятию «жёсткости»! Итак, стержень может быть прямым в одной системе отсчёта и искривлённым — в другой.
Нам ясна теперь сущность этого кажущегося парадокса, и мы знаем, что метровый стержень упадёт в отверстие. В лабораторной системе отсчёта этот вывод напрашивался сам собой: метровый стержень там был укорочен до длины, много меньшей метра, и ему ничего не стоило провалиться в отверстие. В системе отсчёта ракеты, напротив, отверстие сократилось до размеров, намного меньших метра, тогда как метровый стержень приобрёл свою полную длину. При этом, однако, мы должны были признать, что метровый стержень не был — и не мог быть в принципе — абсолютно жёстким, его правый конец выгнулся вниз, этот конец погрузился в отверстие, а за ним туда нырнул и весь стержень. ▲
РЕШЕНИЯ УПРАЖНЕНИЙ К ГЛ. 2
55. Быстрые электроны
а) Энергия, приобретаемая на 1 м пути, равна
40⋅10³ Мэв
3⋅10³ м
≃
13
Мэв
/
м
.
Если бы выполнялись законы механики Ньютона, то энергия электрона, движущегося со скоростью света, была бы равна
1
2
𝑚𝑐²
=
1
2
(0,511
Мэв
)
≈
1
4
Мэв
(по Ньютону)
,
и эта энергия была бы достигнута на дистанции
1/4 Мэв
13 Мэв/м
=
1
52
м
≈
2
см
!
б) Согласно формуле (107), полученной во введении к этим упражнениям,
1-β
≈
𝑚²
2𝐸²
,
если
β
≈
1
.
Здесь величины 𝑚 и 𝐸 выражены в одних и тех же единицах. Так как нас интересует их отношение, то выбор единиц (если они одинаковы для обеих величин!) не играет роли. Тогда, используя единицы Мэв, получим
1-β
≈
(1/2 Мэв)²
2⋅(4⋅10⁴ Мэв)²
≈
1
128
⋅
10⁻⁸
<
10⁻¹⁰
.
Скорость этих электронов отличается от скорости света менее чем на десятимиллиардную часть последней. При состязании на скорость полёта между такими электронами и световой вспышкой на дистанции 1000 км=10⁹ мм свет опередит электроны всего лишь на
(1-β) 10⁹
мм
<
10⁻¹⁰⋅10⁹
мм
=
0,1
мм
.
в) Множитель, характеризующий лоренцево сокращение, равен при этом
1
ch θ
=
𝑚
𝐸
=
0,5 Мэв
40⋅10³ Мэв
=
1,2⋅10⁻⁵
,
так что сократившаяся длина «3000-метровой» трубы при измерении в системе отсчёта ракеты составляет всего
(3⋅10³
м
)⋅1,2⋅10⁻⁵
≈
4⋅10⁻²
м
=
4
см
.
▲
56. Космические лучи
а) Коэффициент, характеризующий замедление времени, определяется формулой (44) из упражнения 10, так что
Δ
𝑡'
=
Δ𝑡
ch θ𝑟
=
Δ
𝑡
𝑚
𝐸
=
Δ
𝑡
⋅
10⁹ эв
10²⁰ эв
,
так что для интервала времени, равного
Δ
𝑡
≈
(10⁵
лет
)
(3⋅10⁷
сек
/
год
)
,
найдём
Δ
𝑡'
=
10⁵⋅3⋅10⁷⋅10⁻¹¹
сек
=
30
сек
.
Пока за свои 30 сек космический путешественник успевает пересечь Галактику, на Земле проходит сто тысячелетий!
б) Коэффициент, характеризующий лоренцево сокращение Галактики, определяется по формуле (38) из упражнения 9 и равен
10⁵ св. лет
10⁻¹⁵ м
=
(10⁵ лет)(3⋅10⁷ сек/год)(3⋅10⁸ м/сек)
10⁻¹⁵ м
=
=
9⋅10²⁰ м
10⁻¹⁵ м
≈
10³⁶
=
ch
θ
𝑟
=
𝑚
𝐸
.
Чтобы протон приобрёл необходимую скорость, ему необходимо придать энергию, равную в единицах массы
𝑇
=
𝐸
-
𝑚
=
10³⁶𝑚
-
𝑚
≈
10³⁶𝑚
≈
≈
10³⁶𝑚
⋅
10³⁶⋅10⁻²⁷
кг
≈
10⁹
кг
,
иначе говоря, потребуется превратить в энергию около одного миллиона тонн массы, чтобы разогнать этот протон! ▲
57. Границы ньютоновской механики
а) Ответ также указан в конце книги!
б) Согласно формуле без номера, находящейся на стр. 155 между формулами (81) и (82), из разложения бинома Ньютона следует разложение по степеням β и для релятивистской энергии:
𝐸
=
𝑚
+
𝑚
β²
2
+
3
8
𝑚β⁴
+
…,
откуда
𝑇
=
𝐸
-
𝑚
=
𝑚
β²
2
+
3
8
𝑚β⁴
+
…
.
Здесь первый член справа — обычное ньютоновское выражение для кинетической энергии. Сравнивая с ним следующий член, найдём, что поправка порядка 10⁻² к ньютоновской механике, рассматриваемая в этом упражнении, будет иметь место при
⎡
⎢
⎣
𝑚β²
+
3
𝑚β⁴
⎤
⎥
⎦
-
𝑚β²
2
8
2
=
10⁻²
,
𝑚β²/2
т.е. когда
β²
=
4
3
⋅
10⁻²
.
Это и есть граница ньютоновской механики; сравните её с другими «границами», найденными в упражнениях 39 и 40 гл. 1. При такой скорости отношение кинетической энергии к энергии покоя равно
𝑚β²
2
⋅
𝑚⁻¹
=
β²
2
=
2
3
⋅
10⁻²
.
В случае протона его кинетическая энергия, соответствующая границе применимости ньютоновской механики, равна
𝑇
𝑝
=
2
3
⋅
10⁻²
𝑚
𝑝
≈
2
3
⋅
10⁻²
Бэв
=
2
3
⋅
10⁻²⋅10⁹
эв
=
2
3
⋅
10⁷
эв
≈
7
Мэв
.
В случае же электрона соответствующая кинетическая энергия равна
𝑇
𝑒
=
2
3
⋅
10⁻²
𝑚
𝑒
≈
2
3
10⁻²⋅10⁶
эв
≈
3
кэв
.
▲
58. Релятивистская ракета
а) Законы сохранения импульса и энергии выражаются как
-
𝑚
sh
θ
выбр
+
𝑀₂sh (𝑑θ)
=
0,
𝑚
ch
θ
выбр
+
𝑀₂ch (𝑑θ)
=
𝑀₁.
Перенесите вторые слагаемые из левых частей обеих формул вправо, разделите соответствующие части получившихся формул друг на друга и учтите соотношения
sh θвыбр
ch θвыбр
=
th
θ
выбр
=
β
выбр
,
sh (𝑑θ)
≈
𝑑θ
,
ch (𝑑θ)
≈
1
.
Вы получите требуемые соотношения.
б) Когда параметр скорости мал, β=θ, так что
𝑣
=
β𝑐
≈
β
выбр
𝑐
ln
𝑀₁
𝑀
=
𝑣
выбр
ln
𝑀₁
𝑀
,
что и требовалось показать.
в) Из закона сохранения энергии легко заключить, что 𝑚+𝑀₂=𝑀₁ так как для того, чтобы получить 𝑀₁, нужно сложить 𝑚 и 𝑀₂, предварительно умноженные на коэффициенты, много большие единицы. Рассматриваемый здесь процесс — это «обращённое неупругое столкновение»: в неупругих столкновениях кинетическая энергия переходит в массу покоя, тогда как здесь, наоборот, масса покоя превращается в кинетическую энергию ракеты и продуктов сгорания топлива.
г) Даже при наибольших допустимых отношениях масс (𝑀₁/𝑀→∞) и при самых высоких скоростях выброса (βвыбр→1) скорость ракеты будет лишь приближаться к скорости счета, но не сможет её превысить:
β
=
th θ
→
1
при
θ
=
β
выбр
ln
𝑀₁
𝑀
→
∞
.
д) Вернёмся к выражению закона сохранения энергии, данному в ответе к части а). При очень большой скорости выброса величина ch θвыбр стремится к бесконечности, и чтобы закон сохранения не нарушался при конечных значениях 𝑀₂ и 𝑀₁, величина массы выбрасываемых продуктов сгорания 𝑚 должна становиться очень малой. Предельный случай достигается для света, когда масса покоя ракетного горючего полностью превращается в энергию излучения.
е) Ракета, работающая на световых вспышках, не очень практична. Предположим (для грубой оценки), что лампа вместе с батарейкой обладает массой 1/2 кг и излучает пучок света мощностью 5 вт; за полчаса (около 2000 сек) излучённая энергия составит тогда 10⁴ вт⋅сек, или 10⁴ дж. Чтобы найти количество массы, перешедшей при этом в энергию, следует разделить 10⁴ дж на 𝑐² Получается приблизительно 10⁻¹³ кг — неудивительно, что наша лампа с батарейкой не становится заметно легче после работы!
Отношение масс для такой «ракеты» составляет
1
2
кг
×
⎛
⎜
⎝
1
2
кг
-
10⁻¹³
кг
⎞
⎟
⎠
,
или приблизительно 1+2⋅10⁻¹³. Чтобы вычислить скорость, приобретённую при этом первоначально покоившейся лампой [формула (110)], нужно найти натуральный логарифм числа 1+2⋅10⁻¹³; логарифм единицы равен нулю, и вблизи этого значения натуральный логарифм возрастает так же, как и его аргумент. Иными словами, ln(1+δ)≈δ при δ≪1. Отсюда и из формулы (110) следует, что скорость, приобретённая лампой, равна
β
≈
θ
=
ln(1+2⋅10⁻¹³)
≈
2⋅10⁻¹³
или
𝑣
=
𝑐β
=
6⋅10⁻⁵
м
/
сек
.
Быстро бы прогорела та пиротехническая компания, которая выпускала бы ракеты весом по полкило, «летающие» с такой скоростью! Причина того, что лампа способна развить лишь такую ничтожную скорость, выясняется при обсуждении, предложенном в тексте упражнения. Дело в том, что «шлак», остающийся при реакции — использованные батареи,— ускоряется здесь вместе с ракетой. Напротив, химическая ракета практичнее, так как выбрасывает свой шлак через сопло. Существует ряд «бесшлаковых» реакций для элементарных частиц, и в случае исходных частиц с отличными от нуля массами покоя потенциально важны реакции типа
(Частица)
+
(Античастица)
→
Излучение.
В качестве пары частица — античастица здесь могут фигурировать, например, электрон и позитрон или протон и антипротон. Ещё практичнее взять электрически нейтральные вещество и антивещество (атомы антиводорода, антижелеза и пр.) и хранить их в отдельных местах. Однако по развитию техники мы ещё очень далеки от возможности производить такие количества антивещества, которые требовались бы для ускорения ракет путём превращения в излучение частиц и античастиц при их аннигиляции в двигателе ракеты или непосредственно за её кормой. В упражнении 104 рассмотрены трудности, с которыми столкнутся проектировщики межзвёздных полётов, когда удастся преодолеть эту техническую трудность.
ж) Когда коэффициент, характеризующий замедление времени, равен 10, это значит, что ch θ=10. Из «способов быстрой оценки для простых смертных» в табл. 8 можно заключить, что при θ≫1 имеет место ch θ≈𝑒θ. Если θ=0, то 𝑒θ≈20, а ch θ≈10, что и требовалось. Если принцип ускорения ракеты основан на полном превращении массы в излучение (без шлака!), то из формулы (110) следует
𝑀₁
=
(Масса при старте)
=
𝑀
⎛
⎜
⎝
Масса после достижения
⎞
⎟
⎠
требуемой скорости
=
𝑒
θ
≈
20
=
⎛
⎜
⎝
Удвоенный коэффициент
замедления времени
⎞
⎟
⎠
.
В случае химической ракеты достижение этой же скорости (или такой же величины коэффициента замедления времени) обходится намного дороже. Скорость выброса берётся равной
β
выбр
=
4⋅10³
3⋅10⁸
=
1,33⋅10⁻⁵
,
и для неё из формулы (108) следует
ln
=
Масса при старте
Масса после набора скорости
=
=
θ
βвыбр
=
3
1,33⋅10⁻⁵
=
2,25⋅10⁵
.
Для того чтобы после разгона ракета ещё имела массу 1 т, необходима в этом случае начальная масса
𝑀₁
=
(1
т
)𝑒²²⁵ ⁰⁰⁰
=
10⁹⁷ ⁶⁰⁰
т
.
Хорошенькая ракета, если вспомнить, что масса наблюдаемой Вселенной оценивается по порядку величины в 10⁵⁰ т! ▲
59. Парадокс центра масс
а) В системе отсчёта ракеты пушечные ядра всё время движутся симметрично по отношению к центру трубы, так что центр масс этой системы ядер совпадает с центром трубы и остаётся неподвижным. Пока что никакого парадокса ещё нет.

Рис. 148
б) В лабораторной системе отсчёта выстрелы, посредством которых ядра вводятся в трубу, производятся не одновременно (см. рис. 148, а также упражнение 11). Первое ядро вводится в левый конец трубы ещё до того, как второе ядро вводится в её правый конец, находящийся впереди по ходу движения трубы в лабораторной системе. В этой системе отсчёта скорости ядер различны, так что различны их энергии и импульсы. Как определять теперь положение «центра масс»: считать массы ядер одинаковыми или учитывать такое различие? Ясно, что в приложении к составным системам, отдельные части которых движутся с релятивистскими скоростями, возникает значительная неоднозначность в определении понятия «центр масс». Поэтому вместо того, чтобы характеризовать здесь систему отсчёта ракеты как «систему центра масс», было бы лучше назвать её «системой нулевого импульса»— это было бы более общее утверждение. Если, несмотря на различие их энергий (иногда говорят: «масс движения», см. конец табл. 13), мы придавали бы обеим сталкивающимся массам одинаковое значение, то тем самым ввели бы фактически такое понятие «центра масс», которое во избежание недоразумений было бы лучше называть «центром барионного числа». Иначе говоря, в этом случае значение тела оценивалось бы не по количеству содержащейся в нем энергии, а по числу входящих в него частиц (протонов и нейтронов, являющихся двумя разновидностями барионов, из которых построено обычное вещество). Мировая линия центра барионного числа наших двух ядер изображена на рис. 148 пунктирной линией. Её можно определить, взяв в соответствующие моменты времени положения обоих ядер и найдя для каждого момента точку, лежащую точно посередине. Найденная линия испытывает колебания, и не удаётся усмотреть связи между её видом и законами, управляющими движением ядер. Поэтому понятие центра барионного числа едва ли может быть плодотворным.
В противоположность пунктирной линии штриховая изображает мировую линию центра гравитационного притяжения, оказываемого системой двух ядер на любую далёкую массу (до того момента, когда одно из ядер соударяется с заглушкой в конце трубы). Такое представление о локализации центра гравитационного притяжения подкрепляется двумя соображениями. Во-первых, рассмотрим в системе отсчёта ракеты положение центра масс ядер; там он всё время совпадает с центром трубы в начале координат системы отсчёта ракеты. Переходя к лабораторной системе отсчёта, получим как раз нашу штриховую линию (скорость βракеты=th ракеты)- Во-вторых, найдём скорость переноса энергии (массы) вправо как сумму переносов, осуществляемых каждым ядром по отдельности. Выясним, с какой скоростью должны были бы двигаться эти ядра, если бы они были объединены, чтобы обеспечить такую же скорость переноса энергии (массы) вправо. Мы придём тогда вновь к только что полученной величине βракеты как скорости движения центра гравитационного притяжения (т.е. придём к штриховой прямой мировой линии, изображающей движение центра трубы; детали вычисления см. в конце этого анализа).
Всё было бы очень просто и сводилось бы к приведённым рассуждениям, если бы не было самой трубы, а ядра после своего столкновения в мировой точке 𝑃 (где они фактически меняются ролями) навсегда разлетелись бы в противоположные стороны. Тогда, конечно, соответствующий ядрам центр гравитационного притяжения навсегда стал бы двигаться по штриховой линии. Но в тот момент, когда первое ядро ударяется в мировой точке 𝑄 с левой заглушкой трубы, оно изменяет направление своего движения на обратное, и оба ядра с этого момента летят вправо. Значит, на некоторый срок скорость переноса энергии (массы) должна возрасти по сравнению с тем, что было получено ранее. Этот срок кончается в момент, соответствующий событию 𝑅, когда скорость переноса возвращается к своему прежнему значению, так что после 𝑅 вновь можно утверждать, что энергия (масса) объединённой системы ядро 1 + ядро 2 движется вправо со скоростью системы отсчёта ракеты βракеты (штриховая линия, проходящая через мировую точку 𝑆 предстоящего столкновения ядер).
Итак, парадокс состоит в том, что в промежуток времени от 𝑡𝑄 до 𝑡𝑅 должен был бы происходить ускоренный перенос энергии (массы) вправо и следовало бы ожидать, что за это время эффективный центр притяжения системы ядер будет ускоренно сдвигаться вправо, а когда он снова приобретёт свою исходную скорость, следовало бы ожидать, что его мировая линия станет проходить несколько правее прежней штриховой линии. Однако такого сдвига не зафиксировано. Как же совместить ускоренный перенос энергии (массы) вправо с тем фактом, что центр притяжения продолжает двигаться по прежней прямой мировой линии?

Рис. 149.
Чтобы найти ответ, рассмотрим такой пример. Пусть некий бездельник подпирает заднюю стенку надстройки на пароме. Тогда он совершает работу, «двигая» стенку, мощностью 𝐹𝑣, если давит своим плечом на неё с силой 𝐹 и движется со скоростью 𝑣. Но в этом нет его заслуги, так как палуба, расходуя такую же мощность, совершает работу над ним. Иначе говоря, мощность 𝐹𝑣 втекает в него через ноги и такая же мощность вытекает из его плеча. Мощность — скорость переноса энергии, и на релятивистском языке её нужно понимать как скорость переноса энергии и массы. Хотя наш бездельник (вопреки своим принципам) невольно совершает перенос энергии (массы), его центр тяжести движется нисколько не быстрее, чем если бы он стоял по стойке «смирно». Аналогичное происходит и с системой двух ядер: не ограничиваясь переносом вправо энергии (массы) с такой скоростью, что их центр притяжения движется по штриховой линии, ядра испытывают через определённые промежутки времени толчки со стороны левой заглушки трубы и переносят эти импульсы правой заглушке (это аналогично постоянному переносу энергии через нашего бездельника, только теперь сила действует прерывисто). Дополнительный перенос энергии (массы), происходящий при этом, вообще не приводит к дополнительному смещению центра притяжения 1).
1) При соударении с заглушкой в конце трубы каждое ядро обменивается с ней импульсом и приводит её, таким образом, в движение. Даже в системе отсчёта ракеты, где соударения в противоположных концах трубы происходят одновременно, импульсы, переданные трубе, не сразу взаимно уничтожаются ввиду конечной скорости распространения акустической волны: хотя суммарный переданный импульс равен нулю, труба должна сначала некоторое время (симметрично) колебаться, и эти колебания, конечно, переносят энергию. В лабораторной системе отсчёта такая симметрия нарушается в силу относительности одновременности, и для полного анализа переноса энергии (массы) здесь следовало бы учесть поток, распространяющийся по самой трубе. Полезно обратить внимание на то, что «неподвижно закреплённая» труба соответствует бесконечно большой массе по крайней мере заглушек, в противном случае ядра не сохраняли бы абсолютной величины своих импульсов. Но в таком случае можно пренебречь энергией, переносимой акустическими волнами, если рассматривать центр гравитационного притяжения всей системы в целом (правда, при этом было бы логично пренебречь и массами самих ядер!). Читатель видит отсюда, что ситуация, имеющая место между моментами 𝑡𝑄 и 𝑡𝑅, описана авторами неполно; ему было бы полезно обдумать вопрос о том, как изменится задача в случае разных масс заглушек и разной степени жёсткости трубы (в обеих системах отсчёта). Разумеется, анализ следует проводить качественно.— Прим. перев.
в) Центр гравитационного притяжения системы труба + ядра движется вправо с постоянной скоростью βракеты в лабораторной системе отсчёта.
Дополнительные данные к части б)
Обозначим значения скорости и параметра скорости ядер в системе отсчёта ракеты через ±β' и ±θ'. Тогда параметры скорости в лабораторной системе отсчёта будут равны θ𝑟+θ' и θ𝑟-θ'. Скорость переноса энергии (массы) даётся выражением
Импульс
=
𝑚β₁
√1-β₁²
+
𝑚β₂
√1-β₂²
=
=
𝑚(sh θ
𝑟
ch θ'
+
ch θ
𝑟
sh θ')
+
+
𝑚(sh θ
𝑟
ch θ'
-
ch θ
𝑟
sh θ')
=
=
2𝑚
ch θ'sh θ
𝑟
.
Полная величина энергии (массы) в системе отсчёта ракеты равна
𝑚
√1-β₁²
+
𝑚
√1-β₂²
=
2𝑚
ch θ'
.
Разделив её на скорость переноса энергии (массы), найдём sh θ𝑟. Итак, параметр скорости системы ядро 1 + ядро 2 совпадает с параметром скорости ракеты θ𝑟 относительно лабораторной системы отсчёта, что и требовалось доказать. ▲
60. Второй вывод релятивистского выражения для импульса
а) В системе отсчёта ракеты шар 𝐴 движется параллельно направлению оси 𝑦 как до, так и после столкновения (см. рис. 83). Поэтому разности координат в системе ракеты между событиями столкновения шаров и ударом шара 𝐴 о верхнюю стенку равны
Δ
𝑥'
=
0
,
Δ
𝑦'
=
Δ
𝑦
и
Δ
𝑡
.
Из формул (42) следует промежуток времени в лабораторной системе
Δ
𝑡
=
Δ
𝑥'
sh
θ
𝑟
+
Δ
𝑡'
ch
θ
𝑟
=
Δ
𝑡'
ch
θ
𝑟
.
Это выражение позволяет определить 𝑦-компоненту скорости шара 𝐴 в лабораторной системе отсчёта через скорость этого шара в системе отсчёта ракеты β=Δ𝑦'/Δ𝑡':
(β
𝐴
𝑦
)
лаб
=
Δ𝑦
Δ𝑡
=
Δ𝑦'
Δ𝑡' ch θ𝑟
=
β
ch θ𝑟
.
б) Сравнивая рис. 83 и 84, видим, что скорость шара 𝐴 в системе отсчёта ракеты равна скорости шара 𝐵 в лабораторной системе отсчёта. Вертикальная компонента скорости шара 𝐴 в лабораторной системе была найдена в части а) этого упражнения. Горизонтальная же компонента скорости шара 𝐴 в лабораторной системе — это просто скорость движения этой системы относительно системы отсчёта ракеты, β𝑟. Подставляя значения компонент скорости и импульса, данные на рис. 101, в закон пропорциональности, выведенный на основании этого же рисунка (см. текст данного упражнения), получим соотношение
𝑝𝑥
2𝑚β
=
th θ𝑟
2β/ch θ𝑟
(равенство этих отношений означает, что векторы импульса и скорости имеют одинаковое направление). Отсюда и следует формула
𝑝
𝑥
𝑚
sh
θ
𝑟
.
▲
61. Второй вывод релятивистского выражения для энергии
а) На основании двух частей рис. 102 можно непосредственно записать закон сохранения импульса в ньютоновском пределе. Из верхней киноленты, снятой в лаборатории, следует закон сохранения в лабораторной системе отсчёта. Когда же на основании нижней киноленты рис. 102, снятой из ракеты, записывается закон сохранения импульса в этой системе, то стоящая в обеих частях уравнения скорость относительного движения систем β𝑟 уничтожается, и остаётся в точности уравнение, уже полученное в лабораторной системе отсчёта. Итак, в системе отсчёта ракеты импульс автоматически сохраняется, если он сохранялся в лабораторной системе; но это верно лишь для столкновений с малыми скоростями.
б) Переходя к релятивистскому анализу, заметим, что в системе отсчёта ракеты (нижняя кинолента на рис. 103) закон сохранения импульса принимает вид
𝑚₁
sh
(θ₁-θ
𝑟
)
+
𝑚₂
sh
(θ₂-θ
𝑟
)
=
=
𝑚₁
sh
(
θ
₁-θ
𝑟
)
+
𝑚₂
sh
(
θ
₂-θ
𝑟
)
.
Воспользовавшись формулой (11) из правого столбца табл. 8, преобразуем здесь каждое из четырёх слагаемых так, чтобы получилось соотношение вида (112). У нас появятся две скобки: первая
(
𝑚₁
sh
θ₁
+
𝑚₂
sh
θ₂
-
𝑚₁
sh
θ
₁
-
𝑚₂
sh
θ
₂
)
и вторая
(
𝑚₁
ch
θ₁
+
𝑚₂
ch
θ₂
-
𝑚₁
ch
θ
₁
-
𝑚₂
ch
θ
₂
)
Каждая из них должна самостоятельно обращаться в нуль, что следует из условия задачи. Значит, должны выполняться уравнения (111) и (113). Короче говоря, чтобы импульс сохранялся в системе отсчёта ракеты, недостаточно его сохранения в лабораторной системе отсчёта, как это было в предельном случае малых скоростей (в ньютоновской механике), но необходимо ещё, чтобы в лабораторной системе сохранялась и энергия, что выражается уравнением (113).
в) Ход приведённых рассуждений в основном останется без изменения, если массы покоя разлетающихся частиц отличаются от масс частиц до соударения. При этом закон сохранения импульса в лабораторной системе отсчёта принимает вид
𝑚₁
sh
θ₁
+
𝑚₂
sh
θ₂
=
𝑚
₁
sh
θ
₁
+
𝑚
₂
sh
θ
₂
,
а закон сохранения энергии (тоже в лабораторной системе) —
𝑚₁
ch
θ₁
+
𝑚₂
ch
θ₂
=
𝑚
₁
ch
θ
₁
+
𝑚
₂
ch
θ
₂
,
Импульс будет сохраняться и в системе отсчёта ракеты, только если выполняются оба эти закона сохранения одновременно.
Что же касается сохранения кинетической энергии, то заметим, что, вычитая в случае упругого столкновения из соответствующих сторон уравнения (113) тождество 𝑚₁+𝑚₂≡𝑚₁+𝑚₂, получим
(𝑚₁ch
θ₁-𝑚₁)
+
(𝑚₂ch
θ₂-𝑚₂)
=
(𝑚₁ch
θ
₁-𝑚₁)
+
(𝑚₂ch
θ
₂-𝑚₂)
,
𝑇₁
+
𝑇₂
=
𝑇
₁
+
𝑇
₂.
Это и есть выражение того факта, что при упругих столкновениях кинетическая энергия сохраняется. В случае неупругих столкновений, когда 𝑚₁≠𝑚₁ и 𝑚₂≠𝑚₂, сохранения кинетической энергии нет и подобного уравнения записать нельзя. Особый интерес представляют неупругие столкновения без излучения, но с переходом части кинетической энергии в массу покоя: 𝑚₁+𝑚₂>𝑚₁+𝑚₂. ▲
62. Задачи на пересчёт
а) 100 вт — это 100 дж/сек, а так как в году около 30 миллионов секунд, то 100-ваттная лампочка излучает в год энергию, равную 3⋅10⁹ дж. Это соответствует массе покоя, равной (3⋅10⁹ дж)/𝑐²=¹/₃⋅10⁻⁷ кг.
б) 10¹² квт⋅ч= 10¹⁵ вт⋅ч= 10¹⁵⋅3600 вт⋅сек= 3,6⋅10¹⁸ дж. Это соответствует массе покоя (3,6⋅10¹⁸ дж)/𝑐²=40 кг. В действительности же в энергию при этом превращается более 40 кг массы, так как производство электроэнергии неизбежно сопровождается тепловыми потерями (часть массы «уходит» в тепло): так, теряется часть теплоты при использовании химической энергии (при сжигании угля), теряется теплота, возникающая в результате трения из механической энергии (в генераторах гидростанций). Конечно, оценка зависит от того, в каких масштабах рассматривать, например, струи газов, извергаемые трубами тепловой электростанции, работающей на угле. На микроскопическом уровне можно провести деление на массу покоя отдельных молекул и на кинетическую энергию их теплового движения. Напротив, в крупных масштабах получится, что эти горячие газы имеют массу покоя, превышающую сумму масс покоя отдельных составляющих их молекул (см. замечания по поводу «ящика с нагретым газом» на стр. 176). Конечно, та же участь ожидает и большую часть благополучно генерированной «полезной» электроэнергии, ведь её поглотят и превратят в теплоту стены освещённой с её помощью комнаты и т.д. и т.п. Так часть массы покоя угля превращается в электроэнергию, а потом —снова в массу покоя там, где эта энергия потребляется. И за целый год не найти ни одного момента, когда хоть сколько-нибудь заметная часть этих 40 кг энергии существовала в форме электроэнергии.
в) Студент производит энергию со скоростью (мощностью) в 2 лошадиные силы (л. с.): 1/2 л. с. полезной мощности + 3⋅½ л. с. превращается в теплоту (2 л. с. ≈ 1500 вт). Срок, необходимый для того, чтобы превратить 1 кг массы в энергию, можно найти по формуле
1500
вт
⋅𝑡
сек
=
1
кг
⋅𝑐²
,
откуда получается 𝑡сек=6⋅10¹⁴ сек — больше десяти миллионов лет! Конечно, чтобы похудеть на 1 кг, никому не потребуется так долго крутить педали— химические процессы «горения» в организме чрезвычайно расточительны (коэффициент перевода массы в энергию невероятно мал), и удаление продуктов сгорания приводит к намного более быстрой потере массы, чем если бы она превращалась в энергию.
г) Полное количество световой энергии, испускаемой за одну секунду Солнцем, можно подсчитать, умножив величину энергии излучения, проходящую за 1 сек через 1 м² поверхности, перпендикулярной падающим лучам вблизи Земли (т.е. солнечную постоянную), на площадь в квадратных метрах воображаемой сферы радиуса, равного радиусу орбиты Земли, с центром в Солнце. Этот радиус равен приблизительно 𝑟=150 млн. км=1,5⋅10¹¹ м, площадь же соответствующей сферы составляет
4π𝑟²
≈
3⋅10³³
м
²
.
Количество энергии в джоулях, уходящей сквозь эту воображаемую поверхность каждую секунду, равно
(1,4
дж
/
сек
⋅
м
²)
(3⋅10²³
м
²)
≈
4⋅10²³
дж
/
сек
,
что соответствует скорости потери массы Солнцем
(4⋅10²³
дж
/
сек
)/𝑐²
≈
4⋅10⁶
кг
/
сек
—
приблизительно 4000 т в 1 сек. Такова та часть массы Солнца, которая ежесекундно теряется им вследствие превращения вещества в свет. Количество массы такого же порядка излучается Солнцем в форме нейтрино. Ещё большую роль в потерях массы Солнцем играет «солнечный ветер»— непосредственное выбрасывание вещества в пространство. Земля преграждает путь этим потокам на площади, приблизительно равной
π𝑟²
Земля
≈
3⋅(6⋅10⁶
м
)²
≈
10¹⁴
м
²
,
так что на неё падает в секунду около 1,4⋅10¹⁴ дж энергии в форме солнечного света. В год это составляет примерно 4⋅10²¹ дж — почти 50 000 кг энергии (массы). Часть падающего на неё света, конечно, отражается Землёй, а ещё некоторая часть снова излучается ею в космос в других диапазонах частот.
д) Скорость каждого поезда, выраженная в метрах пути на метр светового времени, равна
β
=
𝑣
𝑐
=
45 м/сек
3⋅10⁸ м/сек
=
1,5⋅10⁻⁷
.
При этом полная кинетическая энергия очень близка к той, которую даёт теория Ньютона:
𝑇
полн
≈
𝑚β²
2
≈
(10⁶
кг
)(2⋅10⁻¹⁴)
=
2⋅10⁻⁸
кг
=
=
2⋅10⁻⁵
г
=
20
мк
.
Такова кинетическая энергия двух поездов до столкновения; она и переходит в ту добавочную массу покоя, на которую увеличивается масса поездов, рельсов и насыпи сразу же после столкновения. ▲
63. Релятивистская химия
10⁸ дж энергии соответствуют (10⁸ дж)/𝑐²≈10⁻⁹ кг. Это составляет примерно 10⁻¹⁰ от тех 9 кг воды, которые получаются при полном соединении водорода и кислорода, а самые чувствительные химические весы неспособны зарегистрировать изменение веса, менее чем в 1000 раз превышающее эту величину. ▲
64. Релятивистский осциллятор
а) Нет, инженер не сможет получить здесь сколь угодно высокой частоты. Так как скорость электрона не может быть больше скорости света, период одного колебания не удастся неограниченно уменьшать (в системе отсчёта ящика).
б) Когда напряжение возрастает вдвое, кинетическая энергия электрона в соответствующих точках его траектории также удваивается. Однако ньютоновское выражение для кинетической энергии, справедливое при малых скоростях, имеет вид ½⋅𝑚β², и поэтому скорость β увеличивается в √2=1,414… раз при удвоении величины напряжения. Во столько же раз, следовательно, увеличится при этом и частота.
в) Вывод, полученный в части б), наводит на мысль, что частота колебаний электрона увеличивается пропорционально корню квадратному из величины приложенного напряжения. Чтобы найти коэффициент пропорциональности, заметим, что электрон подвергается постоянному ускорению в каждой половине ящика, причём на него действует сила, равная 𝑞𝑉₀/(𝐿/2) Здесь 𝑞 — заряд электрона, а 𝐿 — ширина ящика (равная в нашем случае 1 м). Тогда ускорение равно 𝑎=𝑞𝑉₀/(𝑚𝐿/2), а время 𝑡, необходимое для того, чтобы электрон прошёл путь от одной стенки ящика (где он покоился) до его центра, определяется из обычного уравнения равноускоренного движения, 𝑠=½⋅𝑎𝑡². В нашем случае 𝑠=𝐿/2 и 𝑡=𝑇/4 (четверть периода), тогда как 𝑎 даётся приведённым выше выражением. Отсюда
𝐿
2
=
1
2
2𝑞𝑉₀
𝑚𝐿
⎛
⎜
⎝
𝑇
2
⎞²
⎟
⎠
и следовательно,
ν²
=
⎛
⎜
⎝
1
𝑇
⎞²
⎟
⎠
=
𝑞𝑉₀
8𝑚𝐿²
.
Действительно, полученное выражение для частоты оказывается пропорционально квадратному корню из величины приложенного напряжения 𝑉₀.
г) В крайнем ультрарелятивистском случае электрон большую часть времени движется почти со скоростью света. В результате величина периода 𝑇мин становится близка к тому времени, за которое свет покрывает расстояние 2𝐿:
𝑇
мин
=
2𝐿
𝑐
или
ν
макс
=
1
𝑇мин
=
𝑐
2𝐿
.
д) Начертить предлагаемый график проще, если взять не самую величину ν, а безразмерное отношение
ν
νмакс
=
⎛
⎜
⎝
𝑞𝑉₀
2𝑚𝑐²
⎞½
⎟
⎠
(ньютоновский предел),
ν
νмакс
=
1
(ультрарелятивистский предел).

Рис. 150.
Этим формулам нетрудно дать простое истолкование. Величина 𝑞𝑉₀ представляет собой потенциальную энергию электрона, когда он покоится около стенки ящика; эта же величина равна и кинетической энергии электрона при прохождении им через сетку в центре ящика. В любом случае она определяет энергию электрона как колеблющегося грузика. Величина же 𝑚𝑐² — это просто масса покоя электрона, выраженная в единицах энергии. Разумеется, ньютоновская формула выполняется, когда частота много меньше своего ультрарелятивистского предела, иначе говоря, если кинетическая энергия электрона много меньше его энергии покоя. Иными словами, область перехода от ньютоновского предела к ультрарелятивистскому определяется соотношением 𝑞𝑉₀≈2𝑚𝑐²=1 Мэв, т.е. 𝑉₀≈1 000 000 в. ▲
65. Импульс без массы?
а) Скорость переноса массы равна просто 𝑑𝐸/𝑑𝑡, если выразить энергию в единицах массы.
б) Импульс равен
𝑥
𝑑𝑚
𝑑𝑡
=
𝑥
𝑑𝐸
𝑑𝑡
.
в) Движение платформы происходит оттого, что центр масс системы в целом 1) не может начать двигаться. Так как масса покоя передаётся от аккумулятора воде, платформа должна двигаться влево (см. рис. 105) для того, чтобы центр масс всей системы сохранял неизменное положение. После того как заряд аккумулятора истощится, масса покоя перестанет передаваться воде, а вместе с этим отпадёт необходимость в компенсирующем движении платформы — она остановится. Окончательный сдвиг платформы ε будет составлять крайне малую часть её длины 𝑥. Пусть вся израсходованная аккумулятором энергия равна 𝐸, так что воде была передана соответствующая ей масса (в форме теплоты). Положим полную массу платформы и всей её нагрузки равной 𝑀 (исключая массу 𝐸). Тогда условие неподвижности центра масс можно выразить формулой
1) Авторы используют здесь свой термин «центр импульса». См. по этому поводу наше примечание на стр. 214 — Прим. перев.
𝑀ε
+
𝐸𝑥
=
0,
откуда окончательный сдвиг платформы определяется в виде
ε
=-
𝐸𝑥
𝑀
.
г) Любой объект, покоящийся в данной системе отсчёта, не совершает в ней механической работы. Поэтому в системе отсчёта платформы перенос энергии слева направо может осуществляться лишь посредством движущейся ремённой передачи. В системе отсчёта стола, если считать, что платформа катится по нему без трения, движение энергии (массы) платформы в целом влево или вправо невозможно. Поэтому масса платформы 𝑀 отступает влево в точности настолько, чтобы компенсировать перенос ремённой передачей энергии (массы) вправо. В этой системе отсчёта скорости переноса энергии платформой и ремённой передачей в точности равны друг другу, но противоположно направлены. Наконец, в системе отсчёта наблюдателя, движущегося вместе с ремённой передачей в какую-то одну сторону, будет значительно ускорен перенос энергии в противоположную сторону встречным движением ремня, так как увеличится относительная скорость, и с этим наблюдателем нельзя не согласиться — ведь для него масса всей системы в целом несомненно находится в быстром движении. ▲
66. Частицы нулевой массы покоя
Вывод соотношения 𝐸²-𝑒²=𝑚² основывается (см. рис. 88 и 89), во-первых, на инвариантности интервала и, во-вторых, на существовании множителя 𝑚, переводящего единичный 4-вектор, касательный к мировой линии, в вектор энергии-импульса, также к ней касательный. В пределе исчезающе малой массы покоя это соотношение принимает вид
𝑒²
=
𝐸²
или
|𝑝⃗|
=
𝐸
,
формула же (90) справедлива для всех скоростей и масс покоя:
𝑝
=
β𝐸
.
Поэтому, если 𝑝𝐸 скорость рассматриваемой частицы β должна быть равна единице: частица должна двигаться со скоростью света. Однако скорость связана с параметром скорости соотношением
β
=
𝑝
𝐸
=
𝑚 sh θ
𝑚 ch θ
=
th θ
.
Отсюда, если скорость равна скорости света, должны быть равны друг другу ch θ и sh θ; следовательно, параметр скорости θ должен быть бесконечно большим. Если рассматривать теперь объект нулевой массы покоя из системы отсчёта ракеты, двигающейся относительно лабораторной системы со скоростью β𝑟 (параметр скорости θ𝑟), то параметр скорости этого объекта будет равен θ'=θ-θ𝑟. Каким бы большим ни был параметр θ𝑟, θ будет бесконечен ввиду бесконечности θ. Следовательно, свет распространяется с одной и той же скоростью в любой инерциальной системе отсчёта, и невозможно найти систему, в которой бы он покоился. Это верно и для любых других частиц, масса покоя которых равна нулю; все они движутся со скоростью света. См. также обсуждение на стр. 159—161. ▲
67. Эйнштейновский вывод принципа эквивалентности энергии и массы покоя — подробный пример
Решение дано в тексте.
68. Устойчивость фотона

Рис. 151
Диаграмма на рис. 151 изображает сохранение импульса в ходе предполагаемого дробления фотона на два других фотона, не сохраняющих его первоначального направления движения. Треугольник образован трёхмерными векторами импульса и построен в обычном трёхмерном эвклидовом пространстве. Поэтому сумма длин его боковых сторон должна быть больше длины основания, т.е.
⎛
⎜
⎜
⎝
Модуль импульса
первого
дочернего фотона
⎞
⎟
⎟
⎠
+
⎛
⎜
⎜
⎝
Модуль импульса
второго
дочернего фотона
⎞
⎟
⎟
⎠
>
>
⎛
⎜
⎝
Модуль импульса
исходного фотона
⎞
⎟
⎠
.
Однако импульс фотона по модулю равен его энергии. Значит, сумма энергий двух дочерних фотонов должна превосходить энергию исходного фотона, а это невозможно. Следовательно, одновременное сохранение и импульса, и энергии невозможно, если только фотоны — продукты дробления — не продолжают двигаться в том же направлении, в котором двигался первоначальный фотон. ▲
69. Давление света
а) Свет лампочки мощностью 1 вт приносит на поглощающую его поверхность 1 дж энергии каждую секунду. 1 дж эквивалентен энергии (массе), равной (1 дж)/𝑐²≈10⁻¹⁷ кг. Эта поверхность поглощает за одну секунду столько же импульса (выраженного в единицах массы); переход к обычным единицам осуществляется путём умножения на скорость света 𝑐 (см. стр. 141), что даёт в данном случае 3⋅10⁻⁹ кг⋅м/сек импульса, поступающего на поглощающую поверхность в секунду. Это соответствует силе, равной 3⋅10⁻⁹ кг⋅м/сек² т.е. 3⋅10⁻⁹ н.
б) Сила, действующая на каждый квадратный метр поглощающего спутника, в 1400 раз больше только что найденной, т.е. равна около 4⋅10⁻⁶ н. Когда свет падает на идеально отражающую поверхность, он отражается от неё в обратную сторону, так что изменение его импульса вдвое превышает полученную прежде величину — мы имеем теперь 8⋅10⁻⁶ н на каждый квадратный метр поверхности. В случае «реальных» поверхностей давление должно быть промежуточным между этими двумя значениями, цвет же поверхности играет роль лишь постольку, поскольку он характеризует её отражательную способность.
в) Запишем выражение для силы, действующей со стороны Солнца на частицу массы 𝑚 как 𝑚𝑎Солнце где 𝑎Солнце=𝐺𝑀/𝑅² — гравитационное ускорение, вызванное притяжением Солнца. (Что касается закона тяготения, см. введение к упражнению 73; вблизи Земли ускорение силы тяжести, вызываемое Солнцем, равно 6⋅10⁻³ м/сек² см. стр. 21). Сила, действующая со стороны солнечного света, представляет собой давление [см. часть б) этого упражнения], умноженное на эффективную поглощающую площадь частицы. Пусть частица имеет сферическую форму и полностью поглощает падающий на неё свет; тогда её поперечное сечение равно π𝑟². Обозначим давление солнечного света через 𝑃. Тогда отталкивающая сила будет равна 𝑃π𝑟², сила же гравитационного притяжения к Солнцу будет 𝑚𝑎Солнце. Нас интересует, каких размеров должна быть частица, чтобы эти силы в точности уравновешивали друг друга:
𝑚𝑎
Солнце
=
π𝑃𝑟²
.
Масса шарообразной частицы связана с её плотностью ρ и радиусом 𝑟 по формуле
𝑚
=
4π
3
𝑟³ρ
.
Подставляя её в уравнение баланса сил, найдём оттуда величину критического радиуса
𝑟
=
3
4
𝑃
ρ𝑎Солнце
.
Чтобы определить численное значение 𝑟, необходимо задаться величиной плотности ρ; предположим поэтому, что она равна плотности воды, 10³ кг/м³. Используя также данные о давлении солнечного света вблизи Земли и о величине солнечного гравитационного ускорения в этой же области, найдём
𝑟
=
3
4
4⋅10⁻⁶ н/м²
(10³ кг/м³)(6⋅10⁻³ м/сек²)
=
5⋅10⁻⁷
м
.
Итак, частица должна быть довольно маленькой — радиусом примерно 1000 атомов. Интересно, что расстояние от Солнца при вычислениях сокращается. Отметим, что мы сделали здесь следующие предположения:
1) частица шарообразна,
2) частица полностью поглощает падающий на неё свет,
3) плотность частицы равна плотности воды. ▲
70. Эффект Комптона
В подписи к рис. 109 дано уравнение, выражающее закон сохранения импульса. Однако нас больше интересует здесь энергия, почему мы и произведём в нем замены
𝑝
=
𝐸
фотон
,
𝑝
=
𝐸
фотон
,
𝑃
²
=
𝐸
²-𝑚².
В результате получим уравнение
𝐸²
-
𝑚²
=
𝐸
фотон
²
+
𝐸
фотон
²
-
2
𝐸
фотон
𝐸
фотон
cos φ
,
в то время как собственно закон сохранения энергии даёт
𝐸
фотон
+
𝑚
=
𝐸
фотон
+
𝐸
,
если учесть, что электрон первоначально находился в покое, так что его полная энергия сводилась к энергии покоя 𝑚. Теперь нас не интересует энергия 𝐸 электрона после столкновения, и мы исключим её из полученных двух уравнений, получив, наконец, энергию фотона, рассеянного в направлении угла φ:
𝐸
фотон
=
𝐸
фотон
.
1
+
𝐸
фотон
(1-cos φ)
𝑚
Разделив левую и правую стороны этого равенства на массу покоя электрона 𝑚, рассмотрим случай, когда 𝐸фотон/𝑚=2:
𝐸фотон
𝑚
=
2
1+2(1-cos φ)
.
Когда электрон крепко связан в атоме, в качестве массы 𝑚 выступает масса этого атома в целом, и тогда эффективная величина отношения 𝐸фотон/𝑚 оказывается в 20 тысяч раз меньше, чем при рассеянии фотонов на свободных электронах. В случае крепко связанных электронов знаменатель в формуле, описывающей эффект Комптона, становится практически равным единице при любых углах φ, так что энергия рассеянного фотона оказывается очень близка к энергии падающего.

Рис. 152.
▲
71. Измерение энергии фотона

Рис. 153.
На рис. 153 изображена диаграмма импульсов, причём через 𝑃 обозначен импульс электрона после столкновения. Для этого прямоугольного треугольника можно записать
𝑃
²
=
𝑝²
+
𝑝
²
=
𝐸
фотон
²
+
𝐸
фотон
²
,
𝑝
𝑝
=
𝐸фотон
𝐸фотон
=
3
4
.
С другой стороны, имеют место закон сохранения энергии
𝐸
фотон
+
𝑚
=
𝐸
фотон
+
𝐸
и релятивистское соотношение между энергией и импульсом для электрона
𝐸
²
-
𝑃
²
=
𝑚²
.
Из этих уравнений можно найти энергию падающего фотона
𝐸
фотон
=
4𝑚
12
(проверку выполнения всех этих уравнений можно осуществить, используя следующие вспомогательные величины:
𝐸
фотон
=
3𝑚
12
,
𝐸
=
13𝑚
12
,
𝑝
=
5𝑚
12
⎞
⎟
⎠
.
▲
72. Энергия и частота фотона
а) В случае фотона, движущегося вдоль оси 𝑥, формулы преобразования энергии и импульса (78) сводятся к одному-единственному равенству
𝐸'
=
𝐸 ch
θ
𝑟
-
𝑝 sh
θ
𝑟
=
𝐸(ch
θ
𝑟
-
sh
θ
𝑟
)
=
𝐸𝑒⁻
θ𝑟
,
где мы учли формальные определения функций ch θ и sh θ, приведённые в табл. 8.
б) Нулевая вспышка (𝑛=0) проходит через начало координат в момент 𝑡=0, и её распространение описывается в дальнейшем уравнением 𝑥=𝑡, т.е. 𝑡-𝑥=0. Вспышка № 1 (𝑛=1) проходит через начало координат в момент 𝑡=𝑐/ν, так что величина её 𝑥-координаты всегда на 𝑐/ν меньше, чем этой же координаты нулевой вспышки:
𝑥
=
𝑡
-
𝑐
ν
т.е.
1
=
ν
𝑐
(𝑡-𝑥)
.
Вспышка № 𝑛 проходит через начало координат в момент 𝑛𝑐/ν, и её 𝑥-координата всегда на 𝑛𝑐/ν меньше, чем у нулевой вспышки: 𝑥=𝑡-𝑛𝑐/ν, т.е. 𝑛=ν/𝑐⋅(𝑡-𝑥).
Это и есть то уравнение, которое требовалось получить. Свет распространяется с одной и той же скоростью 𝑐 и в лабораторной системе отсчёта, и в системе ракеты, так что те же рассуждения, взятые в применении к системе отсчёта ракеты, дают уравнение
𝑛
=
ν'
𝑐
(𝑡'-𝑥')
.
Подставим сюда значения 𝑡' и 𝑥' из формул преобразования Лоренца; мы получим
𝑛
=
ν'
𝑐
(𝑡-𝑥)(
ch
θ
𝑟
+
sh
θ
𝑟
),
𝑛
=
ν'
𝑐
(𝑡-𝑥)
𝑒
θ𝑟
.
Приравнивая друг другу выражения для 𝑛, полученные в лабораторной системе отсчёта и в системе ракеты, найдём
ν'
=
ν
𝑒⁻
θ𝑟
.
в) Равенства, полученные в частях а) и б) этого упражнения, выглядят одинаково, и это говорит за то, что энергия фотона 𝐸 пропорциональна его классической частоте (как в лабораторной системе отсчёта, так и в системе ракеты). Коэффициент пропорциональности определяется на основании других экспериментов, которых мы здесь не касаемся; окончательно получим
𝐸
=
ℎ
𝑐²
ν
.
Умножая энергию, выраженную в единицах массы, на квадрат скорости света, получим 𝐸обычн — энергию, измеренную в обычных единицах (см. разд. 10 гл. 2):
𝐸
обычн
=
ℎν
.
г) Если это последнее соотношение подставить в формулу, описывающую эффект Комптона (упражнение 70), то получится формула (116). ▲
73. Гравитационное красное смещение
а) Работа, затрачиваемая на единицу массы при переходе от 𝑟 к 𝑟+𝑑𝑟, выражается формулой (117) и представляет собой вклад в потенциальную энергию частицы. Вблизи поверхности Земли 𝑟≈𝑟Земля, и мы получим
𝑑𝑊
𝑚
=
𝑚*
𝑟Земля²
𝑑𝑟
=
𝑔*
𝑑𝑟
.
Подставляя 𝑔≈10 м/сек² приближённо найдём
𝑔*
=
𝑔
𝑐²
≈
10 м/сек²
9⋅10¹⁶ м²/сек²
≈
10⁻¹⁶
м
/
м
²
,
так что относительное изменение массы покоя частицы при подъёме на 170 м равно
𝑑𝑊
𝑚
≈
1,7⋅10⁻¹⁴
≈
2⋅10⁻¹⁴
.
б) Отношение же полной работы к массе даётся формулой (118); если взять в ней в качестве 𝑚* массу Земли, равную 4,4⋅10⁻³ м, а за исходный радиус принять радиус Земли 𝑟Земля мы получим
𝑊
𝑚
=
𝑚*
𝑟Земля
≈
4,4⋅10⁻³ м
6,7⋅10⁶ м
≈
7⋅10⁻¹⁰
.
Отношения, полученные в частях а) и б) этого упражнения, не включают в правой стороне самую массу поднимающейся частицы.
в) Заменяя в формуле, полученной в части a), 𝑑𝑟 на 𝑧, а 𝑑𝑊/𝑚 — на отношение (изменение энергии)/(полная энергия), получим, учитывая формулу (115), требуемый результат. Знак минус в нем появился ввиду того, что изменение энергии отрицательно (она уменьшается с высотой) 1.
1 В отличие от кинетической энергии, потенциальная энергия пробной массы в гравитационном поле с точки зрения теории Ньютона всегда отрицательна и обращается в нуль на бесконечности, где поле отсутствует; таким образом, энергия возрастает с высотой. Авторы в действительности имеют в виду работу, необходимую для удаления массы из гравитационного поля, равную по абсолютной величине потенциальной энергии этой массы, но обратную ей по знаку. Возрастание потенциальной энергии с высотой отражает тот факт, что гравитация создает силы притяжения, а не отталкивания между массами (по принципу минимума энергии).— Прим. перев.
г) Формула (119) непосредственно следует из ответа на часть б) этого упражнения. Для Земли (𝑀*=4,44⋅10⁻³ м, 𝑟Земля6,7⋅10⁶ м) относительная величина гравитационного красного смещения равна
⎛
⎜
⎝
Δν
ν
⎞
⎟
⎠
Земля
≈
-7⋅10⁻¹⁰
,
т.е. численно совпадает с ответом на часть б). Для Солнца (𝑀*=1,47⋅10³ м, 𝑟Солнце7⋅10⁸ м) относительная величина гравитационного красного смещения равна
⎛
⎜
⎝
Δν
ν
⎞
⎟
⎠
Солнце
≈
-2⋅10⁻⁶
.
▲
74. Плотность спутника Сириуса
Из формулы (119) следует величина радиуса
𝑟
=
𝑀*
-Δν/ν
=
1,5⋅10³ м
7⋅10⁻⁴
≈
2⋅10⁶
м
(менее одной трети радиуса Земли!). Плотность равна
𝑀
=
2⋅10³⁰
кг
≈
6⋅10¹⁰
кг
/
м
³
=
6⋅10⁷
г
/
см
³
4π
𝑟²
4⋅8⋅10¹⁸
м
³
3
— в шестьдесят миллионов раз больше плотности воды! ▲
75. Формулы Допплера
а) В системе отсчёта ракеты
𝑝'
𝑥
=
𝑝' cos φ',
𝑝'
𝑦
=
𝑝' sin φ'.
Подставляя эти выражения для компонент импульса в формулы преобразования Лоренца (78), найдём
𝐸'
=
-𝑝
cos φ
sh
θ
𝑟
+
𝐸
ch
θ
𝑟
,
𝑝'cos φ'
=
𝑝
cos φ
sh
θ
𝑟
-
𝐸
ch
θ
𝑟
,
𝑝'sin φ'
=
𝑝
sin φ
.
Но для фотона 𝑝=𝐸, и первое из уравнений записывается в виде
𝐸'
=
𝐸
ch
θ
𝑟
(1-β
𝑟
cos φ)
,
как это требовалось показать [уравнение (120)]. Найдём теперь из второго уравнения cos φ' и исключим из него 𝐸 пользуясь (120):
cos φ'
=
𝐸 cos φ ch θ𝑟-𝐸 sh θ𝑟
𝐸 ch θ𝑟(1-β𝑟 cos φ)
,
cos φ'
=
cos φ-β𝑟
1-β𝑟 cos φ
.
б) Будем исходить из формул, обратных (78):
𝐸
=
𝑝'
𝑥
sh θ
𝑟
+
𝐸' ch θ
𝑟
,
𝑝
𝑥
=
𝑝'
𝑥
ch θ
𝑟
+
𝐸' sh θ
𝑟
,
𝑝
𝑦
=
𝑝'
,
𝑝
𝑧
=
𝑝'
𝑧
.
Вновь производя уже знакомые подстановки
𝑝'
𝑥
=
𝑝' cos φ'
=
𝐸' cos φ'
,
𝑝'
𝑦
=
𝑝' sin φ'
=
𝐸' sin φ'
и т.д., найдём из приведённой выше формулы преобразования энергии
𝐸
=
𝐸' ch
θ
𝑟
(1+β
𝑟
cos φ')
.
Подставляя этот результат в выписанную выше первую формулу для компонент импульса, найдём из неё
cos φ
=
cos φ'+β𝑟
1+β𝑟cos φ'
.
Эти результаты приведены в упражнении 76, а последняя формула была выведена также в упражнении 22 [уравнение (50)].
в) Энергия фотона 𝐸 и соответствующая ей классическая частота электромагнитной волны ν связаны друг с другом равенством 𝐸=ℎ/𝑐²⋅ν (см. упражнение 72). Поэтому уравнение (120) переписывается для частот в виде
ν'
=
ν ch
θ
𝑟
⋅
(1-β
𝑟
cos φ)
.
Зная лишь, какая частота наблюдается в данной системе отсчёта, ещё невозможно сказать, чему равна частота в той системе, где источник излучения покоится. Итак, когда мы измеряем в нашей системе отсчёта частоту, мы никоим образом не получаем прямой информации о скорости источника относительно нашей системы. ▲
76. Распад π⁰-мезона; подробный пример
Решение дано в тексте.
77. Полёт неоновой лампочки
Пока неоновая лампочка находится на большом расстоянии от наблюдателя и быстро к нему приближается, её свет для наблюдателя очень ярок (эффект прожектора; упражнение 22) и далеко сдвинут в синюю сторону (частоты в диапазоне фиолетовых и ультрафиолетовых волн — эффект Допплера; упражнение 75). Затем яркость резко понизится (наблюдатель окажется вне «луча прожектора»), когда косинус угла, образованного лучом зрения и осью 𝑥, станет равен β𝑟. В момент наибольшего сближения лампочки с наблюдателем её свет будет уже испытывать красное смещение (см. формулу (120) при φ=90°, cos φ=0). Когда лампочка будет улетать прочь, её свет будет очень слабым и далеко сдвинут в красную сторону (частоты в диапазоне дальних красных и инфракрасных волн). ▲
78. Физик и светофор
Учитывая в уравнении (120), что энергия 𝐸 пропорциональна частоте ν, а cos φ=-1, получим
ν'
=
ν ch
θ
𝑟
⋅
(1+β
𝑟
)
ν
⎛
⎜
⎝
1+β𝑟
1-β𝑟
⎞½
⎟
⎠
.
Подставляя сюда ν=𝑐/λ, найдём
λ'
λ
=
⎛
⎜
⎝
1-β𝑟
1+β𝑟
⎞½
⎟
⎠
или
β
𝑟
=
1-(λ'/λ)²
1+(λ'/λ)²
.
При λ'/λ=(5300 Å)/(6500 Å)=0,81
(λ'/λ)²
=
0,66
,
так что
β
𝑟
=
0,34/1,66
=
0,20
.
откуда
𝑣
𝑟
=
β
𝑟
𝑐
=
6⋅10⁷
м
/
сек
=
=
216⋅10⁶
км
/
час
=
13⋅10⁷
миль
/
час
,
так что штраф составит приблизительно 130 миллионов долларов. ▲
79. Допплеровское смещение на краю диска Солнца
На экваторе Солнца линейная скорость вращения, направленная по касательной к его поверхности, равна
𝑣
=
2π𝑟
𝑇
=
2π
2π10⁸ м
(24,7 дней)(86 400 сек/день)
=
=
2,1⋅10³
м
/
сек
,
так что
β
=
𝑣
𝑐
=
7⋅10⁻⁶
.
Из формулы (120) для эффекта Допплера, приняв φ=0, а cos φ=1, получим
ν'
=
ν
⎛
⎜
⎝
1-β𝑟
1+β𝑟
⎞½
⎟
⎠
или
λ
=
λ'
⎛
⎜
⎝
1-β𝑟
1+β𝑟
⎞½
⎟
⎠
≈
λ'
⎛
⎜
⎝
1
-
7⋅10⁻⁶
2
⎞
⎟
⎠
⎛
⎜
⎝
1
-
7⋅10⁻⁶
2
⎞
⎟
⎠
≈
≈
λ'
(1-7⋅10⁻⁶)
,
так что
Δλ
λ
=-
Δν
ν
≈
7⋅10⁻⁶
.
Сдвиг будет происходить в голубую сторону, когда излучающая точка приближается к Земле, и в красную, когда она удаляется от Земли. Полученная величина относительного допплеровского сдвига частоты сравнима с величиной относительного гравитационного сдвига также в случае Солнца 2⋅10⁻⁶ (см. упражнение 73). ▲
80. Расширяющаяся Вселенная
а) Согласно условиям задачи,
λ'
=
4870 Å
,
λ
=
7300 Å
,
φ
=
φ'
=
π
.
Формулу (120) можно записать в виде
𝐸
𝐸'
=
λ'
λ
=
⎛
⎜
⎝
1-β𝑟
1+β𝑟
⎞½
⎟
⎠
или
β
𝑟
=
1-(λ'/λ)²
1+(λ'/λ)²
.
Так как λ'/λ=0,67, (λ'/λ)²=0,45 то скорость равна
β
𝑟
=
0,55
1,45
=
0,38
.
б) Для того чтобы со скоростью β=0,38 (в единицах скорости света) пройти расстояние 5⋅10⁹ световых лет, требуется (5⋅10⁹)/0,38=13⋅10⁹ лет. Если на более раннем этапе скорость была больше (гравитация произвела в дальнейшем торможение), то это же расстояние могло быть пройдено за более короткий срок. Поэтому, учитывая замедляющее влияние тяготения в прошлом, мы придём к меньшему сроку, прошедшему с момента начала расширения. ▲
81. Анализ парадокса часов с помощью эффекта Допплера
Пусть время путешествия туда и обратно равно 𝑡 в системе отсчёта Павла и 𝑡' — в системе отсчёта Петра. Тогда полное число пульсаций переменной звезды одно и то же в обеих системах отсчёта и равно соответственно ν'𝑡'=ν𝑡. Промежуток времени 𝑡, который покажут часы брата, оставшегося на Земле, равен 𝑡=(ν'/ν)𝑡. Найдём отношение частот по формуле (122), имея в виду, что переменная наблюдается домоседом Павлом под углом 90° к направлению движения Петра (φ=90°, cos φ=0). Отсюда получим
𝑡
=
𝑡'
ch
θ
𝑟
.
В упражнении 27 было указано, что скорость равна β𝑟=24/25, так что
ch
θ
𝑟
=
(1-β
𝑟
²)⁻¹
/
²
=
[1-(24/25)]⁻¹
/
²
=
=
(69/625)⁻¹
/
²
=
25/7
.
Поэтому, если 𝑡'=7 лет, то 𝑡=255 лет, что уже было получено в упражнении 27. ▲
82. «Не превышайте скорости»
Скорость приближающейся машины равна 𝑣𝑟=80 миль/час=36 м/сек. Отсюда
β
𝑟
=
𝑣𝑟
𝑐
=
12⋅10⁻⁸
Частота ν' в системе отсчёта машины может быть получена из уравнения (122), если принять φ=π. Ограничиваясь в разложении членами первой степени по β𝑟, найдём
ν'
=
ν
пад
⎛
⎜
⎝
1+β𝑟
1-β𝑟
⎞½
⎟
⎠
≈
ν
пад
⎛
⎜
⎝
1
+
β𝑟
2
⎞
⎟
⎠
⎛
⎜
⎝
1
+
β𝑟
2
⎞
⎟
⎠
,
ν'
=
ν
пад
(1+β
𝑟
).
Затем радиолокационный луч отражается от машины в противоположном направлении, и при этом в системе отсчёта машины частота ν' остаётся неизменной. Частоту, наблюдаемую в системе отсчёта автострады (лаборатории), можно найти из уравнения, обратного (122) (см. первую формулу в упражнении 76),
ν
отр
=
ν'
ch
θ
𝑟
⋅
(1+β
𝑟
cos φ').
Теперь φ'=0, так что
ν
отр
=
ν'
⎛
⎜
⎝
1+β𝑟
1-β𝑟
⎞½
⎟
⎠
≈
ν'
(1+β
𝑟
).
Подставляя сюда полученное выше выражение для ν' найдём
ν
отр
≈
ν
пад
(1+β
𝑟
)²
≈
ν
пад
(1+2β
𝑟
).
Сдвиг частоты приблизительно равен
ν
отр
-
ν
пад
=
ν
пад
⋅
2β
𝑟
=
(2455
Мгц
)⋅2⋅12⋅10⁻⁸
≈
≈
590⋅10⁻⁶
Мгц
=
590
гц
.
Наименьшее изменение частоты, поддающееся обнаружению, равно
Δ
ν
отр
=
2ν
пад
Δ
β
𝑟
.
Если Δ𝑣𝑟=10 миль/час=4,47 м/сек, то Δβ𝑟≈10⋅10⁻⁸, и мы получим относительный сдвиг частоты
Δ
ν
отр
/
ν
пад
=
2
Δ
β
𝑟
≈
3⋅10⁻⁸
.
▲
83. Допплеровское уширение спектральных линий
Приравняйте ньютоновское выражение для кинетической энергии её выражению через температуру:
1
2
𝑚
〈𝑣²〉
ср
=
3
2
𝑘𝑇
.
Отсюда
⎛
⎝
〈𝑣²〉
ср
⎞½
⎠
=
⎛
⎜
⎝
3𝑘𝑇
𝑚
⎞½
⎟
⎠
и
β
𝑟
≈
1
𝑐
⎛
⎝
〈𝑣²〉
ср
⎞½
⎠
=
⎛
⎜
⎝
3𝑘𝑇
𝑚𝑐²
⎞½
⎟
⎠
.
Возьмите уравнение, обратное (122),
ν
=
ν'
ch
θ
𝑟
⋅
(1+β
𝑟
cos φ')
для того, чтобы определить сдвиг частот; положите здесь φ'=0 и используйте приближение для малых β𝑟:
ν
=
ν'
⎛
⎜
⎝
1+β𝑟
1-β𝑟
⎞½
⎟
⎠
≈
ν'
⎛
⎜
⎝
1+
1
2
β
𝑟
⎞
⎟
⎠
⎛
⎜
⎝
1+
1
2
β
𝑟
⎞
⎟
⎠
≈
≈
ν'
(1+β
𝑟
).
Тогда
ν-ν'
ν'
≈
Δν
ν
=
β
𝑟
=
⎛
⎜
⎝
3𝑘𝑇
𝑚𝑐²
⎞½
⎟
⎠
.
Наблюдаемая частота будет выше для тех частиц, которые приближаются к наблюдателю, и ниже для тех, которые удаляются. В целом при температурах, совместимых с ньютоновским приближением, должен наблюдаться эффект разброса частот, выражаемый полученной выше формулой («допплеровское уширение спектральных линий»). ▲
84. Изменение энергии фотона вследствие отдачи излучателя
а) Воспользуемся законами сохранения для того, чтобы определить энергию и импульс частицы, испытывающей отдачу:
𝑚
ch
θ
𝑟
=
𝑚
-
𝐸
(энергия),
𝑚
sh
θ
𝑟
=
𝐸
(импульс).
Возведите каждое из этих равенств в квадрат и вычтите первое из второго
𝑚
²
(ch²
θ
𝑟
-
sh²
θ
𝑟
)
=
𝑚
²
=
(𝑚-𝐸)²
-
𝐸²
=
=
𝑚²
-
2𝑚𝐸
.
Отсюда следует выражение для энергии
𝐸
=
𝑚²-𝑚²
2𝑚
.
В частном случае, когда отношение
𝑚-𝑚
𝑚
мало',
𝐸
=
(𝑚+
𝑚
)
𝑚-𝑚
2𝑚
≈
𝑚
-
𝑚
=
𝐸₀
(тем самым определяется 𝐸₀). В точном выражении заменим повсюду 𝑚 по формуле 𝑚=𝑚-𝐸₀; получим
𝐸
=
𝐸₀
𝑚-𝑚
2𝑚
=
𝐸₀
𝑚+𝑚-𝐸₀
2𝑚
=
𝐸₀
⎛
⎜
⎝
1
-
𝐸₀
2𝑚
⎞
⎟
⎠
,
что и требовалось показать.
б) Относительная поправка за счёт отдачи при излучении атомами видимого света составляет
Δ𝐸
𝐸₀
≈
3 эв
2⋅10¹⁰ эв
=
1,5⋅10⁻¹⁰
(отдача).
Если 𝑘𝑇≈1/40 эв, то формула, полученная в упражнении 83, даёт
Δν
ν
=
Δ𝐸
𝐸₀
=
√3/40
√10⋅10⁹
≈
3⋅10⁻⁶
(по Допплеру).
Мы видим, что допплеровское уширение частот видимого света, излучаемого атомами, намного больше, чем эффект сдвига энергии фотона за счёт отдачи атома. ▲
85. Эффект Мёссбауэра
Возьмём из предыдущего упражнения уравнение (123)
Δ𝐸
𝐸₀
=-
𝐸₀
2𝑚
.
Как энергию испущенного фотона 𝐸₀=14,4⋅10³ эв, так и массу покоя 𝑚 испустившей его частицы нужно выразить в одних и тех же единицах. Масса покоя протона приблизительно равна 10⁹ эв (см. данные в конце книги); масса покоя 𝙵𝚎⁵⁷, состоящего из 26 протонов и 31 нейтрона, превышает эту величину примерно в 57 раз. Следовательно,
Δ𝐸
𝐸₀
≈-
14⋅10³ эв
2⋅57⋅10⁹ эв
≈-
10⁷
.
б) Когда 𝑚=1 г=10⁻³/(1,7⋅10⁻²⁷ кг/протон)≈0,6⋅10²⁴ масс протонам ≈0,6⋅10³³ эв, мы получим
Δ𝐸
𝐸₀
≈-
14⋅10³ эв
6⋅10³² эв
≈-
2⋅10⁻²⁹
— относительный сдвиг, намного меньший, чем в случае свободного атома железа! [ср. часть а)].
в) Воспользовавшись результатами упражнения 72, найдём частоту:
𝐸₁
обычн
=
(14,4⋅10³
эв
)
(1,6⋅10⁻¹⁹
дж
/
эв
)
=
=
23⋅10⁻¹⁶
дж
=
ℎν₀
или
ν₀
=
23⋅10⁻¹⁶ дж
6,6⋅10⁻³⁴ дж/сек
=
3,5⋅10¹⁸
гц
.
Ширина линии Δν в герцах равна
Δ
ν
=
Δν
ν₀
ν₀
=
3⋅10⁻¹³⋅3,5⋅10¹⁸
гц
=
10⁶
гц
.
Относительная ширина спектральной линии, равная 3⋅10⁻¹³, намного меньше, чем относительный сдвиг, обусловленный отдачей свободного атома [т.е. 10⁻⁷ — результат, полученный в части а)], и вместе с тем намного больше, чем относительный сдвиг в процессе без отдачи [2⋅10⁻²⁹ для однограммового образца; см. часть б)]. ▲
86. Резонансное рассеяние
Фотон выполняет двоякую роль. Во-первых, он возбуждает атом, прежде находившийся в состоянии с основной энергией (массой) 𝑚, переводя его в состояние с 𝑚. Для этого он должен столкнуться с атомом и поглотиться им, а значит, передать ему нежелательный толчок. Следовательно, и это во-вторых, фотон передаёт атому также кинетическую энергию отдачи. Если у фотона запас энергии будет достаточен лишь для выполнения первой роли, то он никак не сможет выполнить ни её, ни вторую роль. Если, однако, атом обладает очень большой массой, то при отдаче он приобретёт весьма малую скорость и потеря энергии на отдачу будет мала. Тогда энергия фотона может быть очень близкой к разности 𝑚-𝑚. Кинетическую энергию, переданную атому, в случае таких малых скоростей можно рассчитывать с помощью законов ньютоновской механики:
𝑇
≈
(Импульс)²
2⋅(Масса)
≈
(𝑚-𝑚)²
𝑚
.
Отсюда можно заключить, что относительная поправка для энергии отдачи приближённо выражается как
Энергия отдачи
Энергия возбуждения
=
𝑇
𝑚-𝑚
≈
𝑚-𝑚
𝑚
.
В случае свободного атома железа 𝙵𝚎⁵⁷ это отношение равно
14,4 кэв
2⋅57⋅931 000 кэв
=
1,4⋅10⁻⁷
т.е. оно слишком велико, чтобы его «не заметил» атом железа. Атом (точнее, его ядро) требует, чтобы энергия падающего фотона выдерживалась с относительной точностью около 3⋅10⁻¹³, иначе этот фотон не будет поглощён. Если же атом принадлежит кристаллу и речь идёт о «поглощении без отдачи», то отдачу приобретает масса кристалла, равная целому грамму, а это 10²² атомов. Увеличение знаменателя дроби в 10²² раз приводит к тому, что вместо прежней относительной поправки на энергию отдачи, равной 1,4⋅10⁻⁷, мы получаем 1,4⋅10⁻²⁹, за которой никакой атом железа не «уследит», и фотон будет поэтому поглощён. ▲
87. Измерение допплеровского смещения по резонансному рассеянию
Возьмём первую формулу из упражнения 76
𝐸
=
𝐸
'
ch
θ
𝑟
⋅
(1+β
𝑟
cos
φ')
(источник в системе отсчёта ракеты, поглощающий атом — в лабораторной системе отсчёта). Положим здесь φ'=0 и 𝐸 '=𝐸₀ и запишем результат приближённо для малых скоростей β𝑟:
𝐸
=
𝐸₀
⎛
⎜
⎝
1+β𝑟
1-β𝑟
⎞
⎟
⎠
≈
𝐸₀
⎛
⎜
⎝
1
+
β𝑟
2
⎞
⎟
⎠
⎛
⎜
⎝
1
+
β𝑟
2
⎞
⎟
⎠
≈
≈
𝐸₀
(1+β
𝑟
)
или
𝐸-𝐸₀
𝐸₀
≈
Δ𝐸
𝐸₀
≈
β
𝑟
.
Относительный допплеровский сдвиг частоты, равный 3⋅10⁻¹³, получается, когда скорость также составляет 3⋅10⁻¹³ скорости света, т.е.
𝑣
𝑟
=
3⋅10⁻¹³⋅3⋅10⁸
м
/
сек
≈
10⁻⁴
м
/
сек
=
10⁻²
см
/
сек
.
Число зарегистрированных счётчиком гамма-квантов при этом увеличится, так как поглотитель беспрепятственно пропустит сквозь себя больше падающих на него фотонов, не подвергнув их резонансному рассеянию. Когда источник фотонов удаляется от поглотителя, относительный сдвиг частоты будет отличаться от случая приближения источника лишь знаком, что соответствует изменению знака β𝑟. В целом поведение счётчика изображено на рис. 154.

Рис. 154.
▲
88. Проверка эффекта гравитационного красного смещения с помощью эффекта Мёссбауэра
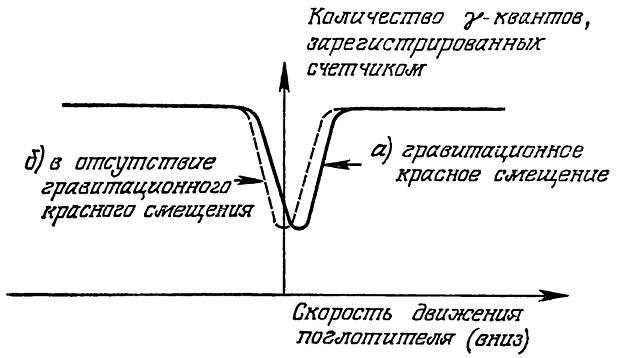
Рис. 155.
Возьмём формулу, полученную в части в) упражнения 73,
Δ𝐸
𝐸₀
=
Δν
ν₀
=-
𝑔*𝑧
,
где 𝑔*=𝑔/𝑐²=(9,8 м/сек²)/(3⋅10⁸ м/сек)²≈1,1⋅10⁻¹⁶ м/м² для точек на поверхности Земли. Если 𝑧=22,5 м, получим
Δν
ν
≈-
(22,5
м
)(1,1⋅10⁻¹⁶
м
⁻¹)
≈-
2,5⋅10⁻¹⁵
.
Необходимо, чтобы резонансный поглотитель приближался к источнику гамма-квантов; тогда в системе отсчёта поглотителя благодаря эффекту Допплера будет компенсировано гравитационное красное смещение, наблюдаемое в лабораторной системе отсчёта. Вспомним, что в предыдущем упражнении относительная скорость β𝑟, нужная для оптимального поглощения, была найдена равной относительному сдвигу частоты излучения, которое требуется поглотить. Значит, скорость движения поглотителя должна быть равна
β
𝑟
=
2,5⋅10⁻¹⁵
или
𝑣
𝑟
≈
10⁻⁶
м
/
сек
=
10⁻⁴
см
/
сек
(см. рис. 155).
Результаты эксперимента Паунда и Ребки, приведённые на стр. 209, получены путём сравнения двух опытных фактов:
1) результатов измерений сдвига частоты, когда источник находился внизу, а поглотитель — вверху, как и описано в этом упражнении (уменьшение энергии поднимающегося фотона), и 2) результатов измерений этого сдвига, когда источник находился вверху, а поглотитель — внизу (увеличение частоты опускающегося фотона). Следовало ожидать, что относительный сдвиг частоты в обоих случаях должен быть одинаковым, но разного знака; поэтому при вычитании одного результата из другого должен получаться «сдвиг», вдвое больший, чем просто при движении фотона вверх (Паунд и Ребка назвали такой сдвиг «сдвигом в два конца»). Половинное значение численных результатов, полученных Паундом и Ребкой, хорошо согласуется с результатами проведённых нами здесь вычислений. ▲
89. Проверка парадокса часов с помощью эффекта Мёссбауэра
При малых β коэффициент, характеризующий относительное различие в старении атомов-близнецов, можно приближённо представить, пользуясь первыми членами разложения бинома Ньютона:
1
-
√
1-β²
≈
1
-
⎛
⎜
⎝
1
-
1
2
β²
⎞
⎟
⎠
=
1
2
β²
Число тик-так за 1 сек приблизительно равно ν₀⋅( сек); поэтому накопление нехватки этих тик-так за одну секунду составит около
ν₀
⎛
⎜
⎝
β²
2
⎞
⎟
⎠
ср
(1
сек
)
,
а относительная нехватка будет равна (β²/₂)ср. Произвести оценку этой величины можно исходя из элементарной кинетической теории теплоты, затронутой в обсуждении (см. текст упражнения). Мы получим
Δν
ν₀
=
⎛
⎜
⎝
β²
2
⎞
⎟
⎠
ср
=
³/₂⋅𝑘𝑇
𝑚𝙵𝚎𝑐²
=
=
³/₂⋅1,38⋅10⁻²³ дж/град
57⋅(1,6⋅10⁻²⁷ кг)(9⋅10¹⁶ м²/сек²
⋅
𝑇
=
2,5⋅10⁻¹⁵ 𝑇
,
т.е. 2,5⋅10⁻¹⁵ на градус. Этот результат хорошо согласуется (конечно, как оценочный) с экспериментальными данными Паунда и Ребки. ▲
90. Симметричное упругое столкновение
Обозначим через 𝑇 и 𝑝 соответственно кинетическую энергию и импульс налетающей частицы, а через 𝑇 и 𝑝 — кинетическую энергию и абсолютную величину импульса каждой из рассеянных частиц. Тогда для рассматриваемого случая упругого рассеяния законы сохранения будут выражаться уравнениями
𝑇
+
𝑚
+
𝑚
=
2
𝑇
+
2𝑚
или
𝑇
=
2
𝑇
и
𝑝
=
2
𝑝
cos
α
2
.
Выражая импульс через кинетическую энергию, получим
𝑝
=
√
𝐸²-𝑚²
=
√
(𝑇+𝑚)²-𝑚²
=
√
𝑇²+2𝑚𝑇
.
Используя в уравнении сохранения импульса это выражение и равенство 𝑇=𝑇/2, найдём
√
𝑇²+2𝑚𝑇
=
2
⎡
⎢
⎣
⎛
⎜
⎝
𝑇
2
⎞²
⎟
⎠
+
2𝑚
⎛
⎜
⎝
𝑇
2
⎞
⎟
⎠
⎤½
⎥
⎦
cos
α
2
.
Возведём этот результат в квадрат и найдём cos ½α:
cos²
α
2
=
𝑇+2𝑚
𝑇+4𝑚
.
Это и требовалось получить. Формула (124) непосредственно следует отсюда ввиду указанного в условии упражнения тригонометрического тождества. Если упругое столкновение рассматривать в ньютоновском приближении, то кинетическую энергию 𝑇 налетающей частицы следует считать много меньшей, чем массу покоя любой из частиц. Тогда из нашего уравнения следует cos α=0 и α=90°, т.е. вывод механики Ньютона. В ультрарелятивистском случае кинетическая энергия 𝑇 намного превышает массу покоя 𝑚, и поэтому можно пренебречь членом 4𝑚 по сравнению с 𝑇 в знаменателе правой части формулы (124). Тогда cos α=1 и α=0 — обе частицы летят после столкновения вперёд. Сравните этот вывод с результатом, полученным в упражнении 68, где показано, что одиночный фотон (самая релятивистская из всех частиц!) может спонтанно распадаться на два фотона, лишь если эти последние движутся в том же направлении, что исходный фотон. ▲
91. Давид и Голиаф — подробный пример
Решение дано в тексте.
92. Абсолютно неупругое столкновение
Решение этого упражнения проведено в гл. 2 на стр. 161 и 162, причём ответ записан в виде уравнения (92). Величина 𝑚конечн=𝑚=𝑚₁+𝑚₂, так как кинетическая энергия налетающей частицы 𝑇 намного меньше, чем масса покоя любой из частиц. При этом условии ещё допустим ньютоновский подход к данной задаче с его «принципом сохранения масс». ▲
93. Порождение частиц протонами
а) Система частиц, изображённая на рис. 119, обладала импульсом до столкновения, но после этого её импульс равен нулю. Поэтому такая реакция не могла бы удовлетворять закону сохранения импульса, а значит, она невозможна.
б) Рассмотрим кадр «после» на рис. 120. Взяв вместо разлетающихся четырёх частиц конечного состояния такие же покоящиеся частицы, можно «сэкономить» избыточную кинетическую энергию и уменьшить на эту величину энергию, которая была первоначально придана двум сталкивающимся протонам (кадр «до», на рис. 120). Кинетическая энергия сталкивающихся частиц целиком переходит в массу покоя, лишь если все частицы конечного состояния покоятся.
в) Пусть 𝐸=𝑇+𝑚 — энергия и 𝑝 — импульс налетающего протона (рис. 121), 𝐸=𝑇+𝑚 — соответственно энергия и импульс каждой частицы после реакции. Законы сохранения имеют вид:
𝑇
+
𝑚
+
𝑚
=
4(
𝑇
+𝑚)
или
𝑇
=
1
4
𝑇
-
1
2
𝑚
и
𝑝
=
4
𝑝
или
⎛
⎝
𝑇²
+
2𝑚𝑇
⎞½
⎠
=
4
⎛
⎝
𝑇
²
+
2𝑚
𝑇
⎞½
⎠
.
Исключая из последнего уравнения 𝑇 и решая его затем относительно 𝑇, получим
𝑇
=
6𝑚
.
Это и есть пороговая энергия порождения протон-антипротонной пары. Так как масса покоя протона 𝑚 составляет 1 Бэв=10⁹ эв, то
𝑇
порог
=
6
Бэв
.
г) Из формулы в части в)
𝑇
=
1
4
𝑇
-
1
2
𝑚
находим, полагая 𝑇=6𝑚, что 𝑇=𝑚.
Энергетический баланс для пороговой реакции можно кратко охарактеризовать таким образом: из всей первоначальной кинетической энергии 6𝑚 в массы покоя протона и антипротона превращается энергия 2𝑚, и все 4 частицы, имеющиеся по окончании реакции, приобретают кинетическую энергию 𝑚 каждая.
д) Согласно уравнению (92) на стр. 162,
𝑚
²
=
(𝑚₁+𝑚₂)²
+
2𝑇₁𝑚₂
,
в случае 𝑚₁=𝑚₂=𝑚 и 𝑚=4𝑚 получим
16𝑚²
=
4𝑚²
+
2𝑇₁𝑚
и
𝑇₁
=
6𝑚
,
что уже было найдено в части в).
е) Собственно, как мишень тяжёлое ядро ничем не примечательно. Лучше всего представлять себе, что налетающий протон сталкивается в мишени с одним-единственным протоном, а не сразу со многими (сравните это с выстрелом пулей в стаю птиц). Новым качеством протона в ядре является его движение там. Даже если это движение совершается с умеренной кинетической энергией (𝑇₂=25 Мэв) навстречу налетающему протону, это уже даёт огромное преимущество, позволяя получать пары при гораздо более низких энергиях. Законы сохранения имеют вид
𝑚
+
𝑇₁
+
𝑚
+
𝑇₂
=
4(𝑚+
𝑇
)
(энергия),
√
𝑇₁²+2𝑚𝑇₁
-
√
𝑇₂²+2𝑚𝑇₂
=
=
4
⎛
⎝
𝑇
²
+
2𝑚
𝑇
⎞½
⎠
(импульс).
Исключая из второго уравнения 𝑇 с помощью первого, можно найти 𝑇₁:
𝑇₁
=
6𝑚
+
7𝑇₂
-
4√
3𝑇₂²+6𝑇₂𝑚
.
Если кинетическая энергия 𝑇₂ мала, приближённо получим
𝑇₁
≈
6𝑚
-
4√
6𝑇₂𝑚
.
Полагая 𝑇₂=25 Мэв, найдём отсюда пороговую энергию
𝑇₁
≈
6000
Мэв
-
4⋅4000
Мэв
=
4400
Мэв
,
при этом всё равно, какое было выбрано ядро мишени — гелия или свинца! В формулу входит квадратный корень из энергии протона мишени, так как он даёт скорость этого протона. Такое движение навстречу «обстреливающему» протону делает его кинетическую энергию (в системе центра масс) много большей, чем в лабораторной системе отсчёта. Какие-то 25 Мэв позволяют сэкономить целых 1600 Мэв! ▲
94. Порождение частиц электронами
Разберитесь сначала в решении упражнения 93. Воспользуйтесь уравнением (92) на стр. 162, приняв 𝑚₁=𝑚𝑒 в качестве массы налетающего электрона, 𝑚₂=𝑚𝑝 — массы протона мишени и 𝑚=𝑚𝑒+3𝑚𝑝 — массы продуктов реакции (электрон, два протона и антипротон). Тогда это уравнение даст
(𝑚
𝑒
+3𝑚
𝑝
)²
=
(𝑚
𝑒
+𝑚
𝑝
)²
+
2𝑇
𝑒
𝑚
𝑝
,
откуда следует величина пороговой кинетической энергии электрона
𝑇
𝑒
=
4𝑚
𝑝
+
2𝑚
𝑒
.
Масса покоя протона соответствует 10³ Мэв, а электрона 1/2 Мэв, так что ею можно практически пренебречь по сравнению с массой протона. Поэтому пороговая энергия приблизительно равна 4𝑚𝑝=4000 Мэв. ▲
95. Фоторождение пары одиночным фотоном
Рис. 156. Диаграмма предполагаемой реакции: слева одиночный фотон до реакции, справа — предполагаемый результат реакции (пара электрон и позитрон). Реакция не идёт.
а) Предполагаемая реакция изображается диаграммой на рис. 156. Законы сохранения имеют вид:
𝐸
фотон
=
𝐸
+
+
𝐸
-
(энергия),
𝐩
=
𝐩
+
+
𝐩
-
(импульс).
Вместо того чтобы рассматривать все компоненты 4-вектора энергии-импульса, достаточно будет взять его квадрат,
(Энергия)
²
-
(Импульс)
²
,
величина которого не должна изменяться в ходе реакции. Возводя в квадрат уравнения, описывающие законы сохранения, и вычитая полученные выражения друг из друга, найдём
(Энергия)
²
-
(Импульс)
²
=
=
(
𝐸
+
²
+
2
𝐸
+
𝐸
-
+
𝐸
-
²)
-
(
𝑝
+
²
+
2
𝐩
+
𝐩
_
+
𝑝
+
²)
=
=
𝐸
фотон
²
-
𝑝
фотон
²
.
Вспомним, что разность 𝐸²-𝑝² в случае электрона равна просто 𝑚², а для фотона она даёт нуль. Кроме того, 2𝐩+𝐩-=2𝑝+𝑝- cos φ, где φ — угол между направлениями вылета электрона и позитрона. Разделив на 2, получим уравнение
𝑚²
+
𝐸
+
𝐸
-
-
𝑝
+
𝑝
-
cos φ
=
0
или
cos φ
=
𝑚²+𝐸+𝐸-
𝑝+𝑝-
.
Однако 𝐸+=(𝑚²+𝑝+²)¹/² всегда больше, чем 𝑝+, а 𝐸- всегда больше, чем 𝑝- Значит, косинус равен величине, явно превышающей единицу, и поэтому ему не может соответствовать никакой реальный угол φ. Заключение: предполагаемая реакция невозможна.
Это можно доказать намного проще и изящнее, если перейти к системе центра масс предполагаемой электрон-позитронной пары. К такой системе отсчёта, где полный импульс обращается в нуль, всегда можно перейти, если в рассматриваемой физической системе хотя бы у одной частицы масса покоя отлична от нуля. Но в этой системе в момент «до» (рис. 156) импульс исходного одиночного фотона никак не может быть равен нулю: иначе была бы равна нулю и энергия фотона, так как для фотонов 𝐸=𝑝, и этого фотона попросту бы не существовало! Значит, предполагаемая нами реакция нарушает законы сохранения.

Рис. 157. Диаграмма реально происходящей реакции: кроме фотона, в ней на начальной стадии должна участвовать заряженная частица с ненулевой массой покоя.
б) Рассуждения, проведённые в упражнении 93, показывают, что при пороговой реакции все её продукты двигаются совместно с одинаковыми скоростями (рис. 157). Законы сохранения тогда записываются в виде
𝐸
фотон
+
𝑚
=
3
𝐸
и
𝑝
=
𝐸
фотон
=
3
𝑝
.
Возводя в квадрат и вычитая друг из друга соответствующие части получающихся уравнений, найдём
𝐸
фотон
²
+
2𝑚𝐸
фотон
+
𝑚²
-
𝐸
фотон
²
=
=
9(
𝐸
²
-
𝑝
²
)=
9𝑚²
.
Отсюда следует величина пороговой энергии, равная
𝐸
фотон
=
4𝑚
=
4⋅(1/2
Мэв
)
=
2
Мэв
.
▲
96. Фоторождение пары двумя фотонами

Рис. 158. Диаграмма реально происходящей реакции: до реакции два фотона, после реакции — электрон-позитронная пара. Показан случай порогового рождения пары, когда электрон и позитрон неподвижны относительно друг друга.
Сначала рассмотрим пороговую реакцию, после которой возникающие электрон и позитрон не разлетаются (рис. 158; см. также упражнение 93). Запишем компоненты 4-вектора энергии-импульса до и после реакции и приравняем их:
𝐸₁
+
𝐸₂
=
2
𝐸
,
𝐩₁
+
𝐩₂
=
2
𝐩
.
Найдём квадрат этого 4-вектора:
(Энергия)
²
-
(Импульс)
²
=
=
𝐸₁²
+
2𝐸₁𝐸₂
+
𝐸₂²
-
𝑝₁²
-
2𝑝₁𝑝₂
cos φ
-
𝑝₂²
=
=
4
𝐸
²
-
4
𝑝
²
.
Полученное уравнение упрощается, если учесть, что разность 𝐸²-𝑝² равна 0 для фотонов и 𝑚 для электронов или позитронов, а также что 1-cos φ=2 sin² ½φ. В результате найдём
𝐸₁
𝐸₂
sin²
φ
2
=
𝑚²
.
Выполнение этого условия соответствует тому, что реакция идёт на пределе (пороговое условие). Если слева будет стоять большая величина, то это значит, что энергии, которой два фотона обладают в системе центра масс (когда их суммарный импульс равен нулю), в принципе было бы достаточно для образования пары более массивных частиц, чем электрон и позитрон. Этот избыток энергии (величины в левой части равенства) означает также, что, если на самом деле рождается пара (𝑒⁺, 𝑒⁻), то её компоненты будут находиться в относительном движении и их кинетическая энергия не будет равна нулю в системе центра масс; иначе говоря, мы будем иметь дело уже с надпороговой реакцией. ▲
97. Аннигиляция электрон-позитронной пары
а) В системе центра масс перед аннигиляцией полный импульс равен нулю. Значит, он должен быть равен нулю и после аннигиляции. Однако одиночный фотон не может обладать нулевым импульсом. Поэтому, чтобы закон сохранения импульса не нарушался, должно быть испущено по крайней мере два фотона (рис. 159).

Рис. 159.
б) Запишем закон сохранения энергии:
𝐸
+
𝑚
=
𝐸
₁
+
𝐸
₂
или
𝐸
₂²
=
⎛
⎝
𝐸
+
𝑚
-
𝐸
₁
⎞²
⎠
.
Закон сохранения импульса ясен из рис. 160.
Рис. 160.
Воспользуемся законом косинусов
𝐸
₂²
=
𝐸
₁²
+
𝑝²
-
2𝑝
𝐸
₁
cos φ₁
=
=
𝐸
₁²
+
𝐸²
-
𝑚²
-
2𝑝
𝐸
₁
cos φ₁
.
Приравнивая друг другу два выражения для 𝐸₂² найдём
𝐸²
+
𝑚²
+
𝐸
₁²
+
2𝑚𝐸
-
2𝐸
𝐸
₁
-
2𝑚
𝐸
₁
=
=
𝐸
₁²
+
𝐸²
-
𝑚²
-
2𝑝
𝐸
₁
cos φ₁
.
Отсюда следует выражение для 𝐸₁:
𝐸
₁
=
𝑚(𝑚+𝐸)
𝐸+𝑚-𝑝 cos φ₁
=
𝑚(2𝑚+𝑇)
2𝑚+𝑇-cos φ₁√𝑇²+2𝑚𝑇
или, наконец, в единицах массы электрона 𝑚,
𝐸
₁
=
1
.
𝑚
1
-
cos φ₁
√
1+2𝑚/𝑇
в) При заданной кинетической энергии сталкивающегося позитрона 𝑇 максимальная энергия гамма-кванта реализуется при cos φ₁=1, т.е. φ₁=0, и равна
⎛
⎜
⎝
𝐸₁
𝑚
⎞
⎟
⎠
макс
=
1
1-(1+2𝑚/𝑇)⁻¹/²
.
Минимальная энергия фотона соответствует cos φ₁=-1, т.е. φ₁=π, и равна
⎛
⎜
⎝
𝐸₁
𝑚
⎞
⎟
⎠
мин
=
1
1+(1+2𝑚/𝑇)⁻¹/²
.
г) При очень малых 𝑇 (очень больших отношениях 𝑚/𝑇) максимальная и минимальная энергии приближённо равны друг другу:
⎛
⎜
⎝
𝐸₁
𝑚
⎞
⎟
⎠
макс
≈
⎛
⎜
⎝
𝐸₁
𝑚
⎞
⎟
⎠
мин
≈
1
(малые
𝑇
).
Каждый фотон уносит энергию, равную энергии покоя одного электрона; первоначальной кинетической энергией можно пренебречь.
При очень больших 𝑇 (очень малых отношениях 𝑚/𝑇) максимальная и минимальная энергии испущенных фотонов резко отличаются друг от друга:
⎛
⎜
⎝
𝐸
₁
⎞
⎟
⎠
макс
≈
1
=
𝑇
,
𝑚
1
-
⎛
⎜
⎝
1
-
𝑚
⎞
⎟
⎠
𝑚
𝑇
⎛
⎜
⎝
𝐸₁
𝑚
⎞
⎟
⎠
мин
≈
1
2
(большие
𝑇
).
В этом случае самый богатый энергией из испущенных фотонов уносит с собой кинетическую энергию сталкивающегося позитрона, которая очень велика. Минимальная энергия здесь составляет половину массы покоя электрона. ▲
98. Проверка принципа относительности

Рис. 161.
а) Схему на рис. 122 можно представить в виде диаграммы (рис. 161). Законы сохранения записываются как
𝐸
+
𝑚
=
𝐸
₁
+
𝐸
₂
,
𝑝
=
𝐸
₁
cos 30°
-
𝐸
₂
sin 30°
,
0
=
𝐸
₁
sin 30°
-
𝐸
₂
cos 30°
.
Из последних двух уравнений следует
𝐸
₂
=
𝐸
₁
sin 30°
cos 30°
=
0,58
𝐸
₁
,
и
𝑝
=
𝐸
₁
⎛
⎜
⎝
cos 30°
-
sin² 30°
cos 30°
⎞
⎟
⎠
=
0,58
𝐸
₁
.
Подставляя эти выражения в уравнение для сохранения энергии, найдём
𝐸
+
𝑚
=
𝑝
0,58
+
𝑝
=
2,75𝑝
=
2,75√
𝐸²-𝑚²
=
=
2,75
√
𝐸+𝑚
√
𝐸-𝑚
или
√
𝐸+𝑚
=
2,75
√
𝐸-𝑚
.
Возводя в квадрат, получим
𝐸+𝑚
=
7,6
(𝐸-𝑚)
,
откуда следует величина энергии
𝐸
=
1,3𝑚
.
Кинетическая энергия налетающего позитрона, регистрируемого таким способом, равна
𝑇
=
𝐸
-
𝑚
=
0,3𝑚
=
0,3⋅0,5⋅10⁶
эв
=
150
кэв
.
При этом скорость не близка к единице, и её величину приходится находить непосредственным вычислением:
𝐸
=
𝑚 ch
θ
𝑟
=
𝑚(1-β²)
-½
=
1,3𝑚
,
1
-
β²
=
0,59
,
β
=
0,64
.
б) Следовало бы регистрировать разность времён между попаданиями гамма-квантов в счётчики 𝐴 и 𝐵, расположенные на равных расстояниях от мишени. Если бы такая разность была обнаружена, она свидетельствовала бы о различии величины скорости света в зависимости от того, вперёд или назад был он испущен движущейся частицей. Соответствующие экспериментальные результаты приведены на рис. 123. ▲
99. Отождествление частиц по трекам в пузырьковой камере
а) Лабораторная система отсчёта является одновременно и системой центра масс; в ней законы сохранения принимают вид
𝑚
π
=
𝐸
μ
+
𝐸
𝑥
=
√
𝑝
μ
²+𝑚
μ
²
+
√
𝑝
𝑥
²+𝑚
𝑥
²
,
𝑝
μ
=
58,2𝑚
𝑒
=
𝑝
𝑥
.
Подставим значение 𝑝, следующее из второго уравнения, в первое и используем значения масс покоя мезонов, указанные в условиях задачи. С точностью логарифмической линейки найдём
58𝑚
𝑒
=
√
58,2𝑚
𝑒
+𝑚
𝑥
²
.
Это уравнение заставляет думать, что 𝑚𝑥 либо точно равняется нулю, либо намного меньше, чем 𝑚𝑒.
б) Спиновый момент импульса неизвестной частицы должен уничтожаться в сумме со спиновым моментом μ+-мезона ½ℏ. Отсюда следует, что спиновый момент неизвестной частицы по абсолютной величине равен ½ℏ и направлен в сторону, противоположную спиновому моменту μ+-мезона. ▲
100. Накопительные кольца и встречные пучки

Рис. 162.
В лабораторной системе отсчёта полная величина энергии, которая может реализоваться во взаимодействии, равна суммарной кинетической энергии сталкивающихся электронов, т.е. 500 Мэв + 500 Мэв = 1000 Мэв = 1 Бэв, плюс энергия покоя этих электронов, т.е. 1/2 Мэв + 1/2 Мэв = 1 Мэв, которой можно пренебречь по сравнению с кинетической энергией. В любой другой системе отсчёта полная величина энергии, которая может реализоваться во взаимодействии, будет такой же. На рис. 162 представлены ситуации в лабораторной системе и в системе отсчёта ракеты. В последней один из электронов первоначально покоится; найдём кинетическую энергию другого. Частица 1 может покоиться в той системе, параметр скорости которой определяется соотношением
𝐸
=
𝑚 ch
θ
𝑟
или
ch
θ
𝑟
=
𝐸
𝑚
≈
𝑇
𝑚
≈
1000
.
При столь больших скоростях из равенства (89), 𝐸≈𝑝, следует, что sh θ𝑟≈ch θ𝑟≈1000. Поэтому формула преобразования энергии записывается для частицы 2 (с импульсом -𝑝) в виде
𝐸₂'
=
𝐸₂
ch
θ
𝑟
-
𝑝₂
sh
θ
𝑟
=
𝐸
ch
θ
𝑟
-
𝑝
sh
θ
𝑟
≈
≈
2𝐸
ch
θ
𝑟
≈
2𝐸
𝑇
𝑚
≈
(2⋅500
Мэв
)⋅1000
=
=
10⁶
Мэв
=
10³
Бэв
.
Такова кинетическая энергия, которую следует придать одиночному электрону, налетающему на покоящийся электрон, чтобы полная энергия, которая может реализоваться во взаимодействии, составляла 1000 Мэв.
Если взять для протонов (у которых 𝑚=1 Бэв) 𝐸₂'=10³ Бэв, то, читая предыдущие соотношения в обратном порядке, получим
2𝐸
𝑝
=
𝑇𝑝
𝑚
≈
2
𝑇𝑝²
𝑚
≈
10³
Бэв
или
𝑇
𝑝
²
=
𝑚
2
⋅
10²
Бэв
²
≈
500
Бэв
²
,
𝑇
𝑝
=
22
Бэв
.
Значит, протоны, «консервируемые» в накопительных кольцах, должны обладать энергией 22 Бэв, и полная энергия взаимодействия составит 22+22+1+1=46 Бэв. ▲
101. Де Бройль и Бор
Из упражнения 72 известно, что
𝐸
=
𝑝
=
ℎ
𝑐²
ν
.
однако
ν
=
𝑐
λ
,
так что
𝑝
=
ℎ
λ𝑐
или
λ
=
ℎ
𝑝𝑐
=
ℎ
𝑝обычн
,
где 𝑝обычн=𝑝𝑐 — импульс, выраженный в обычных единицах. Потребуем, чтобы для электрона, движущегося по орбите вокруг ядра, выполнялось равенство
𝑛λ
=
2π𝑟
,
𝑛
=
1,
2,
3,
…,
или
𝑛ℎ
𝑝обычн
=
2π𝑟
,
или
𝑟𝑝
обычн
=
𝑛
ℎ
2π
=
𝑛ℏ
,
𝑛
=
1,
2,
3,
…,
Отсюда следует, что орбитальный момент импульса электрона 𝑟𝑝обычн должен быть равен целому кратному ℏ «кванта момента импульса».
Приравняем силу электрического притяжения 𝐾𝑍𝑒²/𝑟² электрона (заряд 𝑒) к ядру (заряд 𝑍𝑒) центробежной силе
𝑚𝑣²
𝑟
=
𝑚²𝑣²
𝑚𝑟
=
(𝑝обычн)²
𝑚𝑟
,
необходимой для удержания электрона на круговой орбите. Постоянная 𝐾 зависит от выбора системы единиц (в единицах СГС 𝐾=1; в системе СИ, или МКС, 𝐾=1/(4 πε₀) н⋅м²/к²:
(𝑝обычн)²
𝑚𝑟
=
𝐾𝑍𝑒²
𝑟²
или
(𝑟𝑝
обычн
)²
=
𝑛²ℏ²
𝐾𝑍𝑒²𝑚𝑟
,
откуда получим
𝑟
=
𝑛²ℏ²
𝐾𝑍𝑒²𝑚
.
Формула (126а) получится, если использовать систему 𝐾=1/(4 πε₀) мула (126б) — если положить 𝐾=1.
Величину скорости β можно найти из формулы, справедливой в случае малых скоростей:
β
=
𝑝обычн
𝑚𝑐
=
𝑛ℏ
𝑚𝑟𝑐
=
𝑛ℏ
𝑚𝑐𝑛²ℏ²/(𝐾𝑍𝑒²𝑚)
=
=
𝐾𝑍𝑒²
𝑛ℏ𝑐
=
𝐾𝑒²
ℏ𝑐
⋅
𝑍
𝑛
=
α𝑍
𝑛
.
▲
102. Ви'дение посредством электронов
В формулу для импульса 𝑝=ℎ/λ𝑐 подставим значения λ=10⁻⁶ м и λ=10⁻¹⁵ м а затем найдём соответствующие значения энергии по формуле 𝐸/𝑚=√1+(𝑃/𝑚)². При λ=10⁻⁶ м энергия получается приближённо равной
𝐸
𝑚
≈
1
+
3⋅10⁻¹²
,
так что
𝑇
≈
3⋅10⁻¹²
𝑚
.
Примем 𝑚=0,5 Мэв; необходимая кинетическая энергия будет тогда равна
𝑇
≈
1,5⋅10⁻⁶
эв
.
Чтобы электронный микроскоп обладал достаточной разрешающей способностью для наблюдения бактерий, электроны должны пропускаться через разность потенциалов не менее одного микровольта. Такие низкие напряжения на практике трудно поддерживать стабильно; более того, столь медленные электроны вовсе не способны пройти даже сквозь высушенную бактерию. Поэтому пользуются электронами с энергиями в несколько тысяч электронвольт, и это позволяет наблюдать детали строения бактерий. При λ=10⁻¹⁵ м энергия должна быть равна
𝐸
𝑚
=
2,4⋅10³
≈
𝑇
𝑚
,
𝑇
=
2,4⋅10³⋅0,5
Мэв
≈
10⁹
эв
=
1
Бэв
.
Для выявления деталей структуры протонов и нейтронов необходимы электроны, ускоренные не менее чем до таких энергий. ▲
103. Прецессия Томаса
Все этапы решения этой задачи подробно изложены в тексте.
104. Трудности межзвёздных полётов
а) Требуемую величину параметра скорости можно определить по коэффициенту замедления времени, ch θ=10. По «способам быстрой оценки для простых смертных» (см. табл. 8 на стр. 78) для параметра скорости приближённо найдём 𝑒θ=20 или θ=3. Отношение начальной массы ракеты к конечной для одного этапа ускорения из состояния покоя до данного конечного значения параметра скорости (или для замедления от данного значения параметра скорости до состояния покоя) можно вычислить по формуле (110) из упражнения 58:
θ
=
ln
𝑀₁
𝑀
.
Отсюда следует искомое отношение масс
𝑀₁
𝑀
=
𝑒
θ
=
20
.
Полезный груз ракеты равен 10⁵ кг; поэтому суммарная масса полезного груза и горючего перед последним торможением при возвращении на Землю составляет 20⋅10⁵ кг. Но при предшествовавшем ускорении от далёкой звезды к Земле ускорять приходится не только полезный груз, но и горючее, необходимое для конечного торможения. Поэтому при прощании со звездой полная масса космического корабля должна быть равна 20⋅20⋅10⁵ кг. Продолжая эти рассуждения назад во времени вплоть до самого отлёта с Земли, для исходного значения массы корабля получим
20⋅20⋅20⋅20⋅10⁵
кг
3,2⋅10¹⁰
кг
,
т.е. 32 миллиона тонн! Из этой общей массы полезный груз составляет всего 100 тонн, а остальное — горючее.
б) Полёт в одну сторону (быстрое ускорение не в счёт, важен лишь длительный полёт по инерции, когда ch θ=10) занимает 50 лет времени астронавта или 50⋅10 лет= 500 лет на Земле. Космический корабль летит почти со скоростью света:
1
-
β²
=
1
ch²θ
=
10⁻²
=
(1-β)
(1+β)
≈
2(1-β)
,
или
1-β
≈
0,5⋅10⁻²
.
Поэтому он может достигнуть звезды, удалённой от нас самое большее на 500 световых лет. Всё путешествие займёт тысячу земных лет.
в) Коэффициент замедления времени равен ch θ=10, поэтому энергия атома водорода (масса покоя 𝑚) составляет
𝐸
=
𝑚 ch θ
=
10𝑚
или
𝑇
=
𝐸
-
𝑚
=
9𝑚
≈
9
Бэв
.
Лоренцево сокращение, происходящее в направлении движения, также определяется коэффициентом ch θ=10. Поэтому в системе отсчёта ракеты, движущейся со своей полной скоростью, на каждый кубический сантиметр будет приходиться не один атом водорода, а целых десять, т.е. 10⋅10²⋅10²⋅10²=10⁷ атомов на один кубометр. В этой системе отсчёта они будут лететь почти со скоростью света, так что в секунду на каждый квадратный метр лобовой поверхности космического корабля будет обрушиваться 3⋅10⁸ кубических метров частиц — 3⋅10¹⁵ атомов. Это в 300 раз превышает мощность пучка протонов высокой энергии от ускорителя.
Подведём итоги:
1) Расстояние (около 500 световых лет), достижимое в космическом полёте человеком за время его жизни, намного меньше, чем расстояния до самых далёких из наблюдаемых нами звёзд (от 5 до 9 миллиардов световых лет).
2) Даже в случае «идеальной» ракеты отношение начальной массы к конечной, необходимое для полёта туда и обратно «всего лишь» на расстояние 500 световых лет, недопустимо велико.
3) Астронавт-человек нуждается во время такого полёта в массивном защитном щите, что несовместимо с предположением об идеальной ракете, принятым при выводе двух предыдущих заключений. ▲
Некоторые физические постоянные
Скорость света в вакууме
𝑐
=
2,997925
⎧
⎨
⎩
10⁸
м
/
сек
10¹⁰
см
/
сек
𝑐
=
⎧
⎨
⎩
1
метр пути/метр светового времени
1
сантиметр пути/сантиметр светового времени
Гравитационная постоянная
𝐺
=
6,670
×
⎧
⎨
⎩
10⁻¹¹
м
³/
кг
⋅
сек
⁻²
10⁻⁸
см
³/
г
⋅
сек
⁻²
Постоянная Планка
ℎ
=
6,6256 ×
⎧
⎨
⎩
10⁻³⁴
кг
⋅
м
²/
сек
10⁻²⁷
г
⋅
см
²/
сек
Квант момента импульса
ℏ
=
1,0545 ×
⎧
⎨
⎩
10⁻³⁴
кг
⋅
м
²/
сек
10⁻²⁷
г
⋅
см
²/
сек
Постоянная Больцмана
𝑘
=
1,38054 ×
⎧
⎨
⎩
10⁻²³
джоуль
/°𝖪
10⁻¹⁶
эрг
/°𝖪
Элементарный заряд
𝑒
=
⎧
⎨
⎩
1,60210⋅10⁻¹⁹
кулон
4,80298⋅10⁻¹⁰
CGSE или
г
¹
/
²⋅
см
³
/
²
сек
Масса покоя электрона
𝑚
𝑒
=
9,1091×
⎧
⎨
⎩
10⁻³¹
кг
10⁻²⁸
г
Энергия покоя электрона
𝑚
𝑒
𝑐²
=
8,1869×
⎧
⎨
⎩
10⁻¹⁴
джоуль
10⁻⁷
эрг
=
0,510984
Мэв
Масса покоя протона
𝑚
𝑝
=
1,67252×
⎧
⎨
⎩
10⁻²⁷
кг
10⁻²⁴
г
Энергия покоя протона
𝑚
𝑝
𝑐²
=
1,503186×
⎧
⎨
⎩
10⁻¹⁰
джоуль
10⁻³
эрг
=
938,232
Мэв
Масса Земли
𝑀
⨁
=
5,977×
⎧
⎨
⎩
10²⁴
кг
10²⁷
г
Радиус сферы тогоже объёма, что и Земля
𝑅
⨁
=
6,371×
⎧
⎨
⎩
10⁶
м
10⁸
см
Среднее расстояние от Солнца до Земли (астрономическая единица)
АЕ
=
1,495985×
⎧
⎨
⎩
10¹¹
м
10¹³
см
Средняя скорость движения Земли по орбите вокруг Солнца
𝑣
𝑒
=
29,8
км
/
сек
Среднее расстояние от Земли до Луны
3,84×
⎧
⎨
⎩
10⁸
м
10¹⁰
см
Масса Солнца
𝑀
☉
=
1,989×
⎧
⎨
⎩
10³⁰
кг
10³³
г
Средний радиус Солнца
𝑅
☉
=
6,9598×
⎧
⎨
⎩
10⁸
м
10¹⁰
см
Множители перехода
1
сек
=
2,997925×
⎧
⎨
⎩
10⁸
м
светового времени
10¹⁰
см
1
м
светового времени
=
3,335640⋅10⁻⁹
сек
1
см
светового времени
=
3,335640⋅10⁻¹¹
сек
1
год
=
3,156⋅10⁷
сек
=
9,460×
⎧
⎨
⎩
10¹⁵
м
светового времени
10¹⁷
см
1
км
=
0,6214
мили
1
электронвольт
эв
=
1,602⋅10⁻¹⁹
джоуль
=
1,602⋅10⁻¹²
эрг
Резюме главы 1. СРАВНЕНИЕ ЭВКЛИДОВЫХ ПОВОРОТОВ И ПРЕОБРАЗОВАНИИ ЛОРЕНЦА
𝗘
Эвклидова геометрия трёхмерного пространства
𝗟
Лоренцева геометрия четырёхмерного мира
Задача: найти связь между
𝗘
координатами точки в исходной (нештрихованной) системе координат и координатами той же точки в штрихованной системе координат, повёрнутой относительно предыдущей
𝗟
координатами (в том числе и временем) события в лабораторной системе отсчёта (нештрихованные координаты) и координатами того же события в системе отсчёта ракеты (штрихованные координаты)
Для упрощения исследования берётся частный случай, когда
𝗘
начала обеих систем совпадают
поворот берётся в плоскости 𝑥𝑦, причём ось 𝑦' составляет с осью 𝑦 угол θ𝑟 (наклон 𝑆𝑟=tg θ𝑟) 𝑧=𝑧'
все координаты измеряются в метрах
𝗟
начала совпадают при 𝑡=𝑡'=0 (опорное событие)
система отсчёта ракеты движется в положительном направлении оси 𝑥 лабораторной системы отсчёта, причём параметр скорости равен θ𝑟 (скорость β𝑟=th θ𝑟), 𝑦=𝑦', 𝑧=𝑧'
все координаты измеряются в метрах (в том числе время, измеряемое в «метрах светового времени»)
Сохраняющий одно и то жe значение в обеих системах инвариант имеет вид
𝗘
(Длина)²=𝐿²=𝑥²+𝑦²+𝑧²
Таким образом,
𝑥²+𝑦²=𝑥'²+𝑦'²
𝗟
(Пространственный интервал)²=σ²=-(Временноподобный интервал)²=-τ²=𝑥²+𝑦²+𝑧²-𝑡²
Таким образом,
𝑥²-𝑡²=𝑥'²-𝑡'²
При проверке выполнения последнего условия используется общее свойство
𝗘
cos²θ+sin²θ=1
тригонометрических функций
ch²+sh²=1
гиперболических функций
Преобразование от штрихованных к нештрихованным координатам
𝗘
(преобразование эвклидова поворота)
𝑥=𝑥'cos θ𝑟+𝑦'sin θ𝑟 =
𝑥'+𝑆𝑟𝑦'
√1+𝑆𝑟² ; 𝑦=-𝑥'sin θ𝑟+𝑦'cos θ𝑟 =
-𝑆𝑟𝑥'+𝑦'
√1+𝑆𝑟² ;
𝗟
(преобразование Лоренца)
𝑥=𝑥'ch θ𝑟+𝑡'sh θ𝑟 =
𝑥'+β𝑟𝑡'
√1+β𝑟² ; 𝑡=𝑥'sh θ𝑟+𝑡'ch θ𝑟 =
β𝑟𝑥'+𝑦'
√1-β𝑟² ;
Преобразование от нештрихованных к штрихованным координатам
𝗘
𝑥'=𝑥 cos θ𝑟-𝑦 sin θ𝑟 =
𝑥-𝑆𝑟𝑦
√1-𝑆𝑟² ;
𝑦'=𝑥 sin θ𝑟+𝑦 cos θ𝑟 =
𝑆𝑟𝑥+𝑦
√1+𝑆𝑟² .
𝗟
𝑥'=𝑥 ch θ𝑟+𝑡 sh θ𝑟 =
𝑥-β𝑟𝑡
√1-β𝑟² ;
𝑡'=-𝑥 sh θ𝑟+𝑡 ch θ𝑟 =
-β𝑟𝑥+𝑦
√1-β𝑟² .
Фундаментальный закон сложения
𝗘
наклонов:
если некоторая линия образует угол θ с повёрнутой осью 𝑦', то угол θ, образуемый этой же линией с исходной осью 𝑦, определяется выражением
θ=θ'+θ𝑟,
или для относительных наклонов tg θ =
tg θ'+tg θ𝑟
1-tg θ' tg θ𝑟 , 𝑆 =
𝑆'+𝑆𝑟
1-𝑆'𝑆𝑟
𝗟
скоростей:
если пуля движется в направлении оси 𝑥 и параметр её скорости равен θ' в штрихованной системе отсчёта ракеты, то параметр скорости пули относительно нештрихованной лабораторной системы отсчёта θ определяется выражением
θ=θ'+θ𝑟,
или для относительных скоростей th θ =
th θ'+th θ𝑟
1+th θ' th θ𝑟 , β =
β'+β𝑟
1+β'β𝑟
Сводка формул главы 2, выраженных в единицах массы и в обычных единицах
𝗠
Формулы, включающие 𝑝, 𝐸, 𝑇, выраженные в единицах массы
𝗢
Формулы, включающие 𝑝обычн=𝑝𝑐, 𝐸обычн=𝐸𝑐², 𝑇обычн=𝑇𝑐², выраженные в обычных единицах
𝗙
Номера формул
Единицы измерения
Импульс
𝗠
килограммы, граммы или, например, жетоны для автоматов, продающих подсолнечное масло
𝗢
кг⋅м/сек, г⋅м/сек или (например) жетон⋅вершок/сек
Энергия
𝗠
килограммы, граммы или, например, те же жетоны
𝗢
джоуль, Мэв, эрг или, например, фунт⋅вершок
Ньютоновские формулы (приближение малых скоростей)
𝗠
𝑝 = 𝑚β , 𝑇 =
1
2 𝑚β²
𝗢
𝑝обычн = 𝑚β𝑐 = 𝑚𝑣 𝑇обычн =
1
2 𝑚β²𝑐² =
1
2 𝑚𝑣²
𝗙
67, 68
Релятивистские формулы
Компоненты 4-вектора энергии-импульса
𝗠
𝑝 𝑡 = 𝐸 = 𝑚
𝑑𝑡
𝑑τ 𝑝 𝑥 = 𝑚
𝑑𝑥
𝑑τ 𝑝 𝑦 = 𝑚
𝑑𝑦
𝑑τ 𝑝 𝑧 = 𝑚
𝑑𝑧
𝑑τ
𝗢
𝐸обычн = 𝑚𝑐²
⎛
⎜
⎝
𝑑𝑡
𝑑τ
⎞
⎟
⎠ 𝑝обычн𝑥 = 𝑚𝑐
⎛
⎜
⎝
𝑑𝑥
𝑑τ
⎞
⎟
⎠ 𝑝обычн𝑦 = 𝑚𝑐
⎛
⎜
⎝
𝑑𝑦
𝑑τ
⎞
⎟
⎠ 𝑝обычн𝑧 = 𝑚𝑐
⎛
⎜
⎝
𝑑𝑧
𝑑τ
⎞
⎟
⎠
𝗙
77
Абсолютная величина импульса
𝗠
𝑝 = √(𝑝𝑥)²+(𝑝𝑦)²+(𝑝𝑧)² = = 𝑚
𝑑𝑟
𝑑τ = = 𝑚 sh θ = =
𝑚β
√1-β²
𝗢
𝑝обычн = =
⎡
⎣
⎛
⎝ 𝑝обычн𝑥
⎞²
⎠ +
⎛
⎝ 𝑝обычн𝑦
⎞²
⎠ +
⎛
⎝ 𝑝обычн𝑧
⎞²
⎠
⎤½
⎦ = = 𝑚𝑐
⎛
⎜
⎝
𝑑𝑟
𝑑τ
⎞
⎟
⎠ = = 𝑚𝑐 sh θ = =
𝑚𝑣
√1-β²
𝗙
73
Полная энергия
𝗠
𝐸 = 𝑚 ch θ =
𝑚
√1-β²
𝗢
𝐸обычн = 𝑚𝑐²ch θ =
𝑚𝑐²
√1-β²
𝗙
81
Энергия покоя
𝗠
𝐸покоя=𝑚
𝗢
𝐸покоя обычн=𝑚𝑐²
𝗙
83,84
Кинетическая энергия
𝗠
𝑇 = 𝑚 (ch θ-1) = = 𝑚
⎛
⎜
⎝
1
√1-β² - 1
⎞
⎟
⎠
𝗢
𝑇обычн = 𝑚𝑐² (ch θ-1) = = 𝑚𝑐²
⎛
⎜
⎝
1
√1-β² - 1
⎞
⎟
⎠
𝗙
85
4-вектор энергии-импульса
𝗠
𝐸² - 𝑝² = 𝑚²
𝗢
𝐸обычн² = 𝑝обычн²𝑐² = 𝑚²𝑐⁴
𝗙
86
Выражение скорости частицы через её импульс и энергию
𝗠
β = th θ =
sh θ
ch θ =
𝑚 sh θ
𝑚 ch θ =
𝑝
𝐸
𝗢
𝑣 = 𝑐 th θ =
𝑝обычн𝑐²
𝐸обычн
𝗙
90
Законы преобразования (штрихованные величины измерены в системе отсчёта ракеты)
𝗠
𝐸' =- 𝑝 𝑥 sh θ𝑟 + 𝐸 ch ch θ𝑟 𝑝 𝑥' = 𝑝 𝑥 ch θ𝑟 - 𝐸 sh ch θ𝑟 𝑝 𝑦' = 𝑝 𝑦 𝑝 𝑧' = 𝑝 𝑧
𝗢
𝐸обычн'
𝑐 =- 𝑝обычн𝑥 sh θ𝑟 +
𝐸обычн
𝑐 ch θ𝑟 𝑝обычн𝑥' = 𝑝обычн𝑥 ch θ𝑟 -
𝐸обычн
𝑐 sh θ𝑟 𝑝обычн𝑦' = 𝑝обычн𝑦 𝑝обычн𝑧' = 𝑝обычн𝑧
𝗙
78
Обратные преобразования
𝗠
𝐸 = 𝑝 𝑥' sh θ𝑟 + 𝐸' ch θ𝑟 𝑝 𝑥 = 𝑝 𝑥' ch θ𝑟 + 𝐸' sh θ𝑟 𝑝 𝑦 = 𝑝 𝑦' 𝑝 𝑧 = 𝑝 𝑧'
См. также рис. 91 на стр. 160
𝗢
𝐸обычн
𝑐 = 𝑝обычн𝑥' sh θ𝑟 +
𝐸обычн'
𝑐 ch θ𝑟 𝑝обычн𝑥 = 𝑝обычн𝑥' ch θ𝑟 +
𝐸обычн'
𝑐 sh θ𝑟 𝑝обычн𝑦 = 𝑝обычн𝑦' 𝑝обычн𝑧 = 𝑝обычн𝑧'
ОГЛАВЛЕНИЕ
Предисловие к русскому переводу
5
1. ГЕОМЕТРИЯ ПРОСТРАНСТВА-ВРЕМЕНИ
9
1. Притча о землемерах
9
2. Инерциальная система отсчёта
15
3. Принцип относительности
21
4. Координаты события
27
5. Инвариантность интервала
33
6. Пространственно-временные диаграммы. Мировые линии
41
7. Подразделения пространства-времени
51
8. Преобразование Лоренца
55
9. Параметр скорости
65
Упражнения к главе 1
79
Предварительные замечания
79
A. Интервал пространства-времени (разд. 5—7)
81
Б. Преобразование Лоренца (разд. 8 и 9)
84
B. Загадки и парадоксы
92
Г. Основания теории
96
Д. Приближение малых скоростей
112
Е. Физика пространства-времени. Новые факты
119
Ж. Геометрическое истолкование
124
3. Винегрет
129
2. ИМПУЛЬС И ЭНЕРГИЯ
139
10. Введение. Импульс и энергия, выраженные в единицах массы
139
11. Импульс
142
12. 4-вектор энергии-импульса
150
13. Эквивалентность энергии и массы покоя
161
Упражнения к главе 2
179
A. Общие задачи
181
Б. Эквивалентность энергии и массы покоя
188
B. Фотоны
191
Г. Допплеровское смещение
202
Д. Столкновения
210
Е. Атомная физика
221
Ж. Межзвёздные полёты
228
3. ФИЗИКА ИСКРИВЛЁННОГО ПРОСТРАНСТВА-ВРЕМЕНИ
229
Притча о двух путешественниках
239
4. РЕШЕНИЯ УПРАЖНЕНИЙ
253
Решения упражнений к главе 1
253
Решения упражнений к главе 2
279
Некоторые физические постоянные
315
Множители перехода
316
Резюме главы 1
317
Сводка формул главы 2
318
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, её оформлении, качестве перевода и другие, просим присылать по адресу: Москва, И-278, 1-й Рижский пер., д. 2, издательство «Мир».
Э. Тейлор, Дж. Уилер
ФИЗИКА ПРОСТРАНСТВА-ВРЕМЕНИ
Редакторы
Л. В. Самсоненко
,
Э. А. Медушевская
Художник
В. А. Медников
Художественный редактор
В. М. Варлашин
Технический редактор
И. К. Дерва
Корректор
О. К. Румянцева
Сдано в набор 6/XI 1970 г. Подписано к печати 8/IV 1971 г. Бумага № 1 70x108¹/₁₆= 10 бум. л. Уел. печ. л. 28. Уч.-изд. л. 26.04. Изд. № 27/5952. Цена 2 р. 25 к. Зак. 543
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Московская типография № 16 Главполиграфпрома Комитета по печати при Совете Министров СССР
Москва, Трёхпрудный пер., 9

«Физика пространства - времени» рассчитана на студента, только что приступившего к занятиям физикой, и призвана продемонстрировать пользу знакомства с великими открытиями Эйнштейна и других с самого начала изучения физики, а не в конце его.
Книга даёт элементарное, но последовательное и строгое изложение основ теории относительности, и мы надеемся, что она поможет студенту чувствовать себя в геометрии пространства-времени столь же привычно, как в прошлом столетии его предшественники чувствовали себя в мире эвклидовой геометрии.
ФИЗИКА ПРОСТРАНСТВА-ВРЕМЕНИ
Принципы частной теории относительности замечательно просты. Они много проще аксиом геометрии Эвклида или правил управления автомобилем. Однако и геометрия Эвклида, и автомобиль были созданы поколениями обыкновенных людей, даже не испытавшими в полной мере удивления, которого заслуживали плоды их творчества. Некоторые из лучших умов XX века выступали против идей теории относительности, и не потому что темна их природа, а по той простой причине, что человеку трудно преодолеть установившийся взгляд на вещи. Теперь относительность уже окончательно выиграла сражение. Мы уже можем выразить её понятия так просто, что правильный взгляд на вещи устанавливается сам собой.