Teacher.elementary.school
Методика преподавания математики в начальной школе
Умозаключения
I. Умозаключения.
1. Понятие «умозаключения».
2. Виды умозаключений:
а) дедуктивное,
б) неполная индукция,
в) аналогия.
II. Схемы дедуктивных умозаключений.
III. Способы математического доказательства.
1. Понятие доказательства.
2. Основные законы построения дедуктивных умозаключений.
3. Виды доказательств:
а) прямое,
б) косвенное,
в) полная индукция.
В математике знания чаще получают в процессе рассуждений. Для того, чтобы знание было истинным, рассуждение должно строится в соответствии с правилами, лежащими в основе логики. Считают, что рассуждения используют при доказательствах. Для обучения учащихся учитель должен владеть глубокими знаниями построения верных рассуждений, о структуре и способах доказательств.
В логике понятие рассуждения заменяется словом «умозаключение».
Умозаключение – это форма мышления, посредством которой из одного или нескольких высказываний, называемых посылками, выводится высказывание, содержащее новое знание, называемое заключением.
Рассмотрим образцы умозаключений, используемых в начальном курсе математики:
1) При выполнении устных вычислительных приемов с числами учащиеся применяют различные математические понятия, в том числе и понятия, связанные с десятичной системой счисления, которой мы пользуемся в современной математике. Например, в случае
42 + 6 учащиеся должны владеть разрядным составом двузначного числа. Объясняя способ вычисления, дети говорят: «Число 42 – двузначное. Все двузначные числа можно представить в виде суммы двух разрядных слагаемых – десятков и единиц. Следовательно, 42 = 40 + 2».
Это умозаключение состоит из трех предложений. Первое и второе предложение – посылки:
1-ое предложение – частная посылка, она дает характеристику числу 42;
2-ое предложение – посылка общего характера, которая указывает на особенность двузначных чисел – состоят из двух разрядов (десятков, единиц).
3-е предложение является заключением, оно формулируется после слова «следовательно», и также носит частный характер, т.к. в нем идет речь о конкретном числе – 42.
2) При ознакомлении учащихся с переместительным (коммутативным) свойством умножения создается проблемная ситуация, в процессе разрешения которой учащиеся самостоятельно формулируют свойство:
На сколько квадратов разделен каждый прямоугольник? Посчитай разными способами. Объясни свои действия.
Учащиеся с помощью системы вопросов учителя предлагают по два способа вычисления к каждому из рисунков:
4 × 3 = 3 × 4 9 × 3 = 3 × 9.
Затем учащиеся делают вывод: для всех натуральных чисел верно равенство
а × в = в × а.
В данном умозаключении посылками являются два равенства. В них утверждается, что для конкретных натуральных чисел выполняется переместительное свойство. Заключением же в этом случае является утверждение общего характера – от перестановки множителей значение произведения не изменяется.
3) При ознакомлении младших школьников со случаями деления на однозначное число, дети должны уяснить, что деление связано с умножением. А следовательно, чтобы найти значение выражения, например 56 : 7, нужно знать табличные случаи умножения числа 7. На какое число нужно умножить 7, чтобы получить 56 – делимое:
«Мы знаем, что 7 × 8 = 56. Если произведение разделить на один из множителей, получится другой множитель. Следовательно, 56 : 7 = 8».
Таким же образом, учащиеся рассуждают, находя результат в случаях 27 : 9, 36 : 6 и т.д.
Рассмотрев эти случаи, мы видим, что умозаключения бывают разными. В логике рассмотренные нами называют дедуктивными.
Дедуктивными называют умозаключения, в которых посылки и заключения находятся в отношении логического следования.
Посылки дедуктивного следования обозначают так –
А1 , А2 , …, Аn , а заключение буквой
В. Схематично само умозаключение можно представить так:
А1, А2, …, Аn => В. Часто используют и такую запись:
А1 , А2 , …, Аn .
В
В ней черта обозначает слово «следовательно».
В дедуктивном умозаключении при истинности посылок, истинно и заключение.
Во втором случае рассматриваются две посылки частного характера, показывающие, что некоторые натуральные числа обладают переместительным свойством при выполнении умножения. На этой основе сделан вывод, что этим свойством обладают все натуральные числа. Такие умозаключения – неполная индукция.
Неполная индукция – умозаключение, в котором на основании того, что некоторые объекты класса обладают определенным свойством, делают вывод, что этим свойством обладают все объекты данного класса.
Неполная индукция не является дедуктивным умозаключением.
Рассмотрим как образец пары выражений:
3 + 5 и 3 × 5; 2 + 7 и 2 × 7; 4 + 8 и 4 × 8. Можно с уверенностью утверждать, что сумма этих чисел меньше произведения. На основании этого можно сделать вывод, что этим свойством обладают все натуральные числа:
(Ұ а,в Є N)[а + в < а × в].
Но это утверждение ложно, т.к. можно привести контрпример: числа 1 и 2 – натуральные, но их сумма больше, чем произведение
1 + 2 < 1 × 2. Значит, к выводам, полученным с помощью неполной индукции, важно относится осторожно. Они носят характер предположения (гипотезы) и нуждаются в проверке. Их доказывают или опровергают.
Таким образом, неполная индукция и дедуктивные умозаключения взаимосвязаны. Все математические утверждения (теоремы, аксиомы, определения, правила), используемые в дедуктивных умозаключениях, часто являются результатом индуктивного обобщения. А индуктивного умозаключения расширяют математические знания.
В третьем случае используется аналогия (греч. – «сходство, соответствие»).
Аналогия – умозаключение, в котором на основании сходства объектов по некоторым признакам и при наличии другого признака у одного из них, делается вывод о наличии этого признака у другого объекта.
Термином «объект» называются реальные предметы, модели, рисунки, числовые и буквенные выражения, задачи. Аналогия помогает открывать новые и использовать усвоенные способы действия в измененных условиях. Выводы по аналогии также требуют доказательства или опровержения, т.к. носят характер предположения.
Например, при изучении понятия о десятичной системе счисления, учащиеся изучают названия классов и разрядов. Изучая класс единиц, дети знакомятся с разрядами единиц, десятков, сотен, в классе тысяч – единицами тысяч, десятками тысяч, сотнями тысяч. По аналогии они уже могут назвать разряды классов миллионов и миллиардов.
Знакомясь с дистрибутивным свойством умножения, учащиеся используют его при выполнении умножения двузначных чисел:
23 × 4 = (20 + 3) × 4 = 20 × 4 + 3 × 4 = 80 + 12 = 92
По аналогии они выполняют умножение трехзначных чисел:
123 × 4 = (100 + 20 + 3) × 4 = 100 × 4 + 20 × 4 + 3 × 4 = 400 + 80 + 12 = 492
По аналогии они выполняют умножение четырехзначных чисел:
5123 × 4 = ……………..
А далее делается обобщение: выводится алгоритм умножения многозначного числа на однозначное –
неполная индукция.
Практическая работа
Выделите в перечисленных умозаключениях посылки и заключения.
а) Если запись числа оканчивается нулем, то оно кратно 10. Число 260 оканчивается нулем. Следовательно, число 260 кратно 10.
б) Если запись числа оканчивается нулем, то оно кратно 10. Если число кратно 10, то оно четное. Следовательно, если запись числа оканчивается 0, то оно четное.
в) Если запись числа оканчивается нулем, то оно кратно 10. Число 263 не кратно 10. Следовательно, оно не оканчивается нулем.
II. Согласно определению, в дедуктивном умозаключении посылки и заключение находятся в отношении логического следования. Это означает, что в нем всегда из истинных посылок следует истинное заключение.
Важно знать, как строить такие умозаключения и проверять их правильность.
В логике считают, что правильность умозаключения определяется его формой и не зависит от его конкретного содержания входящих в него утверждений. Математика предлагает такие правила, соблюдая которые можно строить дедуктивные умозаключения. Эти правила называются
правилами вывода или
схемами дедуктивных умозаключений:
1. А(х) => В(х), А(а) –
правило заключения;
В(а)
2. А(х) => В(х), В(а) –
правило отрицания;
А(а)
3. А(х) => В(х), В(х) => С(х)
– правило силлогизма.
А(х) => В(х)
В
правиле заключения обозначены две посылки: А(х) => В(х) и А(а). Первую называют общей (это может быть определение, правило, теорема), а вторую – частной (она получается из условия А(х) при х = а).
Например:
Если запись числа
х оканчивается цифрой 5, то число
х делится на 5. Запись числа 135 оканчивается цифрой 5. Следовательно, число 135 делится на 5.
Данное умозаключение можно записать так – А(х) => В(х), А(а), где
А(х) – общая посылка – «запись числа
х оканчивается цифрой 5», а
В(х) – «число
х делится на 5»;
А(а) – частная посылка – «число 135 оканчивается цифрой 5», при х = 135;
В(а) – заключение – «число 135 делится на 5».
Для
правила отрицания приведем такой пример:
Если запись числа
х оканчивается цифрой 5, то число
х делится на 5. Число 137 не делится на 5. Следовательно, оно не заканчивается цифрой 5.
Это умозаключение можно записать так – А(х) => В(х), В(а), где:
А(х) => В(х) – общая посылка такая же, как и в первом случае – «запись числа
х оканчивается цифрой 5, то число
х делится на 5»;
В(а) – частная посылка – отрицание – «число 137 не делится на 5», при х = 137;
А(а) – заключение – отрицание – «число 137 не оканчивается цифрой 5».
К
правилу силлогизма приведем такой пример:
Если число
х кратно 12, то оно кратно 6. Если
х кратно 6, то оно кратно 3. Следовательно, если число
х кратно 12, то оно кратно 3.
В этом умозаключении две посылки вида «если А(х), то В(х)» и «если В(х), то С(х)», где
А(х) – «х кратно 12»,
В(х) – «х кратно 6»,
С(х) – «х кратно 3».
Заключение представляет собой «если А(х), то С(х)».
Выполняя рассуждения по этим правилам, мы всегда будем получать истинные заключения, что и требуется в дедуктивном заключении.
В логике существуют различные способы проверки истинности заключений, но часто используются круги Эйлера.
Задача.
«Если запись числа оканчивается цифрой 5, то число делится на 5. Число125 делится на 5. Следовательно, запись числа оканчивается на 5».
Правильно ли это заключение?
Данное умозаключение выполнено по схеме А(х) => В(х), В(125)
А(125)
В общем виде ее можно представить так: А(х) => В(х), В(а)
А(а)
Такой схемы из тех, которые нами рассмотрены, нет. Для определения, является ли это умозаключение дедуктивным, воспользуемся кругами Эйлера. На теоретико-множественном языке запишем правило так
ТА c ТВ, а Є ТА
а Є ТВ
Тв
. а
тТтттТ
Та
ТА – множество чисел, оканчивающихся на 5;
ТВ – множество чисел, делящихся на 5;
а = 125.
Мы изобразили на кругах Эйлера множества истинности ТА, ТВ и элемент а, который принадлежит множеству ТА. Но он может содержаться и в множестве ТВ, а может ему и не принадлежать. Значит, эта схема не гарантирует истинность умозаключения, т.к. оно не может быть дедуктивным. Данное умозаключение не является истинным, т.к. не выполнено по схеме.
Важно отметить, что
1) выполняя умозаключение, можно менять очередность посылок и начинать с заключения, а потом воспроизводить посылки;
2) если общие посылки рассмотренных в правилах дедуктивных умозаключений содержат более одной переменной, то это не нарушает их смысл.
Практическая работа
1. Определите логическую структуру умозаключений.
а) Во всяком прямоугольнике противоположные стороны равны. Четырехугольник АВСD – прямоугольник. Следовательно, его противоположные стороны равны.
б) Все прямоугольники являются параллелограммами. Во всех параллелограммах противоположные стороны равны. Следовательно, в любом прямоугольнике противоположные стороны равны.
в) Все числа кратные 2, являются четными. Число 17 не является четным. Следовательно, оно не делится на 2.
г) Равные треугольники имеют равные площади. Треугольники АВС и МНР имеют равные площади. Следовательно, они равны.
2. Закончите умозаключения так, чтобы они были дедуктивными.
а) Все квадраты – прямоугольники. Все прямоугольники – многоугольники. Следовательно, … .
б) В любом прямоугольнике сумма внутренних углов равна 360̊ . Четырехугольник АВСD – … .
III. Обычно, в математике, когда говорят о доказательстве, имеют в виду проверку высказанного утверждения.
Доказать какое-либо утверждение – это значит показать, что это утверждение логически следует из системы истинных и связанных с ним утверждений.
В логике считают, что если рассматриваемое утверждение логически следует из уже доказанных утверждений, то оно обоснованно и также истинно, как и они. Т.е. основным способом доказательства является дедуктивный вывод.
Доказательство – это логическая операция, в процессе которой обосновывается истинность какого-либо утверждения с помощью других истинных и связанных с ним утверждений. Для этого строится конечная цепочка умозаключений, причем заключение каждого из них (кроме последнего) является посылкой в одном из последующих умозаключений.
Доказательство в виде цепочки умозаключений выполняется в соответствии с правилами вывода и указанием всех посылок, оно не предназначено для постоянного использования на практике, где чаще пользуются свернутыми схемами умозаключений.
Применяются не только правила построения дедуктивных умозаключений, но и четыре основных закона логики:
1. Закон тождества.
Каждая мысль, повторяемая в рассуждении, должна быть тождественна самой себе. Это означает, что в процессе рассуждения нельзя подменять одну мысль другой, а одно понятие другим. Нельзя тождественные мысли выдавать за различные, а различные за тождественные.
2.Закон непротиворечия.
Высказывание и его отрицание не могут быть одновременно истинными, одно из них всегда ложно.
Если в в мышлении или речи человека обнаружено логическое противоречие, то такое мышление считается неправильным, а суждение вытекающее из него – ложным.
3. Закон исключенного третьего.
Из двух противоречивых высказываний об одном и том же предмете, одно – истинно, другое – ложное, третьего быть не может.
Этот закон требует выбора одной из взаимоисключающих альтернатив.
4. Закон достаточного основания.
Всякое истинное утверждение должно быть обосновано с помощью других утверждений, истинность которых уже доказана.
Т.е. истинность утверждения нельзя принимать на веру. В качестве аргументов для доказательств используются определения понятий, доказанные теоремы и правила.
Следовательно, при доказательстве необходимо
1) иметь то утверждение, истинность которого нужно доказывать;
2) понимать, что доказательство- это цепочка дедуктивных умозаключений, выполняемых по правилам и законам логики;
3) понимать, какие истинные утверждения можно использовать в процессе доказательства.
Доказательства существуют трех видов:
1) прямое,
2) косвенное,
3) полная индукция.
Прямое доказательство – это построение цепочки дедуктивных умозаключений, выполняемых последовательно от А => В с соблюдением правил и законов логики, истинность которых доказана.
В доказательстве об утверждении, что четырехугольник, у которого три углы прямые, то это прямоугольник, является прямым, т.к. основываясь на истинном предложении с учетом теоремы, строится цепочка дедуктивных утверждений, приводящая к истинному заключению.
Косвенное доказательство – доказательство методом от противного. При доказательстве теоремы – А => В, допускают, что заключение В – ложно, а отрицание истинно. Предложение В (не В) присоединяется к совокупности истинных посылок, и строится умозаключение до тех пор, пока не получится противоречивое утверждение для А. Устанавливают противоречие, на основании закона о непротиворечии, и делают вывод, что предположение было ложным. Значит, на основании закона исключения третьего истинно В, т.е. то, что и требовалось доказать.
Полная индукция – метод доказательства, при котором истинность утверждения следует из истинности его во всех частных случаях.
Способы определения понятий в начальном курсе математики
План:
I. Понятия, изучаемые в курсе начальной математики.
II. Объем и содержание понятия.
III. Отношения между понятиями.
IV. Определение понятий.
1. Понятие определения.
2. Виды определений.
3. Определение через род и видовое отличие.
I. Понятия, изучаемые в курсе начальной математики.
Понятия, которые изучаются в начальном курсе математики, разбивают на четыре группы:
1) арифметические понятия, связанные с числами и операциями над ними (число, цифра, сложение, слагаемое и др.);
2) алгебраические понятия (выражения, равенства, неравенства, уравнение и др.);
3) геометрические понятия (прямая, отрезок, треугольник и др.);
4) понятия, связанные с величинами и их измерением.
В логике
понятие рассматривают как форму мышления, отражающую объекты (предметы или явления) в их существенных и общих свойствах. Языковой формой понятия является слово или группа слов.
Понятия не существуют в объективном мире. Они возникают в сознании человека и заменяют предметы и явления этого мира, являясь их идеальными образами.
Иметь понятие об объекте – это значит уметь выделить его существенные признаки и отличить от всех других объектов. Математические понятия, как и другие, существуют лишь в мышлении человека, отражены в математическом языке (математических знаках и символах).
Учитель должен владеть объемом и содержанием понятий, об отношениях между ними и об операциях с ними.
II. Объем и содержание понятия
Всякий математический объект обладает определенными свойствами, среди которых выделяют существенные и несущественные.
Свойства называются существенными, если без них объект существовать не может, т.е. они ему присущи.
Ярко это можно продемонстрировать на геометрических понятиях. Любой прямоугольник имеет четыре стороны, четыре угла, равные диагонали. Но без третьего свойства он существовать не может: все четыре угла – прямые. А квадрат имеет четыре прямых угла, равные диагонали, четыре стороны. Существенное свойство – все стороны равны.
Следовательно, когда говорят о математическом понятии, то подразумевают множество объектов, называемых одним словом или группой слов (термином). Если говорят о прямоугольниках, то это все те фигуры, у которых все четыре угла прямые, а квадраты – это прямоугольники, у которых все стороны равны.
Считается, что множество всех квадратов составляет объем понятия «квадрат».
Объем понятия – это множество всех объектов, которые обобщаются в понятии и обозначаются одним термином.
Любое понятие имеет содержание.
Содержание понятия – это множество всех существенных свойств объекта, отраженных в этом понятии.
Объем понятия прямоугольник – это множество различных прямоугольников, а в его содержание входят такие свойства прямоугольника:
– «иметь четыре стороны»,
– «иметь четыре прямых угла»,
– «иметь равные противоположные стороны»,
– «иметь равные диагонали».
III. Отношения между понятиями
Между объемом понятия и его содержанием существует взаимосвязь:
если увеличивается объем понятия, то уменьшается его содержание, и наоборот, с уменьшением объема понятия – увеличивается его содержание.
Например, объем понятия «квадрат» является частью объема понятия «прямоугольник», а в содержании, понятия «квадрат» содержится больше свойств, чем в содержании понятия «прямоугольник» («все стороны равны», «диагонали взаимно перпендикулярны», «диагонали равны» и другие).
Любое понятие нельзя усвоить, не осознавая его взаимосвязи с другими понятиями. Поэтому важно знать, в каких отношениях могут находиться эти понятия, и уметь устанавливать эти связи.
Понятия обозначают строчными буквами латинского алфавита:
а, b,
c,
d, …, z. Поэтому, если заданы два понятия
а и
b, то объемы этих понятий обозначают соответственно
А и
В.
Они могут находится в различных отношениях.
Если
А c В (А ≠
В), то говорят, что понятие
а –
видовое по отношению к понятию
b, а понятие
b –
родовое по отношению к понятию
а.
Например: если
а – это «прямоугольник»,
b – это «четырехугольник», то их объемы
А и
В находятся в отношении включения (
А c В и
А ≠
В ), т.к. каждый прямоугольник является четырехугольником. Поэтому можно утверждать, что понятие «прямоугольник» – видовое по отношению к понятию «четырехугольник», а понятие «четырехугольник» – родовое по отношению к понятию «прямоугольник».
Если
А = В, то говорят, что понятия
а и
b тождественны.
1) Понятия рода и вида относительны: одно и то же понятие может быть родовым по отношению к одним понятиям и видовым по отношению к другим. Например: понятие «прямоугольник» – родовое по отношению к понятию «квадрат» и видовым по отношению к понятию «четырехугольник».
2) Для понятия прямоугольник существует несколько родовых понятий – «четырехугольник», «параллелограмм», «многоугольник». Среди них можно указать ближайшее – параллелограмм».
3) Видовое понятие обладает всеми свойствами родового понятия. Квадрат являясь видовым понятием по отношению к понятию «прямоугольник», обладает всеми свойствами, присущими прямоугольнику.
Отношения между понятиями, изображая объемы, можно показать с помощью кругов Эйлера.
Например:
а)
а – «прямоугольник»,
b – «ромб»: объемы пересекаются, но ни одно множество не является подмножеством другого, следовательно понятия «прямоугольник» и «ромб» не находятся в отношении рода и вида.
А В
б)
а – «многоугольник»,
b – «параллелограмм»: объемы данных понятий находятся в отношении включения, но не совпадают – всякий параллелограмм является многоугольником, но не наоборот. Следовательно, понятие «параллелограмм» – видовое по отношению к понятию «многоугольник», а понятие «многоугольник» – родовое по отношению к понятию «параллелограмм».
А
В
в)
а – «прямая»,
b – «отрезок»: объемы понятий не пересекаются, т.к. ни про один отрезок нельзя сказать, что он является прямой, и ни одна прямая не может быть названа отрезком. Следовательно, данные понятия не находятся в отношении рода и вида (отрезок – часть прямой, т.е. наблюдается отношение целого и части).
А В
IV. Определение понятий
1. Понятие определения.
Определение понятий – это логическая операция, с помощью которой раскрывается содержание понятия, либо устанавливается значение термина.
2. Виды определений.
По способу выявления содержания понятия различают
явные и
неявные определения.
К неявным определениям относят
остенсивные. Это определения, раскрывающие существенные свойства (признаки) предметов путем указания, показа, демонстрации объектов, которые этими терминами обозначают.
Например, при ознакомлении с алгебраическими понятиями пользуются остенсивными определениями так:
4 · 7 < 4 · 9 8 · 7 = 56
23 + 8 > 30 9 · 6 = 6 · 9
93 – 8 < 93 – 6 46 + 7 = 62 – 9
Это неравенства. Это равенства.
Наиболее часто применяются остенсивные определения при изучении геометрических понятий.

Остенсивные определения характеризуются незавершенностью. Поэтому впоследствии требуется подробное изучение этих понятий.
Также применяют описание или сравнение объектов.
К неявным определениям относят и
контекстуальные – через отрывок текста, через контекст, через анализ конкретной ситуации, описывающей смысл понятия.
Через текст устанавливается связь определяемого понятия с другими, уже известными понятиями, раскрывая его содержание.
Например, при изучении понятия уравнения (2 класс):
– 5 = 4
Из какого числа нужно вычесть 5, чтобы получилось 4?
Обозначим неизвестное число латинской буквой х:
х – 5 = 4 – это уравнение.
Решить уравнение – это значит найти неизвестное число. В данном уравнении неизвестное число равно 9, так как 9 – 5 = 4.
Объясни, почему числа 0, 10, 8 не подходят.
3. Определение через род и видовое отличие.
Среди явных определений в математике чаще всего используются определения через род и видовое отличие.
Например: «Прямоугольник – это четырехугольник, у которого все углы прямые».
В этом определении есть две части – определяемое понятие (прямоугольник) и определяющее понятие (четырехугольник, у которого все углы прямые). Если обозначить через
а первое понятие, а через
b – второе, то данное определение можно представить в таком виде:
а есть (по определению)
b или
а <=>
b
опр.
Читают запись так: «
а равносильно
b по определению» или «
а тогда и только тогда, когда
b».
В определении прямоугольника можно выделить в определяющем понятии:
а) понятие «четырехугольник», которое является родовым по отношению к понятию «прямоугольник»;
б) свойство «иметь все углы прямые», которое позволяет выделить из всевозможных четырехугольников один вид – прямоугольники; поэтому его называют видовым отличием.
Видовое отличие – это свойство (одно или несколько), которые позволяют выделять определяемые объекты из объема родового понятия.
Это можно показать на схеме:
Определяемое понятие <=> Родовое понятие + Видовое отличие
Определяющее понятие
Схему можно заменить формулой:
а <=> с + Р
опр. b
Формулируя определения понятий через род и видовое отличие, применяют следующие правила:
1) определение должно быть соразмерным;
2) в определении не должно быть порочного круга;
3) определение должно быть ясным;
4) одно и то же понятие определить через род и видовое отличие, соблюдая правила можно по-разному.
Натуральные числа и 0.
Методика изучения нумерации натуральных чисел и 0 в начальном курсе математики
План:
1. Из истории возникновения и развития понятий натурального числа.
2. Отрезок натурального ряда. Счет элементов конечного множества.
3. Теоретико-множественный смысл натурального числа и нуля.
1. Из истории возникновения и развития понятий натурального числа и нуля
В начальной школе большое внимание уделяется изучению нумерации целых неотрицательных чисел, а также действий над ними. Это является одной из центральных тем курса начальной математики, так как всю жизнь человек пользуется различного рода вычислениями, счетом предметов и т.д. Следовательно, учитель должен хорошо представлять себе, с какой системой счисления он работает, каковы ее особенности и как она появилась.
В школьном учебнике математики программы «Перспектива» 2 класс, 2 часть под редакцией Л.Г. Петерсон для учащихся начальных классов кратко, но емко изложена эта история.
Еще в самые отдаленные времена людям понадобились арифметические знания, чтобы определять, когда надо засевать поля, начинать полив, когда ждать потомства от животных. Надо было знать; сколько овец в стаде, сколько мешков зерна положено в амбары. Однако первобытные люди не умели считать. И вот много тысяч лет тому назад древние пастухи стали делать из глины кружки – по одному на каждую овцу. Чтобы узнать, не пропала ли за день хоть одна овца, пастух откладывал в сторону по одному кружку каждый раз, когда очередное животное проходило в загон. И только убедившись, что овец вернулось столько же, сколько было кружков, он спокойно шел спать.
Но в стаде у первобытных людей были не только овцы – они пасли и коров, и коз, и ослов. Поэтому пришлось делать из глины и другие фигурки. А земледельцы с помощью глиняных фигурок, камушков, зарубок вели учет собранного урожая. Они отмечали, сколько мешков зерна положено в амбар, сколько кувшинов масла выжато из оливок, сколько соткано кусков льняного полотна. Складывая и вычитая множества предметов, они решали простейшие задачи на сложение и вычитание. Так, еще не умея считать, древние люди занимались арифметикой. Перекладывать камушки и глиняные фигурки с места на место было довольно утомительным занятием. Но прошло много тысячелетий, прежде чем люди научились пересчитывать предметы. Для этого им пришлось придумывать названия для чисел.
О том, как появились имена у чисел, ученые узнают, изучая языки различных племен и народов. Например, оказалось, что «у нивхов, живущих на Сахалине, числительные зависят от того, какие предметы считают. Важную роль играет форма предмета, так что по-нивсхи в сочетаниях «два яйца», «два камня», «два глаза» и так далее числительные различны. Одному и тому же русскому слову «два» у них соответствует несколько десятков различных слов. Нечто подобное было и древних людей. И должно было много столетий, а может быть и тысячелетий, прежде чем одни и те же числительные стали применять к предметам любого вида. Вот тогда и появились общие названия для чисел. Сначала названия получили только числа 1 и 2. Название для числа «один» связывалось обычно со словом «солнце», а название для числа «два» – с предметами, встречающимися попарно: крыльями, ушами и так далее. Но бывало, что числам 1 и 2 давали иные имена. Иногда их связывали с местоимениями «я» и «ты». А были языки, где «один» звучало так же как «мужчина», а «два» – как «женщина». У некоторых племен еще совсем недавно не было других числительных, кроме «один» и «два». А все, что шло после двух, называлось «много» Но потом понадобилось называть и другие числа. Ведь и собак у охотника, и стрел у него, и овец у пастуха может быть больше, чем две. И тут придумали замечательный выход: числа стали называть, повторяя несколько раз названия для единиц и двоек».
На языке некоторых папуасских племен, живущих на острове Новая Гвинея в Тихом океане, и сейчас числительное «один» звучит «урапун», «два» – «окоза», а число 3 они называют «оказа – урапун», число 4 «окоза – окоза». Так они дошли до числа 6, которое получило имя «окоза – окоза – окоза». Позднее другие племена дали особое имя числительному, которое мы называем «три». А так как до того они считали «один», «два», «много», то это новое числительное стали применять вместо слова «много». Иногда числом 3 обозначали окружающий человека мир – его делили на земное, подземное и небесное царства. Поэтому число 3 стало у многих народов священным. Когда они придумывали легенды о богах, то выделяли из них трех самых главных.
По нашему мнению, в русских сказках число 3 также играло особую роль. Во многих из них участвуют три брата, герой сражается с трехглавым змеем, проходит 3 царства – медное, серебряное и золотое. Число 4 встречается в сказках куда реже. Когда – то за числом 4 и в русском языке начиналась необозримая область «много».
На более поздних этапах в роли слова «много» выступало число 7. Об этом говорят различные пословицы и поговорки: «Семеро одного не ждут», «Семь раз отмерь – один раз отрежь», «Один с сошкой – семеро с ложкой», «Семь бед – один ответ». Так постепенно люди осваивали счет.
Первые названия чисел некоторые племена стали применять 20 – 25 тысяч лет тому назад. А вот слово для обозначения числа 1000 возникло лишь 5 – 7 тысяч лет назад.
Людям приходилось считать на пальцах очень большие совокупности предметов к счету привлекали больше участников. Один считал единицы, второй – десятки, а третий – сотни, т.е. десятки десятков. Он загибал один палец, лишь после того, как у второго участника счета оказывались загнутыми все пальцы обеих рук. Сначала говорили так: пять пальцев третьего человека, восемь пальцев второго и шесть пальцев первого. Но ведь это сколько времени надо произносить! Поэтому постепенно стали произносить короче. Вместо «палец второго человека» – появилось слово «десять», а вместо «палец третьего человека» – «сто». Вот и получилось: пятьсот восемьдесят шесть.
Счет единицами, затем десятками десятков, а там десятками сотен и так далее лег в основу системы счисления, принятой почти у всех народов мира. Она называется
десятичной системой.
Сейчас десятичная система счисления применяется почти повсеместно. Но и теперь есть еще племена, которые довольствуются при счете пальцами одной руки. У них система счета оказалась пятеричной. В странах, где люди ходили босиком, по пальцам легко было считать до 20. Поэтому довольно большое распространение получила двадцатеричная система счета. Следы этого сохранились, например, во французском языке, где слово «восемьдесят» звучит как «четыре раза двадцать».
Самым серьезным соперником десятичной системы счета оказалась двенадцатеричная. Вместо десятков применяли при счете дюжины, т.е. группы из двенадцати предметов. Во многих странах даже теперь некоторые товары, например, ножи, ложки, вилки, пр продают дюжинами.
Долгое время после того, как появились названия чисел, люди их не записывали. Причина для этого была самая уважительная – они еще не умели писать. Поэтому, если кому-нибудь надо было переслать другому человеку сведения, где участвовали числа, прибегали к зарубкам на дереве или на кости, к узелкам на веревках, рисункам на мягкой глине и так далее. Такие знаки уже нельзя было перекладывать с места на место, убирать одни и добавлять другие. Вместо этого приходилось думать, мысленно выполнять операции над знаками.
Знаки на глине обозначали не числа, а предметы – головы скота, мешки с зерном, кувшины масла. Их приходилось изображать столько же, сколько было предметов. С этим еще можно было мириться, пока учет велся в пределах одного хозяйства, одной деревни. Но когда возникли государства, старые методы обозначения чисел стали невыгодными. Для записи больших чисел уже нельзя было обойтись ни зарубками на бирках, ни узелками, ни глиняными фигурками.
И вот примерно 5 тысяч лет тому назад было сделано замечательное открытие, люди догадались, что можно обозначать знаком не одну голову скота, а сразу 10 или 100 голов, не один мешок зерна, а сразу 6 или 60 мешков.
Например, египтяне обозначали десяток знаком

(единицу они обозначали просто вертикальной черточкой

, как это делаем и мы), десять десятков, то есть сотню – знаком
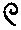
. Появились знаки для тысячи

(цветок лотоса), десятка тысяч

(поднятый кверху палец), ста тысяч

(сидящая лягушка) и миллиона
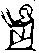
(человек с поднятыми руками).
Писать много раз один и тот же знак, разумеется, весьма неудобно. Более экономной является
позиционная система записи чисел, где имеет значение не только начертание цифры, но и ее позиция, положение среди других цифр. Первая позиционная система записи чисел появилась в Вавилоне. Единица в ней обозначалась клином
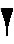
, а десяток – знаком

. В основном разница между вавилонской и современной записью чисел была в одном: вместо числа 10 вавилоняне приняли за основу системы счисления число 60. Но было еще одно отличие, делавшее вавилонскую систему записи не совсем удобной: вавилоняне долгое время не знали нуля.
Мы рассмотрели историю возникновения систем счисления, а теперь мы рассмотрим одно из важнейших чисел этой системы – число нуль.
Первыми нуль был придуман вавилонянами примерно две тысячи лет тому назад. Но они применяли его лишь для обозначения пропущенных разрядов в середине числа. Писать нули в конце записи числа они не догадались. В Индии примерно полторы тысячи лет тому назад нуль был присоединен к девяти цифрам и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно было. И самое главное, запись таких гигантских чисел стала довольно короткой. Если бы живший 30 тысячелетий тому назад древний человек имел представление о миллионе и захотел бы изобразить это число с помощью зарубок на волчьих костях, ему пришлось бы истребить 20 тысяч волков. А для записи миллиарда не хватило бы волков во всех европейских лесах.
Индийской системой обозначений мы пользуемся до сих пор. Это не значит, что индийские цифры имели с самого начала современный вид. В течение многих столетий, переходя от народа к народу, они много раз изменялись, пока приняли современную форму. Арабы заимствовали у индийцев цифры и позиционную десятичную систему записи чисел. Европейцы в свою очередь узнали ее от арабов. Поэтому наши цифры, в отличие от римских, стали называться арабскими. Правильнее было бы назвать их индийскими. Они употребляются в нашей стране, начиная примерно с ХVII века.
Математики Древней Греции долгое время пользовались буквенной нумерацией и нуля не применяли. Слово нуль они перевели на свой язык говорили «сифр». В Х – ХII веках индийская система счисления через арабов проникла в Европу, слово сифр не перевели, а немного видоизменили сначала в слово шифр, а позже в слово цифра.
Самый древний документ в Европе, в котором для нуля имеется свой знак (0), относится к IX в. В одной из книг, написанной на латинском языке в XIII веке, нулем назван «кружок», или цифра, или знак ничего. С тех пор за ним утвердилось название «фигура нуль», что означало «никакой знак». Словом
цифра стали называть знаки, обозначающие число единиц в любом разряде, в том числе цифрой назвали и единицу, а позже и сам нуль.
В первом русском учебнике «Арифметика» Л.Ф.Магницкого, напечатанном в 1689г., нуль назван цифрой или ничем. Спустя несколько лет и в России знак 0 стали называть нулем, а знаки чисел 1,2,3,4…9 называли цифрами. Однако и на этом открытие нуля не закончилось, хотя он приобрел свой вид, получил название, обрел свое место. Но не было решено – нуль цифра или число; если число, то какое: четное или нечетное?
В результате длительных обсуждений математике пришли к заключено: нуль – это число, обозначают его цифрой 0, к натуральному ряду он не принадлежит. С нулем можно производить все действия, за исключением деления на нуль.
Как мы узнали из исторической справки, данной профессором Л.П.Стойловой, о возникновении понятия числа было важнейшим моментом в развитии математики. Появилась возможность изучать эти числа независимо от тех конкретных задач, в связи с которыми они возникли. Теоретическая наука, которая стала изучать числа и действия над ними, получила название «арифметика». Слово «арифметика» происходит от греческого
arithmos, что значит «число». Следовательно, арифметика – это наука о числе.
Арифметика возникла в странах Древнего Востока: Вавилоне, Китае, Индии и Египте. Накопленные в этих странах математические знания были развиты и продолжены учеными Древней Греции. В средние века большой вклад в развитие арифметики внесли математики Индии, стран арабского мира и Средней Азии, а начиная с ХIII века – европейские ученые.
Термин «натуральное число» впервые употребил в V веке римский ученый А. Боэций, который известен как переводчик работ известных математиков прошлого на латинский язык и как автор книги «О введении в арифметику», которая до ХVI века была образцом для всей европейской математики.
Во второй половине ХIХ века натуральные числа оказались фундаментом всей математической науки, от состояния которого зависела и прочность всего здания математики. В связи с этим появилась необходимость в строгом логическом обосновании понятия натурального числа, в систематизации того, что с ним связано.
2. Отрезок натурального ряда. Счет элементов конечного множества
Аксиоматическая теория описывает натуральное число как элемент бесконечного ряда, в котором числа располагаются в определенном порядке: имеется первый элемент, для каждого имеется последующий и предыдущий. Т.е. натуральное число имеет порядковый смысл. Но число имеет и количественный смысл.
С этой целью используется понятие отрезка натурального ряда.
Определение:
Отрезком Na натурального ряда называется множество натуральных чисел, не превосходящих натурального числа а.
Это записывается так:
Na ={ х | х € N и х ≤
а}.
Например:
N7 ={1, 2, 3, 4, 5, 6, 7}.
Отрезок натурального ряда обладает двумя свойствами:
1) любой отрезок натурального ряда
Na содержит единицу (по аксиоме);
2) если число х содержится в отрезке
Na и х ≠
а, то и непосредственно следующее за ним число х + 1 также содержится в
Na.
Действительно, если
х € N
a и х ≠
а, то х <
а. А это значит, что существует такое натуральное число
с, что
а = х + с.
Если
с = 1, то
а = х + 1. Следовательно,
х + 1 содержится в
Na.
Если с > 1, то
с – 1 – натуральное число, и следовательно,
а = х + с =(х + 1) + (с – 1). Но тогда
х + 1 < а, т.е.
х + 1 – натуральное число, принадлежащее отрезку
Na.
Для выполнения счета элементов в множестве важно определение конечного множества:
Множество А называют конечным, если оно равномощно некоторому отрезку Na натурального ряда.
Если посчитать количество сторон в квадрате, то это конечное множество В, т.к. оно равномощно отрезку
N4 ={1, 2, 3, 4}, В ~
N4.
Определение счета:
Счетом называется установление взаимно-однозначного соответствия между каждым предметом данного множества и словами-числительными, называемыми в определенной последовательности (последовательности N – натурального ряда чисел).
Результат счета не зависит от порядка, в котором считаются элементы данного множества.
В слове квадрат можно посчитать буквы в разном порядке: слева направо и справа налево. Количество букв не изменится – 7.
В математике дают определение числу, полученному при счете так:
Если непустое конечное множество А равномощно отрезку Na, то натуральное число а называют числом элементов множества А и пишут
n(А) = а .
Значит, множество сторон квадрата
n(А) = 4.
В процессе счета используют и порядковые и количественные числительные. Они взаимосвязаны: элементы множества упорядочиваются с помощью отрезка натуральных чисел: первый, второй, третий, … и т.д.
А
первый второй третий
четвертый пятый
После того как каждый элемент пронумерован, можно дать ответ на вопрос: «Сколько элементов в множестве?»
Но можно при счете использовать и количественные числительные. При этом мы называем количественное число (один, два, три, … и т.д.), показывая все предметы, обозначаемые этим числительным.
А
один
два
три
четыре
пять
При порядковом счете указывается каждый элемент, а при количественном – группы предметов.
При счете важно знать
правила правильного
счета:
1) счет начинается с единицы;
2) нельзя пропускать ни одного предмета;
3) нельзя предметы указывать дважды;
при счете используются порядковые числительные, последнее числительное обозначает количество предметов в данном множестве.
3. Теоретико-множественный смысл натурального числа и нуля
Если выполнять счет, то все непустые множества можно разбить на классы равномощных множеств (отношение равномощности является отношением эквивалентности). Множества одного класса могут быть различными по своей природе, но содержать одинаковое число элементов. Это число будет общим свойством классов конечных множеств:
n(А) = а, n(В) = в.
Если
n(В) = а, то множества
А и
В равномощны.
Значит,
с теоретико-множественной точки зрения, натуральное число – это общее свойство класса конечных равномощных множеств.
Число «нуль» с теоретико-множественной позиции – число элементов пустого множества, т.е. множества не содержащего ни одного элемента:
0 = n(Ø).
Итак, натуральное число а как характеристику количества можно рассматривать:
1) как число элементов в множестве А, получаемое при счете: а = n(А), причем А ~ Nа;
2) как общее свойство класса конечных равномощных множеств.
Теоретико-множественный смысл отношения «меньше» на множестве натуральных чисел
Устанавливая связь между конечными множествами и натуральными числами, можно дать теоретико-множественное толкование отношения «меньше».
В аксиоматической теории это отношение определяется таким образом:
а < b <=> (Ɏ с ЄN) [а + с = b].
Если а < b, то это означает, что отрезок натурального ряда чисел Nа является собственным подмножеством отрезка Nb, т.е.
Nа c Nb и Nа ≠ Nb.
Справедливо и обратное утверждение, что: если Nа – собственное подмножество Nb, то а < b.
Тем самым отношение «меньше» приобретает смысл:
а < b в том и только том случае, когда отрезок натурального ряда чисел Nа является собственным подмножеством отрезка Nb:
а < b <=> Nа c Nb и Nа ≠ Nb.
Например: 5 < 8 следует из того, что А = {1, 2, 3, 4, 5}; В = {1, 2, 3, 4, 5, 6, 7, 8};
А ={1, 2, 3, 4, 5} c В={1, 2, 3, 4, 5, 6, 7, 8}.
В начальной школе об этом говорят так: «Число а меньше
b тогда и только тогда, когда число
а называется раньше числа
b».
Такая трактовка отношения «меньше» позволяет сравнивать числа, опираясь на знание натурального ряда чисел и места каждого числа в нем.
Но часто сравнивают числа, используя связь их с конечными множествами.
Например:
Если 6 – это число треугольников, а 8 – это число квадратов, то 6 < 8, потому что во втором множестве можно выделить собственное подмножество, равномощное множеству треугольников. Т.е. множество треугольников равномощно отрезку N6, а множество квадратов равномощно отрезку N8 и
N6 c N8.
В общем виде этот подход обосновывается так:
Пусть
а = n (A), b = n (B), и а < b.
Тогда
А ~Nа, B ~Nb и Nа c Nb.
Последнее отношение означает, что в множестве
В можно выделить подмножество
В1, равномощное множеству
А, т.е.
а < b <=> А ~ В1, где
В1 с В, В1 ≠ В, В1 ≠ Ø.
Таким образом, с теоретико-множественной позиции отношение «меньше» приобретает смысл: если
а = n (A), b = n (B) и множество
А равномощно собственному подмножеству множества
В, то
а < b.
Заметим, что эти трактовки основываются на понятии конечного множества, т.к. мы имеем дело с конечными множествами, а любое подмножество конечного множества – конечно.
При определении натурального числа соответствующего множеству
А приходиться осуществлять счет, а для этого нужен отрезок натурального ряда чисел. Поэтому курс математики начальных классов начинается с изучения чисел в пределах десятка.
Каждое число изучается как количественное натуральное число, являющееся свойством класса конечных равномощных множеств. Число элементов в множестве определяется путем счета. Количественный и порядковый смысл числа и его запись выступают в тесной взаимосвязи.
Методика изучения нумерации целых неотрицательных чисел
в концентре «Числа от 1 до 100»
План:
I. Изучение нумерации чисел от 11 до 20 в начальной школе.
II. Методика изучения нумерации чисел в пределах сотни в начальной школе.
I. Изучение нумерации чисел от 11 до 20 в начальной школе
Изучение чисел до 20 выделяется в особый этап. С чем это связано? Дети знакомятся с новой счетной единицей – десятком и с важнейшим понятием десятичной системы счисления – понятием разряда.
Название чисел второго десятка (двенадцать, тринадцать и т.д.) образуются из тех же слов, что и названия разрядных чисел (двадцать, тридцать и т.д.). Но слова «два» (двенадцать), «три» (тринадцать) обозначают в числах до 20 число единиц, тогда как в числительных двадцать, тридцать и они обозначают число десятков. Кроме того, только в числах второго десятка не совпадают названия составляющих их разрядных чисел и порядок «записи»: называют сначала единицы (две-на-дцать), а пишется первым десяток (12). Во всех остальных случаях чтение и «запись» разрядных чисел совпадают (54, 32, 87 и т.д.).
Эти особенности требуют внимания к изучению чисел второго десятка.
Дети должны познакомиться
– с новой счетной единицей – десятком,
– усвоить принцип образования, названия и «запись» двузначных чисел в пределах 20,
– научить понимать и «записывать» отношения равенства, неравенства между этими числами, т.е. сравнивать числа,
– овладеть приемами устных вычислений (увеличить, уменьшить число на один),
– уметь «записать» это при помощи цифр и знаков.
Прежде всего детей необходимо познакомить с новой счетной единицей – десятком, которая лежит в основе всех чисел второго десятка, объяснить, как образуется эта счетная единица. Для этого учитель выставляет на доске десять счетных палочек, пересчитывает их вместе с детьми, обозначает соответствующей цифрой 10 и говорит, что десять палочек иначе называются «десяток». Чтобы дети уяснили, что десять палочек и один десяток палочек – понятия идентичные, рекомендуем несколько раз повторить такую операцию: десять палочек выставляются по одной, пересчитываются, после чего связываются в пучок: «Итак, у нас десять палочек или один десяток». Можно дать сведения о том, что раньше это количество называлось «дцать».
Только после этого можно начать знакомство с числами второго десятка.
Остановимся на этом подробнее и приведем пример фрагмента урока:
– Сегодня вы узнаете, что можно называть не только до 10, но и далее. Сейчас мы говорим «десять», а когда-то, очень давно люди говорили «дцать», а не десять. Сейчас так не говорят, но слово «дцать» сохранилось в названиях всех чисел, которые вы сегодня узнаете. Послушайте: один-на-дцать, две-на-дцать, три-на-дцать и т.д. Когда клали после десяти еще один (учитель кладет на пучок палочек, еще одну палочку), то говорили: «один-на -дцать, т.е. один-на-десять». Воспитатель ставит еще одну палочку: «А теперь – «две-на-дцать», т.е. две-на-десять».
Таким образом, учитель может продемонстрировать на доске образование всех чисел второго десятка. Чтобы дети более глубоко и осмысленно воспринимали десяток, как новую более крупную единицу счета, рекомендуем использовать магнитную доску «Числа от 1 до 20».
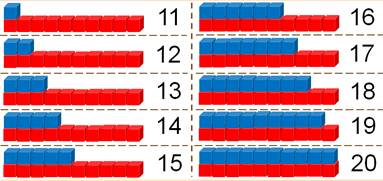
Можно воспользоваться и палочками. Учитель вместе с детьми считает десяток палочек – дцать, сверху кладет еще одну: один на дцать.
Детям предлагают сделать у себя на столах то же самое. Учитель обращает внимание детей на то, что в числе 10 цифра 1 обозначает количество десятков в числе, а 0 отсутствие единиц. После такого объяснения воспитатель ставит рядом с десятком палочек на доске еще одну палочку (дети то же делают у себя на столах), получилось один-на-дцать. Чтобы обозначить это число цифрой, вместо нуля ставится единица – это обозначает, что к одному десятку добавили единицу – и получается – 11». Дети убирают у цифры 10 ноль и ставят вместо него единицу или закрывают ноль единицей. Таким же образом учитель объясняет, как «записать» все остальные числа до 19. При этом единица, обозначающая десяток, не убирается, меняются лишь цифры, обозначающие количество единиц в числе. Показав, как записывается число девятнадцать, воспитатель предлагает к имеющимся десяти палочкам (положенным к связанному десятку палочек) положить еще одну. Итак, на столе перед детьми лежат два десятка палочек – один, положенный в начале, другой, полученный путем прибавления палочек. Детям предлагается вначале самим подумать, как можно «записать» число. Выслушав ответы детей, воспитатель объясняет, что стало два десятка палочек (два-дцать), поэтому цифру, обозначающую число десятков, надо заменить и поставить вместо цифры 1 цифру 2. Отсутствие единиц в этом числе обозначается цифрой 0. Таким образом, дети знакомятся с записью числа 20.
На последующих занятиях воспитатель должен закрепить принцип «записи» двузначных чисел в пределах 20. Рекомендуем делать это с опорой на наглядный материал. Приведем пример. Воспитатель предлагает отсчитать десять палочек, связать их, положить перед собой.
– Сколько перед вами десятков? (Один.)
– Обозначьте это соответствующей цифрой. Положите под десятком цифру 1. (Дети выполняют задание.)
– А единиц сверх десятков сколько? (Ни одной.)
– Какой цифрой это можно обозначить? (Цифрой 0.)
– Положите эту цифру рядом с цифрой 1 и прочитайте, какое число вы выложили. (Десять.)
– Теперь сверху над связанным десятком палочек положите еще две палочки. Сколько десятков перед вами? (Один десяток.)
– А единиц сверху над десятком сколько? (Две.)
– Что надо изменить, чтобы правильно показать число палочек? (Надо изменить число единиц, т.к. их стало две – вместо нуля поставить цифру 2.)
– Какое число получилось? (Двенадцать.)
В некоторых программах курса начальной математики (учебники Л.Г. Петерсон, Н.Б. Истоминой) десяток обозначается треугольником, а единицы кружками:

Такие и подобные занятия знакомят детей с десятичным составом и натуральным следованием чисел до 20. Для закрепления знания натуральной последовательности чисел воспитатель может использовать различные упражнения. Например, детям предлагается положить перед собой 12 палочек, потом придвигать по одной палочке и каждый раз говорить, сколько палочек стало. Или положить 18 палочек, потом откладывать в сторону по одной, каждый раз называя, сколько палочек осталось.
НАТУРАЛЬНОЕ ЧИСЛО КАК МЕРА ВЕЛИЧИНЫ
Понятие положительной скалярной величины
и ее измерения
План:
I. Понятие величины.
II. Особенности величин.
III. Измерение величин.
IV. Сравнения и действия с числами, выражающими меру величин.
I. Понятие величины
В математике начальной школы понятие натурального числа является основным. Именно с него начинается обучение. Натуральное число обладает различными функциями:
– количественной характеристикой предметного множества,
– характеристика порядка,
– значение величины при выбранной единице, т.е. мера величины,
– компонент вычислений.
С этими функциями числа необходимо познакомить младших школьников. А поэтому учителю начальных классов важно овладеть теориями, обосновывающими различные подходы к определению натурального числа и действий над ними:
– аксиоматической,
– теоретико-множественной, а также и
– с точки зрения меры величины.
Следовательно, натуральное число является и значением при измерении величин – один из подходов к трактовке числа в начальном обучении.
Натуральное число рассматривается в связи с измерением таких величин как
длина,
масса,
емкость,
площадь,
время,
а также величины, используемые при решении задач с различными
процессами:
скорость,
цена,
количество товара,
стоимость,
производительность и т.д.
Величина – особое свойство окружающих нас предметов и явлений, которое проявляется при сравнении предметов и явлений по этому свойству, причем каждая из величин связана с определенным способом сравнения.
Все величины, выражающие одно и то же свойство, называются величинами одного рода или однородными.
II. Особенности величин
При работе с величинами необходимо знать их особенности:
1. Любые две величины одного рода сравнимы: одна может быть равна другой или меньше другой, при этом могут быть отношения «равно», «меньше», «больше»: А = В, А < В, А > В.
2. Отношение «меньше» для однородных величин транзитивно: если А < В,
В < С, то А < С.
3. Величины одного рода можно складывать, в результате получается величина того же рода.
Для любых двух величин А и В определяется величина С = А + В, которую называют суммой этих величин – А и В.
Сложение величин коммутативно и ассоциативно.
Например:
а) Если масса яблок – А, а масса груш – В, то А + В – это масса яблок и груш. Из этого очевидно, что А + В = В + А.
б) Если масса яблок – А, а масса груш – В, а С – масса слив, то (А + В) – это масса яблок и груш, а (А + В) + С – масса яблок, груш и слив. А (В + С) – масса груш и слив, а А + (В + С) – масса яблок, груш и слив. Из этого очевидно, что (А + В) + С = А + (В + С).
4. Величины одного и того же рода можно вычитать, в результате получается величина того же рода.
Вычитание определяют через сложение, т.к. эта операция обратная сложению:
Разностью величин А и В называется такая величина С, что С = А – В, что А = В + С. Разность существует тогда и только тогда, когда А > В.
b c
_________________________
a
5. Величину можно умножать на положительное действительное число, в результате получают величину того же рода:
для любой величины
А и любого положительного числа
х существует единственная величина
В = х · А.
Например,
А – масса одной коробки печенья, то масса пяти таких коробок
(х = 5): В = 5 · А.
6. Величины одного и того же рода можно делить, получая в результате число. Деление определяют через умножение величины на число:
частным величин
А и
В называется такое положительное действительное число
х =А : В, что
А = х · В:
b
__________________________
a
III. Измерение величин
Величины обладают особенностью – их можно оценить количественно, т.е. измерить. Для измерения выбирают величину, называемую единицей измерения.
Например, при измерении длины:
е
____
а
____________________
____
Измерить величину а – это значит найти такое положительное действительное число
х, что
А = х · е, при этом число
х называют численным значением величины А при единице
е и пишут
х = m (A).
Число х показывает, во сколько раз величина А больше (или меньше) величины е , принятой за единицу измерения.
Например, если А – длина отрезка
a,
е – длина отрезка
b, то А = 4 е. Число 4 – это численное значение длины А при единице измерения длины
е.
А, следовательно, а = 4
· е, m (a) = 4.
Таким образом, натуральное число
х как значение длины отрезка а показывает – из скольких выбранных единичных отрезков е состоит отрезок а и это число единственное. При переходе к другим единицам длины, численное значение будет меняться. Например:
е
__
а
____________________
__
А = 8 е
m (a) = 8
Величина, определяемая одним численным значением, называется скалярной величиной.
IV. Сравнения и действия с числами, выражающими меру величин
Сравнение величин, действия с ними позволяют переходить к сравнению и действиям с числами:
1. Отношения между величинами А и В при сравнении, будут такими же как и между их численными значениями: А = В => m(A) = m(B);
А < В => m(A) < m(B);
A > B => m(A) > m (B).
2. Чтобы найти численное значение суммы, достаточно сложить численное значение величин:
А + В = С <=> m(A + B) = m(A) + m(B).
3. Чтобы найти численное значение величины В, если В =
х · А и величина измерена единицей
е, то В =
х · А <=> m(B) =
х · m(A) – т.е. достаточно умножить число
х на число m(A).
Длина отрезка и ее измерение
План:
I. Геометрические величины.
II. Понятие длины отрезка.
III. Методика изучения понятия длины и ее измерения в начальной школе.
I. Геометрические величины
Величина – особое свойство окружающих нас предметов и явлений и проявляется при сравнении предметов и явлений по этому свойству, причем каждая из величин связана с определенным способом сравнения.
Геометрическими величинами являются длина линии (отрезка, ломаной, кривой), площадь фигуры, объем тела, величина угла.
Каждой величине ставят в соответствие положительное действительное число, которое называется его численным значением или мерой. Процесс нахождения этого числа называется измерением величины.
В геометрии, прежде всего, изучают то число, которое получается в результате измерения величины, т.е. меру величины при выбранной единице величины. Поэтому это число называют длиной, площадью, объемом.
Геометрические величины имеют особенности, связанные с их сравнением и измерением (рассмотрены ранее).
II. Понятие длины отрезка
Длиной отрезка называется положительная величина, определенная для каждого отрезка и обладающая следующими свойствами:
• равные отрезки имеют равные длины;
• если отрезок состоит из конечного числа отрезков, то его длина равна сумме длин этих отрезков;
• существует отрезок, длина которого равна 1.
Измерение длины отрезка
х состоит в сравнении его длины с длиной отрезка, принятого за единицу. Результатом измерения отрезка является положительное действительное число
а, которое называют численным значением длины отрезка
х при выбранной единице длины
е, или мерой длины отрезка
х при выбранной единице длины
е, или просто длиной отрезка
х:
а = mе (x) или
х = а · е.
Число, полученное при измерении длины отрезка, обладает свойствами:
1. При выбранной единице длины длина любого отрезка выражается положительным действительным числом, т.е.
m (x) > 0 и для каждого такого числа есть отрезок, длина которого выражена этим числом.
2. Если два отрезка равны, то численные значения их длин также равны, и обратно: если численные значения двух длин отрезков равны, то равны и сами отрезки:
х = у <=>
m (x) =
m (у).
3. Если данный отрезок состоит из нескольких отрезков, то численное значение его длины равно сумме численных значений длин всех отрезков, и обратно: если численное значение длины отрезка равно сумме численных значений нескольких отрезков, то сам отрезок состоит из этих отрезков,
т.е. z = x + y <=>
m (z) =
m (x) + m (у).
4. Если длины отрезков
х и
у таковы, что
у = ах, где
а – положительное действительное число и длина измерена с помощью единицы
е, то для нахождения численного значения длины отрезка
у при единице
е, достаточно число
а умножить на численное значение длины отрезка
х при единице
е, т.е.
у = а· х <=>
m (у) = а · m (х).
5. При замене единицы длины численное значение длины увеличивается (уменьшается) во столько раз, во сколько раз новая единица больше (меньше) старой, т.е.
m1 (x) и
m2(x) – численные значения длины отрезка
х при единицах длины
е1 и
е2 , то выполняется равенство
m(х) =
m (e1) = m(е2).
III. Методика изучения понятия длины и ее измерения
Методисты считают, что учащиеся начальных классов должны
– получить конкретные представления о величинах,
– ознакомиться с единицами их измерения,
– овладеть умениями измерять величины,
– научиться выражать результаты измерений в различных единицах,
– выполнять различные действия над ними.
По мнению Н.Б. Истоминой можно выделить восемь этапов изучения величин:
1-й этап – выяснение и уточнение представлений школьников о данной величине (обращение к опыту ребёнка);
2-й этап – сравнение однородных величин:
а) визуально (на «глаз»);
б) с помощью ощущений (ощупывание, «взвешивание» на руках);
в) наложением, приложением;
г) с помощью различных мерок.
3-й этап – знакомство с единицей данной величины и с измерительным прибором.
4-й этап – формирование измерительных умений и навыков.
5-й этап – сложение и вычитание однородных величин, выраженных в единицах одного наименования.
6-й этап – знакомство с новыми единицами величин в тесной связи с изучением нумерации и сложения чисел. Перевод однородных величин, выраженных в единицах одного наименования, в величины, выраженные в единицах двух наименований, и наоборот.
7-й этап – сложение и вычитание величин, выраженных в единицах двух наименований.
8-й этап – умножение и деление величин на число.
Знакомство с понятиями длины осуществляется еще в дошкольный период: учащиеся получают представления о понятиях – длинный – короткий, широкий – узкий, высокий – низкий, а коррекция этих понятий осуществляется в концентре «Подготовка к изучению чисел» в 1 классе. К сожалению, многие дети, приходя из детского сада, считают, что длина, ширина и высота – это разные величины.
Н.Б.Истомина отмечает, что в процессе изучения длины как величины учитель решает следующие задачи:
Сформировать понятие длины как свойства предметов.
Познакомить с единицами длины и соотношениями между ними.
Сформировать умения измерять длину данных отрезков и чертить отрезки заданной длины, сравнивать длины.
Научить выражать величины в меньших и больших единицах.
Научить выполнять арифметические действия над величинами.
Ученики нередко также смешивают единицы длины с инструментом, при помощи которого производится измерение,– с линейкой. Чтобы избежать этого и достигнуть достаточно глубокого понимания детьми сущности измерения, целесообразно использовать четкую методику работы с длиной как величиной.
I эт. – выяснение и уточнение представлений школьников о данной величине (обращение к опыту ребёнка). При введении понятия «длина» внимание учащихся необходимо сосредоточить на самом термине «длина», разъяснив соответствующим образом его значение. Учащиеся рассматривают предметы и сравнивают их по своему усмотрению. Так, при проведении беседы можно предложить учащимся сравнить длину карандаша и ручки, которые лежат у них на партах.
II эт. – сравнение однородных величин: визуально (на «глаз»); наложением, приложением. Эти способы сравнения можно назвать опосредованными способами сравнения.
При сравнении используется прием приложения. Затем можно предложить сравнить по картинке длину ручки и кисточки (ручка короче, кисточка длиннее). В данной ситуации дети используют сравнение длин предметов визуально или расположением предметов друг под другом, т.к. изображения нельзя сравнить наложением.

Представления учащихся уточняются: нарисованные предметы обладают свойством, которое называется длина. Данные предметы можно сравнивать по длине. На рисунке должно быть хорошо видно, длина какого отрезка больше, а какого меньше.
Далее отмечается, что отрезки тоже можно сравнивать по длине. Для ознакомления со способами сравнения длин отрезков рекомендуется организовывать практическую работу. Используя полоски из различных материалов, различных цветов, различной длины как модели отрезков, учащиеся сравнивают длины отрезков с помощью различных
мерок.
Понятие мерки можно раскрыть на примере мультфильма «38 попугаев».
Можно провести беседу по иллюстрации или просмотренному фрагменту мультфильма:
– Как называется мультфильм, героев которого вы видите?
– Кто герои мультфильма?
– Кого измеряли звери?
– Кем измеряли? Каким способом?
– Чем были слон, мартышка и попугай? (МЕРКАМИ)
– К какому выводу пришел удав? (А в попугаях я длиннее, …)
– Что такое МЕРКА?
Меркой длины могут выступать полоски бумаги.


При использовании различных мерок для измерения одного отрезка учащиеся получают различные числовые результаты. В процессе выполнения практических упражнений они должны осознать зависимость числового результата от величины той мерки, с помощью которой измерялся данный отрезок.
Чаще используются несколько ситуаций:
1 сит. – измеряем отрезки меркой синего цвета, получаем результат: 3 < 4;
2 сит. – измеряем меркой красного цвета: 2 < 3;
3 сит. – измеряем зеленый отрезок синей меркой, а оранжевый – красной:
3 = 3.
Ситуация абсурдна, т.к. визуально видно, какой отрезок больше. Ищем причину, почему так получилось: измеряли длины отрезков разными мерками. Делаем вывод об измерении отрезков при сравнении их: необходимо пользоваться одной меркой.
III эт. – знакомство с единицей данной величины и с измерительным прибором.
После проведения предыдущей практической работы у учащихся возникает проблема, как же договориться, как измерять длину, чтобы при измерении равных отрезков у всех были одинаковые результаты? Делается вывод, что необходима единая единица длины.
Такой единицей измерения является сантиметр. Учитель демонстрирует модель сантиметра. Сантиметр сравнивается с шириной пальца, с длиной двух клеточек тетради.
Затем учитель знакомит учащихся с линейкой, с правилами пользования данным инструментом измерения длин отрезков.
На парте у каждого ученика должна быть модель сантиметра, изготовленная учителем ранее. При помощи модели ученики должны уметь решать, например, следующие задачи:
1. Измерить заданный отрезок. При этом ученик должен
а) пересчитывая количество вложенных в отрезок моделей, сделать вывод о длине отрезка в сантиметрах;
б) с помощью карандаша на отрезке отмечать конец модели сантиметра и посчитать, сколько таких моделей укладывается в отрезке.
2. Начертить отрезок заданной длины. При этом ученик должен:
а) провести по линии в тетради прямую;
б) отметить на ней точку отсчета;
в) в нужном направлении отложить длину, ставя карандашом засечки, отметив второй конец отрезка.
Такое пошаговое построение позволяет сформировать у детей необходимые в дальнейшем представления о предупреждении ошибок при измерении.
По нашему мнению, целесообразно четко работать с линейкой как инструментом. Знакомясь с линейкой, ученики могут выделить на ней отрезок в 1 см. Кроме того важно ввести
правило измерения:
прикладывать линейку так, чтобы начало отрезка совпадало с числом 0 на линейке.
С каким числом на линейке будет совпадать конец отрезка – такова и его длина.
Переходя к знакомству с новой для детей единицей длины – дециметром, учитель должен так построить свой урок, чтобы подвести их к самостоятельному выводу о том, что измерять отрезки не всегда удобно сантиметром (длину парты). Моделью сантиметра длину парты измерять долго. Нужна новая единица измерения. Учитель сообщает, что помимо единицы длины – сантиметра, существуют и другие единицы измерения. Так, вторая единица носит название дециметр. Ученики чертят в тетрадях отрезок в 10 см и записывают: 10 см = 1 дм.
Методика изучения метра, километра и миллиметра аналогична.
Площадь фигуры и ее измерение
План:
I. Понятие площади фигуры и ее измерения.
II. Методика изучения площади фигуры и ее измерения в начальной школе.
I. Понятие площади фигуры и ее измерения
Все люди представляют, что такое площадь помещения, где оно находится, площадь участка земли, где располагается дача, площадь поверхности, которую надо застеклить, покрасить. Многие обращают внимание, что площади одинаковых комнат или участков равны, а чтобы узнать общую площадь квартиры, нужно сложить площади всех ее помещений. Эти представления применяются и в геометрии.
Чтобы найти площадь фигуры иногда первоначально находят площади фигур, из которых она состоит.
Если фигура
F состоит из фигур
F1 и
F2, то подразумевают, что она является их объединением, и у них нет внутренних общих точек. Поэтому говорят, что фигура
F разбита на фигуры
F1 и
F2, т.е.
F = F1 + F2.
F
F1 F2
Площадью фигуры называется положительная величина, определенная для каждой фигуры и обладающая свойствами:
– равные фигуры имеют равные площади;
– если фигура состоит из конечного числа фигур, то ее площадь равна сумме их площадей;
– существует фигура, площадь которой равна 1.
Измерение площади фигуры
F состоит в сравнении ее площади с площадью квадрата со стороной, равной
1 длины. Если его обозначить буквой
е, то
результатом сравнения является положительное действительное число Se(F), которое называют численным значением площади фигуры F при выбранной единице площади е, или мерой площади F, или площадью фигуры F.
Получаемое при измерении число обладает свойствами, аналогичными свойствам длины отрезка (важно учесть, что это относится к плоским фигурам).
Фигуры, площади которых равны, называются равновеликими.
Площадь фигуры
F можно найти с помощью палетки – квадратной сетки, нанесенной на прозрачный материал. Длина стороны квадрата сетки принимается за единицу длины, а площадь квадрата – за единицу площади.
Площадь фигуры подсчитывают по формуле:
S(F) = m + n/2 (ед. 2).
Другим способом нахождения площади фигуры является использование готовых формул. Существуют теоремы, в которых обосновываются основные формулы:
1)
Площадь квадрата равна квадрату длины его сторон, т.е. S = а2, где а – длина стороны квадрата.
2)
Площадь прямоугольника равна произведению длин его смежных сторон, т.е. S = a · b, где а и b – длины смежных сторон прямоугольника.
В некоторых случаях, чтобы найти площадь нужно найти площадь геометрических фигур из которых состоит данная фигура. Поэтому фигуры разбивают на фигуры, площадь, которых можно найти по формулам и выполняют вычисления. Например, так находят площадь параллелограмма. При этом используют определение равносоставленных фигур:
Два многоугольника называются равносоставленными, если каждый из них можно разбить на одно и то же количество попарно равных между собой фигур.
В С
В
ha
А F D E
Площадь параллелограмма находится по формуле: S = a · ha
Задание для самостоятельной работы
Площадь прямоугольника равна 12 см
2 , длины его сторон выражаются натуральными числами. Сколько различных прямоугольников можно построить согласно этим условиям?
II. Методика изучения площади фигуры и ее измерения в начальной школе
Методика изучения площади также имеет свои особенности.
Подготовка к изучению понятия площади ведётся еще в первом классе. Спрашивая, какой треугольник больше – красный или синий, учитель показывает, как можно сравнить эти треугольники. Визуально или наложив один треугольник на другой, дети устанавливают, что синий треугольник поместился внутри красного, значит, синий треугольник меньше красного. При этом, конечно, термин «площадь» учитель не использует.
В качестве подготовительных упражнений можно использовать упражнения, в которых следует установить, из скольких одинаковых квадратов, прямоугольников или треугольников составлены разные геометрические фигуры.
По мнению методистов, ввести и закрепить понятие площади можно при помощи фронтальной и индивидуальной работы с учениками. На доске, фланелеграфе, наборном полотне прикрепляются различные геометрические фигуры (2 квадрата, 2 круга, 2 треугольника разных размеров), у детей на партах соответствующий раздаточный материал для проведения сравнения. Допустим, берем большой круг и маленький треугольник. Вопрос: какая фигура поместится во вторую? Покажите это. Наложением дети показывают, что треугольник поместится в середину круга. На доске тоже сначала закрепляется круг, а потом на него треугольник. Вывод: этот треугольник «часть» этого круга, значит, его площадь меньше площади круга. Можно сказать, что «площадь – это место, которое занимает фигура на плоскости». Представления о площади закрепляются у детей аналогичной практической работой, а обобщение проводят по учебнику, рассматривая фигуры различные по площади. Для закрепления понятия площади имеет смысл брать модели фигур различной конфигурации и цвета, чтобы предупредить ошибочное мнение учеников, что площадь имеют только прямоугольник квадрат. Однако спрашивать, что такое площадь у детей не стоит – понятие формируется на интуитивно-практическом уровне.
Следующим шагом будет практическая работа над фигурами, которые не вмещаются одна в другую. При выполнении этого задания нужно познакомить детей со сравнением фигур при помощи их разбиения на отдельные квадраты. На обратной стороне фигур разлинованы квадраты (одинаковые и неодинаковые). Пересчитывается их количество, и делаются выводы.
Затем аналогичные упражнения выполняются по учебнику и чертежам на доске. Требуется показать случаи, когда разные по форме фигуры имеют одинаковую площадь. Упражнения: подсчитайте квадраты, входящие в данную фигуру; начертите фигуры, состоящие из … квадратов:
1 2
Эти упражнения помогают наглядно формировать понятие площади как количества квадратных единиц.
Для ознакомления с квадратным сантиметром Н.Б.Истомина предлагает беседу и практическую работу с мерками-квадратами:
– Какие единицы длины вы знаете? (см, мм, дм, м, км)
– Покажите длины на линейке.
– Запишите обозначение всех единиц, которые назвали.
После этого сообщается, что для измерения площади используется единица, которая называется квадратный сантиметр. Затем, ученики чертят в тетради квадрат со стороной 1 см и называют его квадратным сантиметром. Площадь этого квадрата принимают за единицу измерения площади. Вводится правило записи и чтения: 5 см
2 – пять квадратных сантиметров. После введения понятия проводится его закрепление.
Далее в квадратных сантиметрах измеряется площадь прямоугольника: измеряемый прямоугольник расчерчивается на квадратные сантиметры, и их число подсчитывается. После этого учащихся обучают правилу вычисления площади прямоугольника. При знакомстве с переместительным свойством умножения они подсчитывают число квадратов, на которые разбивался прямоугольник, двумя способами:
1) определяется число квадратов, уложенных в одном ряду, и число рядов; полученные числа умножаются;
2) определяется число квадратов в столбце и число столбцов; полученные числа умножаются.
Эти способы подсчета числа квадратов в прямоугольнике применяются и для определения площади прямоугольника. Например, учитель предлагает детям такое упражнение: установить площадь каждого прямоугольника, изображенного на доске.
Следовательно, выполняя его, учащиеся усваивают алгоритм вычисления площади прямоугольника:
1) измеряется длина прямоугольника, его ширина;
2) вычисляется произведение полученных чисел.
Полученное число и соответствует значению площади прямоугольника в квадратных сантиметрах.
Н.Б.Истомина для определения площади фигур, имеющих форму, отличную от прямоугольника, предлагает использовать, как инструмент – палетку. До введения палетки можно провести практическую работу по определению площади прямоугольников, начерченных на миллиметровой бумаге. Учитель обращает внимание детей на то, что одни неполные квадраты можно «сложить» с другими так, что они образуют квадратный сантиметр. Учащиеся убеждаются в возможности замены неполных квадратов полными: число полных квадратов составляет примерно половину числа неполных.
Правила применения палетки:
1) разместить палетку поверх фигуры так, чтобы в ней поместилось максимальное количество целых квадратов – квадратных сантиметров;
2) отдельно пересчитать количество полностью заполненных фигурой квадратов и тех, которые заняты только частично;
3) разделить количество неполных квадратов на 2 и сложить результат с количеством целых квадратов;
4) полученный результат и будет показывать, сколько квадратных сантиметров содержится в данной фигуре, т.е. ее площадь.
Детям необходимо объяснить, что измерение площади неправильной фигуры при помощи палетки дает приближенные результаты.
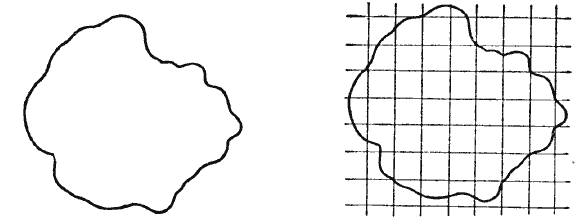
Далее учеников знакомят с квадратным дециметром. Новая единица вводится аналогично квадратному сантиметру, на наглядной основе.
При знакомстве учащихся с квадратным метром следует его модель разбить на квадратные дециметры, а один из квадратных дециметров – на квадратные сантиметры.
Но площадь измеряется не только в квадратных сантиметрах, дециметрах и метрах, но и такими единицами как ар и гектар. Знакомство с ними происходит в 4 классе.
Впоследствии работа над темой площадь, также должна включать систему упражнений, раскрывающих некоторые свойства понятия площади фигуры, а также подтверждающих справедливость математических законов.
Текстовая задача и процесс ее решения
I.
Понятие «задача»
Для формирования у учащихся представлений о математической науке используются различные понятия, предложения, доказательства. Осваивая их, младшие школьники выполняют разнообразные задания. Их называют задачами.
В математике начальной школы преобладают такие, которые имеют определенные характеристики. Они являются
1) текстовыми – т.к. сформулированы на естественном языке в описательной форме;
2) сюжетными – т. к. в них описывается количественная сторона какой-то жизненной ситуации;
3) арифметическими или вычислительными – т. к. сводятся к поиску неизвестной величины с помощью арифметических действий.
Перед задачами в начальной школе стоят следующие цели:
1. В сюжетах находят выражение практические ситуации, с которыми дети уже знакомы, поэтому при решении они используют свой жизненный опыт. Это даёт возможность осознать количественные отношения между различными объектами (величинами), углубить и расширить представления о реальной действительности.
2. Решение задач помогает ребёнку осознать практическую значимость математических понятий, которыми он овладевает.
3. В процессе решения задач у ребёнка формируются знания, умения, навыки, необходимые для решения любой математической задачи:
выделять данное и искомое (условие и вопрос),
устанавливать зависимость между ними,
строить умозаключение,
моделировать,
проверять полученный результат.
Текстовая задача –
это описание некоторой ситуации или ситуаций на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между ее компонентами или определить вид этого отношения.
Любая текстовая задача состоит из двух частей:
утверждение и
требование. Утверждение называется по-другому условием, а требование – вопросом.
Утверждение – часть задачи, где сообщаются сведения об объектах и некоторых величинах, характеризующих данные объекты, об известных и неизвестных значениях этих величин, об отношениях между ними.
В задаче может быть несколько элементарных условий, а не одно. Они представляют собой количественные и качественные характеристики объектов задачи и отношений между ними.
Требование задачи – это указание того, что нужно найти. Оно может быть выражено предложением в повествовательной форме или в вопросительной:
– Вычислить площадь и периметр прямоугольника.
– Чему равна площадь прямоугольника и периметр?
Требований в задаче также может быть несколько.
Практическая работа
Задача. На торжественной линейке первоклассники выстроились в 2 ряда по 25 человек, а выпускники в 4 ряда по 12 человек. Сколько всего учащихся было на линейке? На сколько больше было первоклассников, чем старшеклассников?
Утверждения:
1. На линейке первоклассники выстроились в 2 ряда.
2. На линейке первоклассники выстроились по 25 человек в ряд.
3. На линейке выпускники выстроились в 4 ряда.
4. На линейке выпускники выстроились по 12 человек в ряд.
Требование:
1. Сколько всего учащихся было на линейке?
2. На сколько больше было первоклассников, чем старшеклассников?
II. Этапы решения задачи:
Ознакомление с содержанием задачи.
Поиск решения задачи.
Составление плана решения задачи.
Запись решения и ответа.
Проверка решения задачи.
Ознакомление с содержанием задачи.
– Прочитайте текст задачи. (Уч-ся читают про себя – 1 раз; вслух хорошо читающий ученик – 2 раз.)
– Кто присутствовал на торжественной линейке?
– Как стояли дети?
– Сколько рядов первоклассников было на линейке?
– Сколько первоклассников было в каждом ряде?
– Сколько рядов выпускников было на линейке?
– Сколько выпускников было в каждом ряде?
– Каков вопрос задачи?
– Каков первый вопрос?
– Каков второй вопрос?
2. Поиск решения задачи.
– Прочитайте первый вопрос задачи?
– Прочитайте второй вопрос задачи?
– Что нужно знать, чтобы ответить на эти вопросы?
(Сколько всего первоклассников и сколько всего выпускников.)
– Мы это знаем?
– Как узнать, сколько всего первоклассников?
– Каким действием?
– Как узнать, сколько всего выпускников?
– Каким действием?
– Каким действием узнаем, сколько всего учащихся на линейке?
– А как ответить на второй вопрос задачи?
– Каким правилом воспользовались?
– Ответили мы на вопросы задачи?
3. Составление плана решения задачи.
– Расскажите план решения этой задачи.
1) ×
2) ×
3) +
4) –
Запись решения иответа.
– Запишите решение задачи в тетради.
1) (чел.) – было первоклассников
2) (чел.) – было выпускников
3)
4)
– Сформулируйте ответ. Запишите его.
Ответ: всего на линейке 98 учеников, первоклассников было на 2 больше, чем выпускников.
Арифметические действия
и методика их изучения в курсе математики начальной школы.
Формирование вычислительных навыков
у учащихся начальной школы
Теоретико-множественный смысл
суммы
План:
I. Теоретико-множественный смысл суммы целых неотрицательных чисел.
II. Теоретико-множественный смысл равенства
а + 0 = а.
III. Теоретико-множественный смысл свойств сложения.
I. Теоретико-множественный смысл суммы целых неотрицательных чисел
Все действия над числами связываются с действиями над множествами.
Суммой целых неотрицательных чисел а и b,
таких что а = n (A),
а b = n (B), является численность объединения непересекающихся множеств А и В –
a + b = n (A U B), где A ∩ B= Ø .
Т.е. с теоретико-множественных позиций сумма натуральных чисел
а и
b представляет собой число элементов в объединении конечных непересекающихся множеств А и В, таких, что
а = n (A), b = n (B):
а + b = n (A) + n (B) = n(A U B), если A ∩ B= Ø.
Например:
А = {х, у}; В = {а, в, с}, n (A)= 2, n (B)=3, то A U B = {а, в, с, х, у}
а + b = n(A U B) = n (A) + n (B) = 2 + 3 = 5
Взаимосвязь сложения целых неотрицательных чисел и объединения множеств позволяет также обосновывать с теоретико-множественных позиций выбор арифметических действий при решении текстовых задач различных видов.
Например:
Коля взял с тарелки 6 слив, а Катя – 4. Сколько слив было на тарелке?
В задаче рассматривается три множества: А – множество слив Коли, В – множество слив Кати и их объединение. Требуется узнать число элементов этого объединения, а оно находится сложением. Т.к.
n(A) = 6, а n(В)= 4 и
A ∩ B= Ø, то
n(A U B) = n (A) + n (В) = 6 + 4.
Сумма 6 + 4 – это математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на поставленный вопрос задачи:
6 + 4 = 10. Следовательно, ребята с тарелки взяли 10 слив.
II. Теоретико-множественный смысл равенства а + 0 = а.
Пользуясь этими сведениями, раскроем теоретико-множественный смысл равенства
а + 0 = а.
Если
а = n (A), 0 = n(Ø), то согласно описанному выше
а + 0 = n (A) + n (Ø) = n(A U Ø) = n (A) = а.
Следовательно
А U Ø = А, а значит
n(A U Ø) = n (A), откуда и взято правило
а + 0 = а (Если к любому числу прибавить 0, то получится то же самое число).
III. Теоретико-множественный смысл свойств сложения.
Взаимосвязь сложения целых неотрицательных чисел и объединения множеств позволяет истолковать с теоретико-множественных позиций и свойства сложения:
коммутативность – переместительность
для любых множеств А и В –
A U B = В U А.
Если
а = n (A), b = n (B) и A ∩ B= Ø, то
а + b = n(A U B)= n(В U А) = b + а;
Следовательно,
а + b = b + а.
 ассоциативное свойство – сочетательное
(A U B) U С = А U (В U С)
ассоциативное свойство – сочетательное
(A U B) U С = А U (В U С)
Если
а = n (A), b = n (B), с =n(C) и A ∩ B= Ø, A ∩ С = Ø, В ∩ С= Ø, то
(а + b) + с = n(A U B) + n(C) = n((A U B) U С) = n(A U (B U С)) =
= n(A) + n(B U С) = a + (b + c).
Следовательно,
(а+в) + с = а + (в+с).
 Теоретико-множественный смысл
разности
План:
Теоретико-множественный смысл
разности
План:
I. Теоретико-множественный смысл разности целых неотрицательных чисел.
II. Теоретико-множественный смысл равенств
а – 0 = а и
а – а = 0.
III. Теоретико-множественный смысл правил вычитания числа из суммы и суммы из числа.
IV. Теоретико-множественный смысл понятий
«больше на …», «меньше на …».
I. Теоретико-множественный смысл разности целых неотрицательных чисел.
Пусть
А – конечное множество и
В – его собственное подмножество. Тогда множество
А \ В (когда В c А, можно обозначить
В´ ) тоже конечно, причем выполняется равенство
n(А \ В) = n (A) – n (B)
Доказательство:
Так по условию В – собственное подмножество множества А, то с помощью кругов Эйлера их можно представить так:
А
А \ В
А
В
Разность
А \ В на этом рисунке заштрихована. Хорошо видно, что
В и
А \ В не пересекаются и их объединение равно
А. Поэтому число элементов в множестве
А можно найти по формуле
n (A) = n (B) + n(A \
B), откуда по определению вычитания как операции обратной сложению, получаем
n(A \
B) = n (A) – n (B).
Из этого следует определение разности натуральных чисел:
С теоретико-множественной позиции разность натуральных чисел а и b представляет собой число элементов в дополнении множества В до множества А, если а = n (A), b = n (B) и В c А:
а – b = n (A) – n (B) = n(A \
B), если В c А, В ≠ А, В = Ø.
Взаимосвязь вычитания и разности множеств позволяет обосновывать выбор действия при решении текстовых задач. Выясним, почему задача решается действием вычитания:
У Антона 11 машинок. 3 машинки он подарил другу. Сколько машинок стало у Антона?
В задаче рассматриваются три множества: множество А – машинки у Антона; множество В – машинки подаренных Антоном другу, которое является подмножеством множества А; множество С – дополнение множества В до множества А – машинки, оставшиеся у Антона после того, как он подарил несколько другу. В задаче нужно найти число элементов в дополнении. Т.к. по условию
n (A) = 11, n (B) = 3 и
В c А, то
n(C) =
n(A \
B) = n (A) – n (B) = 11 – 3. Разность 11 – 3 – это математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на вопрос задачи: 11 – 3 = 8. Следовательно, у Антона осталось 8 машинок.
Задание для самостоятельной работы
Обоснуйте с теоретико- множественной точки зрения выбор действий при решении текстовых задач.
а) В корзине 7 морковок, 3 из них отдали кроликам. Сколько морковок осталось в корзине?
б) Во дворе гуляли 6 мальчиков, трое из них ушли. Сколько мальчиков осталось во дворе?
II. Теоретико-множественный смысл равенств а – 0 = а и а – а = 0.
По аналогии трактуется вычитание нуля и вычитание
а из
а.
Т.к.
А \ Ø = А, А \ А = Ø, то а – 0 = а и
а – а = 0.
III. Теоретико-множественный смысл правил вычитания числа из суммы и суммы из числа.
Рассматриваемый подход позволяет толковать правила, которыми пользуются при рациональных способах вычитания:
– вычитание числа из суммы,
– вычитание суммы из числа.
Если а, b, с – натуральные числа, то (а + b) – с = (a – c) + b.
a + (b – c)
Доказательство:
Пусть
А, В и
С – такие множества, что
а = n (A), b = n (B) и
A ∩ B= Ø, С c А.
Докажем, что (А U В) \ С = (А \ С) U В.
n ((А U В) \ С) = n(А U В) – n(C) = (а + b) – c
n((А \ С) U В) = n(A \
C) + n(B) = (a – c) + b
И, следовательно,
(а + b) – c = (a – c) + b, если а > с.
А
А
С
В
а – (b + с) = (a – b) – c.
(a – c) – b.
IV.
Теоретико-множественный смысл понятий «больше на …», «меньше на …».
В аксиоматической теории понятия «меньше на …» («больше на …») вытекает из определения отношения «меньше».
Из того, что
а < b, тогда и только тогда, когда существует число
с, что
а + с = b. А значит,
«а меньше b на с» или
«b больше а на с».
Если
а = n (A), b = n (B) и установлено, что
а < b, то опираясь на теоретико-множественный подход понятия «меньше», в множестве
В можно выделить собственное подмножество
В1, равномощное множеству
А, и непустое множество
В \ В1.
Если число элементов в множестве
В \ В1 обозначить как
с (с ≠ 0), то в множестве
В будет столько же элементов, сколько их в множестве
А и еще
с:
n (B) = n (B)+ n (B \ В1) или
b = а + с, что подразумевает, что
«а меньше b на с» («b больше а на с»).
Таким образом, с теоретико-множественной позиции понятия
«а меньше b на с» («b больше а на с») означают, что
если а = n (A), b = n (B),
то в множестве В содержится столько же элементов, сколько в множестве А и еще с элементов.
Пользуясь этим можно вывести способ действия при сравнении числа элементов в множествах.
Т.к.
с = n (B \ В1), где В1 с В, где n (B) = b,
n (B1) = а, то по определению разности
с = а – b. Следовательно, можно вывести правило:
Чтобы узнать, на сколько одно число меньше или больше другого, нужно из большего числа вычесть меньшее.
Это правило применяется при решении текстовых задач на разностное сравнение:
Мальчики играли в футбол. Юра забил 8 голов, а Толя – 6 голов. Кто из мальчиков забил голов больше и на сколько?
В задаче три множества: А множество голов, забитых Юрой, В – множество голов забитых Толей и С – множество голов, являющихся дополнением множества В до множества А – множество голов, являющихся дополнением к множеству голов, забитых Толей до множества голов, забитых Юрой. А значит, чтобы узнать численность дополнения, нужно из численности множества голов, забитых Юрой вычесть численность множества голов, забитых Толей (из большего вычесть меньшее):
А
А1 А \ А1
В
( где А \ А1 = С)
В задачах с понятиями
«больше на …», «меньше на …» также можно обосновать выбор действий с точки зрения теории множеств, переводя их на действия с числами:
Катя знает 7 стихотворений, а Маша выучила на одно стихотворение больше. Сколько стихотворений знает Маша?
В задаче два множества – множество стихотворений, которые знает Катя – (А) и множество стихотворений, выученных Машей – (В). Известно, что в первом множестве 7 элементов, т.е.
n (A) = 7. Число элементов во втором множестве требуется найти при условии, что в нем на 1 элемент больше, чем в первом множестве. Отношение «на одно больше» означает, что в множестве В элементов столько же, сколько их в множестве А, и еще 1 элемент.
А
В1 В \ В1
В
Т.е. Маша выучила столько же стихотворений, сколько Катя и еще одно. Используя правило подсчета элементов в объединении непересекающихся множеств, получаем:
n (B) = n (B1)+ n (B \ В1)= 7 + 1. Т.к. 7 + 1 = 8, то ответ – Маша выучила 8 стихотворений.
Рассмотрим другую задачу:
Маша съела 6 печений, а Катя на 3 печенья меньше. Сколько печений съела Катя?
В задаче два множества – множество печений, съеденных Катей (А) и множество печений, съеденных Машей (А). Известно, что в первом множестве 6 элементов, т.е.
n (A) = 6. Число элементов во втором надо найти при условии, что в нем на 3 элемента меньше, чем в первом. Отношение «на одно меньше» означает, что в множестве
В элементов столько же, сколько их в множестве А, но без трех.
А
А1 А \А1
В
Это значит, что n(B) = n(A1) = n(A) – n(А \А1) = 6 – 3 = 3.
Арифметические действия
и методика их изучения в курсе математики начальной школы.
Формирование вычислительных навыков
у учащихся начальной школы
Устные приемы сложения и вычитания целых неотрицательных чисел.
Методика формирования вычислительного навыка младших школьников в пределах 10
План:
I. Понятия вычислительного приема.
II. Вычислительный навык и его характеристика.
III. Устные приемы сложения и вычитания однозначных чисел в пределах десятка.
I. Понятия вычислительного приема
Формирование вычислительных умений считается одной из ведущих и самых «трудоёмких» тем в начальной школе. Вопрос о значимости формирования устных вычислительных навыков на сегодняшний день является весьма дискуссионным в методическом плане, так считает С.В. Белошистая: «Программа по математике требует от учителя формирования у детей твердых навыков устных и письменных вычислений. Однако широкое распространение калькуляторов «жёсткой» отработки этих умений под сомнение, поэтому многие не связывают хорошее владение арифметическими вычислениями с математическими способностями и с математической одаренностью. Однако внимание к устным арифметическим вычислениям является особенностью для русской методической школы. В связи с этим значительная часть материала во всех существующих сегодня учебниках математики для начальной школы отведена формированию устных вычислительных умений и навыков». С этой целью учащиеся знакомятся с рациональными приемами вычислений.
Вычислительные приёмы – это последовательность выполняемых операций, каждое из которых опирается на какое-то математическое понятие.
II. Вычислительный навык и его характеристика
Вычислительный навык – это высокая степень овладения вычислительными приёмами. Приобрести вычислительные навыки – значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнять эти операции достаточно быстро.
Полноценный
вычислительный навык характеризуется
– правильностью,
– осознанностью,
– рациональностью,
– обобщенностью,
– автоматизмом,
– прочностью.
Правильность – это характеристика действия, при котором ученик верно находит результат арифметического действия, то есть оптимально выбирает и выполняет операции, составляющие приём.
Осознанность – ученик понимает, на основе каких знаний выбраны операции и установлен порядок их выполнения, в любой момент может объяснить, как он решал и почему так целесообразно действовать.
Рациональность – ученик выбирает для данного случая более короткий способ действия, то есть выбирает те из возможных операций, выполнения которых легче других и быстрее приводит к результату.
Обобщенность – ученик может применить приём вычисления к большому числу случаев, то есть, способен перенести определенный приём вычисления на новые случаи.
Автоматизм – ученик выполняет и выделяет операции быстро и в свернутом виде, но всегда может вернуться к объяснению выбора системы операций.
Высокая степень автоматизации должна быть достигнута по отношению к табличным случаям сложения и вычитания, умножения и деления.
Прочность – ученик сохраняет сформированные вычислительные навыки на длительное время.
Формируя устные вычислительные навыки у младших школьников, учитель знакомит их с рациональными приемами вычислений, которые каждый человек выполняет ежедневно, практически не замечая этого. Т.е. для обладания навыками вычислений нужно владеть знаниями наиболее удобных способов при нахождении результата арифметических действий. Ими и являются вычислительные приемы.
III. Устные приемы сложения и вычитания однозначных чисел в пределах десятка
Все вычислительные приемы имеют теоретическую основу, т.е. это те математические факты (понятия), на которые опираются при выполнении каждой из операций приема.
В приведённой ниже таблице отражены основные виды устных вычислительных приёмов сложения и вычитания однозначных чисел в пределах 10 (1 класс).
Первоначально дети знакомятся со сложением и вычитанием однозначных чисел, результат которых не превышает число 10.
Виды
вычислительных приёмов
Необходимые знания
(теоретическая основа)
1. Присчитывание и отсчитывание по единице:
7 + 1, 4 – 1.
Знание натурального ряда чисел и принципа его построения.
2.Прибавление 2, 3, 4 (по частям):
5 + 4, 8 – 3.
1) знание смысла действий сложения и вычитания,
2) знание состава чисел 2, 3, 4.
3.Прибавление 5, 6, 7, 8, 9:
3 + 6, 2 + 8.
Знание переместительного свойства сложения.
4. Вычитание 5, 6, 7, 8, 9, 10:
9 – 6, 7 – 5.
1) знание взаимосвязи между компонентами и результатом сложения;
2) знание состава однозначных чисел (таблица сложения однозначных чисел).
1) Прибавляя и вычитая 1, например: 7 + 1 = 8, 9 – 1 = 8, учащиеся при этом рассуждают так: «Если к числу прибавить 1, то значит, получится следующее число ряда. Если из числа вычесть 1, то получится предыдующее число ряда».
2) Прибавляя числа по частям в случаях 4 + 3 = 7, 8 – 2 = 6
учащиеся выполняют действия по частям: «К 4 прибавим вначале 1 – получим 5, а потом еще 2 – получим 7». По аналогии и вычитают.
3) В дальнейшем действия осуществляют на основе переместительности и взаимосвязи между компонентами и результатом сложения:
3 + 6 = 9
«Чтобы к 3 прибавить 6 поменяем местами слагаемые, т.к. от перестановки слагаемых сумма не изменится. К 6 прибавим 3 по частям (2 и 1), получим 9».
4) Вычитая числа 5, 6, 7, 8, 9, рассуждают таким образом: «7 – это 5 и 2. Значит, если из 7 вычесть 5, то получим 2»: 7 – 5 = 2.
Арифметические действия
и методика их изучения в курсе математики начальной школы.
Формирование вычислительных навыков
у учащихся начальной школы
Устные приемы сложения и вычитания
двузначных чисел в пределах 100.
Методика формирования вычислительного навыка младших школьников
План:
I. Устные приемы сложения и вычитания двузначных чисел.
II. Приемы сложения и вычитания с трехзначными, четырехзначными и т.д. числами.
III. Методические приемы формирования устных вычислительных навыков сложения и вычитания.
I. Устные приемы сложения и вычитания однозначных чисел в пределах десятка
Во втором классе учащиеся подробно изучаю уже устные вычислительные приемы сложения и вычитания двузначных чисел, не являющихся табличными, т.к. сложение однозначных обобщено таблицей. Поэтому они так и называются
внетабличными, а значит, их нельзя заучить. Важно видеть рациональный способ вычисления.
Виды
вычислительных приёмов
Необходимые знания и умения
(теоретическая основа)
1.Сложение и вычитание двузначных чисел, оканчивающихся 0:
30 + 20,
80 – 30.
1) знание разрядного состава двузначного числа;
2) умение выполнять действия с разрядными единицами;
3) знание таблицы сложения однозначных чисел в пределах 10 и соответствующих случаев вычитания.
2.Сложение и вычитание двузначного числа и однозначного числа (без перехода через разряд):
53 + 4,
68 – 5.
1) знание разрядного состава двузначных чисел;
2) знание сочетательного свойства сложения; правило вычитания числа из суммы;
3) знание таблицы сложения однозначных чисел в пределах 10 и соответствующих случаев вычитания.
3.Сложение и вычитание двузначных чисел, одно из которых оканчивается 0:
63 + 20,
72 – 60.
1) знание разрядного состава числа;
2) знание сочетательного свойства сложения;
3) знание соотношения между разрядными единицами;
4) знание таблицы сложения однозначных чисел в пределах 10 и соответствующих случаев вычитания;
5) умение выполнять действия с двузначными числами также как с однозначными.
4.Сложение и вычитание двузначного числа и однозначного с переходом через разряд:
62 + 9,
73 – 7.
1) знание разрядного состава числа;
2) знание сочетательного свойства сложения;
4) знание таблицы сложения однозначных чисел и соответствующих случаев вычитания с переходом через десяток в пределах 20.
5.Сложение двузначного и однозначного числа, когда в результате получается число оканчивающейся 0, вычитание из числа, оканчивающегося 0:
52 + 8,
60 – 4.
1) знание разрядного состава числа;
2) знание состава числа 10;
3) знание соотношения между разрядными единицами;
4) знание таблицы сложения однозначных чисел в пределах 10.
6. Прибавление двузначного числа к двузначному, оканчивающемуся 0; вычитание двузначного числа из двузначного, оканчивающегося нулем:
60 + 32,
90 – 32
1) знание разрядного состава числа;
2) знание состава числа 10;
3) знание соотношения между разрядными единицами;
4) знание таблицы сложения однозначных чисел в пределах 10.
7. Сложение и вычитание двух двузначных чисел, без перехода через разряд:
34 + 13,
76 – 14.
1) знание разрядного состава двузначного числа;
2) знание сочетательного свойства сложения;
3) знание соотношения между разрядными единицами;
4) знание таблицы сложения однозначных чисел в пределах 10 и соответствующих случаев вычитания.
II. Приемы сложения и вычитания с трехзначными, четырехзначными числами.
По аналогии выделяются приемы сложения и вычитания с трехзначными, четырехзначными и т.д. числами. Но базой для выполнения действия, и конкретно каждого шага преобразований с ними в процессе вычисления результата являются действия с однозначными числами или двузначными числами.
Виды
вычислительных приёмов
Необходимые знания и умения
1.Сложение и вычитание трехзначных чисел, оканчивающихся нулями (как однозначных):
300 + 200, 400 – 100.
1) знание соотношения между разрядными единицами;
2) знание табличного сложения однозначных чисел и соответствующих случаев вычитания;
3) умение складывать и вычитать однозначные числа.
2.Сложение и вычитание трехзначных чисел, оканчивающихся 0 (как двузначных):
530 + 140,
680 – 500.
1) знание разрядного состава числа;
2) знание соотношения между разрядными единицами;
3) знание сочетательного свойства сложения и правила вычитания числа из суммы;
4) умение складывать и вычитать двузначные числа.
3.Сложение и вычитание двух трехзначных чисел, оканчивающихся 0, с переходом через разряд (как двузначных):
340 + 190, 760 – 190.
1) знание разрядного состава трехзначного числа;
2) знание сочетательного свойства сложения;
3) знание соотношения между разрядными единицами;
4) знание таблицы сложения однозначных чисел с переходом через десяток в пределах 20 и соответствующих случаев вычитания.
Для осознанного выполнения приемов сложения и вычитания двузначных и трехзначных чисел учащиеся должны хорошо знать:
а) нумерацию чисел в пределах 100 (разрядный состав чисел, соотношение между разрядными единицами);
б) табличное сложение и соответствующие случаи вычитания в пределах 10, в пределах 20 с переходом через десяток;
в) свойства действий сложения и вычитания: переместительное, сочетательное и правила вычитания числа из суммы и суммы из числа.
II. Методические приемы формирования устных вычислительных навыков сложения и вычитания
Работа над формированием вычислительными навыками (при выполнении всех вычислительных приемов устных и письменных) строится в соответствии с этапами:
I этап – подготовка к изучению вычислительного приема (изучение теоретической основы);
II этап – ознакомление с вычислительным приемом;
III этап – закрепление вычислительного умения, формирование вычислительного навыка.
При ознакомлении с каждым из вычислительных приёмов используются методические приёмы, способствующие их качественному усвоению. Долгие годы методическая копилка учителей пополнялась такими приемами. Эти приемы способствуют решению задачи – вооружить младших школьников устными вычислениями так, чтобы навык мог характеризоваться теми качествами, которые мы указали выше: правильностью, осознанностью, рациональностью, автоматизмом, прочностью.
Один из первых таких приемов, который применяется на первом же уроке ознакомления с любым из вычислительных приемов – это развернутая объяснительная запись. Ее мы видим почти во всех учебниках математики начальной школы (А.М.Моро – программа «Школа России», Л.Г.Петерсон – программа «Перспектива», В.Н.Рудницкая – «Школа 2100»):
43 + 4 = 49 + (1 + 3) = (49 + 1) + 3 = 50 + 3 = 53
48 – 3 = (40 + 8) – 3 = 40 + (8 – 3) = 40 + 5 = 45
Такая
объяснительная запись показывает не просто все шаги тождественных преобразований в процессе выполнения каждой операции приема, но и раскрывает теоретическую основу приема. Ее мы рассмотрели выше в таблицах.
На последующих уроках, закрепляя вычислительные приёмы, необходимо сокращать объяснительную запись. Учителя в начальной школе используют для этого методические приёмы, раскрытые С.Н. Лысенковой:
1) «
метод связывающих дуг»:
50
49 + 4 = 49 + (1 + 3) = 53,
90
73 + 20 = (70 + 3) + 20 = 93
2) «
метод штриха»
48 – 3 = 45;
3. «
метод усов»
45 + 8 = 40 + 13 = 53
40 5
Данные приёмы чаще всего применяются комбинированно:
49 + 4 = 53
49 + (1 + 3) = 50 + 3 = 53
При существующем многообразии методических приёмов для раскрытия приемов, выбор их зависит от специфики работы каждого учителя индивидуально, а так же от особенностей каждого класса в отдельности, но методика работы над каждым вычислительным приёмом содержит одни и те же этапы:
I этап – развернутая (пошаговая) запись вычислительно приёма на доске и в тетрадях
II этап – сокращение записи с помощью одного или нескольких методических приёмов;
III этап – краткая запись выражений с устными пояснениями для повышения качества формирования вычислительного навыка.
В процессе формирования вычислительных навыков осуществляется контроль его уровня.
Вместе с тем, учитывая, что ученик при выполнении вычислительного приёма, должен отдавать себе отчёт в правильности и целесообразности каждого выполненного действия, то есть постоянно контролировать себя, соотнося выполняемые операции с образцом – системой операций.
Арифметические действия
и методика их изучения в курсе математики начальной школы.
Формирование вычислительных навыков
у учащихся начальной школы
Устные приемы сложения и вычитания однозначных чисел с переходом через десяток в пределах 20.
Методика формирования вычислительного навыка младших школьников
После изучения приемов сложения и вычитания чисел в пределах десяти, на их основе учащиеся знакомятся с приемами сложения и вычитания однозначных чисел с переходом через разряд – через десяток в пределах 20 (концентр «Числа от 1 до 20»).
Представим в таблице эти приемы:
Виды
вычислительных приёмов
Необходимые знания
(теоретическая основа)
1. Сложение однозначных чисел с переходом через десяток:
6 + 8.
1) знание состава чисел в пределах десяти (таблица сложения однозначных чисел);
2) знание разрядного состава двузначных чисел.
2. Вычитание однозначных чисел с переходом через десяток:
12 – 7.
1) знание состава чисел в пределах десяти (таблица сложения однозначных чисел);
2) знание разрядного состава двузначных чисел.
3. Вычитание однозначных чисел с переходом через десяток:
12 – 7.
Знание состава двузначных чисел в пределах двадцати (таблица сложения однозначных чисел с переходом через десяток).
Прием сложения однозначных чисел состоит из 3 операций:
1) разложение второго слагаемого на сумму чисел, одно из которых может дополнить первое слагаемое до 10 (теоретическая основа – состав однозначных чисел, раскрытый в таблице сложения в пределах десятка);
6 + 8 =
4 4
2) прибавление к первому слагаемому, дополняя его до десяти (состав числа 10 – таблица сложения в пределах 10);
= (6 + 4) + 4 =
3) прибавление к полученному десятку оставшихся единиц от второго слагаемого (теоретическая основа – разрядный состав двузначных чисел).
= 10 + 4 = 14
Учащиеся рассуждают так: «8 – это 4 и 4. К 6 прибавим 4 до десяти. К десяти прибавим оставшиеся 4 единицы, получаем 14».
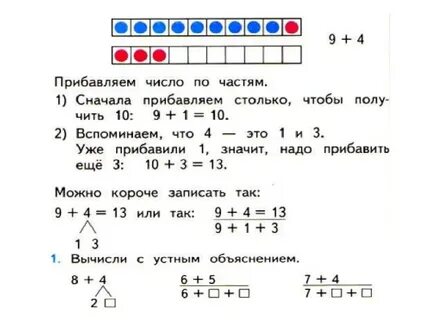
Данный прием четко показан в учебнике программы «Школа России» Математика. 1 класс. 2 часть.
Сложение рассматривается в последовательности прибавления чисел – 2, 3, 4, 5, 6, 7, 8, 9 с переходом через десяток. Эти случаи запоминаются учениками. А на уроке обобщения объединяются в таблицу, называемую «таблицей сложения однозначных чисел в пределах 20».

Вычитание демонстрируется с помощью двух способов.
I способ состоит из трех операций и выполняется по аналогии со сложением – по частям:
1) вычитаемое представляется в виде двух чисел, одно из которых равно разрядным единицам уменьшаемого (теоретическая основа – состав однозначных чисел, раскрытый в таблице сложения в пределах десятка);
12 – 7 = 12 – (2 + 5) =
2 5
2) из уменьшаемого вычитаем число равное единицам уменьшаемого до десятка (теоретическая основа – разрядный состав двузначных чисел);
= (12 – 2) – 5 =
3) из полученного десятка вычитаем оставшиеся единицы вычитаемого (состав числа 10 – таблица сложения в пределах 10).
= 10 – 5 = 5
Учащиеся рассуждают так: «Вычтем по частям. 7 – это 2 и 5. Из 12 вычтем 2 до 10. А теперь из 10 вычтем 5, получим 5».
II способ состоит из 2 операций:
1) уменьшаемое представляется в виде двух чисел, одно из которых равно вычитаемому (теоретическая основа – состав двузначных чисел, раскрытый в таблице сложения в пределах 20);
12 – 7 = (7 + 5) – 7 =
7 5
2) вычитание из суммы чисел слагаемого равного вычитаемому (теоретическая основа: особый случай вычитания – а – а =0).
(7 – 7) + 5 = 5
Учащиеся при этом рассуждают так: «12 – это 7 и 5. Значит, если из 12 вычесть 7, то получим 5». Так рассуждают дети.
– Найдите в учебнике Математика.1 класс. 2 часть урок, раскрывающий приемы вычитания.
– Чем изложенный материал на странице учебника отличается от представленного преподавателем?
Арифметические действия
и методика их изучения в курсе математики начальной школы.
Формирование вычислительных навыков
у учащихся начальной школы
Теоретико-множественный смысл произведения
План:
I. Теоретико-множественный смысл произведения целых неотрицательных чисел. Теоретико-множественный смысл равенств
0 × а = а и
а × 0 = 0.
II. Теоретико-множественный смысл свойств умножения.
I. Теоретико-множественный смысл произведения целых неотрицательных чисел.
Теоретико-множественный смысл равенств а × 1= а и а × 0 = 0.
В школьном курсе математики используется определение умножения, которое связывается со сложением одинаковых слагаемых:
Если а и b – целые неотрицательные числа, то произведением а × b называется число, удовлетворяющее следующим условиям:
1) а × b = а + а + . . . + а + а, при b > 1;
b раз
2) а × b = а, при b = 1;
3) а × b = 0, при b = 0.
Первое условие можно обосновать с теоретико-множественной точки зрения так.
Если множества
А1, А2, …, Аb имеют по
а элементов каждое, причем никакие два из них не пересекаются, то их объединение
А1UА2U …U Аb содержит
а ×
b элементов.
Таким образом, с теоретико-множественной позиции
произведение
а ×
b, при b > 1, представляет собой число элементов в объединении b множеств, каждое из которых содержит по а элементов и никакие два из них не пересекаются:
а ×
b= n(А1 U А2 U …U Аb), если n(А1) = n(А2) = … = n(Аb)= а и А1, А2, …, Аb попарно не пересекаются.
Такой подход позволяет обосновывать выбор умножения при решении текстовых задач, связывая умножение натуральных чисел с операцией объединения.
Каждому ребенку дали по 3 конфеты. Сколько конфет у четырех детей?
Выясним выбор действия для ответа на вопрос этой задачи.
В задаче речь идет о четырех множествах, в каждом из которых три элемента. Требуется узнать число элементов в объединении этих четырех множеств. Если
n(А1) = n(А2) = n(А3)= n(А4)= 3, то
n(А1 U А2 U А3 U А4) = n(А1) + n(А2) + n(А3) + n(А4)= 3 + 3 + 3 + 3= 3 × 4. Произведение 3 × 4 является математической моделью данной задачи. Т.к. 3 × 4 = 12, то получаем ответ на вопрос: у четырех детей 12 конфет.
Существует другое толкование умножения с теоретико-множественной позиции, которое связано с понятием декартова произведения множеств.
Этот подход следует из теоремы:
Пусть
А и
В конечные множества. Тогда их декартово произведение также является конечным множеством, причем выполняется равенство:
n(A × B) = n(A) · n(B).
Тогда
A × B состоит из пар вида
(a ,
b), (a ,
b), …, (a ,
b), число которых равно
n.
Если n = 1, то n(A)= а, n(B) = 1, то в этом случае имеем: n(A × B) = n(A)· n(B) = а · 1 = а.
При k = 0 данное равенство также верно, поскольку B = Ø и n(A × Ø) = n(A)· n(Ø) = а · 0 = 0.
Из этого следует, что с теоретико-множественной с теоретико-множественной точки зрения
произведение а · b целых неотрицательных чисел есть число элементов в декартовом произведении множества А и В, таких, что а = n (A), b = n (B):
а · b = n(A) · n(B) = n(A × B).
II. Теоретико-множественный смысл свойств умножения
Благодаря такому подходу и смысл свойств умножения как арифметического действия:
1) коммутативное свойство – а · b = b · a,
2) ассоциативное свойство – (а · b) · c = a · (b · c),
3) дистрибутивное свойство – (a + b) · c = a · c + b · c.
1) Смысл равенства
а · b = b · a
Хотя множества
A × B и
В × А различны, они являются равномощными: каждой паре (а, b) из множества
A × B можно поставить в соответствие единственную пару
(b,
a) из множества
В × А, и наоборот. Значит,
n(A × B) = n(В × A) и поэтому
а · b = b · a.
а · b = n(A × B) = n(В × A) = b · a
2) Ассоциативность (
а · b) · c = a · (b · c) доказывается аналогично.
Множества
A × (B ×
С) и
(A × B) ×
С различны, но равномощны: каждой паре (а, (b, с)) из множества
A × (B ×
С) соответствует единственная пара ((а, b), с) из множества
(A × B) ×
С и наоборот. Поэтому
n(A × (B ×
С)) = n ((A × B) ×
С), а следовательно
a (b c)= (
а b) c.
3)
Дистрибутивность умножения относительно сложения выводится из равенства *
А ×(В U С) = (А × В) U (А × С), а вычитания из равенства
А ×(В \ С) = (А × В) \ (А × С).
(Ұ а, b,c Є Z) a · (b + c)= a· b + a·c (a +b) · c= a· с + b ·c
а = n (A), b = n (B), с = n (С):
Если А умножить на В и С, то А ×(В U С) = (А × В) U (А × С)
a · (b · c) = n (A) × n(В U С) = n(A ×(В U С)) = n((А × В) U (А × С))=
на основе рав.*
= n(А × В) + n(А × С) = a· b + a·c
Таким образом, умножение определяется через сложение, а особые случаи умножения с нулем принимаются по определению:
а · 1 = а, а · 0 = 0.
Теоретико-множественный смысл частного
План:
I. Теоретико-множественный смысл частного целых неотрицательных чисел.
II. Теоретико-множественный смысл правил деления суммы на число и числа на сумму.
III. Теоретико-множественный смысл отношений «больше в», «меньше в».
IV. Теоретико-множественный смысл деления с остатком.
I. Теоретико-множественный смысл частного целых неотрицательных чисел
С теоретико-множественной точки зрения деление чисел – операция обратная умножению и
связывается с разбиением конечного множества на равночисленные попарно непересекающиеся подмножества и с его помощью решаются задачи двух видов:
– деление на равные части (нахождение числа элементов в каждом подмножестве разбиения);
– деление по содержанию (отыскание числа таких подмножеств).
Если а = n (A) и множество А разбито на попарно непересекающиеся равночисленные подмножества и если:
b – число подмножеств, то частное а : b – число элементов в каждом подмножестве;
b – число элементов в каждом подмножестве, то частное а : b – число таких подмножеств.
В соответствии с этим обосновывается выбор арифметического действия для решения задач:
а)
Мама дала Пете 15 орехов. Он раздал поровну своим друзьям – Диме и Сереже, а также себе. Сколько орехов получил каждый мальчик?
В задаче рассматривается множество, в котором 15 элементов – орехов. Это множество разбивается на 3 равночисленных подмножества, т.к мальчиков трое. Требуется узнать число элементов в каждом таком подмножестве. Это число можно найти с помощью деления: 15 : 3. Вычислив значение этого выражения, получаем ответ на вопрос задачи: каждый мальчик получил по 5 орехов.
б)
Доктор раздал 12 таблеток витаминов по 3 каждому ребенку. Сколько детей получили таблетки витаминов?
Множество из 12 элементов разбивается на подмножества, в каждом из которых по 3 элемента. Требуется узнать число таких подмножеств. Его можно найти с помощью деления: 12 : 3. Вычислив значение этого выражения – 12 : 3 = 4, получаем ответ на вопрос задачи: таблетки получили четыре ребенка.
II. Теоретико-множественный смысл правил деления суммы на число и числа на сумму
В математике при различных вычислениях пользуются правилами деления суммы на число. Дадим теоретико-множественное обоснование этим правилам.
Правило деления суммы на число:
Если частные
а : с и
b : с существуют, то
(а + b) : с = а : с + b : с.
Пусть
а = n (A), b = n (B) и
A ∩ B= Ø. Если множества
А и
В можно разбить на равночисленные подмножества, состоящие из
с элементов каждое, то и объединение этих множеств допускает такое же разбиение. Если при этом множество
А состоит из
а : с подмножеств, а множество
В – из
b : с подмножеств, то
А U В состоит из
а : с+ b : с подмножеств. Это и значит, что
(а + b) : с = а : с+ b : с.
III. Теоретико-множественный смысл отношений «больше в», «меньше в»
С теоретико-множественной точки зрения рассматриваются и отношения «больше в», «меньше в», которые рассматриваются в текстовых задачах.
В аксиоматической теории определение этих отношений вытекает из определения натуральных чисел: если
а : b = c, то можно говорить,
что
«а больше b в с раз» или что
«b меньше а в с раз». И чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее разделить на меньшее.
Если
а = n (A), b = n (B) и известно, что
«а меньше b в с раз», то поскольку
а < b , то в множестве
В можно выделить собственное подмножество, равномощное множеству
А , но так как
«а меньше b в с раз», то множество
В можно разбить на
с подмножеств, равночисленных множеству
А.
Так как
с – это число подмножеств в разбиении множества
В, содержащего
b элементов, а в каждом подмножестве –
а элементов, то
с = b : а.
а) У Дениса было 3 тетрадей в клетку, а в линию в 4 раза больше. Сколько тетрадей было у Дениса?
В задаче речь идет о двух множествах: множестве тетрадей в клетку
(А) и множестве тетрадей в линию
(В). Известно, что
n (A) = 3 и что в множестве
В элементов в 4 раза больше, чем в множестве
А. Требуется найти число элементов в множестве
В, т.е. n (B).
Т.к. в множестве
В элементов в 4 раза больше, чем в множестве
А, то множество
В можно разбить на 4 подмножества, равномощных множеству
А. Поскольку в каждом подмножестве содержится по три элемента, то всего в множестве
В будет содержатся четыре раза по 3 элемента:
3 + 3 + 3 + 3 или
3 × 4 элементов. Выполнив вычисления, получаем ответ на вопрос задачи: тетрадей в линию у Дениса 12.
А
В
б) У Дениса 10 солдатиков, а у Толи в 2 раза меньше. Сколько солдатиков у Толи?
В задаче речь идет о двух множествах: множестве солдатиков у Дениса
(А) и множестве солдатиков у Толи
(В). Известно, что
n (A) = 10 и что в множестве
В элементов в 2 раза меньше, чем в множестве
А. Требуется найти число элементов в множестве
В, т.е. n (B).
Т.к. в множестве
А элементов в 2 раза больше, чем в множестве
А, т.к. сказано, что в множестве
В элементов меньше. То множество
А можно разбить на 2 равночисленных подмножества, равномощных множеству
В. Требуется узнать число элементов в каждом таком подмножестве. Это число можно найти с помощью деления: 10 : 2. Вычислив значение этого выражения, получаем ответ на вопрос задачи: у Толи 5
солдатиков.
А
В


 (единицу они обозначали просто вертикальной черточкой
(единицу они обозначали просто вертикальной черточкой  , как это делаем и мы), десять десятков, то есть сотню – знаком
, как это делаем и мы), десять десятков, то есть сотню – знаком 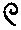 . Появились знаки для тысячи
. Появились знаки для тысячи  (цветок лотоса), десятка тысяч
(цветок лотоса), десятка тысяч  (поднятый кверху палец), ста тысяч
(поднятый кверху палец), ста тысяч  (сидящая лягушка) и миллиона
(сидящая лягушка) и миллиона 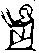 (человек с поднятыми руками).
Писать много раз один и тот же знак, разумеется, весьма неудобно. Более экономной является позиционная система записи чисел, где имеет значение не только начертание цифры, но и ее позиция, положение среди других цифр. Первая позиционная система записи чисел появилась в Вавилоне. Единица в ней обозначалась клином
(человек с поднятыми руками).
Писать много раз один и тот же знак, разумеется, весьма неудобно. Более экономной является позиционная система записи чисел, где имеет значение не только начертание цифры, но и ее позиция, положение среди других цифр. Первая позиционная система записи чисел появилась в Вавилоне. Единица в ней обозначалась клином  , а десяток – знаком
, а десяток – знаком  . В основном разница между вавилонской и современной записью чисел была в одном: вместо числа 10 вавилоняне приняли за основу системы счисления число 60. Но было еще одно отличие, делавшее вавилонскую систему записи не совсем удобной: вавилоняне долгое время не знали нуля.
Мы рассмотрели историю возникновения систем счисления, а теперь мы рассмотрим одно из важнейших чисел этой системы – число нуль.
Первыми нуль был придуман вавилонянами примерно две тысячи лет тому назад. Но они применяли его лишь для обозначения пропущенных разрядов в середине числа. Писать нули в конце записи числа они не догадались. В Индии примерно полторы тысячи лет тому назад нуль был присоединен к девяти цифрам и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно было. И самое главное, запись таких гигантских чисел стала довольно короткой. Если бы живший 30 тысячелетий тому назад древний человек имел представление о миллионе и захотел бы изобразить это число с помощью зарубок на волчьих костях, ему пришлось бы истребить 20 тысяч волков. А для записи миллиарда не хватило бы волков во всех европейских лесах.
Индийской системой обозначений мы пользуемся до сих пор. Это не значит, что индийские цифры имели с самого начала современный вид. В течение многих столетий, переходя от народа к народу, они много раз изменялись, пока приняли современную форму. Арабы заимствовали у индийцев цифры и позиционную десятичную систему записи чисел. Европейцы в свою очередь узнали ее от арабов. Поэтому наши цифры, в отличие от римских, стали называться арабскими. Правильнее было бы назвать их индийскими. Они употребляются в нашей стране, начиная примерно с ХVII века.
Математики Древней Греции долгое время пользовались буквенной нумерацией и нуля не применяли. Слово нуль они перевели на свой язык говорили «сифр». В Х – ХII веках индийская система счисления через арабов проникла в Европу, слово сифр не перевели, а немного видоизменили сначала в слово шифр, а позже в слово цифра.
Самый древний документ в Европе, в котором для нуля имеется свой знак (0), относится к IX в. В одной из книг, написанной на латинском языке в XIII веке, нулем назван «кружок», или цифра, или знак ничего. С тех пор за ним утвердилось название «фигура нуль», что означало «никакой знак». Словом цифра стали называть знаки, обозначающие число единиц в любом разряде, в том числе цифрой назвали и единицу, а позже и сам нуль.
В первом русском учебнике «Арифметика» Л.Ф.Магницкого, напечатанном в 1689г., нуль назван цифрой или ничем. Спустя несколько лет и в России знак 0 стали называть нулем, а знаки чисел 1,2,3,4…9 называли цифрами. Однако и на этом открытие нуля не закончилось, хотя он приобрел свой вид, получил название, обрел свое место. Но не было решено – нуль цифра или число; если число, то какое: четное или нечетное?
В результате длительных обсуждений математике пришли к заключено: нуль – это число, обозначают его цифрой 0, к натуральному ряду он не принадлежит. С нулем можно производить все действия, за исключением деления на нуль.
Как мы узнали из исторической справки, данной профессором Л.П.Стойловой, о возникновении понятия числа было важнейшим моментом в развитии математики. Появилась возможность изучать эти числа независимо от тех конкретных задач, в связи с которыми они возникли. Теоретическая наука, которая стала изучать числа и действия над ними, получила название «арифметика». Слово «арифметика» происходит от греческого arithmos, что значит «число». Следовательно, арифметика – это наука о числе.
Арифметика возникла в странах Древнего Востока: Вавилоне, Китае, Индии и Египте. Накопленные в этих странах математические знания были развиты и продолжены учеными Древней Греции. В средние века большой вклад в развитие арифметики внесли математики Индии, стран арабского мира и Средней Азии, а начиная с ХIII века – европейские ученые.
Термин «натуральное число» впервые употребил в V веке римский ученый А. Боэций, который известен как переводчик работ известных математиков прошлого на латинский язык и как автор книги «О введении в арифметику», которая до ХVI века была образцом для всей европейской математики.
Во второй половине ХIХ века натуральные числа оказались фундаментом всей математической науки, от состояния которого зависела и прочность всего здания математики. В связи с этим появилась необходимость в строгом логическом обосновании понятия натурального числа, в систематизации того, что с ним связано.
. В основном разница между вавилонской и современной записью чисел была в одном: вместо числа 10 вавилоняне приняли за основу системы счисления число 60. Но было еще одно отличие, делавшее вавилонскую систему записи не совсем удобной: вавилоняне долгое время не знали нуля.
Мы рассмотрели историю возникновения систем счисления, а теперь мы рассмотрим одно из важнейших чисел этой системы – число нуль.
Первыми нуль был придуман вавилонянами примерно две тысячи лет тому назад. Но они применяли его лишь для обозначения пропущенных разрядов в середине числа. Писать нули в конце записи числа они не догадались. В Индии примерно полторы тысячи лет тому назад нуль был присоединен к девяти цифрам и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно было. И самое главное, запись таких гигантских чисел стала довольно короткой. Если бы живший 30 тысячелетий тому назад древний человек имел представление о миллионе и захотел бы изобразить это число с помощью зарубок на волчьих костях, ему пришлось бы истребить 20 тысяч волков. А для записи миллиарда не хватило бы волков во всех европейских лесах.
Индийской системой обозначений мы пользуемся до сих пор. Это не значит, что индийские цифры имели с самого начала современный вид. В течение многих столетий, переходя от народа к народу, они много раз изменялись, пока приняли современную форму. Арабы заимствовали у индийцев цифры и позиционную десятичную систему записи чисел. Европейцы в свою очередь узнали ее от арабов. Поэтому наши цифры, в отличие от римских, стали называться арабскими. Правильнее было бы назвать их индийскими. Они употребляются в нашей стране, начиная примерно с ХVII века.
Математики Древней Греции долгое время пользовались буквенной нумерацией и нуля не применяли. Слово нуль они перевели на свой язык говорили «сифр». В Х – ХII веках индийская система счисления через арабов проникла в Европу, слово сифр не перевели, а немного видоизменили сначала в слово шифр, а позже в слово цифра.
Самый древний документ в Европе, в котором для нуля имеется свой знак (0), относится к IX в. В одной из книг, написанной на латинском языке в XIII веке, нулем назван «кружок», или цифра, или знак ничего. С тех пор за ним утвердилось название «фигура нуль», что означало «никакой знак». Словом цифра стали называть знаки, обозначающие число единиц в любом разряде, в том числе цифрой назвали и единицу, а позже и сам нуль.
В первом русском учебнике «Арифметика» Л.Ф.Магницкого, напечатанном в 1689г., нуль назван цифрой или ничем. Спустя несколько лет и в России знак 0 стали называть нулем, а знаки чисел 1,2,3,4…9 называли цифрами. Однако и на этом открытие нуля не закончилось, хотя он приобрел свой вид, получил название, обрел свое место. Но не было решено – нуль цифра или число; если число, то какое: четное или нечетное?
В результате длительных обсуждений математике пришли к заключено: нуль – это число, обозначают его цифрой 0, к натуральному ряду он не принадлежит. С нулем можно производить все действия, за исключением деления на нуль.
Как мы узнали из исторической справки, данной профессором Л.П.Стойловой, о возникновении понятия числа было важнейшим моментом в развитии математики. Появилась возможность изучать эти числа независимо от тех конкретных задач, в связи с которыми они возникли. Теоретическая наука, которая стала изучать числа и действия над ними, получила название «арифметика». Слово «арифметика» происходит от греческого arithmos, что значит «число». Следовательно, арифметика – это наука о числе.
Арифметика возникла в странах Древнего Востока: Вавилоне, Китае, Индии и Египте. Накопленные в этих странах математические знания были развиты и продолжены учеными Древней Греции. В средние века большой вклад в развитие арифметики внесли математики Индии, стран арабского мира и Средней Азии, а начиная с ХIII века – европейские ученые.
Термин «натуральное число» впервые употребил в V веке римский ученый А. Боэций, который известен как переводчик работ известных математиков прошлого на латинский язык и как автор книги «О введении в арифметику», которая до ХVI века была образцом для всей европейской математики.
Во второй половине ХIХ века натуральные числа оказались фундаментом всей математической науки, от состояния которого зависела и прочность всего здания математики. В связи с этим появилась необходимость в строгом логическом обосновании понятия натурального числа, в систематизации того, что с ним связано.





 Далее учеников знакомят с квадратным дециметром. Новая единица вводится аналогично квадратному сантиметру, на наглядной основе.
При знакомстве учащихся с квадратным метром следует его модель разбить на квадратные дециметры, а один из квадратных дециметров – на квадратные сантиметры.
Но площадь измеряется не только в квадратных сантиметрах, дециметрах и метрах, но и такими единицами как ар и гектар. Знакомство с ними происходит в 4 классе.
Впоследствии работа над темой площадь, также должна включать систему упражнений, раскрывающих некоторые свойства понятия площади фигуры, а также подтверждающих справедливость математических законов.
Далее учеников знакомят с квадратным дециметром. Новая единица вводится аналогично квадратному сантиметру, на наглядной основе.
При знакомстве учащихся с квадратным метром следует его модель разбить на квадратные дециметры, а один из квадратных дециметров – на квадратные сантиметры.
Но площадь измеряется не только в квадратных сантиметрах, дециметрах и метрах, но и такими единицами как ар и гектар. Знакомство с ними происходит в 4 классе.
Впоследствии работа над темой площадь, также должна включать систему упражнений, раскрывающих некоторые свойства понятия площади фигуры, а также подтверждающих справедливость математических законов.



